Как решать дробные уравнения? | Александр Будников
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений – дробными уравнениями.
Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)
Дробные уравнения – незаменимая вещь во многих других темах математики. Особенно – в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1. Дроби и действия с дробями и дробными выражениями.
2. Тождественные преобразования уравнений.
3. Решение линейных и квадратных уравнений.
Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем – настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Итак, вперёд!
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
Или такое:
Или вот такое:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.
Например:
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей – четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка – не икс, и деления на неизвестное в дроби нету.
В общем, вы поняли.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей!
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум – перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае – при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой – на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные – не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно – только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации
Умножаем:
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача – дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
2∙3 = х+3
А его (надеюсь) уже решит каждый:
х = 3
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».
Вперёд!
А вот теперь – снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 – х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.
(9 – х)∙х = 20
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
9х – х2 = 20
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение. Но минус перед квадратом икса – нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
х1 = 4
х2 = 5
И все дела.)
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь – квадратным.
А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми – всё равно всё посокращается и останется железное равенство 3=3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми – всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее –
Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
x(x2+2x)(x+2)
и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)
А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х2+2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
х2+2х = х(х+2)
Отлично. Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя – на х(х+2).
Вот на х(х+2) и умножаем:
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем – вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х – 3) в числителе первой дроби – думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
(x-3)(x+2) + 3 = x
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
x2 + 2x – 3x – 6 + 3 – х = 0
x2 – 2x – 3 = 0
И снова получили квадратное уравнение.) Решаем и получаем два корня:
x1 = -1
x2 = 3
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители – обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Ну что, порешаем?)
Решить уравнения:
Ответы (как обычно, вразброс):
x = 3
x1 = 0,5; x2 = 3
x = 2
х = 6
x = 2,6
x1 = 2; x2 = 5
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути – избавление от дробей. Осталась вторая. Не менее важная!
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…
Но об этом – дальше.)
Как решать уравнения с дробями. Показательное решение уравнений с дробями.
Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.
Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.
Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.
Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45
x=45-20=25
Другой пример, когда неизвестное находится в знаменателе:
b/x + c = d
Уравнения такого типа называются дробно-рациональными или просто дробными.
Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:
- значение переменной, обращающее в 0 знаменатель, корнем быть не может;
- нельзя делить или умножать уравнение на выражение =0.
Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.
Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.
Например, требуется решить дробное уравнение:
1/x + 2 = 5
Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.
Избавляемся от знаменателя путем умножения всех членов уравнения на х
1 + 2x = 5х
И решаем обычное уравнение
5x – 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3
Решим уравнение посложнее:
Здесь также присутствует ОДЗ: х -2.
Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.
Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):
Это самое обычное умножение дробей, которое мы уже рассмотрели выше
Запишем это же уравнение, но несколько по-другому
Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:
4 = х + 2
х = 4 – 2 = 2, что соответствует нашей ОДЗ
Ответ: х = 2.
Для закрепления материала рекомендуем еще посмотреть видео.
Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Практика. Решение квадратных и дробно-рациональных уравнений
Математической моделью практических задач могут быть разные уравнения. В школе мы чаще всего будем сталкиваться с линейными и квадратными уравнениями, которые уже умеем решать. Но иногда могут встречаться и более сложные уравнения. Существуют компьютерные алгоритмы, которые позволяют приближенно найти решение практически любого уравнения, а вот точное решение найти удастся не всегда. На этом уроке мы рассмотрим некоторые приемы, которые позволяют эквивалентными преобразованиями свести более сложные уравнения к тем, которые мы уже умеем решать, – линейным и квадратным.
Задание 1. Решить уравнение:
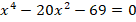
Решение.
Воспользуемся свойством степеней 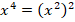 и перепишем уравнение в виде:
и перепишем уравнение в виде:
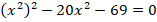
Обратим внимание, что неизвестная величина 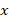 присутствует в уравнении только в составе «конструкции»
присутствует в уравнении только в составе «конструкции» 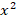 . В таком случае применяют метод замены переменной.
. В таком случае применяют метод замены переменной.
Суть его состоит в том, что эту повторяющуюся конструкцию мы заменяем новой переменной:
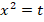
Заменяя 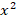 на
на 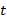 , получаем уравнение:
, получаем уравнение:

Получили квадратное уравнение. С его решением вы можете ознакомиться ниже.
Решение квадратного уравнения с помощью дискриминанта
Имеем следующее квадратное уравнение:

Решим уравнение с помощью дискриминанта. Коэффициенты из общего вида квадратного уравнения:
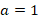
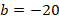
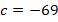
Тогда:
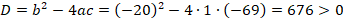
Найдем корни квадратного уравнения:
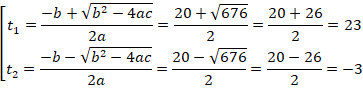
Ответ: 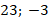 .
.
Далее решения линейных и квадратных уравнений не будут разбираться подробно. Внимание будет сконцентрировано на том, как свести более сложное уравнение к линейному или квадратному. Если же у вас возникают проблемы при решении линейных или квадратных уравнений, пересмотрите соответствующие уроки:
- «Линейное уравнение с одной переменной (Г.Г. Гаицгори)»;
- «Квадратные уравнения».
Решаем уравнение, получаем корни:
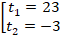
Мы нашли значения 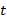 . Но в исходном уравнении фигурировала переменная
. Но в исходном уравнении фигурировала переменная 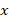 , и решить уравнение – значит, найти значения
, и решить уравнение – значит, найти значения 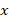 . Вернемся к замене:
. Вернемся к замене:
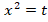
Тогда:
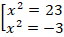
Получили два квадратных уравнения. Первое уравнение 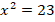 имеет два решения:
имеет два решения:
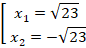
Второе уравнение не имеет действительных корней.
Ответ: 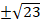 .
.
В процессе решения нам пришлось дважды решать квадратные уравнения: сначала для переменной 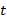 , затем для переменной
, затем для переменной 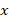 . Поэтому такие уравнения, в которых присутствуют только
. Поэтому такие уравнения, в которых присутствуют только 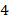 -я и
-я и 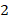 -я степень неизвестной, а также свободный член, называются биквадратными уравнениями, т. е. «дважды квадратными»:
-я степень неизвестной, а также свободный член, называются биквадратными уравнениями, т. е. «дважды квадратными»:
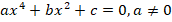
Теперь перейдем к решению дробно-рациональных уравнений. По названию понятно – это те уравнения, которые содержат в себе дробно-рациональные выражения. Если вы забыли, что это за выражения и как с ними работать, рекомендуем пересмотреть соответствующий видеоурок: «Дробно-рациональные выражения».
При решении дробно-рациональных уравнений важно:
- в самом начале найти ОДЗ выражений, которые встречаются в уравнении;
- после нахождения корней нужно проверить, входят ли они в ОДЗ.
Рассмотрим несколько примеров простейших дробно-рациональных уравнений.
Задание 2.Решить уравнение:
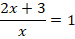
Решение.
Знаменатель дроби не должен равняться нулю, т. е. ОДЗ:
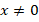
Поскольку 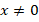 , можем умножить обе части уравнения на
, можем умножить обе части уравнения на 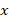 , чтобы избавиться от дроби, тогда:
, чтобы избавиться от дроби, тогда:
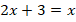
Получили линейное уравнение, решением которого является 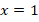 . Это решение входит в ОДЗ, ведь
. Это решение входит в ОДЗ, ведь 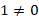 .
.
Ответ: 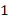 .
.
Задание 3.Решить уравнение:
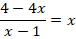
Решение.
Выпишем ОДЗ:
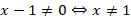
Чтобы избавиться от дроби, умножим обе части уравнения на 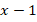 . Мы это можем сделать, поскольку
. Мы это можем сделать, поскольку 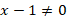 , тогда:
, тогда:
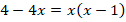
Раскроем скобки, перенесем все слагаемые в одну сторону, приведем подобные слагаемые. Получим квадратное уравнение:
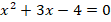
Найдем корни этого уравнения:
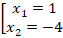
Первый корень не входит в ОДЗ. Поэтому 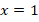 не является решением уравнения.
не является решением уравнения.
Ответ: 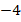 .
.
Решим более сложные дробно-рациональные уравнения.
Задание 4. Решить уравнение:
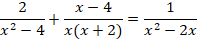
Решение.
Выпишем ОДЗ:
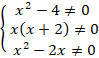
Решим каждое из этих неравенств:
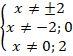
Можем объединить эти неравенства в одно:
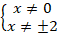
Перенесем все слагаемые в одну сторону:
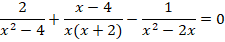
Выполним сложение дробей – для этого разложим знаменатели на множители:
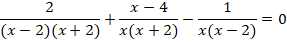
Приведем все дроби к общему знаменателю 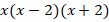 :
:
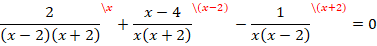
Тогда:
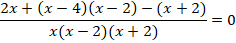
Дробь равна 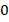 , если ее числитель равен
, если ее числитель равен 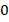 :
:
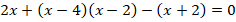
Раскрыв скобки и приведя подобные слагаемые, получаем квадратное уравнение:

Найдем корни квадратного уравнения:
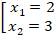
Корень 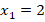 не входит в ОДЗ.
не входит в ОДЗ.
Ответ: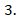
Отметим, что для решения дробно-рациональных уравнений можно использовать разные способы. Первый – это умножить обе части уравнения на некоторые выражения так, чтобы избавиться от дробей. Таким способом мы решили первые два примера с дробно-рациональными выражениями. Второй способ – перенести все слагаемые в одну сторону, преобразовать выражение и приравнять числитель полученной дроби к нулю. Так мы решили последний пример. Вы можете выбрать тот способ, который вам удобнее и понятнее. Главное в каждом из них – не забывать про ОДЗ.
Задание 5. Решить уравнение:
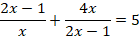
Решение.
Выпишем ОДЗ:
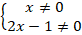
Решим эти неравенства:
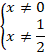
Обратим внимание, что неизвестная 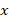 присутствует в уравнении в похожих конструкциях
присутствует в уравнении в похожих конструкциях 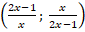 , которые являются взимнообратными выражениями. В таком случае можно применить метод замены переменной:
, которые являются взимнообратными выражениями. В таком случае можно применить метод замены переменной:
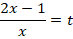
Тогда:
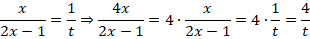
Исходное уравнение будет иметь вид:
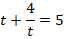
Чтобы избавиться от дроби, умножим обе части уравнения на 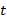 , при этом
, при этом 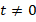 , поскольку
, поскольку 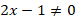 :
:
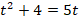
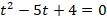
Получили квадратное уравнение, решениями которого являются:
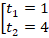
Вернемся к замене:
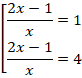
Решаем первое уравнение:
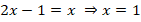
Решаем второе уравнение:
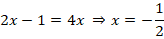
Полученные корни удовлетворяют ОДЗ.
Ответ: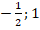 .
.
Задание 6. Решить уравнение:
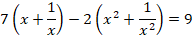
Решение.
Выпишем ОДЗ:
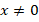
В подобных уравнениях стандартной является замена:
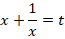
Чтобы выразить 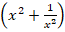 через
через 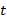 , произведем следующие действия:
, произведем следующие действия:
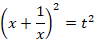
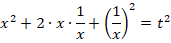
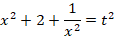

После замены исходное уравнение будет иметь вид:
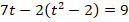
Преобразуя это выражение, получаем квадратное уравнение:
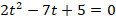
Найдем корни уравнения:
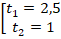
Вернемся к замене:
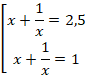
Поскольку 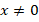 , можем умножить обе части каждого из уравнений на
, можем умножить обе части каждого из уравнений на 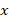 и получить квадратные уравнения:
и получить квадратные уравнения:
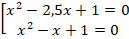
Первое уравнение имеет решения:
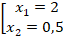
Оба решения удовлетворяют ОДЗ. Второе уравнение не имеет вещественных корней.
Ответ: 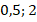 .
.
Теперь перейдем к решению иррациональных уравнений. Так называются уравнения, которые содержат операцию извлечения корня из переменной.
Задание 7. Решить уравнение:
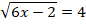
Решение.
Как мы знаем, выражение 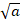 имеет смысл только для значения
имеет смысл только для значения 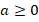 . Поэтому ОДЗ для данного уравнения будет следующей:
. Поэтому ОДЗ для данного уравнения будет следующей:
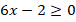
Чтобы привести иррациональное уравнение к линейному или квадратному, нужно избавиться от иррациональности. В данном случае – избавиться от квадратного корня. Для этого воспользуемся свойством корня:
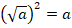
Возведем обе части уравнения в квадрат:
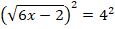
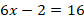
Получили линейное уравнение, корнем которого является:
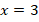
Полученное значение входит в ОДЗ:
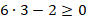
При решении уравнения мы возвели обе части уравнения в квадрат, при этом могли возникнуть посторонние корни, т. е. те, которые не являются решением исходного уравнения.
Посторонние корни
Операция возведения в квадрат обеих частей равенства не является равносильным преобразованием. При применении этой операции можно получить из неправильного равенства правильное. Например, равенство 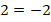 очевидно неправильное. Но при возведении в квадрат получим правильное:
очевидно неправильное. Но при возведении в квадрат получим правильное:
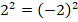
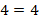
При этом из правильного равенства мы не получим неправильное, ведь если числа равны, то их квадраты также равны. Поэтому любой корень исходного уравнения является корнем уравнения, полученного после возведения в квадрат обеих частей. Но не все корни полученного уравнения являются корнями исходного. Могут возникнуть посторонние корни. Чтобы исключить их, проще всего выполнить проверку, подставив полученные значения в исходное уравнение.
Выполним проверку. Подставим полученный корень в исходное уравнение:
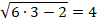
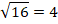
Мы получили правильное равенство, значит, 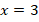 является решением уравнения.
является решением уравнения.
Ответ: 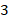 .
.
Задание 8. Решить уравнение:
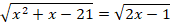
Решение.
Подкоренные выражения должны быть неотрицательными. Поэтому ОДЗ будет следующей:
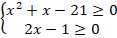
Возведем обе части уравнения в квадрат:
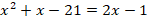
После преобразования получим квадратное уравнение:
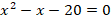
Найдем корни уравнения:
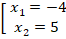
Проверим, входят ли корни в ОДЗ.
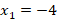 :
:
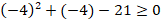
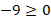
Неравенство неверное, значит, корень 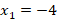 не входит в ОДЗ и не является решением исходного уравнения.
не входит в ОДЗ и не является решением исходного уравнения.
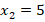 :
:
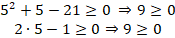
Корень входит в ОДЗ.
Теперь выполним проверку, подставив 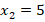 в исходное уравнение:
в исходное уравнение:
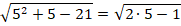
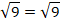
Получили правильное равенство, следовательно, исходное уравнение имеет один корень 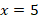 .
.
Ответ: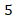 .
.
Заключение
Итак, сегодня мы познакомились с некоторыми приемами, которые позволяют свести уравнения высших порядков, дробно-рациональные и иррациональные уравнения к квадратным и линейным уравнениям.
Список литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра, 8 класс. Учебник. – М.: ФГОС, издательство «Просвещение», 2018.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра, 8 класс. Учебник. – М.: «Просвещение», 2018.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б./Под ред. Теляковского С.А. Алгебра, 8 класс. Учебник. – М.: «Просвещение», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал youclever.org (Источник)
- Интернет-портал kontromat.ru (Источник)
Домашнее задание
1. Решить биквадратное уравнение:
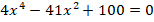
2. Решить дробно-рациональное уравнение:
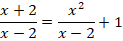
3. Решить иррациональное уравнение:
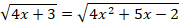
Линейные уравнения с дробями | Алгебра
Линейные уравнения с дробями не содержат переменной в знаменателе. Чтобы решить линейное уравнение с дробями, удобно избавиться от знаменателей.
Для этого нужно найти наименьший общий знаменатель всех входящих в уравнение дробей и обе части уравнения умножить на это число.
Наименьший общий знаменатель данных дробей равен 6. Дополнительный множитель к первой дроби равен 2, ко второй — 3, к 5 — 6. Умножаем обе части уравнения на наименьший общий знаменатель:
В результате наименьший общий знаменатель и знаменатель каждой дроби сокращаются, и получаем линейное уравнение, не содержащее дробей.
Раскроем скобки и приведём подобные слагаемые:
Обе части уравнения делим на число, стоящее перед иксом:
Из полученной неправильной дроби выделяем целую часть
Ответ: -4 6/7.
Наименьший общий знаменатель данных дробей равен 20. Найдем дополнительный множитель к каждой дроби и умножим обе части уравнения на 20:
Можно, конечно, сразу же умножить дополнительный множитель на числитель каждой дроби. Но, к сожалению, наибольшее количество ошибок при решении линейных уравнений с дробями допускается именно на этом шаге. Скобки — друзья ученика :). Поэтому лучше воспользоваться их помощью:
Особенно полезны скобки в случае, когда перед дробью стоит знак «минус».
После раскрытия скобок можно сразу же перенести неизвестные в одну сторону уравнения, известные — в другую (не забыв при переносе изменить их знаки), а можно сначала упростить каждую часть, приведя подобные слагаемые, а потом уже переносить.
Ответ: -34.
Здесь наименьший общий знаменатель дробей равен 12. Находим дополнительный множитель к каждой дроби и умножаем обе части уравнения на 12:
Раскрываем скобки и упрощаем
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: -5.
Уравнения такого вида можно решить, использовать основное свойство пропорции (в верной пропорции произведение крайних членов равно произведению средних членов):
при делении двух отрицательных чисел получается положительное число, поэтому минусы можно сразу же не писать.
Если это возможно, лучше ответ записать в виде десятичной дроби:
Ответ: 0,1875.
Решение дробных рациональных уравнений
Сегодня мы разберемся, как решать дробные рациональные уравнения.
Посмотрим: из уравнений
(1) 2х + 5 = 3(8 – х),
(2) ,
(3)
(4)
дробными рациональными уравнениями являются только (2) и (4), а (1) и (3) это целые уравнения.
Предлагаю решить уравнение (4), а затем сформулировать правило.
Поскольку уравнение дробное, то надо найти общий знаменатель. В этом уравнении это выражение 6(х – 12)(х – 6). Затем мы умножаем обе части уравнения на общий знаменатель:
После сокращения получаем целое уравнение:
6(х – 6)2 – 6(х – 12)2 = 5(х – 12)(х – 6).
Решив это уравнение надо обязательно проверить не обращают ли полученные корни в нуль знаменатели дробей в исходном уравнении.
Раскрываем скобки:
6х2 – 72х + 216 – 6х2 + 144х – 864 = 5х2 – 90х + 360, упрощаем уравнение: 5х2 – 162х + 1008 = 0.
Находим корни уравнения
D = 6084, √D = 78,
х1= (162 – 78)/10= 84/10 = 8,4 и х2 = (162 + 78)/10 = 240/10 = 24.
При х = 8,4 и 24 общий знаменатель 6(х – 12)(х – 6) ≠ 0, значит эти числа являются корнями уравнения (4).
Ответ: 8,4; 24.
Решив предложенное уравнение, приходим к следующим положениям:
1) Находим общий знаменатель.
2) Умножаем обе части уравнения на общий знаменатель.
3) Решаем полученное целое уравнение.
4) Проверяем, какие из корней обращают общий знаменатель в нуль и исключаем их из решения.
Посмотрим теперь на примере, как работают полученные положения.
Решить уравнение:
1) Общий знаменатель: х2 – 1
2) Умножаем обе части уравнения на общий знаменатель, получаем целое уравнение: 6 – 2(х + 1) = 2(х2 – 1) – (х + 4)(х – 1)
3) Решаем уравнение: 6 – 2х – 2 = 2х2 – 2 – х2 – 4х + х + 4
х2 – х – 2 = 0
х1 = — 1 и х2 = 2
4) При х = -1, общий знаменатель х2 – 1 = 0. Число -1 корнем не является.
При х = 2, общий знаменатель х2 – 1 ≠ 0. Число 2 – корень уравнения.
Ответ: 2.
Как видите, наши положения работают. Не бойтесь, у вас все получится! Самое главное правильно найдите общий знаменатель и аккуратно выполните преобразования. Надеемся, что при решение дробных рациональных уравнений у вас всегда будут получаться правильные ответы. Если у вас остались вопросы или вы хотите попрактиковаться в решении подобных уравнений, записывайтесь на уроки к автору этой статьи, репетитору Валентине Галиневской.
Также рекомендуем посмотреть новый видеоурок по данной теме от нашего репетитора Ольги Лукашонок.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Уравнения с дробями | Математика
Линейные уравнения с дробями в 6 классе можно решать по обычной схеме: неизвестные — в одну сторону, известные — в другую, изменив при этом их знак. Другой путь — предварительно упростить уравнение, превратив его из линейного уравнения с дробями в линейное уравнение с целыми числами.
Сначала на примере одного линейного уравнения с дробями рассмотрим оба способа решения.
1 способ: Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Приводим к общему знаменателю дроби в каждой части уравнения:
Это — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:
При делении чисел с разными знаками получаем отрицательное число. По правилу деления дробей:
После сокращения имеем:
(В данном случае ответ можно записать и в виде десятичной дроби: х=-0,8).
2 способ:
Обе части уравнения умножим почленно на наименьший общий знаменатель всех входящих в него дробей, в данном случае он равен 24:
При умножении на знаменатель дроби сокращаются, в знаменателе остается единица, которую не пишем. От линейного уравнения с дробями перешли к линейному уравнению с целыми числами:
Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: -4/5.
Как видите, второй способ существенно упрощает решение линейного уравнения с дробями.
Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей. Здесь он равен 60:
Вместо линейного уравнения с дробями получили линейное уравнение с целыми числами. Неизвестные переносим в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Сокращаем дробь на 3:
Ответ: 5/11.
Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей:
В результате линейное уравнение с дробями заменили на линейное уравнение с целыми числами:
Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: 2,9.
В следующий раз рассмотрим линейные уравнения с смешанными дробями.
Как в уравнении избавиться от дроби — kak.manesu.com
Уравнения с дробями – нестандартный вид уравнений, имеющий свои специфические особенности и тонкие моменты. Испробуем в них разобраться.
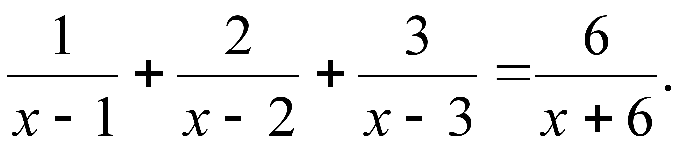
Содержание статьи:
Инструкция
1. Вероятно, самый явственный момент тут – это, безусловно, знаменатель. Числовые дроби не представляют никакой угрозы (дробные уравнения, где во всех знаменателях стоят только числа, вообще будут линейными), а вот если в знаменателе стоит переменная, то это неукоснительно надобно рассматривать и прописывать. Во-первых, это значит, что значение х, обращающее в 0 знаменатель, корнем быть не может, и вообще необходимо отдельно прописать тот факт, что икс не может равняться этому числу. Даже если у вас получится, что при подстановке в числитель всё восхитительно сходится и удовлетворяет условиям. Во-вторых, мы не можем умножать либо разделять обе части уравнения на выражение, равное нулю.
2. Позже этого решение такого уравнения сводится к переносу всех его членов в левую часть так, дабы в правой остался 0.Надобно привести все члены к всеобщему знаменателю, домножив, где надобно, числители на недостающие выражения.Дальше решаем обыкновенное уравнение, написанное в числителе. Можем переносить всеобщие множители за скобки, использовать формулы сокращённого умножения, приводить сходственные, вычислять корни квадратного уравнения через дискриминант и т.д.
3. В результате должно получиться разложение на множители в виде произведения скобок (х-(i-ый корень)). Также сюда могут входить многочлены, не имеющие корней, скажем, квадратный трёхчлен с дискриминантом, меньшим нуля (если, финально, в задаче требуется обнаружить только действительные корни, как почаще каждого и бывает).Неукоснительно надобно разложить на множители и знаменатель с целью нахождения там скобок, теснее содержащихся в числителе. Если в знаменателе стоят выражения типа (х-(число)), то класснее при приведении к всеобщему знаменателю стоящие в нём скобки не перемножать “в лоб”, а оставить в виде произведения начальных примитивных выражений.Идентичные скобки в числителе и знаменателе дозволено сократить, прописав заранее, как говорилось выше, данные на х.Результат записывается в фигурных скобках, как уйма значений х, либо легко перечислением: x1=…, х2=… и т.д.
Решение уравнений – то, без чего невозможно обойтись в физике, математике, химии. Как минимум. Учимся основам их решения.
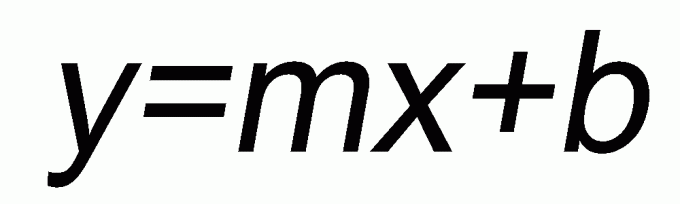
Инструкция
1. В самой всеобщей и легкой систематизации уравнения дозволено поделить по числу переменных, в них содержащихся, и по степеням, в которых эти переменные стоят.Решить уравнение значит обнаружить все его корни либо подтвердить, что их нет.Всякое уравнений имеет не больше P корней, где P – максимальная степень данного уравнения.Но часть этих корней может и совпадать. Так, скажем, уравнение х^2+2*x+1=0, где ^ – значок возведения в степень, сворачивается в квадрат выражения (х+1), то есть в произведение 2-х идентичных скобок, вся из которых даёт х=-1 в качестве решения.
2. Если в уравнении каждого одна неведомая, это значит, что вам удастся в очевидном виде обнаружить его корни (действительные либо комплексные).Для этого скорей каждого потребуются, разные реформирования: формулы сокращённого умножения, формула вычисления дискриминанта и корней квадратного уравнения, перенос слагаемых из одной части в иную, приведение к всеобщему знаменателю, умножение обоих частей уравнения на одно и тоже выражение, возведение в квадрат и другое.Реформирования, не влияющие на корни уравнения, именуются тождественными. Они применяются для облегчения процесса решения уравнения.Также вы можете взамен традиционного аналитического воспользоваться графическим способом и записать данное уравнение в виде функции, проведя после этого её изыскание.
3. Если в уравнении незнакомых огромнее одной, то вам удастся лишь выразить одну из них через иную, показав тем самым комплект решений. Таковы, скажем, уравнения с параметрами, в которых присутствует незнакомая x и параметр а. Решить параметрическое уравнение – значит для всех а выразить х через а, то есть разглядеть все допустимые случаи.Если в уравнении стоят производные либо дифференциалы незнакомых (смотри картинку), поздравляю, это дифференциальное уравнение, и здесь вам не обойтись без высшей математики).
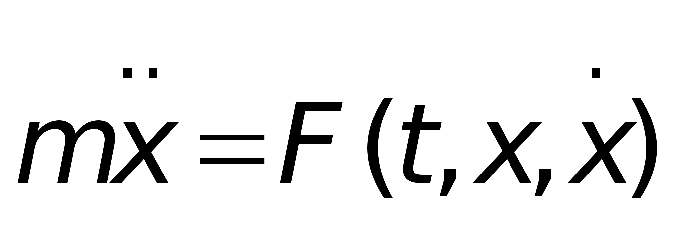
Дабы решить задачу с дробями , необходимо обучиться делать с ними арифметические действия. Они могут быть десятичные, но почаще каждого применяются естественные дроби с числителем и знаменателем. Только позже этого дозволено переходить на решения математических задач с дробными величинами.

Вам понадобится
- – калькулятор;
- – умения свойств дробей;
- – знание изготавливать действия с дробями.
Инструкция
1. Дробью называют запись деления одного числа на другое. Нередко это сделать нацело невозможно, следственно и оставляют это действие «неоконченным . Число, которое является делимым (оно стоит над либо перед знаком дроби), именуются числителем, а второе число (под знаком дроби либо позже него) – знаменателем. Если числитель огромнее знаменателя, дробь именуется неправильной, и из нее дозволено выделить целую часть. Если числитель поменьше знаменателя, то такая дробь именуется верной, и ее целая часть равна 0.
2. Задачи с дробями делятся на несколько видов. Определите, к какому из них относится задача. Примитивный вариант – нахождение доли числа, выраженной дробью. Для решения этой задачи довольно умножить это число на дробь. Скажем, на склад завезли 8 т картошки. В первую неделю было продано 3/4 от ее всеобщего числа. Сколько картошки осталось? Дабы решить эту задачу, число 8 умножьте на 3/4. Получится 8?3/4=6 т.
3. Если надобно обнаружить число по его части, умножьте вестимую часть числа на дробь, обратную той, которая показывает какова доля данной части в числе. Скажем, 8 человек из класса составляют 1/3 от всеобщего числа учеников. Сколько детей учится в классе? От того что 8 человек это часть, которая представляет 1/3 от каждого числа, то обнаружьте обратную дробь, которая равна 3/1 либо примитивно 3. После этого для приобретения числа учеников в классе 8?3=24 ученика.
4. Когда необходимо обнаружить какую часть числа составляет одно число от иного, поделите число, которое представляет часть на то, которое является целым. К примеру, если расстояние между городами 300 км, а автомобиль проехал 200 км, какую часть данный составит от каждого пути? Поделите часть пути 200 на полный путь 300, позже сокращения дроби получите итог. 200/300=2/3.
5. Дабы обнаружить часть неведомую долю от числа, когда есть вестимая, возьмите целое число за условную единицу, и отнимите от нее знаменитую долю. Скажем, если теснее прошло 4/7 части урока, сколько еще осталось? Возьмите каждый урок как условную единицу и отнимите от нее 4/7. Получите 1-4/7=7/7-4/7=3/7.
Дроби – это математическая форма записи простого разумного числа. Она представляет собой число, которое состоит из одной либо нескольких долей единицы, может быть как в десятичном, так и в обыкновенном виде. Сегодня операции по реформированию дробей имеют большое значение не только в математике, но и в иных областях умений.
Инструкция
1. Как водится, множество обычных дробей бывают неправильными, и в таком случае они требуют определенных действий со стороны того, кто решает примеры и задачи с данной дробью.
2. Возьмите учебник со своей задачей. Наблюдательно ознакомьтесь с условием, прочитав его несколько раз, и перейдите к решению. Посмотрите, какие дроби имеются в решаемых вами действиях. Это могут быть неправильные, положительные либо десятичные дроби. Переведите верные дроби в неправильные, но при этом помните, что для записи результата все действия придется исполнить обратно, преобразовав теснее неправильную дробь в верную. У неправильной дроби число над дробной чертой (числитель) неизменно огромнее числа под чертой – знаменателя. Для того дабы сделать перевод из положительной дроби в неправильную нужно исполнить следующие шаги.
3. Умножьте знаменатель на целое число и прибавьте к полученному итогу числитель. К примеру, если дробь вида 2 целых 7/9, нужно 9 умножить на 2 и потом к 18 прибавить 7 – финальным итогом будет 25/9.
4. Произведите все нужные действия по своей задаче (сложения, вычитания, деления, умножения), применяя преобразованные дроби.Возьмите свой результат, его нужно будет представить в обычной дроби. Для этого поделите числитель на знаменатель. К примеру, если нужно перевести число 25/9 в верную дробь, поделите 25 на 9. Потому что 25 на 9 нацело не делится, в результате получается 2 целых и семь (числитель) девятых (знаменатель). Сейчас получена верная дробь, где числитель огромнее знаменателя и имеется целая часть.
5. Запишите результат задачи положительной дробью. Проведите проверку своим действиям, в случае если ее требует сделать условие задачи либо преподаватель.
Source: jprosto.ru
Читайте также
