Как в уравнении убрать дробь: § Как решить уравнение с неизвестным в дроби

Содержание

Как избавиться от знаменателя в дроби

Как решать дробные уравнения?

Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.

Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)

Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:

1. Дроби и действия с дробями и дробными выражениями.

3. Решение линейных и квадратных уравнений.

Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т. д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)

Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.

Что такое дробное уравнение? Примеры.

Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.

Например, вот такое уравнение:

И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.

Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.

Или такое уравнение:

Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.

В общем, вы поняли.

Как решать дробные уравнения? Убираем дроби!

Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?

Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)

Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?

Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее. )

Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:

Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.

А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?

Давайте его конструировать.) Смотрим ещё раз на уравнение:

Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)

Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.

Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).

Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:

Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!

А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:

Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:

А его (надеюсь) уже решит каждый:

Решаем следующий примерчик:

И опять избавляемся от того, что нам не нравится.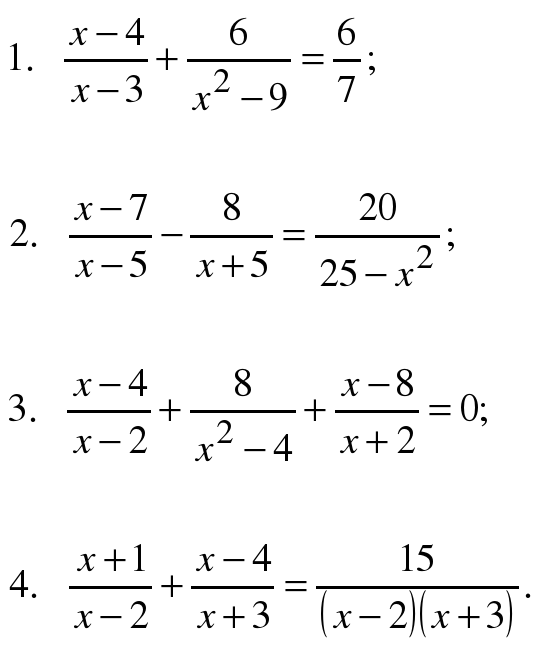 В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.

Вот и домножаем! Всю левую часть и всю правую часть:

Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».

А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!

Дело всё в том, что частенько после умножения народ записывает левую часть вот так:

Это категорически неверно. Дальше можно уже не решать, да…)

Но у нас всё хорошо, будем дорешивать.

С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.

Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:

Переносим всё влево и приводим к стандартному виду:

Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:

Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:

Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.

А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.

Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…

Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)

Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.

Раскладываем на множители!

Решаем третье уравнение по списку:

А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить

и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?

Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)

А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х 2 +2х вполне себе раскладывается! Выносим один икс за скобку и получаем:

Отлично. Вставим наше разложение в исходное уравнение:

Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).

Вот на х(х+2) и умножаем:

И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:

А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:

Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)

С удовольствием сокращаем все дроби:

Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:

И снова получили квадратное уравнение.) Решаем и получаем два корня:

Вот и всё. Это и есть ответ.)

Из этого примера можно сделать важный вывод:

Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!

Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)

Ну что, порешаем?)

Ответы (как обычно, вразброс):

Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)

Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!

Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…

Как решать уравнения с дробями. Показательное решение уравнений с дробями.

Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.

Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.

Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.

Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45

Другой пример, когда неизвестное находится в знаменателе:

Уравнения такого типа называются дробно-рациональными или просто дробными.

Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:

значение переменной, обращающее в 0 знаменатель, корнем быть не может;
нельзя делить или умножать уравнение на выражение =0.

Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.

Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.

Например, требуется решить дробное уравнение:

Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.

Избавляемся от знаменателя путем умножения всех членов уравнения на х

И решаем обычное уравнение

5x – 2х = 1
3x = 1
х = 1/3

Решим уравнение посложнее:

Здесь также присутствует ОДЗ: х -2.

Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.

Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):

Это самое обычное умножение дробей, которое мы уже рассмотрели выше

Запишем это же уравнение, но несколько по-другому

Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:

х = 4 – 2 = 2, что соответствует нашей ОДЗ

Для закрепления материала рекомендуем еще посмотреть видео.

Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.

Решение уравнений с дробями

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Что поможет в решении:

если а не равно нулю, то у уравнения единственный корень: х = −b : а;
если а равно нулю, а b не равно нулю — у уравнения нет корней;
если а и b равны нулю, то корень уравнения — любое число.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

подобрать число, которое можно разделить на каждый из знаменателей без остатка;
умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

если значение переменной обращает знаменатель в 0, значит это неверное значение;
делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Пример 2. Найти корень уравнения

Область допустимых значений: х ≠ −2.
Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Пример 3. Решить дробное уравнение:

как решать, алгоритм, примеры с ответами для 9 класса

Что такое дробно-рациональные уравнения

Определение

Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:

P(x)Q(x)=0,

при P(x) и Q(x) в виде выражений, содержащих переменную.

Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.

Пример 1

Дробно-рациональные уравнения:

9×2-13x=0

12x+xx+1=12

6x+1=x2-5xx+1

Уравнения, которые не являются дробно-рациональными:

9×2-13=0

x2+8×2=6

СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).

Как решаются дробно-рациональные уравнения

В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.

Алгоритм действий при стандартном способе решения:

Выписать и определить ОДЗ.
Найти общий знаменатель для дробей.
Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
Записать уравнение со скобками.
Раскрыть скобки для приведения подобных слагаемых.
Найти корни полученного уравнения.
Выполним проверку корней в соответствии с ОДЗ.
Записать ответ.

Пример 1

Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:

xx-2-7x+2=8×2-4

Начать следует с области допустимых значений:

x-2≠0⇔x≠2

x+2≠0⇔x≠-2

x2-4≠0⇔x≠±2

Воспользуемся правилом сокращенного умножения:

x2-4=(x-2)(x+2)

В результате общим знаменателем дробей является:

(x-2)(x+2)

Выполним умножение каждого из членов выражения на общий знаменатель:

xx-2-7x+2=8×2-4

x(x-2)(x+2)x-2-7(x-2)(x+2)x+2=8(x-2)(x+2)(x-2)(x+2)

После сокращения избавимся от скобок и приведем подобные слагаемые:

x(x+2)-7(x-2)=8

x2+2x-7x+14=8

x2-5x+6=0

Осталось решить квадратное уравнение:

x2-5x+6=0

x1=2

x2=3

Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:

x =3

Примеры задач с ответами для 9 класса

Задача 1

Требуется решить дробно-рациональное уравнение:

xx+2+x+1x+5-7-xx2+7x+10=0

Решение

Проанализируем выражение:

xx+2+x+1x+5-7-xx2+7x+10=0

Определим область допустимых значений:

ОДЗ:x+2≠0⇔x≠-2

x+5≠0⇔x≠-5

x2+7x+10≠0

D=49-4·10=9

x1≠-7+32=-2

x2≠-7-32=-5

Квадратный трехчлен x2+7x+10 следует разложить на множители, руководствуясь формулой:

ax2+bx+c=a(x-x1)(x-x2)

xx+2+x+1x+5-7-x(x+2)(x+5)=0

Заметим, что общим знаменателем для дробей является: (x+2)(x+5). Умножим на этот знаменатель уравнение:

xx+2+x+1x+5-7-x(x+2)(x+5)=0

Сократим дроби, избавимся от скобок, приведем подобные слагаемые:

x(x+2)(x+5)x+2+(x+1)(x+2)(x+5)x+5-

-(7-x)(x+2)(x+5)(x+2)(x+5)=0

x(x+5)+(x+1)(x+2)-7+x=0

x2+5x+x2+3x+2-7+x=0

2×2+9x-5=0

Потребуется решить квадратное уравнение:

2×2+9x-5=0

x1=-5;

x2=12.

Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.

Ответ: x=12

Задача 2

Дано дробно-рациональное уравнение, корни которого требуется найти:

4x-2-3x+4=1

Решение

В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:

4\(x+4)x-2-3\(x-2)x+4-1\(x-2)(x+4)=0

4(x+4)-3(x-2)-(x-2)(x+4)(x-2)(x+4)=0

4x+16-3x+6-(x2+4x-2x-8)(x-2)(x+4)=0

x+22-x2-4x+2x+8(x-2)(x+4)=0

Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:

-x2-x+30(x-2)(x+4)=0⇔-x2-x+30=0(x-2)(x+4)≠0

Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:

(x-2)(x+4)≠0

x-2≠0;

x+4≠0

x≠2;

x≠-4

Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:

-x2-x+30=0___·(-1)

x2+x-30=0

Получилось квадратное уравнение, которое можно решить:

x1=5;

x2=-6

Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.

Ответ: 5; -6

Задача 3

Нужно решить дробно-рациональное уравнение:

x+2×2-2x-xx-2=3x

Решение

На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:

x+2\1x(x-2)-x\xx-2-3\(x-2)x=0

x+2-x2-3(x-2)x(x-2)=0

x+2-x2-3x+6x(x-2)=0

-x2-2x+8x(x-2)=0⇔-x2-2x+8=0x(x-2)≠0

x(x-2)≠0

x≠0;

x≠2

Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.

-x2-2x+8=0___·(-1)

Корни квадратного уравнения:

x2+2x-8=0

x1=-4;x2=2

Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.

Ответ: -4

Задача 4

Найти корни уравнения:

x2-x-6x-3=x+2

Решение

Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:

x2-x-6\1x-3-x\(x-3)-2\(x-3)=0

x2-x-6-x(x-3)-2(x-3)x-3=0

x2-x-6-x2+3x-2x+6x-3=0

0xx-3=0⇔0x=0x-3≠0

Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:

x≠3

Получим уравнение:

0x = 0

Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.

Ответ: х — любое число, за исключением 3.

Задача 5

Требуется вычислить корни дробно-рационального уравнения:

5x-2-3x+2=20×2-4

Решение

На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:

5\(x+2)x-2-3\(x-2)x+2-20\1(x-2)(x+2)=0

5(x+2)-3(x-2)-20(x-2)(x+2)=0

5x+10-3x+6-20(x-2)(x+2)=0

2x-4(x-2)(x+2)=0⇔2x-4=0(x-2)(x+2)≠0

(x-2)(x+2)≠0

x≠2;

x≠-2

Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.

2x — 4 = 0

x = 2

Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.

Ответ: корни отсутствуют

Задача 6

Нужно найти корни уравнения:

x-3x-5+1x=x+5x(x-5)

Решение

Начнем с определения ОДЗ:

-5≠0 x≠0 x(x-5)≠0 x≠5 x≠0

При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:

x-3x-5+1x=x+5x(x-5)·x(x-5)

(x-3)x(x-5)x-5+x(x-5)x=(x+5)x(x-5)x(x-5)

(x-3)x+x=x+5

Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:

x2-3x+x-5=x+5→x2-2x-5-x-5=0→x2-3x-10=0

Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x2, который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:

x1·x2=-10 x1+x2=3

В этом случае подходящими являются числа: -2 и 5.

Второе значение не соответствует области допустимых значений.

Ответ: -2.

Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).

Вставка уравнений — ONLYOFFICE

специальные символы
- Вставка уравнений
- Вставка уравнений
- Вставка уравнений
- Функции автозамены
- Функции автозамены
- Функции автозамены
математические формулы
- Вставка уравнений
- Вставка уравнений
- Вставка уравнений
- Функции автозамены
- Функции автозамены
- Функции автозамены

В редакторе документов вы можете создавать уравнения, используя встроенные шаблоны, редактировать их, вставлять специальные символы (в том числе математические знаки, греческие буквы, диакритические знаки и т.

д.).

Добавление нового уравнения

Чтобы вставить уравнение из коллекции,

установите курсор на нужной строке,
перейдите на вкладку Вставка верхней панели инструментов,
нажмите на стрелку рядом со значком Уравнение на верхней панели инструментов,
в открывшемся выпадающем списке выберите нужную категорию уравнений. В настоящее время доступны следующие категории: Символы, Дроби, Индексы, Радикалы, Интегралы, Крупные операторы, Скобки, Функции, Диакритические знаки, Пределы и логарифмы, Операторы, Матрицы,
щелкните по определенному символу/уравнению в соответствующем наборе шаблонов.

Выбранный символ или уравнение будут вставлены в позиции курсора. Если выбранная строка пуста, уравнение будет выровнено по центру. Чтобы выровнять такое уравнение по левому или правому краю, щелкните по рамке уравнения и используйте значки или на вкладке

Главная верхней панели инструментов.

Каждый шаблон уравнения представляет собой совокупность слотов. Слот — это позиция для каждого элемента, образующего уравнение. Пустой слот, также называемый полем для заполнения, имеет пунктирный контур . Необходимо заполнить все поля, указав нужные значения.

Примечание: чтобы начать создание уравнения, можно также использовать сочетание клавиш Alt + =.

К уравнению также можно добавить подпись. Для получения дополнительной информации о работе с подписями к уравнениям вы можете обратиться к этой статье.

Ввод значений

Курсор определяет, где появится следующий символ, который вы введете. Чтобы точно установить курсор, щелкните внутри поля для заполнения и используйте клавиши со стрелками на клавиатуре для перемещения курсора на один символ влево/вправо или на одну строку вверх/вниз.

Если в выбранном шаблоне требуется добавить новое поле для заполнения под слотом, в котором находится курсор, нажмите клавишу Enter.

Когда курсор будет установлен в нужную позицию, можно заполнить поле:

введите требуемое цифровое или буквенное значение с помощью клавиатуры,
вставьте специальный символ, используя палитру Символы из меню Уравнение на вкладке Вставка верхней панели инструментов или вводя их с клавиатуры (см. описание функции Автозамена математическими символами),
добавьте шаблон другого уравнения с палитры, чтобы создать сложное вложенное уравнение. Размер начального уравнения будет автоматически изменен в соответствии с содержимым. Размер элементов вложенного уравнения зависит от размера поля начального уравнения, но не может быть меньше, чем размер мелкого индекса.

Для добавления некоторых новых элементов уравнений можно также использовать пункты контекстного меню:

Чтобы добавить новый аргумент, идущий до или после имеющегося аргумента в Скобках, можно щелкнуть правой кнопкой мыши по существующему аргументу и выбрать из контекстного меню пункт Вставить аргумент перед/после.
Чтобы добавить новое уравнение в Наборах условий из группы Скобки (или в уравнениях других типов, в которых вы ранее добавили новые поля для заполнения путем нажатия на Enter), можно щелкнуть правой кнопкой мыши по пустому полю для заполнения или по введенному в него уравнению и выбрать из контекстного меню пункт Вставить уравнение перед/после. 3).
При вводе значений математических выражений не требуется использовать клавишу Пробел, так как пробелы между символами и знаками действий устанавливаются автоматически.
Если уравнение слишком длинное и не помещается на одной строке, перенос на другую строку в процессе ввода осуществляется автоматически. Можно также вставить перенос строки в строго определенном месте, щелкнув правой кнопкой мыши по математическому оператору и выбрав из контекстного меню пункт Вставить принудительный разрыв. Выбранный оператор будет перенесен на новую строку. После добавления принудительного разрыва строки можно использовать клавишу Tab, чтобы выровнять новую строку по какому-либо математическому знаку из предыдущей строки. Чтобы удалить добавленный принудительный разрыв строки, щелкните правой кнопкой мыши по математическому оператору в начале новой строки и выберите пункт меню Удалить принудительный разрыв.
Форматирование уравнений
Чтобы увеличить или уменьшить
размер шрифта в уравнении, щелкните мышью внутри рамки уравнения и используйте кнопки и на вкладке Главная верхней панели инструментов или выберите нужный размер шрифта из списка. Все элементы уравнения изменятся соответственно.
По умолчанию буквы в уравнении форматируются курсивом. В случае необходимости можно изменить стиль шрифта (выделение полужирным, курсив, зачеркивание) или цвет для всего уравнения или его части. Подчеркивание можно применить только ко всему уравнению, а не к отдельным символам. Выделите нужную часть уравнения путем перетаскивания. Выделенная часть будет подсвечена голубым цветом. Затем используйте нужные кнопки на вкладке Главная верхней панели инструментов, чтобы отформатировать выделенный фрагмент. Например, можно убрать форматирование курсивом для обычных слов, которые не являются переменными или константами.

Для изменения некоторых элементов уравнений можно также использовать пункты контекстного меню:
- Чтобы изменить формат Дробей, можно щелкнуть правой кнопкой мыши по дроби и выбрать из контекстного меню пункт Изменить на диагональную/горизонтальную/вертикальную простую дробь (доступные опции отличаются в зависимости от типа выбранной дроби).
- Чтобы изменить положение Индексов относительно текста, можно щелкнуть правой кнопкой мыши по уравнению, содержащему индексы, и выбрать из контекстного меню пункт Индексы перед текстом/после текста.
- Чтобы изменить размер аргумента для уравнений из групп Индексы, Радикалы, Интегралы, Крупные операторы, Пределы и логарифмы, Операторы
  , а также для горизонтальных фигурных скобок и шаблонов с группирующим знаком из группы Диакритические знаки, можно щелкнуть правой кнопкой мыши по аргументу, который требуется изменить, и выбрать из контекстного меню пункт Увеличить/Уменьшить размер аргумента.
- Чтобы указать, надо ли отображать пустое поле для ввода степени в уравнении из группы Радикалы, можно щелкнуть правой кнопкой мыши по радикалу и выбрать из контекстного меню пункт Скрыть/Показать степень.
- Чтобы указать, надо ли отображать пустое поле для ввода предела в уравнение из группы Интегралы или Крупные операторы, можно щелкнуть правой кнопкой мыши по уравнению и выбрать из контекстного меню пункт Скрыть/Показать верхний/нижний предел.
- Чтобы изменить положение пределов относительно знака интеграла или оператора в уравнениях из группы Интегралы или Крупные операторы, можно щелкнуть правой кнопкой мыши по уравнению и выбрать из контекстного меню пункт Изменить положение пределов. Пределы могут отображаться справа от знака оператора (как верхние и нижние индексы) или непосредственно над и под знаком оператора.
- Чтобы изменить положение пределов относительно текста в уравнениях из группы Пределы и логарифмы и в шаблонах с группирующим знаком из группы Диакритические знаки, можно щелкнуть правой кнопкой мыши по уравнению и выбрать из контекстного меню пункт Предел над текстом/под текстом.
- Чтобы выбрать, какие из Скобок надо отображать, можно щелкнуть правой кнопкой мыши по выражению в скобках и выбрать из контекстного меню пункт Скрыть/Показать открывающую/закрывающую скобку.
- Чтобы управлять размером Скобок, можно щелкнуть правой кнопкой мыши по выражению в скобках.
  Пункт меню Растянуть скобки выбран по умолчанию, так что скобки могут увеличиваться в соответствии с размером выражения, заключенного в них, но вы можете снять выделение с этой опции, чтобы запретить растяжение скобок. Когда эта опция активирована, можно также использовать пункт меню Изменить размер скобок в соответствии с высотой аргумента.
- Чтобы изменить положение символа относительно текста для горизонтальных фигурных скобок или горизонтальной черты над/под уравнением из группы Диакритические знаки, можно щелкнуть правой кнопкой мыши по шаблону и и выбрать из контекстного меню пункт Символ/Черта над/под текстом.
- Чтобы выбрать, какие границы надо отображать для Уравнения в рамке из группы Диакритические знаки, можно щелкнуть правой кнопкой мыши по уравнению и выбрать из контекстного меню пункт Свойства границ, а затем — Скрыть/Показать верхнюю/нижнюю/левую/правую границу или Добавить/Скрыть горизонтальную/вертикальную/диагональную линию.
- Чтобы указать, надо ли отображать пустые поля для заполнения в Матрице, можно щелкнуть по ней правой кнопкой мыши и выбрать из контекстного меню пункт Скрыть/Показать поля для заполнения.
Для выравнивания некоторых элементов уравнений можно использовать пункты контекстного меню:
- Чтобы выровнять уровнения в Наборах условий из группы Скобки (или в уравнениях других типов, в которых вы ранее добавили новые поля для заполнения путем нажатия на Enter), можно щелкнуть правой кнопкой мыши по уравнению, выбрать из контекстного меню пункт Выравнивание, а затем выбрать тип выравнивания: По верхнему краю, По центру или По нижнему краю.
- Чтобы выровнять Матрицу по вертикали, можно щелкнуть правой кнопкой мыши по матрице, выбрать из контекстного меню пункт Выравнивание матрицы, а затем выбрать тип выравнивания: По верхнему краю, По центру или По нижнему краю.
- Чтобы выровнять по горизонтали элементы внутри отдельного столбца Матрицы, можно щелкнуть правой кнопкой мыши по полю для заполнения внутри столбца, выбрать из контекстного меню пункт Выравнивание столбца, а затем выбрать тип выравнивания: По левому краю, По центру или По правому краю.
Удаление элементов уравнения
Чтобы удалить часть уравнения, выделите фрагмент, который требуется удалить, путем перетаскивания или удерживая клавишу Shift и используя клавиши со стрелками, затем нажмите на клавиатуре клавишу Delete.
Слот можно удалить только вместе с шаблоном, к которому он относится.
Чтобы удалить всё уравнение, выделите его полностью путем перетаскивания или с помощью двойного щелчка по рамке уравнения и нажмите на клавиатуре клавишу Delete.
Для удаления некоторых элементов уравнений можно также использовать пункты контекстного меню:
- Чтобы удалить Радикал, можно щелкнуть по нему правой кнопкой мыши и выбрать из контекстного меню пункт Удалить радикал.
- Чтобы удалить Нижний индекс и/или Верхний индекс, можно щелкнуть правой кнопкой мыши по содержащему их выражению и выбрать из контекстного меню пункт Удалить верхний индекс/нижний индекс. Если выражение содержит индексы, расположенные перед текстом, доступна опция Удалить индексы.
- Чтобы удалить Скобки, можно щелкнуть правой кнопкой мыши по выражению в скобках и выбрать из контекстного меню пункт Удалить вложенные знаки или Удалить вложенные знаки и разделители.
- Если выражение в Скобках содержит несколько аргументов, можно щелкнуть правой кнопкой мыши по аргументу, который требуется удалить, и выбрать из контекстного меню пункт Удалить аргумент.
- Если в Скобках заключено несколько уравнений (а именно, в Наборах условий), можно щелкнуть правой кнопкой мыши по уравнению, которое требуется удалить, и выбрать из контекстного меню пункт Удалить уравнение. Эта опция также доступна для уравнений других типов, в которых вы ранее добавили новые поля для заполнения путем нажатия на Enter.
- Чтобы удалить Предел, можно щелкнуть по нему правой кнопкой мыши и выбрать из контекстного меню пункт Удалить предел.
- Чтобы удалить Диакритический знак, можно щелкнуть по нему правой кнопкой мыши и выбрать из контекстного меню пункт Удалить диакритический знак, Удалить символ или Удалить черту (доступные опции отличаются в зависимости от выбранного диакритического знака).
- Чтобы удалить строку или столбец Матрицы, можно щелкнуть правой кнопкой мыши по полю для заполнения внутри строки/столбца, который требуется удалить, выбрать из контекстного меню пункт Удалить, а затем — Удалить строку/столбец.
Преобразование уравнений
Если вы открываете существующий документ с уравнениями, которые были созданы с помощью старой версии редактора уравнений (например, в версиях, предшествующих MS Office 2007), эти уравнения необходимо преобразовать в формат Office Math ML, чтобы иметь возможность их редактировать.
Чтобы преобразовать уравнение, дважды щелкните по нему. Откроется окно с предупреждением:
Чтобы преобразовать только выбранное уравнение, нажмите кнопку Да в окне предупреждения. Чтобы преобразовать все уравнения в документе, поставьте галочку Применить ко всем уравнениям и нажмите кнопку Да.
После преобразования уравнения вы сможете его редактировать.
Вернуться на предыдущую страницу
Попробуйте бесплатно Попробуйте и примите решение Не нужно ничего устанавливать,
чтобы увидеть все функции в действии
2.3: Удаление дробей и десятичных знаков
1. Последнее обновление
2. Сохранить как PDF
Идентификатор страницы
19858

Дэвид Арнольд
Колледж Редвудс

В этом разделе мы познакомим вас с методами, которые убирают дроби и десятичные дроби из уравнений, что значительно упрощает решение полученного уравнения. При очистке дробей от уравнения вам нужно будет упростить продукты, подобные тем, которые представлены в следующих примерах.

Пример \(\PageIndex{1}\)

Упрощение: \(12\left(\dfrac{2}{3} x\right)\).

Решение

Когда мы умножаем три числа, такие как \(12\), \(2/3\) и \(x\), ассоциативное свойство умножения говорит нам, что не имеет значения, какие два числа числа, которые мы сначала умножаем. Мы используем свойство ассоциативности для перегруппировки, затем перемножаем числители и знаменатели и упрощаем результат.

\[\begin{align} 12\left(\dfrac{2}{3} x\right) &=\left(12 \cdot \dfrac{2}{3}\right) x \quad \color{ Red} \text{Ассоциативное свойство умножения.}\\ &=\dfrac{24}{3} x \quad \color{Red} \text { Умножить: } 12 \cdot 2=24 \\ &=8 x \ quad \color{Red} \text { Разделить: } 24 / 3=8 \end{aligned} \nonumber \]

Упражнение \(\PageIndex{1}\)

Упрощение: \(15\left(\dfrac{3}{5} x\right)\).

Ответить: \(9х\)

В примере \(\PageIndex{1}\) показаны все шаги, необходимые для получения ответа. Однако целью этого раздела является выполнение этого расчета в уме. Поэтому мы просто «умножаем \(12\) и \(2\), чтобы получить \(24\), затем делим \(24\) на \(3\), чтобы получить \(8\)». Такой подход позволяет нам записать ответ, не выполняя никакой работы.

\[12\влево(\dfrac{2}{3} х\вправо)=8 х \номер \]

Вы должны практиковаться в этом вычислении в уме, пока не сможете записать ответ, не записывая шагов.

Пример \(\PageIndex{2}\)

Упрощение: \(18 \left(\dfrac{2}{9} x\right)\).

Решение

На этот раз мы производим расчеты в уме. Умножьте \(18\) и \(2\), чтобы получить \(36\), затем разделите \(36\) на \(9\), чтобы получить \(4\).

\[18\влево(\dfrac{2}{9} x\вправо)=4 x \не число \]

Упражнение \(\PageIndex{2}\)

Упрощение: \(14 \left(\dfrac{3}{7} x\right)\).

Ответить: \(6x\)

Чем больше число, тем сложнее считать в уме. Например, рассмотрим \[72\left(\dfrac{8}{9} x\right) \nonumber \]

В этом случае работа «умножить \(72\) и \(8\), чтобы получить \(576\), затем разделить \(576\) на \(9\), чтобы получить \(64\)» немного трудно держать в голове. Однако тут на помощь приходит калькулятор.

Пример \(\PageIndex{3}\)

Используйте калькулятор, чтобы упростить \(72 \left(\dfrac{8}{9)} х\справа)\).

Решение

С помощью калькулятора умножьте \(72\) и \(8\), затем разделите на \(9\). Введите 72*8/9 и нажмите клавишу ENTER.

Таким образом, \(72\влево(\dfrac{8}{9} x\вправо)=64 x\).

Упражнение \(\PageIndex{3}\)

Используйте калькулятор для упрощения: \(81 \left(\frac{5}{9} x\right)\).

Ответить: \(45х\)

Отмена более эффективна

В примерах \(\PageIndex{1}\), \(\PageIndex{2}\) и \(\PageIndex{3}\) мы умножали числители, а затем делили на единственный знаменатель. Мы также увидели, что немного трудно удерживать работу в голове, когда числа становятся все больше. В главе 1, разделе 3 мы видели, что отмена уменьшает размер чисел и упрощает работу.

Пример \(\PageIndex{4}\)

Упрощение: \(72 \left(\dfrac{8}{9} x\right)\).

Решение

В примере \(\PageIndex{3}\) мы использовали наш калькулятор для умножения \(72\) и \(8\), чтобы получить \(576\), затем разделили \(576\ ) на \(9\), чтобы получить \(64\). В этом решении мы делим \(9\) на \(72\), чтобы получить \(8\), затем умножаем \(8\) на \(8\), чтобы получить \(64\). Мы получаем тот же ответ, но поскольку промежуточные числа намного меньше, вычисления в уме проводить намного проще.

\[\begin{align} 72\left(\dfrac{8}{9} x\right) &=\left(72 \cdot \dfrac{8}{9}\right) x \quad \color{ Красный} \text{Ассоциативное свойство умножения}\\ &=(8 \cdot 8) x \quad \color{Красный} \text { Разделить: } 72 / 9=8 \\ &=64 x \quad \color{ Красный} \text { Умножить: } 8 \cdot 8=64 \end{выровнено} \nonumber \]

Упражнение \(\PageIndex{4}\)

Упрощение: \(64 \left(\dfrac{5}{8} x\right)\).

Ответить: \(40х\)

Пример \(\PageIndex{4}\) показывает все шаги, необходимые для получения ответа. Опять же, цель этого раздела состоит в том, чтобы выполнить это вычисление в уме, поэтому мы просто «разделим \(9\) на \(72\), чтобы получить \(8\), затем умножим \(8\) на \(8\). ), чтобы получить \(644\)».

\[72\left(\frac{8}{9} x\right)=64 x \nonnumber \]

Такой подход не только позволяет нам записать ответ без выполнения какой-либо работы, но и в численных расчетах используются меньшие числа. Вы должны практиковать этот умственный расчет, пока не сможете записать ответ, не записывая никаких шагов.

Пример \(\PageIndex{5}\)

Упрощение: \(27\left(\dfrac{5}{9} x\right)\).

Решение

Разделите \(9\) на \(27\), чтобы получить \(3\), затем умножьте \(3\) на \(5\), чтобы получить \(15\). \[27\влево(\dfrac{5}{9} x\right)=15 x \nonumber \]

Упражнение \(\PageIndex{5}\)

Упрощение: \(18\left(\dfrac{3}{2} x\right)\).

Ответить: \(27х\)

Примечание

Техника, показанная в примерах \(\PageIndex{4}\) и \(\PageIndex{5}\), будет использоваться в оставшейся части этого раздела. Деление (сокращение) сначала гораздо эффективнее, поскольку меньшие числа позволяют нам производить вычисления в уме.

Удаление дробей из уравнения

Теперь, когда мы выполнили необходимую работу с дробями, теперь мы можем сосредоточиться на очистке дробей из уравнения. Как только дроби удалены из уравнения, полученное эквивалентное уравнение решить намного проще, чем исходное.

Удаление дробей из уравнения

Чтобы удалить дроби из уравнения, умножьте обе части уравнения на наименьший общий знаменатель.

Пример \(\PageIndex{6}\)

Добавьте сюда текст.

Решение

Добавьте сюда текст.

Упражнение \(\PageIndex{6}\)

Добавьте сюда текст упражнений.

Ответить: Добавьте сюда текст. Не удаляйте этот текст первым.

	[латекс]\Large\frac{1}{8}\normalsize x+\Large\frac{1}{2}=\Large\frac{1}{4}\normalsize\quad{LCD=8}[/latex ]
Умножьте обе части уравнения на этот LCD, [латекс]8[/латекс]. Это очищает дроби.	[латекс]\color{red}{8(}\Large\frac{1}{8}\normalsize x+\Large\frac{1}{2}\color{red}{)}=\normalsize\color{ красный {8(}\Large\frac{1}{4}\color{red}{)}[/latex]
Используйте Распределительное свойство.	[латекс]8\cdot\Large\frac{1}{8}\normalsize x+8\cdot\Large\frac{1}{2}\normalsize=8\cdot\Large\frac{1}{4} [/латекс]
Упростите — и заметьте, больше никаких дробей!	[латекс]x+4=2[/латекс]
Решите, используя общую стратегию решения линейных уравнений.	[латекс]x+4\цвет{красный}{-4}=2\цвет{красный}{-4}[/латекс]
Упрощение.	[латекс]x=-2[/латекс]
Проверить: Пусть [латекс]x=-2[/латекс][латекс] \большой\фрак{1}{8}\нормальный размер х+ \большой\фракция{1}{2}= \большой\фракция{1 {4}[/латекс] [латекс] \Large\frac{1}{8}\normalsize(\color{red}{-2})+ \Large\frac{1}{2}\normalsize\stackrel{\text{?}}{ =} \Large\frac{1}{4}[/latex] [латекс] \Large\frac{-2}{8}+ \Large\frac{1}{2}\normalsize\stackrel{\text{?}}{=} \Large\frac{1}{4} [/латекс] [латекс] \Large\frac{-2}{8}+ \Large\frac{4}{8}\normalsize\stackrel{\text{?}}{=} \Large\frac{1}{4} [/латекс] [латекс] \Large\frac{2}{8}\normalsize\stackrel{\text{?}}{=} \Large\frac{1}{4}[/latex] [латекс] \Large\frac{1}{4}= \Large\frac{1}{4}\quad\checkmark[/latex]

Как избавиться от знаменателя в дроби

Как решать дробные уравнения?

Как решать уравнения с дробями. Показательное решение уравнений с дробями.

Решение уравнений с дробями

Основные свойства дробей

Понятие уравнения

Понятие дробного уравнения

Как решать уравнения с дробями

1. Метод пропорции

2. Метод избавления от дробей

Что еще важно учитывать при решении

Универсальный алгоритм решения

Примеры решения дробных уравнений

как решать, алгоритм, примеры с ответами для 9 класса

Что такое дробно-рациональные уравнения

Как решаются дробно-рациональные уравнения

Примеры задач с ответами для 9 класса

Вставка уравнений — ONLYOFFICE

Добавление нового уравнения

Ввод значений

Форматирование уравнений

Удаление элементов уравнения

Преобразование уравнений

2.3: Удаление дробей и десятичных знаков

Отмена более эффективна

Удаление дробей из уравнения

Решение уравнений путем удаления дробей

Результаты обучения

ПРИМЕР

Попробуй

Решите уравнения, очистив знаменатели

Пример

Попробуйте

Внимание!

Пример

Попробуйте

ПРИМЕР

Попробуйте

Как избавиться от показателей в алгебраическом уравнении

Упрощение и комбинирование похожих членов

Ищите возможности разложения на множители

Изолировать и применить радикал

Добавить комментарий Отменить ответ