Решение
Вычисление матрицы $D$ начнем с нахождения результата произведения $AB$. Матрицы $A$ и $B$ можно перемножать, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. Обозначим $F=AB$. При этом матрица $F$ будет иметь три столбца и три строки, т.е. будет квадратной (если этот вывод кажется неочевидным, посмотрите описание умножения матриц в первой части этой темы). Найдем матрицу $F$, вычислив все её элементы:
$$
F=A\cdot B=\left(\begin{array} {cccc}
1 & 0 & -1 & 2 \\
3 & -2 & 5 & 0 \\
-1 & 4 & -3 & 6
\end{array} \right)\cdot \left(\begin{array} {ccc}
-9 & 1 & 0 \\
2 & -1 & 4 \\
0 & -2 & 3 \\
1 & 5 & 0
\end{array} \right)\\
\begin{aligned}
& f_{11}=1\cdot (-9)+0\cdot 2+(-1)\cdot 0+2\cdot 1=-7; \\
& f_{12}=1\cdot 1+0\cdot (-1)+(-1)\cdot (-2)+2\cdot 5=13; \\
& f_{13}=1\cdot 0+0\cdot 4+(-1)\cdot 3+2\cdot 0=-3;\\ \\
& f_{21}=3\cdot (-9)+(-2)\cdot 2+5\cdot 0+0\cdot 1=-31;\\
& f_{22}=3\cdot 1+(-2)\cdot (-1)+5\cdot (-2)+0\cdot 5=-5;\\
& f_{23}=3\cdot 0+(-2)\cdot 4+5\cdot 3+0\cdot 0=7;\\ \\
& f_{31}=-1\cdot (-9)+4\cdot 2+(-3)\cdot 0+6\cdot 1=23; \\
& f_{32}=-1\cdot 1+4\cdot (-1)+(-3)\cdot (-2)+6\cdot 5=31;\\
& f_{33}=-1\cdot 0+4\cdot 4+(-3)\cdot 3+6\cdot 0=7.
Умножим матрицы в правой части равенства на соответствующие числа (т.е. на 2, 3 и 7):
$$ 2\cdot \left(\begin{array} {ccc} -7 & 13 & -3 \\ -31 & -5 & 7 \\ 23 & 31 & 7 \end{array} \right)-3\cdot \left(\begin{array} {ccc} -5 & 10 & 3 \\ -20 & 12 & -15 \\ 13 & 9 & 8 \end{array} \right)+7\cdot \left(\begin{array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)=\\= \left(\begin{array} {ccc} -14 & 26 & -6 \\ -62 & -10 & 14 \\ 46 & 62 & 14 \end{array} \right)-\left(\begin{array} {ccc} -15 & 30 & 9 \\ -60 & 36 & -45 \\ 39 & 27 & 24 \end{array} \right)+\left(\begin{array} {ccc} 7 & 0 & 0 \\ 0 & 7 & 0 \\ 0 & 0 & 7 \end{array} \right) $$
Выполним последние действия: вычитание и сложение:
$$
\left(\begin{array} {ccc}
-14 & 26 & -6 \\
-62 & -10 & 14 \\
46 & 62 & 14
\end{array} \right)-\left(\begin{array} {ccc}
-15 & 30 & 9 \\
-60 & 36 & -45 \\
39 & 27 & 24
\end{array} \right)+\left(\begin{array} {ccc}
7 & 0 & 0 \\
0 & 7 & 0 \\
0 & 0 & 7
\end{array} \right)=\\
=\left(\begin{array} {ccc}
-14-(-15)+7 & 26-30+0 & -6-9+0 \\
-62-(-60)+0 & -10-36+7 & 14-(-45)+0 \\
46-39+0 & 62-27+0 & 14-24+7
\end{array} \right)=
\left(\begin{array} {ccc}
8 & -4 & -15 \\
-2 & -39 & 59 \\
7 & 35 & -3
\end{array} \right).
Ответ: $f(A)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right)$.
Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
а в 1 степени матрица
Вы искали а в 1 степени матрица? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и а в степени 1 матрица, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «а в 1 степени матрица».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как а в 1 степени матрица,а в степени 1 матрица,возведение в квадрат матрицы,возведение в степень 1 матрицы,возведение в степень матриц,возведение в степень матрицы,возведение матриц в степень,возведение матрицы в 1 степень,возведение матрицы в квадрат,возведение матрицы в степень,возведение матрицы в степень 1,возвести в квадрат матрицу,возвести в степень матрицу,возвести матрицу в квадрат,возвести матрицу в степень,как возвести в квадрат матрицу,как возвести в куб матрицу,как возвести матрицу в 1 степень,как возвести матрицу в квадрат,как возвести матрицу в куб,как возвести матрицу в минус 1 степень,как возвести матрицу в степень,как возвести матрицу в степень 1,как возвести матрицу в степень минус 1,как возводить в квадрат матрицу,как возводить в степень матрицу,как возводить матрицу в квадрат,как возводить матрицу в степень,как матрицу возвести в 1 степень,как матрицу возвести в квадрат,как матрицу возвести в куб,как матрицу возвести в степень,как матрицу возводить в квадрат,как найти матрицу а в минус 1 степени,как найти матрицу в 1 степени,квадрат матрицы,матрица 2 на 2 обратная,матрица а в 1 степени,матрица а в минус первой степени,матрица а в степени 1,матрица в 1 степени,матрица в 1 степени онлайн,матрица в 1 степени пример,матрица в квадрате,матрица в квадрате онлайн,матрица в квадрате пример,матрица в кубе,матрица в минус 1 степени,матрица в минус первой,матрица в минус первой степени,матрица в минус первой степени решение онлайн,матрица в отрицательной степени,матрица в степени,матрица в степени 1,матрица в степени 1 онлайн,матрица в степени минус 1,матрицу возвести в квадрат,матрицу возвести в степень,матрицу возвести в степень онлайн,матрицы степень,обратная 2 на 2 матрица,обратная матрица 2 на 2,онлайн возведение матрицы в квадрат,онлайн матрица в квадрате.
Решить задачу а в 1 степени матрица вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Видео с вопросами: Возведение матрицы в квадрат и куб ноль, ноль, ноль, пять, ноль, ноль, ноль, два. Затем нам нужно найти 𝐴 в квадрате, а затем используйте это, чтобы найти 𝐴 в кубе.
Ну, сколько будет 𝐴 в квадрате
это матрица один, ноль, ноль, ноль, пять, ноль, ноль, ноль, два, умноженная на
матрица один, ноль, ноль, ноль, пять, ноль, ноль, ноль, два.
И мы знаем, что они могут быть
умножаются друг на друга, потому что количество столбцов в матрице один такое же, как
количество строк в матрице два. И это потому, что они оба,
на самом деле, матрицы три на три. И поэтому наш результат также
будет матрица три на три.
Теперь, чтобы рассчитать первый элемент в нашей матрице будет, что мы делаем, так это умножаем соответствующие элементы из первой строки нашей первой матрицы и первого столбца нашей второй матрицы, а затем сложить их вместе. Итак, у нас есть один, умноженный на один плюс ноль умножить на ноль плюс ноль умножить на ноль.
Итак, из следующего элемента
вместе, на этот раз мы смотрим на второй столбец в нашей второй матрице. Итак, на этот раз у нас будет
единица, умноженная на ноль, ноль, умноженная на пять, и ноль, умноженная на ноль. Итак, наконец, напоследок
элемент в нашей первой строке, то, что у нас будет, это единица, умноженная на ноль, нуль
умножить на ноль, а ноль умножить на два.
Хорошо, отлично. Итак, теперь у нас есть процесс. Мы используем это только для заполнения остальная часть матрицы. Итак, когда мы переходим к следующей строке вниз, мы просто перемещаем строку вниз в первой матрице, а затем перезапустите сначала с первого столбца во второй матрице. Значит ноль умножить на один плюс пять умножить на ноль плюс ноль умножить на ноль. Итак, мы просто продолжаем нашу шаблон и используйте его, чтобы завершить нашу матрицу. Итак, мы сделали это здесь. Итак, теперь у нас есть все расчеты на месте.
Теперь нам нужно сделать следующее.
вычислить каждый из элементов нашей матрицы 𝐴 в квадрате. Ну, наш первый элемент один
потому что мы получили один плюс ноль плюс ноль, затем ноль, затем снова ноль. Итак, это наш первый ряд
полный.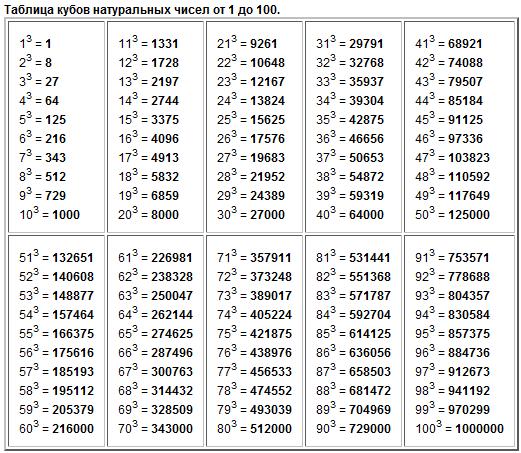
А затем для нашего второго ряда мы
собираюсь получить ноль, 25 и ноль. Итак, для нашего последнего ряда мы
собираешься получить ноль, ноль, четыре. Так здорово, мы нашли нашу матрицу для
𝐴 в квадрате. И это один, ноль, ноль, ноль,
25, ноль, ноль, ноль, четыре.
Итак, теперь нам нужно двигаться на 𝐴 в кубе. Ну а чтобы найти 𝐴 в кубе, что это будет равно матрице для квадрата 𝐴, умноженной на матрицу для 𝐴. Так что это будет матрица один, ноль, ноль, ноль, 25, ноль, ноль, ноль, четыре, умноженные на матрицу один, ноль, ноль, ноль, пять, ноль, ноль, ноль, два. И мы делаем это так же, как мы перемножил две матрицы ранее.
Чтобы быстро напомнить нам, у нас есть
посмотрите на первый элемент. Итак, что мы делаем, так это умножаем
соответствующие элементы из первой строки первой матрицы и первого столбца
второй матрицы и сложим их вместе.
Итак, мы получаем единицу, умноженную на
один добавить ноль, умножить на ноль добавить ноль, умножить на ноль. Итак, мы используем этот метод для переноса
для завершения остальной части нашей матрицы. Итак, мы видим здесь, что мы написали
все расчеты, которые нам нужны. Итак, наша первая строка матрицы 𝐴
в кубе будет единица, ноль, ноль. В следующей строке будет ноль, 125,
нуль. Так что это даст нам последний ряд
ноль, ноль, восемь.
Отлично, мы смогли решить проблема, потому что мы можем сказать, что если мы возьмем матрицу 𝐴, которая равна единице, нулю, нулю, ноль, пять, ноль, ноль, ноль, два, тогда 𝐴 в квадрате будет единица, ноль, ноль, ноль, 25, ноль, ноль, ноль, четыре. И 𝐴 в кубе будет единица, ноль, ноль, ноль, 125, ноль, ноль, ноль, восемь.
Обзор | RGB LED Matrix Cube с 25 000 светодиодов
Обзор
Сохранить Подписаться
Пожалуйста, войдите, чтобы подписаться на это руководство.
После входа в систему вы будете перенаправлены обратно к этому руководству и сможете подписаться на него.
Светодиодов никогда не бывает слишком много… но мы не позволим этому помешать нам попробовать . Этот проект объединяет почти 25 000 полноцветных светодиодов в завораживающем, автономном интерактивном кубе, а маленький и могучий Raspberry Pi 4 — Altoid компьютеров — управляет шоу. Возможно, самый показной проект, который мы когда-либо пробовали!
- Ваш браузер не поддерживает видео тег.
3D PixelDust
Демонстрация плавного пиксельного песка использует акселерометр для создания завораживающего эффекта движения.
Песчинки стекают вниз и перемещаются по всем шести панелям, что делает эту физическую игрушку непохожей ни на что другое.
Необычное руководство
ВАЖНО: мы присвоили этому руководству редкую рекомендацию уровня «Продвинутый». Не то, чтобы это было особенно глубоко или технично, но мы должны признать, что это дорого. Почти в любой день мы праздновали обучение на ошибках новичков… но здесь один неверный шаг, например подключение неправильного источника питания, может разрушить сотен по частям. Это лучше всего подходит для людей, которые опытным путем выработали терпение и тщательность.
Эта сборка также необычна тем, что она нелинейная, с несколькими циклическими этапами между 3D-печатью, пайкой и подключением, установкой и тестированием кода… это не просто одно за другим. Это позволяет проводить тестирование и устранение неполадок при первой возможности, пока все открыто, чтобы избежать длительных неудач позже (см. «Терпение и тщательность благодаря опыту» выше). А начиная с 3D-печати, можно выполнять многозадачность… вы можете начать работу, пока электроника находится в пути, и выполнить начальное тестирование платы и кода по мере постепенного продвижения печати.
Перед совершением пролистайте руководство, чтобы узнать, что все это влечет за собой.
Уход и кормление вашего куба
Это один из наших самых амбициозных проектов «сделай сам», с большим количеством дорогостоящих деталей и точных допусков, и вам нужно заботиться о нем . Светодиодные матрицы предназначены для цифровых вывесок, а не для портативного использования. При грубом обращении отдельные светодиоды могут быть срезаны по краям и углам. Остальная часть матрицы все равно будет работать, будут только белые пятна и вам будет немного грустно.
Следовательно:
- Поднимите куб обеими руками вплотную к граням, не по краям. Аккуратно передайте его от плоской ладони к плоской ладони.
- Аккуратно откройте куб с помощью пластиковой лопатки, не царапайте его пальцами. Гитарный медиатор, старая кредитная или транспортная карта могут отлично сработать!
- Сопротивляйтесь непреодолимому желанию раскрутить кубик пальцами на противоположных углах.
Детали от Adafruit
Ваш браузер не поддерживает видео тег.Светодиодная матричная RGB-панель 64×64 с шагом 2 мм
Зима в городе может быть суровой. Небо серое. Погода непредсказуема. Так что избавьтесь от сезонной хандры с помощью ослепления Таймс-сквер…
Светодиодная матричная RGB-панель 64×64 с 45-градусным срезом бордюра — шаг 2,5 мм
Зимой в городе может быть сурово. Небо серое. Погода непредсказуема. Так что избавьтесь от этой сезонной хандры с ослепительным блеском Таймс-сквер из этого…
Матричная крышка Adafruit RGB для Raspberry Pi
Теперь вы можете создать ослепительный дисплей с Raspberry Pi с помощью матричной крышки Adafruit RGB Matrix. Эти платы подключаются к вашему Pi и делают его превосходным…
Raspberry Pi 4, модель B — 2 ГБ ОЗУ
ПРИМЕЧАНИЕ. Из-за ограниченного запаса мы можем предложить возмещение или сохранить кредит только для Pi, которые неисправны, повреждены или потерянный в.
..
Трехосевой акселерометр Adafruit LIS3DH (+-2g/4g/8g/16g)
LIS3DH — очень популярный трехосевой акселерометр с низким энергопотреблением. Это недорого, но в нем есть почти все «дополнительные функции», которые вам нужны…
2 х Шина распределения питания
Цельная латунь диаметром 7 x 6 мм
В корзину 2 шт.
1 х Adafruit RGB Matrix HAT + RTC для Raspberry Pi
Adafruit RGB Matrix HAT + RTC для Raspberry Pi
Добавить в корзину
1 х Кабель USB-C на USB-A
Черный плетеный прямоугольный кабель USB C на USB A, длина 0,2 м
Нет в наличии
1 х STEMMA QT / Qwiic JST SH 4-контактный кабель для вилки премиум-класса
Длина 150 мм
Добавить в корзину
1 х Комплект крепежных деталей M2.5 из черного нейлона
Комплект крепежных деталей M2.
5 из черного нейлона
Добавить в корзину
1 х Комплект крепежных деталей M3 из черного нейлона
Комплект крепежных деталей M3 из черного нейлона
Добавить в корзину
Детали из других источников
1 х Неодимовые магниты
Диаметр 1/4 дюйма x толщина 1/8 дюйма 1D42 – Количество x48
Купить
2 х Батарея USB 5 В 3 А
Батарея USB 10000 мАч
Купить сейчас
1 х Кабель USB-A/DC
Разъем USB-Darrel Jack Штекер постоянного тока 5 В Кабель питания 2,1 мм
Купить
Вам также понадобится
- Паяльник и сопутствующие принадлежности. Там очень мало пайки требуется, но не ноль.
- Основные инструменты для изготовления, такие как плоскогубцы и небольшие отвертки (для винтовых клемм питания постоянного тока).
- Пластиковый инструмент «spudger» для открывания собранного куба или импровизированный эквивалент (гитарный медиатор, старая кредитная карта), возможно, шлифование одного края для лучшей подачи в узкие щели.
