Глава 02. Действия над матрицами
1. Сложение матриц.
Пусть
|
; . |
(1.2.1) |
Суммой двух матриц A и B одинаковой размерности называется матрица C = A + B той же размерности, элементы которой равны сумме соответствующих элементов матриц A и B, т. е.
|
(I= 1, 2, …, N; K= 1, 2, …, M). |
(1.2.2) |
Пример
, , .
2. Умножение матрицы на число.
Произведением матрицы A на число l называется матрица C = lA, элементы которой равны элементам матрицы A, умноженным на число l, т. е.
|
, (I= 1, 2, …, N; K= 1, 2, …, M). |
(1. |
Матрица –A = (–1)×A называется противоположной матрице A. Очевидно, что A + (–A) = 0, где 0 – нулевая матрица той же размерности, что и матрица A.
Легко проверить, что операции сложения матриц и умножения матрицы на число, называющиеся линейными операциями, обладают следующими свойствами:
|
(1.2.4) | |
3. Вычитание матриц.
Разностью матриц A и B одинаковой размерности называется такая матрица C = A – B, сумма которой с матрицей B равна матрице A.
|
(1. |
2.5)Чтобы получить матрицу C = A – B, достаточно из элементов матрицы A вычесть соответствующие элементы матрицы B:
|
(i= 1, 2, …, n; k= 1, 2, …, m). |
(1.2.7) |
4. Умножение матриц.
Произведением двух матриц A и B, заданных в указанном порядке, называется такая матрица С = A×B, каждый элемент которой Cik равен сумме произведений элементов I–ой строки матрицы A на соответствующие элементы K–го столбца матрицы B.
Матрицы A и B можно перемножить, если количество элементов в строке матрицы A равно количеству элементов в столбце матрицы
Пример
; . Найти A×B.
Решение
Замечание
Произведение матриц BA рассмотренных в приведенном выше примере, не существует, т.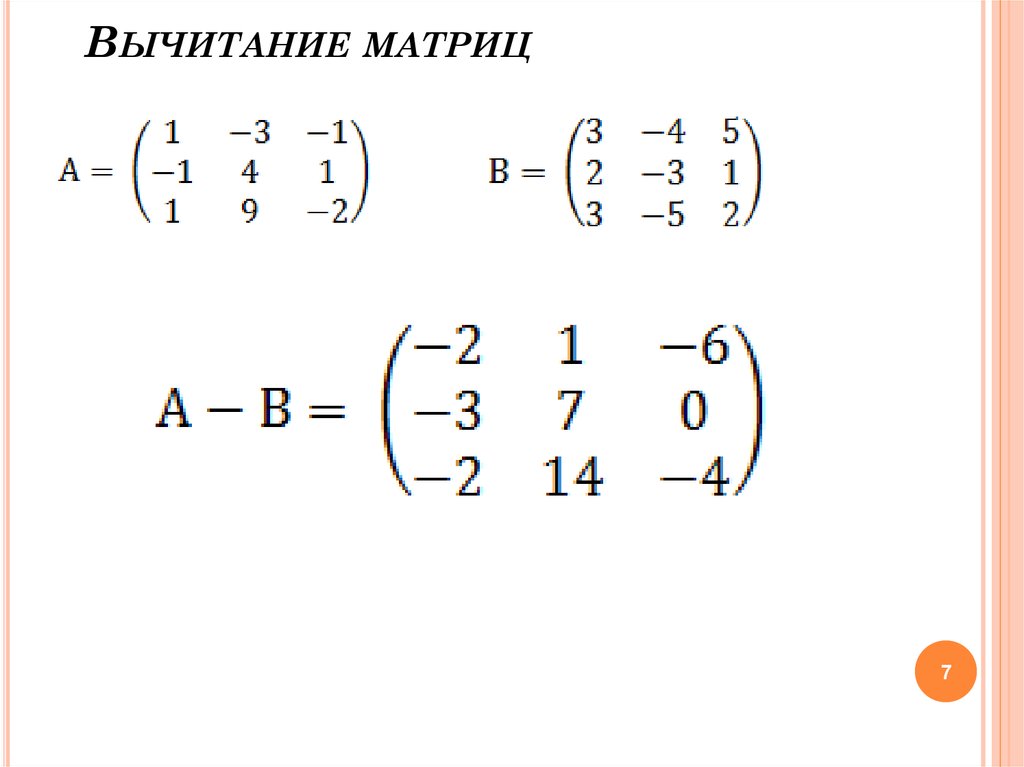
к. число столбцов (2) матрицы B (первого множителя) не равно числу строк (3) матрицы A (второго множителя).
Пример
Найти A×B и B×A.
Решение
, .
Как видим из примера, A×B ¹ B×A, т. е. произведение матриц не обладает коммутативным свойством.
Свойства произведения матриц:
|
(1.2.8) | |
| < Предыдущая | Следующая > |
|---|
Операции (действия) над матрицами — Vmatematika.ru
Сами по себе матрицы, как таблицы чисел, не представляли бы никакого интереса, если бы с ними не возможно было производить действия.
В этой статье мы познакомимся с основными действиями (операциями) над матрицами: сложением и вычитанием матриц, умножением матрицы на число, умножением матриц, транспонированием матриц.
Содержание Сложение матриц Сумма матриц Пример нахождения суммы матриц Вычитание матриц Разность матриц Пример нахождения разности матриц Умножение матрицы на число (скаляр) Произведение матрицы на число Пример нахождения произведения матрицы на число (скаляр) Противоположная матрица Теорема о единственности противоположной матрицы Свойства операций сложения, вычитания и умножения матриц на число Умножение матриц Произведение матриц Пример нахождения произведения матриц Перестановочные матрицы Свойства операции умножения матриц Транспонирование матриц Пример транспонирования матрицы Элементарные преобразования над матрицами Каноническая форма матрицы
На множестве матриц одного и того же размера можно ввести внутреннюю бинарную операцию сложение матриц, при такой операции двум матрицам и одинакового размера ставится в соответствие матрица того же размера, матрицу-результат будем называть суммой матриц и обозначать
Определение 1.
Суммой матриц и называется матрица где каждый элемент т.е.
Таким образом, для нахождения суммы матриц надо сложить их соответствующие элементы.
Например,
Аналогичным образом на множестве матриц одного и того же размера вводится внутренняя бинарная операция вычитание матриц, при такой операции двум матрицам и одинакового размера ставится в соответствие матрица того же размера, матрицу-результат будем называть разностью матриц и и для обозначения использовать запись
Определение 2. Разностью матриц и называется матрица где т.е.
Таким образом, для нахождения разности двух матриц надо от элементов первой матрицы вычесть соответствующие элементы второй матрицы.
Например,
На множестве матриц введем внешнюю бинарную операцию умножение матрицы на число, при такой операции матрице и числу ставится в соответствие матрица того же размера, что и матрица Матрицу-результат будем называть произведением матрицы
Определение 3.
Произведением матрицы на число называется матрица где т.е.
Таким образом, для нахождения произведения матрицы на число надо каждый элемент матрицы умножить на число
Например,
Противоположная матрица
Определение 4. Противоположной матрицей к матрице называется матрица, обозначаемая такая, что где — нулевая матрица того же размера, что и матрица
Теорема 1. Каждая матрица имеет единственную противоположную матрицу, причем
Доказательство. Пусть произвольная матрица. Тогда из задания операций сложения матриц и умножения матрицы на число, следует, что для матрицы существует противоположная матрица
Докажем единственность противоположной матрицы. Предположим, что матрица имеет противоположную матрицу отличную от матрицы Тогда
Мы получили, что каждый элемент матрицы равен соответствующему элементу матрицы а значит, матрицы и равны.
Полученное противоречие (по предположению матрицы и не равны) доказывает то, что у матрицы не существует противоположной матрицы отличной от
Разность матриц и можно определить через сумму матрицы и противоположной матрицы
Пусть и произвольные матрицы размера а и любые действительные числа, тогда справедливы следующие утверждения.
На множестве матриц вводится операция (действие) умножение матриц. При умножении матрицы размера и матрицы размера им ставится в соответствие матрица размера называемая произведением матрицы на матрицу
Определение 5. Произведением матрицы на матрицу называется матрица где
Таким образом, для того чтобы найти матрицу-произведение надо вычислить все ее элементы. При этом, для элемента находящегося в -ой строке и -ом столбце матрицы-произведения (матрицы ), надо взять элементы -ой строки первой матрицы (матрицы ) и умножить их на соответствующие элементы -го столбца второй матрицы (матрицы ), полученные произведения следует сложить (рис.
1). Произведение можно найти лишь в том случае, когда количество столбцов матрицы совпадает с количеством строк матрицы У матрицы-произведения количество строк совпадает с количеством строк первой матрицы (матрицы ), а количество столбцов совпадает с количеством столбцов второй матрицы (матрицы ).
Рис. 1
Заметим, что произведение в общем случае не совпадает с произведением более того, иногда одно из этих произведений может и не существовать.
Например, для матриц
произведение
В этом примере произведение не определено, так как у матрицы число столбцов — 3, а у матрицы две строки.
Определение 6. Если то матрицы и называются перестановочными матрицами.
Свойства операции умножения матриц
Каждой матрице размера можно поставить в соответствие транспонированную матрицу размера у которой каждая строка с номером будет состоять из элементов (в порядке их следования) столбца с номером матрицы Такая операция называется транспонированием матрицы.
Например,
Выделим преобразования матрицы, которые принято называть элементарными:
- Перестановка местами строк (столбцов) матрицы;
- Умножение или деление на ненулевое число всех элементов строки (столбца) матрицы;
- Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца) умноженных на один и тот же скаляр (число).
Определение 7. Если матрица получается из матрицы с помощью элементарных преобразований, то матрицы и называются эквивалентными матрицами.
Если матрицы и эквивалентны, то это будем записывать следующим образом:
Элементарные преобразования над матрицами обычно применяются для перехода от матрицы к эквивалентной ей матрице в канонической форме (матрице у которой в начале главной диагонали находятся подряд несколько единиц), что позволяет определить ранг матрицы. Так же проведение таких преобразований над строками матриц позволяет перейти от матрицы к эквивалентной ей ступенчатой матрице, что широко применяется в методе Гаусса решения систем линейных уравнений.
M2 Сложение и вычитание матриц
14 июля 2021 г., 11:06 — AJ (e67821)
Open image
Матрица — это массив чисел. Существуют правила сложения и вычитания матриц, которые рассматриваются в этом модуле. Матрицы одинаковой формы (одинаковое количество строк и столбцов) можно складывать и вычитать.
Сложение
Матрицы одинаковой формы (одинаковое количество строк и столбцов) могут быть добавлены путем добавления соответствующих элементов.
Например, пусть \[\begin{align*} A & =\left[\begin{массив}{ccc} 3 и 2 и -1\\ 1 и 5 и -4 \end{массив}\right],\,B=\left[\begin{массив}{ccc} 1 и 0 и 2\\ 3 и 1 и -2 \end{массив}\right]\;\textrm{and $C=\left[\begin{массив}{cc} 2 и -3\\ 4 и 3 \end{массив}\right]$ }. \end{align*}\] Обратите внимание, что \(A\) и \(B\) имеют одинаковую форму \(\left(2\times3\right)\), а \(C\) — это \(\left( 2\раз2\справа)\).
Тогда \(A+B\) имеет смысл, потому что они оба \(\left(2\times3\right)\), и у нас есть \[\begin{align*}
A+B & =\left[\begin{массив}{ccc}
3 и 2 и -1\\
1 и 5 и -4
\end{массив}\right]+\left[\begin{массив}{ccc}
1 и 0 и 2\\
3 и 1 и -2
\конец{массив}\справа]\\
& =\left[\begin{массив}{ccc}
3+1 и 2+0 и -1+2\\
1+3 и 5+1 и -4+(-2)
\конец{массив}\справа]\\
& =\left[\begin{массив}{ccc}
4 и 2 и 1\\
4 и 6 и -6
\end{массив}\right].
\end{выравнивание*}\]
Однако \(A+C\) не определено, поскольку \(A\) равно \(\left(2\times3\right)\) и \(C\) равно \(\left(2\times2\right) )\). Вы не можете добавлять матрицы, которые имеют различную форму.
Обратите внимание, что порядок сложения такой же, как и для действительных чисел. То есть: \[\begin{align*} А+В и =В+А \end{align*}\]
Вычитание
Матрицы одинаковой формы могут быть вычтены путем вычитания соответствующих элементов. Например, пусть \[\begin{align*}
A & =\left[\begin{массив}{ccc}
3 и 2 и -1\\
1 и 5 и -4
\end{массив}\right],\,B=\left[\begin{массив}{ccc}
1 и 0 и 2\\
3 и 1 и -2
\end{массив}\right]\;\textrm{and $C=\left[\begin{массив}{cc}
2 и -3\\
4 и 3
\end{массив}\right]$ }.
\end{align*}\] Тогда \(AB\) имеет смысл, потому что они оба \(\left(2\times3\right)\), и у нас есть \[\begin{align*}
AB & =\left[\begin{массив}{ccc}
3 и 2 и -1\\
1 и 5 и -4
\end{массив}\right]-\left[\begin{массив}{ccc}
1 и 0 и 2\\
3 и 1 и -2
\конец{массив}\справа]\\
& =\left[\begin{массив}{ccc}
3-1 и 2-0 и -1-2\\
1-3 и 5-1 и -4-(-2)
\конец{массив}\справа]\\
& =\left[\begin{массив}{ccc}
2 и 2 и -3\\
-2 и 4 и -2
\end{массив}\right].
\end{выравнивание*}\]
Однако \(A-C\) не определяется, поскольку \(A\) равно \(\left(2\times3\right)\) и \(C\) равно \(\left(2\times2\right)\ ). Вы не можете вычесть матрицы, которые имеют различную форму. В качестве другого примера рассмотрим \(BA\), у нас есть \[\begin{alignat*}{1} BA & =\left[\begin{массив}{ccc} 1 и 0 и 2\\ 3 и 1 и -2 \end{массив}\right]-\left[\begin{массив}{ccc} 3 и 2 и -1\\ 1 и 5 и -4 \конец{массив}\справа]\\ & =\left[\begin{массив}{ccc} 1-3 и 0-2 и 2-(-1)\\ 3-1 и 1-5 и -2-(-4) \конец{массив}\справа]\\ & =\left[\begin{массив}{ccc} -2 и -2 и 3\\ 2 и -4 и 2 \конец{массив}\справа] \end{alignat*}\] Обратите внимание, что \(A-B\neq B-A\). Порядок вычитания матриц важен так же, как и при вычитании действительных чисел. На самом деле, \(B-A=-\left(A-B\right)\).
Скалярное умножение
Матрицы можно умножать на числа. Для этого каждый элемент матрицы умножается на число.
Например, пусть \[\begin{align*}
A & =\left[\begin{массив}{cc}
1 и 2\\
5 и 4
\end{массив}\right]\textrm{ и $B=\left[\begin{массив}{cc}
2 и -3\\
0 и -1
\end{массив}\right]$ }
\end{align*}\], затем \[\begin{align*}
5A & =5\times\left[\begin{массив}{cc}
1 и 2\\
5 и 4
\конец{массив}\справа]\\
& =\left[\begin{массив}{cc}
5\раз1 и 5\раз2\\
5\х5 и 5\х4
\конец{массив}\справа]\\
& =\left[\begin{массив}{cc}
5 и 10\\
25 и 20
\end{массив}\right].
\end{выравнивание*}\]
Другой пример: \[\begin{align*} -2A & =-2\times\left[\begin{массив}{cc} 1 и 2\\ 5 и 4 \конец{массив}\справа]\\ & =\left[\begin{массив}{cc} -2\раз1 и -2\раз2\\ -2\х5 и -2\х4 \конец{массив}\справа]\\ & =\left[\begin{массив}{cc} -2 и -4\\ -10 и -8 \end{массив}\right]. \end{align*}\]
Вы также можете использовать скалярное умножение со сложением или вычитанием. Например: \[\begin{выравнивание*}
5A-2B & =5\times\left[\begin{массив}{cc}
1 и 2\\
5 и 4
\end{массив}\right]-2\times\left[\begin{массив}{cc}
2 и -3\\
0 и -1
\конец{массив}\справа]\\
& =\left[\begin{массив}{cc}
5\раз1 и 5\раз2\\
5\х5 и 5\х4
\end{массив}\right]-\left[\begin{массив}{cc}
2\раз2 и 2\раз\влево(-3\вправо)\\
2\times0 и 2\times\влево(-1\вправо)
\конец{массив}\справа]\\
& =\left[\begin{массив}{cc}
5 и 10\\
25 и 20
\end{массив}\right]-\left[\begin{массив}{cc}
4 и -6\\
0 и -2
\конец{массив}\справа]\\
& =\left[\begin{массив}{cc}
5-4 и 10-\влево(-6\вправо)\\
25-0 и 20-\влево(-2\вправо)
\конец{массив}\справа]\\
& =\left[\begin{массив}{cc}
1 и 16\\
25 и 22
\end{массив}\right].
\end{выравнивание*}\]
Упражнения
Учитывая \[\begin{align*} A & =\left[\begin{массив}{c} 2\\ 3 \end{массив}\right],\;B=\left[\begin{массив}{cc} 1 и 2\\ 4 и 3 \end{массив}\right],\;C=\left[\begin{массив}{cc} 5 и 3\\ -1 и 2 \end{массив}\right],\;D=\left[\begin{массив}{cc} 2 и 3\конец{массив}\справа],\;E=\влево[\начало{массив}{cc} -1 и 0\\ 2 и -1 \конец{массив}\справа], \end{align*}\] найдите, если возможно: \[\begin{align*} \begin{массив}{lllll} a)\,A+B & b)\,B-C & c)\,A-D & d)\,B+E & e)\,E-D.\end{массив} \end{выравнивание*}\]
Дано \[\begin{align*} A=\left[\begin{массив}{ccc} 2 и 3 и 1\\ 0 и 1 и 2 \end{массив}\right],\;B=\left[\begin{массив}{c} 4\\ -1\\ 2 \end{массив}\right],\;C=\left[\begin{массив}{ccc} 1 и -1 и 2\\ 2 и 0 и 1 \end{массив}\right],\;D=\left[\begin{массив}{c} 1\\ 0\\ -1 \end{массив}\right],\;E=\left[\begin{массив}{ccc} 0 и 1 и 3\\ 1 и 0 и 2 \конец{массив}\справа], \end{align*}\] найдите, если возможно: \[\begin{align*} \begin{массив}{lllll} a)\,2A+B & b)\,4D-B & c)\,3C-A & d)\,B+2D+E & e)\,3C-A+2E\end{массив}.
\end{выравнивание*}\]
Ответы
\[\begin{выравнивание*} \начать{массив}{llllll} 1. & a)\,\textrm{Невозможно} & b)\,\left[\begin{array}{cc} -4 и -1\\ 5 и 1 \end{массив}\right] & c)\,\textrm{Невозможно} & d)\,\left[\begin{массив}{cc} 0 и 2\\ 6 и 2 \end{массив}\right] & e)\,\textrm{Невозможно}.\end{массив} \end{выравнивание*}\]
\[\begin{выравнивание*} \начать{массив}{llllll} 2. & a)\,\textrm{Невозможно} & b)\,\left[\begin{array}{c} 0\\ -1\\ -6 \end{массив}\right] & c)\,\left[\begin{массив}{ccc} 1 и -6 и 5\\ 6 и -1 и 1 \end{массив}\right] & d)\,\textrm{Невозможно} & e)\,\left[\begin{array}{ccc} 1 и -4 и 11\\ 8 и -1 и 5 \конец{массив}\справа].\конец{массив} \end{выравнивание*}\]
Скачать эту страницу, M2 Сложение и вычитание матриц (PDF 110 КБ)
Что дальше… M3 Умножение матриц
Ключевые слова:
Математика
Матрицы
Объяснение вычитания матриц, Математика Unacademy
Вычитание матриц включает вычитание соответствующих элементов из двух или более матриц. Однако, прежде чем мы продолжим обсуждение вычитания матриц, давайте разберемся, что такое матрица. Матрица — это математический формат, в котором данные и элементы располагаются с помощью строк и столбцов.
Обычно вычитание матриц выполняется посредством поэлементного вычитания матриц. К матрицам можно применять различные операции, включая сложение, вычитание и умножение.
В этой статье мы сосредоточимся на подробном рассмотрении вычитания матриц. Вычитание матриц выполняется точно так же, как и сложение матриц. Это означает, что условия, применимые для сложения матриц, и аналогичные условия применяются для вычитания матриц.
Вычитание матриц
Вычитание матриц — это операция, при которой поэлементное вычитание применяется к матрицам одного порядка, что по существу означает, что вычитание между двумя матрицами может происходить только тогда, когда обе они имеют одинаковое количество строк и столбцы.
Если количество горизонтальных строк в матрице равно «m», а количество столбцов равно «n», матрица имеет порядок x n». Для вычитания матриц обе матрицы должны быть одного порядка, чтобы вычесть соответствующие элементы матриц.
Возьмем пример.
Существует матрица a = [aij] m x n и b = [bij] m x n
, так что теперь
, если a = b =
Затем
A-B =
Субтрикция матриц из порядка 2 x 2. 2
Поскольку мы знаем, что вычитание матриц возможно только тогда, когда обе матрицы имеют одинаковое количество столбцов и строк, для вычитания матриц порядка 2 x 2 матрицы должны иметь две строки и 2 столбца.
Возьмем пример.
Рассмотрим две матрицы A и B порядка 2 x 2. Итак, чтобы вычесть B из A, нам нужно вычесть элементы B из соответствующих элементов A.
Итак, если
A= и B =
Тогда
A-B =
Вычитание матриц порядка 3 x 3
Тот же принцип будет работать в случае матриц 3 x 3, когда матрицы должны быть вычтены одна из другой с 3 строками и 3 столбцами. Для вычитания матриц нам нужно вычесть элементы из одной матрицы с соответствующими элементами другой матрицы.
Итак, если
A= B=
Тогда
A-B=
A-B=
Свойства вычитания матриц
Условия сложения матриц также применимы к вычитанию матриц. Однако есть некоторые исключения. Существуют определенные законы, которым не следует матричное вычитание. Итак, давайте рассмотрим некоторые свойства и условия вычитания матриц.
Количество строк и столбцов должно быть одинаковым для операции вычитания матриц.
Вычитание матриц не является коммутативным, что означает A-B ≠ B-A.
Также вычитание матриц не является ассоциативным, что означает (A-B) – C ≠ A- (B-C).
Вычитание матрицы из самой себя приводит к нулевой матрице; это означает, что A-A= 0.
Вычитание матриц — это добавление отрицательного значения матрицы к другой матрице, что означает A — B = A + (-B).
При вычитании матрицы мы обычно используем
Поэлементное вычитание матриц
В этом типе для вычитания двух матриц мы вычитаем элементы в каждой строке и столбце до соответствующих элементов строк и столбцов следующей матрицы.
Так, например, A = [aij]m x n и B = [bij] m x n — это две матрицы, поэтому, вычитая их, мы получаем A-B = [aij]mxn — [bij] m x n = [aij — bij] mxn, где ij обозначает положение каждого элемента в i-й строке и j-м столбце.
Примеры вычитания матриц
- Определите элемент в первой строке и третьем столбце матрицы Q-P с помощью вычитания определения матриц, где p13 = 14 — элемент в P, а q13 = -3 — элемент в B.
Теперь пусть мы пытаемся решить ее.
Чтобы определить элемент в первой строке и третьем столбце матрицы Q-P, нам сначала нужно вычислить значение q13 – p13 с помощью матричного вычитания
q13 – p13 = -3 -14 = -17.