Геометрическая прогрессия калькулятор
Вычислить:
Член геометрической прогрессии с номером nСумма первых n членов геометрической прогрессииСумма членов геометрической прогрессии от n-ого до m-огоПроизведение первых n членов геометрической прогрессииПроизведение членов геометрической прогрессии от n-ого до m-огоЗнаменатель геометрической прогрессииПостроить геометрическую прогрессию
Известный член геометрической прогрессии
bm =
Номер m известного члена прогрессии
m =
Номер n члена геометрической прогрессии (который необходимо найти)
n =
Знаменатель геометрической прогрессии
q =
Отобразить члены геометрической прогрессии без нумерациис нумерациейв строкув столбик
с по
(диапазон не может быть больше 10)
Идет расчет …
Геометрическая прогрессия
Геометрическая прогрессия – это числовая последовательность, в которой числа отличны от нуля, каждый член в которой начиная со второго, равен предыдущему члену, умноженному на одно и то же число q.
Число q – называется знаменателем прогрессии.
Приведем примеры, построим геометрическую прогрессию со знаменателем q = 2, первый член которой b1 будет равен 3, тогда прогрессия будет построена следующим образом:
3, 3·2, (3·2)·2, (3·2·2)·2, (3·2·2·2)·2… либо
3, 3·2, 6·2, 12·2, 24·2… либо
3, 3·2, 3·22, 3·23, 3·24… и так далее, прогрессия имеет вид:
3, 6, 12, 24, 48…
Приведем еще один пример, построим геометрическую прогрессию с шагом d = −2, первый член которой b 1 равен 5, тогда прогрессия будет построена следующим образом:
5, 5·(-2), (5·(-2))·(-2), (5·(-2)·(-2))·(-2), (5·(-2)·(-2)·(-2))·(-2)… либо
5, 5·(-2), -10·(-2), 20·(-2), -40·(-2)… либо
5, 5·(-2), 5·(-2)2, 5·(-2)3, 5·(-2)4… и так далее, прогрессия имеет вид:
5, -10, 20, -40, 80…
Геометрическая прогрессия бывает четырех типов:
1. Возрастающая геометрическая прогрессия, если b1 > 0 и q > 1.
Возрастающая геометрическая прогрессия, если b1 > 0 и q > 1.
Например: 3, 6, 12, 24, 48, 96…
2. Убывающая геометрическая прогрессия, если 0 .
Например: 1, 0.5, 0.25, 0.125, 0.0625, 0.03125, 0.015625, 0.0078125, 0.00390625, 0.001953125…
3. Знакочередующаяся геометрическая прогрессия, если q .
Например: 1, -2, 4, -8, 16, -32, 64, -128, 256, -512…
4. Стационарная геометрическая прогрессия, если q = 1.
Например: 5, 5, 5, 5, 5, 5…
Любой член bn геометрической прогрессии может быть вычислен по формуле:
bm − известный член геометрической прогрессииm − номер m известного члена прогрессии
n − номер n члена геометрической прогрессии (который необходимо найти)
q − знаменатель геометрической прогрессии
Возьмём для примера, заданную выше прогрессию 3, 6, 12, 24, 48… и найдем ее 4-й член. В данной прогрессии q = 2. В качестве b m − мы можем использовать любой известный член прогрессии, возьмем b2 = 6, тогда
В данной прогрессии q = 2. В качестве b m − мы можем использовать любой известный член прогрессии, возьмем b2 = 6, тогда
bn = qn−m · bm
b4 = (2)4 − 2 · (6) = 24
Знаменатель геометрической прогрессии
bn − известный член геометрической прогрессии член с номером nbn+1 − следующий известный член геометрической прогрессии член с номером n+1
Приведем пример. Дана прогрессия (bn): 1 , -7 , 49 , -343 , 2401… найти ее знаменатель. В качестве bn, возьмём 3-й член в качестве bn+1 четвертый.
bn = 49
bn+1 = -343 тогда:
q =
bn+1
bn
=
-343
49
=
-7
Сумма членов геометрической прогрессии
Сумма первых n членов геометрической прогрессииbn − член геометрической прогрессии (последний член суммы)
n − номер n члена геометрической прогрессии (количество суммируемых членов)
q − знаменатель геометрической прогрессии
Приведем пример. Дана прогрессия (bn): -2 , -8 , -32 , -128, -512… Знаменатель q = 4. Найти сумму первых четырех членов.
Дана прогрессия (bn): -2 , -8 , -32 , -128, -512… Знаменатель q = 4. Найти сумму первых четырех членов.
Sn =
bn · q − b1
q − 1
=
(-128 · 4) − (-2)
4 − 1
=
-170
Сумма членов геометрической прогрессии от n-ого до m-огоbn − член геометрической прогрессии член с номером nbm − член геометрической прогрессии член с номером m
n − номер n члена геометрической прогрессии
m − номер m члена геометрической прогрессии
q − знаменатель геометрической прогрессии
Приведем пример. Дана прогрессия (bn): -2 , -8 , -32 , -128, -512… Знаменатель q = 4. Найдем сумму с 2-го по 4-й член.
Sn,m =
bm · q − bn
q − 1
=
(-128 · 4) − (-8)
4 − 1
=
-168
Произведение членов геометрической прогрессии
Произведение первых n членов геометрической прогрессииb1 − первый член геометрической прогрессииbn − член геометрической прогрессии (последний член произведения)
n − номер n члена геометрической прогрессии (количество членов произведения)
Приведем пример.
Pn = (b1 · bn)n/2 =
(-2 · (-128))4/2 =
65536
Произведение членов геометрической прогрессии от n-ого до m-огоb1 − первый член геометрической прогрессииbn-1 − член геометрической прогрессии с номером n-1
bm − член геометрической прогрессии член с номером m (последний член произведения)
n − номер n члена геометрической прогрессии
m − номер m члена геометрической прогрессии Произведение членов геометрической прогрессии от n-ого до m-огоq − знаменатель геометрической прогрессии
b1 − первый член геометрической прогрессии
n − номер n члена геометрической прогрессии
m − номер m члена геометрической прогрессии
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
| Справочник по математике | Алгебра | Последовательности чисел |
| Бесконечно убывающая геометрическая прогрессия |
Определение 1. Числовую последовательность
Числовую последовательность
b1 , b2 , … bk , …
все члены которой отличны от нуля, называют геометрической прогрессией, если справедливы равенства
Определение 2. Если последовательность чисел
b1 , b2 , … bk , …
является геометрической прогрессией, то число q , определенное формулой
называют знаменателем этой геометрической прогрессии.
Из определений 1 и 2 следует, что для того, чтобы задать геометрическую прогрессию, нужно знать два числа, например, первый член геометрической прогрессии b1 и знаменатель геометрической прогрессии q . Если числа b1 и q известны, то все остальные члены прогрессии можно найти по формулам:
| (1) |
По этой причине многие задачи на геометрическую прогрессию удобно решать при помощи составления системы уравнений для определения чисел b1 и q.
Из формул (1) вытекает общая формула
| bk = b1qk – 1, k = 1, 2, 3, … | (2) |
позволяющая по любому номеру k вычислить член bk геометрической прогрессии, зная первый член и знаменатель прогрессии. Эта формула носит название формулы общего члена геометрической прогрессии.
Из формулы (2) вытекает утверждение, называемое характеристическим свойством геометрической прогрессии. Это свойство формулируется так: — «Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению своих соседних членов». Таким образом, характеристическое свойство геометрической прогрессии утверждает, что при справедливо равенство
| (3) |
В случае, когда
b1 > 0 и q > 0
все члены геометрической прогрессии будут положительными, и формулу (3) можно переписать в другом виде:
| (4) |
Равенство (4) означает, что каждый член такой геометрической прогрессии, начиная со второго, равен среднему геометрическому своих соседних членов.
Если для суммы первых k членов геометрической прогрессии ввести обозначение
Sk = b1 + b2 + … + bk ,
k = 1, 2, 3, …
то, воспользовавшись равенствами (1), получаем
q Sk =
= b1q + b2q + … + bk q =
= b2 + b3 + … + bk +1 .
Следовательно,
Sk – q Sk = b1 – bk +1 .
Таким образом , при будет справедливо равенство
которое называется формулой для суммы первых k членов геометрической прогрессии.
В случае, когда q = 1, все члены геометрической прогрессии равны, что не представляет особого интереса.
Определение 3. Геометрическую прогрессию называют бесконечно убывающей, если её знаменатель удовлетворяет неравенству
| q | < 1 .
В этом случае выполнено равенство
а величину S называют суммой бесконечно убывающей геометрической прогрессии.
Более подробно с понятием предела числовой последовательности можно ознакомиться в в разделе «Пределы числовых последовательностей» нашего справочника.
С примерами решений различных задач по теме «Геометрическая прогрессия» можно ознакомиться в нашем учебном пособии «Арифметическая и геометрическая прогрессии».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Геометрические последовательности и ряды
Геометрические последовательности
Геометрическая последовательностьПоследовательность чисел, в которой каждое последующее число является произведением предыдущего числа и некоторой константы r . , или геометрическая прогрессияИспользуется при ссылке на геометрическую последовательность., представляет собой последовательность чисел, где каждое последующее число является произведением предыдущего числа и некоторой константы r .
, или геометрическая прогрессияИспользуется при ссылке на геометрическую последовательность., представляет собой последовательность чисел, где каждое последующее число является произведением предыдущего числа и некоторой константы r .
an=ran−1 Geometic Sequence
И поскольку anan−1=r, постоянный множитель равен r называется обыкновенным отношением. Константа r получается при делении любых двух последовательных членов геометрической прогрессии; anan−1=r.. Например, следующая геометрическая последовательность
9,27,81,243,729…
Здесь a1=9, а отношение между любыми двумя последовательными членами равно 3. Мы можем построить общий член an= 3an−1 где
a1=9a2=3a1=3(9)=27a3=3a2=3(27)=81a4=3a3=3(81)=243a5=3a4=3(243)=729⋮
In в общем, учитывая первый член a1 и обыкновенное отношение r геометрической прогрессии можно записать следующее: мы видим, что любая геометрическая последовательность может быть записана через ее первый элемент, ее знаменатель и индекс следующим образом: представляет собой геометрическую последовательность.
Пример 1
Найдите уравнение для общего члена данной геометрической прогрессии и используйте его для вычисления его 10 th член: 3,6,12,24,48…
Решение:
Начните с нахождения знаменателя,
r=63=2
Обратите внимание, что отношение между любыми двумя последовательными членами равно 2. последовательность действительно является геометрической прогрессией, где a1=3 и r=2.
an=a1rn−1=3(2)n−1
Следовательно, мы можем записать общий член an=3(2)n−1, а 10 -й член можно вычислить следующим образом:
a10 =3(2)10−1=3(2)9=1,536
Ответ: an=3(2)n−1; а10=1,536
Члены между заданными членами геометрической последовательности называются средними геометрическими. Члены между заданными членами геометрической прогрессии. Другими словами, найдите все средние геометрические между членами 1 и 4 .
Решение:
Начните с нахождения знаменателя r . В этом случае нам даны первый и четвертый члены:
an=a1rn−1 Use n = 4. a4=a1r4−1a4=a1r3
a4=a1r4−1a4=a1r3
Подставьте a1=-5 и a4=-135 в приведенное выше уравнение и затем найдите r .
−135=−5r327=r33=r
Затем используйте первый член a1=−5 и знаменатель r=3, чтобы найти уравнение для n -го члена последовательности.
an=a1rn−1an=−5(3)n−1
Теперь мы можем использовать an=−5(3)n−1, где n — натуральное число, чтобы определить недостающие члены.
a1=-5(3)1-1=-5⋅30=-5a2=-5(3)2-1=-5⋅31=-15a3=-5(3)3-1=-5⋅ 32=−45 } геометрическое среднее4=−5(3)4−1=−5⋅33=−135
Ответ: −15, −45,
Первый член геометрической прогрессии не может быть задан.
Пример 3
Найдите общий член геометрической прогрессии, где a2=−2 и a5=2125.
Решение:
Чтобы определить формулу для общего члена, нам нужны a1 и r. Нелинейная система с этими переменными может быть сформирована с использованием данной информации и an=a1rn−1:
{a2=a1r2−1a5=a1r5−1 ⇒ {−2=a1r2125=a1r4 Use a2=−2. Используйте a5=2125.
Используйте a5=2125.
Найдите a1 в первом уравнении,
{ −2=a1r ⇒ −2r=a12125=a1r4
Подставим a1=−2r во второе уравнение и найдем r .
2125=a1r42125=(−2r)r42125=−2r3−1125=r3−15=r
Обратно заменить, чтобы найти a1:
a1=−2r=−2(−15)=10
Следовательно, a1 =10 и r=-15.
Ответ: an=10(−15)n−1
Попробуйте! Найдите уравнение для общего члена данной геометрической прогрессии и используйте его для вычисления его 6-го -го -го члена: 2,43,89,…
Ответ: an=2(23)n−1; a6=64243
(нажмите, чтобы посмотреть видео)
Геометрический ряд
Геометрический рядСумма членов геометрической прогрессии. представляет собой сумму членов геометрической прогрессии. Например, сумма первых 5 членов геометрической последовательности, определяемой выражением an=3n+1, выглядит следующим образом:
S5=Σn=153n+1=31+1+32+1+33+1+34+1+35 +1=32+33+34+35+36=9+27+81+243+729=1,089
Можно сложить 5 положительных целых чисел. Однако задача добавления большого количества терминов не стоит. Поэтому далее мы разрабатываем формулу, которую можно использовать для вычисления суммы первых n членов любой геометрической прогрессии. В общем,
Однако задача добавления большого количества терминов не стоит. Поэтому далее мы разрабатываем формулу, которую можно использовать для вычисления суммы первых n членов любой геометрической прогрессии. В общем,
Sn=a1+a1r+a1r2+…+a1rn−1
Умножая обе части на r , мы можем написать,
rSn= a1r+a1r2+a1r3+…+a1rn
Вычитая эти два уравнения, затем получаем,
Sn−rSn=a1−a1rnSn(1−r)=a1(1−rn)
Предполагая, что r≠1 делит обе части на (1−r), мы получаем формулу для n -го частичного сумма геометрической прогрессииСумма первых n членов геометрической прогрессии, заданная формулой: Sn=a1(1−rn)1−r, r≠1.:
Sn=a1(1−rn)1−r(r≠1)
Другими словами, n -я частичная сумма любой геометрической последовательности может быть вычислена с использованием первого члена и знаменателя. Например, чтобы вычислить сумму первых 15 членов геометрической последовательности, определяемой выражением an=3n+1, используйте формулу с a1=9 и r=3.
S15=a1(1−r15)1−r=9⋅(1−315)1−3=9(−14 348 906)−2=64 570 077
Пример 4
Найдите сумму первых 10 членов заданная последовательность: 4, −8, 16, −32, 64,…
Решение:
Определите, есть ли общее отношение между данными терминами.
r=-84=-2
Обратите внимание, что отношение между любыми двумя последовательными членами равно -2; следовательно, данная последовательность является геометрической последовательностью. Используйте r=−2 и тот факт, что a1=4, чтобы вычислить сумму первых 10 членов,
Sn=a1(1−rn)1−rS10=4[1−(−2)10]1−(− 2)=4(1−1,024)1+2=4(−1,023)3=−1,364
Ответ: S10=−1,364
Пример 5
Оценка: Σn=162(−5)n.
Решение:
В этом случае нас просят найти сумму первых 6 членов геометрической последовательности с общим членом an=2(−5)n. Используйте это, чтобы определить член 1 st и обыкновенное отношение r :
a1=2(−5)1=−10
Чтобы показать, что существует общее отношение, мы можем использовать последовательные члены в целом следующим образом :
r=anan-1=2(-5)n2(-5)n-1=(-5)n-(n-1)=(-5)1=-5
Использовать a1=-10 и r=-5 для вычисления частичной суммы 6 th .
Sn=a1(1−rn)1−rS6=−10[1−(−5)6]1−(−5)=−10(1−15 625)1+5=−10(−15 624)6 =26 040
Ответ: 26 040
Попробуйте! Найдите сумму первых 9 членов данной последовательности: −2, 1, −1/2,…
Ответ: S9=−171128
(нажмите, чтобы посмотреть видео)
Если обыкновенное отношение r бесконечной геометрической последовательности является дробью, где |r|<1 (то есть −1
1−(110)2=1−0,01=0,991−(110)4=1−0,0001=0,99991−(110)6=1 −0,000001=0,999999
Здесь мы видим, что этот коэффициент становится все ближе и ближе к 1 для все больших значений n . Это иллюстрирует идею предела, важное понятие, широко используемое в математике высокого уровня, которое выражается с использованием следующих обозначений:
limn→∞(1−rn)=1 где |r|<1 , “предел (1−rn) как n приближается к бесконечности равно 1». Хотя это дает представление о том, что вас ждет в дальнейшем изучении математики, в данный момент мы занимаемся разработкой формулы для специальных бесконечных геометрических рядов. Рассмотрим n -ю частичную сумму любой геометрической прогрессии,
Хотя это дает представление о том, что вас ждет в дальнейшем изучении математики, в данный момент мы занимаемся разработкой формулы для специальных бесконечных геометрических рядов. Рассмотрим n -ю частичную сумму любой геометрической прогрессии,
Sn=a1(1−rn)1−r=a11−r(1−rn)
поскольку n приближается к бесконечности, существует, и мы можем написать,
Sn=a11−r(1−rn) ⇒n→∞ S∞=a11−r⋅1
Таким образом, сходящийся геометрический ряд Бесконечный геометрический ряд, где |r|<1, сумма которого определяется формулой: S∞=a11−r. — бесконечный геометрический ряд, где |r|<1; его сумму можно вычислить по формуле:
S∞=a11−r
Пример 6
Найти сумму бесконечного геометрического ряда: 32+12+16+118+154+⋯
Решение:
Определить обыкновенное отношение,
r=1232=12⋅23=13
Поскольку обыкновенное отношение r=13 представляет собой дробь от −1 до 1, это сходящийся геометрический ряд. Используйте первый член a1=32 и обыкновенное отношение, чтобы вычислить его сумму.
S∞=a11−r=321−(13)= 32 23=32⋅32=94
Ответ: S∞=94
Примечание : В случае бесконечного геометрического ряда, где |r|≥ 1 ряд расходится и говорят, что суммы нет. Например, если an=(5)n−1, то r=5 и мы имеем
S∞=Σn=1∞(5)n−1=1+5+25+⋯
Мы видим, что эта сумма неограниченно растет и не имеет суммы.
Попробуйте! Найдите сумму бесконечного геометрического ряда: Σn=1∞−2(59)n−1.
Ответ: −9/2
(нажмите, чтобы посмотреть видео)
Повторяющаяся десятичная дробь может быть записана в виде бесконечного геометрического ряда, общий коэффициент которого равен степени 1/10. Следовательно, формулу сходящегося геометрического ряда можно использовать для преобразования повторяющейся десятичной дроби в дробь.
Пример 7
Запишите в виде дроби: 1,181818…
Решение:
Начните с определения повторяющихся цифр справа от десятичной дроби и запишите в виде геометрической прогрессии.
0,181818…=0,18+0,0018+0,000018+…=18100+1810 000+181 000 000+…
В этой форме мы можем определить знаменатель отношения для вычисления бесконечной суммы:
S∞=a11−r=181001−(1100)=1810099100=18100⋅10099=211
Следовательно, 0,181818…=211 и мы имеем,
1,181811…=1+1+181811
Ответ: 1211
Пример 8
Некоторый мяч отскакивает на две трети высоты, с которой он упал. Если этот мяч первоначально падает с высоты 27 футов, оцените приблизительное общее расстояние, которое пройдет мяч.
Решение:
Мы можем рассчитать высоту каждого последовательного отскока:
27=23 = 18 футов высоты первого отскока18 порядка 23 = высота 12 футов второго отскока12 порядка 23 = 8 футов высоты третьего отскока
Общее расстояние, пройденное мячом, равно сумме расстояний, на которые он падает, и расстояний, на которые мяч поднимается. Расстояния, на которые падает мяч, составляют геометрический ряд:
27+18+12+⋯ Расстояние падения мяча
, где a1=27 и r=23. Потому что r — дробь от −1 до 1, эту сумму можно рассчитать следующим образом:
Потому что r — дробь от −1 до 1, эту сумму можно рассчитать следующим образом:
S∞=a11−r=271−23=2713=81
Следовательно, мяч падает с общей высоты 81 фут. . Расстояния, на которые поднимается мяч, составляют геометрический ряд:
18+12+8+⋯ Расстояние на мяч поднимается
, где a1=18 и r=23. Вычислите эту сумму аналогичным образом:
S∞=a11−r=181−23=1813=54
Следовательно, мяч поднимается на общее расстояние 54 фута. Приблизительно общее пройденное расстояние путем сложения общих расстояний подъема и опускания:
81+54=135 футов
Ответ: 135 футов
Ключевые выводы
- Геометрическая последовательность — это последовательность, в которой отношение r между последовательными членами является постоянным.
- Общий член геометрической прогрессии можно записать через его первый член a1, знаменатель r и индекс n следующим образом: an=a1rn−1.

- Геометрический ряд – это сумма членов геометрической прогрессии.
- n -я частичная сумма геометрической прогрессии может быть вычислена с использованием первого члена a1 и знаменателя r следующим образом: Sn=a1(1−rn)1−r.
- Бесконечная сумма геометрической последовательности может быть вычислена, если знаменатель представляет собой дробь между −1 и 1 (то есть |r|<1) следующим образом: S∞=a11−r. Если |r|≥1, то суммы не существует.
Тематические упражнения
а1=1; г=5
а1=1; г=3
а1=2; г=3
а1=5; г=4
а1=2; г=-3
а1=6; г=-2
-
а1=3; г=23
а1=6; г=12
а1=1,2; г=0,6
а1=-0,6; г=-3
7, 28, 112,…
−2, −10, −50,…
2, 12, 18,…
1, 25, 425,…
8, 4, 2,…
6, 2, 23,…
−1, 23, −49,…
2, −32, 98,…
13, −2, 12,…
25, −2, 10,…
−3,6, −4,32, −5,184,…
0,8, −2,08, 5,408,…
Найдите общий член и используйте его для определения 20-го члена в последовательности: 1, x2, x24,…
Найдите общий член и используйте его для определения 20-го члена в последовательности: 2, −6x, 18×2,…
Количество клеток в культуре определенных бактерий удваивается каждые 4 часа.
 Если изначально присутствует 200 клеток, напишите последовательность, показывающую популяцию клеток через каждые и 4-часовых периодов в течение одного дня. Напишите формулу, которая дает количество клеток через любой 4-часовой период.
Если изначально присутствует 200 клеток, напишите последовательность, показывающую популяцию клеток через каждые и 4-часовых периодов в течение одного дня. Напишите формулу, которая дает количество клеток через любой 4-часовой период.Определенный мяч отскакивает назад на половине высоты, с которой он упал. Если этот мяч первоначально падает с высоты 12 футов, найдите формулу, определяющую высоту мяча на 9-м метре.0005 n -й отскок и используйте его, чтобы найти высоту мяча при 6 -м -м отскоке.
Для заданной геометрической последовательности, определяемой рекуррентным соотношением an=4an−1, где a1=2 и n>1, найдите уравнение, которое дает общий член через a1 и обыкновенное отношение r .
Для заданной геометрической последовательности, определяемой рекуррентным соотношением an=6an−1, где a1=12 и n>1, найдите уравнение, которое дает общий член через a1 и обыкновенное отношение р .

a1=-3 и a6=-96
а1=5 и а4=-40
а1=-2 и а8=-164
а1=34 и а4=-136
а2=18 и а5=486
а2=10 и а7=320
a4=−2 и a9=64
а3=-43 и а6=3281
а5=153,6 и а8=9830,4
a4=-2,4× 10-3 и a9=-7,68× 10-7
а1=2 и а4=250
а1=13 и а6=-196
a2=-20 и a5=-20 000
a3=49 и a6=-16 807
Часть A: геометрические последовательности
Запишите первые 5 членов геометрической прогрессии, зная ее первый член и знаменатель. Найдите формулу для его общего члена.
Учитывая геометрическую последовательность, найдите формулу для общего члена и используйте ее для определения 5 -го члена в последовательности.
Зная члены геометрической прогрессии, найдите формулу для общего члена.
Найдите все средние геометрические между данными терминами.
ан=2n+1; S12
ан=(-2)n+1; S12
ан=(12)n; С7
ан=(23)n-1; S6
ан=5(-3)n-1; S5
ан=-7(-4)n; S5
ан=2(-14)n; S5
ан=13(2)n+1; S10
∑n=155n
∑n=16(−4)n
∑к=1102к+1
∑k=1142k−1
∑k=110−2(3)k
∑k=185(−2)k
∑n=152(12)n+2
∑n=14−3(23)n
ан=(15)n; S∞
ан=(23)n-1; S∞
ан=2(-34)n-1; S∞
ан=3(-16)n; S∞
ан=-2(12)n+1; S∞
an=-13(-12)n; S∞
∑n=1∞2(13)n−1
∑n=1∞(15)n
∑n=1∞3(2)n−2
∑n=1∞−14(3)n−2
∑n=1∞12(−16)n
∑n=1∞13(−25)n
1,222…
5,777 …
2.252525…
3,272727…
1,999…
1.0
Предположим, вы согласились работать за копейки в день в течение 30 дней. Вы заработаете 1 пенни в первый день, 2 пенни во второй день, 4 пенни в третий день и так далее. Сколько всего пенни вы заработаете в конце 30-дневного периода? Какая сумма в долларах?
Первоначальная ставка в рулетке в размере 100 долларов сделана (на красное) и проиграна.
 Чтобы компенсировать разницу, игрок удваивает ставку, делает ставку в размере 200 долларов и проигрывает. Опять же, чтобы компенсировать разницу, игрок удваивает ставку до 400 долларов и проигрывает. Если игрок продолжит удваивать свою ставку таким образом и проиграет 7 раз подряд, сколько всего он проиграет?
Чтобы компенсировать разницу, игрок удваивает ставку, делает ставку в размере 200 долларов и проигрывает. Опять же, чтобы компенсировать разницу, игрок удваивает ставку до 400 долларов и проигрывает. Если игрок продолжит удваивать свою ставку таким образом и проиграет 7 раз подряд, сколько всего он проиграет?Определенный мяч отскакивает на половину высоты, с которой он упал. Если этот мяч изначально падает с высоты 12 футов, оцените приблизительное общее расстояние, которое пройдет мяч.
Мяч для гольфа отскакивает от бетонного тротуара на три четверти высоты, с которой он упал. Если мяч первоначально падает с 8 метров, оцените общее расстояние, которое пролетел мяч.
Структурированное урегулирование дает сумму в долларах каждый год, представленную n , в соответствии с формулой pn=6000(0,80)n−1.
 Какова общая сумма, полученная от урегулирования через 10 лет?
Какова общая сумма, полученная от урегулирования через 10 лет?Начав с квадрата, каждая сторона которого равна 1 единице, впишите другой квадрат, соединив середины каждой стороны. Продолжайте вписывать квадраты таким образом до бесконечности, как показано на рисунке:
Найдите сумму площадей всех квадратов на рисунке. (Подсказка: начните с нахождения последовательности, состоящей из площадей каждого квадрата.)
Часть B: Геометрический ряд
Рассчитайте указанную сумму.
Запишите как смешанное число.
−12, 24, −48,…
−7,−5,−3,…
−3,−11,−19,…
4,9,16,…
2,32,43,…
43,89,1627,…
16,−16,−12,…
13,14,316,…
12,14,16…
−110,−15,−310,…
1,26,0,252,0,0504,…
0,02,0,08,0,18,…
1, −1, 1, −1,…
0, 0, 0,…
ан=3(5)n-1; С8
ан=5-6н; S22
ан=2n; S14
ан=2n; S10
ан=-2(17)n-1; S∞
an=-2+17n; С8
∑n=150(3n−5)
∑n=125(4−8n)
∑n=112(−2)n−1
∑n=1∞5(−12)n−1
∑n=1405
∑n=1∞0,6n
Часть C: Последовательности и серии
Классифицировать последовательность как арифметическую, геометрическую или ни одну из них. Укажите общую разность или отношение, если оно существует.
Классифицируйте последовательность как арифметическую или геометрическую, а затем вычислите указанную сумму.
Рассчитайте указанную сумму.
Используйте приемы, описанные в этом разделе, чтобы объяснить, почему 0,999…=1.

Построить геометрическую прогрессию, где r=1. Исследуйте частичную сумму n такой последовательности. Какие выводы мы можем сделать?
Часть D: Дискуссионная доска
Ответы
1, 5, 25, 125, 625; ан=5n−1
2, 6, 18, 54, 162; an=2(3)n−1
2, -6, 18, -54, 162; an=2(−3)n−1
3, 2, 43, 89, 1627; an=3(23)n−1
1,2, 0,72, 0,432, 0,2592, 0,15552; an=1,2(0,6)n−1
an=7(4)n−1, a5=1,792
an=2(14)n−1, a5=1128
ан=8(12)n−1, а5=12
an=-(-23)n-1, a5=-1681
an=13(−6)n−1, a5=432
an=-3,6(1,2)n-1, a5=-7,46496
an=(x2)n−1; а20=х19219
400 ячеек; 800 ячеек; 1600 ячеек; 3200 ячеек; 6400 ячеек; 12 800 ячеек; pn=400(2)n−1 клеток
ан=2(4)n−1
ан=-3(2)n-1
ан=-2(12)n-1
ан=6(3)n−1
an=14(−2)n−1
ан=0,6(4)n−1
10, 50
−200; −2 000
16 380
127128
305
−205512
3 905
4,092
−177 144
3164
14
87
−1
3
Нет суммы
−114
129
22599
2
1 073 741 823 пенни; 10 737 418,23
долларов США36 футов
26 778,77 $
Геометрический; г=-2
Арифметика; г=-8
Ни
Арифметика; д=-13
Ни
Геометрический; г=0,2
Геометрический; г=-1
Геометрический; 292 968
Арифметика; 210
Геометрический; −73
3 575
−1 365
200
Ответ может отличаться
- 9{th}$ частичная сумма геометрической прогрессии.
 {th}$ член — $g_n$.
Это означает, что любая геометрическая прогрессия $(g_n )_{n\in N}$ имеет следующий вид 94,\ldots$$
{th}$ член — $g_n$.
Это означает, что любая геометрическая прогрессия $(g_n )_{n\in N}$ имеет следующий вид 94,\ldots$$, где ненулевая константа $r$ является знаменателем. Первый член $g_1$ называется начальным. Обратите внимание, что обыкновенное отношение $r$ не может быть равно нулю. С другой стороны, прогрессия $(g_n )_{n\in N}$ является геометрической прогрессией со знаменателем $r$, если отношения между последовательными членами равны, т.е.
$$\frac{g_2}{g_1 }=\frac{g_3}{g_2}=\ldots=\frac{g_n}{g_{n-1}} =r$$
- Если $r>1$, то геометрическая прогрессия является возрастающей и он держит
$$g_1\lt g_2\lt \ldots\lt g_{n-1}\lt g_n$$ - Если $0\lt r\lt 1$, то геометрическая прогрессия является убывающей и имеет место
$$ g_1>g_2>\ldots>g_{n-1}>g_n$$ - Если $r=1$, то геометрическая прогрессия является постоянной прогрессией и выполняется
$$g_1=g_2=\ldots=g_{n -1}=g_n$$ Постоянная прогрессия — это только прогрессия, которая является одновременно и геометрической, и геометрической.
Члены между двумя непоследовательными членами геометрической прогрессии $(g_n )_{n\in N}$ называются средними геометрическими этих членов. Например, среднее геометрическое между $g_1$ и $g_5$ равно $g_2$, $g_3$ и $g_5$. Если заданы два непоследовательных члена геометрической прогрессии $(g_n )_{n\in N}$ и число средних геометрических между ними, то геометрическая прогрессия полностью определена. 9{th}$ частичная сумма геометрической прогрессии, в которой членов геометрической прогрессии $5$, первый член равен $2$, а знаменатель равен $4$. Для любых других комбинаций количества членов, первого члена и общего отношения просто укажите другие числа в качестве входных данных и нажмите кнопку «СОЗДАТЬ РАБОТУ». Учащиеся начальной школы могут использовать этот калькулятор геометрической прогрессии для создания работы, проверки результатов или эффективного решения домашних заданий.
Реальные задачи с использованием геометрической прогрессии 9{th}$ член этой прогрессии равен $g_n=1.
 03g_{n-1}$, а начальный член равен $g_1=100$.
03g_{n-1}$, а начальный член равен $g_1=100$.
Геометрическая прогрессия может представлять рост или распад.- Если обыкновенное отношение $r$ больше $1$, $r>1$, то геометрическая прогрессия может моделировать рост. Например, рост населения.
- Если знаменатель $r$ положителен и меньше $1$, $0\lt r\lt 1$, то геометрическая прогрессия может моделировать распад. Например, предположим, что новый автомобиль теряет одну пятую своей стоимости.
каждый год. Сколько стоит этот автомобиль через 3 года, если сейчас он стоит $\$30,0000$. 9x,\;x>0,$ получаем следующие графики:
Практические задачи на геометрическую прогрессию
Практическая задача 1:
У нас есть $\$12$ и мы идем в банк, чтобы внести деньги. Банк предлагает нам следующий вариант: в первый месяц мы получаем $\$18$, во второй месяц мы получаем $\$27$ и т.д. Сколько денег мы получим через $10$ месяцев?Практическая задача 2:
Дана последовательность рекуррентным соотношением $g_{n+1}=6g_n$ и $g_1=3$. Найдите сумму первых $10$ членов геометрической прогрессии. 9{th}$ член геометрической прогрессии и сумма $n$ чисел геометрической прогрессии, пример вычисления (работа с шагами), реальные задачи и практические задачи будут очень полезны для учащихся начальных классов (K-12 образование) в изучении рядов и последовательностей и в решении проблем в банковском деле, биологии и других областях реальной жизни.
Найдите сумму первых $10$ членов геометрической прогрессии. 9{th}$ член геометрической прогрессии и сумма $n$ чисел геометрической прогрессии, пример вычисления (работа с шагами), реальные задачи и практические задачи будут очень полезны для учащихся начальных классов (K-12 образование) в изучении рядов и последовательностей и в решении проблем в банковском деле, биологии и других областях реальной жизни.- Калькулятор отношений и пропорций
- Калькулятор логарифмов
- Калькулятор антилогарифма
- Калькулятор простых или составных чисел
- Прайс -калькулятор факторизации
- Кальфлятор арифметического прогрессирования
- миллиард — миллион — кроры — конвертер
- Двоирный до децимального, Hex & Octal Converter
- . Восьмеричный преобразователь
- Восьмеричное в десятичное, двоичное и шестнадцатеричное преобразование
- Калькулятор средневзвешенных значений
Геометрическая прогрессия — Уроки Византа
Прогрессия — это еще один способ сказать последовательность, таким образом, геометрическая прогрессия — это число
, также известное как геометрическая последовательность.
Геометрическая прогрессия — это особая последовательность, определяемая тем особым свойством, что
отношение двух последовательных членов одинаково для всех членов последовательности.
В то время как в арифметической прогрессии мы говорили о разнице, здесь мы говорим о соотношениях
что означает, что когда вы делите текущий член на предыдущий член, число, которое
, которое вы получите, должно быть отличной от нуля константой, одинаковой для всех последовательных пар
терминов в последовательности. Это число известно как обыкновенное отношение и обозначается как
буквой r .Например, учитывая последовательность ниже
чтобы последовательность квалифицировалась как геометрическая прогрессия, следующее должно быть
истиннымпоэтому, поскольку мы установили вышеуказанное соотношение, мы заключаем, что следующее
должно быть верныма также на 4 срок
и последний член
Так ты уже ничего не заметил?
Выражение для последнего члена дает нам общее выражение для нахождения любого члена
в геометрической прогрессии. Все, что вам нужно, это первый член и обыкновенное отношение
Все, что вам нужно, это первый член и обыкновенное отношение
, затем примените следующее:Например; найдите 5-й и 8-й члены геометрической прогрессии, если
первый член равен 2, а знаменатель равен 3Решение:
Поскольку у нас есть первый член и знаменатель r , все, что нам нужно сделать, это
подставить в формулу, чтобы получить нужные нам члены:Геометрическая серия
Поскольку у нас есть геометрическая последовательность, вы также должны ожидать, что у вас будет геометрическая последовательность
для суммы членов в геометрической прогрессии.Используя обозначение серии, геометрическую серию можно представить как
.

Подобно тому, что мы делали в арифметической прогрессии, мы можем вывести формулу для нахождения суммы
геометрической прогрессии.Первый шаг состоит в том, чтобы заменить различные термины и представить все выражение 91 284 в терминах только первого члена.
поскольку первый член является общим для всего выражения, мы можем выделить его как
следующим образом:Если бы мы умножили эту сумму на обыкновенное отношение r , то получили бы
после.
Затем мы приступаем к вычитанию вышеуказанного из исходного выражения суммы, поскольку
следует за.
что после некоторых очень долгих и утомительных манипуляций, что вам не стоит слишком беспокоиться
о даетвынес сумму
что оставляет следующую формулу для нахождения суммы геометрического ряда
который также выражается как
Примеры геометрической прогрессии
Пример 1
Найдите сумму первых 10 членов следующего геометрического ряда
Этап 1
Сумму геометрического ряда можно найти по следующей формуле:
Этап 2
Из приведенной выше формулы видно, что нам нужен только первый член, обычное отношение
и количество членов в ряду, чтобы вычислить сумму.
- Если $r>1$, то геометрическая прогрессия является возрастающей и он держит


 Если изначально присутствует 200 клеток, напишите последовательность, показывающую популяцию клеток через каждые и 4-часовых периодов в течение одного дня. Напишите формулу, которая дает количество клеток через любой 4-часовой период.
Если изначально присутствует 200 клеток, напишите последовательность, показывающую популяцию клеток через каждые и 4-часовых периодов в течение одного дня. Напишите формулу, которая дает количество клеток через любой 4-часовой период.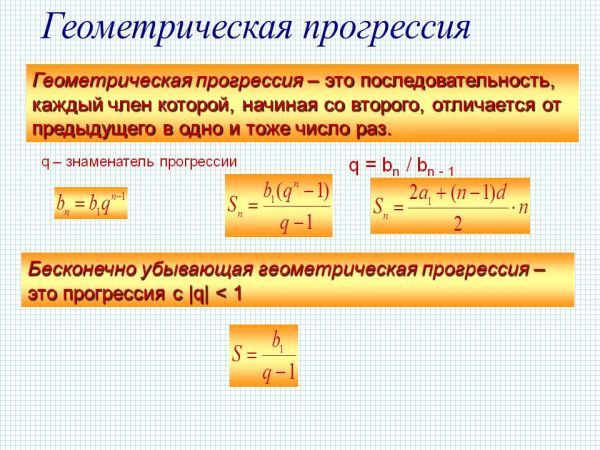
 Чтобы компенсировать разницу, игрок удваивает ставку, делает ставку в размере 200 долларов и проигрывает. Опять же, чтобы компенсировать разницу, игрок удваивает ставку до 400 долларов и проигрывает. Если игрок продолжит удваивать свою ставку таким образом и проиграет 7 раз подряд, сколько всего он проиграет?
Чтобы компенсировать разницу, игрок удваивает ставку, делает ставку в размере 200 долларов и проигрывает. Опять же, чтобы компенсировать разницу, игрок удваивает ставку до 400 долларов и проигрывает. Если игрок продолжит удваивать свою ставку таким образом и проиграет 7 раз подряд, сколько всего он проиграет? Какова общая сумма, полученная от урегулирования через 10 лет?
Какова общая сумма, полученная от урегулирования через 10 лет?
 {th}$ член — $g_n$.
Это означает, что любая геометрическая прогрессия $(g_n )_{n\in N}$ имеет следующий вид 94,\ldots$$
{th}$ член — $g_n$.
Это означает, что любая геометрическая прогрессия $(g_n )_{n\in N}$ имеет следующий вид 94,\ldots$$
 03g_{n-1}$, а начальный член равен $g_1=100$.
03g_{n-1}$, а начальный член равен $g_1=100$.  Найдите сумму первых $10$ членов геометрической прогрессии. 9{th}$ член геометрической прогрессии и сумма $n$ чисел геометрической прогрессии, пример вычисления (работа с шагами), реальные задачи и практические задачи будут очень полезны для учащихся начальных классов (K-12 образование) в изучении рядов и последовательностей и в решении проблем в банковском деле, биологии и других областях реальной жизни.
Найдите сумму первых $10$ членов геометрической прогрессии. 9{th}$ член геометрической прогрессии и сумма $n$ чисел геометрической прогрессии, пример вычисления (работа с шагами), реальные задачи и практические задачи будут очень полезны для учащихся начальных классов (K-12 образование) в изучении рядов и последовательностей и в решении проблем в банковском деле, биологии и других областях реальной жизни.
 Все, что вам нужно, это первый член и обыкновенное отношение
Все, что вам нужно, это первый член и обыкновенное отношение 
