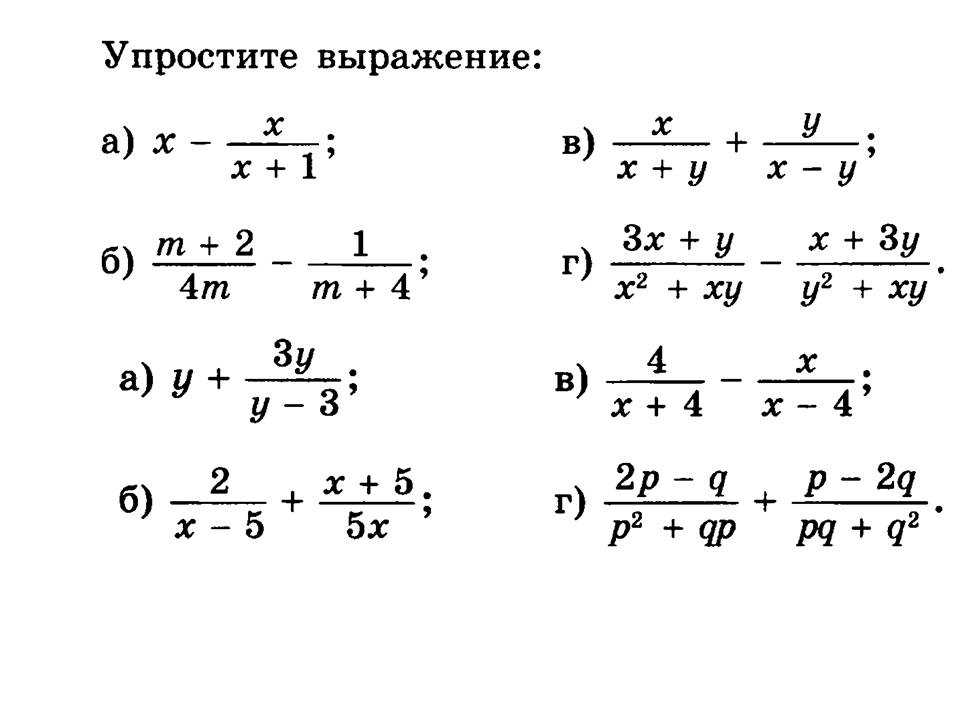Как выразить неизвестное из формулы: Выражение неизвестной, учимся выражать

Выражение неизвестной величины из формулы.

Для очень многих учеников это неумение является камнем преткновения при решении задач.

Хотя нужно уметь применять всего лишь два правила решения уравнений, которые изучаются еще в 7-м классе на алгебре и заменяют собой шесть правил нахождения неизвестной величины, знакомых вам  с начальных классов.

А ведь любая физическая формула по сути – это уравнение.

Вот они: эти правила.

1. Если слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
2. Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получим уравнение, равносильное данному.

В дополнение ко второму правилу добавляем еще правило сокращения дробей.

И в некоторых формулах потребуется извлечение корня.

Смотрите видеоурок.

На уроках математики ученики худо-бедно применяют эти правила, но и то часто делают ошибки. А уж если нужно перенести данную информацию на задачу с физическим содержанием, то многие впадают в полный ступор.

Давайте сегодня с вами решим эту проблему раз и навсегда. После этого мастер-класса у вас не будет никаких непоняток в плане выражения неизвестной величины из формулы.

Первая часть:

Начнем с самых простых формул, которые включают в себя три буквы.

Формула пути при равномерном движении:

 

Если нужно из этой формулы выразить время, то применяем второе правило: обе части уравнения делим на одно и то же число  (на одну и ту же букву). Делим на ту букву, от которой нужно избавиться. Затем сокращаем. В данном случае нужно избавиться от величины скорости.

Пишем короче:

Рассмотрим формулу давления столба жидкости.

 

Рассмотрим формулу плотности.

Чтобы выразить массу, нужно обе части уравнения умножить на объем. Затем сократить.

 

Если нужно выразить величину, которая стоит в знаменателе дроби, то сначала перетащим ее из знаменателя в числитель.

Итак, выражаем величину объема. Обе части уравнения умножаем на объем, извлекая его таким образом из знаменателя.

Сокращаем дробь в правой части на v.

Теперь, чтобы избавиться от плотности, делим на нее обе части

 

Встречаются формулы, в которых какая-то величина в степени.

Например, формула кинетической энергии

Нужно выразить скорость. Сначала выражаем квадрат скорости. Для этого обе части уравнения разделим на массу и умножим на 2.

 

Сокращаем на m и на 2, и получаем

Мы выразили квадрат скорости. Чтобы найти скорость, нужно избавиться от квадрата. Для этого из обеих частей уравнения извлекаем квадратный корень.

Записывается, конечно, все это короче.

 

На первых порах вы можете расписывать все подробно, когда же эти правила доведете до автоматизма, тогда уже сокращайте записи.

Для тренировки выпишите все известные вам формулы, похожие на те, которые мы сегодня разбирали и потренируйтесь в выражении. Если не помните формулы, воспользуйтесь справочником.

Формула плеча силы в физике

Формула плеча силы в физике

Определение и формула плеча силы

Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${\overline{F}}_1$ и ${\overline{F}}_2$, действующие на рычаг направлены в одну сторону.

Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.

Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $\left|OA\right|=d_1$- плечо силы $F_1$; $\left|OA\right|=d_2$- плечо силы $F_2$.

Рычаг находится в состоянии равновесия, если выполняется равенство:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1\right).\]

Предположим, что материальная точка движется по окружности (рис.2) под действием силы $\overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($\varepsilon $) точки определяется тангенциальной составляющей ($F_{\tau }$) силы $\overline{F}$:

\[mR\varepsilon =F_{\tau }\left(2\right),\]

где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{\tau }$ — проекция силы на направление скорости движения точки.

Если угол $\alpha $ — это угол между вектором силы $\overline{F}$ и радиус — вектором $\overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.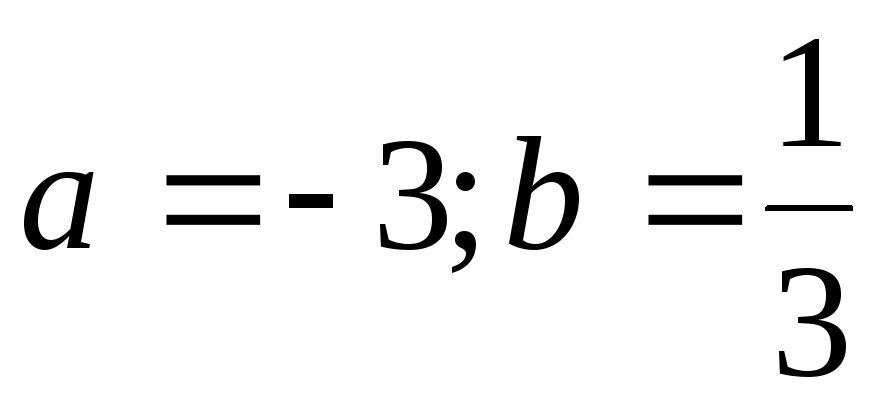 2), тогда:

\[F_{\tau }=F{\sin \alpha \ \left(3\right).\ }\]

Расстояние $d$ между центром O и линией действия силы $\overline{F}$ называют плечом силы. Из рис.2 следует, что:

\[d=R{\sin \alpha \ \left(4\right).\ }\]

Если на точку будет действовать сила ($\overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $\alpha $ станет равен $\frac{\pi }{2}$.

Момент силы и плечо

Понятие плечо силы иногда используют, для записи величины момента силы ($\overline{M}$), который равен:

\[\overline{M}=\left[\overline{r}\overline{F}\right]\left(5\right),\]

где $\overline{r}$ — радиус — вектор проведенный к точке продолжения силы$\ \overline{F}$. Модуль вектора момента силы равен:

\[M=F{r\sin \alpha =\ }Fd\ \left(6\right).\]

Построение плеча силы

И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз).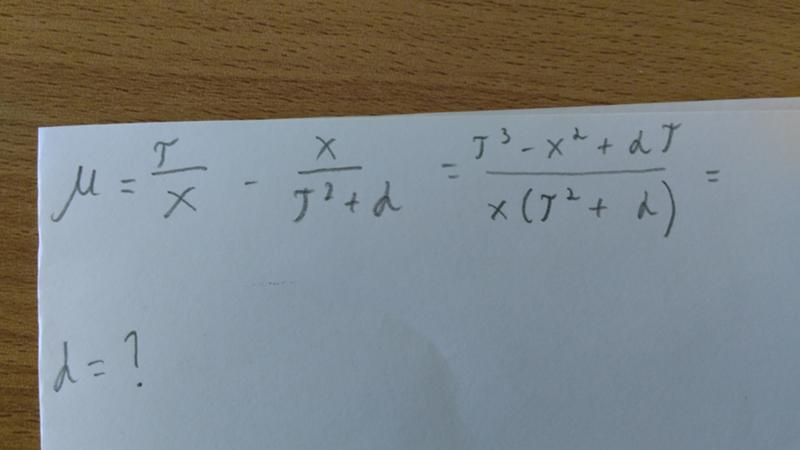 При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.

Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).

Примеры задач с решением

Пример 1

Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={\rm 2\ }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?

Решение. Основой решения задачи является правило равновесия рычага:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1.1\right),\]

где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:

\[\frac{m_1g}{m_2g}=\frac{d_2}{d_1}\to \frac{m_1}{m_2}=\frac{d_2}{d_1}\left(1.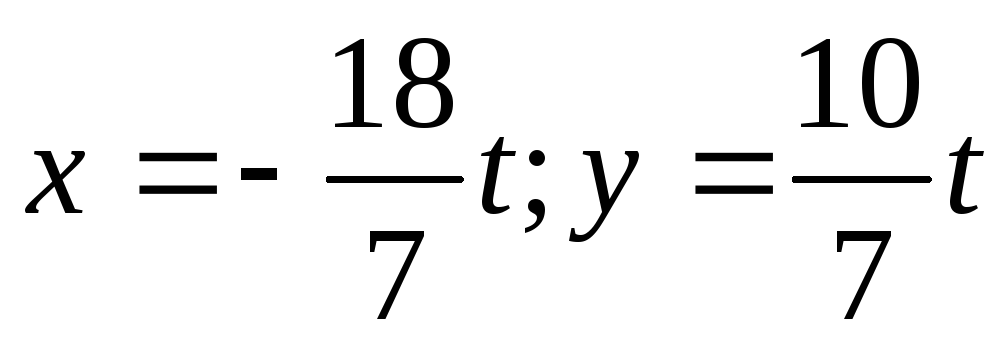 2\right).\]

Из выражения (1.2) получим искомую массу $m_1$:

\[m_1=\frac{m_2d_2}{d_1}.\]

Вычислим искомую массу:

\[m_1=2\cdot \frac{1}{4}=0,5\ (кг).\]

Ответ. $m_1=0,5\ кг$

Пример 2

Задание. Однородный стержень длинной $l\ $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $\alpha $. На стержне на расстоянии $b\ $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?

Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $M\overline{g}$, вес груза, расположенного на нем $\overline{P}=m_1\overline{g}$, сила реакции наклонной плоскости: $\overline{N}$; сила реакции опоры в точке A: $\overline{N}’$.

Плечи сил будем искать относительно точки A. Плечо силы $\overline{N’}$ будет равно нулю, так как сила приложена к стержню в точке А:

\[d_{N’}=0\ \left(2.1\right).\]

Плечо другой силы реакции опоры ($\overline{N}$) равно длине перпендикуляра AC:

\[d_N=l{\sin (90-\alpha )\ }=l{\cos \alpha \ \left(2.2\right).\ }\]

Плечо силы $M\overline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:

\[d_{Mg}=\frac{l}{2}\left(2.3\right).\]

Плечо силы $m_1\overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:

\[d_{m_1g}=b.\]

Ответ. $d_{N’}=0;;\ d_N=l{sin (90-\alpha )\ }=l{cos \alpha \ \left(м\right),\ }d_{Mg}=\frac{l}{2},\ d_{m_1g}=b$

Читать дальше: формула полезной мощности.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

1. Что такое алгебра?: Нахождение неизвестных…

Глава 1. Что такое алгебра?: Нахождение неизвестных…

Вы когда-нибудь хотели знать больше, чем знать?

В этом вся суть алгебры: делать неизвестные известными. К тому времени, когда вы через эту первую главу вы уже будете иметь представление о том, что X — это много больше, чем отметка, где зарыто сокровище. Вы разберетесь с уравнений , сохраняя обе части уравнения сбалансированный , и почему решение неизвестных на самом деле не такая уж большая задача иметь дело. Чего ты ждешь? Иди и начни!

Все началось с большой игровой распродажи

Джо некоторое время наблюдал за битвами игровой системы теперь и, наконец, определилась с тем, кого она хочет. Ее любимая система в продаже на этой неделе, и она готова купить. Но может ли она себе это позволить? Это где ей нужна небольшая помощь от вас.

Что на самом деле делает система Стоимость?

Когда покупаешь вещи, особенно дорогие электронные вещи — есть много вещей, которые добавляют в цену, помимо только номер на рекламном проспекте: налог с продаж, расширенная гарантия, доставка и управление и т. д. Так сколько же на самом деле будет стоить система KillerX?

Система облагается налогом…

Базовая цена системы составляет 199 долларов США. После этого нам нужно подумайте о налогах, которые составляют 5%. Давайте подсчитаем, сколько у Джо будет платить налоги:

… и расширенная гарантия тоже.

Джо собирается потратить 199 долларов на игровой автомат, и она хочет приобретите план расширенной гарантии за дополнительные 20 долларов. Давайте положим что и в цене. Какую цену придется заплатить Джо?

Вычисление суммы было не просто сложением! Это было решение для неизвестного — и это алгебра. В данном случае неизвестно, сколько всего было будет стоить.

Алгебра — это решение неизвестные

Алгебра заключается в том, чтобы найти недостающее число . информацию , которую вы ищете, используя информацию у тебя уже есть. Неизвестным может быть стоимость автокредита, количество газировки, которое вам нужно, или как высоко вы можете бросить воздушный шар с водой. Если вы этого не знаете, это неизвестный .

Все остальное, чему вы научитесь по алгебре, — это просто способы покачивайте вещи, чтобы помочь вам найти часть недостающей информации. Существуют правила о том, когда вы можете умножать вещи или когда вы можете сталкиваться что-то с одной стороны знака равенства на другую, но в конце день, все они просто уловки, чтобы помочь вам найти недостающую часть информацию, которую вы ищете.

У Джо есть еще неизвестные

Итак, Джо знает, сколько потребуется, чтобы купить потрясающую игру системы, включая расширенную гарантию. Но у нее до сих пор нет игры… или другой контроллер… или гарнитура.

Джо начала с 315,27 долларов на банковском счете. Теперь, когда она заплатила для консоли, сколько Джо может потратить на аксессуары? Начнем с запишем это прописью:

Мы знаем, сколько стоит консоль ($228,95), и мы знаем, сколько У Джо есть на ее счету (315,27 долларов США). Теперь просто заполните пробелы, и мы сможем вычислить бюджет аксессуаров Джо:

Решение любого неизвестного — это алгебра.

X обозначает неизвестное место

x просто удобная замена неизвестного блока, который мы использовали ранее. x легче написать, и это то, что вы искать, когда вы решаете уравнение. Неизвестное в любой заданной ситуацию называют переменной.

В реальном мире проблемы возникают каждый день; Идет перевод их в математические уравнения позволяет решить их.

Уравнения математические предложения

Уравнения, подобные тому, которое вы использовали ранее, чтобы выяснить, как сколько Джо могла бы потратить на аксессуары, это просто математические предложения. Они математический способ сказать что-либо. Итак, когда мы говорили о Джо баланс счета, мы фактически использовали уравнение:

Наше уравнение означает « Баланс счета минус сколько мы тратим на консоль столько, сколько у нас осталось аксессуары. » Значит, значит, счет баланс должен равняться стоимости консоли плюс деньги за аксессуары . Если мы запишем это предложение в виде уравнения, оно выглядит так:

Уравнения можно переставить как фразы.

Оба предложения означают одно и то же; они просто сформулированы иначе. На следующих нескольких страницах вы узнаете, как изменить математические предложения и убедитесь, что вы не меняете никаких значений.

Теперь РЕШИТЕ ​​для неизвестно

Джо пытается решить, стоит ли ей покупать ЖИВАЯ подписка. У нее 10 игр, и в 7 из них нет онлайна. играть в. Сколько у нее есть, что можно играть онлайн? Это делает смысл для нее покупать подписку?

Что нас действительно волнует здесь, так это то, что такое x — неизвестное количество игр. мы не действительно заботятся о семи играх в левой части уравнения. В на самом деле, мы можем избавиться от этой семерки, если мы убедимся, что делаем то же самое для обеих сторон уравнения.

Знак равенства означает, что обе стороны одинаковы. Итак, если мы отнимите 7 от одной стороны, мы должны сделать то же самое с другой стороны уравнения:.

Итак, что у нас осталось:

Для этого не нужны картинки алгебра.

Вам нужен способ использования операций, которые вы уже знаете (сложение, вычитание, умножение и деление) для решения уравнения.

Сложная часть? Вы должны сохранить равенство. Равенство означает одинаковый. Когда ты что-то делаешь с одной стороны уравнения, вы должны сделать то же самое с другой сторону уравнения.

Вот еще один способ взглянуть на онлайн-проблему Джо без картинки:

себя, вы изолируете переменная. Это самая важная часть решения уравнение. Изоляция переменной означает, что вы получили переменную себя в левой части уравнения, а все остальное складывается справа. Если вы можете изолировать переменную, значит, вы решили задачу. уравнение — ответ просто выскакивает, например, х = 3 .

Знание того, что вашей целью является выделение переменной, означает, что вы знать, какие числа отойти от левой стороны. Поскольку вы пытаетесь чтобы получить только x , это означает, что вы двигай семерку, а не 10!

Итак, когда какую операцию вы используете?

Противоположностью сложения является вычитание. Итак, если некоторые число добавляется к одной стороне уравнения, и вы хотите переместить это число на другую сторону, вы можете вычесть это число из обоих стороны. Математический термин, описывающий противоположные операции, называется обратными операциями.

Основными математическими операциями являются сложение, вычитание, умножение и деление. Обратная операция – это операция, которая отменяет операцию (как сложение отменяет вычитание). Обратный операции позволяют сдвигать число или переменную с одной стороны уравнение к другому, «отменив» это число на одной стороне уравнение.

Когда вы хотите решить уравнение:

1. Посмотрите на уравнение и решите какие числа двигать.

   Используя уравнение Джо, мы должны были избавиться от 7. Это потому что мы пытаемся изолировать переменную x.

2. Выясните, какую операцию использовать.

   Вам нужно использовать обратную операцию для числа, чтобы удалить Это. Для вычитаемого числа прибавьте. Для разделенного числа умножить, и так далее.

3. Сохранить равенство.

   Что бы вы ни решили сделать с одной частью уравнения, вы должен сделать с другим. Это сохраняет уравнение прежним.

Сила мозга

Существуют и другие обратные операции. Ты можешь думать о другие рабочие пары, которые работают?

Кто бы ни думал, что использовать x для обозначения типичного неизвестного, по-видимому, было хорошей идеей. не возражал против путаницы, которую это могло вызвать со знаком умножения, Икс. Тем не менее, многие другие люди сделали это.

Они отказались от использования x для умножение и придумал несколько более удобных для чтения вариантов:

И сдачу на дивизию тоже…

Знак дивизии, который вы привыкли видеть, тоже выбросили. Вместо этого вы увидите такие вещи:

Джо готова к аксессуарам!

Джо выяснила, что на ее счету осталось 86,32 доллара на аксессуары. Она решила, что хочет получить больше игр и не волноваться про гарнитуру только пока.

Джо быстро сделала алгебру, чтобы выяснить, сколько игр она может купить:

Проверка Проверка вашего work…

По мере изучения алгебры вы обнаружите, что задачи усложняются, и ошибиться довольно легко. Джо не правильно поделила, вот и достала! Проверка вашей работы не просто просматривая то, что вы сделали. Это также означает использование определенного техника под названием замена .

Замена использует ваше решение в оригинале уравнение

Замена означает замену чего-то другим. А замещающий учитель вместо обычного учителя, верно? К проверьте свою работу, вы подставляете найденный ответ на переменная в исходном уравнении.

Замена — это процесс, который можно использовать не только для проверки вашей работе, но и для других вещей тоже. Когда мы доберемся до более сложных уравнения и уравнения с более чем одной переменной, вы захотите использовать замену как часть процесса решения.

Обучение уравнениям

Давайте объединим все ваши сумасшедшие навыки решения уравнений, чтобы решить реальную задачу с помощью алгебры:

У Джо потрясающая установка!

После поездки, чтобы продать 4 игры и купить гарнитуру, Джо вошла в ЖИВИТЕ и купили этот новый уровень, и она готова к игре!

Джо собирается часами заниматься своим новым игру, но когда она закончит, будет легко понять, в какую игру она может позволить себе следующий!

Math Toolbox

Переменные алгебраических выражений как неизвестные величины

• Home /
• Algebra /
• Algebraic Expressions /
• Topics /
• Variables /
• Variables as Unknown Quantities

• Variables /
• Variables as Unknown Quantities

Topics

• Введение
• Темы
• Variables
• Variables as Unknown Quantities
• Variable Notations
• Constants
• Expressions and Equations
• Combining Like Terms
• Equations, Functions, and Formulas
• Toolbox Applications
• Geometric Formulas
• Unit Conversion
• In the Реальный мир
• Примеры
• Упражнения
• Задачи Math Shack
• Условия
• Лучшее из Интернета
• Викторины
• Раздаточный материал
• Содержание

•  НАЗАД
• СЛЕДУЮЩИЙ

Иногда нам дают заманчивую информацию о числе, и нам нужно выяснить, что это за число.

Пример задачи

Заполните пропуск: 2 + ? = 10.

Ответ равен 8, так как 2 + 8 = 10. Это решение может быть особенно полезным для тех, у кого 2 пальца на одной руке и 8 пальцев на другой.

Пример задачи

Какое число, удвоенное, равно 24?

Другими словами, если бы вам пришлось спать полдня, сколько бы это было?

В символах мы знаем, что 2 · ☐ = 24, и нам нужно заполнить поле соответствующей цифрой. В этом случае ответ будет 12, так как 2 · 12 = 24. Вы, должно быть, съели тонну индейки перед тем, как лечь спать прошлой ночью. Или двойная доза NyQuil.

В приведенных выше примерах используются заполнители «?» и «☐» для обозначения неизвестных чисел. Хотя эти заполнители хорошо подходят для таких простых примеров, они не будут работать так же хорошо для задач, в которых имеется более одной неизвестной величины. Кроме того, на большинстве клавиатур нет клавиши «коробка». Если вы действительно расстроены этим фактом, вам нужно спросить об этом у Geek Squad в Best Buy. По этим причинам мы используем буквы в качестве заполнителей для неизвестных чисел и называем эти буквы переменными. Потому что они «очень умеют» представлять числа. О, круто. Мы  – это  команда гиков.

Переменная, выражающая неизвестную величину, подобна ячейке, ожидающей заполнения. Чтобы переписать предыдущие примеры с переменными, мы пишем буквы вместо вопросительных знаков или квадратиков. Однако не выбрасывайте коробки. Возможно, скоро вам придется переехать.

Вместо «Заполните пропуск: 2 + ? = 10» мы пишем «Найдите значение х , для которого 2 + х = 10».

А вместо «Какое число удвоенное равно 24?» мы могли бы написать «Для какого значения x делает 2 · x = 24?»

Иногда информации, которую мы получили, недостаточно, чтобы заставить переменную быть одним конкретным числом. Информация может ограничивать возможные значения, которые может иметь переменная. В этом случае нам нужно определить все возможные значения или диапазон значений, которые решат данную проблему.