Официальный сайт МБОУ СОШ с.Паниковец
| Размер шрифта: | Межстрочный интервал: стандартный средний большой |
| Цвет фона: | Межбуквенный интервал: стандартный средний большой |
Версия для слабовидящих Отключить версию для слабовидящих
Липецкая область, Задонский район, с. Пани́ковец, ул. Запрудная, д. 18. Телефон: 8 (47471) 4-72-12
Электронная почта школы: [email protected]
02.02.2023
Сталинград. Победа, изменившая мир
С 1995 года 2 февраля в России отмечают как день Победы советского народа в Сталинградской битве.
Читать далее
Изобретательно и занимательно
В современном творчестве очень популярным стало lego – конструирование.
Читать далее
30.01.2023
Помни. Не забывай…
Хотя уже прошло две трети века, я не нашел ответа на вопрос:
Читать далее
27.01.2023
Девятьсот дней мужества
На окне моем горит свеча
Читать далее
26.01.2023
Предстоит учиться мне в университете
25 января в России отмечается день студента. История праздника студенчества тесно связана с историей Московского государственного университета. Так случилось, что именно в Татьянин день, 25 января в 1775 году императрица Елизавета Петровна подписала указ «Об учреждении Московского университета», и Татьянин день стал официальным праздником всех студентов, Святая Татьяна их небесной покровительницей.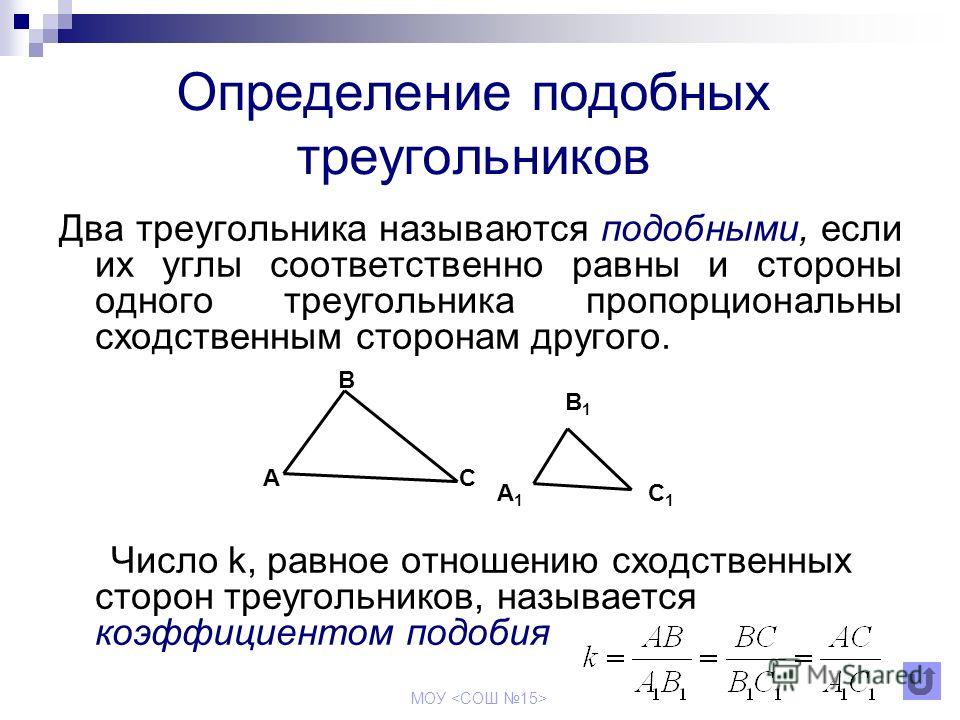
Читать далее
20.01.2023
Дорожная азбука
Липецкая область один из немногих регионов России, где проводится профильная Олимпиада по основам дорожной безопасности. Организаторами «Дорожной азбуки» являются областные Госавтоинспекция и управление образования и науки, а целями – повышение знаний учащихся школ в области транспортной безопасности и культуры. Мероприятие проводится в рамках реализации федерального проекта «Безопасность дорожного движения» национального проекта «Безопасные качественные дороги».
Читать далее
01.01.2023
Год педагога и наставника
2023 год Указом Президента России Владимира Путина объявлен Годом педагога и наставника. Миссия Года – признание особого статуса педагогических работников, в том числе выполняющих наставническую деятельность. Мероприятия Года педагога и наставника будут направлены на повышение престижа профессии учителя.
Читать далее
28.12.2022
Акция «Дед Мороз за БДД»
В канун новогодних праздников традиционно проводятся профилактические мероприятия. Наша школа охотно поддержала акцию по безопасности дорожного движения «Дед Мороз за БДД». Дед Мороз с ребятами из отряда ЮИД в игровом занятии проверили свои знания по ПДД, призывали всех позаботиться о своей безопасности, быть внимательными и осторожными при переходе дороги, а автомобилистам напомнили о том, что скоро зимние каникулы, когда нужно быть особенно внимательными. Дед Мороз поздравил всех с наступающим Новым годом.
Читать далее
23.12.2022
Этой силе имя есть – Россия!
25 декабря 2000 года президент России Владимир Владимирович Путин подписал федеральные законы о государственных символах Российской Федерации – флаге, гербе и гимне.
Читать далее
20.12.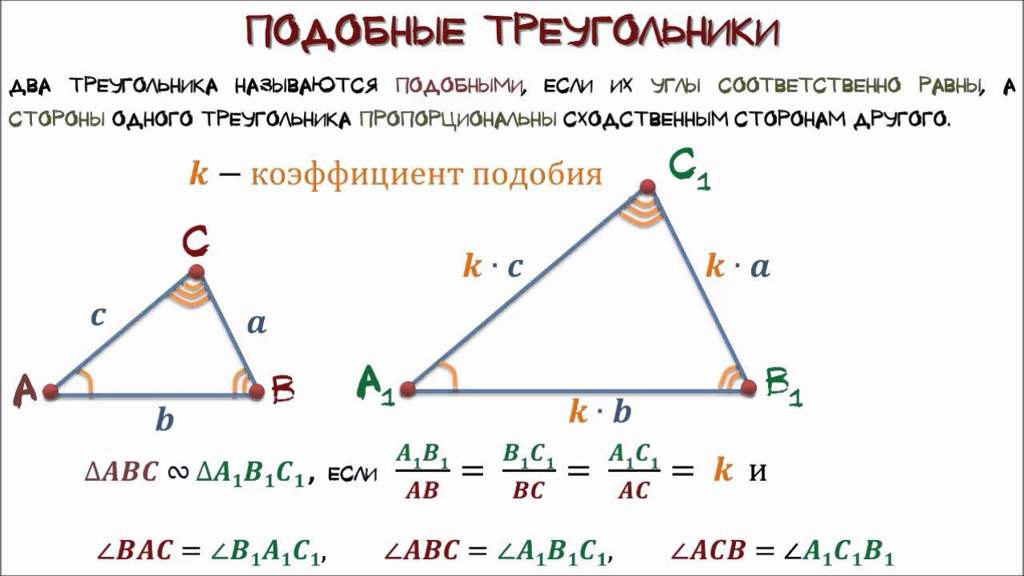 2022
2022
Правила поведения на водоёмах в зимний период
1. Необходимо помнить, что выходить на лед можно только в крайнем случае с максимальной осторожностью.
Читать далее
Все новости >>>
Что такое коэффициент подобия фигур?
Что такое коэффициент подобия фигур?
Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников. Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.
Чему равен квадрат коэффициента подобия?
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия S ABC S DEF = k 2 .
Как записывается Подобие треугольников?
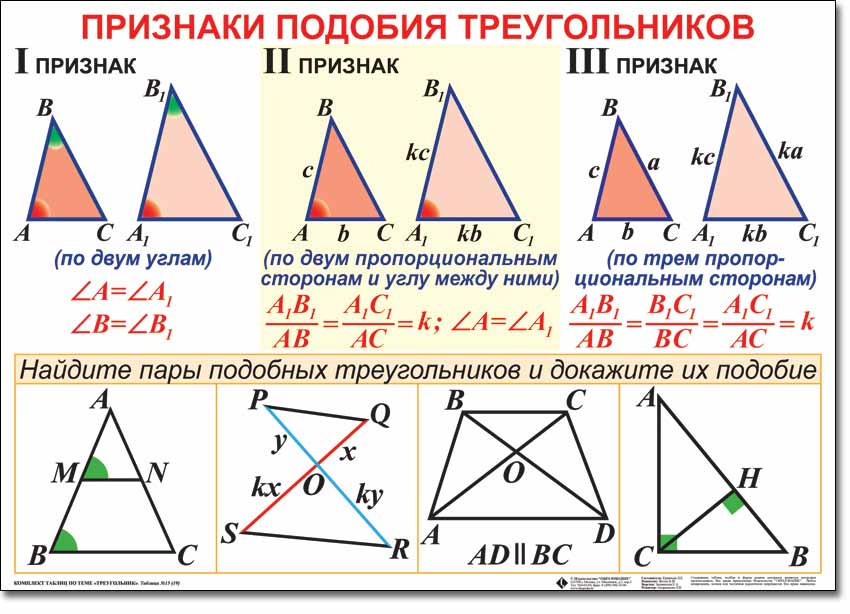
-Если угол одного треугольника,равен углу другого треугольника,то такие треугольники (пропорциональные в равном отношении)то такие треугольники подобны. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого,то такие треугольники подобны.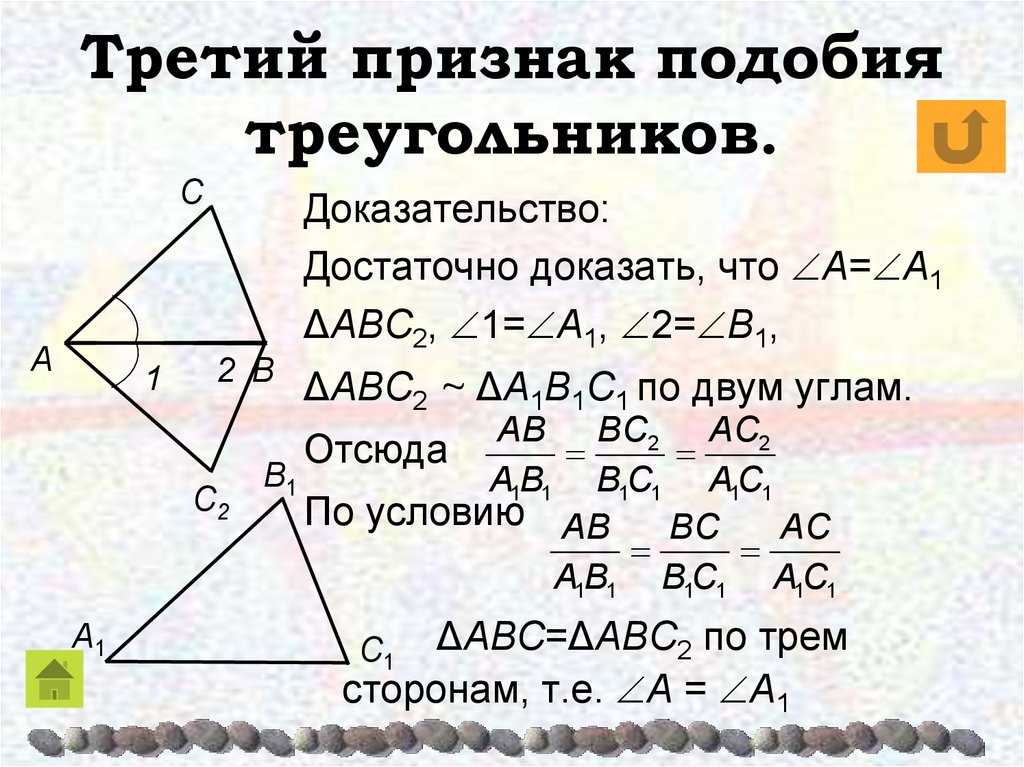
Как найти площадь подобных треугольников?
Площади подобных треугольников относятся как квадраты их соответствующих сторон, то есть отношение площадей подобных треугольников равно квадрату коэффициента подобия. Что и требовалось доказать.
Как найти угол в треугольнике?
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
Чему равны углы прямоугольного треугольника?
Прямоугольный треугольник Прямоугольным треугольником называется треугольник, у которого один угол прямой (равен 90∘). Стороны треугольника, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, − гипотенузой.
Чему равен катет прилежащий к углу 30 градусов?
Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
Чему равен катет в прямоугольном треугольнике?
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Чему равен угол лежащий против угла в 60 градусов?
Катет, лежащий против угла 60 градусов равен: То есть равен произведению гипотенузы на √3/2.
Чему равен катет лежащий против угла?
Катет прямоугольного треугольника, лежащий против угла , равен половине гипотенузы (см. Рис. 8).
Как найти гипотенузу зная катет и угол 60?
Если вам дан длинный катет (противолежащий углу в 60 градусов), просто умножьте длину этого катета на 2/√3, чтобы найти длину гипотенузы. Например, если короткий катет равен 4, то гипотенуза равна 4,62.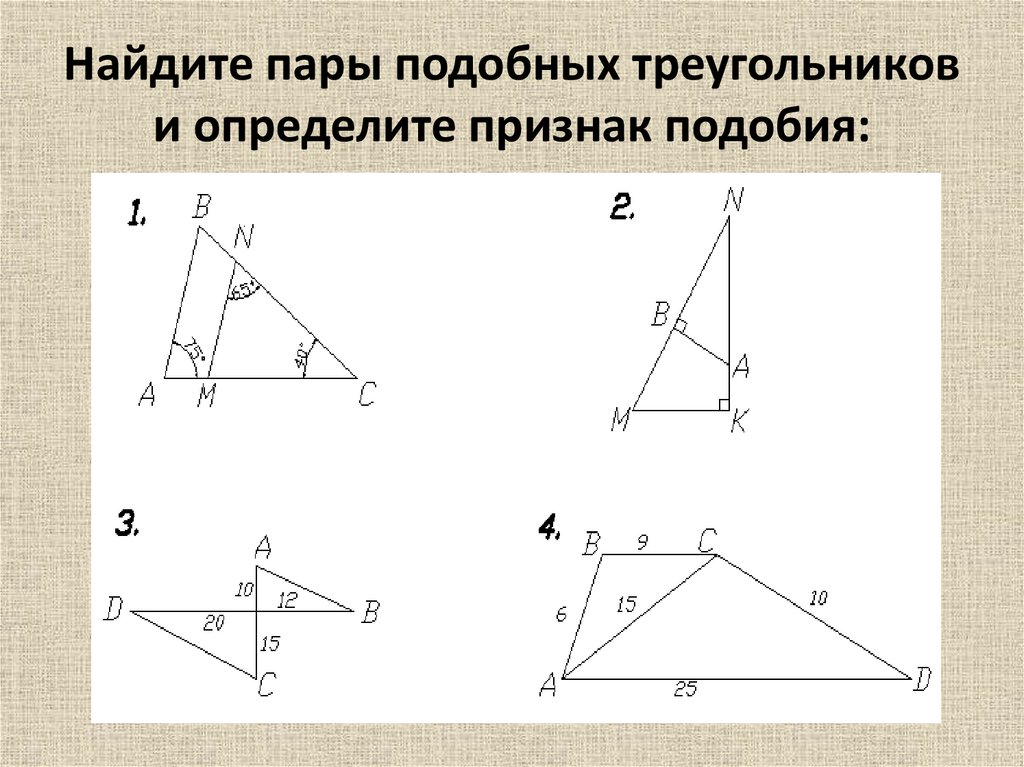
подобных треугольников | Определение, примеры, правила, теорема, резюме
Введение
Задумывались ли вы когда-нибудь над разнообразием геометрических фигур, с которыми мы сталкиваемся ежедневно, как соотнести две фигуры относительно их размера и ориентации? Оказывается, математики нашли ответ на этот вопрос — понятие подобия.
В этой статье мы вводим эту концепцию, сравнивая треугольники. Сначала мы вернемся к определению и свойствам треугольника с некоторыми соответствующими уравнениями, а затем покажем различные теоремы, связанные с подобными треугольниками. Попутно мы также попробуем несколько примеров в качестве дополнения к обучению.
Что такое треугольник?
В геометрии треугольником называется фигура, состоящая из набора трех прямых или сторон , трех внутренних углов , образованных парой сторон, и трех вершин или точек пересечения линий, образующих треугольник.
Треугольник также может иметь внешний угол .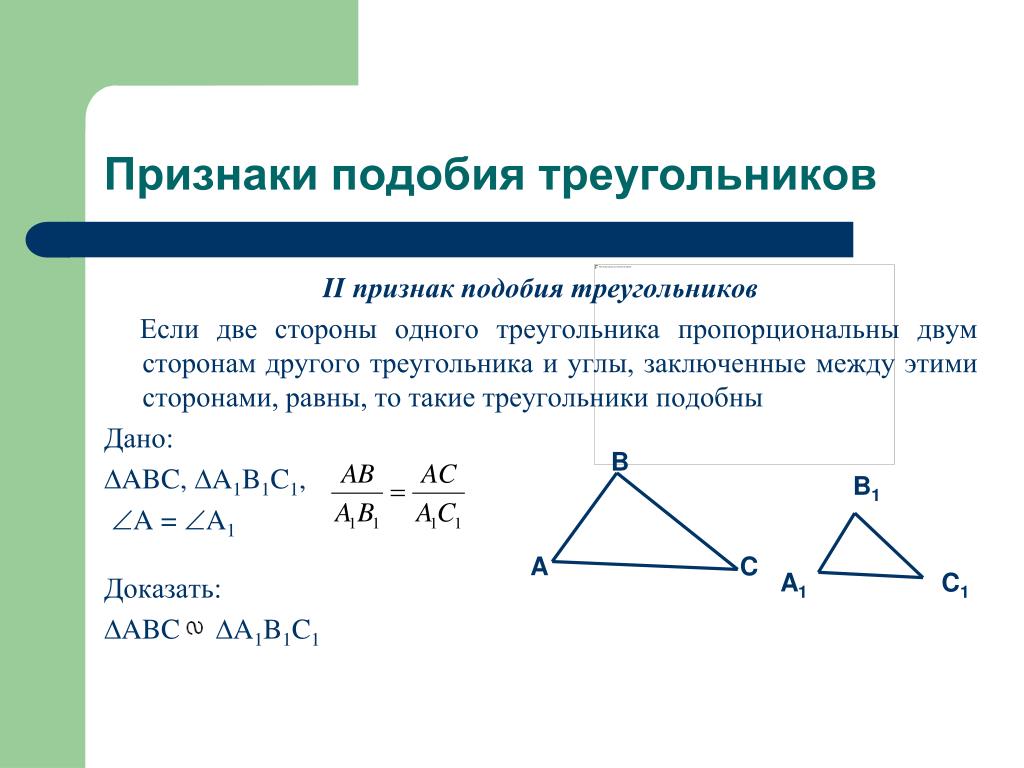 Это происходит, когда мы расширяем одну сторону треугольника и берем угол, который образует удлиненная линия в его вершине с другой стороной.
Это происходит, когда мы расширяем одну сторону треугольника и берем угол, который образует удлиненная линия в его вершине с другой стороной.
Какие свойства треугольников?
Прежде всего заметим, что сумма длин двух сторон треугольника больше длины его третьей стороны. И наоборот, можно сказать, что разница между длинами двух сторон всегда меньше длины третьей стороны.
Во-вторых, мы замечаем, что для любого треугольника сумма его внутренних углов составляет в сумме 180°. Это называется Свойством суммы углов .
В-третьих, заметим, что сумма мер внутреннего угла треугольника и прилежащего к нему внешнего угла является дополнительной. Другими словами, эти углы в сумме составляют 180°.
Что такое закон синусов?
Закон синусов , также известный под другими названиями, такими как закон синусов, правило синусов или формула синусов, представляет собой уравнение, связывающее углы треугольника с соответствующей стороной, противоположной его вершине.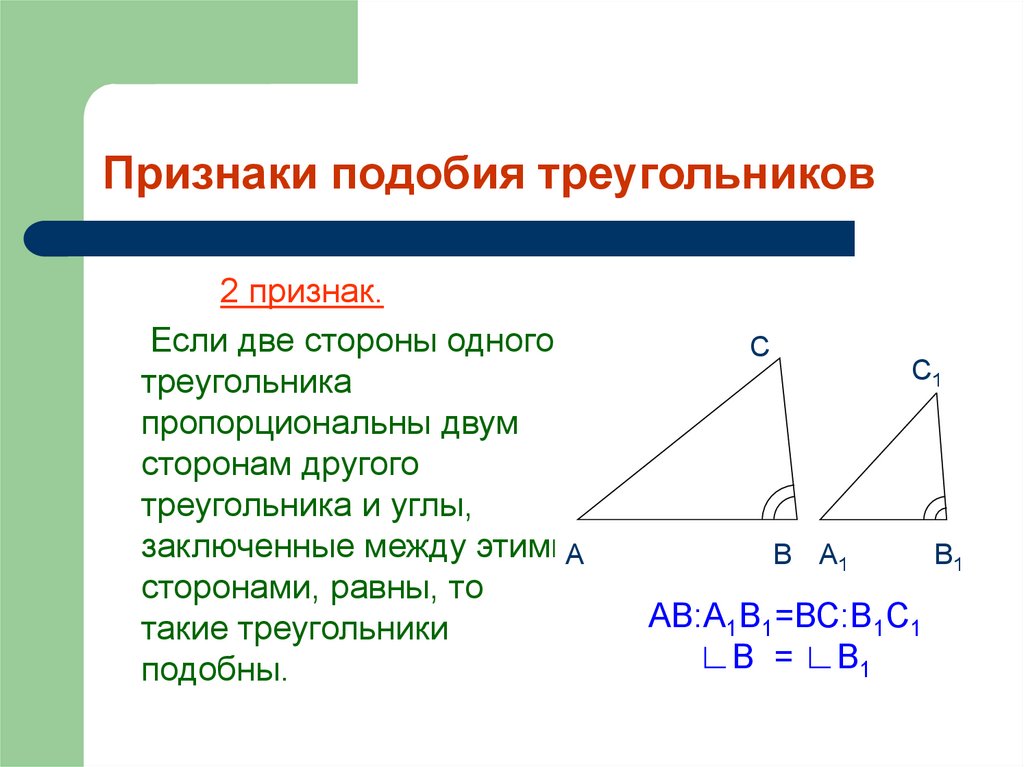
Утверждается, что отношение длины стороны треугольника к синусу угла при противоположной вершине одинаково для всех сторон и углов любого треугольника:
$\frac{a}{sinsin A} = \frac {b}{sinsin B} = \frac{c}{sinsin C}$
Мы можем использовать закон синусов, чтобы найти неизвестные стороны или углы треугольника с помощью набора заданной информации:
- Два угла треугольника и одна сторона, в которую он входит
- Два угла треугольника и один не- включенная сторона
- Две стороны треугольника и один угол, противолежащий каждой стороне
Что такое закон косинусов?
Закон косинусов , также называемый законом косинуса, правилом косинуса или формулой косинуса, представляет собой еще одно уравнение, связывающее углы треугольника с длинами его сторон.
Утверждается, что квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное их произведение и косинус угла между ними:
c 2 = a 2 + b 2 – 2ab coscos C
Альтернативно, мы можем написать аналогичные уравнения для оставшихся двух сторон:
б 2 = а 2 + c 2 – 2ac coscos B
Мы можем использовать закон косинусов, чтобы найти следующие неизвестные:
- Неизвестная сторона треугольника по двум сторонам и одному углу
- Неизвестные углы треугольника по всем трем стороны
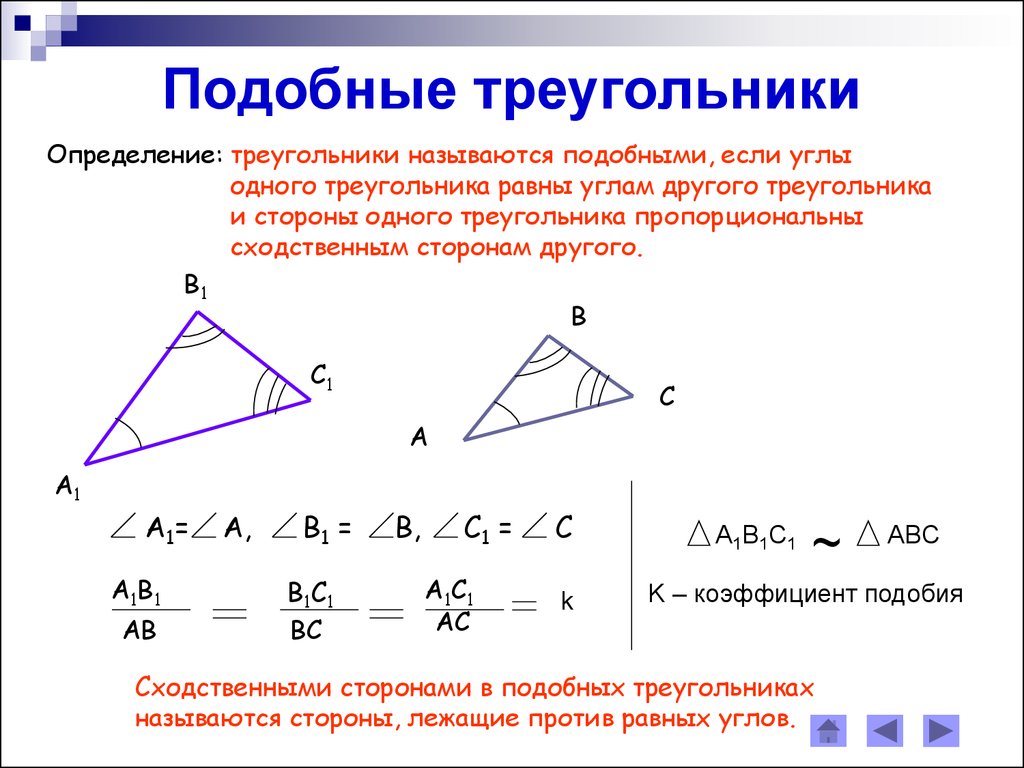
Подобные треугольники
Теперь мы переходим от основных понятий к основной теме. Сходство , по определению, есть сходство или сходство двух геометрических объектов. Когда мы говорим, что два объекта подобны, мы замечаем, что они выглядят одинаково. Будь то по их размеру или ориентации, мы узнаем, как мы переходим от одной формы к другой в похожих формах.
Сходство , по определению, есть сходство или сходство двух геометрических объектов. Когда мы говорим, что два объекта подобны, мы замечаем, что они выглядят одинаково. Будь то по их размеру или ориентации, мы узнаем, как мы переходим от одной формы к другой в похожих формах.
В случае треугольников мы говорим, что два треугольника подобны, если их размеры пропорциональны и/или один треугольник является либо повернутой, либо перевернутой версией другого: быть подобными , если выполняются следующие условия:
- Длины их сторон пропорциональны друг другу
$\frac{AB}{XY} = \frac{AC}{XZ} = \frac{BC} {YZ}$
- Меры соответствующих углов равны
∠A≅∠X
∠B≅∠Y
∠C≅∠Z
В приведенном выше примере у нас есть треугольники ABC и XYZ, которые являются масштабированными, повернутыми версиями друг друга. Это означает, что они являются подобными треугольниками, или в математической записи: ABC ~ XYZ, где «» — символ, обозначающий сходство.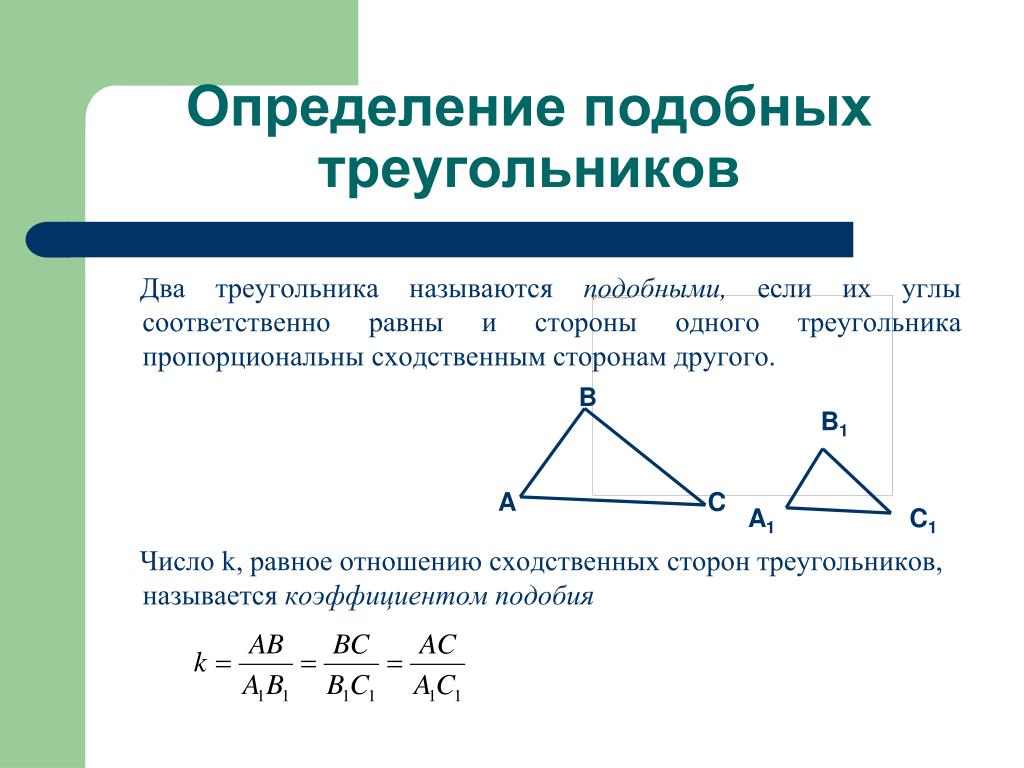
При этих условиях у нас есть следующие теоремы, касающиеся подобия между треугольниками: теорема о подобия угла-угла, теорема о подобия стороне-угла-сторона и теорема о подобия стороне-стороне-стороне.
AA Теорема подобия
Теорема о подобия углах (AA) определяет подобные треугольники на основе пары двух углов в треугольниках. Он гласит, что если мера двух углов треугольника равна величине двух углов другого треугольника, то эти два треугольника подобны.
Это также относится к теореме подобия «угол-угол-угол» (AAA), поскольку по свойству суммы углов мы можем сказать, что третий угол и соответствующий ему угол равны.
Теорема подобия SAS
Теорема о сходстве сторон (SAS) определяет сходство между двумя треугольниками путем сравнения набора двух углов и угла, образованного между этими сторонами.
Он гласит, что если мера длин любых двух сторон в треугольнике пропорциональна длине двух сторон в другом треугольнике, а меры прилежащих к ней углов в обоих треугольниках равны, то они являются подобными треугольниками.
SSS Теорема подобия
Теорема о сходстве сторон (SSS) проверяет, подобны ли два треугольника, основываясь на сравниваемых сторонах обоих треугольников.
Он гласит, что если меры длин всех сторон треугольника пропорциональны длинам сторон другого треугольника, то они подобны.
Примеры решения задач
Теперь мы можем приступить к решению примеров задач, чтобы применить то, что мы уже узнали. Каждая проблема решает различные обсуждаемые формулы и ставит перед нами задачу решить ее с помощью предоставленной нам информации.
Использование теоремы подобия AA
Пример задачи 1:
На рисунке ниже у нас есть два треугольника FGH и JKL. Два треугольника подобны?
Решение:
Сначала отметим данные меры каждого угла:
∠F=40° ∠G=80° ∠H=60°
∠J=80° ∠K=60° ∠L=40 °
Затем мы связываем соответствующие углы обоих треугольников, чтобы установить следующие равенства:
∠F≅∠L
∠G≅∠J
∠H≅∠K
Теперь, поскольку по крайней мере две пары углов имеют одинаковую меру, мы заключаем, что по теореме подобия AA данные треугольники подобны :
△FGH∼△JKL
Пример задачи 2:
Два треугольники CAT и DOG, углы которых даны, показаны ниже:
Нам задают следующие вопросы:
- Какова мера неизвестного угла ∠C?
- Чему равен неизвестный угол ∠D?
- Являются ли CAT и DOG подобными треугольниками?
Решение:
- Сначала рассмотрим треугольник CAT.
 Два его угла задаются с помощью мер:
Два его угла задаются с помощью мер:
∠A=35°
∠T=75°
Тогда с помощью свойства суммы углов мы можем связать сумму внутренних углов CAT как:
∠C+∠ A+∠T=180°
Подставив данные меры угла, получим:
∠C+35°+75°=180°
Далее перепишем уравнение через неизвестный угол, переставив члены вправо -ручная часть уравнения:
∠C=180°-35°-75°
Наконец, мы вычитаем меры углов, чтобы получить меру неизвестного угла:
∠C=70°
Следовательно, мера ∠C равна 70°.
- Следуя шагам, выполненным в части A, рассмотрим другой треугольник DOG и отметим заданные меры его углов:
∠O=70°
∠G=75°
можно соотнести меры внутренних углов DOG следующим образом:
∠D+∠O+∠G=180°
Подставив данные меры угла, получим:
∠D+∠70°+∠75°=180°
Затем перепишем уравнение в терминах неизвестного угла:
∠D=180°-70°-75°
Наконец, мы вычтем указанные меры, чтобы получить меру неизвестного угла:
∠D=35°
Следовательно, мера ∠D равна 35°.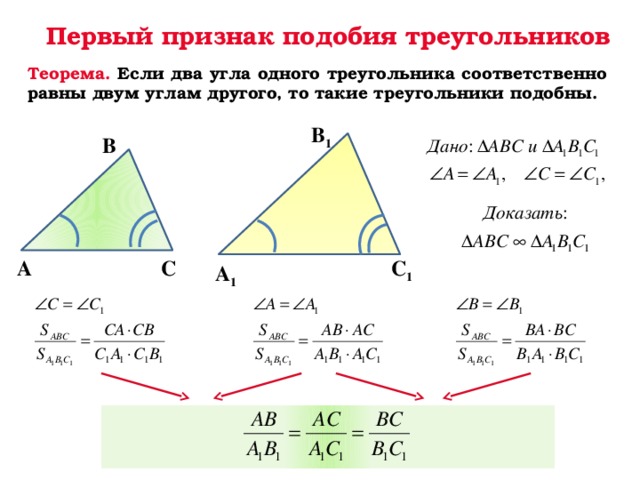
- Из мер углов, полученных из части А и части Б, свяжем соответствующие углы обоих треугольников, установив следующие равенства:
∠C≅∠O
∠A≅∠D
∠T≅∠G
Теперь, поскольку по крайней мере две пары углов имеют одинаковую меру, мы заключаем, что по теореме о подобия АА данные треугольники подобны :
△CAT∼△DOG
Пример задачи 3:
Предположим, у нас есть два треугольника △ELF и △ORC, стороны и углы которых заданы, как показано ниже:
Покажите, что два треугольника подобны через Теорема подобия AA.
Решение:
Чтобы использовать теорему подобия AA, мы должны показать, что по крайней мере две пары углов в △ELF и △ORC равны по мере. Однако для треугольника ELF дан только один угол. Следовательно, мы сначала находим меру либо ∠L, либо ∠F.
В этом случае мы решили найти ∠L, используя закон синусов. Напомним, что для треугольника ELF по закону синусов выполняется следующее равенство:
$\frac{e}{sinsin E} = \frac{l}{sinsin L} = \frac{f}{sinsin F}$
Ориентируясь по заданным углам и длинам сторон, имеем:
$\frac{8}{sinsin 75°} = \frac{7}{sinsin L}$
Переписав уравнение через неизвестную угловую меру L, получим:
sinsin L = $\ frac{7}{8}$ x sinsin 75°
Находя значение sin 75° , мы упрощаем правую часть уравнения до:
sinsin L= $\frac{7}{8}$ × 0,97
Затем мы можем перемножить числа вместе, чтобы получить:
sinsin L=0,85
Наконец, мы берем арксинус обеих частей уравнения, чтобы найти меру ∠L:
L=arcsin arcsin (0,85)
∴L=58°
Теперь заметим, что для данных треугольников мы имеем следующие конгруэнтные углы: Следовательно, по теореме подобия AA заключаем, что оба треугольника подобны :
△ELF∼△ORC
Используя теорему подобия SAS
Пример задачи 4:
Рассмотрим одну и ту же пару треугольников из примера Задача 3:
На этот раз покажите, что △ELF∼△ORC, используя теорему подобия SAS.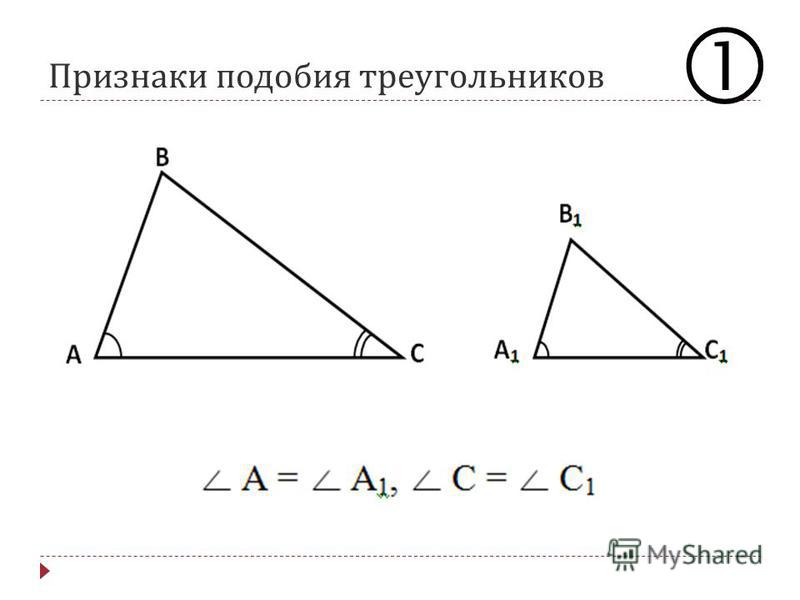
Решение:
Из данного рисунка мы знаем, что углы обоих треугольников равны:
∠E=75°
∠O=47°
∠R=58°
заметим, что меры углов ∠E и ∠C равны:
∠E≅∠C
Далее наблюдаем заданные длины сторон обоих треугольников:
EF=7 LF=8
OC=21 OR=24
Если рассмотреть сторону, противоположную равным углам, и одну сторону, примыкающую к ней, то сравнить отношение их мер между треугольниками △ELF и △ORC, то получим:
$\frac{EF}{OC} = \frac{7}{21} = \frac{1}{3}$
$\frac{LF}{OR} = \frac{8}{24} = \frac{1}{3}$
Следовательно, мы можем сказать, что две стороны обоих треугольников пропорциональны друг другу:
$\frac{EF}{OC} = \frac{LF}{OR}$
Поскольку ∠E≅∠C и $\frac{EF}{OC} = \frac{LF}{OR}$, по теореме подобия SAS мы заключаем, что данные треугольники подобны :
△ ELF ∼ △ORC
Пример задачи 5:
На рисунке ниже у нас есть два равнобедренных треугольника, стороны и углы которых известны:
Два треугольника похожи?
Решение:
Прежде всего заметим, что данные треугольники равнобедренные.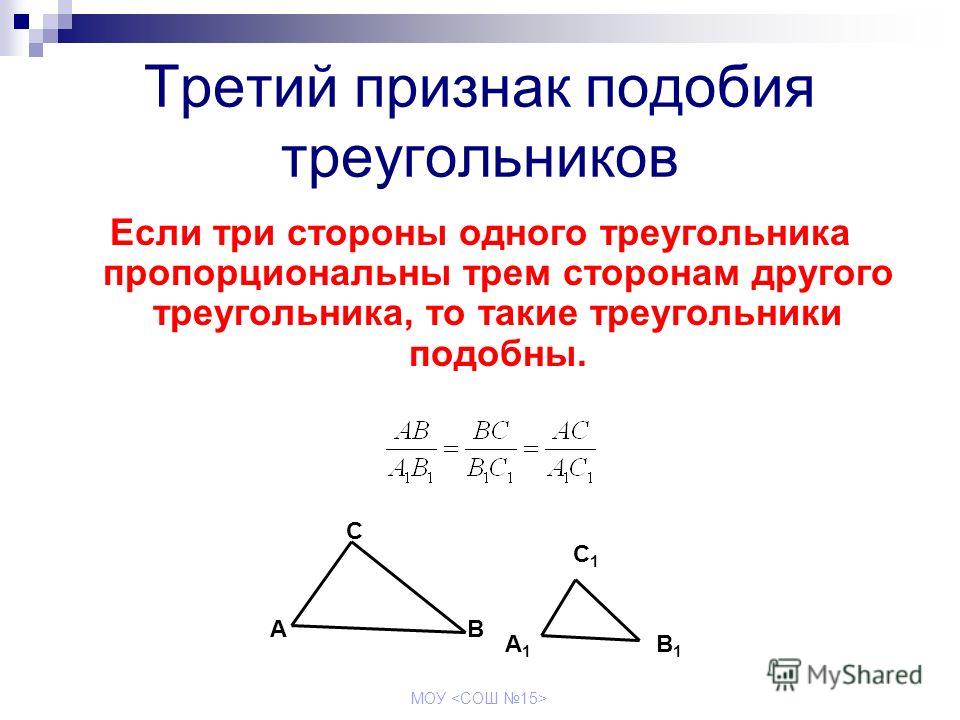 Это означает, что длины двух сторон равны, и меры двух внутренних углов также равны. В этом случае мы имеем следующую информацию:
Это означает, что длины двух сторон равны, и меры двух внутренних углов также равны. В этом случае мы имеем следующую информацию:
∠E=∠R=65°
RD=ED=13
TI=TN=26
Мы хотим найти меру неизвестного угла ∠D. По свойству суммы углов мы можем связать внутренние углы RED таким образом, что:
∠R+∠E+∠D=180°
Подставляя заданные меры углов, получаем:
65°+65°+∠D=180°
Затем переставляем члены, чтобы выделить неизвестный угол ∠D:
∠D=180°-65°-65°
Следовательно, мы можем определить меру угла ∠D, вычитая числа в правой части уравнения:
∠D=50°
Мы обратите внимание, что этот угол имеет меру, равную ∠T. Таким образом, мы можем сказать, что оба угла равны:
∠D≅∠T
Далее, если мы рассмотрим равные стороны обоих треугольников и возьмем их отношение, получим следующие равенства:
$\frac{RD}{TI}=\frac{13}{26}=\frac{1} {2}$
$\frac{ED}{TN}=\frac{13}{26}=\frac{1}{2}$
Таким образом, мы можем сказать, что две стороны обоих треугольников пропорциональны между собой:
$\frac{RD}{TI}=\frac{ED}{TN}$
Наконец, поскольку ∠D≅∠T и $\frac{RD}{TI}=\frac{ED {TN}$, поэтому по теореме подобия SAS мы заключаем, что оба треугольника равны Аналогичный :
△ Red ∼ △ △ TIN
с использованием теоремы SSS сходства
Проблема Проблема 6:
Предположим, что мы имеем два равенственных треугольника △ ABC и △ xyz:
- , если их длина AB=1 и XY=10, подобны ли эти два треугольника?
- Если длины сторон △ABC изменить на AB=20, а △XYZ оставить без изменений, будут ли они по-прежнему подобны треугольникам?
- Можно ли вообще сказать, что все равносторонние треугольники подобны? Почему или почему нет?
Решение:
- Напомним, что у равносторонних треугольников все стороны имеют одинаковую длину.
 Отсюда следует, что длины сторон обоих треугольников равны:
Отсюда следует, что длины сторон обоих треугольников равны:
AB=AC=BC=1
XY=XZ=YZ=10
Теперь, если мы возьмем отношение между соответствующими сторонами обоих треугольников, мы заметим, что они имеют одинаковое значение:
$\frac{AB}{XY}=\frac{1}{10}$
$\frac{AC}{XZ}=\frac{1}{10}$
$\ frac{BC}{YZ}=\frac{1}{10}$
Следовательно, мы можем сказать, что все стороны обоих треугольников пропорциональны друг другу:
$\frac{AB}{XY}=\frac{AC}{XZ}=\frac{BC}{YZ}$
Следовательно, по теореме подобия SSS мы заключаем, что данные треугольники подобны :
△ABC∼△XYZ
- . =BC=20
XY=XZ=YZ=10Мы знаем, что отношение их соответствующих сторон равно:
$\frac{AB}{XY}=\frac{AC}{XZ}=\frac{BC}{YZ}=\frac{20}{10}$
Таким образом, по теореме подобия SSS заключаем что два треугольника также подобны :
△ABC∼△XYZ
- Мы заметили, что изменение длин сторон любого треугольника по-прежнему сохраняет сходство между двумя треугольниками.
 Поскольку длины сторон одного треугольника изменяются пропорционально другим его сторонам, мы ожидаем, что отношение между длинами сторон обоих треугольников останется равным.
Поскольку длины сторон одного треугольника изменяются пропорционально другим его сторонам, мы ожидаем, что отношение между длинами сторон обоих треугольников останется равным.
Благодаря этому наблюдению мы можем сказать, что все равносторонние треугольники подобны .
Пример задачи 7:
Показаны два треугольника △RST и △UVW, длины сторон и меры углов которых заданы:
- Какова длина стороны RS треугольника △RST?
- Два треугольника подобны?
Решение:
- Заметим, что для треугольника △RST даны две стороны и угол между ними. Нам нужно знать все три стороны обоих треугольников, чтобы использовать теорему подобия SSS. Следовательно, мы можем применить закон косинусов для определения длины стороны RS.
Напомним из закона косинусов, что длины сторон △RST можно выразить следующим образом: )
Подставив заданные длины сторон и прилежащий угол, мы получим:
RS 2 =16 2 +14 2 -(2×16×14×coscos 47°)
Затем вычисляем значение тригонометрической функции:
RS 2 =16 2 +14 2 -(2×16×14×0,682)
Далее умножаем числа, заключенные в скобки:
RS 2 =16 2 +14 2 -305,536
Также возьмем квадрат обоих числа в правой части уравнения:
RS 2 =256+196-304,64
Таким образом, мы можем упростить уравнение, складывая/вычитая числа вместе:
RS 2 =146,464
5
4 Извлекаем квадратный корень из обеих сторон, чтобы получить длину стороны RS:
RS=12,102
Округляя до ближайшего целого числа, заключаем, что длина RS равна 12:
RS=12
- Теперь, когда мы знаем, что длины сторон обоих треугольников равны:
8887788888878 гг.RS = 12 RT = 14 ST = 16 VW = 36 UW = 42 UV = 48  имеем следующие значения:
имеем следующие значения:$\frac{RS}{VW}=\frac{12}{36}=\frac{1}{3}$
$\frac{RT}{UW}=\frac{14}{42}= \frac{1}{3}$
$\frac{ST}{UV}=\frac{16}{48}=\frac{1}{3}$Таким образом, мы можем сказать, что все стороны обоих RST и UVW пропорциональны друг другу:
$\frac{RS}{VW}=\frac{RT}{UW}=\frac{ST}{UV}$
Следовательно, по теореме подобия SSS заключаем что оба треугольника подобны :
△RST∼△UVW
Пример задачи 8:
На рисунке, показанном ниже, у нас есть два прямоугольных треугольника △LMN и △OPQ:
- Какова длина гипотенузы △LMN?
- Какова длина стороны OP △OPQ?
- Данные треугольники подобны?
Решение:
- Начнем с определения длины гипотенузы △LMN, применяя теорему Пифагора. Напомним, что для прямоугольного треугольника длина гипотенузы равна:
LN 2 =LM 2 +MN 2
Подставляя данные длины сторон, мы имеем:
LN 2 =8 2 +6 2
Затем мы возьмем квадрат обоих чисел, которые мы подставили ранее, чтобы получить:
LN 2 =64+36
Затем мы складываем оба, числа в правой части уравнения:
LN 2 =100
Наконец, мы извлекаем квадратный корень из обеих частей уравнения, чтобы получить длину гипотенузы:
LN=10
Следовательно , длина гипотенузы LN равна 10,
- Затем мы переходим к нахождению длины неизвестной стороны △OPQ по теореме Пифагора.
 Опять же, для прямоугольного треугольника длины их сторон связаны как:
Опять же, для прямоугольного треугольника длины их сторон связаны как:
OQ 2 =OP 2 +PQ 2
Переписав уравнение с точки зрения неизвестной стороны OP, мы получим:
OP 2 =OQ 2 -PQ 2
Подставив указанные длины сторон, получим:
OP 2 =30 2 8 2 -10061 2
Затем возьмем квадрат обоих чисел, которые мы подставили ранее, чтобы получить:
OP 2 =900-324
Вычитая оба числа в правой части уравнения, мы имеем:
OP 2 =576
Наконец, мы извлекаем квадратный корень из обеих частей уравнения, чтобы получить длину неизвестной стороны OP:
OP=24
Следовательно, длина стороны OP равна 24.
- Из вычислений, сделанных в части A и части B, мы знаем, что длины сторон обоих треугольников равны:
LM = 8 MN = 6 LN = 10 OP = 24 PQ = 18 OV = 24 PQ = 18 OV = 24 PQ = 18 oq = 24 PQ = 18 .  обоих треугольников имеем следующие значения:
обоих треугольников имеем следующие значения:$\frac{LM}{OP}=\frac{8}{24}=\frac{1}{3}$
$\frac{MN}{PQ }=\frac{6}{18}=\frac{1}{3}$
$\frac{LN}{OQ}=\frac{10}{30}=\frac{1}{3}$
Таким образом, мы можем сказать, что все стороны как LMN, так и OPQ пропорциональны друг другу:
$\frac{LM}{OP}=\frac{MN}{PQ}=\frac{LN}{OQ}$
Следовательно, по теореме подобия SSS мы заключаем, что оба треугольника подобны :
△LMN∼△OPQ
Резюме
Треугольник представляет собой форму, образованную набором трех сторон , трех внутренних углов , образованных между сторонами треугольника, и трех вершин, или 9001 пересечения сторон треугольника. Он также может иметь внешних углов , образованный расширением одной из его сторон.
Свойство Сумма углов утверждает, что сумма всех внутренних углов треугольника составляет в сумме 180°.

Закон синусов гласит, что отношение длины стороны треугольника к синусу угла при противоположной вершине одинаково для всех сторон и углов любого треугольника:
$\frac{a}{sinsin A} = \frac{b}{sinsin B} = \frac{c}{sinsin C}$
С другой стороны, Закон косинусов связывает квадраты длин сторон треугольника и косинусы между ними: быть подобными , если выполняются следующие условия:
Длины их сторон пропорциональны друг другу
Меры соответствующих углов равны
Чтобы определить, подобны ли два треугольника, мы используем следующие теоремы подобия:
Теорема о сходстве углов (AA) утверждает, что если мера двух углов треугольника равна мере двух углов другого треугольника, то эти два треугольника подобны.
Теорема подобия Сторона-Угол-Сторона (SAS) утверждает, что если мера длин любых двух сторон в треугольнике пропорциональна длине двух сторон в другом треугольнике, а меры вложенных углов в оба треугольника равны, то они подобны треугольникам.

Теорема о сходстве сторон (SSS) утверждает, что если меры длин всех сторон треугольника пропорциональны длинам сторон другого треугольника, то они подобны.
Часто задаваемые вопросы (FAQ)
Что такое включенная сторона?
Включенная сторона — это сторона, совпадающая с двумя углами. Например, для треугольника FGH сторона $\overline{HF}$ является включенной стороной между двумя углами ∠H и углом ∠F:
По этому рисунку также можно сказать, что $\overline{HG}$ — вложенная сторона между ∠H и ∠G, а $\overline{GF}$ — вложенная сторона между ∠G и ∠F.
Что такое прилежащий угол?
Прилежащий угол — это угол, который совпадает с двумя сторонами. Используя предыдущий пример, угол ∠H является внутренним углом между двумя сторонами $\overline{HF}$ и $\overline{HG}$:
Из этого рисунка также можно сказать, что ∠G является внутренним углом между $ \overline{HG}$ и $\overline{GF}$, а ∠F — внутренний угол между $\overline{HF}$ и $\overline{GF}$.

Что такое не включенная сторона?
Невключенная сторона — это сторона, не совпадающая с двумя углами. Например, для треугольника △FGH стороны $\overline{HG}$ и $\overline{GF}$ являются невключенными сторонами между двумя углами ∠H и углом ∠F:
Из этого рисунка также можно сказать что $\overline{HF}$ и $\overline{GF}$ — невключенные стороны между ∠H и ∠G, а $\overline{HG}$ и $\overline{HF}$ — невключенные стороны между ∠G и ∠F.
Что такое не включенный угол?
Невключенный угол — это угол, который не совпадает с двумя сторонами. Используя предыдущий пример, углы G и ∠F являются невключенными углами между двумя сторонами $\overline{HF}$ и $\overline{GF}$:
Из этого рисунка также можно сказать, что H и ∠F равны невключенные углы между $\overline{HG}$ и $\overline{GF}$, и что H и ∠G являются невключенными углами между $\overline{HF}$ и $\overline{GF}$.
Что такое теорема Пифагора?
Теорема Пифагора связывает все три стороны прямоугольного треугольника уравнением.
 Он утверждает, что квадрат длины его гипотенузы равен сумме квадратов длин других его сторон:
Он утверждает, что квадрат длины его гипотенузы равен сумме квадратов длин других его сторон:c 2 =a 2 +b 2
Как мы используем теорему Пифагора?
Если известны длины сторон прямоугольного треугольника, подставляем их длины в формулу. Затем мы возводим их длины в квадрат и складываем их, чтобы получить квадрат длины гипотенузы. Извлекая квадратный корень из суммы, мы получаем длину гипотенузы c.
Периметр треугольника (на тему Дня Благодарения) Рабочие листы по математике
Прямоугольные треугольники (на тему Хэллоуина) Рабочие листы по математике
Пространственные навыки: треугольники и четырехугольники (на тему зимнего солнцестояния) Рабочие листы по математикеМы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Когда треугольники подобны? (3 способа сказать, с примерами) – JDM Educational
В геометрии вы часто будете сравнивать треугольники, чтобы увидеть, одинаковы ли длины их сторон или углы.
 Конгруэнтные треугольники абсолютно одинаковы с точки зрения длин сторон и углов, но как насчет подобных треугольников?
Конгруэнтные треугольники абсолютно одинаковы с точки зрения длин сторон и углов, но как насчет подобных треугольников?Итак, когда треугольники подобны? Два треугольника подобны, если каждый треугольник имеет одинаковый набор мер угла. Например, если треугольник А имеет углы, равные 20, 50 и 110 градусов, то треугольник В подобен треугольнику А тогда и только тогда, когда его углы равны 20, 50 и 110 градусов.
Конечно, мы можем использовать несколько различных критериев, чтобы определить, когда два треугольника подобны.
В этой статье мы поговорим о подобных треугольниках и о том, как определить, что треугольники подобны. Мы также рассмотрим несколько примеров, чтобы прояснить концепцию в различных сценариях.
Начнем.
Когда треугольники подобны?
Два треугольника подобны, если каждый треугольник имеет точно такой же набор трех мер угла. Например:
- Если треугольник A имеет углы, равные 30, 70 и 80 градусов, а треугольники A и B подобны, то треугольник B также должен иметь углы, равные 30, 70 и 80 градусов.

Для подобных треугольников длина каждой стороны одного треугольника пропорциональна соответствующей длине стороны другого треугольника. Например:
- Если длина сторон треугольника А равна 3, 4 и 5 футам, а длина сторон треугольника В равна 6, 8 и 10, то треугольники А и В подобны, так как пропорция соответствующих сторон равна 2 (6 = 2*3, 8 = 2*4, 10 = 2*5).
Пропорция между двумя подобными треугольниками не обязательно должна быть целым числом. Пропорция может быть любым положительным числом P.
Когда у квадратного уравнения нет решения…
Пожалуйста, включите JavaScript
Когда у квадратного уравнения нет решения?
Отношение между длинами сторон двух подобных треугольников может быть любым положительным числом P.Если треугольник A имеет длины сторон x, y и z, то аналогичный треугольник B будет иметь длины сторон Px, Py и Pz.
 Обратите внимание, что площадь треугольника B будет равна P 2 , умноженной на площадь треугольника A:
Обратите внимание, что площадь треугольника B будет равна P 2 , умноженной на площадь треугольника A:- Площадь треугольника = (основание*высота)/2
Помните, что пара конгруэнтных треугольников подобна, и длины соответствующих сторон также одинаковы.
Примечание: два треугольника могут быть подобны, но не конгруэнтны. Другими словами:
Два треугольника могут быть подобны (одинаковые пары углов), но не равны (разные, но пропорциональные длины сторон).«Если два треугольника равны, то они и подобны. Однако два подобных треугольника могут быть, а могут и не быть конгруэнтными».
Все сводится к пропорции P между соответствующими длинами сторон. Для двух подобных треугольников с пропорцией P между соответствующими длинами сторон:
- Если P = 1, то два подобных треугольника конгруэнтны (они имеют одинаковый размер).
- Если P не равно 1, то два подобных треугольника не равны (у них разные размеры).

Как доказать, что два треугольника подобны
Есть несколько ситуаций, которые помогут вам доказать, что два треугольника подобны:
AA (угол-угол)
AA угол». Если две соответствующие пары углов в треугольнике имеют одинаковую меру, то третья пара углов также должна иметь одинаковую меру.
Это означает, что два треугольника подобны, так как все три пары углов имеют одинаковую меру. Дело в том, что в любом треугольнике сумма углов равна 180 градусам.
Три угла любого треугольника в сумме дают 180 градусов. Если мы знаем угловые меры двух углов (x и y), то мы знаем, что мера третьего угла равна 180 – (x + y).Если треугольник A имеет углы a, b и c, а треугольник B имеет углы x, y и z, причем два угла совпадают (a = x и b = y), то:
- 180 = 180
- a + b + c = x + y + z [сумма трех углов равна 180 в любом треугольнике]
- x + y + c = x + y 01 + 2 z [a = x and b = y]
- c = z
Итак, третья пара углов совпадает, и треугольники подобны.

Пример: Подобные треугольники по AA (угол-угол)
Предположим, что:
- У треугольника A есть углы 20 градусов и 40 градусов
- Угол треугольника B равен 20 и 40 градусов
Тогда треугольники A и B подобны по AA (угол-угол). Мы можем доказать, что третий угол равен 120 градусам, так как:
- a + b + c = 180
- 20 + 40 + c = 180
- 60 + c = 120 120
Итак, углы обоих треугольников равны 20, 40 и 120 градусов. Таким образом, треугольники А и В подобны.
SAS (сторона-угол-сторона)
SAS означает «сторона-угол-сторона». Когда две соответствующие пары сторон в треугольнике пропорциональны (с одинаковой пропорцией) и одна соответствующая пара углов (те, что между двумя сторонами) имеют одинаковую меру, тогда треугольники подобны.
Чтобы использовать SAS (сторона-угол-сторона) для доказательства подобия треугольников, известный угол (A) должен быть «включен» (между двумя известными сторонами).
Подумайте о том, чтобы взять две линии длины x и y и соединить их на концах так, чтобы между ними был фиксированный угол A. Возьмите еще две линии длин Px и Py и соедините их концами так, чтобы между ними был одинаковый угол A.
Третьи стороны треугольников имеют пропорциональную длину (z и Pz), что означает, что треугольники подобны.
Сходство также можно доказать с помощью закона косинусов. Допустим, у нас есть два треугольника, расположенные так, что их общий угол встречается в одной и той же точке (как показано на диаграмме ниже):
Два треугольника расположены так, что они встречаются под общим (общим) углом, C. Маленький треугольник имеет длины сторон a, b и c, а больший треугольник имеет длины сторон Pa, Pb и L.Эти треугольники удовлетворяют SAS, поскольку пары сторон a/Pa и b/Pb пропорциональны (с той же пропорцией P) и имеют общий угол C.
Для меньшего треугольника закон косинусов гласит:
- A 2 + B 2 — 2ABCOS (C) = C 2
Когда мы применяем эту формулу к более крупному треугольнику, мы получаем:
- (PA) 2 +
- .
 (Pb) 2 – 2(Па)(Pb)cos(C) = L 2
(Pb) 2 – 2(Па)(Pb)cos(C) = L 2
After simplifying, we get:
- P 2 a 2 + P 2 b 2 – 2P 2 abcos(C) = L 2
Обратите внимание, что P 2 появляется в каждом члене в левой части уравнения.
После деления на P 2 с обеих сторон получаем:
- a 2 + b 2 – 2abcos(C) = L 2 2 /P
10046
Из первого приведенного выше уравнения, мы знаем, что 2 + B 2 — 2ABCOS (C) = C 2 , SO:
- C 2 = L 2 /P C 2 = L 2 /P 2
- C 2 P 2 = L 2
- CP = L
. б/пб.
Таким образом, два треугольника подобны.

Пример: подобные треугольники по SAS (сторона-угол-сторона)
Допустим, что:
- Треугольник A имеет две длины сторон 3 и 4 с углом между ними 30 градусов.
- Треугольник B имеет две длины сторон 6 и 8 с углом между ними 30 градусов.
Тогда треугольники A и B подобны по SAS (сторона-угол-сторона):
- Пары сторон пропорциональны P = 2, так как 6 = 2*3 и 8 = 2*4.
- Угол между сторонами равен 30 градусов в обоих треугольниках.
SSS (Side-Side-Side)
SSS означает «сторона-сторона-сторона». Когда три соответствующие пары сторон в треугольнике имеют пропорциональную длину (с одинаковой пропорцией), то треугольники подобны.
Доказательство снова будет использовать закон косинусов. Имея длины сторон a, b и c для одного треугольника и длины сторон Pa, Pb и Pc для другого треугольника, мы увидим, что оба угла в каждой соответствующей паре имеют одинаковую градусную меру.

Пример: Подобные треугольники по SSS (сторона-сторона-сторона)
Допустим, что:
- Треугольник A имеет длины сторон 2, 5 и 6.
- Треугольник B имеет длины сторон 8, 20 и 24.
Тогда треугольники A и B подобны треугольникам A и B. SSS (сторона-сторона-сторона):
- Пары сторон пропорциональны P = 4, так как 8 = 2*4, 20 = 5*4 и 24 = 6*4.
HL (Кант гипотенузы)
HL означает катет гипотенузы. В частном случае прямоугольных треугольников мы можем доказать подобные треугольники, если гипотенузы пропорциональны и одна пара катетов пропорциональна (с той же пропорцией).
Два прямоугольных треугольника расположены так, что они встречаются под их общим (общим) углом, прямым углом 90 градусов. У маленького треугольника боковые катеты x и L с гипотенузой H, а у большего треугольника боковые катеты y и PL с гипотенузой PH.For the smaller right triangle, the Pythagorean Theorem applies:
- x 2 + L 2 = H 2
Solving for x 2 , we get:
- x 2 = H 2 — L 2
Применение теоремы Пифагоре в более крупный правый треугольник, мы получаем:
- Y 2 + (PL) 2 9002 = (PH) 1 2 2 + (PL) 2
- = (PH).
 2
2 - = (PH).
- Y 2 + P 2 L 2 = P 2 H 2
- Y 2 = P 2
- Y 2 = P 2
- H 2 = P 2
- 2 2 19 2 69 2 2 19 2 19 2 19 2 19 2 19 2 6 2 2
- . L 2
Обратите внимание, что P 2 появляется в каждом члене правой части уравнения.
После деления на P 2 с обеих сторон мы получаем:
- Y 2 /P 2 = H 2 — L 2
- Y 2 /P 2 = X 2
- Y 2
- Y 2 = P
- Y 2 = P
- Y 2
- Y 2
- y 2
- .
- y = Px
Итак, стороны y и x имеют ту же пропорцию P, что и стороны L/PL и H/PH.

Таким образом, два треугольника подобны.
Пример: подобные треугольники по HL (гипотенуза-каттер)
Допустим, что:
- Прямоугольный треугольник A имеет гипотенузу длины 10 и катет длиной 6.
- Прямоугольный треугольник B имеет гипотенузу длина 50 и отрезок длины 30.
Тогда треугольники A и B подобны по HL (гипотенуза-каттер):
- Пара гипотенуз и пара сторон пропорциональны P = 5, так как 50 = 10*5 и 30 = 6* 5.
Равносторонние треугольники
Любые два равносторонних треугольника автоматически подобны. Помните, что в любом равностороннем треугольнике все три угла равны 60 градусам.
Два равносторонних треугольника автоматически подобны (одинаковые углы и пропорции между длинами сторон). Однако они могут не совпадать из-за разного размера (длины сторон).Итак, каждая пара углов между двумя равносторонними треугольниками совпадает (оба по 60 градусов).
 Помните, что два равносторонних треугольника подобны, но они могут быть или не быть равными (длины сторон могут различаться).
Помните, что два равносторонних треугольника подобны, но они могут быть или не быть равными (длины сторон могут различаться).Транзитивность подобия треугольников
Помните, что подобие треугольников транзитивно. То есть:
«Если треугольник A подобен треугольнику B, а треугольник B подобен треугольнику C, то треугольник A подобен треугольнику C».
Кроме того, мы можем найти пропорцию между треугольниками A и C. Если:
- Длины сторон треугольника A равны P, умноженным на длины сторон треугольника B, и
- Длины сторон треугольника B равны Q, умноженным на длины сторон треугольника C, затем
- Длины сторон треугольника A равны PQ длинам сторон треугольника C, умноженным на PQ.
Заключение
Теперь вы знаете, когда треугольники подобны и как это определить. Вы также знаете несколько ключевых сценариев (AA, SAS, SSS, HL и равносторонние треугольники) и когда треугольники также конгруэнтны.

- Мы заметили, что изменение длин сторон любого треугольника по-прежнему сохраняет сходство между двумя треугольниками.

 Два его угла задаются с помощью мер:
Два его угла задаются с помощью мер: Отсюда следует, что длины сторон обоих треугольников равны:
Отсюда следует, что длины сторон обоих треугольников равны: Поскольку длины сторон одного треугольника изменяются пропорционально другим его сторонам, мы ожидаем, что отношение между длинами сторон обоих треугольников останется равным.
Поскольку длины сторон одного треугольника изменяются пропорционально другим его сторонам, мы ожидаем, что отношение между длинами сторон обоих треугольников останется равным. имеем следующие значения:
имеем следующие значения: Опять же, для прямоугольного треугольника длины их сторон связаны как:
Опять же, для прямоугольного треугольника длины их сторон связаны как: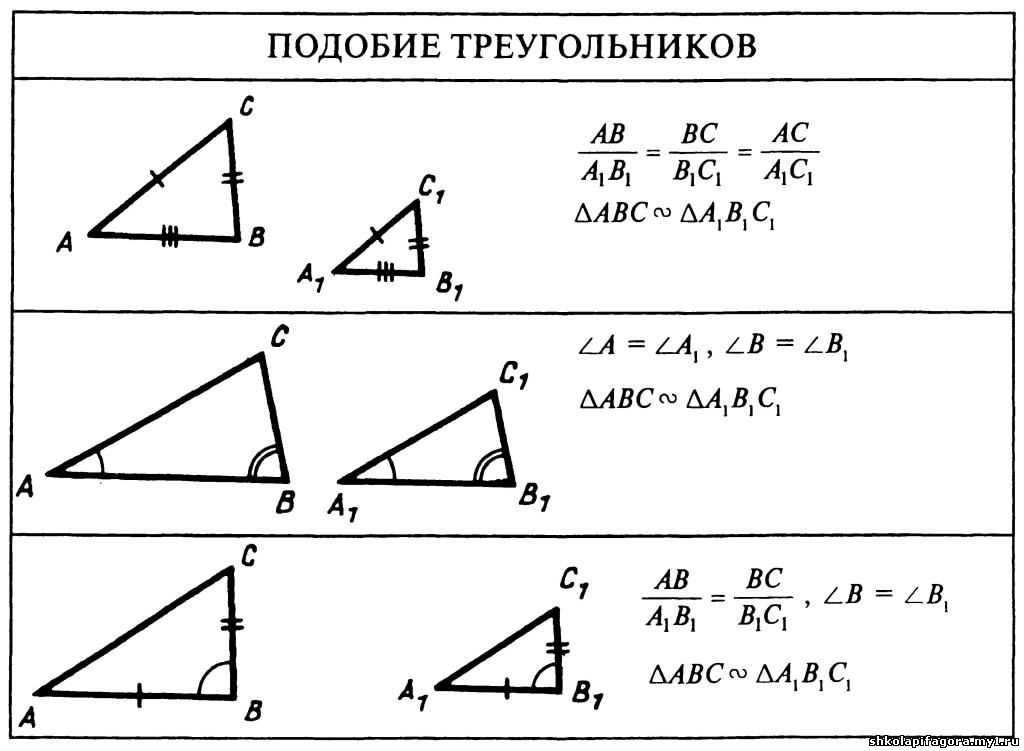 обоих треугольников имеем следующие значения:
обоих треугольников имеем следующие значения: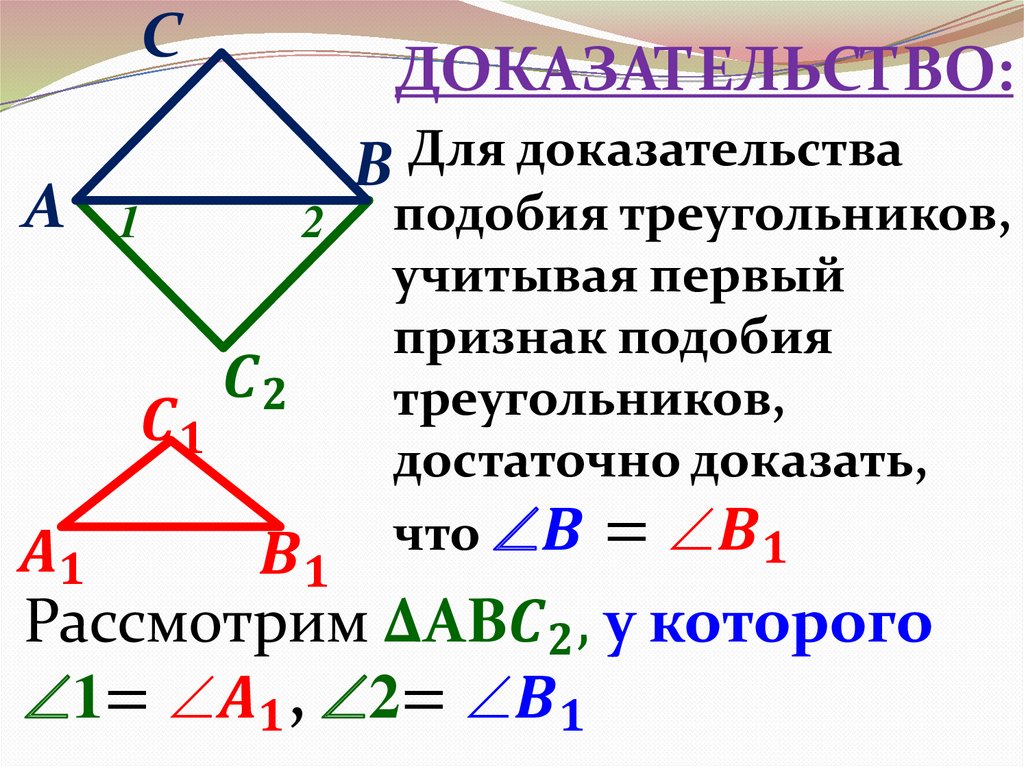

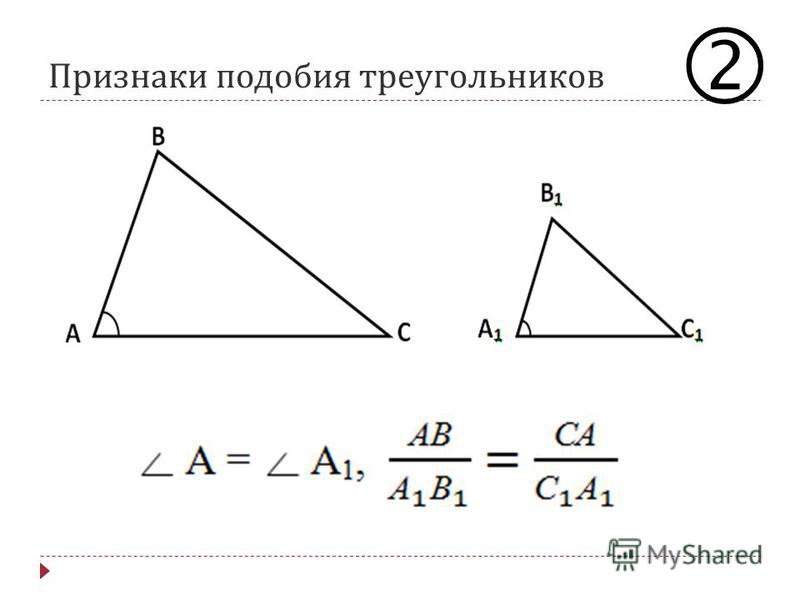
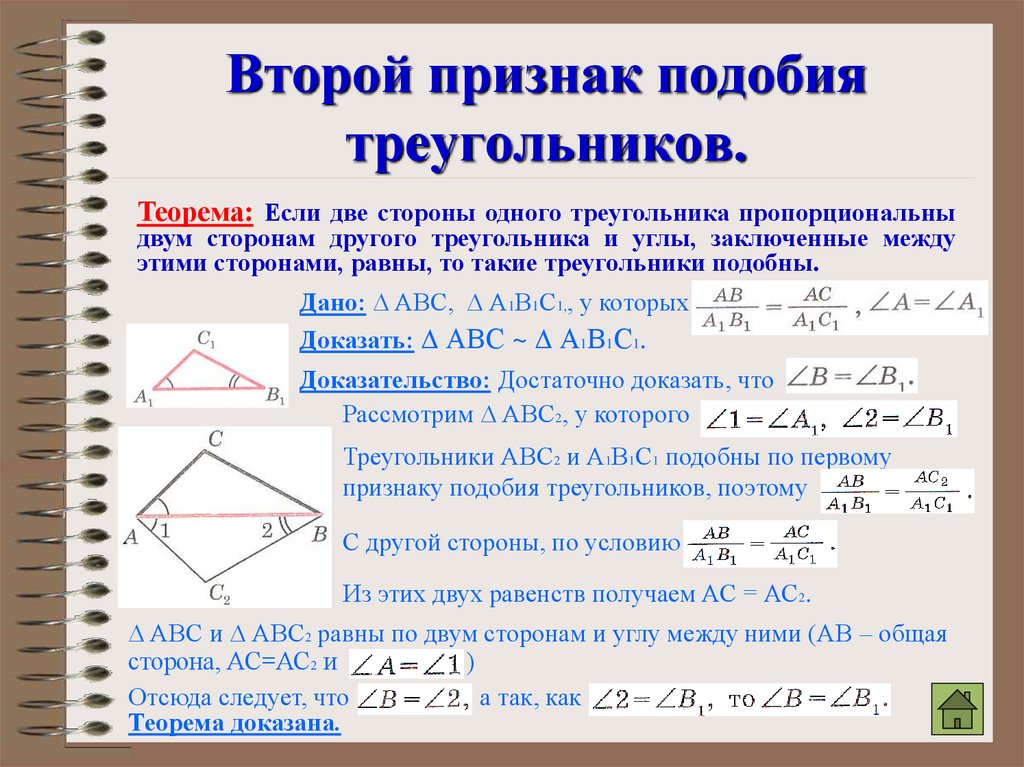 Он утверждает, что квадрат длины его гипотенузы равен сумме квадратов длин других его сторон:
Он утверждает, что квадрат длины его гипотенузы равен сумме квадратов длин других его сторон: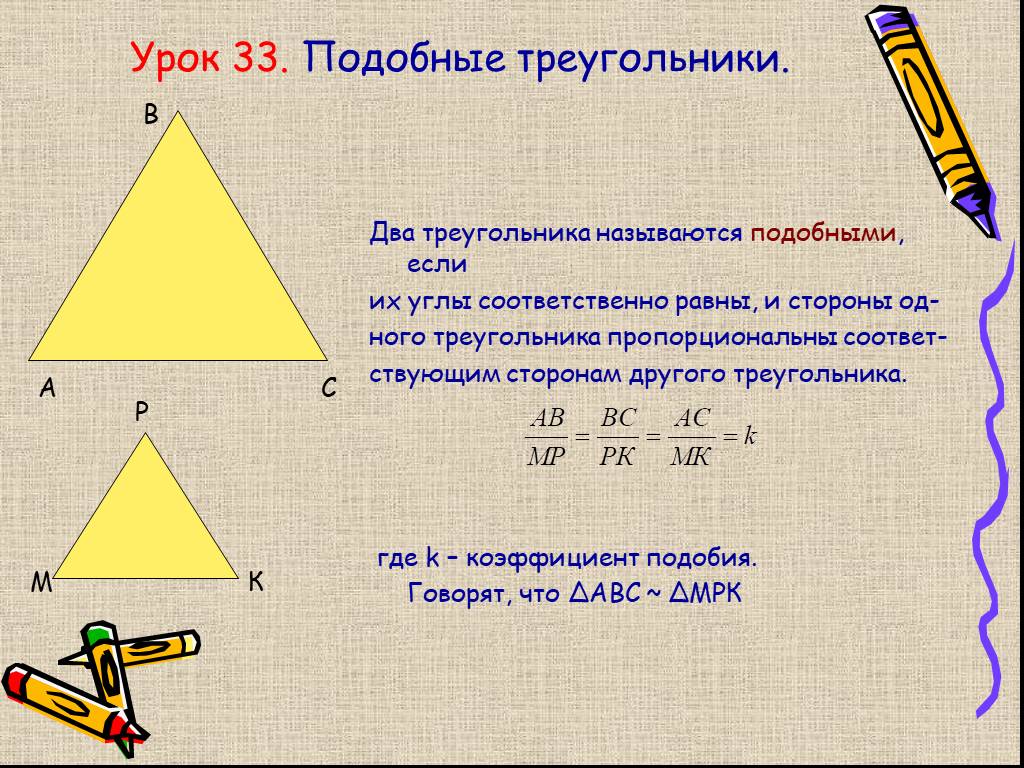 Конгруэнтные треугольники абсолютно одинаковы с точки зрения длин сторон и углов, но как насчет подобных треугольников?
Конгруэнтные треугольники абсолютно одинаковы с точки зрения длин сторон и углов, но как насчет подобных треугольников?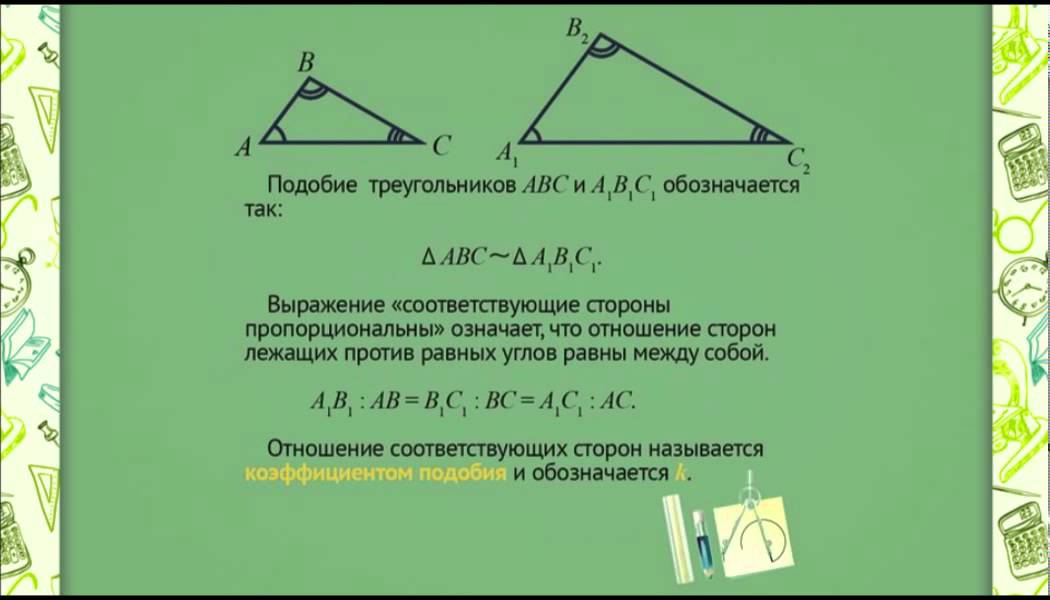
 Обратите внимание, что площадь треугольника B будет равна P 2 , умноженной на площадь треугольника A:
Обратите внимание, что площадь треугольника B будет равна P 2 , умноженной на площадь треугольника A: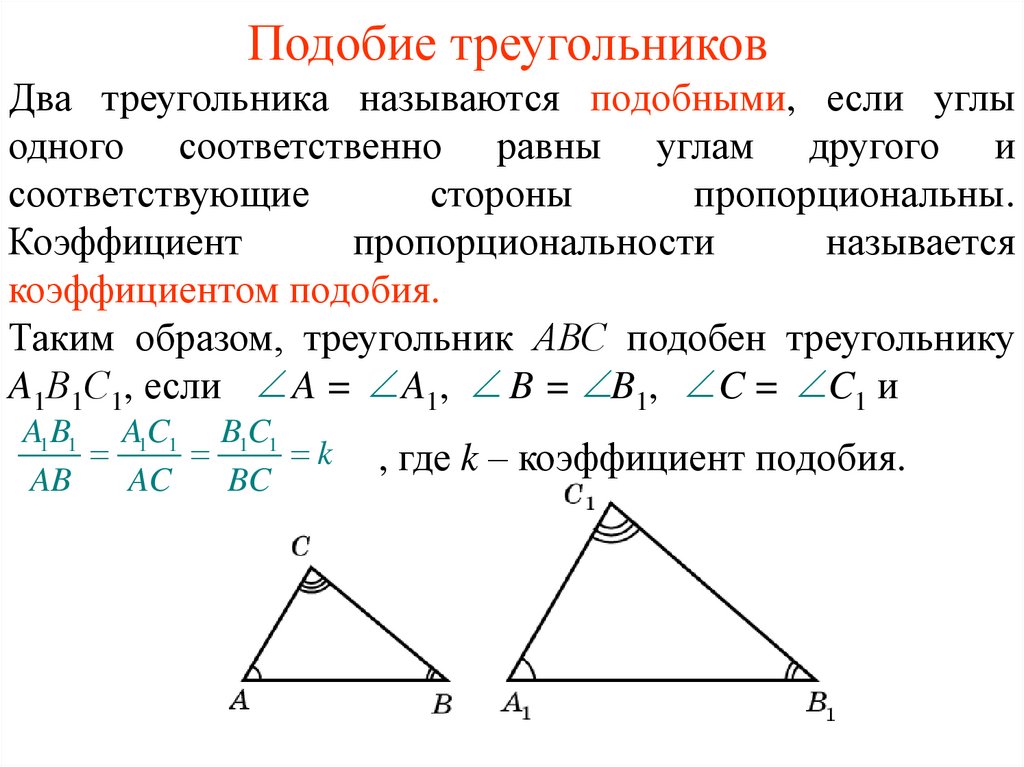


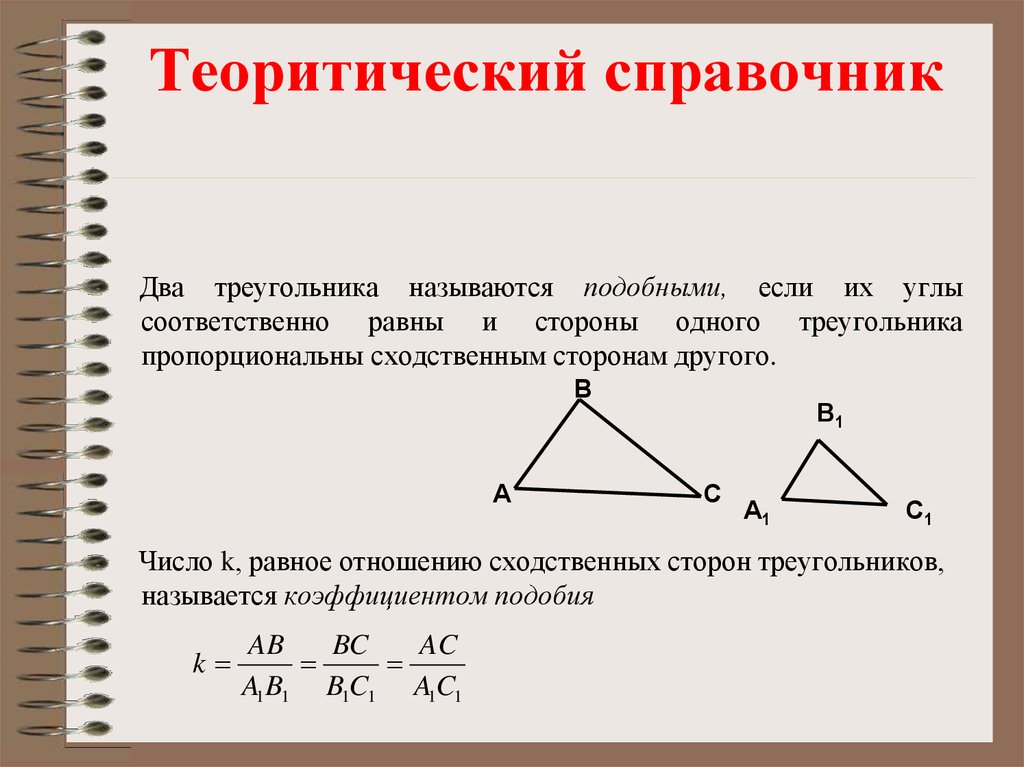 (Pb) 2 – 2(Па)(Pb)cos(C) = L 2
(Pb) 2 – 2(Па)(Pb)cos(C) = L 2 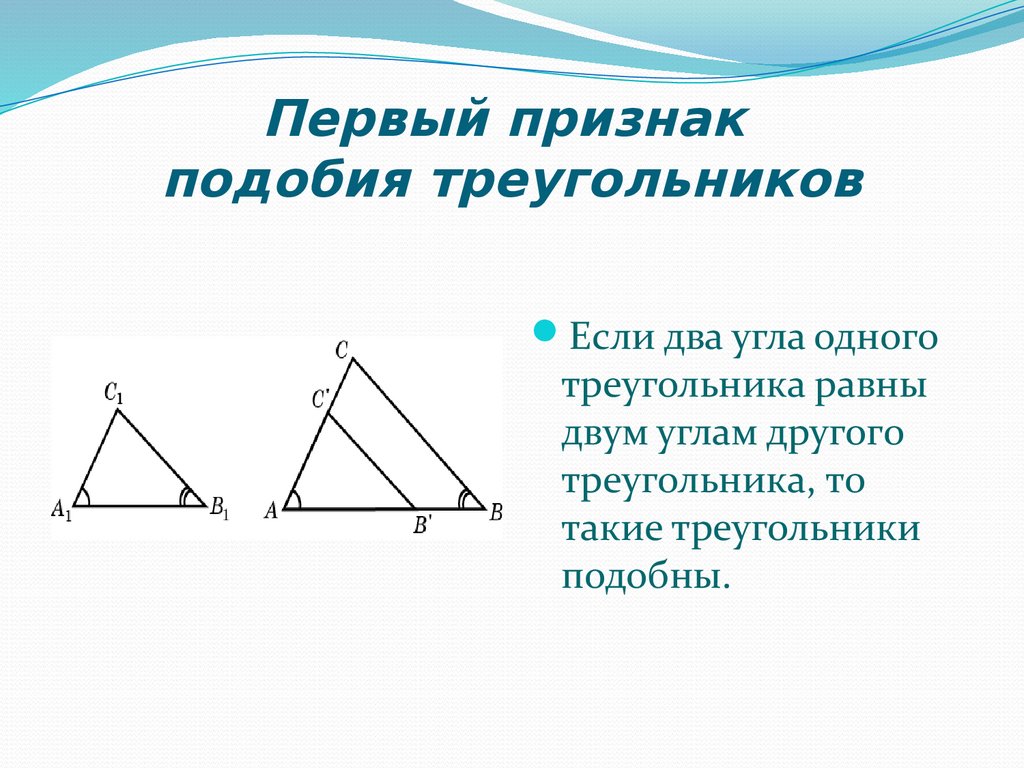

 2
2 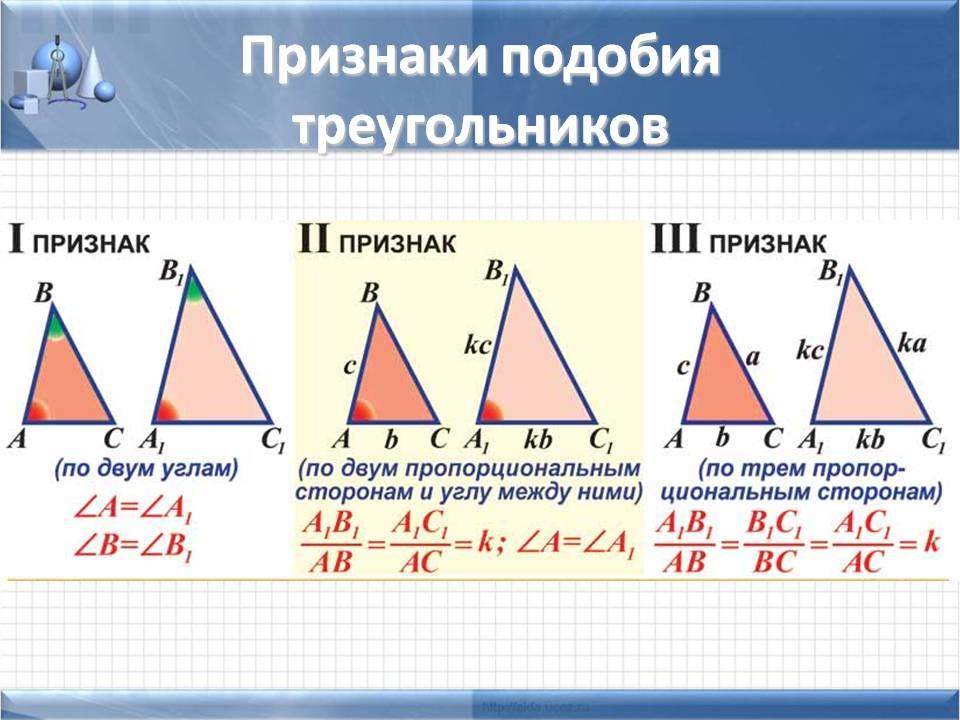
 Помните, что два равносторонних треугольника подобны, но они могут быть или не быть равными (длины сторон могут различаться).
Помните, что два равносторонних треугольника подобны, но они могут быть или не быть равными (длины сторон могут различаться).