Профилактин Лайт, флакон 1000 мл — От насекомых (инсектициды)
|
|
|
||||||||||||||||||||||||||||
|
Минимальная сумма покупки составляет 2 000 ₽. Система скидок. Если вы найдете аналогичный товар дешевле, мы сделаем дополнительную скидку. |
|||||||||||||||||||||||||||||
Описание
Многие проблемы гораздо проще предотвратить. Это относится и к садовым вредителям. Если провести обработку до их выхода из зимовки, они просто не успеют нанести растениям вред. Именно для этих целей предназначен препарат «Профилактин Лайт». Препарат «Профилактин Лайт» продается во флаконах по 1000 мл. По принципу действия вещество относится к классу инсектоакарицидов: помогает очистить стволы плодово-ягодных растений от зимующих насекомых. Средство избавит сад от клещей, тли, медяниц и других вредителей. «Профилактин Лайт» подходит для обработки яблонь, груш, айвы, вишни, крыжовника, смородины, декоративных кустарников.
Инсектоакарицид смешивают с водой в пропорциях, указанных в инструкции, и опрыскивают столы деревьев ранней весной. Обработку нужно проводить после таяния снега, не дожидаясь набухания почек.
Препарат «Профилактин Лайт» действует с высокой эффективностью при температуре воздуха выше +4 ˚C. Раствор для опрыскивания нужно использовать в день приготовления. При хранении более суток эффективность раствора для уничтожения насекомых снижается.
Независимые отзывы о товаре
Mneniya.Pro
К товару » Профилактин Лайт, флакон 1000 мл » рекомендуем:
4. Фертика, жидкие удобрения в ампулах
73 ₽ — 180 ₽
5. Укрытия из кокосового волокна
29.90 ₽ — 36 231 ₽
6. Кокосовые мульчирующие круги, Fibrefamily
30.09 ₽ — 744 ₽
7. Фитоспорин
17.10 ₽ — 25 ₽
8. Глиокладин, от корневых и прикорневых гнилей
72 ₽ — 82 ₽
9. Паста РанНет
70 ₽ — 87 ₽
Функции
ФункцииРанее была задача вычисления числа сочетаний из n элементов по k,
для чего необходимо вычисление факториалов трех величин: n, k и n-k.
Для этого можно сделать три цикла,
что приводит к увеличению размера программы за счет трехкратного повторения похожего кода. Вместо этого
лучше сделать одну функцию, вычисляющую факториал любого данного числа n и трижды использовать
эту функцию в своей программе. Соответствующая функция может выглядеть так:
def factorial(n):
f = 1
for i in range(2, n + 1):
f *= i
return f
Этот текст должен идти в начале программы, вернее, до того места,
где мы захотим воспользоваться функцией factorial.
Первая строчка этого примера является описанием нашей функции. factorial — идентификатор, то есть имя нашей функции.
После идентификатора в круглых скобках идет список параметров,
которые получает наша функция. Список состоит из перечисленных через запятую
идентификаторов параметров. В нашем случае список состоит из одной величины n.
В конце строки ставится двоеточие.
Далее идет тело функции, оформленное в виде блока, то есть с отступом.
Внутри функции вычисляется значение факториала числа n
f. Функция завершается инструкцией return f,
которая завершает работу функции и возвращает значение переменной f.
Инструкция return может встречаться в произвольном месте функции, ее исполнение
завершает работу функции и возвращает указанное значение в место вызова.
Если функция не возвращает значения, то инструкция return используется без возвращаемого значения, также в функциях, не возвращающих значения,
инструкция return может отсутствовать.Теперь мы можем использовать нашу функцию несколько раз.
В этом примере мы трижды вызываем функцию factorial для вычисления трех факториалов: factorial(n), factorial(k), factorial(n-k).
n = int(input()) k = int(input()) print(factorial(n) // (factorial(k) * factorial(n - k)))
Мы также можем, например, объявить функцию binomial, которая принимает два целочисленных параметра n и k и вычисляет число сочетаний из n по k:
def binomial(n, k)
return factorial(n) // (factorial(k) * factorial(n - k))
Тогда в нашей основной программе мы можем вызвать функцию binomial для нахождения числа сочетаний:
print(binomial(n, k))
Вернемся к задаче нахождения наибольшего из двух или трех чисел.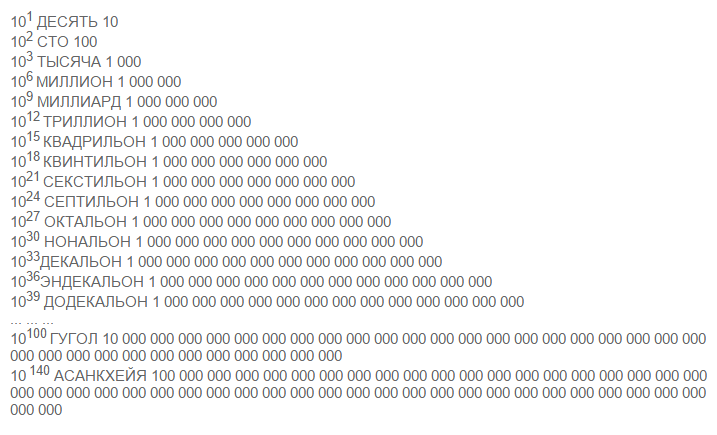
Функцию нахождения максимума из двух чисел можно написать так:
def max(a, b):
if a > b:
return a
else:
return b
Теперь мы можем реализовать функцию max3, находящую максимум трех чисел:
def max3(a, b, c):
return max(max(a, b), c)
Функция max3 дважды вызывает функцию max для двух чисел:
сначала, чтобы найти максимум из a
b, потом чтобы найти максимум из этой
величины и c.Локальные и глобальные переменные
Внутри функции можно использовать переменные, объявленные вне этой функции
def f():
print(a)
a = 1
f()
Здесь переменной a присваивается значение 1, и функция f печатает это значение, несмотря на то, что выше функции f эта переменная
не инициализируется. Но в момент вызова функции f переменной a уже присвоено значение, поэтому функция f может вывести его на экран.
Такие переменные (объявленные вне функции, но доступные внутри функции) называются глобальными.
Но если инициализировать какую-то переменную внутри функции, использовать эту переменную вне функции не удастся. Например:
def f():
a = 1
f()
print(a)
Получим NameError: name 'a' is not defined
Интересным получится результат, если попробовать изменить значение глобальной переменной внутри функции:
def f():
a = 1
print(a)
a = 0
f()
print(a)
Будут выведены числа 1 и 0. То есть несмотря на то, что значение переменной a изменилось внутри функции, то вне функции оно осталось прежним! Это сделано в целях
“защиты” глобальных переменных от случайного изменения из функции
(например, если функция будет вызвана из цикла по переменной i, а в этой функции
будет использована переменная i также для организации цикла, то эти переменные должны
быть различными).
То есть если внутри функции модифицируется значение некоторой переменной,
то переменная с таким именем становится локальной переменной, и ее модификация не приведет
к изменению глобальной переменной с таким же именем.
Более формально: интерпретатор Питон считает переменную локальной, если внутри
нее есть хотя бы одна инструкция, модифицирующая значение переменной (это может быть
оператор =, += и т.д., или использование этой переменной
в качестве параметра цикла for, то эта переменная считается локальной
и не может быть использована до инициализации. При этом даже если инструкция,
модифицирующая переменную никогда не будет выполнена: интерпретатор это проверить
не может, и переменная все равно считается локальной. Пример:
def f():
print(a)
if False:
a = 0
a = 1
f()
Возникает ошибка: UnboundLocalError: local variable 'a' referenced before assignment.
А именно, в функции f идентификатор a становится локальной переменной,
т.
к. в функции есть команда, модифицирующая переменную a, пусть даже никогда и
не выполняющийся (но интерпретатор не может это отследить). Поэтому вывод переменной a приводит к обращению к неинициализированной локальной переменной.
Чтобы функция могла изменить значение глобальной переменной, необходимо объявить эту переменную
внутри функции, как глобальную, при помощи ключевого слова global:
def f():
global a
a = 1
print(a)
a = 0
f()
print(a)
В этом примере на экран будет выведено 1 1, так как переменная a объявлена, как глобальная,
и ее изменение внутри функции приводит к тому, что и вне функции переменная
будет доступна.
Тем не менее, лучше не изменять значения глобальных переменных внутри функции. Если функция должна поменять какую-то переменную, то как правило это лучше сделать, как значение, возвращаемое функцией.
Если нужно, чтобы функция вернула не одно значение, а два или более, то для этого функция может вернуть кортеж из двух или нескольких значений:
return (a, b)
Тогда результат вызова функции тоже нужно присваивать кортежу:
(n, m) = f(a, b)
Эпиграф:
def short_story():
print("У попа была собака, он ее любил.
")
print("Она съела кусок мяса, он ее убил,")
print("В землю закопал и надпись написал:")
short_story()
")
print("Она съела кусок мяса, он ее убил,")
print("В землю закопал и надпись написал:")
short_story()
Как мы видели выше, функция может вызывать другую функцию. Но функция также может вызывать и саму себя! Рассмотрим это на примере функции вычисления факториала. Хорошо известно, что \(0!=1\), \(1!=1\). А как вычислить величину \(n!\) для большого \(n\)? Если бы мы могли вычислить величину \((n-1)!\), то тогда мы легко вычислим \(n!\), поскольку \(n!=n(n-1)\)!. Но как вычислить \((n-1)!\)? Если бы мы вычислили \((n-2)!\), то мы сможем вычисли и \((n-1)!=(n-1)(n-2)!\). А как вычислить \((n-2)!\)? Если бы… В конце концов, мы дойдем до величины \(0!\), которая равна \(1\). Таким образом, для вычисления факториала мы можем использовать значение факториала для меньшего числа. Это можно сделать и в программе на Питоне:
def factorial (n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
Подобный прием (вызов функцией самой себя) называется рекурсией, а сама функция называется рекурсивной.
Рекурсивные функции являются мощным механизмом в программировании. К сожалению, они не всегда эффективны (об этом речь пойдет позже). Также часто использование рекурсии приводит к ошибкам, наиболее распространенная из таких ошибок – бесконечная рекурсия, когда цепочка вызовов функций никогда не завершается и продолжается, пока не кончится свободная память в компьютере. Пример бесконечной рекурсии приведен в эпиграфе к этому разделу. Две наиболее распространенные причины для бесконечной рекурсии:
- Неправильное оформление выхода из рекурсии. Например, если мы в программе вычисления факториала
забудем поставить проверку
if n == 0, тоfactorial(0)вызоветfactorial(-1), тот вызоветfactorial(-2)и т.д. - Рекурсивный вызов с неправильными параметрами. Например, если функция
factorial(n)будет вызыватьfactorial(n), то также получиться бесконечная цепочка.
Поэтому при разработке рекурсивной функции необходимо прежде всего оформлять условия завершения рекурсии
и думать, почему рекурсия когда-либо завершит работу.
Максимальная глубина рекурсии
По умолчанию максимальное число рекурсивных вызовов (последовательных, то есть вложенных функций) примерно равно 1000, то есть вычислить факториал числа 1000 при помощи такой рекурсивной функции не получится. Для повышения максимально разрешенной глубины рекурсии можно использовать функцию setrecursionlimit из модуля sys:
import sys sys.setrecursionlimit(10 ** 9)
чему равен факториал 1000?
Калькулятор факториала До 10 000
Здесь вы можете найти ответы на такие вопросы, как: что такое факториал 1000? Чему равен факториал 1000? Каковы последние цифры факториала 1000? Сколько нулей в конце факториала 1000? Сколько цифр в факториале 1000? Воспользуйтесь приведенным выше калькулятором факториала, чтобы найти факториал любого натурального числа в диапазоне от 0 до 10 000.
Что такое факториал?
Определение факториала
Факториал — это величина, определенная для любого целого числа n, большего или равного 0.
Факториал — это произведение всех целых чисел, меньших или равных n, но больших или равных 1. Значение факториала 0 равно определение равно 1. Для отрицательных целых чисел факториалы не определены. Факториал можно рассматривать как результат умножения последовательности убывающих натуральных чисел (например, 3 × 2 × 1).
Символ факториала — восклицательный знак!.
Формула факториала
Если n — натуральное число, большее или равное 1, то
n! = n x (n — 1) x (n — 2) x (n — 3) … 3 x 2 x 1
Если n = 0, то n! = 1, по соглашению.
Пример: 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
Ярлык для поиска конечных нулей в факториале
Конечные нули представляют собой последовательность нулей в десятичном представлении числа, после которой не следуют никакие другие цифры. В этом видео показано, как легко найти конечные нули факториала.
Таблица факториалов до 30
| нет | нет! |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 47 00 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432 |
| 21 | 51090942171709440000 |
| 22 | 1124000727777607680000 |
| 23 | 25852016738884976640000 |
| 24 | 620448401733239439360000 |
| 25 | 15511210043330985984000000 |
| 26 | 403291461126605635584000000 |
| 27 | 10888869450418352160768000000 |
| 28 | 304888344611713860501504000000 |
| 29 | 8841761993739701954543616000000 |
| 30 | 265252859812191058636308480000000 |
Factorial Calculator
Please ссылка на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
Пример расчета факториала.
- Factorial of 80
- Factorial of 460
- Factorial of 860
- Factorial of 40
- Factorial of 470
- Factorial of 73
- Factorial of 10000
- Factorial of 8000
- Factorial of 1000
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
1000 Факториал — CodeProject
- Загрузить исходный код (факт) — 15,22 КБ
- Загрузить исходный код (факт2) — 14,98 КБ
Введение
Факториал или произведение натуральных чисел или процессов). Многие математические расчеты должны иметь точный результат факториала большого числа, например 1000! найти окончательный ответ с высокой точностью.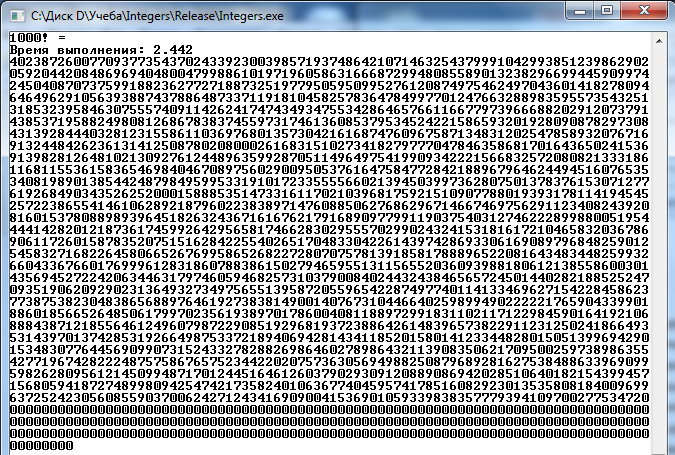
Но проблема в том, что ни в одном языке программирования нет переменной или механизма для хранения такой большой цифры. Все языки программирования и калькуляторы оценивают результат, а затем сохраняют его как научное число. Например, калькулятор Windows XP показывает 1000! вот так:
4.02387260077093773543702433923 e+2567
Вот я и решил придумать алгоритм решения этой задачи.
Алгоритм
Вы знаете, что для вычисления факториала числа нужно умножить все числа от 1 на себя, например:
1000! = 1*2*3*……*998*999*1000
Ни в одном языке программирования нет переменной, которая могла бы точно хранить результат этого умножения; кроме хранения в экспоненциальном представлении. Из-за огромного результата последовательного умножения необходимо найти новую стратегию или механизм.
В рекомендуемом мной алгоритме число не рассматривается как число, вместо этого оно рассматривается как последовательные цифры, каждая из которых имеет свое числовое значение.
На самом деле доступен массив цифр. Каждый раз второе число умножается на каждую цифру первого числа (индекс массива), а затем добавляется с переносом числа вверх от предыдущего умножения.
Этот процесс показан, например 12!:
12! = 11! * 12 11! = 39916800 12! = 4700
- Если результат меньше 10, результат будет помещен в ячейку массива.
- Если оно равно или больше 10, оно будет разделено на 10, а затем остаток будет помещен в ячейку массива, а частное помещено в переменную, которая будет добавлена при следующем ответе умножения.
Примечание: Обратите внимание, что все числа сохраняются с конца массива, как при обычном вычислении (реальном вычислении).
Код программирования
Объявления
int numArr[3000]; целая сумма, рем = 0, счет; зарегистрироваться в я;
В первой строке определяется массив, размер которого зависит от размера факториала.
« rem » определено для хранения остатка от деления.
В конце определяется целочисленная переменная с именем « i «, которая играет роль счетчика циклов и индекса массива, и из-за большого количества доступов она определяется как регистр.
Модификатор типа регистра указывает компилятору сохранить объявленную переменную в регистре ЦП (если возможно) для оптимизации доступа.
Примечание : Современные компиляторы имеют хороший оптимизатор, который решает, какие переменные следует хранить в регистрах. Они сами выбирают регистры, когда включена глобальная оптимизация распределения регистров.
Основная часть кода
i=2999; //начнем с конца массива.
номерАрр[2999]=1;
для (количество = 2; количество <= 1000; количество ++)
{
в то время как (я> 0)
{
итог=numArr[i]*count+rem;
бэр=0;
если(всего>9)
{
numArr[i]=всего%10;
бэр=всего/10;
}
еще
numArr[i]=всего;
я--;
}
бэр=0;
всего=0;
я=2999;
} В соответствии с алгоритмом, который был объяснен ранее, существует цикл, считающий от 2 до 1000, и каждый раз значение ‘ count ‘ умножается на ячейку массива и добавляется к ‘ rem ‘, которое содержит перенос из предыдущего умножения.
Наконец, результат сохраняется в ‘ total ‘ и затем помещается в ячейку массива.
Другой алгоритм
Сначала я нашел другой алгоритм для этой задачи. Он основан на моделировании умножения последовательными сложениями. Например, 20= 4*5, а также 20= (5+5+5+5).
Итак, поместите числа в массив, а затем сложите его с самим собой ‘X’ раз.
Х за 1000! равно:
X= ∑ n
n=1,2,3, … ,999,1000
Примечание : Этот алгоритм не так оптимален, как первый, который я объяснил. Также это слишком скучно и требует несколько больших массивов. Второй ZIP-файл относится к этому алгоритму.
Достопримечательности
Хочу отметить, что алгоритм имеет высокую скорость вычислений, поэтому переводит программу во вполне оптимальное состояние.
Одной из наиболее важных особенностей этого алгоритма является использование только одного массива, в то время как другим алгоритмам требуется больше памяти (использование нескольких массивов для имитации умножения на последовательные суммы).