формула, как найти координаты, вывод уравнения, абсцисса и ордината
Содержание:
- Что такое вершина параболы
- Вывод формулы координат вершины параболы
- Как найти координаты, основные способы
- Примеры решения задач
Содержание
- Что такое вершина параболы
- Вывод формулы координат вершины параболы
- Как найти координаты, основные способы
- Примеры решения задач
Что такое вершина параболы
Определение
Вершина параболы — это точка, в которой наблюдается пересечение параболой оси координат и ее невозможность держать направление выше или ниже в координатной плоскости. 2-7\times3,5+3=-9,25.\)
2-7\times3,5+3=-9,25.\)
Ответ: (3,5; -9,25).
Насколько полезной была для вас статья?
Рейтинг: 2.17 (Голосов: 6)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Нахождение вершины параболы: найти её координаты, способы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Содержание:
- Нахождение вершины параболы: способы, примеры, советы
- Первый способ
- Второй способ
- Третий способ
- Построение параболы
- Советы
- Видео
Нахождение вершины параболы: способы, примеры, советы
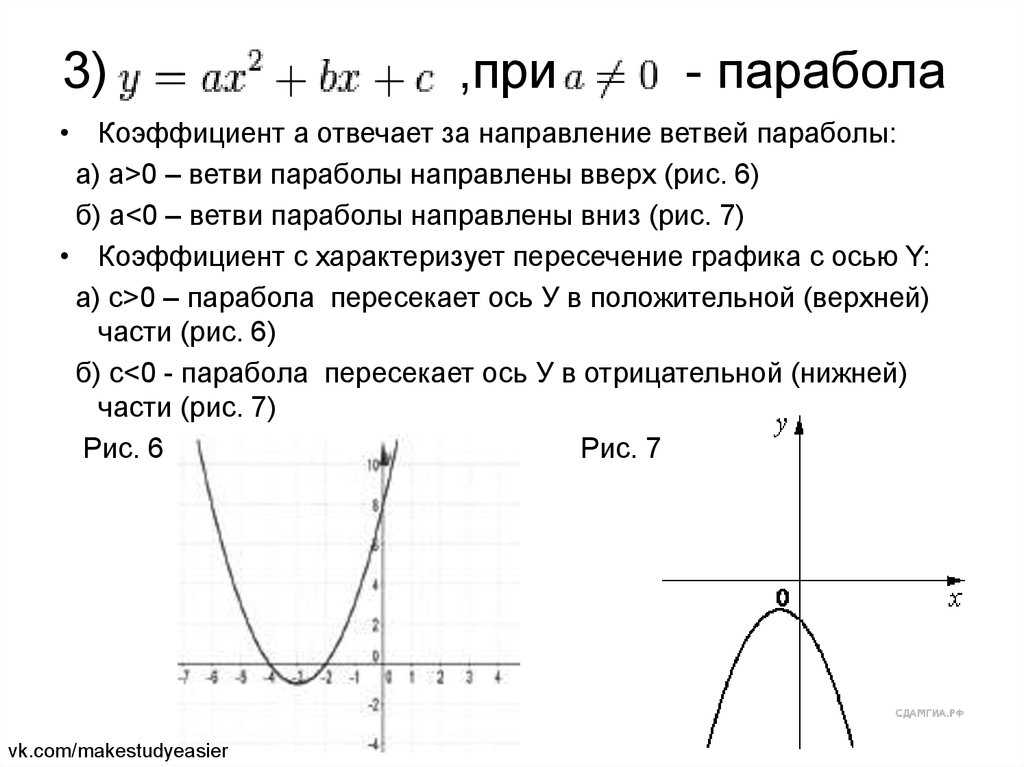
График функции y = ax2+ bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой.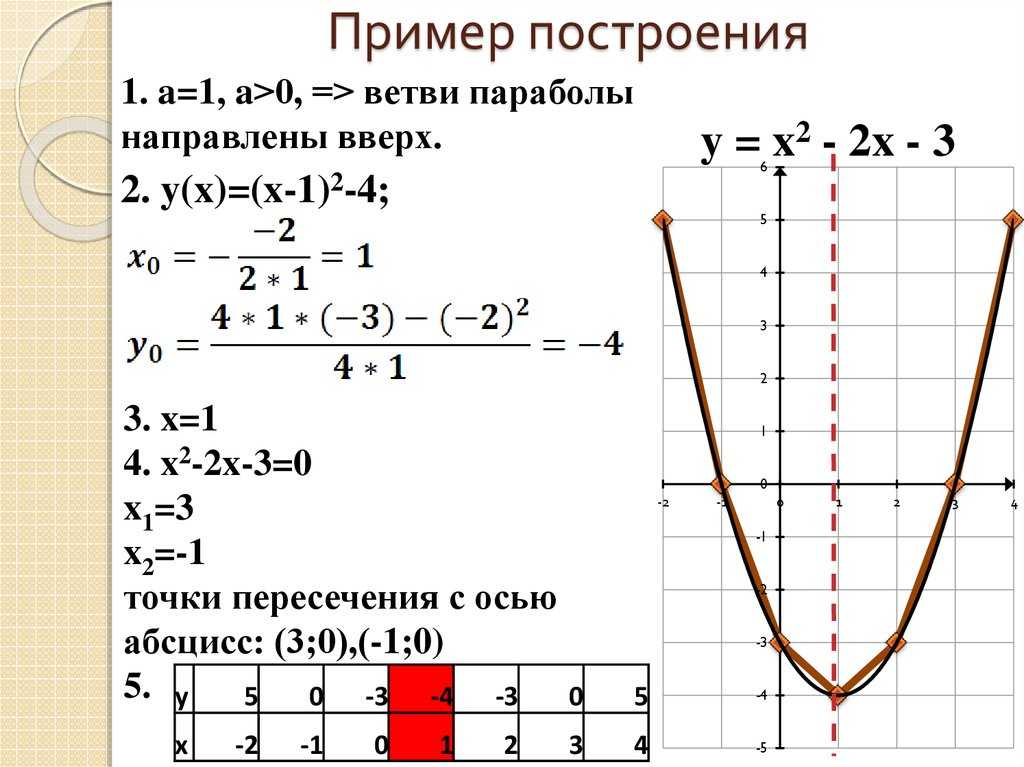 Но обратите внимание на тот факт, что a ≠0.
Но обратите внимание на тот факт, что a ≠0.
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0
.Например, y =x2–8 x +15;
находим первый, второй коэффициенты и свободный член;
- a =1, b =-8, c =15;
подставляем значения a и b в формулу;
- x0=8/2=4;
вычисляем значения y;
- y0 = 16–32+15 = -1;
Значит, вершина находится в точке (4;-1).
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
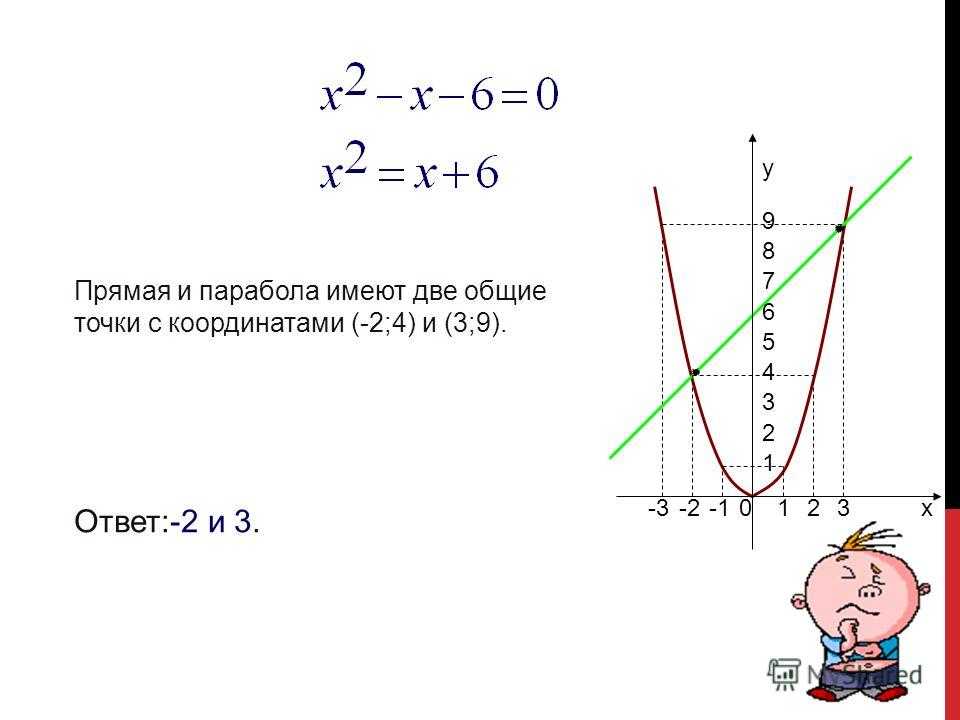
Рассмотрим на примере y =x2–6x+5
1) Приравниваем к нулю:
- x2–6x+5=0.
2) Находим дискриминант, используя формулу: D = b
- D =36–20=16.
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 — первый корень;
- 5 — второй корень.
4) Вычисляем:
- x0 =(5+1)/2=3
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2+8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x2 + 8x = -10.
Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2)2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
x2 + 8x +16= 6.
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4)2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1.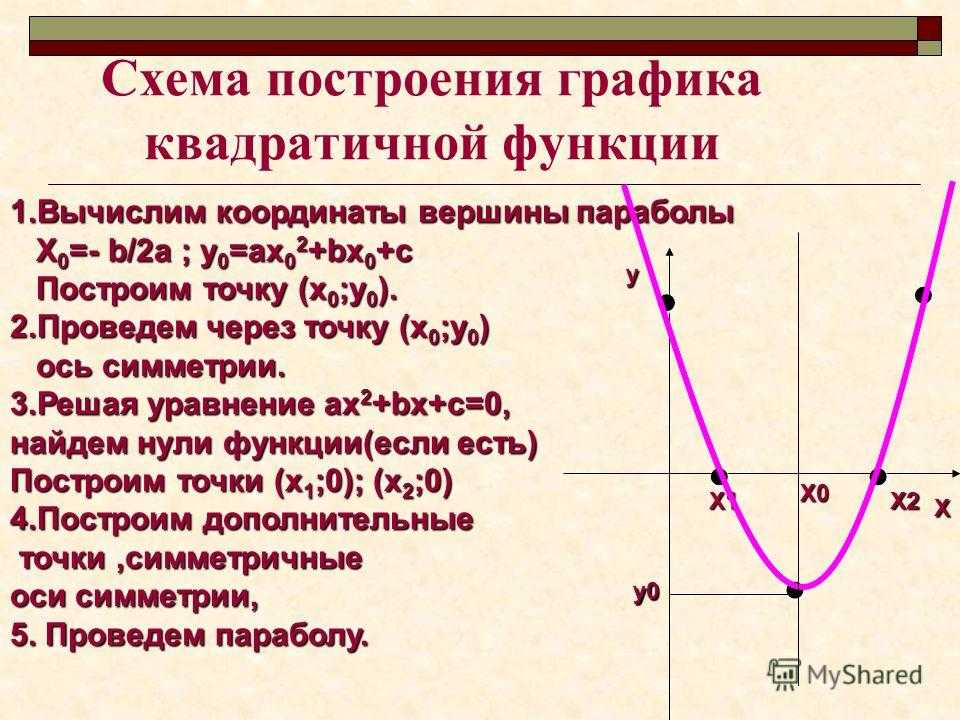 Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
- Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2+11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
| X | 5,5 | ||||
| Y |
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины.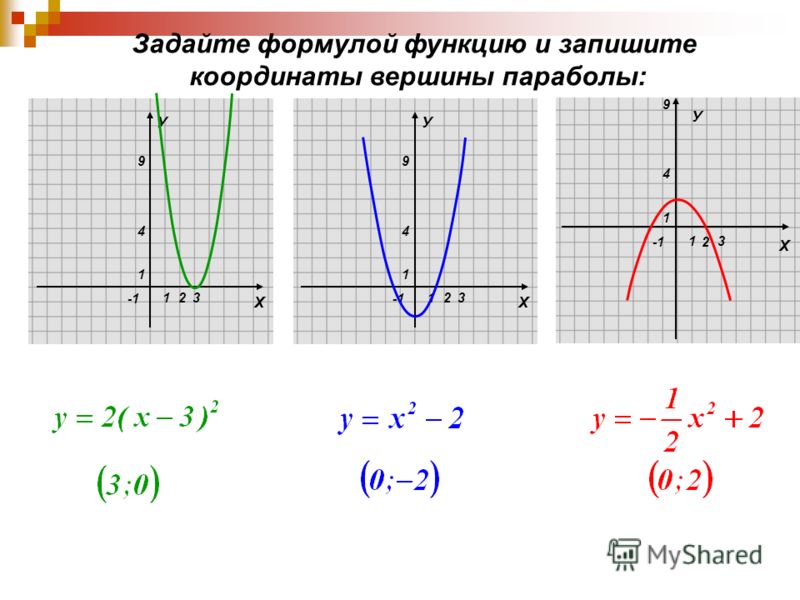
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Видео
Это видео поможет вам научиться находить вершину параболы
Что такое параболы, их уравнения, их правила?
Получение информации из уравнений Получение уравнений из задач и калькуляторов InfoWord
Purplemath
Что такое парабола?
Парабола — это особый тип геометрической кривой, которая алгебраически соответствует квадратному уравнению. Геометрически парабола соответствует краю среза перевернутого конуса; этот срез и есть то, что называется коническим «сечением».
Геометрически парабола соответствует краю среза перевернутого конуса; этот срез и есть то, что называется коническим «сечением».
Содержание продолжается ниже
MathHelp.com
С физической точки зрения, круг представляет собой линию, образованную путем обматывания веревки вокруг палки, воткнутой в песок, другой палки, воткнутой в другой конец нити с петлей, натянутой этой палкой веревки и потянув эту палку вокруг первой палки. Эллипс формируется путем помещения двух палочек в песок, наматывания веревки вокруг них обеих (эта петля должна быть достаточно длинной, чтобы свободно обхватывать палочки), помещения третьей палки в петлю, вытягивания провисания и вытягивания этой палки. вокруг двух палок в земле.
Как строится парабола?
Параболу можно построить с помощью таврового угольника и рельса. Положите Т-образный угольник на рейку. Поместите булавку на доску над рельсом. Вставьте еще одну булавку в верхнюю часть Т-образного квадрата. Натяните нить вдоль вертикального края Т-образного квадрата.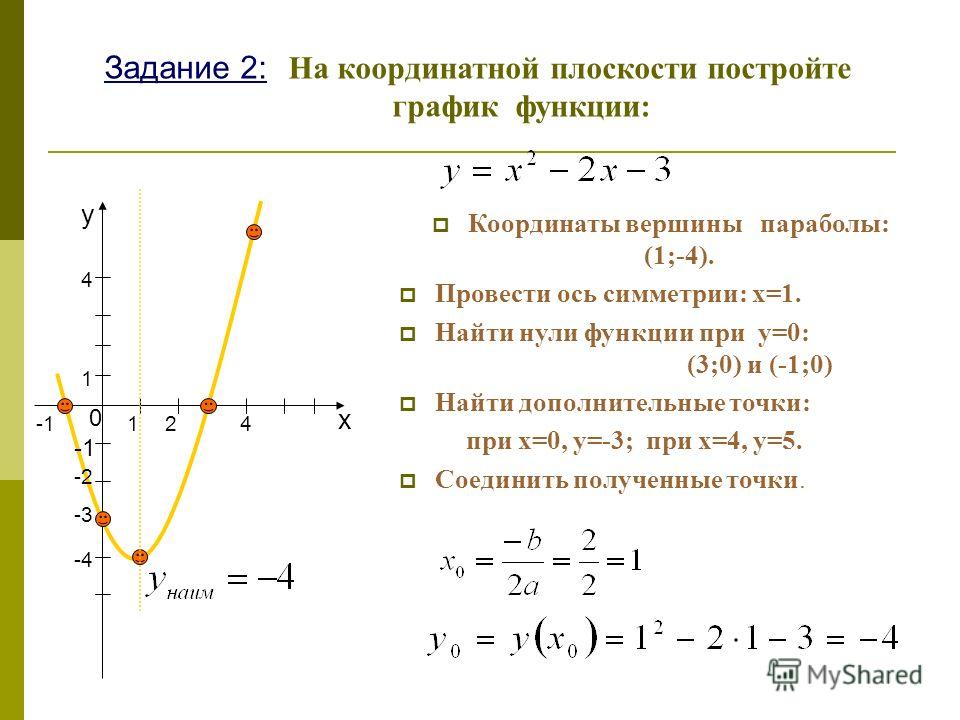 Сдвиньте Т-образный квадрат из стороны в сторону, удерживая маркер и нить напротив вертикального края. Полученная кривая представляет собой параболу.
Сдвиньте Т-образный квадрат из стороны в сторону, удерживая маркер и нить напротив вертикального края. Полученная кривая представляет собой параболу.
(Эти физические чертежи, называемые конструкциями из булавок и струн, может быть трудно представить себе в голове. Если вы хотите увидеть эти конструкции, посмотрите это видео. Парабола начинается прямо на минутной отметке.)
В алгебре работа с параболами обычно означает построение графика квадратичных уравнений или нахождение максимальных/минимальных точек (то есть вершин) парабол для решения квадратных задач. Однако в контексте коников есть некоторые дополнительные соображения.
Каковы ключевые слова для парабол?
Ключевые слова для парабол: вершина, фокус, директриса и ось симметрии. Чтобы сформировать параболу в соответствии с древнегреческими определениями, вы должны начать с прямой линии и точки в одну сторону; линия называется директрисой; точка называется фокусом. Парабола — это кривая, образованная всеми точками ( x , y ), которые равноудалены от директрисы и фокуса.
Линия, перпендикулярная директрисе и проходящая через фокус (т. е. линия, разделяющая параболу посередине), называется осью симметрии. Точка на этой оси, которая находится точно посередине между фокусом и направляющей, является вершиной; вершина — это точка, в которой парабола меняет направление.
Рассмотрим эту «правильную» (то есть прямую или перевернутую, но не боковую) параболу:
На картинке выше сама парабола нарисована синим цветом. Фокус (отмечен зеленым) находится внутри параболы, вершина (отмечена оранжевым) находится в точке поворота графика, директриса (отмечена фиолетовым) — прямая по другую сторону вершины от фокуса, а ось симметрии (отмечена красным) проходит вертикально через фокус и перпендикулярна директрисе.
Вы почти всегда будете иметь дело с вертикальными параболами, как показано выше. Но вы могли бы также (но только в разделе о кониках) иметь дело с горизонтальными, как это:
Это боковая или горизонтальная парабола (синий).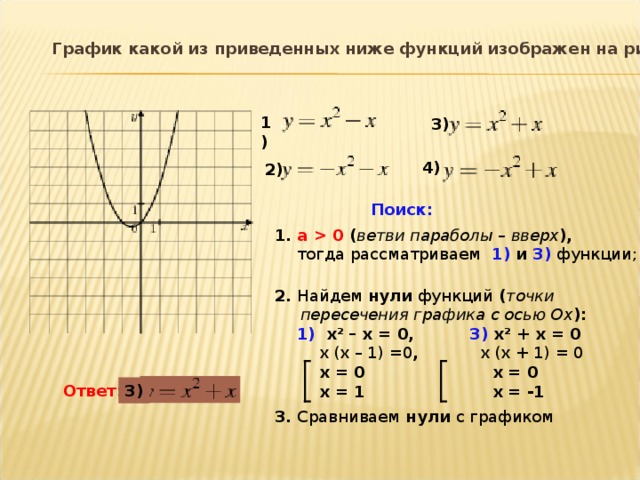 На этом графике вы можете видеть фокус (отмеченный зеленым цветом) внутри параболы, вершину (отмеченную оранжевым цветом) на графике, директрису (отмеченную фиолетовым цветом) по другую сторону от вершины от фокуса и ось симметрии (отмечено красным), проходящей через фокус и перпендикулярной директрисе. Фокус параболы всегда находится внутри параболы; вершина всегда находится на параболе; директриса всегда находится вне параболы.
На этом графике вы можете видеть фокус (отмеченный зеленым цветом) внутри параболы, вершину (отмеченную оранжевым цветом) на графике, директрису (отмеченную фиолетовым цветом) по другую сторону от вершины от фокуса и ось симметрии (отмечено красным), проходящей через фокус и перпендикулярной директрисе. Фокус параболы всегда находится внутри параболы; вершина всегда находится на параболе; директриса всегда находится вне параболы.
Откуда произошло слово парабола?
Название парабола происходит от нового латинского термина, который означает что-то похожее на сравнение или уравновешивание, и относится к тому факту, что расстояние от параболы до фокуса всегда равно (то есть всегда находится в равновесии) расстояние от параболы до директрисы. С практической точки зрения вам, вероятно, нужно будет только знать, что вершина находится точно посередине между директрисой и фокусом.
Какое основное физическое свойство парабол?
Основным свойством парабол в реальной жизни является то, что любой свет, спутниковый сигнал, звуковая волна и т. д., которые входят в параболу параллельно оси симметрии и достигают внутренней поверхности параболической чаши (например, спутниковой антенны), будут отражается обратно в фокус. Параболические антенны, такие как бионические уши и радиотелескопы, используют это свойство для концентрации сигнала на приемнике.
д., которые входят в параболу параллельно оси симметрии и достигают внутренней поверхности параболической чаши (например, спутниковой антенны), будут отражается обратно в фокус. Параболические антенны, такие как бионические уши и радиотелескопы, используют это свойство для концентрации сигнала на приемнике.
Какова общая форма уравнения параболы?
Общая форма уравнения параболы — это квадратное уравнение, к которому вы привыкли:
y = ax 2 + bx + c
— unless the quadratic is sideways, in which case the equation will look something like this:
x = ay 2 + на + c
Важным отличием двух уравнений является то, в какой переменной возводится в квадрат: для правильных (то есть вертикальных) парабол часть x возводится в квадрат; для боковых (то есть для горизонтальных) парабол и часть в квадрате.
Что такое вершинная форма уравнения параболы?
Форма вершины параболы — с вершиной в точке ( h , k ) — равна:
регулярная: y = a ( x ) 5 h 9027 − + к
сбоку: x = a ( y − k ) 2 + h
Форма вершины также может быть выражена как:
regular: y − k = a ( x − h ) 2
sideways: x − h = a ( y − k ) 2
Что такое коническая форма уравнения параболы?
Коническая форма уравнения параболы (которую вы найдете в продвинутых или старых текстах):0027 H ) 2
Боковые пути: 4 P ( x — H ) = ( Y — K ) 2
Why Do
и p в уравнениях параболы? Почему ( h , k ) для вершины и p вместо a в старинной формуле для коник? Не знаю.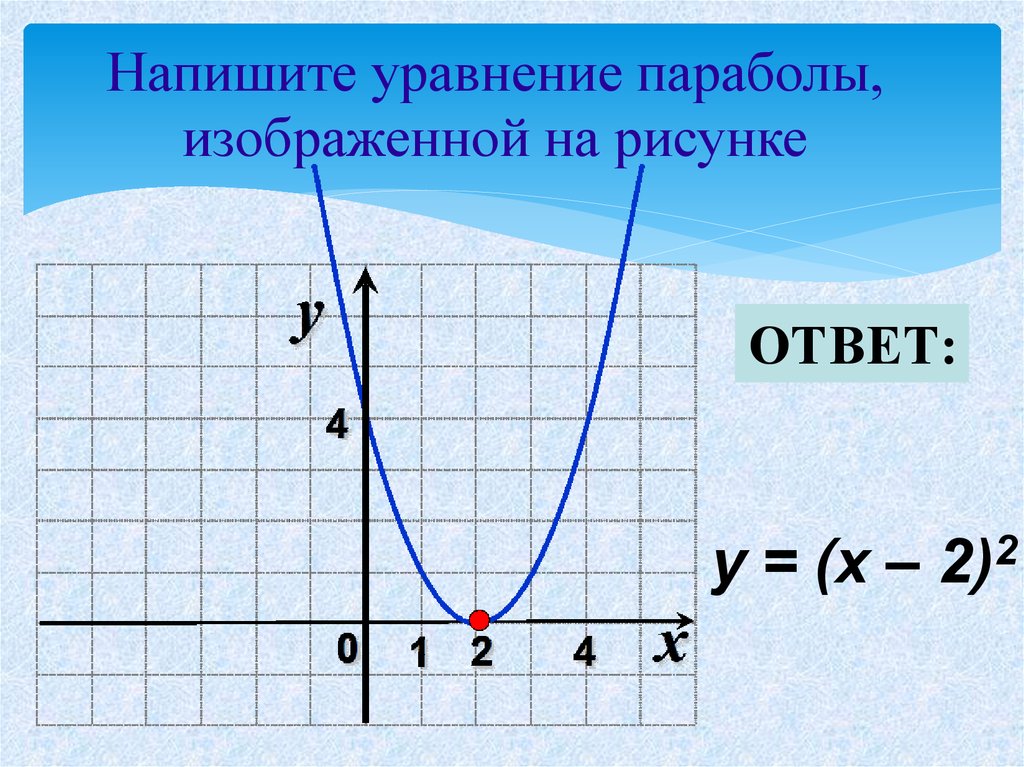 И даже неправда, что «все» используют эти буквы. (Обсуждение Math StackExchange со ссылкой на архивную статью AskDrMath) Так что ваше предположение так же хорошо, как и мое (хотя, если вы столкнетесь с источником, который кажется авторитетным, пожалуйста, напишите мне).
И даже неправда, что «все» используют эти буквы. (Обсуждение Math StackExchange со ссылкой на архивную статью AskDrMath) Так что ваше предположение так же хорошо, как и мое (хотя, если вы столкнетесь с источником, который кажется авторитетным, пожалуйста, напишите мне).
Какая связь между вершинной и геометрической формами уравнения параболы?
Важно отметить, работаете ли вы с вершинной формой или геометрической формой (т. k всегда остается с частью y , и что p всегда находится на неквадратной переменной части .
Фактически связь между вершинной формой уравнения и конической формой уравнения есть не что иное, как перестановка:
y = a ( x − h ) 2 + к
(1/ A ) ( y — K ) = ( y — K ) = ( y — K ) = ( y — K ) = ( y — K ) = ( y — K ) = ( y — K ) = 7.
 ) 2
) 2 4 p ( y − k ) = ( x − h ) 2
Другими словами, значение 4 p 90 на самом деле такое же, как 1 p 90 и ; это просто два способа сказать одно и то же. Но эта новая переменная p — это та переменная, с которой вам нужно иметь возможность работать, когда вы рисуете параболы в контексте коник: она представляет расстояние между вершиной и фокусом, а также то же самое, что и (что также равно) расстоянию между вершиной и направляющей; так 2 p – это расстояние между фокусом и директрисой.
Какая связь между вершиной и общими формами уравнения параболы?
Вершинная форма уравнения параболы преобразуется в общую форму путем умножения всего и выделения неквадратичной переменной с одной стороны знака «равно» с квадратным выражением с другой стороны. Общая форма уравнения параболы преобразуется в форму вершины путем завершения квадрата или с помощью следующей формулы, чтобы получить значение H , являясь x -координат вершины:
H = — B /(2 A )
. Затем подключите значение H в течение
Затем подключите значение H в течение . общую форму параболы и упростите, чтобы получить значение y = k .
Каковы правила парабол?
Правила для парабол таковы:
- Вершина всегда находится в точке ( h , k ; это точка, в которой кривая на графике разворачивается и начинает двигаться в обратном направлении.
- Независимо от того, работаете ли вы с ведущим коэффициентом a или геометрическим коэффициентом p (где p = 1/ a ):
- если коэффициент положительный, то кривая разворачивается вверх (или, если вбок, вправо).
- , если коэффициент отрицательный, то кривая разворачивается вниз (или, если вбок, влево).
- Ось симметрии — это линия, которая делит параболу на две равные половины.
- Если парабола вертикальна, то ось симметрии проходит через вершину и представляет собой вертикальную линию

- Если парабола направлена боком, то ось симметрии проходит через вершину и является горизонтальной линией y = k .
- Если парабола вертикальна, то ось симметрии проходит через вершину и представляет собой вертикальную линию
- Фокус будет в точке p единиц от вершины, и будет находиться внутри параболы на оси симметрии
- Направляющей будет линия p единиц от вершины, и она будет вне параболы и перпендикулярна оси симметрии.
Как вы помните правила построения парабол?
По моему опыту, лучший способ выучить и запомнить правила построения парабол — и особенно отношения между общей, вершинной и геометрической формами — это практиковаться, практиковаться и еще раз практиковаться. Ваш мозг достаточно устанет (или достаточно разочаруется) от необходимости снова и снова искать один и тот же материал, и начнет вспоминать отношения из чистой лени. По крайней мере, так работает *мой* мозг.
URL: https://www. purplemath.com/modules/parabola.htm
purplemath.com/modules/parabola.htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске вершины. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти форму вершины», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и перейдите на следующую страницу.)
Пожалуйста, примите «предпочтительные» файлы cookie, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Стр. 2 Стр. 3 Стр. 4
Стандартное уравнение параболы с примерами
График квадратного уравнения можно назвать параболой. В конических сечениях парабола — это уравнение кривой, где точка на кривой находится в эквидистантной форме фиксированной линии и фиксированной точки на плоскости. Неподвижная линия известна как направляющая параболы, а неподвижная точка известна как фокус параболы.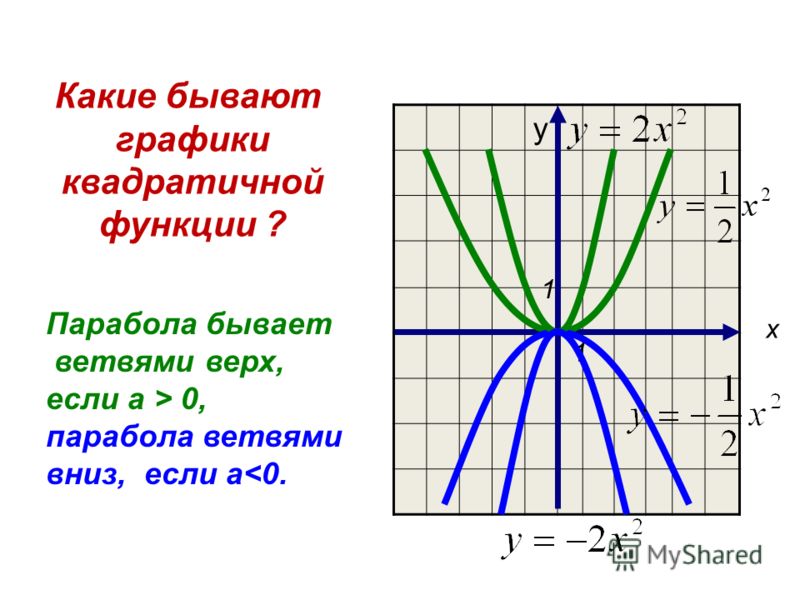 Проще говоря, параболой называется геометрическое место точки, равноудаленной от фиксированной линии (директрисы) и фиксированной точки (фокуса). Ось параболы проходит через фокус и перпендикулярна директрисе параболы. Точка пересечения параболы с осью называется вершиной параболы.
Проще говоря, параболой называется геометрическое место точки, равноудаленной от фиксированной линии (директрисы) и фиксированной точки (фокуса). Ось параболы проходит через фокус и перпендикулярна директрисе параболы. Точка пересечения параболы с осью называется вершиной параболы.
The general equation of a parabola is,
y = 4a(x – h) 2 + k
(or)
x = 4a( y – k) 2 + h
Где (h, k) – вершина параболы.
Некоторые важные термины и части параболы
- Фокус: Фокус — неподвижная точка параболы.
- Директриса: Направляющая параболы — это линия, перпендикулярная оси параболы.
- Фокусная хорда: Хорда, проходящая через фокус параболы и пересекающая параболу в двух различных точках, называется фокальной хордой.

- Фокусное расстояние: Фокусное расстояние — это расстояние от точки (x 1 , y 1 ) на параболе до фокуса.
- Широкая прямая кишка: Широкая прямая кишка представляет собой фокальную хорду, проходящую через фокус параболы и перпендикулярную оси параболы. Длина широкой прямой кишки LL’ = 4а.
- Эксцентриситет: Отношение расстояния точки от фокуса к ее расстоянию от директрисы называется эксцентриситетом (e). Для параболы эксцентриситет равен 1, т. е. e = 1.
Парабола имеет четыре стандартных уравнения, основанных на ориентации параболы и ее оси. Каждая парабола имеет разные поперечную ось и сопряженную ось.
Уравнение параболы | Парабола | Формулы параметров параболы | |||||
|---|---|---|---|---|---|---|---|
y 2 = 4AX | 9003 | ||||||
| 9000 2. |
| Вершина = (0,0) Фокус = (-a, 0) Парабола открывается влево. Equation of the axis is y = 0 Equation of the directrix is x – a = 0 The length of the latus rectum = 4a | |||||
x 2 = 4ay |
| Вершина = (0,0) Фокус = (0, а) Парабола открывается вверх. Уравнение оси x = 0 Уравнение Directrix составляет y + a = 0 Длина Latus rectum = 4a | |||||
x 2 = -4AY | . |
параболы:
- Парабола симметрична относительно своей оси.
Например, y 2 = 4ax симметрично относительно оси x, тогда как x 2 = 4ay симметрично относительно оси y.
- Если парабола симметрична относительно оси x, то парабола открывается вправо, если x-коэффициент положительный, и влево, если x-коэффициент отрицательный.
- Если парабола симметрична относительно оси y, то парабола направлена вверх, если коэффициент y положительный, и вниз, если коэффициент y отрицателен.
Ниже приведены стандартные уравнения параболы, когда ось симметрии параллельна оси x или оси y, а вершина не находится в начале координат.
Equation of the Parabola | Parabola | Formulae of parameters of a parabola | ||
|---|---|---|---|---|
(y – k) 2 = 4a(x – h) |
| Вершина = (h, k) Фокус = (h + a, k) Парабола открывается вправо. Уравнение оси: y = k Уравнение направляющей: x = h – a Длина широкой прямой кишки = 4a x – h) |
| Вершина = (h, k) Фокус = (h – a, k) Парабола открывается влево. Уравнение оси y = k Уравнение Directrix составляет x = h + a Длина латус -прямой кишки = 4a |
(x — h) 2 = 4a (Y — K) | 64649649649649649649649649649649649649649649649649649649649649649649649649649649649649649649649649646464649н. Вершина = (h, k) Фокус = (h, k + a) Парабола открывается вверх. Уравнение оси x = h Уравнение направляющей y = k – a Длина широкой прямой кишки = 4a | |||
(x – h) 2 = -4a(y – k) |
| Вершина = (h, k) Фокус = (h, k – a) Парабола открывается вниз. Уравнение оси составляет x = H Уравнение Directrix IS y = K + A Длина прямой кишки LATUS = 4A |
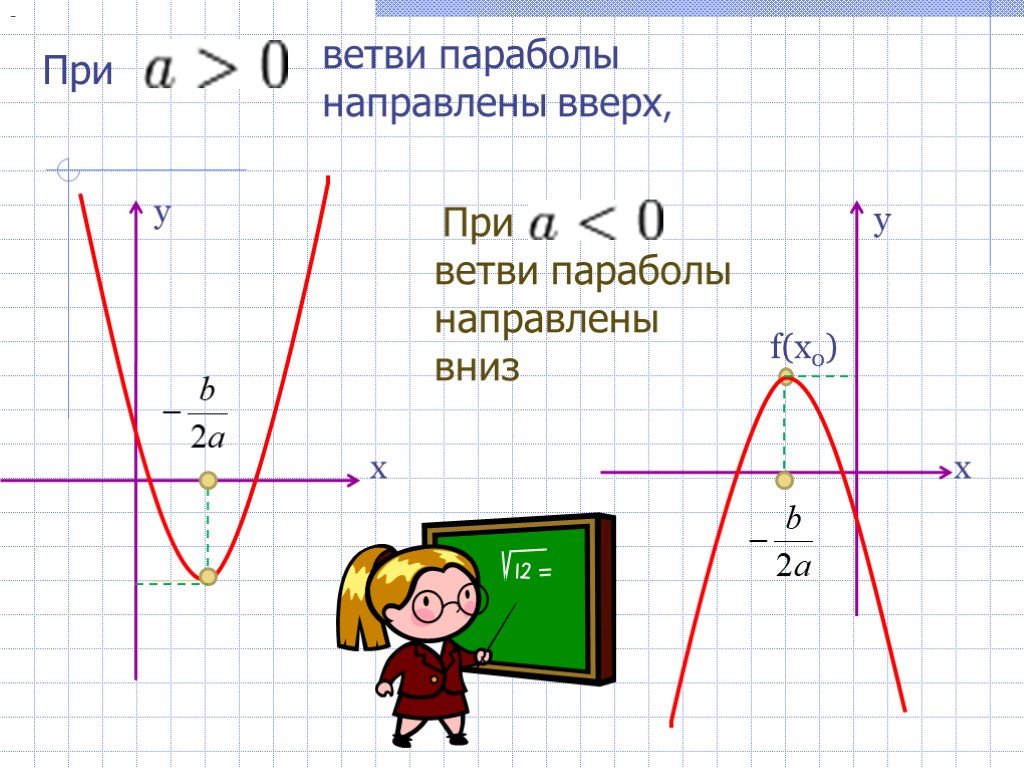 Из определения параболы расстояние точки P до фокуса (F) равно расстоянию той же точки P до директрисы параболы. Теперь рассмотрим точку X на направляющей с координатами (-a, y).
Из определения параболы расстояние точки P до фокуса (F) равно расстоянию той же точки P до директрисы параболы. Теперь рассмотрим точку X на направляющей с координатами (-a, y).
Из определения эксцентриситета параболы имеем
e = PF/PX = 1
⇒ PF = PX
Координаты фокуса равны (a, 0). Теперь, используя формулу координатного расстояния, мы можем найти расстояние от точки P (x, y) до фокуса F (a, 0). — — (1)
Уравнение директрисы: x + a = 0. Чтобы найти расстояние PX, мы используем формулу перпендикулярного расстояния.
PX = (x + a)/√[1 2 + 0 2 ]
⇒ PX = x +a —————— (2)
Мы уже знаем, что PF = PX. Итак, приравняем уравнения (1) и (2).
√[(x – a) 2 + y 2 ] = (x + a)
По возводя в квадрат обе стороны, получаем
⇒ [(x – a) 2 + y 2 ] = (x + a) 2
⇒ x 2 + a 2 – 2ax + y 2 = x 2 9 0 + a 2905
⇒ y 2 – 2ax = 2ax
⇒ y 2 = 2ax + 2ax ⇒ y 2 = 4ax
.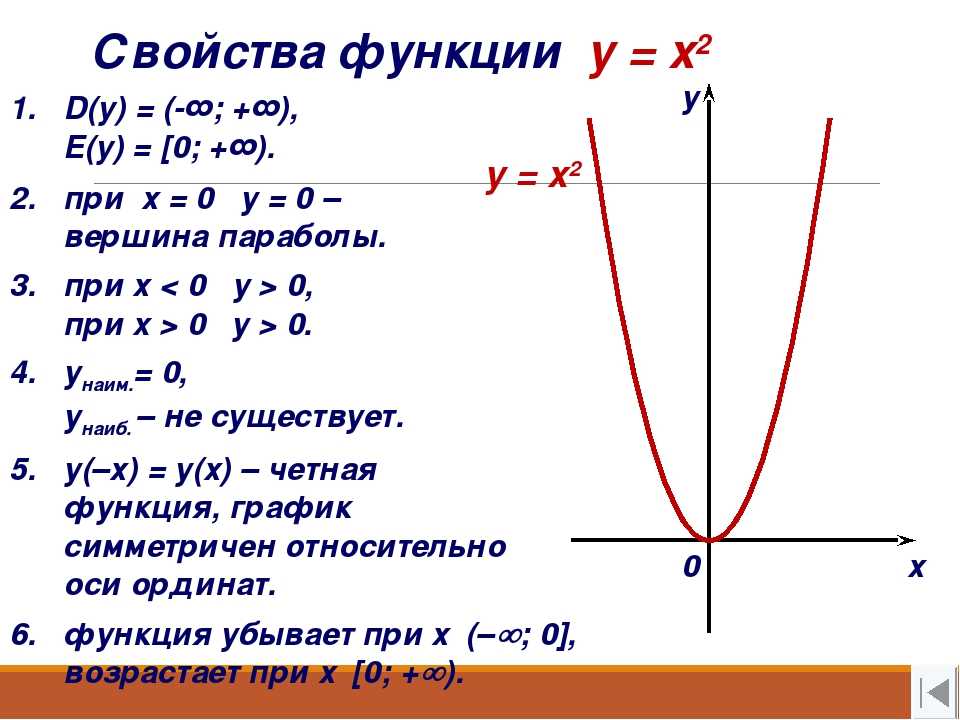 Точно так же мы можем вывести стандартные уравнения трех других парабол.
Точно так же мы можем вывести стандартные уравнения трех других парабол.
- y 2 = -4ax
- x 2 = 4ay
- x 2 = -4ay
y 2 = 4ax, y 2 = -4ax, x 2 = 4ay, а x 2 = -4ay — стандартные уравнения параболы.
Решенные примерыЗадача 1: Найдите длину широкой прямой кишки, фокуса и вершины, если уравнение параболы y 2 = 12x.
Решение:
. ⇒ a = 12/4 = 3
Мы знаем, что
Прямая кишка параболы = 4a = 4 (3) = 12
Теперь фокус параболы = (a, 0) = (3, 0)
Вершина данной параболы = (0, 0)
Задача 2: Найдите уравнение параболы, симметричной относительно оси X и проходящей через точку (-4, 5).
Решение:
Дано,
Парабола симметрична относительно оси X и имеет вершину в начале координат.
Таким образом, уравнение может иметь вид y 2 = 4ax или y 2 = -4ax, где знак зависит от того, направлена ли парабола влево или вправо.
Парабола должна открываться влево, так как она проходит через (-4, 5), лежащую во втором квадранте.
Итак, уравнение будет таким: y 2 = -4ax
Подставив (-4, 5) в приведенное выше уравнение,
⇒ (5) 2 = -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
Следовательно, уравнение параболы: y 2 = -4(25/16)x (или) 4y
2 = -25x.
Задача 3: Найти координаты фокуса, оси, уравнения директрисы и прямой линии параболы x 2 = 16y.
Решение:
,
Уравнение параболы: x 2 = 16y
, сравнивая данное уравнение с стандартной формой x 2 = 4.
4a = 16. ⇒ а = 4
Коэффициент y положительный, поэтому парабола направлена вверх.
Кроме того, ось симметрии проходит вдоль положительной оси Y.
Следовательно,
Фокус параболы равен (a, 0) = (4, 0).
Уравнение направляющей y = -a, т. е. y = -4 или y + 4 = 0.
Длина широкой прямой кишки = 4a = 4(4) = 16.
длина широкой прямой кишки, фокуса и вершины, если уравнение параболы 2(x-2) 2 + 16 = y.
Решение:
Дано,
Уравнение параболы 2(x-2) 2 + 16 = y
Сравнивая данное уравнение с общим уравнением параболы (x – h) 2 + k, получаем
a = 2
(h, k) = (2, 16)
Мы знаем, что
Длина широкой прямой кишки параболы = 4a
= 4(2) = 8
Теперь фокус = (а, 0) = (2, 0)
Теперь вершина = (2, 16).
Задача 5. Уравнение параболы: x 2 – 12x + 4y – 24 = 0, затем найдите ее вершину, фокус и направляющую.
Решение:
,
Уравнение параболы — x 2 — 12x + 4y — 24 = 0
⇒ x 2 — 12x + 36 — 36 + 4y — 24 = = 24 = = 24 = = 24 =.


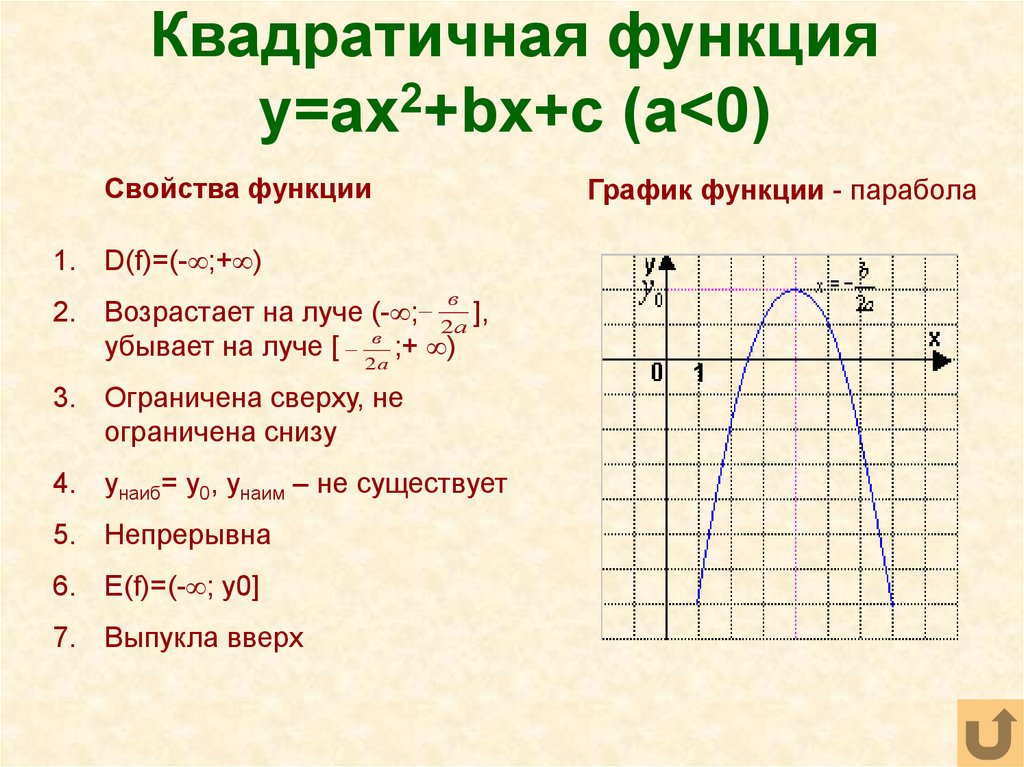
 парабола открывается вправо.
парабола открывается вправо.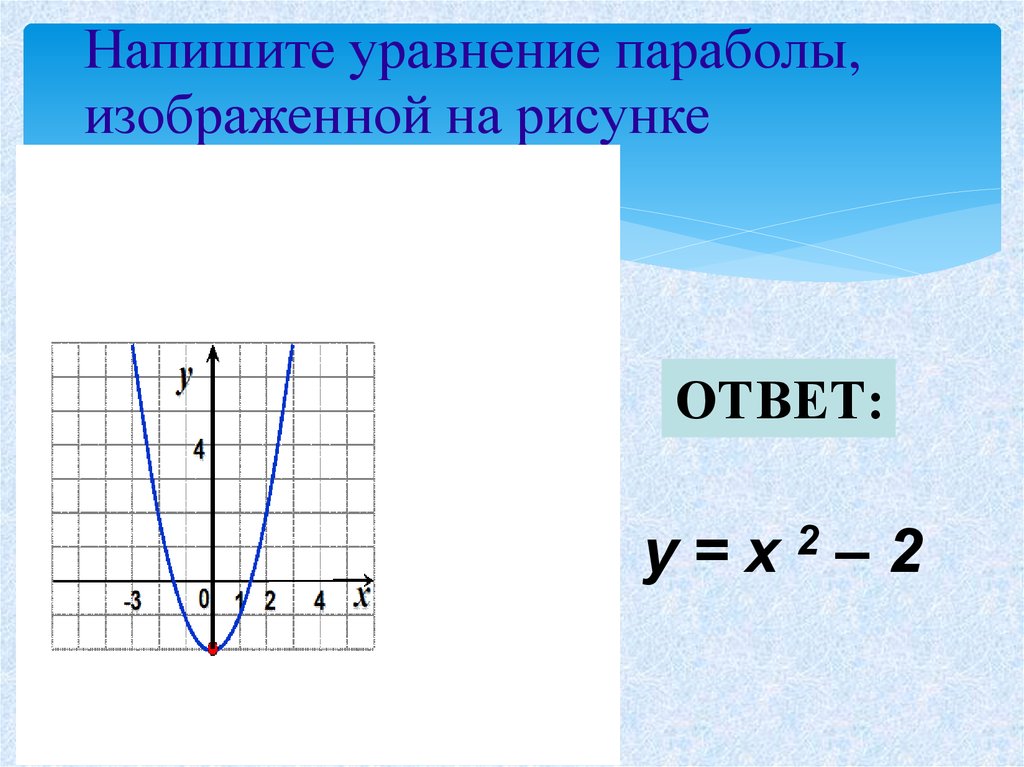 Например, y 2 = 4ax симметрично относительно оси x, тогда как x 2 = 4ay симметрично относительно оси y.
Например, y 2 = 4ax симметрично относительно оси x, тогда как x 2 = 4ay симметрично относительно оси y.