Какие части окружности бывают и чем они различаются | Бери и Делай
В реальной жизни мы достаточно часто имеем дело с окружностью и ее элементами, хотя не всегда замечаем это. К примеру, зная диаметр колеса, как можно узнать расстояние, которое оно преодолевает за 1 оборот? Или как узнать, сколько места в саду займет пруд в форме круга, если вам известен его радиус?
«Бери и Делай» помогает разобраться, что представляет собой окружность, чем отличны и примечательны ее элементы.
Что такое окружность
Если взять множество точек и расположить их последовательно друг за другом, у вас получится линия. Если она не искривляется, не имеет ни начала, ни конца и бесконечно продолжается в обе стороны, то это прямая. Если линия изгибается из-за определенного расположения точек, то это кривая. Концы кривой линии, в свою очередь, могут не соединяться, образуя незамкнутую линию. Когда же они соединяются, получается замкнутая линия. Нарисуйте замкнутую кривую линию так, чтобы все ее точки находились в одной плоскости и на равном расстоянии от заданной точки, которая располагается в той же плоскости, и вы получите отдельную геометрическую фигуру под названием окружность. Если взять только плоскость внутри окружности, то вы получите другую геометрическую фигуру под названием круг. Чтобы построить окружность, используется циркуль — специальный инструмент, позволяющий чертить окружности и дуги.
Нарисуйте замкнутую кривую линию так, чтобы все ее точки находились в одной плоскости и на равном расстоянии от заданной точки, которая располагается в той же плоскости, и вы получите отдельную геометрическую фигуру под названием окружность. Если взять только плоскость внутри окружности, то вы получите другую геометрическую фигуру под названием круг. Чтобы построить окружность, используется циркуль — специальный инструмент, позволяющий чертить окружности и дуги.
Что представляют собой элементы окружности
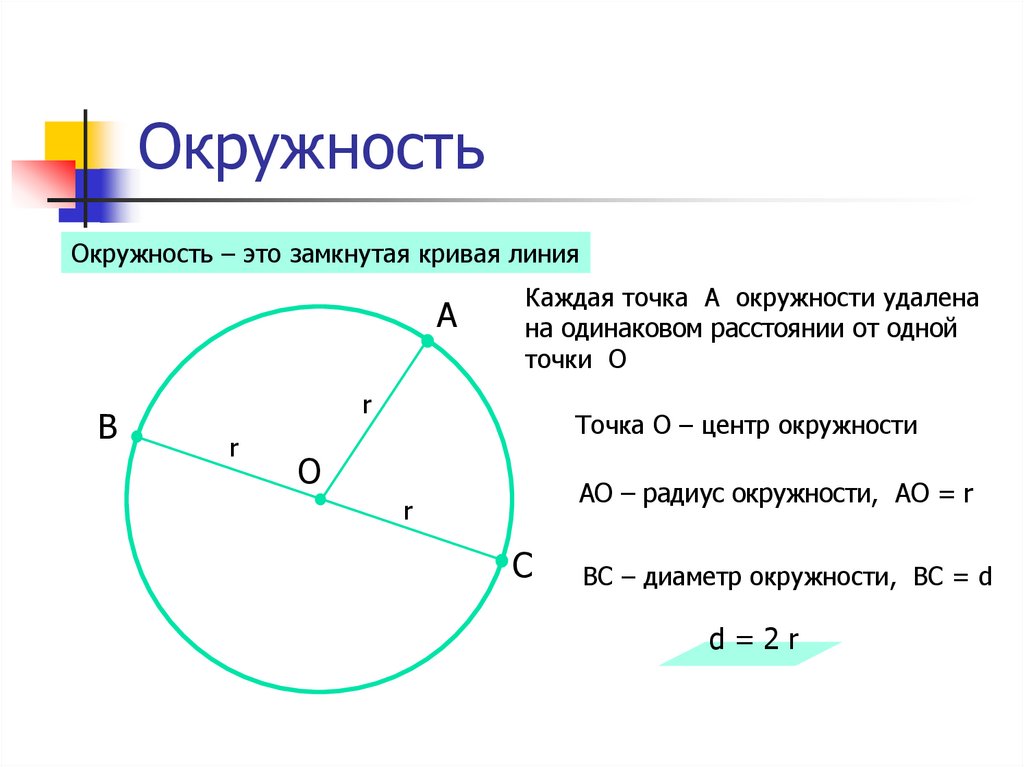
- Длина отрезка от центра окружности до любой ее граничной точки всегда едина и называется радиусом.
- Отрезок, который соединяет 2 любые точки окружности и проходит через центр окружности, называется диаметром. При этом диаметр окружности всегда в 2 раза больше ее радиуса.
- Если измерить длину замкнутой плоской кривой, ограничивающей круг, получится длина окружности. Также можно сказать, что длина окружности является частным случаем периметра, если рассматривать окружность как границу круга.

Обозначим радиус буквой R, диаметр — буквой D, а длину окружности — буквой L. В определении диаметра выше говорится, что диаметр окружности всегда в 2 раза больше ее радиуса: D = 2R Если взять длину окружности и разделить ее на диаметр окружности, вы всегда получите одно и то же число — число пи (π). Оно неизменно, иррационально и имеет бесконечное количество цифр после запятой: π ≈ 3,1415926535897932384626433832795… Таким образом, чтобы узнать длину окружности, достаточно умножить число π на ее диаметр или на 2 радиуса: L = π × D = π × 2R
Зная радиус, легко вычислить площадь круга. Для этого нужно число π умножить на квадрат радиуса круга: S = π × R2 = (π × D2) : 4
- Отрезок, соединяющий 2 любые точки окружности, называется хордой.
- Прямая, которая соединяет 2 любые точки окружности, называется секущей. Таким образом, хорда всегда находится на секущей.
- Если у прямой с окружностью только 1 общая точка, то эта прямая называется касательной. Полезно знать, что касательная всегда перпендикулярна радиусу окружности, проведенному через точку касания.
 И наоборот: если прямая проходит через точку, расположенную на конце радиуса, лежащего на окружности, и перпендикулярна ему, то она называется касательной.
И наоборот: если прямая проходит через точку, расположенную на конце радиуса, лежащего на окружности, и перпендикулярна ему, то она называется касательной.
- Часть окружности называют дугой. Она получается благодаря тому, что окружность любые 2 различные и принадлежащие ей точки разбивают на части, каждая из которых называется дугой.
- Дуга, в свою очередь, может быть полуокружностью, если отрезок, который соединяет ее концы, является диаметром окружности.
- Если от каждого конца дуги окружности провести отрезки к центру окружности, то вы получите угол с вершиной в центре окружности, который называется центральным углом. Таким образом, градусная мера дуги равна градусной мере центрального угла, что видно из картинки выше.
- Если вершина угла находится на окружности, а стороны пересекают окружность, то такой угол называется вписанным углом.
- Часть круга, которая лежит внутри конкретного центрального угла, называется круговым сектором.
- Часть круга, которая заключена между дугой окружности и ее хордой, называется круговым сегментом.
 Если из середины хорды до пересечения с дугой провести перпендикуляр, вы получите стрелку дуги, которая еще называется высотой сегмента.
Если из середины хорды до пересечения с дугой провести перпендикуляр, вы получите стрелку дуги, которая еще называется высотой сегмента. - Если сектор отсечен радиусами, образующими угол в 90°, то он называется квадрантом.
Поделиться в социальных сетях
Вам может понравиться
Окружность
К содержанию
Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка (O) называется центром окружности.
Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности.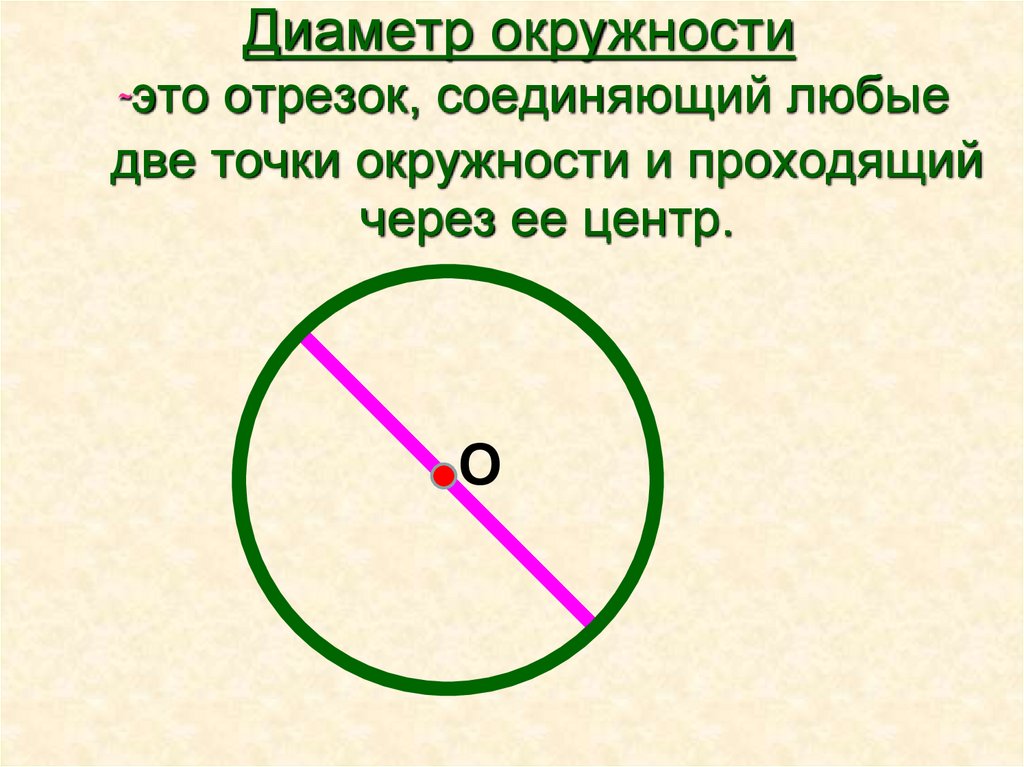 Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Длина единичной полуокружности обозначается через π.
Сумма градусных мер двух дуг окружности с общими концами равна
Часть плоскости, ограниченная окружностью, называется кругом.
Круговой сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора.
Две окружности, имеющие общий центр, называются концентрическими.
Две окружности, пересекающиеся под прямым углом, называются ортогональными.
Взаимное расположение прямой и окружности
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d ), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
 Такая прямая называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Такая прямая называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. - Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .
Центральные и вписанные углы
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
- Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны. - Следствие 2.
Вписанный угол, опирающийся на полуокружность — прямой.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Основные формулы
- Длина окружности:
C = 2∙π∙R
- Длина дуги окружности:
R = С/(2∙π) = D/2
- Диаметр:
D = C/π = 2∙R
- Длина дуги окружности:
l = (π∙R) / 180∙α,
где α — градусная мера длины дуги окружности)
- Площадь круга:
S = π∙R2
- Площадь кругового сектора:
S = ((π∙R2) / 360)∙α
Уравнение окружности
- В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (xо;yо) имеет вид:
(x — xо)2 + (y — yо)2 = r2
- Уравнение окружности радиуса r с центром в начале координат имеет вид:
x2 + y2 = r2
| Площадь круга |
Другие заметки по алгебре и геометрии
Полезная информация?
Каковы некоторые приложения кругов в реальной жизни?
Амина Решма
2 мин чтения
Одним из фундаментальных уроков геометрии является круг. Различные применения кругов в нашей повседневной деятельности показывают, насколько они важны. Каждый день мы сталкиваемся со многими предметами круглой формы; например, солнце, луна, планеты и даже мельчайший атом имеют круглую форму. В реальном мире круги можно найти как в естественном мире, так и в творениях человека.
Круг
Греческие и латинские слова, обозначающие «обруч» и «кольцо», являются источниками слова «круг». 2 Окружность — это двухмерная фигура в геометрии, определяемая как набор точек на плоскости, равноудаленных от определенной фиксированной точки. Радиус круга – это фиксированное расстояние от центра. Диаметр круга вдвое больше его радиуса. 3, 4
Применение кругов в реальном мире.
Существует множество применений кругов в архитектуре, ландшафтном дизайне, графике, инфраструктуре, транспорте и других областях.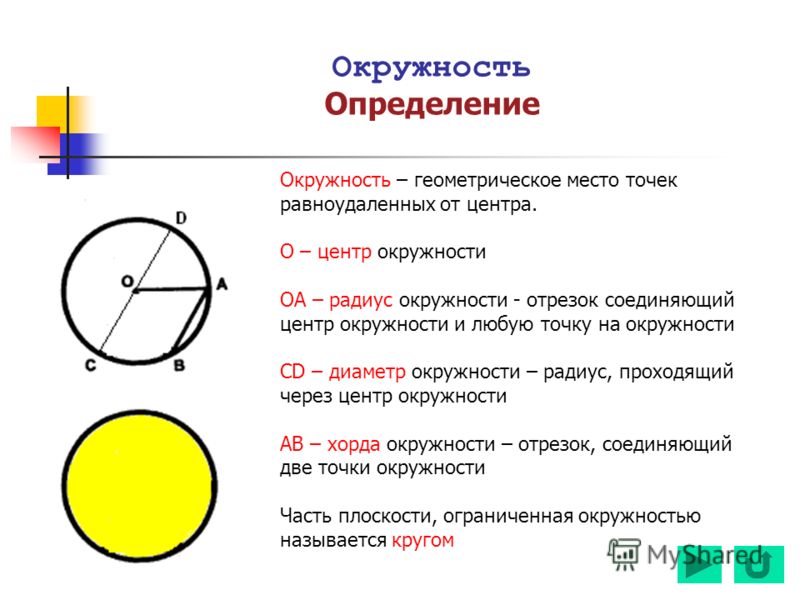 Вот некоторые из них: 4,5
Вот некоторые из них: 4,5
- Круги внесли значительный вклад в цивилизацию. Только посмотрите, как изобретение колеса изменило общество и наши способы передвижения.
- Круги часто используются при проектировании спортивных дорожек, парков отдыха, планов зданий, каруселей, колес обозрения и т. д. благодаря их симметричным свойствам.
- Использование кругов проявляется даже в производстве сфер (шары, воздушные шары, глобусы), цилиндров (трубы, свечи, ведерки) и конусов (рожки для мороженого, шляпы для вечеринок, дорожные конусы).
- Симметричные свойства круга используются инженерами для создания различных объектов, включая часы, автомобили, корабли, самолеты, радиоприемники, телефоны, тачки, кондиционеры, ракеты и многое другое.
- Круги могут быть даже ценным инструментом при работе в саду, поскольку они помогают определить, сколько пространства необходимо растениям для роста вокруг них.

- Архитекторы используют круги при проектировании зданий, особенно при разработке декоративных элементов, таких как купола, арки, круглые балки и криволинейные поверхности.
- Круги используются в графике для вращения объектов на экранах компьютеров и преобразования 2D-концепций в 3D-представления.
- Круги используются GPS для определения расстояния. Он находит точки и определяет их расстояние от спутника, используя теорию окружности.
- Ученые используют круги по-разному, в том числе при проектировании сепараторов частиц, расчетах траекторий, оценке размеров далеких планет и измерении кратеров.
- Круги используются сейсмологами для определения и локализации очагов землетрясений.
Применение кругов практически безгранично. Посетите блог BYJU FutureSchool, чтобы узнать больше о различных математических специальностях, о том, как они применяются в повседневной жизни, а также о ряде других интригующих тем.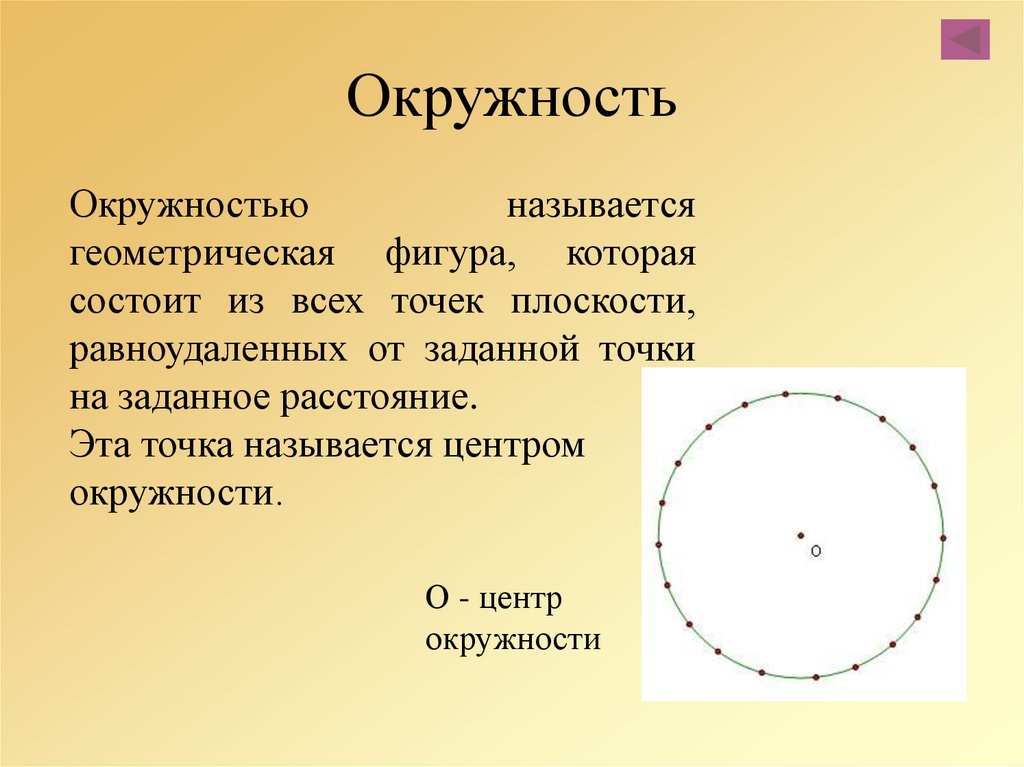
Ссылки:
- CIRCLE GEOMETRY Проект улучшения математического образования в школах (TIMES) . (2011 г.), с https://amsi.org.au/teacher_modules/pdfs/Circle_Geometry.pdf
- круг | Этимология, происхождение и значение круга по etymonline . (н.д.). Получено 30 августа 2022 г. с https://www.etymonline.com/word/circle
- (PDF) ПЛАН УРОКА «Круг и его части или связанные с ним термины». (2019). Получено 30 августа 2022 г. с https://www.researchgate.net/publication/331439467_A_LESSON_PLAN_ON_Circle_and_Its_Parts_or_the_Terms_Related_To_It
- Как круги используются в реальной жизни? (2020). Получено 30 августа 2022 г. с https://www.reference.com/world-view/circles-used-real-life-5a9.cee1968769425
- Применение кругов в реальном мире Патриком Сойером . (2014). Получено 30 августа 2022 г. с https://prezi.com/jhnfzclxankh/applications-of-circles-in-the-real-world/

Учись с математикой, математика
Наука и математика: идеальное сочетаниеЕстествознание и математика — очень взаимосвязанные темы. Импликация одного автоматически подразумевает подразумеваемые части другого. Другими словами, если наука Подробнее…
Как исчисление используется в реальном мире?Исчисление — это математическая отрасль, которая занимается изучением изменений. Он играет важную роль в выводе последствий в системах количественного моделирования, связанных с изменениями. Подробнее…
Как компьютеры повлияли на математику?Более широкое применение компьютеров в математике повлияло на математическое мышление и рассуждения. В 1960-х люди начали осознавать потенциал интеграции компьютеров в Подробнее…
Математика: решение реальных задач Сложные формулы, длинные уравнения, расчеты и т. д. Если вы думаете, что это и есть математика, вы можете изменить свое мнение после прочтения этой статьи.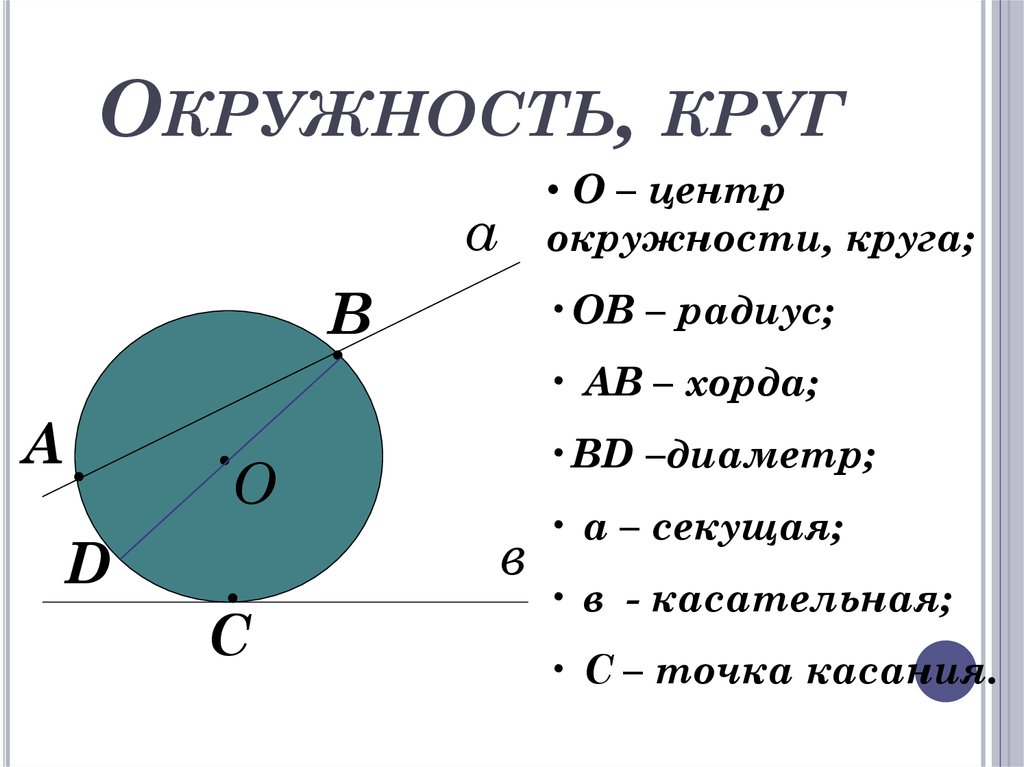 Подробнее…
Подробнее…
Каковы некоторые примеры кругов в реальном мире?
Амина Решма
2 мин чтения
Определение круга
Окружность — это «идеально круглая форма : линия, изогнутая так, что ее концы сходятся, и все точки на линии находятся на одинаковом расстоянии от центра». 1
Вы давно видели круг? Наверняка есть! Круги окружают вас, но вы можете даже не осознавать этого, если один из них находится прямо перед вами, потому что они очень распространены. В реальном мире круги можно найти как в естественном мире, так и в творениях человека. Ниже приведены несколько примеров использования кругов в повседневной жизни:
- Часы
Многие часы, которые мы видим, имеют круглую форму. Большинство настенных, настольных и наручных часов можно считать основными примерами круглых предметов, используемых ежедневно.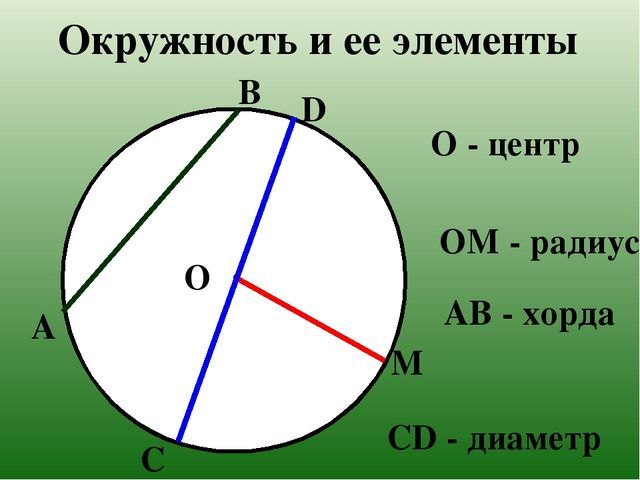
- Зрачок
Зрачок представляет собой округлое отверстие в центре радужной оболочки. Обязательно обратите на это внимание, когда в следующий раз будете стоять перед зеркалом.
- Тарелки и миски
Большинство столовых приборов, таких как миски и тарелки, имеют круглую форму. Таким образом, тарелки могут быть наиболее типичным примером круглого объекта в повседневной жизни.
- Колесо обозрения
При посещении парков развлечений колесо обозрения является одним из главных приманок для большинства детей. Легко заметить, что гигантский аттракцион на колесах имеет круглую форму и может стать одним из самых захватывающих примеров для детей.
- Пицца, пончики, пирожные, леденцы, хлопья и печенье
Какие закуски любят большинство детей? Сколько из этих закусок имеют форму кругов? Чтобы вспомнить определение и словарь, связанный с геометрической фигурой, проверьте форму своей любимой закуски, когда в следующий раз потянетесь за ней.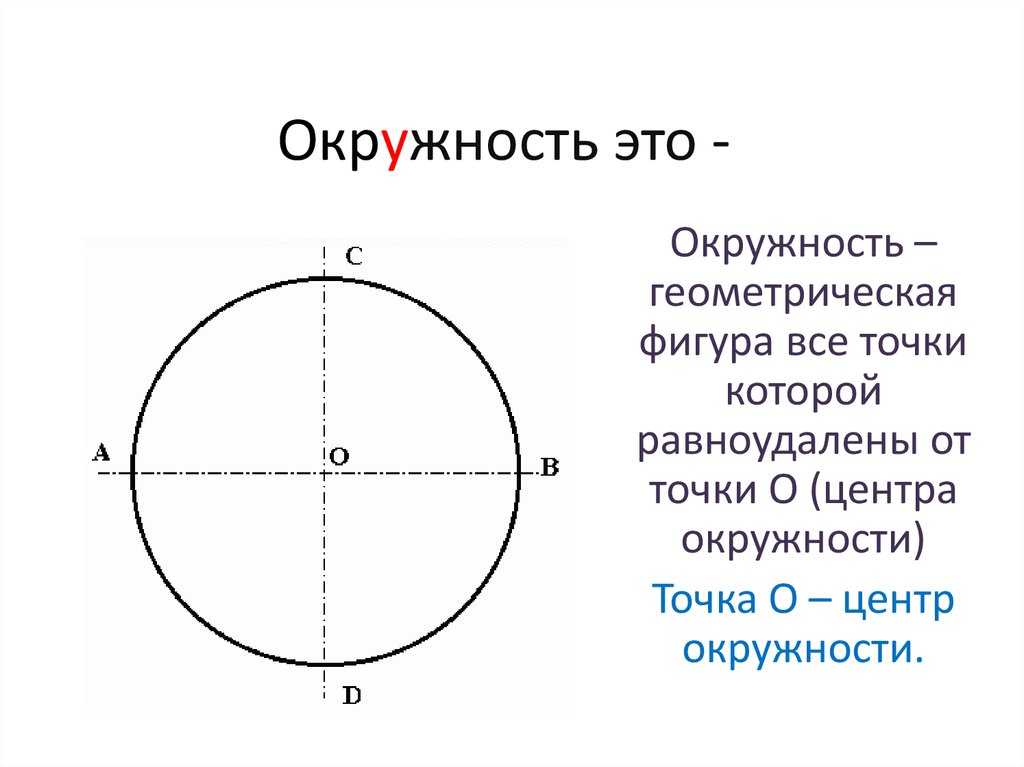
- Венки
Венок представляет собой декоративную композицию из цветов или листьев на круглой основе. Несомненно, это хороший пример для детей. Не так ли?
- Колеса
Видели ли вы какие-нибудь автомобили в последнее время? Велосипед, автомобиль, автобус или велосипед? Другой пример круглого предмета, используемого ежедневно, — это колеса различных транспортных средств.
- Летающая тарелка
Летающая тарелка — это скользящая игрушка или спортивный инвентарь, который бросают вручную. Они также известны как летающие диски или скользящие диски, и большинство детей их обожают. Еще один пример, который понравится детям? Конечно!
- Увеличительное стекло
Лупы также имеют круглую форму. То, что это круги, хорошо видно через внешнюю границу.
- Медали
Медали представляют собой круглые металлические диски, обычно размером с большую монету, украшенные текстом или надписями в честь какого-либо лица, например солдата или спортсмена.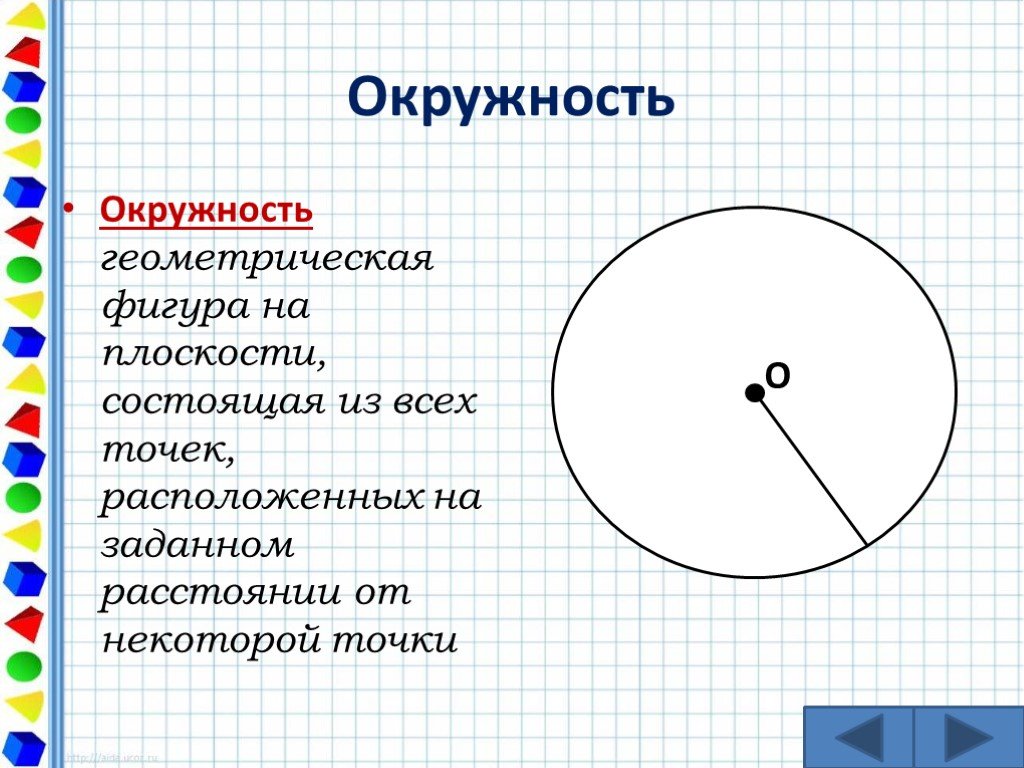 В следующий раз, когда вы будете смотреть Олимпийские игры, пробежите марафон или станете свидетелем того, как ваш ребенок выиграет спортивное мероприятие, у вас будет возможность убедиться в этом лично.
В следующий раз, когда вы будете смотреть Олимпийские игры, пробежите марафон или станете свидетелем того, как ваш ребенок выиграет спортивное мероприятие, у вас будет возможность убедиться в этом лично.
Если вам понравилось читать о примерах кругов, вы также можете узнать больше о треугольниках и золотых пропорциях. Чтобы узнать больше наводящих на размышления статей по математике, посетите блог BYJU FutureSchool.
Ссылки:
- Определение круга и его значение | Британский словарь . (н.д.). Получено 28 августа 2022 г. с https://www.britannica.com/dictionary/circle
- 438 Things That Are Circular . (н.д.). Получено 28 августа 2022 г. с https://thingdb.io/things-that-are-circular/ 9.0032
Математика, Мир математики
Наука и математика: идеальное сочетание Естествознание и математика — очень взаимосвязанные темы. Импликация одного автоматически подразумевает подразумеваемые части другого.


 И наоборот: если прямая проходит через точку, расположенную на конце радиуса, лежащего на окружности, и перпендикулярна ему, то она называется касательной.
И наоборот: если прямая проходит через точку, расположенную на конце радиуса, лежащего на окружности, и перпендикулярна ему, то она называется касательной.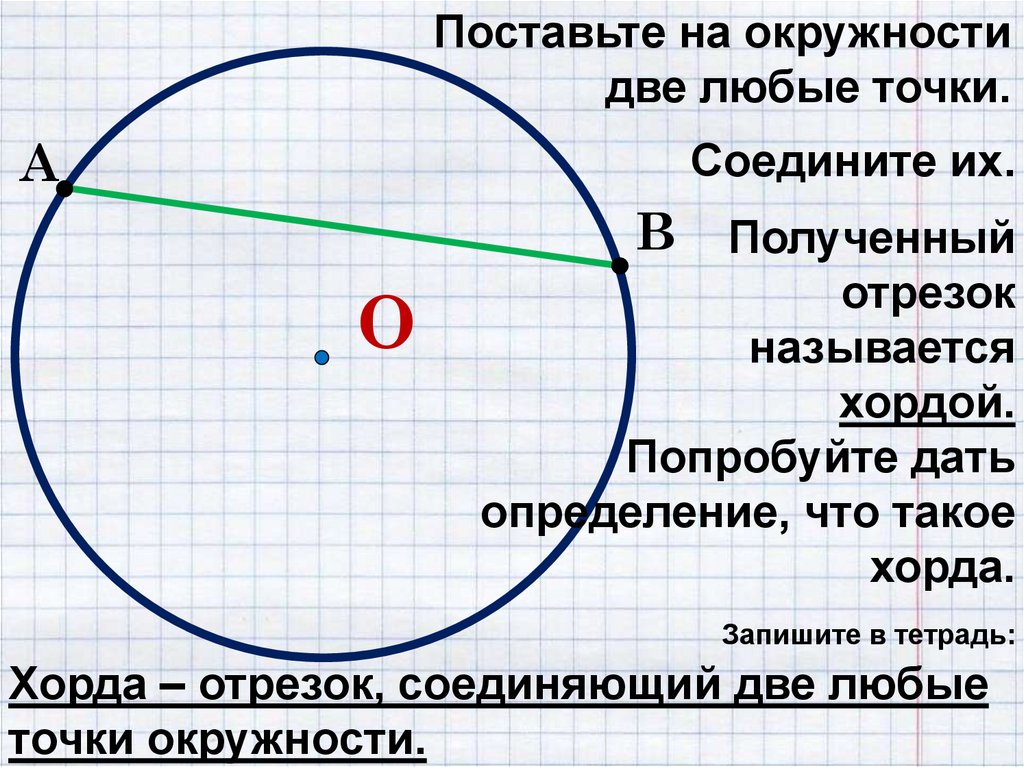 Если из середины хорды до пересечения с дугой провести перпендикуляр, вы получите стрелку дуги, которая еще называется высотой сегмента.
Если из середины хорды до пересечения с дугой провести перпендикуляр, вы получите стрелку дуги, которая еще называется высотой сегмента.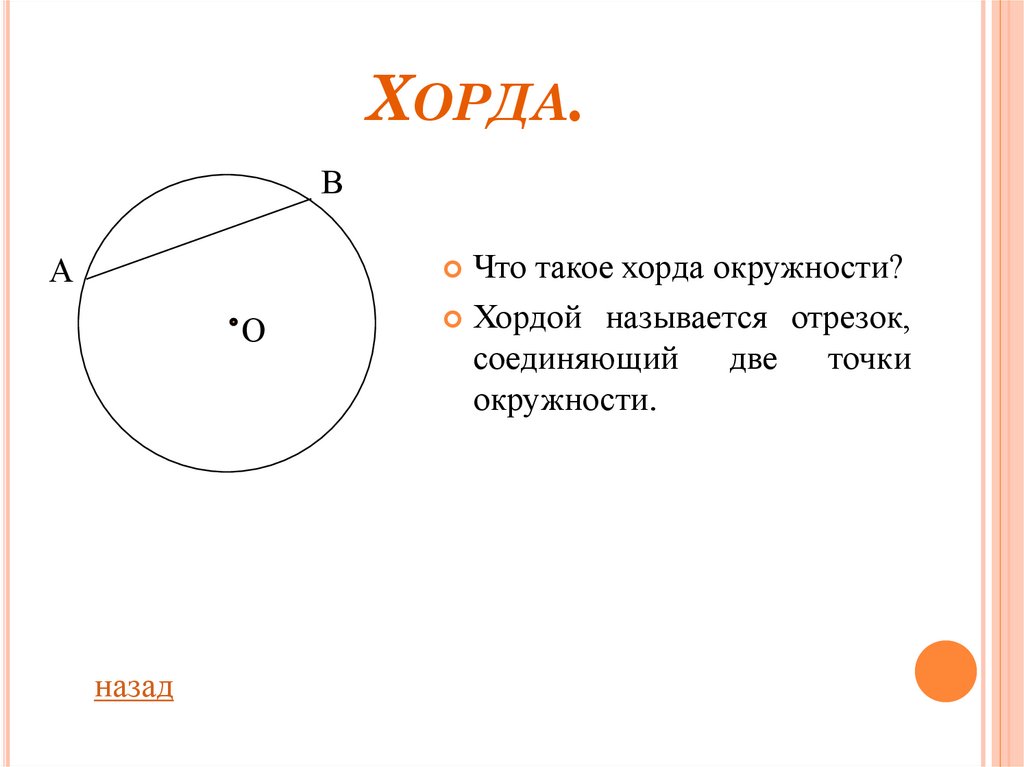 Такая прямая называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Такая прямая называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.