Какие четырехугольники имеют четыре прямых угла: Типы четырехугольников. Геометрия квадрат. Прямоугольник геометрии. Геометрия параллелограмм.

Типы четырехугольников. Геометрия квадрат. Прямоугольник геометрии. Геометрия параллелограмм.

• Альфашкола
• Статьи
• Типы четырехугольников

Различные типы четырехугольников имеют разные свойства, которые определяются различным соотношением сторон и углов четырехугольника. Вполне возможно иметь четырехугольник, в котором никакие две стороны и никакие два угла не совпадают. С другой стороны, любые две или более сторон могут быть равны по длине, а любые два или более углов могут быть одинаковой величины. Кроме того, одна или обе пары противоположных сторон могут быть параллельны. Многие конфигурации приводят к фигурам с определенными именами, и, по крайней мере, некоторые из этих имен, вероятно, вам знакомы. Примеры различных конфигураций показаны ниже, вместе с именем, котор дали к каждой форме и кратко описанием своих характеристик.

Квадрат- самый простой тип четырехугольника. Квадрат называется равносторонним, потому что все четыре стороны имеют одинаковую длину то есть квадрат является правильным многоугольником, и все четыре внутренних угла равны девяносто градусов. Диагонали в квадрате имеют одинаковую длину, пересекают друг друга  перпендикулярно, то есть пересекаются под прямым углом. По определению квадрат- это тоже прямоугольник, параллелограмм и ромб .

 

• Квадрат имеет четыре равные стороны и четыре прямых угла.

 

---

Прямоугольник — четырехугольник, где все четыре внутренних угла имеют прямые углы (т. е. девяносто градусов), только противоположные стороны имеют равную длину. Смежные стороны могут  быть разной длины. По определению прямоугольник является и параллелограммом.

 

• Только противоположные стороны прямоугольника должны быть равны

---

 

Параллелограмм — обе пары противоположных сторон параллельны (отсюда и название), противоположные стороны равны, и противоположные углы равны по величине.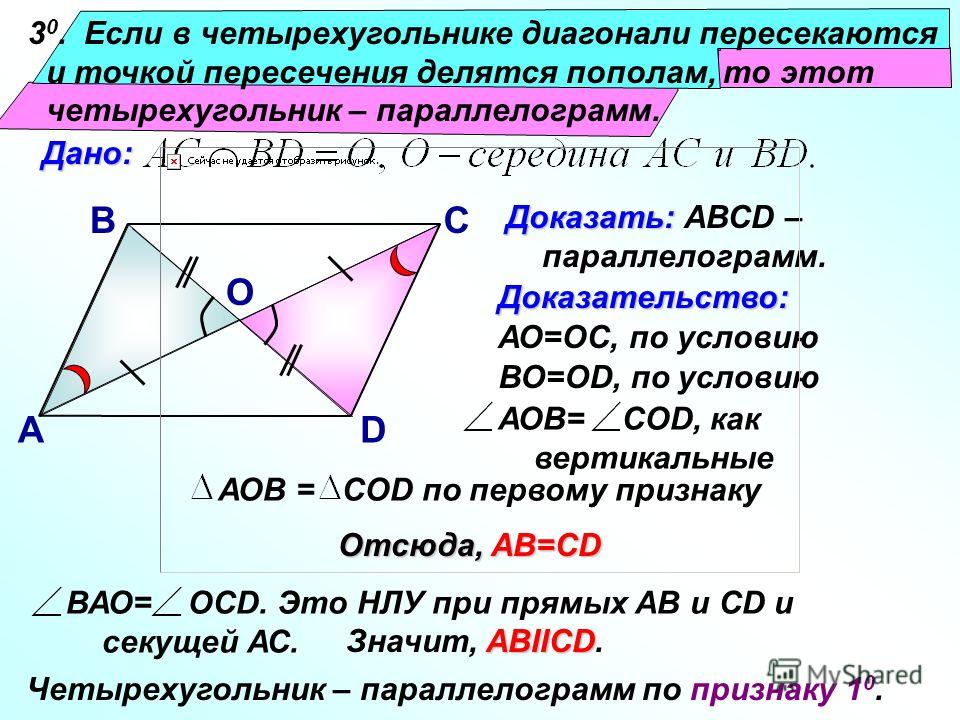 Диагонали, хотя и одинаковой длины, когда параллелограмм представляет собой квадрат или прямоугольник, всегда разделяют друг друга. Диагональ разбивает параллелограмм на два равных треугольников. Последовательные углы являются дополнительными (т. е. они всегда составляют сто восемьдесят градусов). Обратите внимание, что параллелограмм, в котором смежные стороны имеют разную длину и в котором все внутренние углы наклонены, иногда называют ромбом (в отличие от ромба, который является параллелограммом, в котором все четыре стороны имеют одинаковую длину ).

• Параллелограмм, показанный здесь, является ромбом

Ромб-ромб представляет собой равносторонний параллелограмм, т. е. имеет четыре стороны равной длины. Поскольку это параллелограмм, противоположные стороны параллельны, противоположные углы имеют равную величину, последовательные углы являются дополнительными (т. е. они составляют сто восемьдесят градусов), а диагонали разделяют друг друга. Диагонали ромба также рассекают внутренние углы и ортодиагональны (т.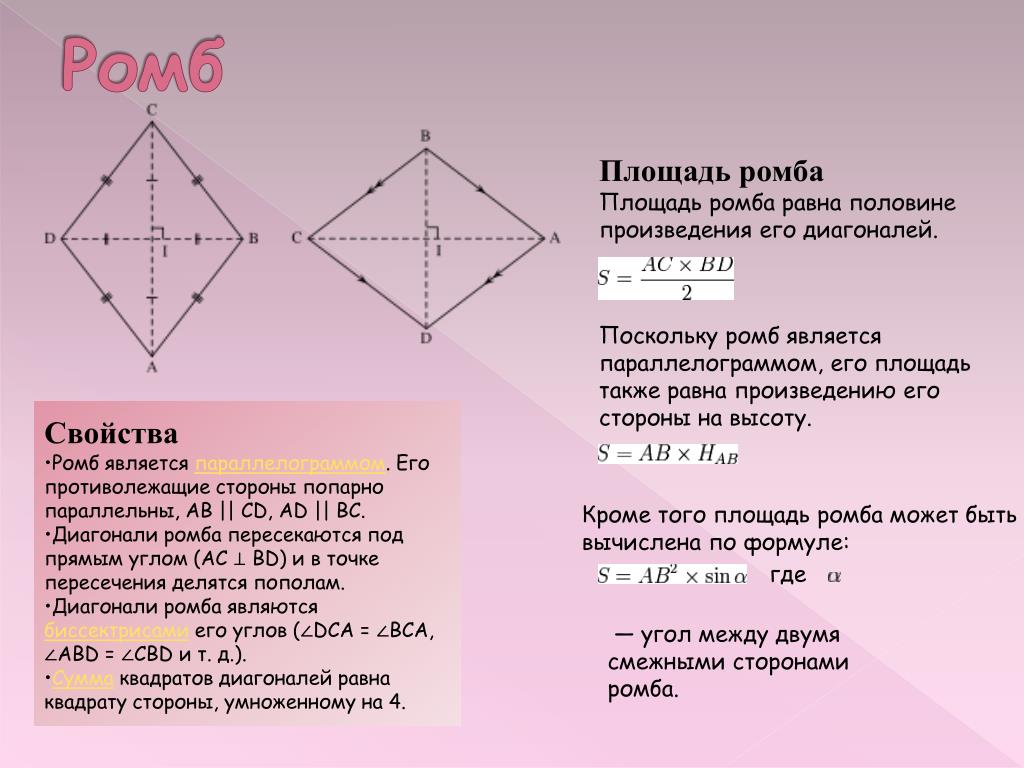

е. пересекаются под прямым углом).

• Ромб-равносторонний параллелограмм

---

Трапеция-это выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. На рисунке ниже показаны три возможных варианта трапеции. На рисунке слева изображена равнобедренная трапеция, в которой углы, прилегающие к каждой из параллельных сторон равны. Центральная фигура имеет одну сторону, перпендикулярную обеим параллельным сторонам, поэтому трапеция содержит два прямых угла. Последняя, самая правая, фигура имеет стороны разной длины, и все внутренние углы разные.

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Денис Александрович Косвинцев

Репетитор по математике

Стаж (лет)

Образование:

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Курс информатики с 7 по 11 класс.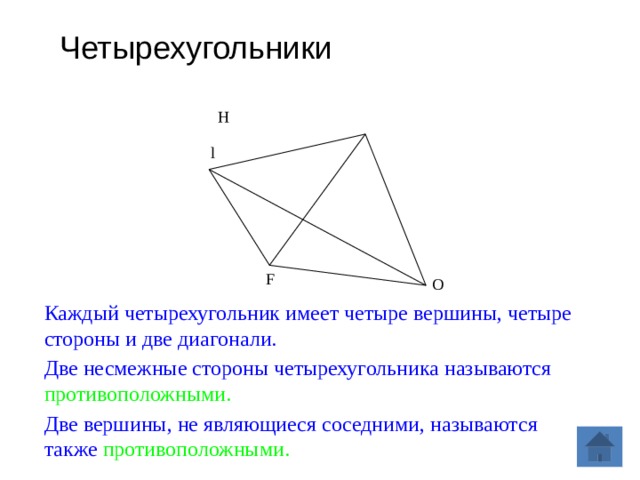 Подготовка к ОГЭ и ЕГЭ (на не Microsoft-ПО). Практические занятия по программированию на Python, Pascal, C или Java и в офисном пакете LibreOffice. Индивидуальные программы обучения по выборочным темам.

Григорий Олегович Курто

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 5-11 классов. Я очень люблю математику, поскольку она блестяще развивает логическое мышление. Каждый раз, решая ту или иную нестандартную задачу, мне приходится осуществлять ее глубокий анализ, и найдя решение, при возможности я стараюсь найти 2-й, 3-й варианты решений и т.д. Такой подход позволяет преподавателю самому конструировать различные модели в голове и придумывать разносортные задачи на любую тему. Что же касается моей собственной методики обучения учащихся, то я стараюсь в работе периодически чередовать методы организации учебно-познавательной деятельности(словесные, наглядные, практические), методы стимулирования учебно-познавательной деятельности(дидактические игры, метод дискуссии), методы контроля за эффективностью учебно-познавательной деятельности(устный, письменный).Особо выделю такой метод как метод дискуссии. На мой взгляд, это очень эффективный метод , потому что в беседе на ту или иную математическую тему у учащегося развивается очень много навыков, что позволяет в дальнейшем совершать прогресс в рабочем процессе. Ученик должен выбрать именно меня, потому что я смогу его научить любить математику, нестандартно мыслить, решать задачи любого уровня, самому находить ошибки в решении (условии) задач и т.

д.

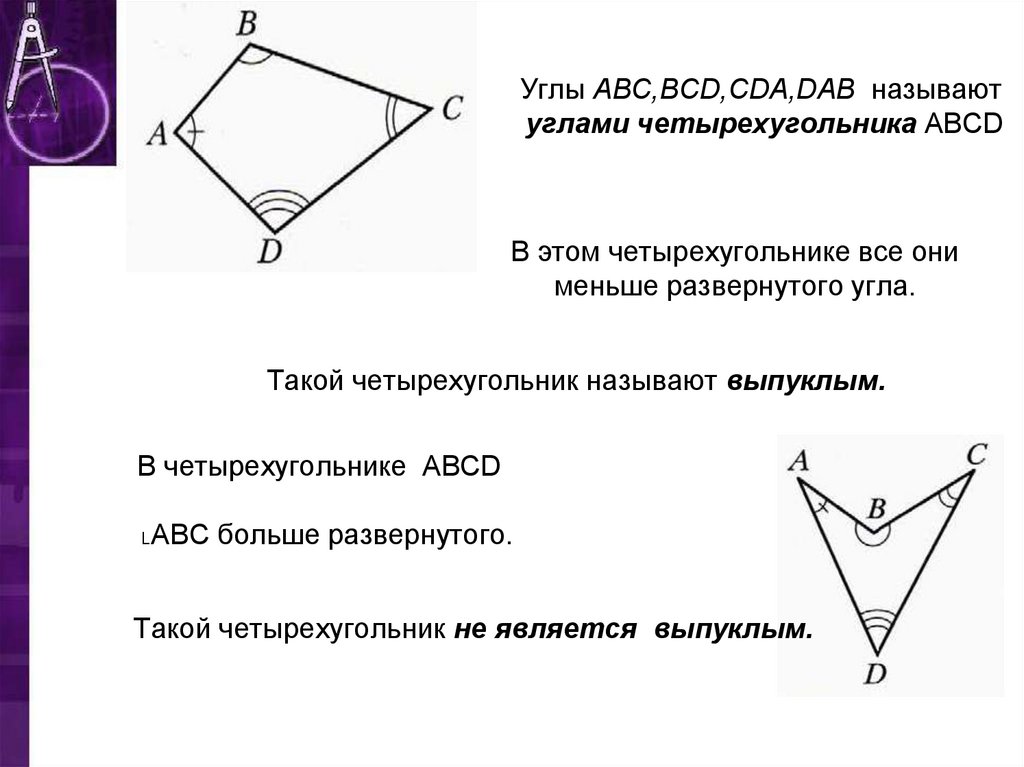
Юлия Геннадьевна Газданова

Репетитор по математике

Стаж (лет)

Образование:

Актюбинский педагогический техникум

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-5 классов. Люблю работать с детьми и умею находить с ними общий язык. Математику люблю за точность и преподаю её так, как хотела бы, чтобы учили моего ребенка. При обучении настраиваю на позитивное восприятие всего нового и непонятного. Весело и интересно объясняю сложный материал.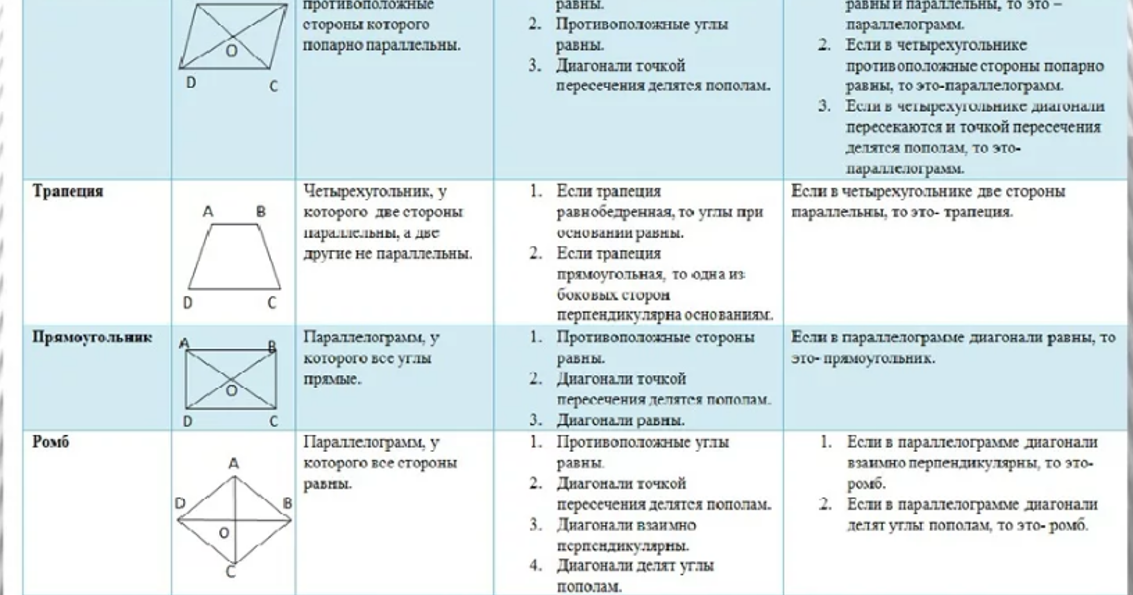

Со мной вашим детям будет легко, занимательно и познавательно. До встречи на уроках!

Похожие статьи

• Что такое рациональные числа
• ЕГЭ по математике, профильный уровень. Иррациональное уравнение
• ЕГЭ по математике, профильный уровень. Неравенства
• ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 1)
• Задачи с прикладным содержанием (вариант 3)
• Тренируемся решать задачи с прикладным содержанием
• Я старший или младший в семье: учимся ладить с братьями и сестрами
• Детское переедание: что делать?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Четырехугольник и его элементы — определение и вычисление с доказательствами и примерами решения

Содержание:

Четырехугольником называют фигуру, состоящую из четырех точек и четырех последовательно соединяющих их отрезков.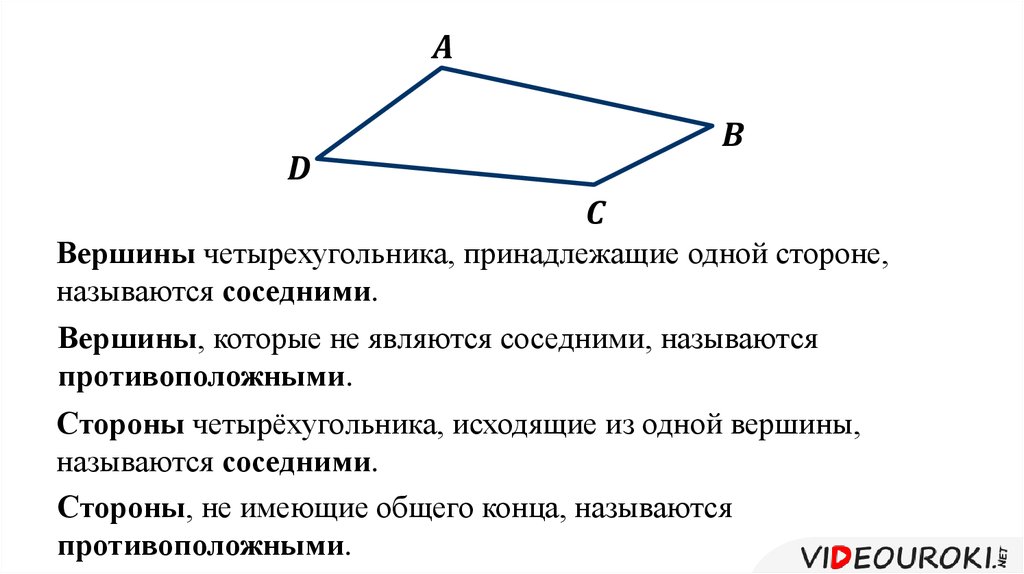

Никакие три из этих точек не должны лежать на одной прямой, а соединяющие их отрезки не должны иметь никаких других общих точек, кроме данных.

Любой четырехугольник ограничивает некоторую часть плоскости, являющуюся внутренней областью четырехугольника.

На рисунке 1 изображен четырехугольник

Вершины четырехугольника, являющиеся концами его стороны, называют соседними, несоседние вершины называют

противолежащими. На рисунке 1 вершины и — соседние, и — противолежащие.

Стороны четырехугольника, имеющие общую вершину, называют соседними, а не имеющие общей вершины — противолежащими. На рис. 1 стороны  и — соседние, и — противолежащие.

Сумму длин всех сторон четырехугольника называют его периметром. Периметр обозначают буквой  Например, периметр четырехугольника  можно обозначить как

Отрезки, соединяющие противолежащие вершины четырехугольника, называют диагоналями четырехугольника.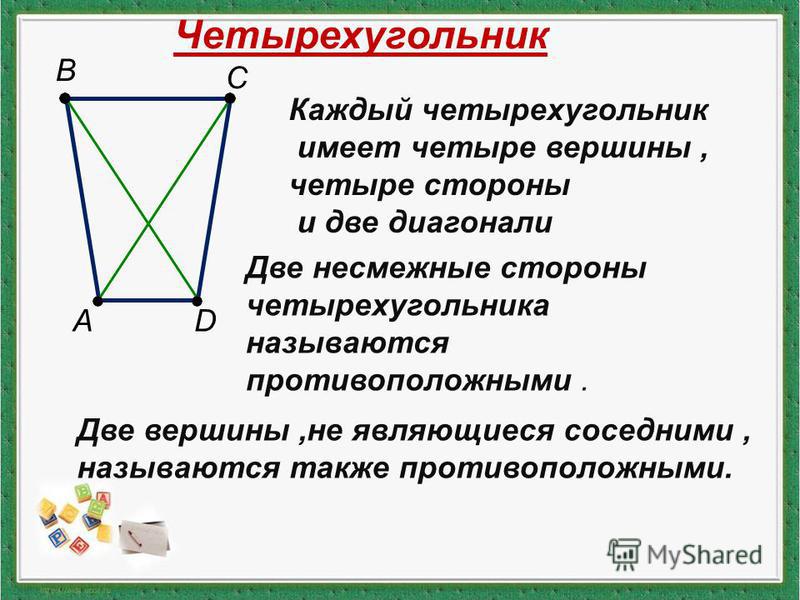

На рисунке 2 отрезки  и — диагонали четырехугольника Каждый четырехугольник имеет две диагонали.

Углами четырехугольника называют углы  и  (рис. 1). Углы четырехугольника называют противолежащими, если их вершины — противолежащие вершины четырехугольника, и соседними, если их вершины — соседние вершины четырехугольника. На рисунке 1 углы и — противолежащие, и — соседние.

Один из углов четырехугольника может быть больше развернутого угла. Например, на рисунке 3 в четырехугольнике угол больше развернутого. Такой четырехугольник называют невыпуклым. Если все углы четырехугольника меньше 180°, его называют выпуклым. Диагонали выпуклого четырехугольника пересекаются (рис. 2), а невыпуклого не пересекаются (рис. 4).

Теорема (о сумме углов четырехугольника). Сумма углов четырехугольника равна 360°.

Доказательство:

Пусть — некоторый четырехугольник. Проведем в нем диагональ  (рис. 5). Тогда Учитывая, что (как сумма углов   (как сумма углов  будем иметь:

Пример:

Найдите углы четырехугольника, если их градусные меры относятся как 3 : 10 : 4 : 1. Выпуклым или невыпуклым является этот четырехугольник?

Решение:

Пусть углы четырехугольника равны и  Имеем уравнение откуда Следовательно, углы четырехугольника равны и Так как один из углов четырехугольника больше 180°, то этот четырехугольник — невыпуклый.

Ответ. 60°, 200°, 80°, 20°; невыпуклый.

На рисунке 1 отрезки АВ и ВС имеют только одну общую точку В, которая является концом каждого из них. Такие отрезки называют соседними. На рисунке 2 каждые два отрезка являются соседними.

Отрезки АВ и CD на рисунке 3 не являются соседними.

Рассмотрим фигуру, состоящую из четырех точек А, В, С, D и четырех отрезков АВ, ВС, CD, DA таких, что никакие два соседних отрезка не лежат на одной прямой и никакие два несоседних отрезка не имеют общих точек (рис. 4, а).

Фигура, образованная этими отрезками, ограничивает часть плоскости, выделенную на рисунке 4, б зеленым цветом. Эту часть плоскости вместе с отрезками АВ, ВС, CD и DA называют четырехугольником. Точки А, В, С, D называют вершинами четырехугольника, а отрезки АВ, ВС, CD, DA — сторонами четырехугольника.

На рисунке 5 изображены фигуры, состоящие из четырех отрезков АВ, ВС, CD, DA и части плоскости, которую они ограничивают. Однако эти фигуры не являются четырехугольниками. Поясните почему.

Стороны четырехугольника, являющиеся соседними отрезками, называют соседними сторонами четырехугольника. Вершины, являющиеся концами одной стороны, называют соседними вершинами многоугольника. Стороны, не являющиеся соседними, называют противолежащими сторонами четырехугольника. Несоседние вершины называют противолежащими вершинами четырехугольника.

На рисунке 6 изображен четырехугольник, в котором, например, стороны MQ и MN являются соседними, а стороны NP и MQ — противолежащими.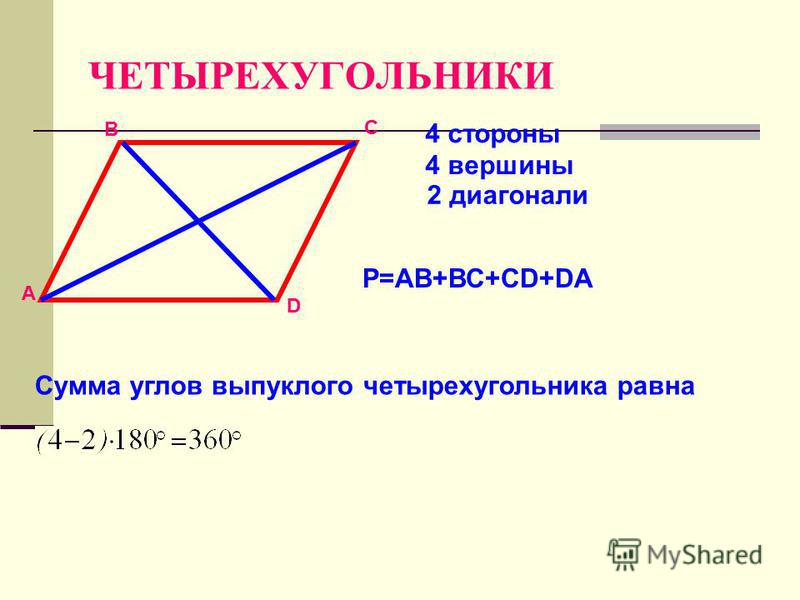 Вершины Q и Р — соседние, а вершины М и Р — противолежащие.   

Четырехугольник называют и обозначают по его вершинам. Например, на рисунке 4, б изображен четырехугольник ABCD, а на рисунке 6 — четырехугольник MNPQ. В обозначении четырехугольника буквы, стоящие рядом, соответствуют соседним вершинам четырехугольника. Например, четырехугольник, изображенный на рисунке 6, можно обозначить еще и так: PQMN, или MQPN, или NPQM и т. д.

Сумму длин всех сторон четырехугольника называют периметром четырехугольника.

Отрезок, соединяющий противолежащие вершины четырехугольника, называют диагональю. На рисунке 7 отрезки АС и BD — диагонали четырехугольника АВСD.

Углы ABC, BCD, CDA, DAB (рис. 8) называют углами четырехугольника ABCD. В этом четырехугольнике каждый из них меньше развернутого угла. Такой четырехугольник называют выпуклым. Однако существуют четырехугольники, в которых не все углы меньше развернутого. Например, на рисунке 9 угол В четырехугольника ABCD больше 180°. Такой четырехугольник называют невыпуклым¹.

Углы АВС и ADC называют противолежащими углами четырехугольника ABCD (рис. 8, 9). Также противолежащими являются углы BAD и BCD.

Теорема 1.1. Сумма углов четырехугольника равна 360°.

Доказательство. Проведем в четырехугольнике диагональ, разбивающую его на два треугольника. Например, на рисунке 10

¹ Более подробно с понятием «выпуклость» вы ознакомитесь в п. 19.

это диагональ BD. Тогда сумма углов четырехугольника ABCD равна сумме углов треугольников ABD и CBD. Поскольку сумма углов треугольника равна 180°, то сумма углов четырехугольника равна 360°. 

Следствие. В четырехугольнике только один из углов может быть больше развернутого.

Докажите это свойство самостоятельно.

Пример:

Докажите, что длина любой стороны четырехугольника меньше суммы  длин трех остальных его сторон.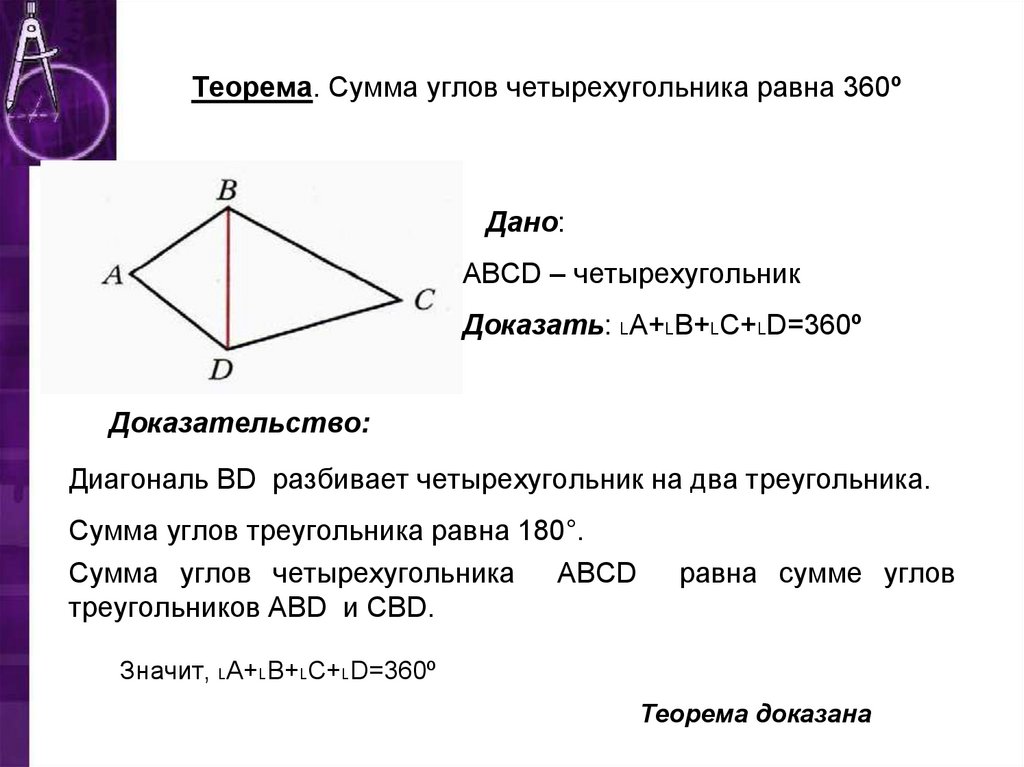

Решение:

Рассмотрим произвольный четырехугольник ABCD (рис. 11). Покажем, например, что АВ

Проведем диагональ АС. Применяя неравенство треугольника для сторон АВ и АС соответственно треугольников АВС и ADC, получаем неравенства: АВ

Отсюда АВ

Следовательно, АВ

Пример:

Постройте четырехугольник по двум соседним сторонам и четырем углам, каждый из которых меньше развернутого.

Решение:

На рисунке 12 изображен четырехугольник ABCD, в котором известны длины сторон АВ и ВС, а также все его углы.
¹ В учебнике задачи на построение не обязательны для рассмотрения.

В треугольнике АВС известны две стороны АВ и ВС и угол В между ними. Следовательно, этот треугольник можно построить. Теперь можем от лучей АВ и СВ отложить углы, равные углам четырехугольника при вершинах А и С.

Проведенный анализ показывает, как строить искомый четырехугольник.

Строим треугольник по двум данным сторонам четырехугольника и углу между ними. На рисунке 12 это треугольник АВС. Далее от лучей АВ и СВ откладываем два известных угла четырехугольника. Два построенных луча пересекаются в точке D. Четырехугольник ABCD — искомый. 

Параллелограмм. Свойства параллелограмма

Определение. Параллелограммом называют четырехугольник, у которого каждые две противолежащие стороны параллельны.

На рисунке 19 изображен параллелограмм ABCD. По определению параллелограмма имеем:

Рассмотрим некоторые свойства параллелограмма.

Теорема 2.1. Противолежащие стороны параллелограмма равны.

Доказательство. На рисунке 19 изображен параллелограмм ABCD. Докажем, что  АВ = CD и ВС = AD.

Проведем диагональ АС. Докажем, что треугольники АВС и CDA равны (рис. 20).

В этих треугольниках сторона АС — общая, углы 1 и 2 равны как накрест лежащие при параллельных прямых ВС и AD и секущей АС, углы 3 и 4 равны как накрест лежащие при параллельных прямых АВ и CD и секущей АС.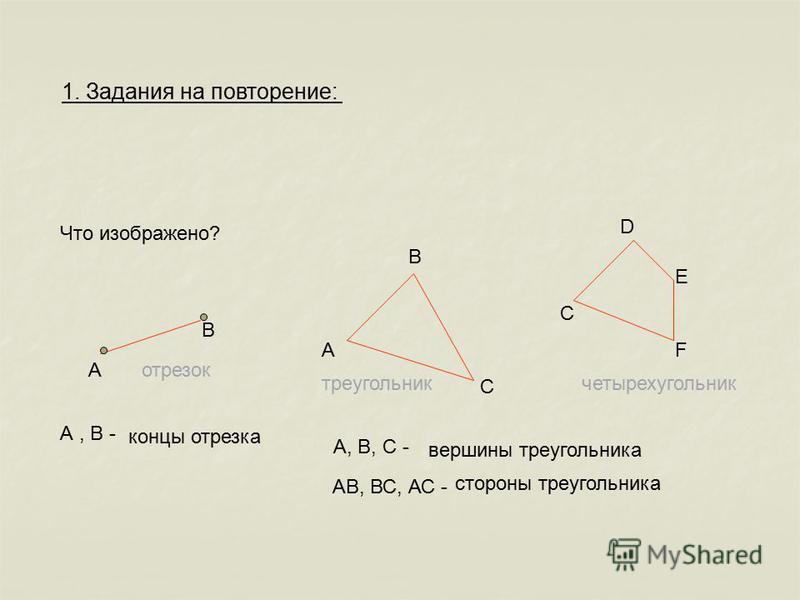 Следовательно, треугольники АВС и CDA равны по второму признаку равенства треугольников. Отсюда АВ = CD и ВС = AD. 

Теорема 2.2. Противолежащие углы параллелограмма равны.

Доказательство. На рисунке 19 изображен параллелограмм ABCD. Докажем, что
При доказательстве предыдущей теоремы было установлено, что (рис. 20). Отсюда Из равенства углов 1 и 2 и равенства углов 3 и 4 следует, что Следовательно,

Теорема 2.3. Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство. На рисунке 21 изображен параллелограмм ABCD, диагонали которого пересекаются в точке О. Докажем, что АО = ОС и ВО = OD.

Рассмотрим треугольники AOD и СОВ.
Имеем: равны как накрест лежащие при параллельных прямых AD и ВС и секущих АС и BD соответственно. Из теоремы 2.1 получаем: AD = ВС.

Следовательно, треугольники AOD и СОВ равны по второму признаку равенства треугольников. Отсюда АО = ОС, ВО = OD. 

Определение.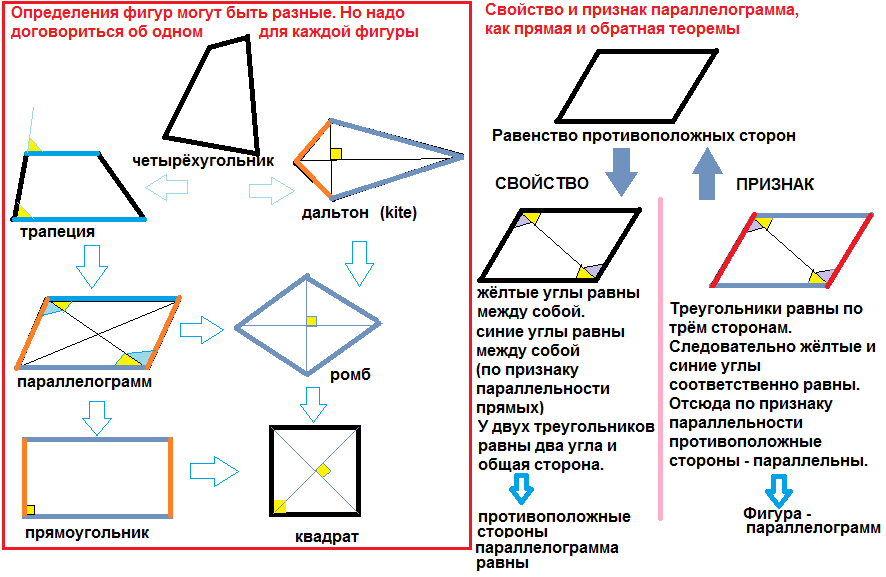 Высотой параллелограмма называют перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону.

На рисунке 22 каждый из отрезков AF, QE, ВМ, PN, СК является высотой параллелограмма ABCD.

Из курса геометрии 7 класса вы знаете, что все точки одной из двух параллельных прямых равноудалены от другой прямой. Поэтому AF = QE и        ВМ = PN = СК.

Говорят, что высоты ВМ, СК, PN проведены к сторонам ВС и AD, а высоты AF, QE — к сторонам АВ и CD.

Пример №1

Докажите, что прямые, содержащие высоты треугольника, переcекаются в одной точке.

Решение:

Через каждую вершину данного треугольника АВС проведем прямую, параллельную противолежащей стороне. Получим треугольник (рис. 23).

Из построения следует, что четырехугольники — параллелограммы. Отсюда Следовательно, точка А является серединой отрезка

Поскольку прямые параллельны, то высота АН треугольника АВС перпендикулярна отрезку Таким образом, прямая АН — серединный перпендикуляр стороны треугольника Аналогично можно доказать, что прямые, содержащие две другие высоты треугольника АВС, являются серединными перпендикулярами сторон треугольника

Так как серединные перпендикуляры сторон треугольника пересекаются в одной точке, то утверждение теоремы доказано.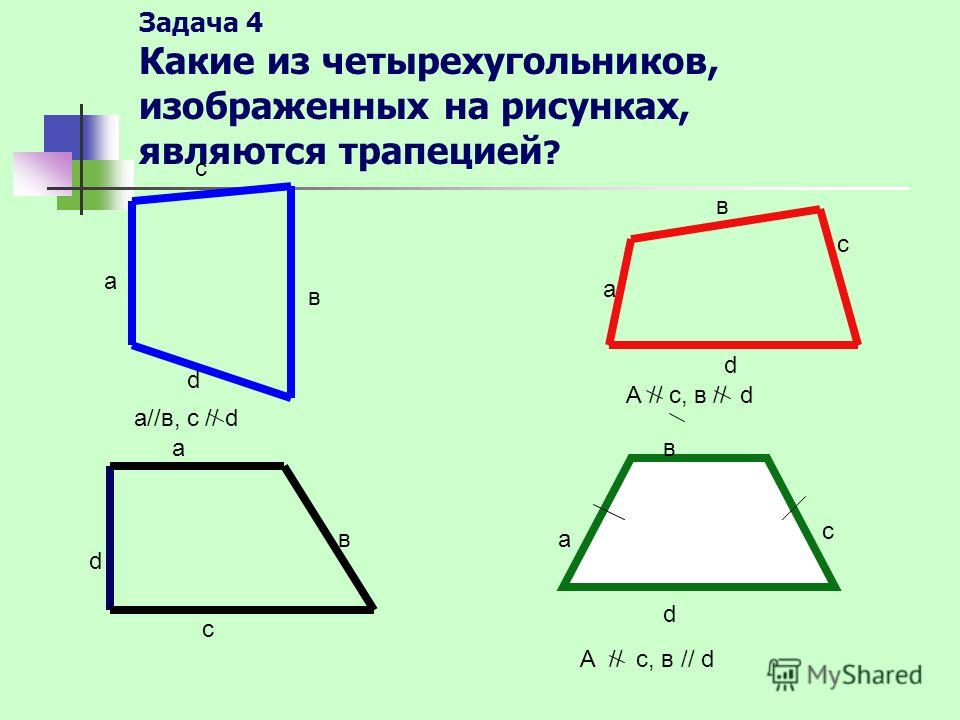

Пример №2

Биссектриса тупого угла параллелограмма делит его сторону в отношении 2 : 1, считая от вершины острого угла. Найдите стороны параллелограмма, если его периметр равен 60 см.

Решение:

Пусть биссектриса тупого угла В параллелограмма ABCD (рис. 24) пересекает сторону AD в точке М. По условию AM : MD = 2 : 1.

Углы ABM и CBM равны по условию.
Углы СВМ и AM В равны как накрест лежащие при параллельных прямых ВС и AD и секущей ВМ.

Тогда Следовательно, треугольник ВАМ равнобедренный, отсюда АВ = AM.

Пусть MD = х см, тогда АВ =АМ = 2х см, AD = Зх см. Поскольку противолежащие стороны параллелограмма равны, то его периметр равен 2 (АВ + AD). Учитывая, что по условию периметр параллелограмма равен 60 см, получаем:

2 (2х + Зх) = 60;
х = 6.

Следовательно, АВ = 12 см, AD = 18 см.

Ответ: 12 см, 18 см. 

Признаки параллелограмма

Определение параллелограмма позволяет среди четырехугольников распознавать параллелограммы. Этой же цели служат следующие три теоремы, которые называют признаками параллелограмма.

Теорема 3.1 (обратная теореме 2.1). Если в четырехугольнике каждые две противолежащие стороны равны, то этот четырехугольник — параллелограмм.

Доказательство. На рисунке 29 изображен четырехугольник ABCD, в котором  АВ = CD и ВС = AD. Докажем, что четырехугольник ABCD — параллелограмм.

Проведем диагональ АС. Треугольники АВС и CDA равны по третьему признаку равенства треугольников. Отсюда и Углы 1 и 3 являются накрест лежащими при прямых ВС и AD и секущей АС. Следовательно, Аналогично из равенства следует, что

Таким образом, в четырехугольнике ABCD каждые две противолежащие стороны параллельны, поэтому этот четырехугольник — параллелограмм. 

Теорема 3.2. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Доказательство. На рисунке 30 изображен четырехугольник ABCD, в котором        ВС = AD и Докажем, что четырехугольник ABCD — параллелограмм.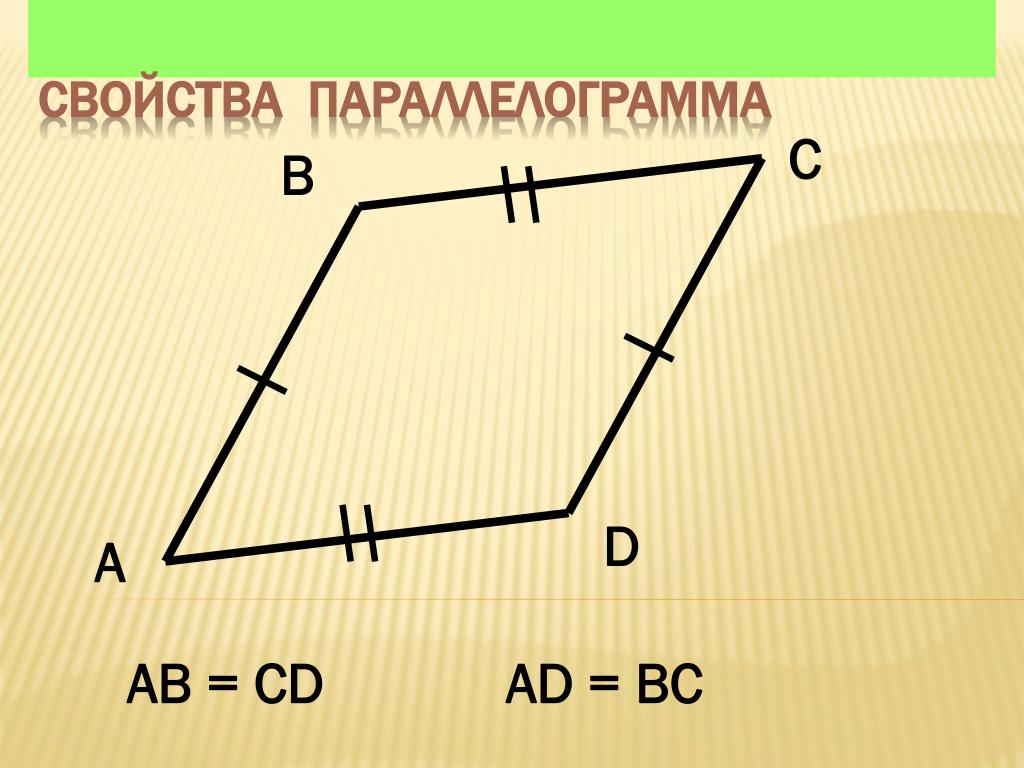

Проведем диагональ АС. В треугольниках АВС и CDA имеем: ВС = AD по условию, углы 1 и 2 равны как накрест лежащие при параллельных прямых ВС и AD и секущей АС, а сторона АС общая. Следовательно, треугольники АВС и CDA равны по первому признаку равенства треугольников. Отсюда АВ = CD. Значит, в четырехугольнике ABCD каждые две противолежащие стороны равны. Поэтому по теореме 3.1 четырехугольник ABCD — параллелограмм. 

Теорема 3.3 (обратная теореме 2.3). Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Доказательство. На рисунке 31 изображен четырехугольник ABCD, в котором диагонали АС и BD пересекаются в точке О, причем АО = ОС и ВО = OD. Докажем, что четырехугольник ABCD — параллелограмм.    

Поскольку углы ВОС и DOA равны как вертикальные, АО = ОС и ВО = OD, то треугольники ВОС и DOA равны по первому признаку равенства треугольников. Отсюда ВС = AD и  Углы 1 и 2 являются накрест лежащими при прямых ВС и AD и секущей АС. Следовательно,

Таким образом, в четырехугольнике ABCD две противолежащие стороны равны и параллельны. По теореме 3.2 четырехугольник ABCD — параллелограмм. 

Вы знаете, что треугольник можно однозначно задать его сторонами, то есть задача построения треугольника по трем сторонам имеет единственное решение. Иначе обстоит дело с параллелограммом. На рисунке 32 изображены параллелограммы стороны которых равны, то есть  Однако очевидно, что сами параллелограммы не равны.

Сказанное означает, что если четыре рейки скрепить так, чтобы образовался параллелограмм, то полученная конструкция не будет жесткой.

Это свойство параллелограмма широко используют на практике. Благодаря его подвижности лампу можно устанавливать в удобное для работы положение, а раздвижную решетку — отодвигать на нужное расстояние в дверном проеме (рис. 33).

На рисунке 34 изображена схема механизма, являющегося частью паровой машины. При увеличении скорости вращения оси шары отдаляются от нее под действием центробежной силы, тем самым поднимая заслонку, регулирующую количество пара. Механизм назван параллелограммом Уатта в честь изобретателя первой универсальной паровой машины.    

Пример №3

Докажите, что если в четырехугольнике каждые два противолежащих угла равны, то этот четырехугольник — параллелограмм.    

Решение:

На рисунке 35 изображен четырехугольник ABCD, в котором Докажем, что четырехугольник ABCD — параллелограмм.

По теореме о сумме углов четырехугольника (теорема 1.1) Учитывая, что получим:

Поскольку углы А и В — односторонние углы при прямых AD и ВС и секущей АВ, а их сумма равна 180°, то
Аналогично доказываем, что

Следовательно, четырехугольник ABCD — параллелограмм.

Необходимо и достаточно

Из курса геометрии 7 класса вы узнали, что большинство теорем состоят из двух частей: условия (то, что дано) и заключения (то, что требуется доказать).

Если утверждение, выражающее условие, обозначить буквой А, а утверждение, выражающее заключение, — буквой В, то формулировку теоремы можно изобразить следующей схемой: если А, то В.
Например, теорему 2.3 можно сформулировать так:

Тогда теорему 3.3, обратную теореме 2.3, можно сформулировать так:

Часто в повседневной жизни в своих высказываниях мы пользуемся словами «необходимо», «достаточно». Приведем несколько примеров.

• Для того чтобы уметь решать задачи, необходимо знать теоремы.
• Если вы на математической олимпиаде правильно решили все предложенные задачи, то этого достаточно для того, чтобы занять первое место.

Употребление слов «необходимо» и «достаточно» тесно связано с теоремами.

Рассмотрим теорему:

Условие А является достаточным для заключения В. Вместе с тем делимость числа нацело на 5 (утверждение В) необходима для делимости числа нацело на 10 (утверждение А).

Приведем еще один пример:

В этой теореме утверждение А является достаточным условием для утверждения В, то есть для того, чтобы два угла были равны, достаточно, чтобы они были вертикальными. В этой же теореме утверждение В является необходимым условием для утверждения А, то есть для того, чтобы два угла были вертикальными, необходимо, чтобы они были равны. Отметим, что утверждение В не является достаточным условием для утверждения А. Действительно, если два угла равны, то это совсем не означает, что они вертикальные.

Итак, в любой теореме вида если А, то В утверждение А является достаточным для утверждения В, а утверждение В — необходимым для утверждения А.

Если справедлива не только теорема если А, то В, но и обратная теорема если В, то А, то А является необходимым и достаточным условием для В, а В — необходимым и достаточным условием для А.

Например, теоремы 3.3 и 2.3 являются взаимно обратными. На языке «необходимо — достаточно» этот факт можно сформулировать так: для того чтобы четырехугольник был параллелограммом, необходимо и достаточно, чтобы его диагонали точкой пересечения делились пополам.

Подчеркнем, что если в теореме есть слова «необходимо и достаточно», то она объединяет две теоремы: прямую и обратную (прямой теоремой может быть любая из двух теорем, тогда другая будет обратной). Следовательно, доказательство такой теоремы должно состоять из двух частей: доказательств прямой и обратной теорем. Теорему, объединяющую прямую и обратную теоремы, называют критерием.

Иногда вместо «необходимо и достаточно» говорят «тогда и только тогда». Например, взаимно обратные теоремы 2.1 и 3.1 можно объединить в следующий критерий:

• четырехугольник является параллелограммом тогда и только тогда, когда каждые две его противолежащие стороны равны.

Сформулируйте самостоятельно теорему 2.2 и ключевую задачу п. 3 в виде теоремы-критерия.

Прямоугольник

Параллелограмм — это четырехугольник, однако очевидно, что не каждый четырехугольник является параллелограммом. В этом случае говорят, что параллелограмм — это отдельный вид четырехугольника. Рисунок 42 иллюстрирует этот факт.

Существуют также отдельные виды параллелограммов.
 

Определение. Прямоугольником называют параллелограмм, у которого все углы прямые.

На рисунке 43 изображен прямоугольник ABCD.
Из определения следует, что прямоугольник имеет все свойства параллелограмма. В прямоугольнике:

• противолежащие стороны равны;
• диагонали точкой пересечения делятся пополам.

Однако прямоугольник имеет свои особые свойства, которыми не обладает параллелограмм, отличный от прямоугольника. Так, из определения следует, что все углы прямоугольника равны. Еще одно свойство прямоугольника выражает следующая теорема.

Теорема 4.1. Диагонали прямоугольника равны.

Доказательство. На рисунке 44 изображен прямоугольник ABCD. Докажем, что его диагонали АС и BD равны.
В прямоугольных треугольниках ABD и DCA катеты АВ и DC равны, а катет AD общий. Поэтому треугольники ABD и DCA равны по двум катетам. Отсюда              BD = АС. 

Определение прямоугольника позволяет среди параллелограммов распознавать прямоугольники. Этой же цели служат следующие две теоремы, которые называют признаками прямоугольника.

Теорема 4.2. Если один из углов параллелограмма прямой, то этот параллелограмм — прямоугольник.

Докажите эту теорему самостоятельно.

Теорема 4.3. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.

Доказательство. На рисунке 45 изображен параллелограмм ABCD, диагонали АС и BD которого равны. Докажем, что параллелограмм ABCD — прямоугольник.

Рассмотрим треугольники ABD и DCА. У них АВ = CD, BD =АС, AD — общая сторона. Следовательно, эти треугольники равны по третьему признаку равенства треугольников. Отсюда Эти углы являются односторонними при параллельных прямых АВ и DC и секущей AD. Таким образом, Тогда Поэтому по теореме 4.2 параллелограмм ABCD — прямоугольник. 

Ромб

Вы уже знаете, что прямоугольник — это отдельный вид параллелограмма. Познакомимся еще с одним видом параллелограмма — ромбом.

Определение. Ромбом называют параллелограмм, у которого все стороны равны.

На рисунке 47 изображен ромб ABCD.
Из определения следует, что ромб имеет все свойства параллелограмма. В ромбе:

• противолежащие углы равны;
• диагонали точкой пересечения делятся пополам.

Однако ромб имеет и свои особые свойства.

Теорема 5.1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. На рисунке 48 изображен ромб ABCD, диагонали которого пересекаются в точке О. Докажем, что и

Поскольку по определению ромба все его стороны равны, то треугольник АВС равнобедренный (АВ = ВС). По свойству диагоналей параллелограмма АО = ОС. Тогда отрезок ВО является медианой треугольника АВС, а значит, и высотой и биссектрисой этого треугольника. Следовательно,

Распознавать ромбы среди параллелограммов позволяют не только определение ромба, но и следующие две теоремы, которые называют признаками ромба.

Теорема 5.2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.

Теорема 5.3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм — ромб.

Докажите эти теоремы самостоятельно.

Квадрат

Определение. Квадратом называют прямоугольник, у которого все стороны равны.

На рисунке 50 изображен квадрат ABCD.

Из приведенного определения следует, что квадрат — это ромб, у которого все углы равны. Значит, квадрат является отдельным видом и прямоугольника, и ромба. Это иллюстрирует рисунок 51. Поэтому квадрат обладает всеми свойствами прямоугольника и ромба. Отсюда следует, что:

• все углы квадрата прямые;
• диагонали квадрата равны, перпендикулярны и являются биссектрисами его углов.

Средняя линия треугольника

Определение. Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.

На рисунке 56 отрезки MN, NE, ЕМ — средние линии треугольника АВС.

Теорема 7.1. Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.

Доказательство. Пусть MN — средняя линия треугольника АВС (рис. 57). Докажем, что

На прямой MN отметим точку Е так, что MN = NE (рис. 57). Соединим отрезком точки Е и С. Поскольку точка N является серединой отрезка ВС, то BN = NC. Углы 1 и 2 равны как вертикальные. Следовательно, треугольники MBN и ECN равны по первому признаку равенства треугольников. Отсюда Учитывая, что AM = ВМ, получим: ЕС = AM. Углы 3 и 4 являются накрест лежащими при прямых АВ и ЕС и секущей ВС. Тогда

Таким образом, в четырехугольнике АМЕС стороны AM и ЕС параллельны и равны. Следовательно, по теореме 3.2 четырехугольник АМЕС является параллелограммом. Отсюда  то есть

Также ME = АС. Поскольку 

Пример №4

Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.

Решение:

В четырехугольнике ABCD точки М, N, К и Р — середины сторон АВ, ВС, CD и AD соответственно (рис. 58).
Отрезок MN — средняя линия треугольника АВС. По свойству средней линии треугольника
Отрезок РК — средняя линия треугольника ADC. По свойству средней линии треугольника  

Поскольку то
Из равенств и получаем:
Следовательно, в четырехугольнике MNKP стороны MN и РК равны и параллельны, поэтому четырехугольник MNKP — параллелограмм. 

Трапеция

Определение. Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Каждый из четырехугольников, изображенных на рисунке 62, является трапецией.

Параллельные стороны трапеции называют основаниями, а непараллельные — боковыми сторонами (рис. 63).

В трапеции ABCD углы Аи D называют углами при основании AD, а углы В и С — углами при основании ВС.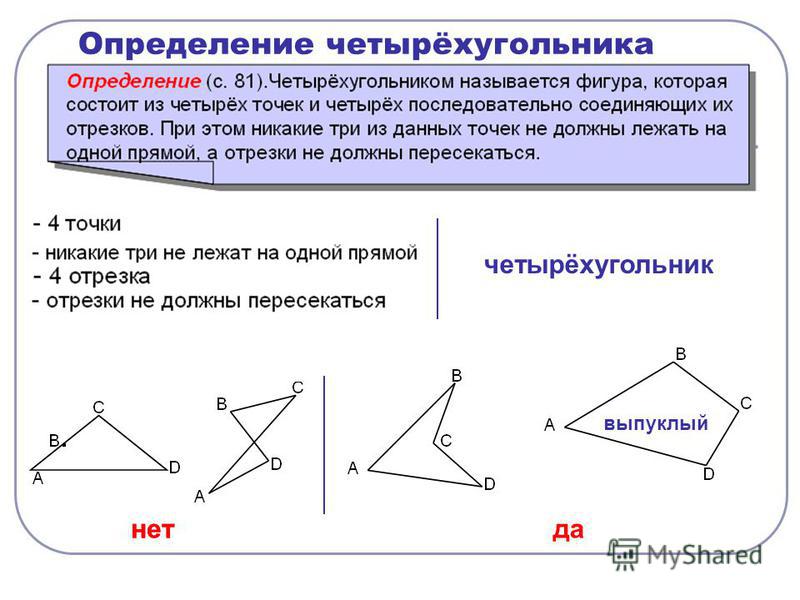

Определение. Высотой трапеции называют перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований, на прямую, содержащую другое основание.

На рисунке 64 каждый из отрезков ВМ, EF, DK, PQ является высотой трапеции ABCD. Длины этих отрезков равны расстоянию между параллельными прямыми ВС и AD. Поэтому ВМ = EF = DK = PQ.

На рисунке 65 изображена трапеция ABCD, у которой боковые стороны АВ и CD равны. Такую трапецию называют равнобокой или равнобедренной.

Если боковая сторона трапеции является ее высотой, то такую трапецию называют прямоугольной (рис. 66).

Трапеция — это отдельный вид четырехугольника. Связь между четырехугольниками и их отдельными видами показана на рисунке 67.

Определение. Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.

На рисунке 68 отрезок MN — средняя линия трапеции ABCD.

Теорема 8.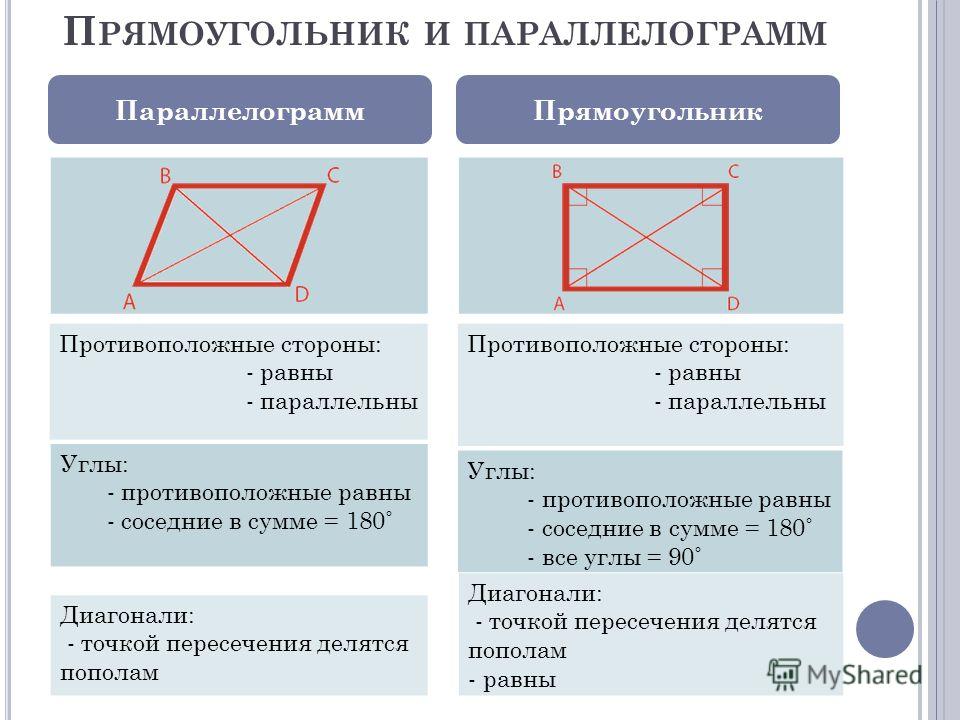 1. Средняя линия трапеции параллельна основаниям и равна половине их суммы.

Доказательство. Пусть MN — средняя линия трапеции ABCD (рис. 69). Докажем, что

Проведем прямую BN и точку ее пересечения с прямой AD обозначим буквой Е.

Поскольку точка N — середина отрезка CD, то CN = ND. Углы 1 и 2 равны как вертикальные, а углы 3 и 4 равны как накрест лежащие при параллельных прямых ВС и АЕ и секущей CD. Следовательно, треугольники BCN и EDN равны по второму признаку равенства треугольников. Отсюда ВС = DE и BN = NE. Тогда отрезок MN — средняя линия треугольника АВЕ. Из этого следует, что  то есть и Имеем: 

Пример №5 (свойства равнобокой трапеции)

Докажите, что в равнобокой трапеции:

1. углы при каждом основании равны;
2. диагонали равны;
3. высота трапеции, проведенная из вершины тупого угла, делит основание трапеции на два отрезка, меньший из которых равен половине разности оснований, а больший — половине суммы оснований (средней линии трапеции).

Решение:

Рассмотрим равнобокую трапецию ABCD (АВ = CD).
1) Проведем высоты ВМ и СК (рис. 70). Поскольку АВ = CD и ВМ = СК, то прямоугольные треугольники АМВ и DKC равны по катету и гипотенузе. Тогда

Имеем: Следовательно,

2) Рассмотрим треугольники ACD и DBA (рис. 71).

Имеем: АВ = CD, AD — общая сторона, углы BAD и CDA равны как углы при основании равнобокой трапеции. Следовательно, треугольники ACD и DBA равны по двум сторонам и углу между ними. Тогда АС = BD.
3) В четырехугольнике ВМКС (рис. 70)  угол ВМК прямой. Следовательно, этот четырехугольник является прямоугольником. Отсюда        МК = ВС.
Из равенства треугольников АМВ и DKC следует, что Тогда 

Центральные и вписанные углы

Определение. Центральным углом окружности называют угол с вершиной в центре окружности.

На рисунке 76 угол АОВ — центральный. Стороны этого угла пересекают окружность в точках А и В. Эти точки делят окружность на две дуги, выделенные на рисунке 76 разным цветом.

Точки А и В называют концами дуги, они принадлежат каждой из выделенных дуг. Каждую из этих дуг можно обозначить так: (читают: «дуга АВ»).

Однако по записи невозможно отличить дуги на рисунке 76. Если на какой-нибудь из двух дуг отметить точку (на рисунке 77 это точка М), то понятно, что обозначение относится к «синей» дуге. Если на одной из двух дуг АВ отмечена точка, то договоримся, что обозначение относится к дуге, которой эта точка не принадлежит (на рисунке 77 это «зеленая» дуга).

Дуга АВ принадлежит центральному углу АОВ (рис. 77). В этом случае говорят, что центральный угол АОВ опирается на дугу АВ.

Каждая дуга окружности, как и вся окружность, имеет градусную меру. Градусную меру всей окружности считают равной 360°. Если центральный угол MON опирается на дугу MN (рис. 78), то градусную меру дуги MN считают равной градусной мере угла MON и записывают: (читают: «градусная мера дуги MN равна градусной мере угла MON). Градусную меру дуги MEN (рис. 78) считают равной 360° —

На рисунке 79 изображена окружность, в которой проведены два перпендикулярных диаметра АВ и CD.

Тогда   Каждую из дуг АСВ и ADB называют полуокружностью. На рисунке 79 полуокружностями являются также дуги CAD и CBD.

О хорде, соединяющей концы дуги, говорят, что хорда стягивает дугу. На рисунке 80 хорда АВ стягивает каждую из дуг АВ и АКВ.

Любая хорда стягивает две дуги, сумма градусных мер которых равна 360°.

Определение. Вписанным углом окружности называют угол, вершина которого принадлежит окружности, а стороны пересекают окружность.

На рисунке 81 угол АВС — вписанный. Дуга АС принадлежит этому углу, а дуга АВС — не принадлежит. В таком случае говорят, что вписанный угол АВС опирается на дугу АС. Также можно сказать, что вписанный угол АВС опирается на хорду АС.

Теорема 9.1. Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Доказательство. О На рисунке 81 угол АВС вписанный.

Докажем, что
Рассмотрим три случая расположения центра О окружности относительно вписанного угла АВС.

Случай 1. Центр О принадлежит одной из сторон угла, например стороне ВС    (рис. 82).
Проведем радиус ОА. Центральный угол АОС — внешний угол равнобедренного треугольника АВО (стороны ОА и ОВ равны как радиусы). Тогда  Однако Отсюда

Случай 2. Центр О принадлежит углу, однако не принадлежит ни одной из его сторон (рис. 83).
Проведем диаметр ВК. Согласно доказанному  
Имеем:

 

Случай 3. Центр О не принадлежит углу (рис. 84).
Для третьего случая проведите доказательство самостоятельно. 

Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 85).
 

Следствие 2. Вписанный угол, опирающийся на диаметр (полуокружность), — прямой (рис. 86).

Докажите эти свойства самостоятельно.

Пример №6 (свойство угла между касательной и хордой).

Отрезок АВ — хорда окружности с центром О (рис. 87). Через точку А проведена касательная MN. Докажите, что

Решение:

Проведем диаметр AD (рис. 87). Тогда угол В равен 90° как вписанный, опирающийся на диаметр AD. В прямоугольном треугольнике ABD Поскольку MN — касательная, то Тогда Получаем, что
Следовательно,
Имеем:

Пример №7

Постройте касательную к данной окружности, проходящую через данную точку, лежащую вне окружности.

Решение:

На рисунке 88 изображены окружность с центром О и точка М, лежащая вне этой окружности.

Пусть X — такая точка окружности, что прямая MX является касательной (рис. 88). Тогда угол МХО прямой. Следовательно, его можно рассматривать как вписанный в окружность с диаметром МО.

Проведенный анализ показывает, как провести построение.

Построим отрезок МО и разделим его пополам (рис. 89). Пусть точка К — его середина. Построим окружность радиуса КО с центром К. Обозначим точки пересечения построенной и данной окружностей буквами Е и F. Тогда каждая из прямых ME и MF является искомой касательной.

Действительно, угол МЕО равен 90° как вписанный угол, опирающийся на диаметр МО. Отрезок ОЕ — радиус данной окружности. Тогда по признаку касательной прямая ME — искомая касательная. 

Описанная и вписанная окружности четырехугольника

Определение. Окружность называют описанной около четырехугольника, если она проходит через все его вершины.

На рисунке 103 изображена окружность, описанная около четырехугольника ABCD. В этом случае также говорят, что четырехугольник вписан в окружность.

Теорема 10.1. Если четырехугольник является вписанным в окружность, то сумма его противолежащих углов равна 180°.

Доказательство. Пусть четырехугольник ABCD вписан в окружность (рис. 103). Докажем, что
Поскольку углы А и С являются вписанными, то
Имеем:
Аналогично можно показать, что

Вы знаете, что около любого треугольника можно описать окружность. Однако не всякий четырехугольник обладает таким свойством. Например, нельзя описать окружность около параллелограмма, отличного от прямоугольника. Распознавать четырехугольники, около которых можно описать окружность, позволяет следующая теорема.

Теорема 10.2 (обратная теореме 10.1). Если в четырехугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность.

Доказательство. Рассмотрим четырехугольник ABCD, в котором Докажем, что около него можно описать окружность.

Предположим, что около этого четырехугольника нельзя описать окружность. Опишем окружность около треугольника ABD. По предположению точка С не принадлежит этой окружности. Поэтому возможны два случая.

Случай 1. Точка С лежит вне описанной окружности треугольника ABD (рис. 104).

Пусть сторона ВС пересекает окружность в точке Четырехугольник вписан в окружность. Тогда по теореме 10.1 получаем, что Но по условию Отсюда Однако это равенство выполняться не может, так как по свойству внешнего угла треугольника

Итак, точка С не может лежать вне окружности, описанной около треугольника ABD.

Случай 2. Точка С лежит внутри описанной окружности треугольника ABD (рис. 105). Рассуждая аналогично, можно показать, что точка С не может лежать внутри рассматриваемой окружности. Убедитесь в этом самостоятельно.

Таким образом, предположив, что точка С не принадлежит окружности, описанной около треугольника ABD, мы получили противоречие. 

Теорему 10.2 можно рассматривать как признак принадлежности четырех точек одной окружности.

Если четырехугольник вписан в окружность, то существует точка, равноудаленная от всех его вершин (центр описанной окружности). Чтобы найти эту точку, достаточно найти точку пересечения серединных перпендикуляров двух соседних сторон четырехугольника.

Определение. Окружность называют вписанной в четырехугольник, если она касается всех его сторон.

На рисунке 106 изображена окружность, вписанная в четырехугольник ABCD. В этом случае также говорят, что четырехугольник описан около окружности.

Теорема 10.3. Если четырехугольник является описанным около окружности, то суммы его противолежащих сторон равны.

Доказательство. Пусть четырехугольник ABCD описан около окружности (рис. 107). Докажем, что АВ + CD = ВС + AD.

Точки М, N, Р, К — точки касания окружности со сторонами четырехугольника.

Поскольку отрезки касательных, проведенных к окружности через одну точку, равны, то АК =АМ, ВМ = BN, CN = СР, DP = DK. Пусть АК = а, ВМ = b, CN = с, DP = d.

Тогда АВ + CD = a + b + c + d,
ВС + AD = b + c + a + d.

Следовательно, АВ + CD = ВС + AD. 

Вы знаете, что в любой треугольник можно вписать окружность. Однако не всякий четырехугольник обладает таким свойством. Например, нельзя вписать окружность в прямоугольник, отличный от квадрата. Распознавать четырехугольники, в которые можно вписать окружность, позволяет следующая теорема.

Теорема 10.4. Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность.

Доказательство. Рассмотрим выпуклый четырехугольник ABCD, в котором АВ + CD = ВС + AD. Докажем, что в него можно вписать окружность.

Пусть биссектрисы углов А и В пересекаются в точке О (рис. 108). Тогда точка О равноудалена от сторон АВ, ВС и AD. Следовательно, существует окружность с центром в точке О, которая касается этих трех сторон.  

Предположим, что эта окружность не касается стороны CD. Тогда возможны два случая. 

Случай 1. Сторона CD не имеет общих точек с построенной окружностью.
Проведем касательную параллельно стороне CD (рис. 108). Четырехугольник описан около окружности. Тогда по теореме 10.3 получаем,  что

Однако по условию

Вычтем из равенства (2) равенство (1):

Отсюда имеем:

Это равенство противоречит утверждению, доказанному в ключевой задаче п. 1.

Итак, сторона CD должна иметь общие точки с рассматриваемой окружностью.

Случай 2. Сторона CD имеет две общие точки с построенной окружностью.

Рассуждая аналогично, можно показать, что сторона CD не может иметь две общие точки с построенной окружностью. Убедитесь в этом самостоятельно.

Таким образом, предположив, что построенная окружность не касается стороны CD, мы получили противоречие. 

Если четырехугольник описан около окружности, то существует точка, равноудаленная от всех его сторон (центр вписанной окружности). Чтобы найти эту точку, достаточно найти точку пересечения биссектрис двух соседних углов этого четырехугольника.

Пример №8 (признак принадлежности четырех точек одной окружности).

Точки А, М, N, В таковы, что причем точки M и N лежат в одной полуплоскости относительно прямой АВ. Докажите, что точки А, М, N, В лежат на одной окружности.

Решение:

Пусть Около треугольника АМВ опишем окружность (рис. 109). Пусть С — произвольная точка окружности, не принадлежащая дуге АМВ. Тогда четырехугольник АСВМ вписан в окружность. Отсюда Имеем: Следовательно, по теореме 10.2 около четырехугольника ACBN можно описать окружность. Поскольку около треугольника АВС можно описать только одну окружность, то этой окружности принадлежат как точка М, так и точка N.

Главное:

Сумма углов четырехугольника

• Сумма углов четырехугольника равна 360°.

Параллелограмм

• Параллелограммом называют четырехугольник, у которого каждые две противолежащие стороны параллельны.

Свойства параллелограмма

• Противолежащие стороны параллелограмма равны.
• Противолежащие углы параллелограмма равны.
• Диагонали параллелограмма точкой пересечения делятся пополам.

Высота параллелограмма

• Высотой параллелограмма называют перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону.

Признаки параллелограмма

• Если в четырехугольнике каждые две противолежащие стороны равны, то этот четырехугольник — параллелограмм.
• Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
• Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Прямоугольник

• Прямоугольником называют параллелограмм, у которого все углы прямые.

Особое свойство прямоугольника

• Диагонали прямоугольника равны.

Признаки прямоугольника

• Если один из углов параллелограмма прямой, то этот параллелограмм — прямоугольник.
• Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.

Ромб

• Ромбом называют параллелограмм, у которого все стороны равны.

Особое свойство ромба

• Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Признаки ромба

• Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
• Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм — ромб.

Квадрат

• Квадратом называют прямоугольник, у которого все стороны равны.

Средняя линия треугольника

• Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

• Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.

Трапеция

• Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Высота трапеции

• Высотой трапеции называют перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований, на прямую, содержащую другое основание.

Средняя линия трапеции

• Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.

Свойство средней линии трапеции

• Средняя линия трапеции параллельна основаниям и равна половине их суммы.

Центральный угол окружности

• Центральным углом окружности называют угол с вершиной в центре окружности.

Вписанный угол окружности

• Вписанным углом окружности называют угол, вершина которого принадлежит окружности, а стороны пересекают окружность.

Градусная мера вписанного угла окружности

• Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.

Свойства вписанных углов

• Вписанные углы, опирающиеся на одну и ту же дугу, равны.
• Вписанный угол, опирающийся на диаметр (полуокружность), — прямой.

Окружность, описанная около четырехугольника

• Окружность называют описанной около четырехугольника, если она проходит через все его вершины.

Свойство четырехугольника, вписанного в окружность

• Если четырехугольник является вписанным в окружность, то сумма его противолежащих углов равна 180°.

Признак четырехугольника, около которого можно описать окружность

• Если в четырехугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность.

Окружность, вписанная в четырехугольник

• Окружность называют вписанной в четырехугольник, если она касается всех его сторон.

Свойство окружности, описанной около четырехугольника

• Если четырехугольник является описанным около окружности, то суммы его противолежащих сторон равны.

Признак четырехугольника, в который можно вписать окружность

• Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность.

Вписанные и описанные четырехугольники

Четырехугольник называют вписанным в окружность, если все его вершины лежат на окружности. Окружность при этом называют описанной около четырехугольника (рис. 92).

Теорема 1 (свойство углов вписанного четырехугольника). Сумма противолежащих углов вписанного четырехугольника равна 180°.

Доказательство:

Пусть в окружность с центром  вписан четырехугольник (рис. 92). Тогда   (по теореме о вписанном угле).

Поэтому  Тогда

Следствие 1. Если около трапеции можно описать окружность, то трапеция равнобокая.

Доказательство:

Пусть трапеция вписана в окружность, (рис. 93). Тогда  Но в трапеции  Поэтому Следовательно, — равнобокая трапеция (по признаку равнобокой трапеции). 

Как известно из курса геометрии 7 класса, около любого треугольника можно описать окружность. Для четырехугольников это не так.

Теорема 2 (признак вписанного четырехугольника). Если в четырехугольнике сумма двух противолежащих углов равна 180°, то около него можно описать окружность.

Доказательство:

Пусть в четырехугольнике Проведем через точки и окружность. Докажем (методом от противного), что вершина четырехугольника также будет лежать на этой окружности.

1) Допустим, что вершина  лежит внутри круга (рис. 94). Продолжим до пересечения с окружностью в точке Тогда (по условию) и (по свойству углов вписанного четырехугольника). Тогда Но — внешний, a — не смежный с ним внутренний угол треугольника  Поэтому должен быть больше, чем  

Пришли к противоречию, значит, наше предположение ошибочно, и точка не может лежать внутри круга.

2) Аналогично можно доказать, что вершина не может лежать вне круга.

3) Следовательно, точка лежит на окружности, ограничивающей круг (рис. 92), а значит около четырехугольника можно описать окружность.

Следствие 1. Около любого прямоугольника можно описать окружность.

Следствие 2. Около равнобокой трапеции можно описать окружность.

Заметим, что, как и в треугольнике, центром описанной около четырехугольника окружности является точка пересечения серединных перпендикуляров к его сторонам, поскольку она равноудалена от всех его вершин. Например, в прямоугольнике такой точкой является точка пересечения диагоналей.

Четырехугольник называют описанным около окружности, если все его стороны касаются окружности. Окружность при этом называют вписанной в четырехугольник (рис. 95).

Теорема 3 (свойство сторон описанного четырехугольника). В описанном четырехугольнике суммы противолежащих сторон равны.

Доказательство:

Пусть четырехугольник — описанный, — точки касания (рис. 96). По свойству отрезков касательных, проведенных из одной точки к окружности,

Ha рисунке 96 равные отрезки обозначены одинаковым цветом.

Тогда

Следовательно, 

Как известно из курса геометрии 7 класса, в любой треугольник можно вписать окружность. Для четырехугольников это не так.

Теорема 4 (признак описанного четырехугольника). Если в четырехугольнике суммы противолежащих сторон равны, то в этот четырехугольник можно вписать окружность.

Доказательство этой теоремы является достаточно громоздким, поэтому его не приводим.

Следствие. В любой ромб можно вписать окружность.

Как и в треугольнике, центром окружности, вписанной в четырехугольник, является точка пересечения биссектрис его углов. Так как диагонали ромба являются биссектрисами его углов, то центр вписанной в ромб окружности — точка пересечения диагоналей.

Теорема Фалеса

Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство:

Пусть параллельные прямые   пересекают стороны угла с вершиной (рис. 101), при этом  Докажем, что

1) Проведем через точки и прямые и параллельные прямой  (по условию),  (как соответственные углы при параллельных прямых  и  (как соответственные углы при параллельных прямых и  Поэтому

 (по стороне и двум прилежащим к ней углам), а значит,  (как соответственные стороны равных треугольников).

2) Четырехугольник — параллелограмм (по построению). Поэтому  Аналогично -параллелограмм, поэтому

Таким образом,  следовательно  что и требовалось доказать. 

Следствие. Параллельные прямые, пересекающие две данные прямые и отсекающие на одной из них равные отрезки, отсекают равные отрезки и на другой прямой.

С помощью линейки без делений по теореме Фалеса возможно разделить отрезок на любое количество равных частей.

Пример №9

Разделите отрезок на б равных частей.

Решение:

1) Пусть — данный отрезок (рис. 102). Проведем произвольный луч и отложим на нем циркулем последовательно 6 отрезков:

2) Через точки и проведем прямую.

3) Через точки  — с помощью угольника и линейки проведем прямые, параллельные прямой  Тогда по теореме Фалеса эти прямые разделят отрезок АВ на 6 равных частей:

А еще раньше:

Фалес Милетский — древнегреческий математик и астроном. По давней традиции его считают одним из так называемых семи мудрецов света, ведь он был одним из самых выдающихся математиков своего времени.

В молодые годы любознательный юноша отправился путешествовать по Египту с целью познакомиться с египетской культурой и Фалес не только быстро изучил то, что в то время уже было известно египетским ученым, но и сделал ряд собственных научных открытий. Он самостоятельно определил высоту египетских пирамид по длине их тени, чем очень удивил египетского фараона Амазиса, а вернувшись на родину, создал в Милети философскую школу.

По мнению историков Фалес был первым, кто познакомил греков с геометрией и стал первым греческим астрономом. Он предсказал солнечное затмение, произошедшее 28 мая 585 года до н. э.

На гробнице Фалеса высечена надпись: «Насколько мала эта гробница, настолько велика слава этого царя астрономов в области звезд».

Как называется фигура с 4 углами. Четырехугольники

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Сегодня рассмотрим геометрическую фигуру — четырехугольник. Из названия этой фигуры уже становится понятно, что у этой фигуры есть четыре угла. А вот остальные характеристики и свойства этой фигуры мы рассмотрим ниже.

Что такое четырех угольник

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Площадь четырехугольника равна полупроизведению его диагоналей и угла между ними.

Четырехугольник — это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.

Виды четырехугольников

• Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
• Четырехугольник, у которого две противоположные стороны параллельны, а две другие − нет, называется трапецией.
• Четырехугольник, у которого все углы прямые, является прямоугольником.
• Четырехугольник, у которого все стороны равны, является ромбом.
• Четырехугольник, у которого все стороны равны и все углы прямые, называется квадратом.

Четырехугольник может быть:

Самопересекающимся

Невыпуклым

Выпуклым

Самопересекающийся четырехугольник — это четырехугольник, у которого любые из его сторон имеют точку пересечения (на рисунке синим цветом).

Невыпуклый четырехугольник — это четырехугольник, в котором один из внутренних углов более 180 градусов (на рисунке обозначен оранжевым цветом).

Сумма углов любого четырехугольника, который не является самоперсекающимся всегда равна 360 градусов.

Особые виды четырехугольников

Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:

• Параллелограмм
• Прямоугольник
• Квадрат
• Трапеция
• Дельтоид
• Контрпараллелограмм

Четырехугольник и окружность

Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).

Главное свойство описанного четырехугольника:

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.

Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)

Главное свойство вписанного четырехугольника:

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.

Свойства длин сторон четырехугольника

Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.

|a — b| ≤ c + d

|a — c| ≤ b + d

|a — d| ≤ b + c

|b — c| ≤ a + d

|b — d| ≤ a + b

|c — d| ≤ a + b

Важно . Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.

В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны .

Важно . При решении задач в пределах школьной программы можно использовать строгое неравенство (

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Четырехугольником ABCD называется фигура, которая состоит из четырех точек А, В, С, D по три, не лежащих на одной прямой, и четырех отрезков AB, BC, CD и AD, соединяющих эти точки.

На рисунках изображены четырехугольники.

Точки А, В, С и D называются вершинами четырехугольника , а отрезки AB, BC, CD и AD — сторонами . Вершины А и С, В и D называются противолежащими вершинами . Стороны AB и CD, BC и AD называются противолежащими сторонами .

Четырехугольники бывают выпуклые (на рисунке — левый) и невыпуклые (на рисунке — правый).

Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника (диагональ АС разделяет ABCD на два треугольника ABC и ACD; диагональ BD — на BCD и BAD). У невыпуклого четырехугольника только одна из диагоналей разделяет его на два треугольника (диагональ AC разделяет ABCD на два треугольника ABC и ACD; диагональ BD — не разделяет).

Рассмотрим основные виды четырехугольников, их свойства, формулы площади:

Параллелограмм

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства:

Признаки параллелограмма:

1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Площадь параллелограмма:

Трапеция

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Основаниями называются параллельные стороны, а две другие стороны — боковыми сторонами .

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

ТЕОРЕМА.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Площадь трапеции:

Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства:

Площадь ромба:

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы равны.

Свойства:

Признак прямоугольника:

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Площадь прямоугольника:

Квадрат

Квадратом называется прямоугольник, у которого все стороны равны.

Свойства :

Квадрат обладает всеми свойствами прямоугольника и ромба (прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом).

Площадь квадрата:

Одна из наиболее интересных тем по геометрии из школьного курса — это «Четырехугольники» (8 класс). Какие виды таких фигур существуют, какими особыми свойствами они обладают? В чем уникальность четырехугольников с углами по девяносто градусов? Давайте разберемся во всем этом.

Какая геометрическая фигура называется четырехугольником

Многоугольники, которые состоят из четырех сторон и, соответственно, из четырех вершин (углов), называются в евклидовой геометрии четырехугольниками.

Интересна история названия этого вида фигур. В российском языке существительное «четырехугольник» образовано от словосочетания «четыре угла» (точно так же, как «треугольник» — три угла, «пятиугольник» — пять углов и т. п.).

Однако на латыни (через посредничество которой пришли многие геометрические термины в большинство языков мира) он называется quadrilateral. Это слово образовано из числительного quadri (четыре) и существительного latus (сторона). Так что можно сделать вывод, что у древних этот многоугольник именовался не иначе как «четырехсторонник».

Кстати, такое название (с упором на наличие у фигур этого вида четырех сторон, а не углов) сохранилось в некоторых современных языках. Например, в английском — quadrilateral и в французском — quadrilatère.

При этом в большинстве славянских языков рассматриваемый вид фигур идентифицируют все так же по количеству углов, а не сторон. Например, в словацком (štvoruholník), в болгарском («четириъгълник»), в белорусском («чатырохкутнік»), в украинском («чотирикутник»), в чешском (čtyřúhelník), но в польском четырехугольник именуют по количеству сторон — czworoboczny.

Какие виды четырехугольников изучаются в школьной программе

В современной геометрии выделяются 4 вида многоугольников с четырьмя сторонами.

Однако из-за слишком сложных свойств некоторых из них на уроках геометрии школьников знакомят только с двумя видами.

• Параллелограмм (parallelogram). Противолежащие стороны четырехугольника такого попарно параллельны между собой и, соответственно, равны также попарно.
• Трапеция (trapezium или trapezoid). Этот четырехугольник состоит из двух противолежащих сторон, параллельных между собой. Однако другая пара сторон не имеет такой особенности.

Не изучаемые в школьном курсе геометрии виды четырехугольников

Помимо вышеперечисленных, существуют еще два вида четырехугольников, с которыми школьников не знакомят на уроках геометрии, из-за их особой сложности.

• Дельтоид (kite) — фигура, в которой каждая из двух пар смежных сторон равна по длине между собою. Свое название такой четырехугольник получил из-за того, что по внешнему виду он довольно сильно напоминает букву греческого алфавита — «дельта».
• Антипараллелограмм (antiparallelogram) — эта фигура так же сложна, как и ее название. В ней две противоположные стороны равны, но при этом они не параллельны между собою. Кроме того, длинные противоположные стороны этого четырехугольника пересекаются между собой, как и продолжения двух других, более коротких сторон.

Виды параллелограмма

Разобравшись с основными видами четырехугольников, стоит обратить внимание на его подвиды. Так, все параллелограммы, в свою очередь, тоже делятся на четыре группы.

• Классический параллелограмм.
• Ромб (rhombus) — четырехугольная фигура с равными сторонами. Ее диагонали пересекаются под прямым углом, деля ромб на четыре равных прямоугольных треугольника.
• Прямоугольник (rectangle). Название это говорит само за себя. Так как это четырехугольник с прямыми углами (каждый из них равен девяноста градусам). Противоположные стороны его не только параллельны между собою, но и равны.
• Квадрат (square). Как и прямоугольник, это четырехугольник с прямыми углами, но у него все стороны равны между собой. Этим данная фигура близка к ромбу. Так что можно утверждать, что квадрат — это нечто среднее между ромбом и прямоугольником.

Особые свойства прямоугольника

Рассматривая фигуры, в которых каждый из углов между сторонами, равен девяноста градусам, стоит более внимательно остановиться на прямоугольнике. Итак, какими особенными он обладает признаками, отличающими его от других параллелограммов?

Чтобы утверждать, что рассматриваемый параллелограмм — прямоугольник, его диагонали должны быть равны между собою, а каждый из углов — прямыми. Кроме того, квадрат его диагоналей должен соответствовать сумме квадратов двух смежных сторон этой фигуры. Иными словами, классический прямоугольник состоит из двух прямоугольных треугольников, а в них, как известно, В роли гипотенузы выступает диагональ рассматриваемого четырехугольника.

Последний из перечисленных признаков этой фигуры является также ее особенным свойством. Помимо этого, есть и другие. Например, то, что все стороны изучаемого четырехугольника с прямыми углами — это одновременно и его высоты.

Кроме того, если вокруг любого прямоугольника начертить круг, его диаметр будет равен диагонали вписанной фигуры.

Среди других свойств четырехугольника этого, то, что он является плоским и в неевклидовой геометрии не существует. Это связано с тем, что в такой системе отсутствуют четырехугольные фигуры, сумма углов которых равна трехстах шестидесяти градусам.

Квадрат и его особенности

Разобравшись с признаками и свойствами прямоугольника, стоит обратить внимание на второй известный науке четырехугольник с прямыми углами (это квадрат).

Являясь по факту тем же прямоугольником, но с равными сторонами, эта фигура обладает всеми его свойствами. Но в отличие от него, квадрат присутствует в неевклидовой геометрии.

Кроме этого, у данной фигуры, есть и другие собственные отличительные черты. Например, то, что диагонали квадрата не просто равны между собою, но и пересекаются под прямым углом. Таким образом, как и ромб, квадрат состоит из четырех прямоугольных треугольников, на которые ее делят диагонали.

Помимо этого, данная фигура является самой симметричным среди всех четырехугольников.

Чему равна сумма углов четырехугольника

Рассматривая особенности четырехугольников евклидовой геометрии, стоит обратить внимание на их углы.

Так, в каждой из вышеперечисленных фигур, независимо от того, есть у нее прямые углы или нет, общая сумма их всегда одинакова — триста шестьдесят градусов. Это уникальная отличительная черта этого вида фигур.

Периметр четырехугольников

Разобравшись с тем, чему равна сумма углов четырехугольника и другими особенными свойствами фигур этого вида, стоит узнать, какими формулами лучше всего пользоваться, чтобы вычислить их периметр и площадь.

Чтобы определить периметр любого четырехугольника, нужно лишь сложить между собою длину всех его сторон.

Например, в фигуре KLMN ее периметр можно вычислить по формуле: Р = KL + LM + MN + KN. Если подставить сюда числа, получится: 6 + 8 + 6 + 8 = 28 (см).

В случае когда рассматриваемая фигура — это ромб или квадрат, для нахождения периметра можно упростить формулу, просто помножив длину одной из его сторон на четыре: Р = KL х 4. Например: 6 х 4=24 (см).

Формулы четырехугольников площади

Разобравшись с тем, как найти периметр любого фигуры с четырьмя углами и сторонами, стоит рассмотреть наиболее популярные и простые способы нахождения ее площади.

Другие свойства четырехугольников: вписанные и описанные окружности

Рассмотрев особенности и свойства четырехугольника как фигуры евклидовой геометрии, стоит обратить внимание на возможность описывать вокруг или вписывать внутри него круги:

• Если суммы противолежащих углов фигуры составляют по сто восемьдесят градусов и попарно равны между собою, то вокруг такого четырехугольника можно свободно описать окружность.
• Согласно теореме Птолемея, если снаружи многоугольника с четырьмя сторонами описан круг, то произведение его диагоналей равно сумме произведений противоположных сторон данной фигуры. Таким образом, формула будет выглядеть так: КМ х LN = KL х MN + LM х KN.
• Если построить четырехугольник, в котором суммы противоположных сторон равны между собою, то в него можно вписать круг.

Разобравшись с тем, что такое четырехугольник, что за виды его существуют, какие из них имеют только прямые углы между сторонами и какими свойствами они обладают, стоит запомнить весь этот материал. В особенности формулы нахождения периметра и площади рассмотренных многоугольников. Ведь фигуры такой формы — одни из самых распространенных, и эти знания могут пригодиться для вычислений в реальной жизни.

Выпуклый четырехугольник – это фигура, состоящая из четырех сторон, соединенных между собой в вершинах, образующих вместе со сторонами четыре угла, при этом сам четырехугольник всегда находится в одной плоскости относительно прямой, на которой лежит одна из его сторон. Другими словами, вся фигура находится по одну сторону от любой из ее сторон.

Как видно, определение довольно легко запоминающееся.

Основные свойства и виды

К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:

1. параллелограмм;
2. квадрат;
3. прямоугольник;
4. трапеция;
5. ромб.

Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:

На рисунке изображена выпуклая трапеция . Тут видно, что трапеция находится на одной плоскости или по одну сторону от отрезка . Если провести аналогичные действия, можно выяснить, что и в случае со всеми остальными сторонами трапеция является выпуклой.

Является ли параллелограмм выпуклым четырехугольником?

Выше показано изображение параллелограмма. Как видно из рисунка, параллелограмм также является выпуклым . Если посмотреть на фигуру относительно прямых, на которых лежат отрезки AB, BC, CD и AD, то становится понятно, что она всегда находится на одной плоскости от этих прямых. Основными же признаками параллелограмма является то, что его стороны попарно параллельны и равны так же, как и противоположные углы равны между собой.

Теперь, представьте себе квадрат или прямоугольник. По своим основным свойствам они являются еще и параллелограммами, то есть все их стороны расположены попарно параллельно. Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат – это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.

В итоге, сумма всех четырех углов четырехугольника должна быть равна 360 градусам . Легче всего это определить по прямоугольнику: все четыре угла прямоугольника прямые, то есть равны 90 градусам. Сумма этих 90-градусных углов дает 360 градусов, другими словами, если сложить 90 градусов 4 раза, получится необходимый результат.

Свойство диагоналей выпуклого четырехугольника

Диагонали выпуклого четырехугольника пересекаются . Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:

На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.

Другие свойства и признаки выпуклости четырехугольника

Конкретно по этому термину очень сложно назвать какие-то определенные свойства и признаки. Легче обособить по различным видам четырехугольников такого типа. Начать можно с параллелограмма. Мы уже знаем, что это четырехугольная фигура, стороны которой попарно параллельны и равны. При этом, сюда же включается свойство диагоналей параллелограмма пересекаться между собой, а также сам по себе признак выпуклости фигуры: параллелограмм находится всегда в одной плоскости и по одну сторону относительно любой из своих сторон.

Итак, известны основные признаки и свойства:

1. сумма углов четырехугольника равна 360 градусам;
2. диагонали фигур пересекаются в одной точке.

Прямоугольник . Эта фигура имеет все те же свойства и признаки, что и параллелограмм, но при этом все углы его равны 90 градусам. Отсюда и название – прямоугольник.

Квадрат, тот же параллелограмм , но углы его прямые как у прямоугольника. Из-за этого квадрат в редких случаях называют прямоугольником. Но главным отличительным признаком квадрата помимо уже перечисленных выше, является то, что все четыре его стороны равны.

Трапеция – очень интересная фигура . Это тоже четырехугольник и тоже выпуклый. В этой статье трапеция уже рассматривалась на примере рисунка. Понятно, что она тоже выпуклая. Главным отличием, а соответственно признаком трапеции является то, что ее стороны могут быть абсолютно не равны друг другу по длине, а также ее углы по значению. При этом фигура всегда остается на одной плоскости относительно любой из прямых, которая соединяет любые две ее вершины по образующим фигуру отрезкам.

Ромб – не менее интересная фигура . Отчасти ромбом можно считать квадрат. Признаком ромба является тот факт, что его диагонали не только пересекаются, но и делят углы ромба пополам, а сами диагонали пересекаются под прямым углом, то есть, они перпендикулярны. В случае, если длины сторон ромба равны, то диагонали тоже делятся пополам при пересечении.

Дельтоиды или выпуклые ромбоиды (ромбы) могут иметь разную длину сторон. Но при этом все равно сохраняются как основные свойства и признаки самого ромба, так и признаки и свойства выпуклости. То есть, мы можем наблюдать, что диагонали делят углы пополам и пересекаются под прямым углом.

Сегодняшней задачей было рассмотреть и понять, что такое выпуклые четырехугольники, какие они бывают и их основные признаки и свойства. Внимание! Стоит напомнить еще раз, что сумма углов выпуклого четырехугольника равна 360 градусам. Периметр фигур, например, равен сумме длин всех образующих фигуру отрезков. Формулы расчета периметра и площади четырехугольников будут рассмотрены в следующих статьях.

Как называется четырехугольник с прямыми углами?

Изучение геометрии начинается с рассмотрения простых фигур на плоскости, которые легко представить, используя абстрактное воображение. Одна из таких фигур — это четырехугольник с прямыми углами. В 3 классе общеобразовательных школ начинают знакомиться с ней и подробно исследуют ее свойства в старших классах. Рассмотрим главные характеристики этой фигуры в статье, а также приведем примеры ее использования в быту.

Как называется с прямыми углами четырехугольник?

Слово «четырехугольник» говорит о том, что рассматриваемая фигура состоит из четырех углов. На плоскости она будет замкнута только в том случае, если имеет четыре прямые стороны. Если противоположные стороны попарно друг другу параллельны, то такая фигура называется параллелограммом. Его четыре угла попарно равны, однако они могут принимать произвольные значения от 0o до 180o. Если все его углы будут равны 90o, то они называются прямыми. Четырехугольник с углами прямыми — это прямоугольник, и одновременно он является параллелограммом.

Прямоугольник характеризуется всего двумя параметрами: длинами его соседних сторон. Далее в статье будем обозначать их a и b. Если эти длины равны друг другу, то прямоугольник вырождается в квадрат.

Формула для площади

Прямоугольник — это совершенная фигура, под которую человек в ходе своей жизнедеятельности старается подогнать окружающие объекты, например кирпич, форму двора перед домом, монитор компьютера и так далее. Поэтому часто возникает задача расчета площади прямоугольника.

Рассчитать площадь рассматриваемой фигуры не представляет никакой сложности. Поскольку прямоугольник — это параллелограмм, то его площадь вычисляется как произведение двух длин: высоты, опущенной на некоторую сторону, и этой стороны. Высота параллелограмма находится как произведение синуса одного из его углов на сторону. Поскольку мы рассматриваем конкретный вид параллелограмма — прямоугольник, то синус прямого угла равен единице, это означает, что искомая формула для площади принимает следующий вид:

S = a*b

Площадь четырехугольника с прямым углом равна произведению длин двух его непараллельных сторон.

Ниже будет показано, как найти площадь прямоугольника, если известны другие его элементы, например длина диагонали.

Диагонали прямоугольника

На рисунке ниже изображен произвольный четырехугольник с прямыми углами и его две диагонали.

Видно, что диагонали разделяют на две части противоположные прямые углы фигуры. Будем обозначать точку пересечения диагоналей символом C. Она имеет важное значение, поскольку является центром симметрии фигуры. Длины обеих диагоналей равны.

Диагонали делят прямоугольник на четыре равнобедренных треугольника, для которых легко вычислить длины сторон и площадь. Каждые два треугольника, основания которых лежат на сторонах равной длины прямоугольника, являются одинаковыми.

Если провести одну диагональ, то она разделит прямоугольник на два совершенно одинаковых прямоугольных треугольника. Этот факт позволяет использовать тиорему Пифагора, чтобы рассчитать длину диагонали, зная катеты треугольника. Ниже рисунок показывает, как можно найти квадрат диагонали c прямоугольника. Здесь диагональ является гипотенузой, а стороны прямоугольника соответствуют катетам треугольника.

Тогда значение длины c будет равно:

c = √(a2 + b2)

Симметрия прямоугольника

Как было отмечено, центр его симметрии — это точка C, образованная пересекающимися диагоналями. Рассматривая фигуру на плоскости, можно сказать, что ось, через эту точку проходящая и параллельная двум сторонам прямоугольника, является осью симметрии второго порядка, то есть поворот вокруг нее на 180o переведет прямоугольник сам в себя. Поскольку рассматриваемый четырехугольник имеет две пары параллельных сторон, то очевидно, что он обладает двумя указанными осями симметрии.

Ось симметрии делит фигуру на два одинаковых прямоугольника со сторонами:

a и b/2 или b и a/2

Некоторые геометрические свойства прямоугольника

Поскольку рассматриваемая фигура обладает некоторой симметрией, имеет прямые углы и попарно параллельные стороны, то для нее можно выделить ряд важных свойств, используемых на практике. Перечислим их:

1. Всякая прямая, которая проходит через центр C фигуры, пересекает ее в двух точках, находящихся на одинаковом расстоянии от точки C. Максимальное расстояние от C до стороны диагонали прямоугольника равно половине длины его диагонали, минимальное же расстояние равно половине длины его меньшей стороны.
2. Если поделить одну сторону прямоугольника точкой пополам, то, соединяя эту точку с вершинами противоположной параллельной стороны, получаем равнобедренный треугольник с площадью, равной половине площади прямоугольника.
3. Если точку, описанную выше, смещать из центра стороны к одному или другому ее концу, то равнобедренность отмеченного треугольника будет нарушаться, однако его площадь будет оставаться неизменной.
4. Любой прямоугольник можно вписать в окружность.

Первое свойство является очевидным, поскольку любая прямая, проходящая через C, будет пересекать параллельные стороны фигуры. Докажем остальные свойства.

Доказательство свойств 2, 3 и 4

Рассмотрим сначала свойства 2 и 3. На рисунке ниже показан прямоугольник, на сторонах которого построены три треугольника:

ABC1, ABC2 и ABC3

Согласно формуле нахождения площади треугольника, для них можно записать:

S1 = 1/2*h2*AB;S2 = 1/2*h3*AB;S3 = 1/2*h4*AB

Видно, что все высоты hi рассматриваемых треугольников равны длине стороны h прямоугольника. Это означает, что и их площади равны:

S1 = S2 = S3

Теперь запишем формулу для площади S прямоугольника и поделим S на площадь одного из изображенных треугольников, получим:

S = AB*h;S/S1 = AB*h/(1/2*h*AB) = 2

Таким образом, прямоугольник имеет площадь в два раза больше, чем любой из изображенных треугольников, то есть мы доказали второе и третье свойства.

Что касается возможности вписывания с прямыми углами четырехугольника в окружность, то здесь следует рассуждать так: проведем диагонали фигуры, они пересекутся в точке C. Поскольку эта точка находится на одинаковом расстоянии от четырех вершин прямоугольника, то она может служить центром окружности. Если радиус окружности равен половине длины диагонали, то линия окружности пройдет через все четыре вершины прямоугольника, то есть он окажется вписанным в нее.

Является ли четырехугольник, у которого один угол прямой, прямоугольником?

Ответ на вопрос будет положительным только в том случае, если рассматриваемый четырехугольник будет параллелограммом. В этом случае, если один угол равен 90o, то два других смежных угла тоже будут прямыми, а значит, четвертый угол тоже будет равен 90o. Мы нашли в четырехугольнике прямые углы все, значит он — прямоугольник.

В случае, если четырехугольник с одним прямым углом не будет иметь попарно параллельные стороны, то прямоугольником он не будет являться.

Где используется прямоугольник и его свойства?

При изготовлении тетрадных листов используют прямоугольную форму, причем отношение длин большей стороны к меньшей равно √2. Такая форма фигуры приводит к тому, что если ее поделить пополам симметричной осью, параллельной большей стороне, то у образованных двух новых прямоугольников отношение сторон также будет равно √2. Такое деление можно продолжать до бесконечности, при этом форма образующихся прямоугольников будет сохраняться.

Прямоугольная форма используется при производстве телевизионных экранов. До эры жидкокристаллических (ЖК) мониторов использовались электронно-лучевые экраны, отношение сторон которых было равно 4:3. С появлением ЖК-мониторов высокого разрешения, стали применять новый стандарт: 16:9.

Мозаика, которой украшают стены зданий, также имеет форму четырехугольника с прямыми углами.

Расчет площади фигуры по известной диагонали

Завершим статью рассмотрением вопроса вычисления площади четырехугольника, вершины прямых углов которого соединены диагональю. Рассчитаем площадь современного ЖК-монитора, если известно, что длина его диагонали с = 35 см.

Решить эту задачу можно потому, что монитор имеет стандартизированное отношение сторон, равное 16:9. Обозначая за x неизвестный коэффициент, получаем длины сторон монитора:

a = 16*x;b = 9*x

Теперь применяем формулу для определения диагонали, получаем:

c2 = a2 + b2 =>352 = x2*(162+92) =>x = 35/√(162+92) ≈ 1,9

Тогда стороны монитора и площадь его равны:

a = 16*x = 30,4 см;b = 9*x = 17,1 см;S = a*b ≈ 520 см2

Отметим еще раз, что определить по значению диагонали площадь можно только в том случае, если известно отношение сторон прямоугольника.

Четырехугольники. Выпуклые четырехугольники. Сумма углов четырехугольника. Параллелограмм. Виды параллелограммов и их свойства. Ромб, прямоугольник, квадрат. Трапеция и ее свойства. Многоугольник, выпуклый многоугольник, четырехугольник

Сегодня рассмотрим геометрическую фигуру — четырехугольник. Из названия этой фигуры уже становится понятно, что у этой фигуры есть четыре угла. А вот остальные характеристики и свойства этой фигуры мы рассмотрим ниже.

Что такое четырех угольник

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Площадь четырехугольника равна полупроизведению его диагоналей и угла между ними.

Четырехугольник — это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.

Виды четырехугольников

• Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
• Четырехугольник, у которого две противоположные стороны параллельны, а две другие − нет, называется трапецией.
• Четырехугольник, у которого все углы прямые, является прямоугольником.
• Четырехугольник, у которого все стороны равны, является ромбом.
• Четырехугольник, у которого все стороны равны и все углы прямые, называется квадратом.

Четырехугольник может быть:

Самопересекающимся

Невыпуклым

Выпуклым

Самопересекающийся четырехугольник — это четырехугольник, у которого любые из его сторон имеют точку пересечения (на рисунке синим цветом).

Невыпуклый четырехугольник — это четырехугольник, в котором один из внутренних углов более 180 градусов (на рисунке обозначен оранжевым цветом).

Сумма углов любого четырехугольника, который не является самоперсекающимся всегда равна 360 градусов.

Особые виды четырехугольников

Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:

• Параллелограмм
• Прямоугольник
• Квадрат
• Трапеция
• Дельтоид
• Контрпараллелограмм

Четырехугольник и окружность

Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).

Главное свойство описанного четырехугольника:

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.

Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)

Главное свойство вписанного четырехугольника:

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.

Свойства длин сторон четырехугольника

Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.

|a — b| ≤ c + d

|a — c| ≤ b + d

|a — d| ≤ b + c

|b — c| ≤ a + d

|b — d| ≤ a + b

|c — d| ≤ a + b

Важно . Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.

В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны .

Важно . При решении задач в пределах школьной программы можно использовать строгое неравенство (

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Выпуклый четырехугольник – это фигура, состоящая из четырех сторон, соединенных между собой в вершинах, образующих вместе со сторонами четыре угла, при этом сам четырехугольник всегда находится в одной плоскости относительно прямой, на которой лежит одна из его сторон. Другими словами, вся фигура находится по одну сторону от любой из ее сторон.

Как видно, определение довольно легко запоминающееся.

Основные свойства и виды

К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:

1. параллелограмм;
2. квадрат;
3. прямоугольник;
4. трапеция;
5. ромб.

Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:

На рисунке изображена выпуклая трапеция . Тут видно, что трапеция находится на одной плоскости или по одну сторону от отрезка . Если провести аналогичные действия, можно выяснить, что и в случае со всеми остальными сторонами трапеция является выпуклой.

Является ли параллелограмм выпуклым четырехугольником?

Выше показано изображение параллелограмма. Как видно из рисунка, параллелограмм также является выпуклым . Если посмотреть на фигуру относительно прямых, на которых лежат отрезки AB, BC, CD и AD, то становится понятно, что она всегда находится на одной плоскости от этих прямых. Основными же признаками параллелограмма является то, что его стороны попарно параллельны и равны так же, как и противоположные углы равны между собой.

Теперь, представьте себе квадрат или прямоугольник. По своим основным свойствам они являются еще и параллелограммами, то есть все их стороны расположены попарно параллельно. Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат – это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.

В итоге, сумма всех четырех углов четырехугольника должна быть равна 360 градусам . Легче всего это определить по прямоугольнику: все четыре угла прямоугольника прямые, то есть равны 90 градусам. Сумма этих 90-градусных углов дает 360 градусов, другими словами, если сложить 90 градусов 4 раза, получится необходимый результат.

Свойство диагоналей выпуклого четырехугольника

Диагонали выпуклого четырехугольника пересекаются . Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:

На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.

Другие свойства и признаки выпуклости четырехугольника

Конкретно по этому термину очень сложно назвать какие-то определенные свойства и признаки. Легче обособить по различным видам четырехугольников такого типа. Начать можно с параллелограмма. Мы уже знаем, что это четырехугольная фигура, стороны которой попарно параллельны и равны. При этом, сюда же включается свойство диагоналей параллелограмма пересекаться между собой, а также сам по себе признак выпуклости фигуры: параллелограмм находится всегда в одной плоскости и по одну сторону относительно любой из своих сторон.

Итак, известны основные признаки и свойства:

1. сумма углов четырехугольника равна 360 градусам;
2. диагонали фигур пересекаются в одной точке.

Прямоугольник . Эта фигура имеет все те же свойства и признаки, что и параллелограмм, но при этом все углы его равны 90 градусам. Отсюда и название – прямоугольник.

Квадрат, тот же параллелограмм , но углы его прямые как у прямоугольника. Из-за этого квадрат в редких случаях называют прямоугольником. Но главным отличительным признаком квадрата помимо уже перечисленных выше, является то, что все четыре его стороны равны.

Трапеция – очень интересная фигура . Это тоже четырехугольник и тоже выпуклый. В этой статье трапеция уже рассматривалась на примере рисунка. Понятно, что она тоже выпуклая. Главным отличием, а соответственно признаком трапеции является то, что ее стороны могут быть абсолютно не равны друг другу по длине, а также ее углы по значению. При этом фигура всегда остается на одной плоскости относительно любой из прямых, которая соединяет любые две ее вершины по образующим фигуру отрезкам.

Ромб – не менее интересная фигура . Отчасти ромбом можно считать квадрат. Признаком ромба является тот факт, что его диагонали не только пересекаются, но и делят углы ромба пополам, а сами диагонали пересекаются под прямым углом, то есть, они перпендикулярны. В случае, если длины сторон ромба равны, то диагонали тоже делятся пополам при пересечении.

Дельтоиды или выпуклые ромбоиды (ромбы) могут иметь разную длину сторон. Но при этом все равно сохраняются как основные свойства и признаки самого ромба, так и признаки и свойства выпуклости. То есть, мы можем наблюдать, что диагонали делят углы пополам и пересекаются под прямым углом.

Сегодняшней задачей было рассмотреть и понять, что такое выпуклые четырехугольники, какие они бывают и их основные признаки и свойства. Внимание! Стоит напомнить еще раз, что сумма углов выпуклого четырехугольника равна 360 градусам. Периметр фигур, например, равен сумме длин всех образующих фигуру отрезков. Формулы расчета периметра и площади четырехугольников будут рассмотрены в следующих статьях.

Определение 1. Четырехугольником называется фигура, состоящая из четырех точек (вершины), никакие три из которых не лежат на одной прямой, и четырех последовательно соединяющих их непересекающихся отрезков (стороны).
Определение 2. Соседними называют вершины, которые являются концами одной стороны.
Определение 3. Вершины, не являющиеся соседними, называют противолежащими.
Определение 4. Отрезки, соединяющие противоположные вершины четырехугольника, называются его диагоналями.
Теорема 1. Сумма углов четырехугольника равна 360 о.
Действительно, поделив четырехугольник диагональю на два треугольника, получаем, что сумма его углов равна сумме углов этих двух треугольников. Зная, что сумма углов треугольника равна 180 о, получаем искомое: 2 * 180 о =360 о
Определение d1. Описанный четырёхугольник — это четырёхугольник, все стороны которого касаются некоторой окружности. Напомним, что понятие стороны, касающейся окружности: окружность считается касающейся данной стороны, если она касается прямой, содержащей эту сторону, и точка касания лежит на этой стороне.
Определение d2. Вписанный четырехугольник — это четырёхугольник, все вершины которого принадлежат некоторой окружности.
Теорема 2. У любого четырехугольника, вписанного в окружность, суммы пар противоположных углов равны 180 о.
Углы А и С оба опираются на дугу BD только с разных сторон, то есть охватывают всю окружность, а сама окружность — это дуга величиной в 360 о, но мы знаем теоремму, которая твердит, что величина вписанного угла равна половине угловой величины дуги, на которую он опирается, поэтому можем утвердить, что сумма этих углов (А и С в частности) равна 180 о. Тем же способом можно жоказать эту теорему и для другой пары углов.
Теорема 3. Если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.
Для доказательства этой теоремы воспользуемся теоремой из темы круг и окружность , которая гласит: Отрезки касательных, проведенных из одной точки к окружности, равны, т.е. ВК=ВР, СР=СН, DH=DT и АТ=АК. Суммируем стороны АВ и CD: AB+CD=(AK+KB)+(DH+HC)=AT+BP+DT+CP=(AT+TD)+(BP+PC)=AD+BC, ч.т.д.

Для теорем 2 и 3 существуют обратные. Запишем их соответственно:

Теорема 4. Около четырехугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равны 180 градусам
Теорема 5. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны.

Доказательство: Пусть ABCD — данный четырехугольник, и него AB + CD = AD + BC. Проведем биссектрисы его углов A и D. Эти биссектрисы непараллельны, а значит, пересекаются в некоторой точке O. Опустим из точки O на стороны AB, AD и CD перпендикуляры OK, OL и OM. Тогда OK=OL, и OL=OM, а значит, окружность с центром в точке O и радиусом OK касается сторон AB, AD и CD данного четырёхугольника. Проведём из точки B касательную к этой окружности. Пусть эта касательная пересекает прямую CD в точке P. Тогда ABPD — описанный четырёхугольник. Следовательно, по свойству описанного четырёхугольника, AB + DP = AD + BP. Также, по условию, AB+ CD = AD + BC. Следовательно, BP + PC = BC, а значит, по неравенству треугольника, точка P лежит на отрезке BC. Следовательно, прямые BP и BC совпадают, а значит, прямая BC касается окружности с центром в точке O, то есть ABCD — описанный четырёхугольник по определению. Теорема доказана.
Теорема 6. Площадь четырехугольника равна половине произведения его диагоналей и синуса угла между ними.

Доказательство: Пусть ABCD — данный четырёхугольник. Пусть также O — точка пересечения диагоналей. Тогда
S ABCD = S ABO + S BCO +S CDO + S DAO =
= 1/2(AO·BO·sin∠ AOB + BO·CO·sin∠ BOC +
+ CO·DO·sin∠ COD + DO·AO·sin∠ AOD) =
= 1/2·sin∠ BOC·(AO + CO)·(BO + DO) =
= 1/2·sin∠ BOC·AC·BD.
Теорема доказана.
Теорема d1. (Вариньона) Четырёхугольник с вершинами в серединах сторон любого четырёхугольника есть параллелограмм, причём площадь этого параллелограмма равна половине площади исходного четырёхугольника.

Доказательство: Пусть ABCD — данный четырёхугольник, а K, L, M и N — середины его сторон. Тогда KL — средняя линия треугольника ABC, а значит, KL параллельно AC. Также LM параллельно BD, MN параллельно AC, а NK параллельно BD. Следовательно, KL параллельно MN, LM параллельно KN. Значит, KLMN — параллелограмм. Площадь этого параллелограмма — KL·KN·sin∠ NKL =
1/2·AC·BD·sin∠ DOC = 1/2S ABCD .
Теорема доказана.

ВПИСАННЫЕ И ОПИСАННЫЕ МНОГОУГОЛЬНИКИ,

§ 106. СВОЙСТВА ВПИСАННЫХ И ОПИСАННЫХ ЧЕТЫРЁХУГОЛЬНИКОВ.

Теорема 1. Сумма противоположных углов вписанного четырёхугольника равна 180° .

Пусть в окружность с центром О вписан четырёхугольник ABCD (черт. 412). Требуется доказать, что / А + / С = 180° и / В + / D = 180°.

/ А, как вписанный в окружность О, измеряется 1 / 2 BCD.
/ С, как вписанный в ту же окружность, измеряется 1 / 2 BAD.

Следовательно, сумма углов А и С измеряется полусуммой дуг BCD и BAD в сумме же эти дуги составляют окружность, т. е. имеют 360°.
Отсюда / А + / С = 360°: 2 = 180°.

Аналогично доказывается, что и / В + / D = 180°. Однако это можно вывести и иным путём. Мы знаем, что сумма внутренних углов выпуклого четырёхугольника равна 360°. Сумма углов А и С равна 180°, значит, на сумму других двух углов четырёхугольника остаётся тоже 180° .

Теорема 2 (обратная). Если в четырёхугольнике сумма двух противоположных углов равна 180°, то около такого четырёхугольника можно описать окружность.

Пусть сумма противоположных углов четырёхугольника ABCD равна 180°, а именно
/ А + / С = 180° и / В + / D = 180° (черт. 412).

Докажем, что около такого четырёхугольника можно описать окружность.

Доказательство . Через любые 3 вершины этого четырёхугольника можно провести окружность, например через точки А, В и С. Где будет находиться точка D?

Точка D может занять только одно из следующих трёх положений: оказаться внутри круга, оказаться вне круга, оказаться на окружности круга.

Допустим, что вершина окажется внутри круга и займёт положение D» (черт. 413). Тогда в четырёхугольнике ABCD» будем иметь:

/ В + / D» = 2d .

Продолжив сторону AD» до пересечения с окружностью в точке Е и соединив точки Е и С, получим вписанный четырёхугольник АВСЕ, в котором по прямой теореме

/ B + / Е = 2d .

Из этих двух равенств следует:

/ D» = 2d — / B;
/ E = 2d — / B;

/ D» = / E,

но этого быть не может, так как / D», как внешний относительно треугольника CD»E, должен быть больше угла Е. Поэтому точка D не может оказаться внутри круга.

Так же доказывается, что вершина D не может занять положение D» вне круга (черт. 414).

Остаётся признать, что вершина D должна лежать на окружности круга, т. е. совпасть с точкой Е, значит, около четырёхугольника ABCD можно описать окружность.

Следствия. 1. Вокруг всякого прямоугольника можно описать окружность.

2. Вокруг равнобедренной трапеции можно описать окружность.

В обоих случаях сумма противоположных углов равна 180°.

Теорема 3. В описанном четырёхугольнике суммы противоположных сторон равны. Пусть четырёхугольник ABCD описан около окружности (черт. 415), т. е. стороны его АВ, ВС, CD и DA — касательные к этой окружности.

Требуется доказать, что АВ + CD =AD + ВС. Обозначим точки касания буквами М, N, К, Р, На основании свойств касательных, проведённых к окружности из одной точки (§ 75), имеем:

АР = АК;
ВР = ВМ;
DN = DK;
CN = СМ.

Сложим почленно эти равенства. Получим:

АР + ВР + DN + CN = АК + ВМ +DK + СМ,

т. е. АВ + CD = AD + ВС, что и требовалось доказать.

Упражнения.

1. Во вписанном четырёхугольнике два противоположных угла относятся как 3: 5,
а другие два относятся как 4: 5. Определить величину этих углов.

2. В описанном четырёхугольнике сумма двух противоположных сторон равна 45 см. Остальные две стороны относятся как 0,2: 0,3. Найти длину этих сторон.

Одна из наиболее интересных тем по геометрии из школьного курса — это «Четырехугольники» (8 класс). Какие виды таких фигур существуют, какими особыми свойствами они обладают? В чем уникальность четырехугольников с углами по девяносто градусов? Давайте разберемся во всем этом.

Какая геометрическая фигура называется четырехугольником

Многоугольники, которые состоят из четырех сторон и, соответственно, из четырех вершин (углов), называются в евклидовой геометрии четырехугольниками.

Интересна история названия этого вида фигур. В российском языке существительное «четырехугольник» образовано от словосочетания «четыре угла» (точно так же, как «треугольник» — три угла, «пятиугольник» — пять углов и т. п.).

Однако на латыни (через посредничество которой пришли многие геометрические термины в большинство языков мира) он называется quadrilateral. Это слово образовано из числительного quadri (четыре) и существительного latus (сторона). Так что можно сделать вывод, что у древних этот многоугольник именовался не иначе как «четырехсторонник».

Кстати, такое название (с упором на наличие у фигур этого вида четырех сторон, а не углов) сохранилось в некоторых современных языках. Например, в английском — quadrilateral и в французском — quadrilatère.

При этом в большинстве славянских языков рассматриваемый вид фигур идентифицируют все так же по количеству углов, а не сторон. Например, в словацком (štvoruholník), в болгарском («четириъгълник»), в белорусском («чатырохкутнік»), в украинском («чотирикутник»), в чешском (čtyřúhelník), но в польском четырехугольник именуют по количеству сторон — czworoboczny.

Какие виды четырехугольников изучаются в школьной программе

В современной геометрии выделяются 4 вида многоугольников с четырьмя сторонами.

Однако из-за слишком сложных свойств некоторых из них на уроках геометрии школьников знакомят только с двумя видами.

• Параллелограмм (parallelogram). Противолежащие стороны четырехугольника такого попарно параллельны между собой и, соответственно, равны также попарно.
• Трапеция (trapezium или trapezoid). Этот четырехугольник состоит из двух противолежащих сторон, параллельных между собой. Однако другая пара сторон не имеет такой особенности.

Не изучаемые в школьном курсе геометрии виды четырехугольников

Помимо вышеперечисленных, существуют еще два вида четырехугольников, с которыми школьников не знакомят на уроках геометрии, из-за их особой сложности.

• Дельтоид (kite) — фигура, в которой каждая из двух пар смежных сторон равна по длине между собою. Свое название такой четырехугольник получил из-за того, что по внешнему виду он довольно сильно напоминает букву греческого алфавита — «дельта».
• Антипараллелограмм (antiparallelogram) — эта фигура так же сложна, как и ее название. В ней две противоположные стороны равны, но при этом они не параллельны между собою. Кроме того, длинные противоположные стороны этого четырехугольника пересекаются между собой, как и продолжения двух других, более коротких сторон.

Виды параллелограмма

Разобравшись с основными видами четырехугольников, стоит обратить внимание на его подвиды. Так, все параллелограммы, в свою очередь, тоже делятся на четыре группы.

• Классический параллелограмм.
• Ромб (rhombus) — четырехугольная фигура с равными сторонами. Ее диагонали пересекаются под прямым углом, деля ромб на четыре равных прямоугольных треугольника.
• Прямоугольник (rectangle). Название это говорит само за себя. Так как это четырехугольник с прямыми углами (каждый из них равен девяноста градусам). Противоположные стороны его не только параллельны между собою, но и равны.
• Квадрат (square). Как и прямоугольник, это четырехугольник с прямыми углами, но у него все стороны равны между собой. Этим данная фигура близка к ромбу. Так что можно утверждать, что квадрат — это нечто среднее между ромбом и прямоугольником.

Особые свойства прямоугольника

Рассматривая фигуры, в которых каждый из углов между сторонами, равен девяноста градусам, стоит более внимательно остановиться на прямоугольнике. Итак, какими особенными он обладает признаками, отличающими его от других параллелограммов?

Чтобы утверждать, что рассматриваемый параллелограмм — прямоугольник, его диагонали должны быть равны между собою, а каждый из углов — прямыми. Кроме того, квадрат его диагоналей должен соответствовать сумме квадратов двух смежных сторон этой фигуры. Иными словами, классический прямоугольник состоит из двух прямоугольных треугольников, а в них, как известно, В роли гипотенузы выступает диагональ рассматриваемого четырехугольника.

Последний из перечисленных признаков этой фигуры является также ее особенным свойством. Помимо этого, есть и другие. Например, то, что все стороны изучаемого четырехугольника с прямыми углами — это одновременно и его высоты.

Кроме того, если вокруг любого прямоугольника начертить круг, его диаметр будет равен диагонали вписанной фигуры.

Среди других свойств четырехугольника этого, то, что он является плоским и в неевклидовой геометрии не существует. Это связано с тем, что в такой системе отсутствуют четырехугольные фигуры, сумма углов которых равна трехстах шестидесяти градусам.

Квадрат и его особенности

Разобравшись с признаками и свойствами прямоугольника, стоит обратить внимание на второй известный науке четырехугольник с прямыми углами (это квадрат).

Являясь по факту тем же прямоугольником, но с равными сторонами, эта фигура обладает всеми его свойствами. Но в отличие от него, квадрат присутствует в неевклидовой геометрии.

Кроме этого, у данной фигуры, есть и другие собственные отличительные черты. Например, то, что диагонали квадрата не просто равны между собою, но и пересекаются под прямым углом. Таким образом, как и ромб, квадрат состоит из четырех прямоугольных треугольников, на которые ее делят диагонали.

Помимо этого, данная фигура является самой симметричным среди всех четырехугольников.

Чему равна сумма углов четырехугольника

Рассматривая особенности четырехугольников евклидовой геометрии, стоит обратить внимание на их углы.

Так, в каждой из вышеперечисленных фигур, независимо от того, есть у нее прямые углы или нет, общая сумма их всегда одинакова — триста шестьдесят градусов. Это уникальная отличительная черта этого вида фигур.

Периметр четырехугольников

Разобравшись с тем, чему равна сумма углов четырехугольника и другими особенными свойствами фигур этого вида, стоит узнать, какими формулами лучше всего пользоваться, чтобы вычислить их периметр и площадь.

Чтобы определить периметр любого четырехугольника, нужно лишь сложить между собою длину всех его сторон.

Например, в фигуре KLMN ее периметр можно вычислить по формуле: Р = KL + LM + MN + KN. Если подставить сюда числа, получится: 6 + 8 + 6 + 8 = 28 (см).

В случае когда рассматриваемая фигура — это ромб или квадрат, для нахождения периметра можно упростить формулу, просто помножив длину одной из его сторон на четыре: Р = KL х 4. Например: 6 х 4=24 (см).

Формулы четырехугольников площади

Разобравшись с тем, как найти периметр любого фигуры с четырьмя углами и сторонами, стоит рассмотреть наиболее популярные и простые способы нахождения ее площади.

Другие свойства четырехугольников: вписанные и описанные окружности

Рассмотрев особенности и свойства четырехугольника как фигуры евклидовой геометрии, стоит обратить внимание на возможность описывать вокруг или вписывать внутри него круги:

• Если суммы противолежащих углов фигуры составляют по сто восемьдесят градусов и попарно равны между собою, то вокруг такого четырехугольника можно свободно описать окружность.
• Согласно теореме Птолемея, если снаружи многоугольника с четырьмя сторонами описан круг, то произведение его диагоналей равно сумме произведений противоположных сторон данной фигуры. Таким образом, формула будет выглядеть так: КМ х LN = KL х MN + LM х KN.
• Если построить четырехугольник, в котором суммы противоположных сторон равны между собою, то в него можно вписать круг.

Разобравшись с тем, что такое четырехугольник, что за виды его существуют, какие из них имеют только прямые углы между сторонами и какими свойствами они обладают, стоит запомнить весь этот материал. В особенности формулы нахождения периметра и площади рассмотренных многоугольников. Ведь фигуры такой формы — одни из самых распространенных, и эти знания могут пригодиться для вычислений в реальной жизни.

Использование предлога in в английском языке

Употребление и произношение in

Лестницы. Входная группа. Материалы. Двери. Замки. Дизайн

Четырехугольник с равными сторонами и углами называется. Четырехугольники. Выпуклые четырехугольники. Сумма углов четырехугольника. Параллелограмм. Виды параллелограммов и их свойства. Ромб, прямоугольник, квадрат. Трапеция и ее свойства

В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.

Итак, что же такое прямоугольник? Определение для 2 класса общеобразовательной школы будет выглядеть так: это четырёхугольник, у которого все четыре угла прямые. Несложно представить себе, как выглядит прямоугольник: это фигура с 4 прямыми углами и сторонами, попарно параллельными друг другу.

Как понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака , по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:

• фигура является четырёхугольником, три угла которого равны 90°;
• представленный четырёхугольник — это параллелограмм с равными диагоналями;
• параллелограмм, который имеет по крайней мере один прямой угол.

Интересно знать: что такое выпуклый , его особенности и признаки.

Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки.

Формулы для вычисления длины сторон

В прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).

Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α – угол между диагональю и длиной, β – острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:

• С использованием диагонали и известной стороны: a = √(d ² – b ²), b = √(d ² – a ²).
• По площади фигуры и одной из её сторон: a = S / b, b = S / a.
• При помощи периметра и известной стороны: a = (P — 2 b) / 2, b = (P — 2 a) / 2.
• Через диагональ и угол между ней и длиной: a = d sinα, b = d cosα.
• Через диагональ и угол β: a = d sin 0,5 β, b = d cos 0,5 β.

Периметр и площадь

Периметром четырёхугольника называют сумму длин всех его сторон. Чтобы вычислить периметр, могут использоваться следующие формулы:

• Через обе стороны: P = 2 (a + b).
• Через площадь и одну из сторон: P = (2S + 2a ²) / a, P = (2S + 2b ²) / b.

Площадь — это пространство, ограниченное периметром . Три основных способа для расчёта площади:

• Через длины обеих сторон: S = a*b.
• При помощи периметра и какой-либо одной известной стороны: S = (Pa — 2 a ²) / 2; S = (Pb — 2 b ²) / 2.
• По диагонали и углу β: S = 0,5 d ² sinβ.

В задачах школьного курса математики часто требуется хорошо владеть свойствами диагоналей прямоугольника . Перечислим основные из них:

1. Диагонали равны друг другу и делятся на два равных отрезка в точке их пересечения.
2. Диагональ определяется как корень суммы обеих сторон, возведённых в квадрат (следует из теоремы Пифагора).
3. Диагональ разделяет прямоугольник на два треугольника с прямым углом.
4. Точка пересечения совпадает с центром описанной окружности, а сами диагонали — с её диаметром.

Применяются следующие формулы для расчёта длины диагонали:

• С использованием длины и ширины фигуры: d = √(a ² + b ²).
• С использованием радиуса окружности, описанной вокруг четырёхугольника: d = 2 R.

Определение и свойства квадрата

Квадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник.

Четырёхугольник называют квадратом в следующих случаях:

1. Если это прямоугольник, у которого длина a и ширина b равны.
2. Если это ромб с равными длинами диагоналей и с четырьмя прямыми углами.

К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:

1. Диагонали перпендикулярны относительно друг друга (свойство ромба).
2. Точка пересечения совпадает с центром вписанной окружности.
3. Обе диагонали делят четырёхугольник на четыре одинаковых прямоугольных и равнобедренных треугольника.

Приведём часто используемые формулы для вычисления периметра, площади и элементов квадрата:

• Диагональ d = a √2.
• Периметр P = 4 a.
• Площадь S = a ².
• Радиус описанной окружности вдвое меньше диагонали: R = 0,5 a √2.
• Радиус вписанной окружности определяется как половинная длина стороны: r = a / 2.

Примеры вопросов и задач

Разберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач.

Задача 1 . Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза?

Решение: Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз.

Вопрос 1. Четырёхугольник с прямыми углами — это квадрат?

Решение: Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником.

Задача 2 . Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ.

Решение: Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16.

Вопрос 2. У прямоугольника все стороны равны или нет?

Решение: Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком.

Задача 3 . Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.

Решение: По формулам для квадрата проведём следующие расчёты:

• Определим, чему равны основные элементы квадрата: a = √ S = √289 = 17; d = a √2 =1 7√2.
• Подсчитаем, чему равен радиус описанной вокруг четырёхугольника окружности: R = 0,5 d = 8,5√2.
• Найдём радиус вписанной окружности: r = a / 2 = 17 / 2 = 8,5.

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Четырехугольником ABCD называется фигура, которая состоит из четырех точек А, В, С, D по три, не лежащих на одной прямой, и четырех отрезков AB, BC, CD и AD, соединяющих эти точки.

На рисунках изображены четырехугольники.

Точки А, В, С и D называются вершинами четырехугольника , а отрезки AB, BC, CD и AD — сторонами . Вершины А и С, В и D называются противолежащими вершинами . Стороны AB и CD, BC и AD называются противолежащими сторонами .

Четырехугольники бывают выпуклые (на рисунке — левый) и невыпуклые (на рисунке — правый).

Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника (диагональ АС разделяет ABCD на два треугольника ABC и ACD; диагональ BD — на BCD и BAD). У невыпуклого четырехугольника только одна из диагоналей разделяет его на два треугольника (диагональ AC разделяет ABCD на два треугольника ABC и ACD; диагональ BD — не разделяет).

Рассмотрим основные виды четырехугольников, их свойства, формулы площади:

Параллелограмм

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства:

Признаки параллелограмма:

1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Площадь параллелограмма:

Трапеция

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Основаниями называются параллельные стороны, а две другие стороны — боковыми сторонами .

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

ТЕОРЕМА.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Площадь трапеции:

Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства:

Площадь ромба:

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы равны.

Свойства:

Признак прямоугольника:

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Площадь прямоугольника:

Квадрат

Квадратом называется прямоугольник, у которого все стороны равны.

Свойства :

Квадрат обладает всеми свойствами прямоугольника и ромба (прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом).

Площадь квадрата:

Выпуклый четырехугольник – это фигура, состоящая из четырех сторон, соединенных между собой в вершинах, образующих вместе со сторонами четыре угла, при этом сам четырехугольник всегда находится в одной плоскости относительно прямой, на которой лежит одна из его сторон. Другими словами, вся фигура находится по одну сторону от любой из ее сторон.

Как видно, определение довольно легко запоминающееся.

Основные свойства и виды

К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:

1. параллелограмм;
2. квадрат;
3. прямоугольник;
4. трапеция;
5. ромб.

Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:

На рисунке изображена выпуклая трапеция . Тут видно, что трапеция находится на одной плоскости или по одну сторону от отрезка . Если провести аналогичные действия, можно выяснить, что и в случае со всеми остальными сторонами трапеция является выпуклой.

Является ли параллелограмм выпуклым четырехугольником?

Выше показано изображение параллелограмма. Как видно из рисунка, параллелограмм также является выпуклым . Если посмотреть на фигуру относительно прямых, на которых лежат отрезки AB, BC, CD и AD, то становится понятно, что она всегда находится на одной плоскости от этих прямых. Основными же признаками параллелограмма является то, что его стороны попарно параллельны и равны так же, как и противоположные углы равны между собой.

Теперь, представьте себе квадрат или прямоугольник. По своим основным свойствам они являются еще и параллелограммами, то есть все их стороны расположены попарно параллельно. Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат – это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.

В итоге, сумма всех четырех углов четырехугольника должна быть равна 360 градусам . Легче всего это определить по прямоугольнику: все четыре угла прямоугольника прямые, то есть равны 90 градусам. Сумма этих 90-градусных углов дает 360 градусов, другими словами, если сложить 90 градусов 4 раза, получится необходимый результат.

Свойство диагоналей выпуклого четырехугольника

Диагонали выпуклого четырехугольника пересекаются . Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:

На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.

Другие свойства и признаки выпуклости четырехугольника

Конкретно по этому термину очень сложно назвать какие-то определенные свойства и признаки. Легче обособить по различным видам четырехугольников такого типа. Начать можно с параллелограмма. Мы уже знаем, что это четырехугольная фигура, стороны которой попарно параллельны и равны. При этом, сюда же включается свойство диагоналей параллелограмма пересекаться между собой, а также сам по себе признак выпуклости фигуры: параллелограмм находится всегда в одной плоскости и по одну сторону относительно любой из своих сторон.

Итак, известны основные признаки и свойства:

1. сумма углов четырехугольника равна 360 градусам;
2. диагонали фигур пересекаются в одной точке.

Прямоугольник . Эта фигура имеет все те же свойства и признаки, что и параллелограмм, но при этом все углы его равны 90 градусам. Отсюда и название – прямоугольник.

Квадрат, тот же параллелограмм , но углы его прямые как у прямоугольника. Из-за этого квадрат в редких случаях называют прямоугольником. Но главным отличительным признаком квадрата помимо уже перечисленных выше, является то, что все четыре его стороны равны.

Трапеция – очень интересная фигура . Это тоже четырехугольник и тоже выпуклый. В этой статье трапеция уже рассматривалась на примере рисунка. Понятно, что она тоже выпуклая. Главным отличием, а соответственно признаком трапеции является то, что ее стороны могут быть абсолютно не равны друг другу по длине, а также ее углы по значению. При этом фигура всегда остается на одной плоскости относительно любой из прямых, которая соединяет любые две ее вершины по образующим фигуру отрезкам.

Ромб – не менее интересная фигура . Отчасти ромбом можно считать квадрат. Признаком ромба является тот факт, что его диагонали не только пересекаются, но и делят углы ромба пополам, а сами диагонали пересекаются под прямым углом, то есть, они перпендикулярны. В случае, если длины сторон ромба равны, то диагонали тоже делятся пополам при пересечении.

Дельтоиды или выпуклые ромбоиды (ромбы) могут иметь разную длину сторон. Но при этом все равно сохраняются как основные свойства и признаки самого ромба, так и признаки и свойства выпуклости. То есть, мы можем наблюдать, что диагонали делят углы пополам и пересекаются под прямым углом.

Сегодняшней задачей было рассмотреть и понять, что такое выпуклые четырехугольники, какие они бывают и их основные признаки и свойства. Внимание! Стоит напомнить еще раз, что сумма углов выпуклого четырехугольника равна 360 градусам. Периметр фигур, например, равен сумме длин всех образующих фигуру отрезков. Формулы расчета периметра и площади четырехугольников будут рассмотрены в следующих статьях.

Сегодня рассмотрим геометрическую фигуру — четырехугольник. Из названия этой фигуры уже становится понятно, что у этой фигуры есть четыре угла. А вот остальные характеристики и свойства этой фигуры мы рассмотрим ниже.

Что такое четырех угольник

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Площадь четырехугольника равна полупроизведению его диагоналей и угла между ними.

Четырехугольник — это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.

Виды четырехугольников

• Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
• Четырехугольник, у которого две противоположные стороны параллельны, а две другие − нет, называется трапецией.
• Четырехугольник, у которого все углы прямые, является прямоугольником.
• Четырехугольник, у которого все стороны равны, является ромбом.
• Четырехугольник, у которого все стороны равны и все углы прямые, называется квадратом.

Четырехугольник может быть:

Самопересекающимся

Невыпуклым

Выпуклым

Самопересекающийся четырехугольник — это четырехугольник, у которого любые из его сторон имеют точку пересечения (на рисунке синим цветом).

Невыпуклый четырехугольник — это четырехугольник, в котором один из внутренних углов более 180 градусов (на рисунке обозначен оранжевым цветом).

Сумма углов любого четырехугольника, который не является самоперсекающимся всегда равна 360 градусов.

Особые виды четырехугольников

Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:

• Параллелограмм
• Прямоугольник
• Квадрат
• Трапеция
• Дельтоид
• Контрпараллелограмм

Четырехугольник и окружность

Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).

Главное свойство описанного четырехугольника:

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.

Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)

Главное свойство вписанного четырехугольника:

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.

Свойства длин сторон четырехугольника

Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.

|a — b| ≤ c + d

|a — c| ≤ b + d

|a — d| ≤ b + c

|b — c| ≤ a + d

|b — d| ≤ a + b

|c — d| ≤ a + b

Важно . Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.

В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны .

Важно . При решении задач в пределах школьной программы можно использовать строгое неравенство (

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Четырехугольники – объяснение и примеры

Различные типы фигур отличаются друг от друга сторонами или углами. Многие фигуры имеют 4 стороны, но разница в углах сторон делает их уникальными. Мы называем эти четырехсторонние фигуры четырехугольниками.

Из этой статьи вы узнаете:

• Что такое четырехугольник.
• Как выглядят различные типы четырехугольников.
• Свойства четырехугольников.

 

Что такое четырехугольник?

Как следует из названия, « Quad » означает «четыре», а « lateral » означает «сторона». Следовательно, четырехугольник — это замкнутый двумерный многоугольник, составленный из 4-х отрезков . Простыми словами, четырехугольник — это фигура с четырьмя сторонами .

Четырёхугольники повсюду! Из книг, диаграммных бумаг, компьютерных ключей, телевизора и мобильных экранов. Список реальных примеров четырехугольников бесконечен.

Типы четырехугольников

В геометрии есть шесть четырехугольников . Некоторые из четырехугольников наверняка вам знакомы, а другие могут быть не так знакомы.

Давайте посмотрим.

• Прямоугольник
• Квадраты
• Trapezium
• Parallelogram
• Rhombus
• Kite

Прямоугольник

Прямоугольник — это квадратный квадратный настрой с 4 правыми уголками (90 °). В прямоугольнике обе пары противоположных сторон параллельны и равны по длине.

Свойства прямоугольников:

• Все углы прямые.
• Диагонали равны.

Прямоугольники очень удобно иметь под рукой. Например, обувные коробки, разделочные доски, листы бумаги, рамки для картин и т. д. имеют прямоугольную форму.

Прямоугольники легко складывать, потому что у них две пары параллельных сторон. Их прямые углы гарантируют, что построенные объекты, такие как дома, офисные здания, школы и т. Д., Стоят прямо и высоко.

Квадрат

Квадрат – это четырехугольник с 4 прямыми углами (90°). В квадрате обе пары противоположных сторон параллельны и равны по длине.

Свойства квадрата:

• Все стороны квадрата равны.
• Все углы прямые по определению.

Квадраты из реальной жизни включают компьютеры, ключи, подставки, пробелы на шахматной доске и т. д.

Параллелограмм

Параллелограмм – это четырехугольник с двумя парами параллельных противоположных и равных сторон. Точно так же противоположные углы в параллелограмме равны по величине.

В параллелограмме PQRS сторона PQ параллельна стороне SR, и сторона PS параллельна стороне QR. Точка M является серединой двух диагоналей параллелограмма.

Следовательно, длина PM = MR, и длина SM = MQ

Ромб

Ромб – это четырехугольник, все четыре стороны которого имеют одинаковую длину. Противоположные стороны ромба равны и параллельны, а противолежащие углы равны.

ABCD является ромбом, в котором AB параллельны и равны DC и AD также параллельны и равны ВС.

Диагонали AC = BD, и M точка пересечения двух диагоналей.

Трапеция

Трапеция или трапеция – это равносторонняя сторона с одной парой противоположных параллельных сторон. Стороны трапеции называются основаниями, а перпендикулярная линия, проведенная из любой вершины трапеции к основанию, называется высотой.

ABCD — трапеция, в которой сторона BD параллельна стороне CA. Перпендикуляр DM есть высота ( h ) трапеции, а BD и CA являются базами.

Воздушный змей

Воздушный змей представляет собой четырехугольник с двумя парами длин сторон, и эти стороны примыкают друг к другу.

Свойства ромба

• Все стороны равны по определению.
• Диагонали делят углы пополам.
• Диагонали воздушного змея делят друг друга пополам под прямым углом.

 

Свойства четырехугольников

К свойствам четырехугольников относятся:

• Каждый четырехугольник имеет 4 стороны, 4 вершины и 4 угла4.
• Сумма всех четырех внутренних углов четырехугольника всегда равна 360 градусам.
• Сумма внутренних углов четырехугольника соответствует формуле многоугольника, т.е.

Сумма внутренних углов = 180° * (n – 2), где n равно количеству сторон многоугольника

• Прямоугольники, ромбы и квадраты — это все виды параллелограммов.
• Квадрат является и ромбом, и прямоугольником.
• Прямоугольник и ромб не являются квадратами.
• Параллелограмм – это трапеция.
• Трапеция не является параллелограммом.
• Воздушный змей не является параллелограммом.

Классификация четырехугольников

Четырехугольники подразделяются на два основных типа:

• Выпуклые четырехугольники: это четырехугольники с внутренними углами менее 180 градусов, и две диагонали находятся внутри четырехугольников. К ним относятся трапеция, параллелограмм, ромб, прямоугольник, квадрат, воздушный змей и т. д.
• Вогнутые четырехугольники: это четырехугольники, у которых хотя бы один внутренний угол больше 180 градусов, и по крайней мере одна из двух диагоналей находится вне четырехугольника. Дротик – вогнутый четырехугольник.

Существует еще один менее распространенный тип четырехугольников, называемый сложными четырехугольниками. Это скрещенные фигуры. Например, скрещенная трапеция, скрещенный прямоугольник, скрещенный квадрат и т. д.

Давайте поработаем над несколькими примерами задач на четырехугольники.

Пример 1

Внутренние углы неправильного четырехугольника равны; x°, 80°, 2x° и 70°. Вычислите значение х.

Решение

По свойству четырехугольников (сумма внутренних углов = 360°) имеем

⇒ x° + 80° + 2x° + 70° =360°

Упростим.

⇒ 3x + 150° = 360°

Вычтите 150° с обеих сторон.

⇒ 3x + 150° – 150° = 360° – 150°

⇒ 3x = 210°

Разделите обе стороны на 3, чтобы получить;

⇒ x = 70°

Следовательно, значение x равно 70°

И углы четырехугольников равны; 70°, 80°, 140° и 70°.

Пример 2

Внутренние углы четырехугольника равны; 82°, (25x – 2)°, (20x – 1)° и (25x + 1)°. Найдите углы четырехугольника.

Решение

Сумма внутренних углов четырехугольника = 360°

⇒ 82° + (25x — 2) ° + (20x — 1) ° + (25x + 1) ° = 360°

⇒ 82 + 25x — 2 + 20x — 1 + 25x + 1 = 360

Упростить.

⇒ 70x + 80 = 360

Вычтите обе стороны на 80, чтобы получить;

⇒ 70x = 280

Разделите обе стороны на 70.

⇒ x = 4

по замене,

⇒ (25x — 2) = 98 °

⇒ (20x — 1) = 79 °

⇒ (25x + 1) = 101°

Следовательно, углы четырехугольника равны; 82°, 98°, 79° и 101°.

 

Q2Определите все четырехугольники, которые имеют a четыре стороны одинаковой длины b четыре прямых угла.

..

Перейти к

• Упражнение 3.1
• Упражнение 3.2
• Упражнение 3.3
• Упражнение 3.4

• Рациональное число
• Линейные уравнения с одной переменной
• Понимание четырехугольников
• Практическая геометрия
• Обработка данных
• Квадраты и квадратные корни
• Кубы и кубические корни
• Сравнение количеств
• Алгебраические выражения и тождества
• Визуализация твердых фигур
• Измерение
• Показатели и силы
• Прямые и обратные пропорции
• Факторизация
• Введение в графики
• Игра с числами

Главная > Решения НЦЭРТ Класс 8 Математика > Глава 3. Понимание четырехугольников > Упражнение 3.4 > Вопрос 11

Вопрос 11 Упражнение 3.4

Q2) Найдите все четырехугольники, которые имеют:

(a) четыре стороны одинаковой длины.

(б) четыре прямых угла.

Ответ:

Решение:

(a) Стороны ромба и квадрата равны.

(b) Квадрат и прямоугольник имеют четыре прямых угла.

Связанные вопросы

**Укажите, верно это или нет:** **Все ромбы — воздушные змеи.**

**Укажите, верно это или нет:** **Все параллелограммы являются трапециями.**

**Укажите, верно это или нет:** **Все прямоугольники являются квадратами.**

**Укажите, верно это или нет:** **Все ромбы являются параллелограммами.**

**Укажите, верно это или нет:** **Все квадраты не являются параллелограммами. **

**Укажите, верно это или нет:** **Все воздушные змеи представляют собой ромбы.**

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 3.1

Упражнение 3.2

Упражнение 3.3

Упражнение 3.4

Главы

Рациональные номера

Линейные уравнения в одной переменной

Понимание четырехугольников

Практическая геометрия

Обработка данных

Squares и Square Roots

Управление данных

и квадратные Roots

KIPES.

Сравнение величин

Алгебраические выражения и тождества

Визуализация объемных фигур

Измерение

Экспоненты и степени

Прямые и обратные пропорции

Факторизация

Введение в графики

Игра с числами

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Свойства четырехугольников — прямоугольник, квадрат, параллелограмм, ромб, трапеция1

представляет собой четырехстороннюю двумерную фигуру, сумма внутренних углов которой равна 360°. Слово «четырехугольник» происходит от двух латинских слов «quadri» и «latus», что означает «четыре» и «сторона» соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников. Итак, каковы свойства четырехугольников? Четырехугольники обладают двумя свойствами:

• Четырехугольник должен быть замкнутой формы с 4 сторонами
• Сумма всех внутренних углов четырехугольника до 360°

В этой статье вы получите представление о 5 типах четырехугольников (прямоугольник, квадрат, параллелограмм , ромб и трапеция) и узнать о свойствах четырехугольников.

Вот пять типов четырехугольников, обсуждаемых в этой статье:

1. Прямоугольник
2. Квадрат
3. Параллелограмм
4. Rombus
5. Trapezium

Вот видео, объясняющее свойства четырехугольника:

Это то, что вы прочитаете в статье:

[Hide]

.

На приведенной ниже схеме изображен четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов равна 360°. Таким образом, ∠A + ∠B + ∠C + ∠D = 360°

Свойства четырехугольников	Rectangle	Square	Parallelogram	Rhombus	Trapezium
All Sides are equal	No	Yes	No	Yes	No
Противоположные стороны равны	Да	Да	Да	Да	Нет
Противоположные стороны параллельны	Yes	Yes	Yes	Yes	Yes
All angles are equal	Yes	Yes	No	No	No
Opposite angles are equal	Yes	Yes	Yes	Yes	No
Sum of two adjacent angles is 180	Yes	Yes	Yes	Yes	No
Bisect each other	Yes	Yes	Yes	Yes	No
Bisect perpendicularly	No	Yes	No	Yes	No

Let’s discuss each из этих 5 четырехугольников в деталях:

Вот вопросы, которые научат вас, как применять свойства всех 5 четырехугольников, которые вы узнаете в этой статье.

Прямоугольник

Прямоугольник – это четырехугольник с четырьмя прямыми углами. Таким образом, все углы прямоугольника равны (360°/4 = 90°). Более того, противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.

Вот три свойства прямоугольника:

• Все углы прямоугольника равны 90°
• Противоположные стороны прямоугольника равны и параллельны
• Диагонали прямоугольника делятся пополам

Формула прямоугольника – площадь и периметр прямоугольника

Если длина прямоугольника равна L, а ширина равна B, то

1. Площадь прямоугольника = длина × ширина или L × B
2. Периметр прямоугольника = 2 × (L + B)

вопросы помогут вам закрепить свойства прямоугольников

Планируете ли вы поступать в лучшие бизнес-школы? Позвольте нам помочь вам пройти первый этап процесса, то есть сдать GMAT. Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2200 отзывами на GMATClub по состоянию на 4 октября 2021 года.

Знаете ли вы, что участники e-GMAT набрали больше 700 баллов, чем когда-либо прежде в истории GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT достиг этого рекордного результата, инвестируя и внедряя инновации с единственной целью — создать платформу, которая позволяет учащимся достигать и показывать свои лучшие результаты.

Квадрат

Квадрат – это четырехугольник с четырьмя равными сторонами и углами. Это также правильный четырехугольник, поскольку обе его стороны и углы равны. Как и у прямоугольника, у квадрата четыре угла по 90° каждый. Его также можно рассматривать как прямоугольник, две соседние стороны которого равны.

Вот три свойства квадрата:

• Все углы квадрата равны 90°
• Все стороны квадрата равны и параллельны друг другу
• Диагонали делят друг друга перпендикулярно

Формула квадрата – площадь и периметр квадрата

Если сторона квадрата равна а, то

1. Площадь квадрата = a × a = a²
2. Периметр квадрата = 2 × (a + a) = 4a

Эти практические вопросы помогут вам закрепить свойства квадратов

Набрав Q50-51 на GMAT, вы получите 700+ баллов за GMAT. Начните свой путь к получению Q50-51 на GMAT с помощью онлайн-курса подготовки e-GMAT на основе искусственного интеллекта. Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant. Посмотрите это видео, чтобы узнать больше:

Параллелограмм

Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, он имеет две пары параллельных сторон. Кроме того, в параллелограмме противоположные углы равны, а их диагонали делят друг друга пополам.

Вот четыре свойства параллелограмма:

• Противоположные углы равны
• Противоположные стороны равны и параллельны
• Диагонали делят друг друга пополам
• Сумма любых двух смежных углов равна 180°

Формулы параллелограмма – площадь и периметр параллелограмма

Если длина параллелограмма ‘l’, ширина ‘b’ и высота ‘h’, тогда:

1. Периметр параллелограмма = 2 × (l + b)
2. Площадь параллелограмма = l × h

Эти практические вопросы помогут вам закрепить свойства параллелограмма

Ромб

четыре стороны равны по длине, а противоположные стороны параллельны друг другу. Однако углы не равны 9.0°. Ромб с прямыми углами станет квадратом. Другое название ромба — «ромб», так как он похож на ромбовидную масть в игральных картах.

Вот четыре свойства ромба:

• Противоположные углы равны
• Все стороны равны и противоположные стороны параллельны друг другу
• Диагонали делят друг друга перпендикулярно
• Сумма любых двух смежных углов равна 180 °

Формулы ромба – площадь и периметр ромба

Если сторона ромба равна а, то периметр ромба = 4а

Если длина двух диагоналей ромба равна d ₁ и d ₂ , то площадь ромба = ½ × d ₁ × d ₂

Эти практические вопросы помогут вам закрепить свойства ромба. Параллельные стороны называются «основаниями», а две другие стороны называются «ногами» или боковыми сторонами.

Трапецией называется четырехугольник, у которого выполняется одно свойство:

• Только одна пара противоположных сторон параллельна друг другу

Формулы трапеции – площадь и периметр трапеции

Если высота трапеции равна ‘ h’  (как показано на диаграмме выше), тогда:

1. Периметр трапеции = сумма длин всех сторон = AB + BC + CD + DA
2. Площадь трапеции = ½ × (сумма длин параллельных сторон) × h = ½ × (AB + CD) × h

Эти практические вопросы помогут вам закрепить свойства трапеции. и периметр различных типов четырехугольников:

Формулы четырехугольника	Прямоугольник	Square	Parallelogram	Rhombus	Trapezium
Area	l × b	a²	l × h	½ × d1 × d2	½ × (сумма параллельных сторон) × высота
Периметр	2 × (L + B)	4A	2 × (L + B)	4A	SUM OF SIHSE SIHSE	4A	SUM OF SIHE0525

Дополнительная литература:

• Формулы окружности – площадь и периметр
• Свойства чисел – четные и нечетные | Прайм | HCF & LCM
• Свойства треугольников – Определение | Типы | Классификация
• Линии и углы – свойства и их применение

Чтобы успешно сдать GMAT, требуется четко определенный учебный план. Сэкономьте 60+ часов на подготовке к GMAT, выполнив следующие три шага:

Четырехсторонний практический вопрос

Давайте попрактикуемся в применении свойств четырехугольников, ответив на следующие примеры вопросов:

GMAT: Практический вопрос четырехугольников 1

Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров. Сколько метров забора он должен купить, чтобы огородить весь сад?

1. 20 метров
2. 25 метров
3. 30 метров
4. 40 метров
5. 50 метров

Решение

Шаг 1: Дано

• У Адама прямоугольный сад.
  • Имеет длину 10 метров и ширину 15 метров.
  • Он хочет построить вокруг него забор.

Шаг 2: Найти

• Длина, необходимая для возведения забора вокруг всего сада.

Этап 3: Подход и разработка

Забор можно построить только вокруг внешних сторон сада.

• Итак, общая длина необходимого забора = сумма длин всех сторон сада.
  • Поскольку сад прямоугольный, сумма длин всех сторон есть не что иное, как периметр сада.
  • Периметр = 2 × (10 + 15) = 50 метров

Отсюда необходимая длина забора 50 метров.

Следовательно, вариант Е является правильным ответом.

GMAT Quadrilaterials Practice Question 2

Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стен составляет 1,5 доллара за квадратный метр. Если длина стены 25 метров, а ширина 18 метров, то какова общая стоимость покраски стены?

1. $ 300
2. $ 350
3. $ 450
4. $ 600
5. $ 675

Решение

Шаг 1: дано

• Стев хочет нарисовать одну стену из его комнаты.
  • Длина стены 25 метров, ширина 18 метров.
  • Стоимость покраски стены $1,5 за квадратный метр.

Шаг 2: Найти

• Общая стоимость покраски стены.

Этап 3: Подход и разработка

• Стена окрашена по всей площади.
  • Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, то мы получим общую стоимость.
  • Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
  • Общая стоимость покраски стены = 450 × 1,5 долл. США = 675 долл. США

Следовательно, правильный ответ — вариант E.

Мы надеемся, что к настоящему моменту вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти понятия для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT. Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить бесплатный доступ, зарегистрировавшись здесь.

Вот еще несколько статей по математике:

1. Повышение точности математических вопросов о полигонах
2. Вопросы по геометрии – самые распространенные ошибки | GMAT Quant Prep

Посмотрите этот вебинар без геометрии GMAT, на котором мы обсуждаем, как решать 700-уровневые вопросы достаточности данных и проблемные вопросы в четырехугольниках GMAT:

Если вы планируете сдавать GMAT, мы можем дать вы получаете доступ к качественному онлайн-контенту для подготовки. Мы являемся самой популярной компанией по подготовке к GMAT на gmatclub с более чем 2200 отзывами по состоянию на 4 октября 2021 года.

 

Напишите нам по адресу [email protected] в случае возникновения вопросов.

Часто задаваемые вопросы

Какие существуют типы четырехугольников?

Существует 5 типов четырехугольников – прямоугольник, квадрат, параллелограмм, трапеция или трапеция и ромб.

Где я могу найти несколько практических вопросов по четырехугольникам?

В этой статье вы можете найти несколько практических вопросов по четырехугольникам.

Чему равна сумма внутренних углов четырехугольника?

Сумма внутренних углов четырехугольника равна 360°.

Что такое четырехугольник? [Определение, факты и примеры]

Значение четырехугольника

Четырехугольник — это многоугольник, имеющий четыре стороны, четыре угла и четыре вершины. Слово «четырехугольник» происходит от латинских слов «quadri», что означает «четыре», и «latus», что означает «сторона».

Изображение выше является примером четырехугольника.

Части четырехугольника

1. ∠A, ∠B, ∠C и ∠D — четыре угла четырехугольника ABCD
2. AB, BC, CD и DA — четыре стороны четырехугольника ABCD.
3. A, B, C и D — четыре вершины четырехугольника ABCD.
4. AC и BD — две диагонали четырехугольника ABCD.

Непримеры четырехугольников

Фигуры, не имеющие четырех сторон или четырех углов, изогнутые стороны или незамкнутые формы, не являются примерами четырехугольников.

Приведенные выше изображения не являются примерами четырехугольников.

Примеры четырехугольников из реальной жизни

Существует много примеров четырехугольников из реальной жизни: карты, шахматные доски, дорожные знаки и т. д.

Свойства четырехугольников

Некоторые свойства являются общими для всех четырехугольников. Вот эти свойства:

• У них четыре вершины.
• У них четыре стороны.
• Сумма всех внутренних углов равна 360°.
• У них две диагонали.
• Четырехугольник может быть правильным и неправильным. Правильный четырехугольник должен иметь 4 равные стороны и 4 равных угла, а его диагонали должны пересекаться пополам. Квадрат — единственный четырехугольник, удовлетворяющий всем этим условиям.

Типы Четырехугольников

Четырехугольники можно разделить на параллелограммы, квадраты, прямоугольники и ромбы. Квадрат, прямоугольник и ромб также являются параллелограммами.

Вот список типов четырехугольников с их названиями, изображениями и свойствами: 

Вогнутые и выпуклые четырехугольники

Вогнутые четырехугольники: В вогнутых четырехугольниках один внутренний угол больше 180°.

Четырехугольник называется вогнутым четырехугольником, если хотя бы одна диагональ, т. е. отрезок, соединяющий вершины, не является частью одной и той же области четырехугольника.

Выпуклые четырехугольники:  В выпуклых четырехугольниках каждый внутренний угол меньше 180°. Четырехугольник выпуклый, если отрезок, соединяющий любую из его двух вершин, лежит в одной области.

Периметр четырехугольника

Периметр четырехугольника — это длина его границы. Это означает, что периметр четырехугольника равен сумме всех сторон. Если ABCD — четырехугольник, то его периметр будет равен: AB + BC + CD + DA

Периметр четырехугольника ABCD = AB + BC + CD + DA

Ниже приведена формула для периметра некоторых обычных четырехугольников:

Четырехугольник Название	Perimeter
Rectangle	2 (length + width)
Square	4 x Side
Rhombus	4 x Side
Parallelogram	2 x sum of смежные стороны
Воздушный змей	2 x сумма смежных сторон

Площадь четырехугольника

Площадь четырехугольника – это область, ограниченная всеми его сторонами. Формулы для определения площади четырехугольников различных типов показаны ниже:

Решенные примеры

Пример 1. Найдите недостающий угол в данном четырехугольнике.

Решение:

Мы знаем, что сумма всех углов четырехугольника равна 360°.

Отсюда можно записать так:

х + 77° + 101° + 67 = 360°

х + 245° = 360°

х = 360° – 245°

Следовательно, х = 115 °

Пример 2: Каков будет периметр четырехугольника со сторонами 6 см, 8 см, 10 см и 12 см?

Решение:

Даны стороны четырехугольника равны 6 см, 8 см, 10 см и 12 см.

Следовательно, периметр четырехугольника равен:

P = 6 см + 8 см + 10 см + 12 см = 36 см

Пример 3: Если площадь ромба 60 квадратных единиц, а его высота 6 единиц, чему будет равна его база?

Решение:

В приведенном выше примере дано, что –

Площадь ромба = 60 квадратных единиц

Высота ромба = 6 единиц

Площадь ромба = основание x высота

60 = основание x 6

Основание = 60/6 = 10 единиц представляет собой замкнутый многоугольник с четырьмя сторонами, четырьмя углами и четырьмя вертикалями. В SplashLearn ваш ребенок может узнать о четырехугольниках в веселой и игровой форме. Этот простой и уникальный метод обучения быстро привлекает внимание юных учеников. Поэтому родители и учителя могут без особых усилий обучать своих детей четырехугольникам.

Если вы являетесь родителем ребенка, который учится в младших классах и ищете надежные образовательные онлайн-платформы, вы можете зарегистрировать их в SplashLearn. Позвольте вашему ребенку бесстрашно заниматься математикой и зарегистрируйтесь в SplashLearn бесплатно.

Практические задачи

Прямоугольник

Параллелограмм

Квадрат

Ничего из перечисленного выше .

3

2

4

1

Правильный ответ: 4
Четырехугольник — это четырехугольник.

120°

360°

520°

Ничего из перечисленного

Правильный ответ: 360° . В SplashLearn ваш ребенок может узнать о четырехугольниках в веселой и игровой форме. Этот простой и уникальный метод обучения быстро привлекает внимание юных учеников. Поэтому родители и учителя могут без особых усилий обучать своих детей четырехугольникам.

Часто задаваемые вопросы

Сколько вершин у четырехугольника?

Четырехугольник имеет четыре вершины.

Можем ли мы сказать, что параллелограмм является четырехугольником?

Да, параллелограмм — это замкнутая фигура с четырьмя углами. Следовательно, его можно назвать четырехугольником.

Как называется четырехугольник, все углы которого равны 90°, а противоположные стороны равны?

Прямоугольник

Могут ли все углы четырехугольника быть острыми?

Нет, все углы четырехугольника не могут быть острыми, потому что тогда сумма углов четырехугольника будет меньше 360°.

Прямоугольники, ромбы и квадраты — Уроки Wyzant

По мере того, как мы продвигались по разделу четырехугольников
, мы становились все более и более конкретными в отношении типа фигур
, с которыми имеем дело. Изначально мы рассматривали всевозможные полигоны, а потом
мы сузили его до четырехугольников, называемых четырехугольниками. Оттуда мы
узнали об особом типе четырехугольника, противоположные стороны которого параллельны,
называемого параллелограммом
. В этом разделе мы станем еще более конкретными, изучая
свойства различных параллелограммов. Давайте узнаем, что делает прямоугольники, ромбы
и квадраты особенными фигурами.

Прямоугольники

Определение: Прямоугольник – это четырехугольник с четырьмя прямыми углами.

Обратите внимание, что мы используем «четырехугольник» в нашем определении прямоугольников. Мы могли бы также сказать
, что прямоугольник является параллелограммом с четырьмя прямыми углами, поскольку
и четырехугольник с четырьмя прямыми углами также являются параллелограммом (поскольку их
противоположные стороны были бы параллельны).

У прямоугольников есть несколько свойств, которые помогают отличить их от других параллелограммов.
Изучая эти свойства, мы сможем различать различные типы
параллелограммов и классифицировать их более конкретно. Имейте в виду, что все
фигур в этом разделе имеют общие свойства параллелограммов. То есть у них всех
есть

(1) противоположные параллельные стороны,

(2) противоположные конгруэнтные углы,

(3) противоположные конгруэнтные стороны,

(4) последовательных углов, являющихся дополнительными, и

(5) диагоналей, которые делят друг друга пополам.

Теперь давайте посмотрим на свойства, которые делают прямоугольники особым типом параллелограмма.

(1) Все четыре угла прямоугольника прямые.

(2) Диагонали прямоугольника равны.

Ромбы

Определение: Ромб – это четырехугольник с четырьмя конгруэнтными сторонами.

Подобно определению прямоугольника, мы могли бы использовать слово «параллелограмм»
вместо «четырехугольник» в нашем определении ромба. Таким образом, ромбы обладают всеми
свойствами параллелограмма (указанными выше) наряду с некоторыми другими. Давайте
посмотрим на эти свойства.

(1) Последовательные стороны ромба равны.

(2) Диагонали ромба делят пары противоположных углов пополам.

(3) Диагонали ромба перпендикулярны.

Квадраты

Определение: Квадрат — это параллелограмм с четырьмя конгруэнтными сторонами и четырьмя
конгруэнтными углами.

Обратите внимание, что определение квадрата представляет собой комбинацию определений прямоугольника
и ромба. Следовательно, квадрат является и прямоугольником, и ромбом,
а это означает, что свойства параллелограмма, прямоугольника и ромба все
относятся к квадратам. Поскольку квадраты сочетают в себе все эти различные свойства,
это очень специфический тип четырехугольника.

Посмотрите на иерархию четырехугольников ниже. На этом рисунке показано развитие наших знаний о многоугольниках, начиная с четырехугольников и заканчивая квадратами.

Обратите внимание на две стрелки, указывающие на квадрат. Это потому, что квадрат
обладает всеми свойствами прямоугольника и ромба.

Теперь, когда мы знаем о свойствах прямоугольников, ромбов и квадратов, давайте поработаем над несколькими упражнениями, которые помогут оценить наше понимание этого материала.

Упражнение 1

Определите каждый параллелограмм как прямоугольник, ромб или квадрат.

Ответ:

Во-первых, давайте взглянем на параллелограмм A. На рисунке показано, что он имеет четыре конгруэнтных
сторон и что его диагонали пересекаются перпендикулярно. Поскольку его стороны равны,
мы знаем, что параллелограмм не является прямоугольником. Тот факт, что
диагоналей параллелограмма А пересекаются перпендикулярно, не помогает нам, потому что и ромбы, и
квадраты имеют эту характеристику. Однако угол при вершине параллелограмма А не является прямым углом. Следовательно, мы знаем, что это не квадрат. Параллелограмм
А является ромбом.

В параллелограмме B мы видим, что есть четыре прямых угла и что пары из
противоположных сторон равны. Однако последовательные стороны не равны, поэтому мы
можем исключить ромбы и квадраты из наших вариантов. Таким образом, параллелограмм B является прямоугольником
.

Давайте теперь посмотрим на параллелограмм С. Заметим, что у него есть пара прямых углов
и четыре равные стороны. Наша склонность наводит нас на мысль, что этот параллелограмм
является квадратом, но на всякий случай удостоверимся. Мы знаем, что данные нам два прямых угла
имеют сумму 180° . Поскольку внутренние углы четырехстороннего
составляют 360 ° , мы знаем, что остальные два угла должны иметь сумму
180 ° (из-за 360-180 = 180 . Противолежащие углы параллелограмма
конгруэнтны, а это значит, что друг другу недостающие углы должны иметь меру
из 90° (поскольку 180÷2=90 ). Это говорит нам о том, что их 9.1281 на самом деле четыре прямых угла в параллелограмме C, поэтому мы знаем, что это квадрат (а
— ромб).

Упражнение 2

Найдите значение x по данному прямоугольнику ABCD ниже.

Ответ:

Мы знаем, что ABCD — это прямоугольник, поэтому давайте воспользуемся некоторыми свойствами прямоугольника
, чтобы понять, что такое 9. 1346 x пикселей. Создается впечатление, что в этом упражнении
основное внимание уделяется диагоналям фигуры. Из вышеизложенного мы знаем, что диагонали
прямоугольника равны, поэтому приравняем отрезки AC и BD
:

Получаем х=12 .

Упражнение 3

Ответ:

Давайте изучим информацию, полученную в ходе упражнения, чтобы
мог извлечь из нее больше информации. Мы знаем, что ЭКИН является параллелограммом,
и что ?1??2 . Так как ЭКИН является параллелограммом, мы знаем, что
его противоположные стороны параллельны. Следовательно, сегменты ЕК и
В параллельны.

Далее, мы можем использовать теорему о альтернативных внутренних углах, чтобы утверждать, что ?1??4
и ?2??3 . Напомним, что параллельные внутренние углы равны 91 281 тогда и только тогда, когда секущая пересекает пару параллельных прямых. В данном случае
наша пара параллельных прямых это ЕК и ИН , а наша поперечная
это отрезок НК .

По транзитивности можно сказать, что ?1??3 и ?2??4 . Давайте
посмотрим на нашу
цепочку сравнений, чтобы убедиться, что предыдущие утверждения
верны.

Диагональ делит наш параллелограмм на два треугольника. На самом деле, поскольку два угла
каждого треугольника равны, мы можем сказать, что ?ЭКН и ?ИНК
равнобедренные треугольники. Обратное утверждение теоремы о равнобедренном треугольнике утверждает,
что стороны, противоположные конгруэнтным углам равнобедренных треугольников, равны,
поэтому мы знаем, что отрезок EK конгруэнтен отрезку EN , и что 3 отрезка EN IK и IN конгруэнтны.

Теперь можно сказать, что сегментов EK и IN конгруэнтны,
как EN и IK , потому что противоположные стороны параллелограмма конгруэнтны . По транзитивности мы знаем, что EN?EK?IN?IK . Давайте посмотрим на
на нашей новой иллюстрации.

Таким образом, параллелограмм EKIN является ромбом, так как у него четыре конгруэнтные
стороны. Наши
геометрическое доказательство в два столбца для этого упражнения показано ниже.

Упражнение 4

Каким должно быть значение y , чтобы ромб PQRS был квадратом?

Ответ:

Прежде чем мы сможем вычислить наши y , мы должны определить, каково значение
x . В конечном итоге нам нужен ромб PQRS должен быть квадратом,
означает, что PQRS должен иметь четыре прямых угла.

Давайте начнем с выяснения, что такое x . Это относительно просто, потому что
мы можем просто установить сегмент PQ равным PS :

Теперь, когда мы знаем, что x , мы можем подставить его в меру угла, данного
мкс. Но сначала нам нужно выяснить, какова общая мера ?QSR . Мы знаем
, что мы хотим, чтобы ?PSR было 90° . Также мы знаем, что диагонали квадрата делят пополам
пару противоположных углов. Следовательно, ?PSR должны быть разделены пополам отрезком QS , разделив
угол вверх на два конгруэнтных угла по 45° (потому что 90÷2=45 ). Теперь мы можем установить
?QSR равным 45° . Получаем:

Теперь заменим 7 на x :

Итак, значение y должно быть 4 , чтобы ромб PQRS также был квадратом.

Какие бывают четырехугольники?

Четырехугольники являются многоугольниками. Они являются частью плоскости, окруженной четырьмя сторонами (quad означает четыре, а lateral означает сторону). Все четырехугольники имеют ровно четыре стороны и четыре угла. Их можно разделить на определенные группы в зависимости от длины их сторон или углов. 9{\circ}$.

Диагонали — это линии, соединяющие противоположные углы.

Деление четырехугольников по диагоналям перпендикулярности и параллельности сторон:

Разносторонний четырехугольник

Первая группа четырехугольников — это разносторонний четырехугольник . Разносторонний четырехугольник — это четырехугольник, не обладающий какими-либо особыми свойствами. Стороны и углы имеют разную длину и размеры.

Трапеции

Четырехугольники, имеющие одну пару параллельных сторон, называются трапециями . Параллельные стороны называются основаниями трапеции, а непараллельные называются катетами .

Равнобедренная трапеция

Трапеции, катеты которых имеют одинаковую длину, называются равнобедренными трапециями .

Диагонали равнобедренных трапеций равны.

Высота или высота трапеции — это длина линии, перпендикулярной основанию и проходящей через противоположную вершину. {\circ} $. 9{\circ}$.

 

Параллелограмм

Параллелограмм — это четырехугольник, противоположные стороны которого равны и параллельны.

Высота или  высота параллелограмма в метке $h$ — это отрезок, соединяющий вершину с противоположной стороной и перпендикулярный этой стороне.

Помимо того, что параллелограммы являются четырехугольниками, существуют определенные формы, которые являются параллелограммами так же, как и четырехугольниками. Это квадрат, прямоугольник и ромб. 9{\circ}.$$

Отсюда следует $\beta = \delta$ и $\alpha = \gamma$.

 

Теорема

Следующие утверждения эквивалентны друг другу:

1) Четырехугольник $ABCD$ является параллелограммом

2) Существуют две противоположные стороны четырехугольника $ABCD$, которые равны и параллельны

3) Каждые две противоположные стороны четырехугольника $ABCD$ равны

4) Диагонали четырехугольника $ABCD$ делят друг друга пополам

5) Обе пары противоположных углов четырехугольника $ABCD$ равны

Каждое из приведенных выше утверждений может быть альтернативным определением параллелограмма. Остальные утверждения нам нужно доказать.

Доказательство.

$1) \Rightarrow 2)$

Пусть $ABCD$ — параллелограмм. Затем $\overline{AB} \| \overline{CD}$ и $\overline{AD} \| \overline{BC}$.

 

 

Так как прямая $AC$ является ходом параллельных прямых $AB$ и $CD$ , то $\angle{ACD} =\angle{CAB}$. Прямая $AC$ также является обходом параллельных прямых $BC$ и $AD$, то есть $\angle{ACB}=\angle{DAC}$.

$\overline{AC}$ также является общей стороной треугольников $ABC$ и $CDA$. По теореме А-С-А о конгруэнтности треугольников треугольники $ABC$ и $CDA$ конгруэнтны. Отсюда следует, что $|AB| = |CD]$ и $|AD| = |BC|$.

$2) \Rightarrow 3)$

В четырехугольнике  $ABCD$ пусть будет $AB \| CD$ и $|AB| = |CD|$.

Так как $AC$ является ходом параллельных прямых $AB$ и $CD$, то $\angle{ACD} =\angle{CAB}$. Сторона $\overline{AC}$ является общей стороной треугольников $ABC$ и $CDB$. По теореме S-A-S о конгруэнтности треугольников треугольники $ABC$ и $CDB$ конгруэнтны. Отсюда следует, что $|BC| = |CD|.$

 

$3) \Rightarrow 4)$

В четырехугольнике $ABCD$ пусть $|AB|=|CD|$ и $|BC| = |CD|$, а точка $S$ является пересечением диагоналей $\overline{AC}$ и $\overline{BD}$.

 

Сначала рассмотрим треугольники $ABC$ и $CDB$. По теореме С-С-С о конгруэнтности треугольников треугольники $ABC$ и $CDB$ конгруэнтны. Отсюда следует, что $\angle{ACB} = \angle {CAD}$.

Углы $ASD$ и $BSC$ являются вертикальными углами. Если теперь рассмотреть треугольники $ASD$ и $BSD$, то следует, что $\angle{ADS} = \angle{CBS}$. Поскольку $|BC|= |AD|$, треугольники $ASD$ и $BSC$ конгруэнтны по теореме A-S-A о конгруэнтности треугольников. Отсюда следует, что $|AS| = |SC|$ и $|BS| = |SD|$, что означает, что точка $S$ является средней точкой $\overline{AC}$ и $\overline{BD}$.

$4) \Rightarrow 5)$

В четырехугольнике $ABCD$ точка $S$ будет серединой диагоналей $\overline{AC}$ и $\overline{AD}$: $|AS|=|CS |$ и $|BS|=|DS|$.

Рассмотрим треугольники $BCS$ и $ADS$. По теореме S-A-S они конгруэнтны ($|CS| = |AS|$ – $\angle{BSC}=\angle{ASB}$ (вертикальные углы) – $|BS|=|DS|$). Отсюда следует, что $\angle{BCS}=\angle{DAS}$ и $\angle{CBS}=\angle{ADS}$.

Треугольники $ABS$ и $CDS$ также конгруэнтны по теореме S-A-S ($|AS|=|CS|$ – $\angle{ASB}=\angle{CSD}$ (вертикальные углы)  – $|BS|= |ДС|$). Отсюда следует, что $\angle{BAS}=\angle{DCS}$ и $\angle{ABS}=\angle{CDS}$. 9{\circ}$, что также является противоречием.

Отсюда следует, что $AB \| AC$.

Аналогично доказывается, что $BC \| AD$.

Ромб

Ромб  это параллелограмм, у которого есть хотя бы одна пара смежных сторон одинаковой длины.

Противоположные углы равновелики: $\alpha = \gamma$, $\beta = \delta$ и что смежные углы являются дополнительными.

Диагонали ромба равны и перпендикулярны.

 

Касательный четырехугольник

Воздушный змей  – это четырехугольник, характеризующий две пары сторон равной длины, смежных друг с другом. Диагонали воздушного змея перпендикулярны, и по крайней мере одна диагональ является линией симметрии. Воздушный змей также является касательным четырехугольником.

Прямоугольник

Прямоугольник  – это параллелограмм, у которого хотя бы один внутренний угол прямой.

Диагонали прямоугольников равны. 92$

 

Площадь четырехугольника

Площадь квадрата равна квадрату длины его стороны.

Далее идет площадь прямоугольника. Площадь прямоугольника равна произведению длин смежных сторон.

Площадь ромба равна произведению длины его стороны на высоту.

Это верно, потому что из рисунка: Если мы перенесём высоту $\overline{BE}$ в точку $A$ и продолжим сторону $ED$ над вершиной $D$, мы получим треугольник $E’DA$, который совпадает с треугольником $ECB$. Если «перевести» треугольник $ECB$ на треугольник $E’DA$, то получится прямоугольник с одной стороной $a$ и другой $h$.

То же, что и для ромба, работает на параллелограмме , площадь параллелограмма является произведением его одной стороны и высоты на этой стороне.

Площадь трапеции равна половине произведения суммы ее оснований и высоты.

Эта формула является результатом деления трапеции на два треугольника $AED$ и $BCF$ и прямоугольник $EFCD$.

Теперь мы можем записать нашу площадь в виде суммы меньших площадей: $ A_{(ABCD)} = A_{(AED)} + A_{(FBC)} + A_{(EFCD)}$.

Мы знаем, что $ A_{(EFCD)} =h \cdot c$.
Теперь нам нужно найти $A_{(AED)}$ и $A_{(FBC)}$. Если мы перенесем сторону $b$ рядом с $AED$, то получим треугольник $AHD$.

Высота треугольника $AHD$ равна высоте трапеции $ABCD$.

А сторона, на которой задана эта высота, равна $a – c$. Это приводит к выводу, что:

$\ A_ {(AHD)} = h \cdot \frac{a – c}{2}$.

Это означает, что:

$$A_ {(ABCD)} = A_ {(AHD)} + A_ {(HBCD)} =$$

$$=\frac{h \cdot (a – c)}{2} + c\cdot h= \frac{a \cdot h – h\cdot c + 2h \cdot c}{2} = \frac {ч \cdot a + h \cdot c}{2} =$$

$$=\frac{h \cdot (a + c)}{2}$$.

 

Что такое четырехугольник?

Четырехугольник — это многоугольник с четырьмя сторонами.

Четырёхугольники какой формы?

Четырехугольники: квадрат, прямоугольник, трапеция, ромб.

Как определить четырехугольник?

Четырехугольник представляет собой плоскую фигуру с четырьмя соединяющимися сторонами. Квадрат означает четыре. Боковая значит боковая. Все линии должны быть соединены. Это также плоская форма, 2-мерная. Одни четырехугольники образуют идентифицируемые формы, другие нет.

Какие 7 четырехугольников?

Четырехугольников семь. Это: квадрат, прямоугольник, ромб, трапеция, равнобедренная трапеция, параллелограмм, касательный четырехугольник (также известный как воздушный змей из-за его формы воздушного змея).

Какие есть 4 типа четырехугольников?

Четырехугольники можно разделить на четыре типа. Это параллелограмм, ромб, квадрат и прямоугольник. Кроме того, ромбы, квадраты, прямоугольники — все это параллелограммы.