Постройте график функции y cos x 2. Графики тригонометрических функций кратных углов
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом.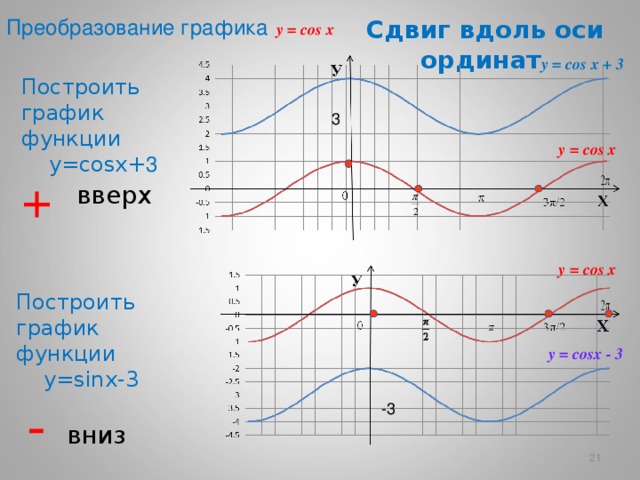
Всего в теме 25 презентаций
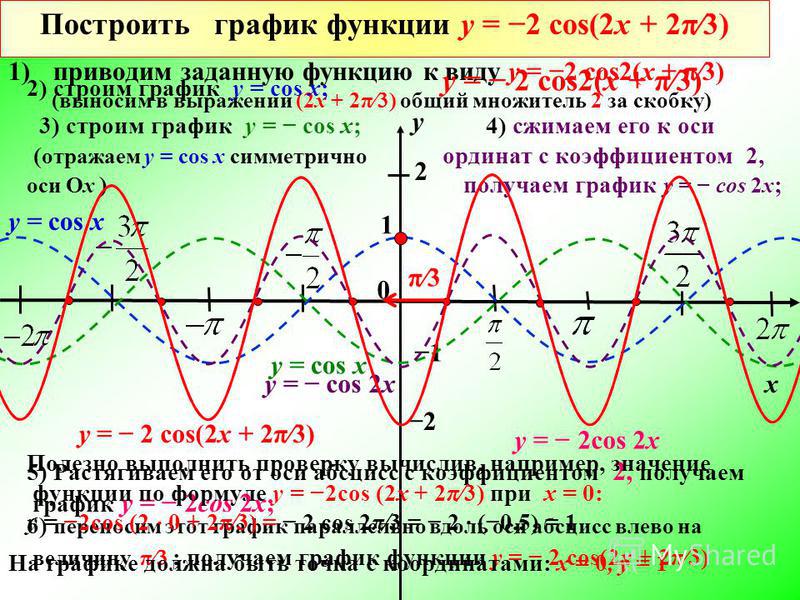
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция
 Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з).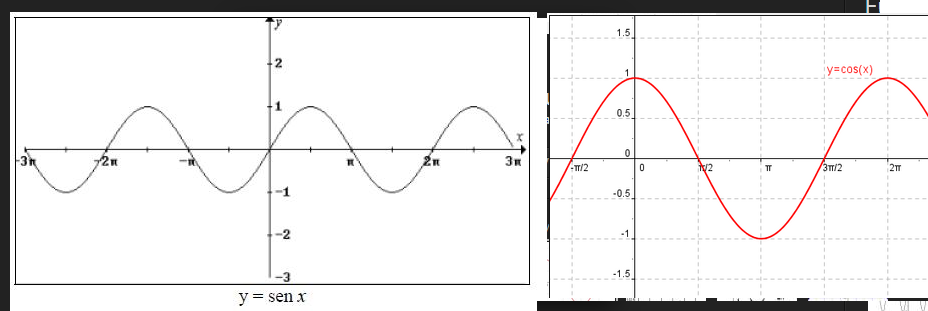 у= ctg x / 3
у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная.
 Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция. - Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
Модуль в тригонометрических уравнениях: найти и обезвредить
Достаточно часто в задачах повышенной сложности встречаются тригонометрические уравнения, содержащие модуль. Большинство из них требуют эвристического подхода к решению, который совсем не знаком большинству школьников.
Предлагаемые ниже задачи призваны познакомить вас с наиболее характерными приемами решения тригонометрических уравнений содержащих модуль.
Задача 1. Найти разность (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 1 + 2sin x · |cos x| = 0.
Решение.
Раскроем модуль:
1) Если cos x ≥ 0, то исходное уравнение примет вид 1 + 2sin x · cos x = 0.
Воспользуемся формулой синуса двойного угла, получим:
1 + sin 2x = 0; sin 2x = -1;
2x = -π/2 + 2πn, n € Z;
x = -π/4 + πn, n € Z. Так как cos x ≥ 0, то x = -π/4 + 2πk, k € Z.
2) Если cos x < 0, то заданное уравнение имеет вид 1 – 2sin x · cos x = 0. По формуле синуса двойного угла, имеем:
1 – sin 2x = 0; sin 2x = 1;
2x = π/2 + 2πn, n € Z;
x = π/4 + πn, n € Z. Так как cos x < 0, то x = 5π/4 + 2πk, k € Z.
3) Наибольший отрицательный корень уравнения: -π/4; наименьший положительный корень уравнения: 5π/4.
Искомая разность: 5π/4 – (-π/4) = 6π/4 = 3π/2 = 3 · 180°/2 = 270°.
Ответ: 270°.
Задача 2. Найти (в градусах) наименьший положительный корень уравнения |tg x| + 1/cos x = tg x.
Решение.
Раскроем модуль:
1) Если tg x ≥ 0, тогда
tg x + 1/cos x = tg x;
1/cos x = 0.
В полученном уравнении корней нет.
2) Если tg x < 0, тогда
-tg x + 1/cos x = tg x;
1/cos x – 2tg x = 0;
1/cos x – 2sin x / cos x = 0;
(1 – 2sin x) / cos x = 0;
1 – 2sin x = 0 и cos x ≠ 0.
С помощью рисунка 1 и условия tg x < 0 находим, что x = 5π/6 + 2πn, где n € Z.
3) Наименьший положительный корень уравнения 5π/6. Переведем это значение в градусы:
5π/6 = 5 · 180°/6 = 5 · 30° = 150°.
Ответ: 150°.
Задача 3. Найти количество различных корней уравнения sin |2x| = cos 2x на промежутке [-π/2; π/2].
Решение.
Запишем уравнение в виде sin|2x| – cos 2x = 0 и рассмотрим функцию y = sin |2x| – cos 2x. Так как функция является четной, то найдем ее нули при x ≥ 0.
sin 2x – cos 2x = 0; разделим обе части уравнения на cos 2x ≠ 0, получим:
tg 2x – 1 = 0;
tg 2x = 1;
2x = π/4 + πn, n € Z;
x = π/8 + πn/2, n € Z.
Воспользовавшись четностью функции, получим, что корнями исходного уравнения являются числа вида
± (π/8 + πn/2), где n € Z.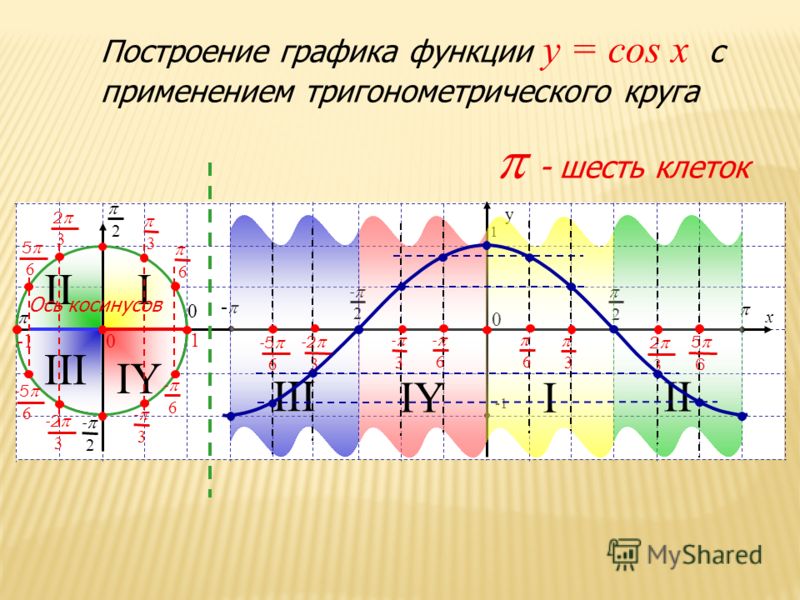
Промежутку [-π/2; π/2] принадлежат числа: -π/8; π/8.
Итак, два корня уравнения принадлежат заданному промежутку.
Ответ: 2.
Данное уравнения можно было бы решить и раскрытием модуля.
Задача 4. Найти количество корней уравнения sin x – (|2cos x – 1|)/(2cos x – 1) · sin2 x = sin2 x на промежутке [-π; 2π].
Решение.
1) Рассмотрим случай, когда 2cos x – 1 > 0, т.е. cos x > 1/2, тогда уравнение принимает вид:
sin x – sin2 x = sin2 x;
sin x – 2sin2 x = 0;
sin x(1 – 2sin x) = 0;
sin x = 0 или 1 – 2sin x = 0;
sin x = 0 или sin x = 1/2.
Используя рисунок 2 и условие cos x > 1/2, найдем корни уравнения:
x = π/6 + 2πn или x = 2πn, n € Z.
2) Рассмотрим случай, когда 2cos x – 1 < 0, т.е. cos x < 1/2, тогда исходное уравнение принимает вид:
sin x + sin2 x = sin2 x;
sin x = 0;
x = 2πn, n € Z.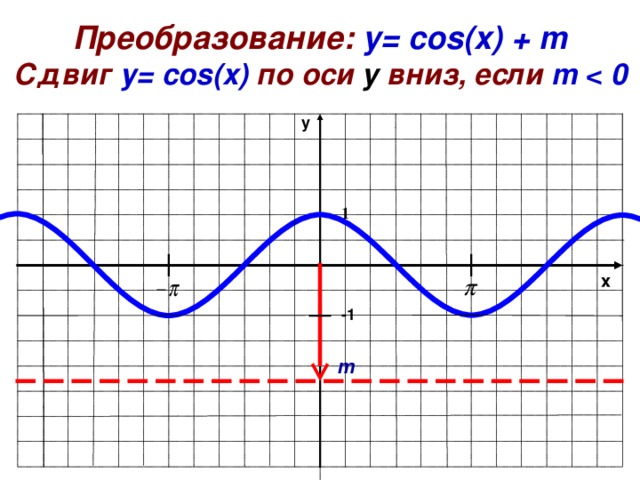
Используя рисунок 2 и условие cos x < 1/2, находим, что x = π + 2πn, где n € Z.
Объединим два случая, получим:
x = π/6 + 2πn или x = πn.
3) Промежутку [-π; 2π] принадлежат корни: π/6; -π; 0; π; 2π.
Таким образом, заданному промежутку принадлежат пять корней уравнения.
Ответ: 5.
Задача 5. Найти количество корней уравнения (x – 0,7)2 |sin x| + sin x = 0 на промежутке [-π; 2π].
Решение.
1) Если sin x ≥ 0, то исходное уравнение принимает вид (x – 0,7)2 sin x + sin x = 0. После вынесения общего множителя sin x за скобки, получим:
sin x((x – 0,7)2 + 1) = 0; так как (x – 0,7)2 + 1 > 0 при всех действительных x, то sinx = 0, т.е. x = πn, n € Z.
2) Если sin x < 0, то -(x – 0,7)2 sin x + sin x = 0;
sin x((x – 0,7)2 – 1) = 0;
sinx = 0 или (x – 0,7)2 + 1 = 0. Так как sin x < 0, то (x – 0,7)2 = 1. Извлекаем квадратный корень из левой и правой частей последнего уравнения, получим:
Извлекаем квадратный корень из левой и правой частей последнего уравнения, получим:
x – 0,7 = 1 или x – 0,7 = -1, а значит x = 1,7 или x = -0,3.
С учетом условия sinx < 0 получим, что sin (-0,3) ≈ sin (-17,1°) < 0 и sin (1,7) ≈ sin (96,9°) > 0, значит только число -0,3 является корнем исходного уравнения.
3) Промежутку [-π; 2π] принадлежат числа: -π; 0; π; 2π; -0,3.
Таким образом, уравнение имеет пять корней на заданном промежутке.
Ответ: 5.
Заняться подготовкой к урокам или экзаменам можно при помощи различных образовательных ресурсов, которые есть в сети. В настоящее время любому человеку просто необходимо использовать новые информационные технологии, ведь правильное, а главное уместное их применение будет способствовать повышению мотивации в изучении предмета, повысит интерес и поможет лучше усвоить необходимый материал. Но не стоит забывать о том, что компьютер не учит думать, полученную информацию обязательно необходимо обрабатывать, понимать и запоминать. Поэтому вы можете обратиться за помощью к нашим онлайн репетиторам, которые помогут вам разобраться с решением интересующих вас задач.
Поэтому вы можете обратиться за помощью к нашим онлайн репетиторам, которые помогут вам разобраться с решением интересующих вас задач.
Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
ДЗ по Алгебре!
Решено
Является ли выражение ( |x| + 1) / (x^2 — 5) все еще рациональным, если в нем присутствует модуль — нерациональное выражение.
ПОЖАЛУЙСТА, НЕ ТРАТЬТЕ ВРЕМЯ НА ЭТО ЗАДАНИЕ. У МЕНЯ ВСЕ-ТАКИ ПОЛУЧИЛОСЬ ЕГО РЕШИТЬ. СПАСИБО
Помогите решить данные интегралы пожалуйста
Решено
Помогите пожалуйста решить данные интегралы, очень срочно нужная помощь пожалуйста
Пользуйтесь нашим приложением
Косинус это проекция на какую ось
Косинус это проекция на какую ось
Чтобы объяснить понятия синуса и косинуса рассмотрим единичную окружность, т.е. окружность, у которой радиус равен 1 (рис. 1).
Единичный радиус-вектор имеет угол с осью Ox. Тогда в этих обозначениях проекция радиус-вектора на ось Ox равна , а проекция на ось Oy — . Например, если , то
Почему и равны этому значению? Это легко объяснить на следующем рисунке (рис. 2)
Проекции синуса и косинуса вместе с радиусом-вектором образуют прямоугольный треугольник. Вспоминая теорему Пифагора, мы знаем, что квадрат гипотенузы равен сумме квадратов катетов.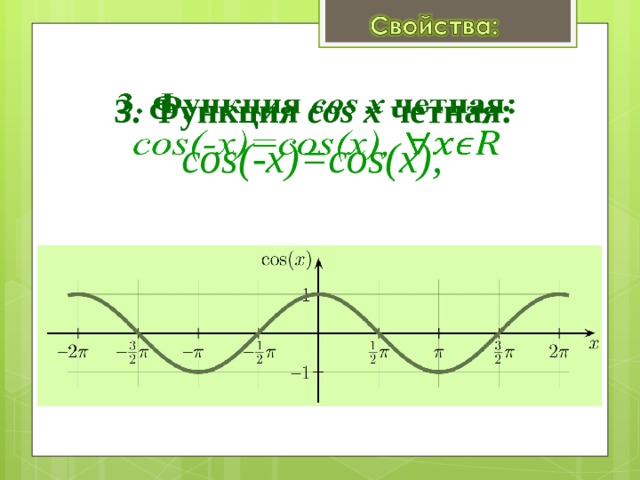 Тогда можно записать
Тогда можно записать
и учитывая, что и равны, то это равенство можно записать и в таких вариантах
Другой случай. Пусть теперь угол , тогда (рис. 3) получается, что
Рассмотрим, как ведут себя функции синуса и косинуса при изменении угла .
Из рис. 4 видно, что если угол меняется от 0 до , то синус остается всегда положительным, а косинус меняет свой знак, как только угол становится больше .
Если же угол меняется от до , то косинус остается положительным, а синус меняет свой знак, когда .
Последнее, что следует указать про функции синуса и косинуса, это то, что они повторяются через каждые радиан или . То есть, если угол взять в , то это будет то же самое, что и и . В этом смысл их периодичности, т.е. повторяемости. Математически это обозначается так
Памятка по проекциям вектора на ось
Здравствуй, дорогой друг! Вот и наступил 11-й класс. Уже совсем скоро начнутся экзамены, а такие слова, как « сила », « проекция на ось », « векторная сумма сил », ставят тебя в тупик… Ну ничего, сейчас я постараюсь помочь тебе разобраться со всеми этими страшными терминами. Погнали!
Погнали!
Итак, первое, с чего нужно начать, это понять, что же от нас хотят. Ведь распространённой ошибкой, которую допускают многие одиннадцатиклассники, является невнимательное чтение вопроса задачи. «ПТУ или СПБ» … нет, что-то не! «Модуль или проекция». Да, да, да… невнимательно прочтённое задание, а вслед за ним, возможно, упущенный «минус» отделяют потенциального инженера-конструктора от заветного бюджетного места в топовом вузе.
Если от нас требуется найти «модуль силы» (в особо изысканных задачах «модуль проекции силы»), то всё не так страшно. Но если же на твою нелёгкую долю, друг, выпала участь отыскать «проекцию» (или «проекцию модуля»), то будь внимательней самого внимательного внимателя.
В первом случае мы видим, что вектор силы F параллелен оси x . Более того, направление вектора совпадает с направлением оси. Тогда проекция вектора равна самому вектору. Во втором случае мы видим, что вектор силы параллелен оси, но его направление уже противоположно. Тогда можно сказать, что проекция также равна самому вектору, но взятому со знаком «минус».
Тогда можно сказать, что проекция также равна самому вектору, но взятому со знаком «минус».
И самый трудный случай, когда вектор даёт проекции сразу на обе оси:
Тут необходимо учитывать угол отклонения вектора от оси. В данном примере взят угол α между самим вектором и осью x . В таком случае проекция вектора на ось x будет равна произведению самого вектора на косинус угла отклонения:
а соответственно, проекция на ось y равна произведению самого вектора на синус угла отклонения:
Также следует внимательно следить за тем, какой угол тебе дан, ведь если взять противоположный угол, то и тригонометрические функции в проекциях поменяются на противоположные.
Надеюсь, прочитав эту маленькую статью, ты стал еще на шаг ближе к своей будущей профессии. Ну а если ты хочешь не просто шагать, а бежать навстречу знаниям, то ждём тебя на занятиях в наших центрах!
Функция y = cos x, её свойства и график
Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
В результате получаем график y=cosx для любого \(x\in\mathbb\).
Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».
п.2. Свойства функции
y=cosx1. Область определения \(x\in\mathbb\) — множество действительных чисел.
2. Функция ограничена сверху и снизу $$ -1\leq cosx\leq 1 $$ Область значений \(y\in[-1;1]\)
3. Функция чётная $$ cos(-x)=cosx $$
4. Функция периодическая с периодом 2π $$ cos(x+2\pi k)=cosx $$
5. Максимальные значения \(y_=1\) достигаются в точках $$ x=2\pi k $$ Минимальные значения \(y_=-1\) достигаются в точках $$ x=\pi+2\pi k $$ Нули функции \(y_=cosx_0=0\) достигаются в точках \(x=\frac\pi2 +\pi k\)
6. 2-\frac\) – парабола ветками вверх, с осью симметрии \(x_0=0\) (ось OY) и вершиной \(\left(0; -\frac\right)\) (см. §29 справочника для 8 класса)
2-\frac\) – парабола ветками вверх, с осью симметрии \(x_0=0\) (ось OY) и вершиной \(\left(0; -\frac\right)\) (см. §29 справочника для 8 класса)
Два корня: \(x_=\pm\frac\pi2\)
Пример 3. Постройте в одной системе координат графики функций $$ y=cosx,\ \ y=-cosx,\ \ y=2cosx,\ \ y=cosx-2 $$
\(y=-cosx\) – отражение исходной функции \(y=cosx\) относительно оси OX. Область значений \(y\in[-1;1]\).
\(y=2cosx\) – исходная функция растягивается в 2 раза по оси OY. Область значений \(y\in[-2;2]\).
\(y=cosx-2\) — исходная функция опускается вниз на 2. Область значений \(y\in[-3;-1]\).
Пример 4. Постройте в одной системе координат графики функций $$ y=cosx,\ \ y=cos2x,\ \ y=cos\frac$$
Амплитуда колебаний у всех трёх функций одинакова, область значений \(y\in[-1;1]\).
Множитель под косинусом изменяет период колебаний.
\(y=cosx\) – главная арка косинуса соответствует отрезку \(-\frac\pi2\leq x\leq\frac\pi2\)
\(y=cos2x\) — период уменьшается в 2 раза, главная арка укладывается в отрезок \(-\frac\pi4\leq x\leq\frac\pi4\). 2}ρ=(x1−x2)2+(y1−y2)2.
2}ρ=(x1−x2)2+(y1−y2)2.
Напишите программу определяющую евклидово расстояние между двумя точками, координаты которых заданы.
Формат входных данных
На вход программе подается четыре вещественных числа, каждое на отдельной строке – x_{1}, \, y_{1}, \, x_{2}, \, y_{2}x1,y1,x2,y2.
Формат выходных данных
Программа должна вывести одно число – евклидово расстояние.
import math x1, x2, y1, y2 = float(input()), float(input()), float(input()), float(input()) print(math.hypot(x1 - y1, x2 - y2))
Площадь и длина
Напишите программу определяющую площадь круга и длину окружности по заданному радиусу RR.
Формат входных данных
На вход программе подается одно вещественное число RR.Формат выходных данных
Программа должна вывести два числа – площадь круга и длину окружности радиуса RR.2 xsinx+cosx+tan2x по заданному числу градусов xx.
Формат входных данных
На вход программе подается одно вещественное число xx измеряемое в градусах.Формат выходных данных
Программа должна вывести одно число – значение тригонометрического выражения.Примечание 1. Тригонометрические функции принимают аргумент в радианах. Чтобы перевести градусы в радианы, воспользуйтесь формулой r = {{x \cdot \pi } \over 180}r=180x⋅π
Примечание 2. Модуль
mathсодержит встроенную функциюradians(), которая переводит угол из градусов в угол в радианах.
from math import * # Поскольку тригонометрические функции работают с радианами, нужно градусы перевести в радианы x = radians(float(input())) print(sin(x) + cos(x) + tan(x)**2)
Пол и потолок
Напишите программу, вычисляющее значение \lceil x\rceil + \lfloor x\rfloor⌈x⌉ +⌊x⌋ по заданному вещественному числу xx.
2 + bx + c = 0.ax2+bx+c=0.Формат входных данных
На вход программе подается три вещественных числа a \neq 0, \, b, \, ca=0,b,c, каждое на отдельной строке.Формат выходных данных
Программа должна вывести вещественные корни уравнения если они существуют или текст «Нет корней» в противном случае.Примечание. Если уравнение имеет два корня, то следует вывести их в порядке возрастания.
from math import *
a = float(input())
b = float(input())
c = float(input())
d = b**2-4*a*c # Ищем дискриминант
if d < 0:
print('Нет корней')
elif d == 0: # если дискриминант ==0 (имеет один корень)
print(-b / (2*a))
elif d > 0: # Если дискриминант >0 то два корня
x1 = (-b - d ** 0.5) / (2*a)
x2 = (-b + d ** 0.5) / (2*a)
print(min(x1, x2))
print(max(x1, x2))Правильный многоугольник
Правильный многоугольник — выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами.
2}{4\tg \left(\dfrac{\pi}{n}\right)}S=4tg(nπ)n⋅a2Даны два числа: натуральное число nn и вещественное число aa. Напишите программу, которая находит площадь указанного правильного многоугольника.
Формат входных данных
На вход программе подается два числа nn и aa, каждое на отдельной строке.Формат выходных данных
Программа должна вывести вещественное число – площадь многоугольника.
from math import * n, a = float(input()), float(input()) ans = (n * pow(a, 2)) / (4 * tan(pi / n)) print(ans)
Разложение Маклорена для cos(x)
Предыдущее: Разложение Маклорена для sin(x)
Далее: Список разложений Маклорена
Пример
Найдите разложение в ряд Маклорена для cos( x ) при
9 x
9 0, и определить его радиус сходимости. Комплексное решение
Шаг 1. Найдите серию Maclaurin
потому что
(
Икс
)
знак равно
г
г
Икс
грех
(
Икс
)
знак равно
г
г
Икс
∑
к
знак равно
0
∞
(
−
1
)
к
(
2
к
+
1
)
!
Икс
2
к
+
1
знак равно
г
г
Икс
(
Икс
−
Икс
3
3
!
+
Икс
5
5
!
−
…
)
знак равно
1
−
Икс
2
2
!
+
Икс
4
4
!
−
…
знак равно
∑
к
знак равно
0
∞
(
−
1
)
к
Икс
2
к
(
2
к
)
!
{\ displaystyle {\ begin {align} \ cos (x) & = {\ frac {d} {dx}} \ sin (x) \\ & = {\ frac {d} {dx}} \ sum _ {k = 0} ^ {\ infty } {\ frac {(-1) ^ {k}} {(2k + 1)!}} x ^ {2k + 1} \\ & = {\ frac {d} {dx} {\ Big (} x — {\ frac {x ^ {3}} {3!}} + {\ frac {x ^ {5}} {5!}} — \ ldots {\ Big )} \\& = 1 — {\ frac {x ^ {2}} {2!}} + {\ frac {x ^ {4}} {4!}} — \ ldots \\& = \ sum _ {k = 0} ^ {\ infty} {\ frac {(-1) ^ {k} x ^ {2k}} {(2k)!}} \ end {выровнено}}}
Шаг 2: Найдите радиус сходимости
Тест соотношения дает нам:
лим
к
→
∞
|
(
−
1
)
к
+
1
(
2
(
к
+
1
)
)
!
Икс
2
(
к
+
1
)
/
(
−
1
)
к
(
2
к
)
!
Икс
2
к
|
знак равно
лим
к
→
∞
(
2
к
)
!
(
2
к
+
2
)
!
|
Икс
|
2
знак равно
лим
к
→
∞
1
(
2
к
+
1
)
(
2
к
+
2
)
|
Икс
|
2
знак равно
0
{\ displaystyle {\ begin {align} \ lim _ {k \ rightarrow \ infty} {\ Big |} {\ frac {(-1) ^ {k + 1}} {(2 (k + 1))!} } x ^ {2 (k + 1)} {\ Bigg /} {\ frac {(-1) ^ {k}} {(2k)!}} x ^ {2k} {\ Big |} & = \ lim _{k\стрелка вправо \infty }{\frac {(2k)!}{(2k+2)!}}|x|^{2}\\&=\lim _{k\стрелка вправо \infty }{\frac {1}{(2k+1)(2k+2)}}|x|^{2}\\&=0\end{выровнено}}}
Поскольку этот предел равен нулю для всех действительных значений x , радиус сходимости разложения равен множеству всех действительных чисел.
Объяснение каждого шага
Шаг 1
Чтобы найти расширение ряда, мы могли бы использовать тот же процесс, что и для sin( x ) и e x 10 90. Но есть способ проще. Мы можем дифференцировать наше известное разложение для функции синуса.
Если вы хотел бы увидеть вывод расширения ряда Маклорена для косинуса, в следующем видео показан этот вывод.
Косинус Ряд Тейлора в 0 Вывод разложения косинуса в ряд Маклорена. Это видео можно найти на веб-сайте Академии Кана, и оно защищено авторскими правами Creative Commons (CC BY-NC-SA 3.0).
Шаг 2
Этот шаг был ничем иным, как подстановкой нашей формулы в формулу для теста соотношения.
Возможные проблемы
Когда мы можем различать степенные ряды?
Для целей этого модуля мы всегда будем предполагать, что можем. Однако существует теорема о дифференциации и интегрировании степенных рядов, о которой вы не должны знать, которая говорит нам, что степенной ряд можно дифференцировать только в том случае, если его радиус сходимости больше нуля.
Скоро появится страница в этом модуле по этой теореме. А пока эта страница в Википедии может помочь.
Приходилось ли нам проверять конвергенцию?
Краткий ответ: нет. Упомянутая выше теорема говорит нам, что, поскольку
- мы получили ряд для cos(x) из ряда для sin(x) дифференцированием, а
- мы уже знаем радиус сходимости sin(x),
радиус сходимости cos(x) будет таким же, как sin(x). Однако мы не ввели эту теорему в этом модуле. Вы можете спросить своего инструктора, должны ли вы знать эту теорему.
Резюме
Разложение Маклорена для cos(x) Расширение ряда Маклорена для cos( x ) определяется выражением потому что
(
Икс
)
знак равно
∑
к
знак равно
0
∞
(
−
1
)
к
Икс
2
к
(
2
к
)
!
знак равно
1
−
Икс
2
2
!
+
Икс
4
4
!
−
Икс
6
6
!
…
{\ displaystyle \ cos (x) = \ sum _ {k = 0} ^ {\ infty} {\ frac {(-1) ^ {k} x ^ {2k}} {(2k)!}} = 1- {\ frac {x ^ {2}} {2!}} + {\ frac {x ^ {4}} {4!}} — {\ frac {x ^ {6}} {6!}} \ ldots}
Эта формула действительна для всех действительных значений x .
Предыдущий: Расширение Маклорена для sin(x)
Далее: Список расширений Маклорена
Основные операции — Документация по SymPy 1.11
Переключить боковую панель оглавления
Здесь мы обсудим некоторые из самых основных операций, необходимых для выражения
манипуляции в SymPy. Некоторые более сложные операции будут обсуждаться позже.
в разделе расширенных операций с выражениями.
>>> из импорта sympy *
>>> x, y, z = символы ("x y z")
Замена
Одна из самых распространенных вещей, которые вы, возможно, захотите сделать с математическим
выражение является заменой. Подстановка заменяет все экземпляры чего-либо
в выражении с чем-то другим. Это делается с использованием метода subs .
Например
>>> выражение = cos(x) + 1
>>> expr.subs(x, y)
потому что (у) + 1
Замена обычно производится по одной из двух причин:
Вычисление выражения в точке. x}}\). Строить
это, мы могли бы начать с
x}}\). Строить
это, мы могли бы начать с x**y и замените y на x**y . Мы
тогда получится x**(x**y) . Если мы заменим на в этом новом выражении
с x**x мы получили бы x**(x**(x**x)) желаемое выражение.
>>> выражение = х**у
>>> выражение
х**у
>>> expr = expr.subs(y, x**y)
>>> выражение
х**(х**у)
>>> expr = expr.subs(y, x**x)
>>> выражение
х**(х**(х**х))
Во-вторых, если мы хотим выполнить очень контролируемое упрощение или
возможно, упрощение, которое SymPy иначе не может сделать. За
например, у нас есть \(\sin(2x) + \cos(2x)\), и мы хотим заменить
\(\sin(2x)\) с \(2\sin(x)\cos(x)\). Как мы узнаем позже, функция expand_trig делает это. Однако эта функция также будет расширяться
\(\cos(2x)\), что может нам и не понадобиться. Хотя есть способы выполнить такие
точное упрощение, и мы изучим некоторые из них в
расширенный раздел обработки выражений,
простой способ — просто заменить \(\sin(2x)\) на \(2\sin(x)\cos(x)\).
>>> выражение = sin(2*x) + cos(2*x)
>>> expand_trig(выражение)
2*sin(x)*cos(x) + 2*cos(x)**2 - 1
>>> expr.subs(sin(2*x), 2*sin(x)*cos(x))
2*sin(x)*cos(x) + cos(2*x)
В отношении сабвуферов следует отметить два важных момента. Во-первых, он возвращает
новое выражение. Объекты SymPy неизменяемы. Это означает, что сабвуферов делает
не изменять его на месте. Например
>>> выражение = cos(x)
>>> expr.subs(x, 0)
1
>>> выражение
потому что (х)
>>> х
Икс
Здесь мы видим, что выполнение expr.subs(x, 0) оставляет expr без изменений.
На самом деле, поскольку выражения SymPy неизменяемы, никакая функция их не изменит.
на месте. Все функции будут возвращать новые выражения.
Чтобы выполнить несколько замен одновременно, передайте список из (старых, новых) пар
до подписки .
>>> выражение = x**3 + 4*x*y - z
>>> expr. subs([(x, 2), (y, 4), (z, 0)])
40
92 - 2х + 3\).
subs([(x, 2), (y, 4), (z, 0)])
40
92 - 2х + 3\).
>>> выражение = х**4 - 4*х**3 + 4*х**2 - 2*х + 3
>>> замены = [(x**i, y**i) для i в диапазоне (5), если i % 2 == 0]
>>> expr.subs(замены)
-4*х**3 - 2*х + у**4 + 4*у**2 + 3
Преобразование строк в выражения SymPy
Функция sympify (это sympify , не путать с упростить ) можно использовать для преобразования строк в выражения SymPy.
Например,
>>> str_expr = "x**2 + 3*x - 1/2"
>>> expr = sympify(str_expr)
>>> выражение
х**2 + 3*х - 1/2
>>> expr.subs(x, 2)
19/2
Предупреждение
sympify использует eval . Не используйте его для непроверенного ввода.
эвалф Чтобы преобразовать числовое выражение в число с плавающей запятой, используйте евальф .
>>> выражение = квадрат (8)
>>> выр.eval()
2,82842712474619
SymPy может вычислять выражения с плавающей запятой с произвольной точностью. По
по умолчанию используются 15 цифр точности, но вы можете передать любое число в качестве
аргумент для
По
по умолчанию используются 15 цифр точности, но вы можете передать любое число в качестве
аргумент для evalf . Давайте вычислим первые 100 цифр \(\pi\).
>>> pi.eval(100)
3.14155897
46264338327950288419716939058209749445
816406286208998628034825342117068
Чтобы численно оценить выражение с символом в точке, мы могли бы использовать сабы за которыми следуют evalf , но это более эффективно и численно
stable для передачи замены на evalf с использованием флага subs , который
берет словарь символов: точка пар.
>>> выражение = cos(2*x)
>>> выражение.evalf(subs={x: 2.4})
0,08749898343
Иногда ошибки округления меньше требуемой точности,
остаются после вычисления выражения. Такие номера могут быть удалены в
усмотрению пользователя, установив пометить флагом True.
>>> один = cos(1)**2 + sin(1)**2
>>> (один - 1). evalf()
-0.e-124
>>> (один - 1).evalf(chop=True)
0
evalf()
-0.e-124
>>> (один - 1).evalf(chop=True)
0
ламбдифай сабвуферы и evalf хороши, если вы хотите сделать простую оценку, но если
вы собираетесь оценивать выражение во многих точках, есть более эффективные
способы. Например, если вы хотите оценить выражение в тысяче
точки, использование SymPy будет намного медленнее, чем должно быть, особенно если вы
заботиться только о точности станка. Вместо этого вы должны использовать такие библиотеки, как
NumPy и SciPy.
Самый простой способ преобразовать выражение SymPy в выражение, которое можно
численно оценивается использование функции lambdify . ламбдифай действует
как функция lambda , за исключением того, что она преобразует имена SymPy в имена
данная числовая библиотека, обычно NumPy. Например
>>> импортировать numpy
>>> a = numpy.arange(10)
>>> выражение = грех(х)
>>> f = lambdify(x, expr, "numpy")
>>> ф(а)
[0,0,84147098 0,743 0,14112001 -0,7568025 -0,958
-0,27 0,6569866 0,985 0,41211849]
Предупреждение
lambdify использует eval . Не используйте его для непроверенного ввода.
Не используйте его для непроверенного ввода.
Вы можете использовать другие библиотеки, кроме NumPy. Например, для использования стандарта
математический модуль библиотеки, используйте "math" .
>>> f = lambdify(x, выражение, "математика")
>>> f(0,1)
0,0998334166468
Чтобы использовать lambdify с числовыми библиотеками, о которых он не знает, передайте
словарь из sympy_name:numerical_function пар. Например
>>> определение mysin(x):
... """
... Мой синус. Обратите внимание, что это верно только для малых x.
... """
... вернуть х
>>> f = lambdify(x, expr, {"sin":mysin})
>>> f(0,1)
0,1
Символическая математика в Python — конспекты лекций Scipy
Автор : Фабиан Педрегоса
Цели
- Вычислять выражения с произвольной точностью.
- Выполнить алгебраические операции с символьными выражениями.
- Выполнение основных вычислительных задач (пределы, дифференцирование и
- интеграции) с символическими выражениями.

- Решите полиномиальные и трансцендентные уравнения.
- Решите несколько дифференциальных уравнений.
Что такое SymPy? SymPy — это библиотека Python для символьной математики. Это
стремится стать альтернативой таким системам, как Mathematica или Maple, сохраняя при этом
код максимально простой и удобный
расширяемый. SymPy полностью написан на Python и не требует никаких
внешние библиотеки.
Документацию Sympy и пакеты для установки можно найти на
http://www.sympy.org/
Содержание глав
- Первые шаги с SymPy
- Использование SymPy в качестве калькулятора
- Символы
- Алгебраические операции
- Развернуть
- Упростить
- Исчисление
- Пределы
- Дифференциация
- Расширение серии
- Интеграция
- Решение уравнения
- Линейная алгебра
- Матрицы
- Дифференциальные уравнения
3.
 2.1.1. Использование SymPy в качестве калькулятора
2.1.1. Использование SymPy в качестве калькулятора SymPy определяет три числовых типа: Действительное , Рациональное и Целое .
Класс Rational представляет рациональное число как пару двоек
Целые числа: числитель и знаменатель, поэтому Rational(1, 2) представляет 1/2, Rational(5, 2) 5/2 и т. д.:
>>> import sympy as sym
>>> a = sym.Rational(1, 2)
>>> а
1/2
>>> а*2
1
SymPy использует mpmath в фоновом режиме, что позволяет
выполнять вычисления с использованием арифметики произвольной точности. Что
Кстати, некоторые специальные константы, такие как , , (Бесконечность),
рассматриваются как
символы и могут быть вычислены с произвольной точностью:
>>> сим.пи**2
пи**2
>>> sym.pi.evalf()
3.141558979
>>> (sym.pi + sym.exp(1)).evalf()
5,85987448204884
как вы видите, evalf оценивает выражение как число с плавающей запятой.
Существует также класс, представляющий математическую бесконечность, называемый оо :
>>> сим. оо > 99999
Истинный
>>> сим.оо + 1
оо
оо > 99999
Истинный
>>> сим.оо + 1
оо
Упражнения
- Расчет со 100 десятичными знаками.
- Считать в рациональной арифметике.
3.2.1.2. Символы
В отличие от других систем компьютерной алгебры, в SymPy вы должны объявить
символьные переменные явно:
>>> x = sym.Symbol('x')
>>> y = sym.Symbol('y')
Затем вы можете манипулировать ими:
>>> x + y + x - y
2*х
>>> (х + у) ** 2
(х + у)**2
Символами теперь можно управлять с помощью некоторых операторов Python: + , -`,
``* , ** (арифметика), &, | , ~ , >>, << (логическое значение).
Печать
Sympy позволяет управлять отображением вывода. Отсюда мы используем
следующие настройки для печати:
>>> sym.init_printing(use_unicode=False, wrap_line=True)
SymPy может выполнять мощные алгебраические операции. Что ж
взгляните на некоторые из наиболее часто используемых: расширить и упростить.
3.2.2.1. Expand
Используйте это, чтобы расширить алгебраическое выражение. Он попытается
степени и умножения:
>>> sym.expand((x + y) ** 3)
3 2 2 3
х + 3*х *у + 3*х*у + у
>>> 3 * х * у ** 2 + 3 * у * х ** 2 + х ** 3 + у ** 3
3 2 2 3
х + 3*х *у + 3*х*у + у
Дополнительные параметры могут быть заданы в виде ключевых слов:
>>> sym.expand(x + y, complex=True)
re(x) + re(y) + I*im(x) + I*im(y)
>>> sym.I * sym.im(x) + sym.I * sym.im(y) + sym.re(x) + sym.re(y)
re(x) + re(y) + I*im(x) + I*im(y)
>>> sym.expand(sym.cos(x + y), trig=True)
-sin(x)*sin(y) + cos(x)*cos(y)
>>> sym.cos(x) * sym.cos(y) - sym.sin(x) * sym.sin(y)
-sin(x)*sin(y) + cos(x)*cos(y)
3.2.2.2. Simplify
Используйте упрощение, если хотите преобразовать выражение в
более простая форма:
>>> sym.simplify((x + x * y) / x)
у + 1
Упрощение — несколько расплывчатый термин, а точнее
существуют альтернативы упрощению: powsimp (упрощение
степени), trigsimp (для тригонометрических выражений) , logcombine , радсимп вместе.
Упражнения
- Рассчитать расширенную форму .
- Упростите тригонометрическое выражение
3.2.3.1. Лимиты
Лимиты просты в использовании в SymPy, они следуют синтаксису limit(функция,
переменная, точка) , поэтому для вычисления предела as
, вы бы выдали limit(f, x, 0) :
>>> sym.limit(sym.sin(x) / x, x, 0)
1
вы также можете вычислить предел на бесконечности:
>>> sym.limit(x, x, sym.oo)
оо
>>> sym.limit(1 / x, x, sym.oo)
0
>>> sym.limit(x ** x, x, 0)
1
3.2.3.2. Дифференциация
Вы можете дифференцировать любое выражение SymPy, используя diff(func,
вар) . Примеры:
>>> sym.diff(sym.sin(x), x)
потому что (х)
>>> sym.diff(sym.sin(2 * x), x)
2*кос(2*х)
>>> sym.diff(sym.tan(x), x)
2
загар (х) + 1
Проверить правильность можно:
>>> sym.limit((sym.tan(x + y) - sym.tan(x)) / y, y, 0)
2
загар (х) + 1
Высшие производные можно рассчитать с помощью diff(func, var, n) method:
>>> sym. diff(sym.sin(2 * x), x, 1)
2*кос(2*х)
>>> sym.diff(sym.sin(2 * x), x, 2)
-4*грех(2*х)
>>> sym.diff(sym.sin(2 * x), x, 3)
-8*cos(2*x)
diff(sym.sin(2 * x), x, 1)
2*кос(2*х)
>>> sym.diff(sym.sin(2 * x), x, 2)
-4*грех(2*х)
>>> sym.diff(sym.sin(2 * x), x, 3)
-8*cos(2*x)
3.2.3.3. Расширение серии
SymPy также знает, как вычислить ряд Тейлора выражения в
точка. Используйте серию (expr, var) :
>>> sym.series (sym.cos (x), x)
2 4
х х / 6\
1 - -- + -- + О\х/
2 24
>>> sym.series(1/sym.cos(x), x)
2 4
х 5*х / 6\
1 + -- + ---- + О\х /
2 24
Упражнения
- Расчет
- Вычислите производную для .
3.2.3.4. Интеграция
SymPy поддерживает неопределенную и определенную интеграцию трансцендентных
элементарные и специальные функции с помощью средства интегрировать() , которое использует
мощный расширенный алгоритм Риша-Нормана и некоторые эвристики и шаблоны
соответствие. Вы можете интегрировать элементарные функции:
>>> sym.integrate(6 * x ** 5, x)
6
Икс
>>> sym.integrate(sym. sin(x), x)
-кос(х)
>>> sym.integrate(sym.log(x), x)
х * журнал (х) - х
>>> sym.integrate(2 * x + sym.sinh(x), x)
2
х + кош(х)
sin(x), x)
-кос(х)
>>> sym.integrate(sym.log(x), x)
х * журнал (х) - х
>>> sym.integrate(2 * x + sym.sinh(x), x)
2
х + кош(х)
Также легко обрабатываются специальные функции:
>>> sym.integrate(sym.exp(-x ** 2) * sym.erf(x), x)
____ 2
\/ пи *erf (x)
--------------
4
Можно вычислить определенный интеграл:
>>> sym.integrate(x**3, (x, -1, 1))
0
>>> sym.integrate(sym.sin(x), (x, 0, sym.pi / 2))
1
>>> sym.integrate(sym.cos(x), (x, -sym.pi/2, sym.pi/2))
2
Также поддерживаются неправильные интегралы:
>>> sym.integrate(sym.exp(-x), (x, 0, sym.oo))
1
>>> sym.integrate(sym.exp(-x ** 2), (x, -sym.oo, sym.oo))
____
\/ Пи
SymPy может решать алгебраические уравнения, в одном и нескольких
переменные, использующие solveset() :
>>> sym.solveset(x ** 4 - 1, x)
{-1, 1, -я, я}
Как видите, в качестве первого аргумента используется выражение, которое
должно быть равно 0. Он также имеет (ограниченную) поддержку трансцендентных
уравнения:
>>> sym. solveset(sym.exp(x) + 1, x)
{I*(2*n*pi + pi) | n в целых числах}
solveset(sym.exp(x) + 1, x)
{I*(2*n*pi + pi) | n в целых числах}
Системы линейных уравнений
Sympy может решить большую часть
полиномиальные уравнения, а также способен решать несколько
уравнения относительно нескольких переменных, дающие кортеж в качестве второго
аргумент. Для этого вы используете команду solve() :
>>> решение = sym.solve((x + 5 * y - 2, -3 * x + 6 * y - 15), (x, y) )
>>> решение[x], решение[y]
(-3, 1)
Другая альтернатива в случае полиномиальных уравнений: фактор . factor возвращает полином, разложенный на неприводимые
условия, и способен вычислить факторизацию по различным
домены:
>>> f = х ** 4 - 3 * х ** 2 + 1
>>> сим.фактор(f)
/ 2 \ / 2 \
\х - х - 1/*\х + х - 1/
>>> sym.factor(f, модуль=5)
2 2
(х - 2) * (х + 2)
SymPy также может решать логические уравнения, т. е. определять,
определенное логическое выражение является выполнимым или нет. Для этого мы используем
выполнимая функция:
Для этого мы используем
выполнимая функция:
>>> sym.satisfiable(x & y)
{х: Истина, у: Истина}
Это говорит нам о том, что (x & y) является истинным, если x и y оба являются истинными.
Если выражение не может быть истинным, то есть никакие значения его аргументов не могут
выражение True, оно вернет False:
>>> sym.satisfiable(x & ~x)
ЛОЖЬ
Упражнения
- Решить систему уравнений ,
- Существуют ли логические значения
x , y , которые делают (~x | y) & (~y | x) истинными?
3.2.5.1. Матрицы
Матрицы создаются как экземпляры класса Matrix:
>>> sym.Matrix([[1, 0], [0, 1]])
[1 0]
[ ]
[0 1]
в отличие от массива NumPy, в него также можно поместить символы:
>>> x, y = sym.symbols('x, y')
>>> A = sym.Matrix([[1, x], [y, 1]])
>>> А
[1 х]
[ ]
[г 1]
>>> А**2
[х*у + 1 2*х]
[ ]
[ 2*у х*у + 1]
3.
 2.5.2. Дифференциальные уравнения
2.5.2. Дифференциальные уравнения SymPy способен решать (некоторые) обыкновенные дифференциальные уравнения.
Для решения дифференциальных уравнений используйте dsolve. Сначала создайте
неопределенная функция путем передачи cls=Function в функцию символов:
>>> f, g = sym.symbols('f g', cls=sym.Function)
Функции f и g теперь не определены. Мы можем вызвать f(x), и это будет представлять
неизвестная функция:
>>> f(x)
е(х)
>>> f(x).diff(x, x) + f(x)
2
г
f(x) + ---(f(x))
2
дх
>>> sym.dsolve(f(x).diff(x, x) + f(x), f(x))
f(x) = C1*sin(x) + C2*cos(x)
Аргументы ключевого слова могут быть переданы этой функции, чтобы помочь, если
найти наилучшую возможную систему разрешения. Например, если вы знаете
что это разделимые уравнения, вы можете использовать ключевое слово подсказка='разделяемый' чтобы заставить dsolve разрешить его как разделимое уравнение:
>>> sym.dsolve(sym.sin(x) * sym. cos(f(x)) + sym.cos(x) * sym.sin(f( x)) * f(x).diff(x), f(x), hint='разделяемый')
/С1\/С1\
[f(x) = - acos|------| + 2*pi, f(x) = acos|------|]
\cos(x)/ \cos(x)/
cos(f(x)) + sym.cos(x) * sym.sin(f( x)) * f(x).diff(x), f(x), hint='разделяемый')
/С1\/С1\
[f(x) = - acos|------| + 2*pi, f(x) = acos|------|]
\cos(x)/ \cos(x)/
Упражнения
- Решение дифференциального уравнения Бернулли
- Решите то же уравнение, используя
hint='Бернулли' . Что вы наблюдаете?
Стандартный кубический фут
Выполняет вычисления самосогласованного поля (Хартри-Фока и теории функционала плотности). Это отправные точки для большинства вычислений, поэтому этот код вызывается в большинстве случаев.
Общая информация о волновой функции
ОСНОВА
Первичный базисный набор
CHOLEKY_TOLERANCE
Допуск для разложения Холецкого тензора ЭРИ
Тип : двойной
По умолчанию : 1e-4
DF_BASIS_SCF
Вспомогательный базисный набор для расчетов плотностной подгонки SCF. По умолчанию используется JKFIT.
По умолчанию используется JKFIT.
DF_SCF_GUESS
Выполнить расчет плотности SCF для сходимости орбиталей перед переключением на использование точных интегралов в расчете SCF_TYPE DIRECT
Тип : логическое значение
По умолчанию : правда
УГАДАЙ
Тип предполагаемых орбиталей. По умолчанию READ для оптимизации геометрии после первого шага, CORE для отдельных атомов и SAD в противном случае. Предположение HUCKEL использует оперативные вычисления, такие как SAD, как описано в документе doi:10.1021/acs.jctc.8b01089, где также описывается предположение SAP.
Тип : строка
Возможные значения : AUTO, CORE, GWH, SAD, SADNO, SAP, HUCKEL, READ
По умолчанию : АВТО
GUESS_MIX
Смешайте HOMO/LUMO в UHF или UKS, чтобы нарушить пространственную симметрию альфа/бета. Полезно для создания неограниченных решений с нарушенной симметрией. Обратите внимание, что эта процедура определена только для вычислений в симметрии C1.
Полезно для создания неограниченных решений с нарушенной симметрией. Обратите внимание, что эта процедура определена только для вычислений в симметрии C1.
Тип : логическое значение
По умолчанию : ложь
GUESS_PERSIST
Если верно, то повторять указанную процедуру определения орбиталей каждый раз, даже во время оптимизации геометрии.
Тип : логический
По умолчанию : ложь
INTS_ДОПУСК
Порог скрининга для выбранного метода скрининга (SCHWARZ, CSAM, DENSITY) Абсолютное значение, ниже которого TEI не учитывается.
Тип : двойной
По умолчанию : 1e-12
МАКС_МЕМ_БУФ
Максимальный объем памяти на буфер для алгоритма PK REORDER, для отладки и настройки
Тип : целое число
По умолчанию : 0
MOLDEN_WRITE
Записать выходной файл MOLDEN? Если это так, имя файла будет заканчиваться на . molden, а префикс определяется WRITER_FILE_LABEL (если он установлен) или именем выходного файла плюс имя текущей молекулы.
molden, а префикс определяется WRITER_FILE_LABEL (если он установлен) или именем выходного файла плюс имя текущей молекулы.
Тип : логический
По умолчанию : ложь
ОРБИТАЛЫ_ЗАПИСЬ
Имя файла (с учетом регистра), в который сериализуются орбитальные данные Wavefunction.
Тип : строка
По умолчанию : Нет по умолчанию
PRINT_BASIS
Печатать базисный набор?
Тип : логическое значение
По умолчанию : ложь
PRINT_MOS
Распечатать молекулярные орбитали?
Тип : логический
По умолчанию : ложь
QCHF
Выполнить расчет QCHF?
Тип : логический
По умолчанию : ложь
ОБОЗНАЧЕНИЕ
Тип эталонной волновой функции. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_REFERENCE
Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_REFERENCE
Тип : строка
Возможные значения : RHF, ROHF, UHF, CUHF, RKS, UKS
По умолчанию : RHF
СОХРАНИТЬ_JK
Сохранить объект JK для дальнейшего использования?
Тип : логическое значение
По умолчанию : ложь
SCF_MEM_SAFETY_FACTOR
Запас памяти для размещения JK
Тип : двойной
По умолчанию : 0,75
SCF_СВОЙСТВА
SCF Свойства для расчета после оценки энергии. Обратите внимание, что это ключевое слово не используется для оценки свойств.
Тип : массив
По умолчанию : Нет по умолчанию
S_CHOLESKY_TOLERANCE
Допуск для частичного разложения Холецкого матрицы перекрытия.
Тип : двойной
По умолчанию : 1e-8
С_ОРТОГОНАЛИЗАЦИЯ
Ортогонализация SO: автоматическая, симметричная или каноническая?
S_ДОПУСК
Минимальное собственное значение S-матрицы до удаления линейных зависимостей.
Тип : двойной
По умолчанию : 1e-7
Контроль конвергенции/стабилизация
BASIS_GUESS
Ускорьте конвергенцию, выполнив предварительную SCF с этим небольшим базисным набором с последующим проецированием на полный целевой базис. Значение TRUE включает проецирование с использованием малого базового набора по умолчанию 3-21G, pcseg-0 или def2-SV(P).
Тип : строка
По умолчанию : ЛОЖЬ
ЗАТУХАНИЕ_КОНВЕРГЕНЦИИ
Порог сходимости плотности, после которого демпфирование больше не выполняется, если оно включено. Рекомендуется оставить демпфирование включенным до сходимости, что является значением по умолчанию. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_DAMPING
Рекомендуется оставить демпфирование включенным до сходимости, что является значением по умолчанию. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_DAMPING
Тип : conv double
По умолчанию : 1.0e-18
DAMPING_PERCENTAGE
Величина (в процентах) демпфирования, применяемая к ранним обновлениям плотности. 0 приведет к полному обновлению, 100 полностью остановит обновление. Значение около 20 (что соответствует 20% плотности предыдущей итерации, смешанной с текущей плотностью) может помочь решить проблемы с колебательной сходимостью.
Тип : двойной
По умолчанию : 0,0
DF_BASIS_GUESS
Когда BASIS_GUESS активен, запустите предварительный scf в режиме подгонки по плотности, используя его в качестве подходящей основы для небольшого базисного набора. Значение
Значение TRUE включает аппроксимацию плотности с базисом по умолчанию, в противном случае используется указанный базис.
ДИИС
Использовать ли экстраполяцию DIIS для ускорения конвергенции?
Тип : логическое значение
По умолчанию : правда
DIIS_MAX_VECS
Максимальное количество векторов ошибок, сохраняемых для экстраполяции DIIS
Тип : целое число
По умолчанию : 10
DIIS_MIN_VECS
Минимальное количество векторов ошибок, сохраненных для экстраполяции DIIS. Будет удалено в v1.7.
Тип : целое число
По умолчанию : 2
DIIS_RMS_ERROR
Использовать среднеквадратичную ошибку вместо более надежной абсолютной ошибки?
Тип : логический
По умолчанию : правда
DIIS_START
Минимальная итерация для начала хранения векторов DIIS и выполнения ADIIS/EDIIS.
Тип : целое число
По умолчанию : 1
DO_LINK
Выполните алгоритм обмена линейным масштабированием (LinK), как описано в [Ochsenfeld:1998:1663]. Применяется только к Direct SCF.
Тип : логический
По умолчанию : ложь
Д_КОНВЕРГЕНЦИЯ
Критерий сходимости плотности SCF, определяемый как среднеквадратичное или максимальное абсолютное значение орбитального градиента. См. Таблицу SCF Convergence & Algorithm для критериев сходимости по умолчанию для различных типов расчета. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_CONV
Тип : conv double
По умолчанию : 1e-6
E_CONVERGENCE
Критерий сходимости энергии СКФ. См. Таблицу SCF Convergence & Algorithm для критериев сходимости по умолчанию для различных типов расчета.
См. Таблицу SCF Convergence & Algorithm для критериев сходимости по умолчанию для различных типов расчета.
Тип : двойной
По умолчанию : 1e-6
FAIL_ON_MAXITER
Ошибка, если мы достигнем maxiter без схождения?
Тип : логический
По умолчанию : правда
ИНФОК
Выполнять инкрементную сборку Fock?
Тип : логический
По умолчанию : ложь
INCFOCK_CONVERGENCE
Порог плотности, при котором прекращается постепенное построение матрицы Фока
Тип : conv double
По умолчанию : 1.0e-5
INCFOCK_FULL_FOCK_EVERY
Частота, с которой вычисляется полная матрица Фока при использовании INCFOCK. N означает перестраивать каждые N итераций SCF, чтобы избежать накопления ошибок из-за инкрементной процедуры.
N означает перестраивать каждые N итераций SCF, чтобы избежать накопления ошибок из-за инкрементной процедуры.
Тип : целое число
По умолчанию : 5
УРОВЕНЬ_SHIFT
Использовать сдвиг уровня?
Тип : двойной
По умолчанию : 0,0
УРОВЕНЬ_SHIFT_CUTOFF
Ошибка DIIS, при которой следует прекратить применение сдвига уровня
Тип : двойной
По умолчанию : 1e-2
LINK_INTS_TOLERANCE
Допуск скрининга, используемый для разреженности ERI/плотности в алгоритме LinK
Тип : conv double
По умолчанию : 1.0e-12
МАКСИТЕР
Максимальное количество итераций. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_MAXCYC
Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_MAXCYC
Тип : целое число
По умолчанию : 100
МОМ_ОСС
Абсолютные индексы орбиталей для возбуждения в MOM (+/- для альфа/бета)
Тип : массив
По умолчанию : Нет по умолчанию
МОМ_СТАРТ
Итерация для запуска MOM (или 0 для отсутствия MOM)
Тип : целое число
По умолчанию : 0
МОМ_ВИР
Абсолютные индексы орбиталей для возбуждения в MOM (+/- для альфа/бета)
Тип : массив
По умолчанию : Нет по умолчанию
SCF_INITIAL_ACCELERATOR
Использовать метод для ускорения первоначальной сходимости SCF? Используйте НЕТ только для DIIS (если он включен) и EDIIS или ADIIS , чтобы иметь выбранный ускоритель и DIIS (если они включены). Для ссылок с ограниченным доступом
Для ссылок с ограниченным доступом EDIIS и ADIIS не действуют.
SCF_INITIAL_FINISH_DIIS_TRANSITION
Ошибка SCF, при которой необходимо завершить линейную интерполяцию между шагами DIIS и шагами начального ускорителя SCF. Значение взято из Garza and Scuseria, DOI: 10.1063/1.4740249
Тип : double
По умолчанию : 1.0e-4
SCF_INITIAL_START_DIIS_TRANSITION
Ошибка SCF, при которой следует запустить линейную интерполяцию между шагами DIIS и шагами начального ускорителя SCF. Значение взято из Garza and Scuseria, DOI: 10.1063/1.4740249
Тип : double
По умолчанию : 1.0e-1
СОСКФ
Использовать методы конвергенции SCF второго порядка?
Тип : логический
По умолчанию : ложь
SOSCF_CONV
Порог сходимости второго порядка. Прекратите микроитерацию на этом значении.
Прекратите микроитерацию на этом значении.
Тип : двойной
По умолчанию : 5.0e-3
SOSCF_MAX_ITER
Максимальное количество выполняемых микроитераций второго порядка.
Тип : целое число
По умолчанию : 5
SOSCF_MIN_ITER
Минимальное количество микроитераций второго порядка для выполнения.
Тип : целое число
По умолчанию : 1
SOSCF_PRINT
Печатаем ли мы микроитерации SOSCF?
Тип : логическое значение
По умолчанию : ложь
SOSCF_START_CONVERGENCE
Когда начинать итерации SCF второго порядка на основе RMS градиента.
Тип : двойной
По умолчанию : 1.0e-2
СТАБИЛЬНОСТЬ_АНАЛИЗ
Следует ли выполнять анализ устойчивости после сходимости. NONE предотвращает выполнение анализа. CHECK распечатает анализ стабильности волновой функции в конце расчета. FOLLOW выполнит анализ и, если будет обнаружена полностью симметричная нестабильность, попытается отследить собственный вектор и повторно запустить вычисления, чтобы найти устойчивое решение.
Дробная занятость UHF/UKS
FRAC_DIIS
Использовать ли экстраполяцию DIIS для ускорения сходимости в ГРП?
Тип : логический
По умолчанию : правда
FRAC_LOAD
Пересчитывать предположения из сохраненных орбиталей?
Тип : логический
По умолчанию : ложь
FRAC_OCC
Абсолютные индексы занятых орбиталей для частичного заполнения (+/- для альфа/бета)
Тип : массив
По умолчанию : Нет по умолчанию
FRAC_RENORMALIZE
Перенормировать матрицы C перед записью в контрольную точку?
Тип : логический
По умолчанию : правда
FRAC_START
Итерация для начала частичного заполнения орбиталей (или 0 для отсутствия частичного заполнения)
Тип : целое число
По умолчанию : 0
FRAC_VAL
Занятия указанных выше орбитальных индексов (\(0. 0\le {\rm occ} \le 1.0\))
0\le {\rm occ} \le 1.0\))
Тип : массив
По умолчанию : нет по умолчанию
Воздействие на окружающую среду
ВНЕШНИЙ
Внешний потенциал (созданный Python или nullptr/None)
Тип : логическое значение
По умолчанию : ложь
ONEPOT_GRID_READ
Считать внешний потенциал из файла .dx?
Тип : логический
По умолчанию : ложь
ВОЗМУЩЕНИЕ_ДИПОЛЯ
Массив длины три, описывающий величину (атомные единицы) поля диполя в направлениях {x,y,z}
Тип : массив
По умолчанию : Нет по умолчанию
ПЕРТУРБ_Ч
Возмущают ли гамильтониан?
Тип : логический
По умолчанию : ложь
ВОЗМУЩЕНИЕ_ВЕЛИЧИНА
Размер возмущения (применяется только к дипольным возмущениям). Устарело — вместо этого используйте PERTURB_DIPOLE
Устарело — вместо этого используйте PERTURB_DIPOLE
Тип : double
По умолчанию : 0,0
ПЕРТУРБ_С
Оператор, используемый для возмущения гамильтониана, если требуется. DIPOLE_X, DIPOLE_Y и DIPOLE_Z будут удалены в пользу опции DIPOLE в будущем
Тип : строка
Возможные значения : DIPOLE, DIPOLE_X, DIPOLE_Y, DIPOLE_Z, EMBPOT, SPHERE, DX
По умолчанию : ДИПОЛЬ
PHI_POINTS
Количество узлов азимутальной сетки для интегрирования сферического потенциала
Тип : целое число
По умолчанию : 360
РАДИУС
Радиус (бор) внешнего потенциала твердой сферы
Тип : двойной
По умолчанию : 10,0
R_POINTS
Количество узлов радиальной сетки для интегрирования сферического потенциала
Тип : целое число
По умолчанию : 100
ТЕТА_ПУНКТОВ
Количество узлов координатной сетки для интегрирования сферического потенциала
Тип : целое число
По умолчанию : 360
ТОЛЩИНА
Толщина (бор) внешнего потенциала твердой сферы
Тип : двойной
По умолчанию : 20,0
Алгоритм DFSCF
DF_BUMP_R0
Функция удара мин. радиус
радиус
Тип : двойной
По умолчанию : 0,0
DF_BUMP_R1
Максимальный радиус функции удара
Тип : двойной
По умолчанию : 0,0
DF_DOMAINS
Алгоритм выбора области геометрической подгонки FastDF
DF_INTS_NUM_THREADS
Количество потоков для интегралов (может быть отклонено, если проблема с памятью). 0 пусто
Тип : целое число
По умолчанию : 0
DF_METRIC
Фитинг FastDF Метрический
DF_THETA
Параметр разделения метрического диапазона FastDF SR Ewald
Тип : двойной
По умолчанию : 1,0
Алгоритм COSX
COSX_INTS_ДОПУСК
Критерии отбора интегралов и промежуточных значений в COSX
Тип : conv double
По умолчанию : 1. 0e-11
0e-11
COSX_RADIAL_POINTS_FINAL
Количество радиальных точек в итоговой сетке COSX.
Тип : целое число
По умолчанию : 35
COSX_RADIAL_POINTS_INITIAL
Количество радиальных точек в исходной сетке COSX.
Тип : целое число
По умолчанию : 25
COSX_SPHERICAL_POINTS_FINAL
Количество сферических точек в итоговой сетке COSX.
Тип : целое число
По умолчанию : 110
COSX_SPHERICAL_POINTS_INITIAL
Количество сферических точек в исходной сетке COSX.
Тип : целое число
По умолчанию : 50
Алгоритм предположения SAD
SAD_D_CONVERGENCE
Критерий сходимости для плотности SCF в расчете SAD, аналог D_CONVERGENCE
Тип : conv double
По умолчанию : 1e-5
SAD_E_CONVERGENCE
Критерий сходимости для энергии SCF в предположении SAD, аналогичный E_CONVERGENCE
Тип : conv double
По умолчанию : 1e-5
ДПФ
ДПФ_АЛЬФА
Параметр точного обмена ДПФ
Тип : двойной
По умолчанию : 0,0
ДПФ_АЛЬФА_С
Гибридный параметр корреляции ДПФ
Тип : двойной
По умолчанию : 0,0
ДПФ_БАЗИС_ДОПУСК
Основа отсечки DFT.
Тип : двойной
По умолчанию : 1.0e-12
ДПФ_БС_РАДИУС_АЛЬФА
Коэффициент эффективного радиуса БС в радиальной сетке.
Тип : двойной
По умолчанию : 1,0
DFT_DISPERSION_PARAMETERS
Параметры, определяющие поправку на дисперсию. См. Функционалы таблицы -D для значений по умолчанию и Коррекции дисперсии таблицы для порядка, в котором параметры должны быть указаны в этой опции массива. Не используется для функционалов, построенных пользователем.
Тип : массив
По умолчанию : Нет по умолчанию
ДФТ_GRAC_АЛЬФА
Градиент регуляризованной асимптотической коррекции альфа-значения
Тип : double
По умолчанию : 0,5
DFT_GRAC_BETA
Градиентное регуляризованное значение бета-асимптотической коррекции
Тип : двойной
По умолчанию : 40,0
DFT_GRAC_SHIFT
Значение сдвига асимптотической коррекции, упорядоченное по градиенту
Тип : double
По умолчанию : 0,0
ДПФ_ЯДЕРНАЯ_СХЕМА
Ядерная схема.
Тип : строка
Возможные значения : TREUTLER, BECKE, NAIVE, STRATMANN, SBECKE
По умолчанию : TREUTLER
ДФТ_ОМЕГА
Параметр разделения диапазонов ДПФ
Тип : двойной
По умолчанию : 0,0
ДФТ_ОМЕГА_С
Параметр разделения диапазона корреляции ДПФ
Тип : двойной
По умолчанию : 0,0
DFT_PRUNING_SCHEME
Выберите подход для обрезки. Options ROBUST and TREUTLER prune based on regions (proximity to nucleus) while FLAT P_GAUSSIAN D_GAUSSIAN P_SLATER D_SLATER LOG_GAUSSIAN LOG_SLATER prune based on decaying functions (experts only!). Рекомендуемая схема
Рекомендуемая схема НАДЕЖНЫЙ .
Тип : строка
По умолчанию : НЕТ
DFT_RADIAL_POINTS
Количество радиальных точек.
Тип : целое число
По умолчанию : 75
ДПФ_РАДИАЛЬНАЯ_СХЕМА
Радиальная схема.
Тип : строка
Возможные значения : TREUTLER, BECKE, MULTIEXP, EM, MURA
По умолчанию : TREUTLER
DFT_SPHERICAL_POINTS
Количество сферических точек (число точек Лебедева).
Тип : целое число
По умолчанию : 302
ДПФ_СФЕРИЧЕСКАЯ_СХЕМА
Сферическая схема.
ДФТ_V2_RHO_CUTOFF
Минимальная отсечка для второй производной
Тип : двойной
По умолчанию : 1.e-6
ДФТ_ВВ10_Б
Определить параметр VV10 b
Тип : двойной
По умолчанию : 0,0
ДФТ_ВВ10_С
Определение параметра VV10 C
Тип : двойной
По умолчанию : 0,0
ДФТ_ВВ10_ПОСТСКФ
коррекция post-scf VV10
Тип : логический
По умолчанию : ложь
ДПФ_ВВ10_РАДИАЛЬНЫЕ_ТОЧКИ
Количество радиальных точек для интегрирования VV10 NL.
Тип : целое число
По умолчанию : 50
DFT_VV10_SPHERICAL_POINTS
Количество сферических точек (количество точек Лебедева) для интегрирования VV10 NL.
Тип : целое число
По умолчанию : 146
ЛОКАЛЬНОЕ_СХОДЕНИЕ
Схождение по процедуре орбитальной локализации
Тип : conv double
По умолчанию : 1e-12
ЛОКАЛЬНЫЙ_МАКСИТЕР
Макситер по процедуре орбитальной локализации
Тип : целое число
По умолчанию : 200
NL_DISPERSION_PARAMETERS
Параметры, определяющие поправку на дисперсию -NL/-V. Сначала b, затем C
Сначала b, затем C
Тип : массив
По умолчанию : нет по умолчанию
СОХРАНИТЬ_УВЧ_НОС
Сохранение NOs УВЧ
Тип : логический
По умолчанию : ложь
UHF_NOONS
Количество ПОЛДЕНИЙ для печати в УВЧ расчете
Тип : строка
По умолчанию : 3
ТДСКФ
TDSCF_COEFF_CUTOFF
Отсечка для печати возбуждений и девозбуждений, влияющих на каждое возбужденное состояние
Тип : двойной
По умолчанию : 0,1
TDSCF_GUESS
Тип предположения, в настоящее время поддерживаются только «знаменатели»
TDSCF_MAXITER
Максимальное количество итераций решателя TDSCF
Тип : целое число
По умолчанию : 60
TDSCF_PRINT
Уровень детализации в TDSCF
Тип : целое число
По умолчанию : 1
TDSCF_R_CONVERGENCE
Порог сходимости для нормы вектора невязки. Если не установлено, по умолчанию используется D_CONVERGENCE
Если не установлено, по умолчанию используется D_CONVERGENCE
Тип : conv double
По умолчанию : 1e-4
TDSCF_STATES
Количество корней (возбужденных состояний), к которым мы должны стремиться. Это может быть либо целое число (общее количество состояний для поиска), либо список (количество состояний за один повтор). Последнее справедливо только в том случае, если система обладает симметрией. Кроме того, при использовании симметрии общее количество состояний будет перераспределяться между невозвратами.
Тип : массив
По умолчанию : Нет по умолчанию
ТДСКФ_ТДА
Работа с приближением Тамма-Данкова (TDA), использует приближение со случайной фазой (RPA), если оно ложно
По умолчанию : ложь
TDSCF_TDM_PRINT
Какие переходные дипольные моменты распечатать: - E_TDM_LEN : электрические переходные дипольные моменты, представление длины - E_TDM_VEL : электрические переходные дипольные моменты, представление скорости - M_TDM : магнитные переходные дипольные моменты
Тип : массив
По умолчанию : Нет по умолчанию
TDSCF_ТРИПЛЕТЫ
Управляет включением триплетных состояний, что допустимо только для ограниченных ссылок. Допустимые варианты: - none : триплеты не вычисляются (по умолчанию) - также : включаются триплеты и синглеты с наименьшей энергией в соотношении 50-50. Обратите внимание, что синглеты являются привилегированными, т. Е. Если вы стремитесь сойтись всего в 5 состояниях, 3 будут синглетами, а 2 будут триплетами. - only : вычисляются только триплетные состояния
Допустимые варианты: - none : триплеты не вычисляются (по умолчанию) - также : включаются триплеты и синглеты с наименьшей энергией в соотношении 50-50. Обратите внимание, что синглеты являются привилегированными, т. Е. Если вы стремитесь сойтись всего в 5 состояниях, 3 будут синглетами, а 2 будут триплетами. - only : вычисляются только триплетные состояния
ВКОМБИН
объединить омега-обмен и обмен Хартри-Фока в одну матрицу для повышения эффективности? Отключено, пока не исправлено.
Тип : логический
По умолчанию : ложь
Эксперт Общая информация о волновой функции ПК_АЛГО
Выберите алгоритм PK для использования. В целях отладки выбор будет автоматизирован позже.
PK_ALL_NONSYM
Все плотности считаются несимметричными, только для отладки.
Тип : логический
По умолчанию : ложь
PK_MAX_BUCKETS
Максимальное количество пакетов для чтения суперматрицы PK.
Тип : целое число
По умолчанию : 500
PK_NO_INCORE
Деактивировать в основном алгоритме. В целях отладки.
Тип : логический
По умолчанию : ложь
ВФН
Тип волновой функции
Эксперт Контроль сходимости/стабилизация FOLLOW_STEP_INCREMENT
При использовании STABILITY_ANALYSIS = FOLLOW приращение для изменения значения FOLLOW_STEP_SCALE, если мы окажемся в одном и том же решении SCF.
Тип : двойной
По умолчанию : 0,2
FOLLOW_STEP_SCALE
При использовании STABILITY_ANALYSIS FOLLOW , на сколько масштабировать шаг вдоль собственного вектора. Полный шаг \(pi/2\) соответствует значению 1,0.
Полный шаг \(pi/2\) соответствует значению 1,0.
Тип : двойной
По умолчанию : 0,5
МАКС. ПОПЫТОК
При использовании STABILITY_ANALYSIS FOLLOW , максимальное количество попыток орбитальной оптимизации, чтобы сделать волновую функцию стабильной.
Тип : целое число
По умолчанию : 1
Эксперт Параллельное выполнение РАСПРЕДЕЛЕННАЯ_МАТРИЦА
Размеры размерности распределенной матрицы
Тип : массив
По умолчанию : Нет По умолчанию
ПАРАЛЛЕЛЬНЫЙ
Запускать параллельно?
Тип : логический
По умолчанию : ложь
PROCESS_GRID
Размеры процессорной сетки
Тип : массив
По умолчанию : Нет по умолчанию
TILE_SZ
Размер плитки для распределенных матриц
Тип : целое число
По умолчанию : 512
Эксперт Разное.
САПТ
Собираетесь делать SAPT? Если да, то какая часть?
Тип : строка
По умолчанию : ЛОЖЬ
Эксперт Алгоритм DFSCF DF_FITTING_CONDITION
Условие подбора, т. е. пороговое значение собственного значения для RI. Аналогично S_TOLERANCE
Тип : двойной
По умолчанию : 1.0e-10
DF_INTS_IO
Кэширование ввода-вывода для поправок CP и т. д.
Эксперт Алгоритм COSX COSX_BASIS_TOLERANCE
Критерии отбора значений базовой функции в сетках COSX
Тип : conv double
По умолчанию : 1.0e-10
COSX_DENSITY_TOLERANCE
Критерии отбора плотности пар оболочек в COSX
Тип : conv double
По умолчанию : 1. 0e-10
0e-10
COSX_INCFOCK
Можно ли повысить эффективность скрининга COSX путем постепенного построения матрицы Фока?
Тип : логический
По умолчанию : ложь
COSX_OVERLAP_FITTING
Уменьшить числовые ошибки COSX с помощью подгонки внахлестку?
Тип : логический
По умолчанию : правда
COSX_PRUNING_SCHEME
Схема обрезки для сетей COSX
Тип : строка
По умолчанию : НАДЕЖНЫЙ
Эксперт Алгоритм предположения SAD DF_BASIS_SAD
Основа фитинга плотности, используемая в SAD
SAD_CHOL_TOLERANCE
SAD порог разложения по плотности приближения
Тип : conv double
По умолчанию : 1e-7
SAD_FRAC_OCC
Принуждать к равномерному распределению занятий по последней частично занятой орбитальной оболочке?
Тип : логический
По умолчанию : правда
SAD_MAXITER
Максимальное количество атомарных итераций SCF в рамках SAD
Тип : целое число
По умолчанию : 50
SAD_PRINT
Количество информации SAD для печати на выходе
Тип : целое число
По умолчанию : 0
SAD_SCF_TYPE
Тип SCF, используемый для атомарных расчетов в SAD-догадке
Тип : строка
Возможные значения : DIRECT, DF, MEM_DF, DISK_DF, PK, OUT_OF_CORE, CD, GTFOCK
По умолчанию : DF
SAD_SPIN_AVERAGE
Использовать усредненные по спину заселенности вместо основного спинового состояния атома в дробном SAD?
Тип : логический
По умолчанию : правда
Эксперт ДПФ DFT_BLOCK_MAX_POINTS
Максимальное количество точек сетки на блок оценки.
Тип : целое число
По умолчанию : 256
DFT_BLOCK_MAX_RADIUS
Максимальный радиус для завершения подразделения блока октодерева [au].
Тип : двойной
По умолчанию : 3.0
DFT_BLOCK_MIN_POINTS
Минимальное количество точек сетки на блок оценки.
Тип : целое число
По умолчанию : 100
DFT_BLOCK_SCHEME
Схема блокировки для ДПФ.
DFT_DENSITY_TOLERANCE
Отсечка по плотности для LibXC. Отрицательное значение отключает эту функцию и используются значения по умолчанию LibXC.
Тип : двойной
По умолчанию : -1,0
ДФТ_GRAC_C_FUNC
Градиентная регуляризованная форма функционала асимптотической коррекции корр.
ДФТ_GRAC_X_FUNC
Градиентная регуляризованная форма функционала асимптотической коррекции.
DFT_GRID_NAME
Спецификация сетки ДПФ, например SG1.
ДПФ_PRUNING_ALPHA
Распространение альфа-канала для логарифмической обрезки.
Тип : двойной
По умолчанию : 1,0
DFT_REMOVE_DISTANT_POINTS
Удалить из квадратурной сетки точки, превышающие пространственную протяженность базисных функций.
Тип : логическое значение
По умолчанию : правда
ДПФ_ВВ10_RHO_CUTOFF
Отсечка Rho для интеграции VV10 NL.
Тип : двойной
По умолчанию : 1. e-8
e-8
ДПФ_ВЕС_ДОПУСК
отсечка по весу сетки. Отключить с -1.0.
Тип : двойной
По умолчанию : 1.0e-15
комплексный синус и косинус
Определим для всех комплексных значений z:
Поскольку эти ряды сходятся для всех действительных значений z, их радиусы сходимости равны ∞, и поэтому они сходятся для всех комплексных значений z (по известному Абелю; ср. серия начального уровня мощности). Тем самым они определяют голоморфные функции во всей комплексной плоскости, т. е. целые функции (точнее, целые трансцендентные функции). Ряд также показывает, что синус — нечетная функция, а косинус — четная функция.
Разложение комплексных экспоненциальных функций eiz и e-iz в ряды по степеням и разделение четных и нечетных степеней дает обобщенные формулы Эйлера
eiz=cosz+isinz,e-iz=cosz-isinz.
Сложение, вычитание и умножение этих двух формул дают соответственно две формулы Эйлера
cosz=eiz+e-iz2,sinz=eiz-e-iz2i (1)
(которые иногда используются для определения косинуса и синуса) и «фундаментальная формула тригонометрии»
cos2z+sin2z= 1.
Как следствие обобщенных формул Эйлера легко получаются формулы сложения синуса и косинуса:
sin(z1+z2)=sinz1cosz2+cosz1sinz2,
cos(z1+z2)=cosz1cosz2-sinz1sinz2;
, поэтому они в ℂ полностью, как в ℝ. Это означает, что все производные от них гониометрические формулы, такие как
sin2z= 2sinzcosz,sin(π-z)=sinz,sin2z=1-cos2z2,
имеют старую форму. См. также постоянство аналитических отношений.
См. также постоянство аналитических отношений.
Формулы сложения могут быть записаны также как
sin(x+iy)=sinxкошy+icosxsinhy,
cos(x+iy)=cosxcoshy-isinxsinhy
из которых следует, если предположить, что x,y∈ℝ, результаты
Re(sin(x+iy))=sinxcoshy, Im(sin(x+iy))=cosxsinhy,
Re(cos(x+iy))=cosxcoshy, Im(cos(x+iy))=-sinxsinhy.
Таким образом, мы получаем оценку модуля
|sin(x+iy)|=sin2xcosh3y+cos2xsinh3y=sin2xcosh3y+(1-sin2x)sinh3y=sin2 x(cosh3y-sinh3y)+sinh3y=sin2x⋅1+sinh3y≥|sinhy|,
который стремится к бесконечности, когда z=x+iy движется к бесконечности вдоль любой линии, непараллельной вещественной оси. Модуль cos(x+iy) ведет себя аналогично.
Другим важным следствием формул сложения является то, что функции sin и cos являются периодическими и имеют 2π в качестве своих значений.
простой период (http://planetmath.org/ComplexExponentialFunction):
sin(z+2π)=sinz,cos(z+2π)=cosz ∀z
Периодичность функций приводит к тому, что их обратные функции, комплексные циклометрические функции, бесконечно многозначны; их можно выразить через комплексный логарифм и квадратный корень (см. общую мощность) как
arcsinz=1ilog(iz+1-z2),arccosz=1ilog(z+i1-z2).
Производные функции синуса и функции косинуса получаются либо из форм ряда, либо из (1):
ддzsinz=cosz,ddzcosz=-sinz
См. высшие производные (http://planetmath.org/HigherOrderDerivativesOfSineAndCosine).
Название комплексный синус и косинус Каноническое имя Сложный синус и косинус Дата создания 22. 03.2013 14:45:25
03.2013 14:45:25 Последнее изменение на 22.03.2013 14:45:25 Владелец пахио (2872) Последнее изменение: пахио (2872) Числовой идентификатор 31 Автор пахио (2872) Тип ввода Определение Классификация мск 30D10 Классификация мск 30B10 Классификация мск 30A99 Классификация мск 33B10 Связанная тема Связь Эйлера Связанная тема Циклометрические функции Связанная тема ПримерTaylorPolynomialsForSinX Связанная тема Сложная экспоненциальная функция Связанная тема Определения в тригонометрии Связанная тема персистенсофаналитикрелейшнс Связанная тема Косинус AtMultiplesOfStraightAngle Связанная тема ХевисайдФормула Связанная тема SomeValuesCharacterisingI Связанная тема УникальностьФури Определяет сложный синус Определяет комплексный косинус Определяет синус Определяет косинус Определяет гониометрическая формула
Формула Эйлера для комплексных чисел
(Есть еще одна «Формула Эйлера» о геометрии ,
эта страница посвящена той, которая используется в комплексных числах)
Во-первых, вы, возможно, видели знаменитую «Тождество Эйлера»:
e 79
9 i π + 1 = 0
Кажется совершенно волшебным, что такое аккуратное уравнение объединяет:
- e (число Эйлера)
- i (мнимый номер блока)
- π (знаменитое число пи, которое встречается во многих интересных областях)
- 1 (первое счетное число)
- 0 (ноль)
А также основные операции сложения, умножения и возведения в степень!
Но если вы хотите совершить интересное путешествие по математике, вы узнаете, как она возникает.
Заинтересованы? Читать дальше!
Открытие
Это было около 1740 года, и математики интересовались мнимыми числами.
Возведение в квадрат мнимого числа дает отрицательный результат
Обычно это невозможно (попробуйте возвести в квадрат некоторые числа, помня, что умножение отрицательных чисел дает положительный результат, и посмотрите, сможете ли вы получить отрицательный результат), но просто представьте, что вы может сделать это!
И у нас может быть этот специальный номер (называется I для воображаемого):
I 2 = −1
Леонард Эулер был наслаждался одним днем, играя с воображением. числа (или мне так кажется!), и он взял эту известную серию Тейлора (почитайте о них, они очаровательны):
e х = 1 + х + х 2 2! + х 3 3! + х 4 4! + х 5 5! + . ..
..
И он положил в него i :
e ix = 1 + ix + (ix) 2 4 2! + (ix) 3 3! + (ix) 4 4! + (ix) 5 5! + ...
И поскольку I 2 = −1 , он упрощает:
E IX = 1 + IX - x 2 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! 2! − ix 3 3! + х 4 4! + ix 5 5! − ...
Теперь сгруппируйте все i Условия в конце:
E IX = (1 - x 2 2! + x 4 4! -) + I (x − 4! -) + I (x. 4! x 3 3! + x 5 5! − ... )
4! x 3 3! + x 5 5! − ... )
И вот чудо... две группы на самом деле представляют собой ряды Taylor и 904 cos для 90 sin :
cos x = 1 − x 2 2! + х 4 4! - ... sin x = x − x 3 3! + х 5 5! - ...
и поэтому он упрощает:
E I x = COS X + I SIN X
Он должен был быть так счастлив, когда он обнаружил это!
Теперь она называется Формула Эйлера .
Давайте давайте попробуйте:
Пример: когда x = 1,1
E I x = COS X + I SIN X
99999999999999999999999999997 SIN x 9999999999999999999999999999999999999997 SIN x 9999999999999999999999999999997997997 9003 1. 1i = COS 1,1 + I SIN 1.1
1i = COS 1,1 + I SIN 1.1 E 1.1I = 0,45 + 0,89 I = 0,45 + 0,89 I = 0,45 + 0,89 I 9004 = 0,45 + 0,89 I = 0,45 + 0,89 I .0010 (до 2 знаков после запятой)
Примечание. Мы используем радианы, а не градусы.
Ответ представляет собой комбинацию действительного и мнимого чисел, которые вместе называются комплексным числом.
На комплексной плоскости можно нанести такое число (действительные числа идут слева направо, а мнимые вверх-вниз):
Здесь мы показываем число 0,45 + 0,89 i
То же, что и e 1.1i
Построим еще!
Круг!
Да, размещение формулы Эйлера на этот график создает круг:
E I x создает круг Radius 1
и, когда мы включим A Radius
и, когда мы включим A RADIUS 47
и, когда мы включим ARIUS 1
и, когда мы включим ARIUS 1
. мы можем превратить любую точку (например, 3 + 4i ) в re i x form by finding the correct value of x and r :
мы можем превратить любую точку (например, 3 + 4i ) в re i x form by finding the correct value of x and r :
Example: the number
3 + 4i To turn 3 + 4i into re i x форму мы делаем декартово преобразование в полярное:
- r = √(3 2 + 4 2 ) = √(9+16) = √25 = 5
- x = тангенс -1 ( 4 / 3 ) = 0,927 (до 3 десятичных знаков)
SO 3 + 4I также может быть 5 E 0,927 I
Это другая форма
Это в основном еще один способ иметь сложный номер.
Это оказывается очень полезным, так как во многих случаях (например, при умножении) проще использовать форму re i x , чем форму a+bi .
Графика
E I π Наконец, когда мы рассчитываем формулу Эйлера для x = π GET:
E I π = COS π + I π = COS π + I π = COS π + I 11011011030303030303030110110110110110 310110110110110110110111.

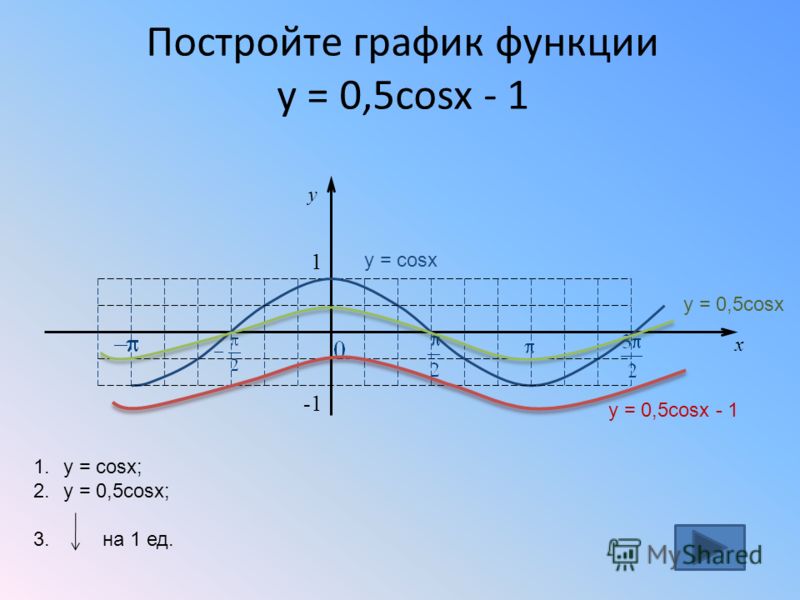

потому что ( Икс ) знак равно ∑ к знак равно 0 ∞ ( − 1 ) к Икс 2 к ( 2 к ) ! знак равно 1 − Икс 2 2 ! + Икс 4 4 ! − Икс 6 6 ! … {\ displaystyle \ cos (x) = \ sum _ {k = 0} ^ {\ infty} {\ frac {(-1) ^ {k} x ^ {2k}} {(2k)!}} = 1- {\ frac {x ^ {2}} {2!}} + {\ frac {x ^ {4}} {4!}} — {\ frac {x ^ {6}} {6!}} \ ldots}
Эта формула действительна для всех действительных значений x .
subs .
Например Вычисление выражения в точке.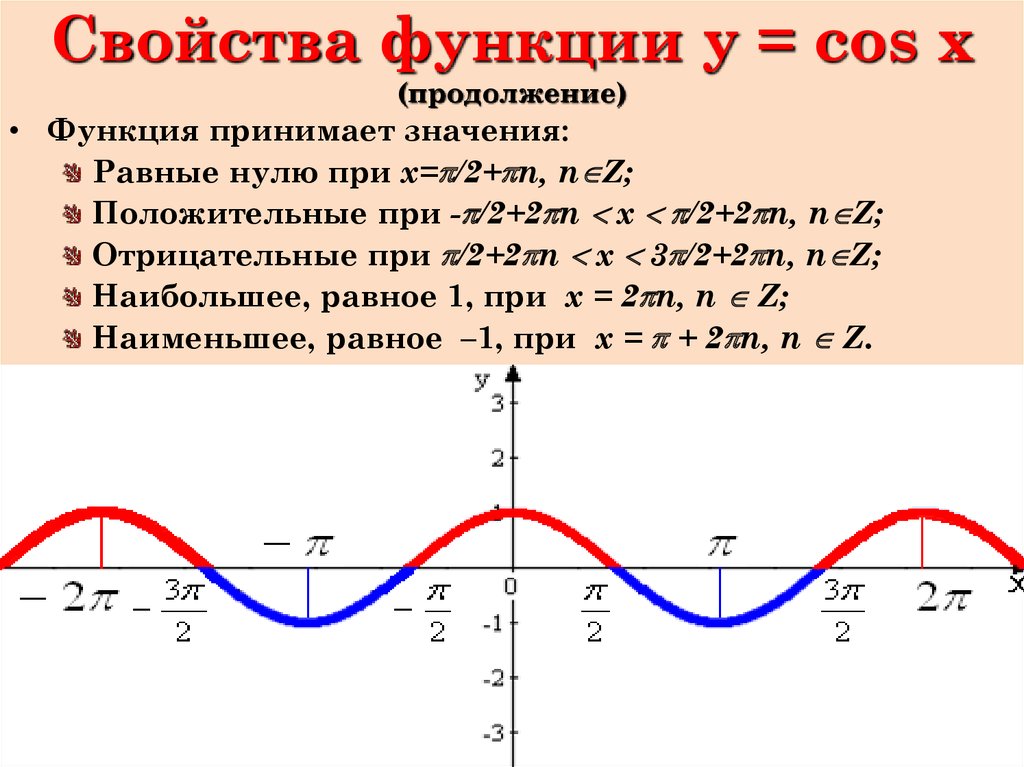 x}}\). Строить
это, мы могли бы начать с
x}}\). Строить
это, мы могли бы начать с x**y и замените y на x**y . Мы
тогда получится x**(x**y) . Если мы заменим на в этом новом выражении
с x**x мы получили бы x**(x**(x**x)) желаемое выражение.
>>> выражение = х**у >>> выражение х**у >>> expr = expr.subs(y, x**y) >>> выражение х**(х**у) >>> expr = expr.subs(y, x**x) >>> выражение х**(х**(х**х))
Во-вторых, если мы хотим выполнить очень контролируемое упрощение или
возможно, упрощение, которое SymPy иначе не может сделать. За
например, у нас есть \(\sin(2x) + \cos(2x)\), и мы хотим заменить
\(\sin(2x)\) с \(2\sin(x)\cos(x)\). Как мы узнаем позже, функция expand_trig делает это. Однако эта функция также будет расширяться
\(\cos(2x)\), что может нам и не понадобиться. Хотя есть способы выполнить такие
точное упрощение, и мы изучим некоторые из них в
расширенный раздел обработки выражений,
простой способ — просто заменить \(\sin(2x)\) на \(2\sin(x)\cos(x)\).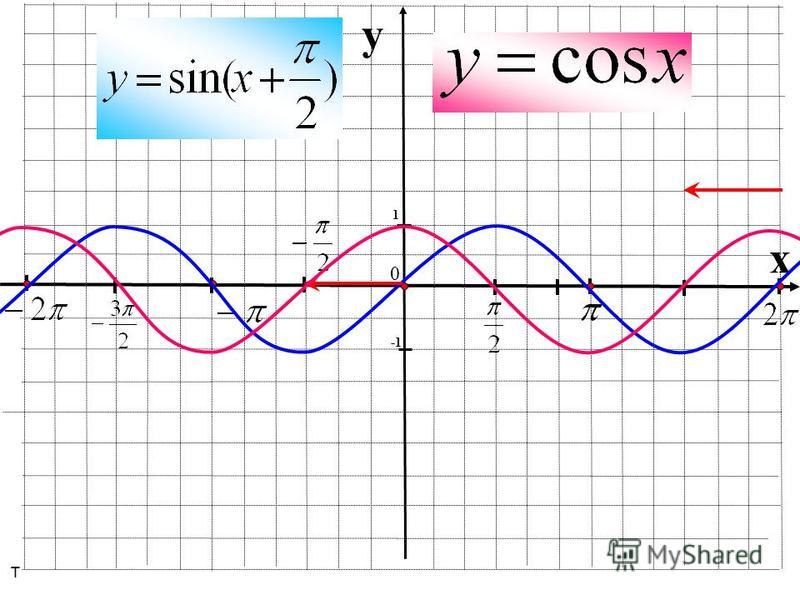
>>> выражение = sin(2*x) + cos(2*x) >>> expand_trig(выражение) 2*sin(x)*cos(x) + 2*cos(x)**2 - 1 >>> expr.subs(sin(2*x), 2*sin(x)*cos(x)) 2*sin(x)*cos(x) + cos(2*x)
сабвуферов следует отметить два важных момента. Во-первых, он возвращает
новое выражение. Объекты SymPy неизменяемы. Это означает, что сабвуферов делает
не изменять его на месте. Например expr.subs(x, 0) оставляет expr без изменений.
На самом деле, поскольку выражения SymPy неизменяемы, никакая функция их не изменит.
на месте. Все функции будут возвращать новые выражения. (старых, новых) пар
до подписки . subs([(x, 2), (y, 4), (z, 0)])
40
92 - 2х + 3\).
subs([(x, 2), (y, 4), (z, 0)])
40
92 - 2х + 3\).
>>> выражение = х**4 - 4*х**3 + 4*х**2 - 2*х + 3 >>> замены = [(x**i, y**i) для i в диапазоне (5), если i % 2 == 0] >>> expr.subs(замены) -4*х**3 - 2*х + у**4 + 4*у**2 + 3
Преобразование строк в выражения SymPy
Функция sympify (это sympify , не путать с упростить ) можно использовать для преобразования строк в выражения SymPy.
Например,
>>> str_expr = "x**2 + 3*x - 1/2" >>> expr = sympify(str_expr) >>> выражение х**2 + 3*х - 1/2 >>> expr.subs(x, 2) 19/2
Предупреждение
sympify использует eval . Не используйте его для непроверенного ввода.
эвалф Чтобы преобразовать числовое выражение в число с плавающей запятой, используйте евальф .
>>> выражение = квадрат (8) >>> выр.eval() 2,82842712474619
SymPy может вычислять выражения с плавающей запятой с произвольной точностью.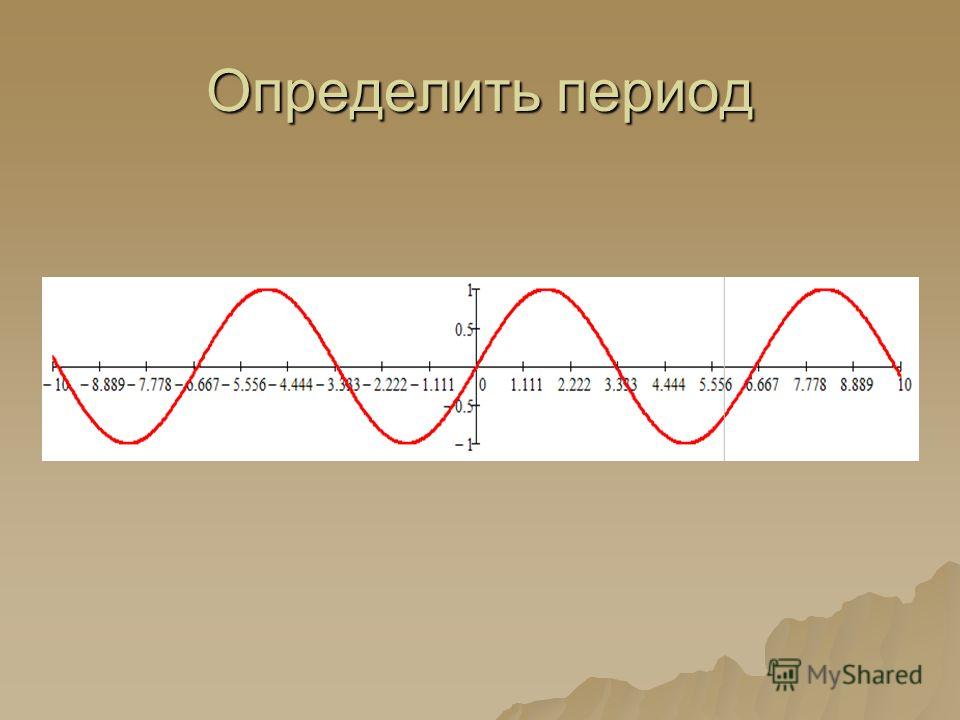 По
по умолчанию используются 15 цифр точности, но вы можете передать любое число в качестве
аргумент для
По
по умолчанию используются 15 цифр точности, но вы можете передать любое число в качестве
аргумент для evalf . Давайте вычислим первые 100 цифр \(\pi\).
>>> pi.eval(100) 3.14155897
46264338327950288419716939058209749445
Чтобы численно оценить выражение с символом в точке, мы могли бы использовать сабы за которыми следуют evalf , но это более эффективно и численно
stable для передачи замены на evalf с использованием флага subs , который
берет словарь символов: точка пар.
пометить флагом True.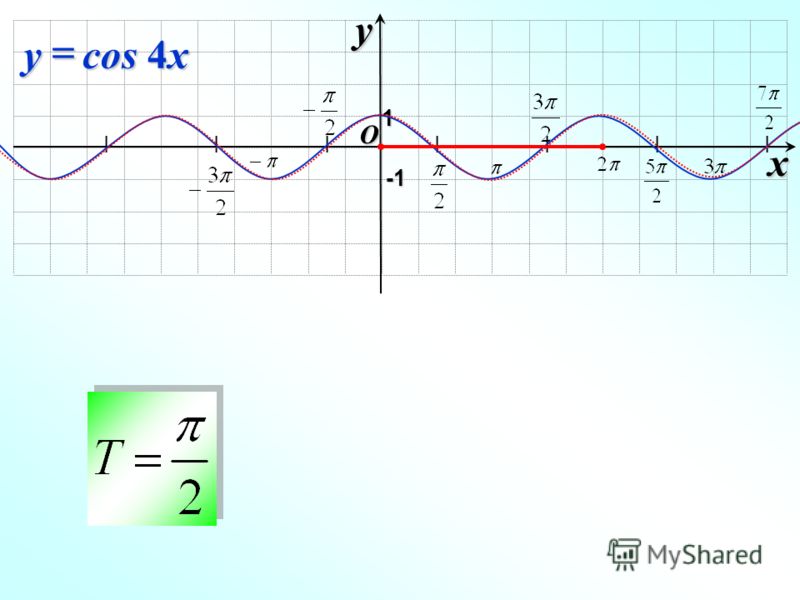 evalf()
-0.e-124
>>> (один - 1).evalf(chop=True)
0
evalf()
-0.e-124
>>> (один - 1).evalf(chop=True)
0
сабвуферы и evalf хороши, если вы хотите сделать простую оценку, но если
вы собираетесь оценивать выражение во многих точках, есть более эффективные
способы. Например, если вы хотите оценить выражение в тысяче
точки, использование SymPy будет намного медленнее, чем должно быть, особенно если вы
заботиться только о точности станка. Вместо этого вы должны использовать такие библиотеки, как
NumPy и SciPy. lambdify . ламбдифай действует
как функция lambda , за исключением того, что она преобразует имена SymPy в имена
данная числовая библиотека, обычно NumPy. Например5 0,41211849]Предупреждение
lambdifyиспользуетeval.Не используйте его для непроверенного ввода.
Вы можете использовать другие библиотеки, кроме NumPy. Например, для использования стандарта математический модуль библиотеки, используйте
"math".>>> f = lambdify(x, выражение, "математика") >>> f(0,1) 0,0998334166468Чтобы использовать lambdify с числовыми библиотеками, о которых он не знает, передайте словарь из
sympy_name:numerical_functionпар. Например>>> определение mysin(x): ... """ ... Мой синус. Обратите внимание, что это верно только для малых x. ... """ ... вернуть х >>> f = lambdify(x, expr, {"sin":mysin}) >>> f(0,1) 0,1Символическая математика в Python — конспекты лекций Scipy
Автор : Фабиан Педрегоса
Цели
- Вычислять выражения с произвольной точностью.
- Выполнить алгебраические операции с символьными выражениями.
- Выполнение основных вычислительных задач (пределы, дифференцирование и
- интеграции) с символическими выражениями.
- Решите полиномиальные и трансцендентные уравнения.
- Решите несколько дифференциальных уравнений.
Что такое SymPy? SymPy — это библиотека Python для символьной математики. Это стремится стать альтернативой таким системам, как Mathematica или Maple, сохраняя при этом код максимально простой и удобный расширяемый. SymPy полностью написан на Python и не требует никаких внешние библиотеки.
Документацию Sympy и пакеты для установки можно найти на http://www.sympy.org/
Содержание глав
- Первые шаги с SymPy
- Использование SymPy в качестве калькулятора
- Символы
- Алгебраические операции
- Развернуть
- Упростить
- Исчисление
- Пределы
- Дифференциация
- Расширение серии
- Интеграция
- Решение уравнения
- Линейная алгебра
- Матрицы
- Дифференциальные уравнения
3.
2.1.1. Использование SymPy в качестве калькулятора
SymPy определяет три числовых типа:
Действительное,РациональноеиЦелое.Класс Rational представляет рациональное число как пару двоек Целые числа: числитель и знаменатель, поэтому
Rational(1, 2)представляет 1/2,Rational(5, 2)5/2 и т. д.:>>> import sympy as sym >>> a = sym.Rational(1, 2) >>> а 1/2 >>> а*2 1SymPy использует mpmath в фоновом режиме, что позволяет выполнять вычисления с использованием арифметики произвольной точности. Что Кстати, некоторые специальные константы, такие как , , (Бесконечность), рассматриваются как символы и могут быть вычислены с произвольной точностью:
>>> сим.пи**2 пи**2 >>> sym.pi.evalf() 3.141558979 >>> (sym.pi + sym.exp(1)).evalf() 5,85987448204884
как вы видите,
evalfоценивает выражение как число с плавающей запятой.Существует также класс, представляющий математическую бесконечность, называемый
оо:>>> сим.оо > 99999 Истинный >>> сим.оо + 1 оо
Упражнения
- Расчет со 100 десятичными знаками.
- Считать в рациональной арифметике.
3.2.1.2. Символы
В отличие от других систем компьютерной алгебры, в SymPy вы должны объявить символьные переменные явно:
>>> x = sym.Symbol('x') >>> y = sym.Symbol('y')Затем вы можете манипулировать ими:
>>> x + y + x - y 2*х >>> (х + у) ** 2 (х + у)**2Символами теперь можно управлять с помощью некоторых операторов Python:
+,-`, ``*,**(арифметика), &, | , ~ , >>, << (логическое значение).Печать
Sympy позволяет управлять отображением вывода. Отсюда мы используем следующие настройки для печати:
>>> sym.init_printing(use_unicode=False, wrap_line=True)SymPy может выполнять мощные алгебраические операции. Что ж взгляните на некоторые из наиболее часто используемых: расширить и упростить.
3.2.2.1. Expand
Используйте это, чтобы расширить алгебраическое выражение. Он попытается степени и умножения:
>>> sym.expand((x + y) ** 3) 3 2 2 3 х + 3*х *у + 3*х*у + у >>> 3 * х * у ** 2 + 3 * у * х ** 2 + х ** 3 + у ** 3 3 2 2 3 х + 3*х *у + 3*х*у + уДополнительные параметры могут быть заданы в виде ключевых слов:
>>> sym.expand(x + y, complex=True) re(x) + re(y) + I*im(x) + I*im(y) >>> sym.I * sym.im(x) + sym.I * sym.im(y) + sym.re(x) + sym.re(y) re(x) + re(y) + I*im(x) + I*im(y) >>> sym.expand(sym.cos(x + y), trig=True) -sin(x)*sin(y) + cos(x)*cos(y) >>> sym.cos(x) * sym.cos(y) - sym.sin(x) * sym.sin(y) -sin(x)*sin(y) + cos(x)*cos(y)3.2.2.2. Simplify
Используйте упрощение, если хотите преобразовать выражение в более простая форма:
>>> sym.simplify((x + x * y) / x) у + 1Упрощение — несколько расплывчатый термин, а точнее существуют альтернативы упрощению:
powsimp(упрощение степени),trigsimp(для тригонометрических выражений) ,logcombine,радсимпвместе.Упражнения
- Рассчитать расширенную форму .
- Упростите тригонометрическое выражение
3.2.3.1. Лимиты
Лимиты просты в использовании в SymPy, они следуют синтаксису
limit(функция, переменная, точка), поэтому для вычисления предела as , вы бы выдалиlimit(f, x, 0):>>> sym.limit(sym.sin(x) / x, x, 0) 1вы также можете вычислить предел на бесконечности:
>>> sym.limit(x, x, sym.oo) оо >>> sym.limit(1 / x, x, sym.oo) 0 >>> sym.limit(x ** x, x, 0) 13.2.3.2. Дифференциация
Вы можете дифференцировать любое выражение SymPy, используя
diff(func, вар). Примеры:>>> sym.diff(sym.sin(x), x) потому что (х) >>> sym.diff(sym.sin(2 * x), x) 2*кос(2*х) >>> sym.diff(sym.tan(x), x) 2 загар (х) + 1Проверить правильность можно:
>>> sym.limit((sym.tan(x + y) - sym.tan(x)) / y, y, 0) 2 загар (х) + 1Высшие производные можно рассчитать с помощью
diff(func, var, n)method:>>> sym.diff(sym.sin(2 * x), x, 1) 2*кос(2*х) >>> sym.diff(sym.sin(2 * x), x, 2) -4*грех(2*х) >>> sym.diff(sym.sin(2 * x), x, 3) -8*cos(2*x)
3.2.3.3. Расширение серии
SymPy также знает, как вычислить ряд Тейлора выражения в точка. Используйте серию
(expr, var):>>> sym.series (sym.cos (x), x) 2 4 х х / 6\ 1 - -- + -- + О\х/ 2 24 >>> sym.series(1/sym.cos(x), x) 2 4 х 5*х / 6\ 1 + -- + ---- + О\х / 2 24Упражнения
- Расчет
- Вычислите производную для .
3.2.3.4. Интеграция
SymPy поддерживает неопределенную и определенную интеграцию трансцендентных элементарные и специальные функции с помощью средства
интегрировать(), которое использует мощный расширенный алгоритм Риша-Нормана и некоторые эвристики и шаблоны соответствие. Вы можете интегрировать элементарные функции:>>> sym.integrate(6 * x ** 5, x) 6 Икс >>> sym.integrate(sym.sin(x), x) -кос(х) >>> sym.integrate(sym.log(x), x) х * журнал (х) - х >>> sym.integrate(2 * x + sym.sinh(x), x) 2 х + кош(х)
Также легко обрабатываются специальные функции:
>>> sym.integrate(sym.exp(-x ** 2) * sym.erf(x), x) ____ 2 \/ пи *erf (x) -------------- 4Можно вычислить определенный интеграл:
>>> sym.integrate(x**3, (x, -1, 1)) 0 >>> sym.integrate(sym.sin(x), (x, 0, sym.pi / 2)) 1 >>> sym.integrate(sym.cos(x), (x, -sym.pi/2, sym.pi/2)) 2Также поддерживаются неправильные интегралы:
>>> sym.integrate(sym.exp(-x), (x, 0, sym.oo)) 1 >>> sym.integrate(sym.exp(-x ** 2), (x, -sym.oo, sym.oo)) ____ \/ ПиSymPy может решать алгебраические уравнения, в одном и нескольких переменные, использующие
solveset():>>> sym.solveset(x ** 4 - 1, x) {-1, 1, -я, я}Как видите, в качестве первого аргумента используется выражение, которое должно быть равно 0. Он также имеет (ограниченную) поддержку трансцендентных уравнения:
>>> sym.solveset(sym.exp(x) + 1, x) {I*(2*n*pi + pi) | n в целых числах}
Системы линейных уравнений
Sympy может решить большую часть полиномиальные уравнения, а также способен решать несколько уравнения относительно нескольких переменных, дающие кортеж в качестве второго аргумент. Для этого вы используете команду
solve():>>> решение = sym.solve((x + 5 * y - 2, -3 * x + 6 * y - 15), (x, y) ) >>> решение[x], решение[y] (-3, 1)Другая альтернатива в случае полиномиальных уравнений: фактор . factor возвращает полином, разложенный на неприводимые условия, и способен вычислить факторизацию по различным домены:
>>> f = х ** 4 - 3 * х ** 2 + 1 >>> сим.фактор(f) / 2 \ / 2 \ \х - х - 1/*\х + х - 1/ >>> sym.factor(f, модуль=5) 2 2 (х - 2) * (х + 2)SymPy также может решать логические уравнения, т. е. определять, определенное логическое выражение является выполнимым или нет.
Для этого мы используем выполнимая функция:
>>> sym.satisfiable(x & y) {х: Истина, у: Истина}Это говорит нам о том, что
(x & y)является истинным, еслиxиyоба являются истинными. Если выражение не может быть истинным, то есть никакие значения его аргументов не могут выражение True, оно вернет False:>>> sym.satisfiable(x & ~x) ЛОЖЬУпражнения
- Решить систему уравнений ,
- Существуют ли логические значения
x,y, которые делают(~x | y) & (~y | x)истинными?3.2.5.1. Матрицы
Матрицы создаются как экземпляры класса Matrix:
>>> sym.Matrix([[1, 0], [0, 1]]) [1 0] [ ] [0 1]в отличие от массива NumPy, в него также можно поместить символы:
>>> x, y = sym.symbols('x, y') >>> A = sym.Matrix([[1, x], [y, 1]]) >>> А [1 х] [ ] [г 1] >>> А**2 [х*у + 1 2*х] [ ] [ 2*у х*у + 1]3.
2.5.2. Дифференциальные уравнения
SymPy способен решать (некоторые) обыкновенные дифференциальные уравнения. Для решения дифференциальных уравнений используйте dsolve. Сначала создайте неопределенная функция путем передачи cls=Function в функцию символов:
>>> f, g = sym.symbols('f g', cls=sym.Function)Функции f и g теперь не определены. Мы можем вызвать f(x), и это будет представлять неизвестная функция:
>>> f(x) е(х) >>> f(x).diff(x, x) + f(x) 2 г f(x) + ---(f(x)) 2 дх >>> sym.dsolve(f(x).diff(x, x) + f(x), f(x)) f(x) = C1*sin(x) + C2*cos(x)Аргументы ключевого слова могут быть переданы этой функции, чтобы помочь, если найти наилучшую возможную систему разрешения. Например, если вы знаете что это разделимые уравнения, вы можете использовать ключевое слово
подсказка='разделяемый'чтобы заставить dsolve разрешить его как разделимое уравнение:>>> sym.dsolve(sym.sin(x) * sym.cos(f(x)) + sym.cos(x) * sym.sin(f( x)) * f(x).diff(x), f(x), hint='разделяемый') /С1\/С1\ [f(x) = - acos|------| + 2*pi, f(x) = acos|------|] \cos(x)/ \cos(x)/
Упражнения
- Решение дифференциального уравнения Бернулли
- Решите то же уравнение, используя
hint='Бернулли'. Что вы наблюдаете?Стандартный кубический фут
Выполняет вычисления самосогласованного поля (Хартри-Фока и теории функционала плотности). Это отправные точки для большинства вычислений, поэтому этот код вызывается в большинстве случаев.
Общая информация о волновой функции
ОСНОВА
Первичный базисный набор
CHOLEKY_TOLERANCE
Допуск для разложения Холецкого тензора ЭРИ
Тип : двойной
По умолчанию : 1e-4
DF_BASIS_SCF
Вспомогательный базисный набор для расчетов плотностной подгонки SCF.
По умолчанию используется JKFIT.
DF_SCF_GUESS
Выполнить расчет плотности SCF для сходимости орбиталей перед переключением на использование точных интегралов в расчете SCF_TYPE
DIRECT
Тип : логическое значение
По умолчанию : правда
УГАДАЙ
Тип предполагаемых орбиталей. По умолчанию
READдля оптимизации геометрии после первого шага,COREдля отдельных атомов иSADв противном случае. ПредположениеHUCKELиспользует оперативные вычисления, такие как SAD, как описано в документе doi:10.1021/acs.jctc.8b01089, где также описывается предположение SAP.
Тип : строка
Возможные значения : AUTO, CORE, GWH, SAD, SADNO, SAP, HUCKEL, READ
По умолчанию : АВТО
GUESS_MIX
Смешайте HOMO/LUMO в UHF или UKS, чтобы нарушить пространственную симметрию альфа/бета.
Полезно для создания неограниченных решений с нарушенной симметрией. Обратите внимание, что эта процедура определена только для вычислений в симметрии C1.
Тип : логическое значение
По умолчанию : ложь
GUESS_PERSIST
Если верно, то повторять указанную процедуру определения орбиталей каждый раз, даже во время оптимизации геометрии.
Тип : логический
По умолчанию : ложь
INTS_ДОПУСК
Порог скрининга для выбранного метода скрининга (SCHWARZ, CSAM, DENSITY) Абсолютное значение, ниже которого TEI не учитывается.
Тип : двойной
По умолчанию : 1e-12
МАКС_МЕМ_БУФ
Максимальный объем памяти на буфер для алгоритма PK REORDER, для отладки и настройки
Тип : целое число
По умолчанию : 0
MOLDEN_WRITE
Записать выходной файл MOLDEN? Если это так, имя файла будет заканчиваться на .
molden, а префикс определяется WRITER_FILE_LABEL (если он установлен) или именем выходного файла плюс имя текущей молекулы.
Тип : логический
По умолчанию : ложь
ОРБИТАЛЫ_ЗАПИСЬ
Имя файла (с учетом регистра), в который сериализуются орбитальные данные Wavefunction.
Тип : строка
По умолчанию : Нет по умолчанию
PRINT_BASIS
Печатать базисный набор?
Тип : логическое значение
По умолчанию : ложь
PRINT_MOS
Распечатать молекулярные орбитали?
Тип : логический
По умолчанию : ложь
QCHF
Выполнить расчет QCHF?
Тип : логический
По умолчанию : ложь
ОБОЗНАЧЕНИЕ
Тип эталонной волновой функции.
Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_REFERENCE
Тип : строка
Возможные значения : RHF, ROHF, UHF, CUHF, RKS, UKS
По умолчанию : RHF
СОХРАНИТЬ_JK
Сохранить объект JK для дальнейшего использования?
Тип : логическое значение
По умолчанию : ложь
SCF_MEM_SAFETY_FACTOR
Запас памяти для размещения JK
Тип : двойной
По умолчанию : 0,75
SCF_СВОЙСТВА
SCF Свойства для расчета после оценки энергии. Обратите внимание, что это ключевое слово не используется для оценки свойств.
Тип : массив
По умолчанию : Нет по умолчанию
S_CHOLESKY_TOLERANCE
Допуск для частичного разложения Холецкого матрицы перекрытия.
Тип : двойной
По умолчанию : 1e-8
С_ОРТОГОНАЛИЗАЦИЯ
Ортогонализация SO: автоматическая, симметричная или каноническая?
S_ДОПУСК
Минимальное собственное значение S-матрицы до удаления линейных зависимостей.
Тип : двойной
По умолчанию : 1e-7
Контроль конвергенции/стабилизация
BASIS_GUESS
Ускорьте конвергенцию, выполнив предварительную SCF с этим небольшим базисным набором с последующим проецированием на полный целевой базис. Значение
TRUEвключает проецирование с использованием малого базового набора по умолчанию 3-21G, pcseg-0 или def2-SV(P).
Тип : строка
По умолчанию : ЛОЖЬ
ЗАТУХАНИЕ_КОНВЕРГЕНЦИИ
Порог сходимости плотности, после которого демпфирование больше не выполняется, если оно включено.
Рекомендуется оставить демпфирование включенным до сходимости, что является значением по умолчанию. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_DAMPING
Тип : conv double
По умолчанию : 1.0e-18
DAMPING_PERCENTAGE
Величина (в процентах) демпфирования, применяемая к ранним обновлениям плотности. 0 приведет к полному обновлению, 100 полностью остановит обновление. Значение около 20 (что соответствует 20% плотности предыдущей итерации, смешанной с текущей плотностью) может помочь решить проблемы с колебательной сходимостью.
Тип : двойной
По умолчанию : 0,0
DF_BASIS_GUESS
Когда BASIS_GUESS активен, запустите предварительный scf в режиме подгонки по плотности, используя его в качестве подходящей основы для небольшого базисного набора.
Значение
TRUEвключает аппроксимацию плотности с базисом по умолчанию, в противном случае используется указанный базис.ДИИС
Использовать ли экстраполяцию DIIS для ускорения конвергенции?
Тип : логическое значение
По умолчанию : правда
DIIS_MAX_VECS
Максимальное количество векторов ошибок, сохраняемых для экстраполяции DIIS
Тип : целое число
По умолчанию : 10
DIIS_MIN_VECS
Минимальное количество векторов ошибок, сохраненных для экстраполяции DIIS. Будет удалено в v1.7.
Тип : целое число
По умолчанию : 2
DIIS_RMS_ERROR
Использовать среднеквадратичную ошибку вместо более надежной абсолютной ошибки?
Тип : логический
По умолчанию : правда
DIIS_START
Минимальная итерация для начала хранения векторов DIIS и выполнения ADIIS/EDIIS.
Тип : целое число
По умолчанию : 1
DO_LINK
Выполните алгоритм обмена линейным масштабированием (LinK), как описано в [Ochsenfeld:1998:1663]. Применяется только к Direct SCF.
Тип : логический
По умолчанию : ложь
Д_КОНВЕРГЕНЦИЯ
Критерий сходимости плотности SCF, определяемый как среднеквадратичное или максимальное абсолютное значение орбитального градиента. См. Таблицу SCF Convergence & Algorithm для критериев сходимости по умолчанию для различных типов расчета. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_CONV
Тип : conv double
По умолчанию : 1e-6
E_CONVERGENCE
Критерий сходимости энергии СКФ.
См. Таблицу SCF Convergence & Algorithm для критериев сходимости по умолчанию для различных типов расчета.
Тип : двойной
По умолчанию : 1e-6
FAIL_ON_MAXITER
Ошибка, если мы достигнем maxiter без схождения?
Тип : логический
По умолчанию : правда
ИНФОК
Выполнять инкрементную сборку Fock?
Тип : логический
По умолчанию : ложь
INCFOCK_CONVERGENCE
Порог плотности, при котором прекращается постепенное построение матрицы Фока
Тип : conv double
По умолчанию : 1.0e-5
INCFOCK_FULL_FOCK_EVERY
Частота, с которой вычисляется полная матрица Фока при использовании INCFOCK.
N означает перестраивать каждые N итераций SCF, чтобы избежать накопления ошибок из-за инкрементной процедуры.
Тип : целое число
По умолчанию : 5
УРОВЕНЬ_SHIFT
Использовать сдвиг уровня?
Тип : двойной
По умолчанию : 0,0
УРОВЕНЬ_SHIFT_CUTOFF
Ошибка DIIS, при которой следует прекратить применение сдвига уровня
Тип : двойной
По умолчанию : 1e-2
LINK_INTS_TOLERANCE
Допуск скрининга, используемый для разреженности ERI/плотности в алгоритме LinK
Тип : conv double
По умолчанию : 1.0e-12
МАКСИТЕР
Максимальное количество итераций.
Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_MAXCYC
Тип : целое число
По умолчанию : 100
МОМ_ОСС
Абсолютные индексы орбиталей для возбуждения в MOM (+/- для альфа/бета)
Тип : массив
По умолчанию : Нет по умолчанию
МОМ_СТАРТ
Итерация для запуска MOM (или 0 для отсутствия MOM)
Тип : целое число
По умолчанию : 0
МОМ_ВИР
Абсолютные индексы орбиталей для возбуждения в MOM (+/- для альфа/бета)
Тип : массив
По умолчанию : Нет по умолчанию
SCF_INITIAL_ACCELERATOR
Использовать метод для ускорения первоначальной сходимости SCF? Используйте
НЕТтолько для DIIS (если он включен) иEDIISилиADIIS, чтобы иметь выбранный ускоритель и DIIS (если они включены).Для ссылок с ограниченным доступом
EDIISиADIISне действуют.SCF_INITIAL_FINISH_DIIS_TRANSITION
Ошибка SCF, при которой необходимо завершить линейную интерполяцию между шагами DIIS и шагами начального ускорителя SCF. Значение взято из Garza and Scuseria, DOI: 10.1063/1.4740249
Тип : double
По умолчанию : 1.0e-4
SCF_INITIAL_START_DIIS_TRANSITION
Ошибка SCF, при которой следует запустить линейную интерполяцию между шагами DIIS и шагами начального ускорителя SCF. Значение взято из Garza and Scuseria, DOI: 10.1063/1.4740249
Тип : double
По умолчанию : 1.0e-1
СОСКФ
Использовать методы конвергенции SCF второго порядка?
Тип : логический
По умолчанию : ложь
SOSCF_CONV
Порог сходимости второго порядка.
Прекратите микроитерацию на этом значении.
Тип : двойной
По умолчанию : 5.0e-3
SOSCF_MAX_ITER
Максимальное количество выполняемых микроитераций второго порядка.
Тип : целое число
По умолчанию : 5
SOSCF_MIN_ITER
Минимальное количество микроитераций второго порядка для выполнения.
Тип : целое число
По умолчанию : 1
SOSCF_PRINT
Печатаем ли мы микроитерации SOSCF?
Тип : логическое значение
По умолчанию : ложь
SOSCF_START_CONVERGENCE
Когда начинать итерации SCF второго порядка на основе RMS градиента.
Тип : двойной
По умолчанию : 1.0e-2
СТАБИЛЬНОСТЬ_АНАЛИЗ
Следует ли выполнять анализ устойчивости после сходимости. NONE предотвращает выполнение анализа. CHECK распечатает анализ стабильности волновой функции в конце расчета. FOLLOW выполнит анализ и, если будет обнаружена полностью симметричная нестабильность, попытается отследить собственный вектор и повторно запустить вычисления, чтобы найти устойчивое решение.
Дробная занятость UHF/UKS
FRAC_DIIS
Использовать ли экстраполяцию DIIS для ускорения сходимости в ГРП?
Тип : логический
По умолчанию : правда
FRAC_LOAD
Пересчитывать предположения из сохраненных орбиталей?
Тип : логический
По умолчанию : ложь
FRAC_OCC
Абсолютные индексы занятых орбиталей для частичного заполнения (+/- для альфа/бета)
Тип : массив
По умолчанию : Нет по умолчанию
FRAC_RENORMALIZE
Перенормировать матрицы C перед записью в контрольную точку?
Тип : логический
По умолчанию : правда
FRAC_START
Итерация для начала частичного заполнения орбиталей (или 0 для отсутствия частичного заполнения)
Тип : целое число
По умолчанию : 0
FRAC_VAL
Занятия указанных выше орбитальных индексов (\(0.
0\le {\rm occ} \le 1.0\))
Тип : массив
По умолчанию : нет по умолчанию
Воздействие на окружающую среду
ВНЕШНИЙ
Внешний потенциал (созданный Python или nullptr/None)
Тип : логическое значение
По умолчанию : ложь
ONEPOT_GRID_READ
Считать внешний потенциал из файла .dx?
Тип : логический
По умолчанию : ложь
ВОЗМУЩЕНИЕ_ДИПОЛЯ
Массив длины три, описывающий величину (атомные единицы) поля диполя в направлениях {x,y,z}
Тип : массив
По умолчанию : Нет по умолчанию
ПЕРТУРБ_Ч
Возмущают ли гамильтониан?
Тип : логический
По умолчанию : ложь
ВОЗМУЩЕНИЕ_ВЕЛИЧИНА
Размер возмущения (применяется только к дипольным возмущениям).
Устарело — вместо этого используйте PERTURB_DIPOLE
Тип : double
По умолчанию : 0,0
ПЕРТУРБ_С
Оператор, используемый для возмущения гамильтониана, если требуется. DIPOLE_X, DIPOLE_Y и DIPOLE_Z будут удалены в пользу опции DIPOLE в будущем
Тип : строка
Возможные значения : DIPOLE, DIPOLE_X, DIPOLE_Y, DIPOLE_Z, EMBPOT, SPHERE, DX
По умолчанию : ДИПОЛЬ
PHI_POINTS
Количество узлов азимутальной сетки для интегрирования сферического потенциала
Тип : целое число
По умолчанию : 360
РАДИУС
Радиус (бор) внешнего потенциала твердой сферы
Тип : двойной
По умолчанию : 10,0
R_POINTS
Количество узлов радиальной сетки для интегрирования сферического потенциала
Тип : целое число
По умолчанию : 100
ТЕТА_ПУНКТОВ
Количество узлов координатной сетки для интегрирования сферического потенциала
Тип : целое число
По умолчанию : 360
ТОЛЩИНА
Толщина (бор) внешнего потенциала твердой сферы
Тип : двойной
По умолчанию : 20,0
Алгоритм DFSCF
DF_BUMP_R0
Функция удара мин.
радиус
Тип : двойной
По умолчанию : 0,0
DF_BUMP_R1
Максимальный радиус функции удара
Тип : двойной
По умолчанию : 0,0
DF_DOMAINS
Алгоритм выбора области геометрической подгонки FastDF
DF_INTS_NUM_THREADS
Количество потоков для интегралов (может быть отклонено, если проблема с памятью). 0 пусто
Тип : целое число
По умолчанию : 0
DF_METRIC
Фитинг FastDF Метрический
DF_THETA
Параметр разделения метрического диапазона FastDF SR Ewald
Тип : двойной
По умолчанию : 1,0
Алгоритм COSX
COSX_INTS_ДОПУСК
Критерии отбора интегралов и промежуточных значений в COSX
Тип : conv double
По умолчанию : 1.
0e-11
COSX_RADIAL_POINTS_FINAL
Количество радиальных точек в итоговой сетке COSX.
Тип : целое число
По умолчанию : 35
COSX_RADIAL_POINTS_INITIAL
Количество радиальных точек в исходной сетке COSX.
Тип : целое число
По умолчанию : 25
COSX_SPHERICAL_POINTS_FINAL
Количество сферических точек в итоговой сетке COSX.
Тип : целое число
По умолчанию : 110
COSX_SPHERICAL_POINTS_INITIAL
Количество сферических точек в исходной сетке COSX.
Тип : целое число
По умолчанию : 50
Алгоритм предположения SAD
SAD_D_CONVERGENCE
Критерий сходимости для плотности SCF в расчете SAD, аналог D_CONVERGENCE
Тип : conv double
По умолчанию : 1e-5
SAD_E_CONVERGENCE
Критерий сходимости для энергии SCF в предположении SAD, аналогичный E_CONVERGENCE
Тип : conv double
По умолчанию : 1e-5
ДПФ
ДПФ_АЛЬФА
Параметр точного обмена ДПФ
Тип : двойной
По умолчанию : 0,0
ДПФ_АЛЬФА_С
Гибридный параметр корреляции ДПФ
Тип : двойной
По умолчанию : 0,0
ДПФ_БАЗИС_ДОПУСК
Основа отсечки DFT.
Тип : двойной
По умолчанию : 1.0e-12
ДПФ_БС_РАДИУС_АЛЬФА
Коэффициент эффективного радиуса БС в радиальной сетке.
Тип : двойной
По умолчанию : 1,0
DFT_DISPERSION_PARAMETERS
Параметры, определяющие поправку на дисперсию. См. Функционалы таблицы -D для значений по умолчанию и Коррекции дисперсии таблицы для порядка, в котором параметры должны быть указаны в этой опции массива. Не используется для функционалов, построенных пользователем.
Тип : массив
По умолчанию : Нет по умолчанию
ДФТ_GRAC_АЛЬФА
Градиент регуляризованной асимптотической коррекции альфа-значения
Тип : double
По умолчанию : 0,5
DFT_GRAC_BETA
Градиентное регуляризованное значение бета-асимптотической коррекции
Тип : двойной
По умолчанию : 40,0
DFT_GRAC_SHIFT
Значение сдвига асимптотической коррекции, упорядоченное по градиенту
Тип : double
По умолчанию : 0,0
ДПФ_ЯДЕРНАЯ_СХЕМА
Ядерная схема.
Тип : строка
Возможные значения : TREUTLER, BECKE, NAIVE, STRATMANN, SBECKE
По умолчанию : TREUTLER
ДФТ_ОМЕГА
Параметр разделения диапазонов ДПФ
Тип : двойной
По умолчанию : 0,0
ДФТ_ОМЕГА_С
Параметр разделения диапазона корреляции ДПФ
Тип : двойной
По умолчанию : 0,0
DFT_PRUNING_SCHEME
Выберите подход для обрезки. Options
ROBUSTandTREUTLERprune based on regions (proximity to nucleus) whileFLATP_GAUSSIAND_GAUSSIANP_SLATERD_SLATERLOG_GAUSSIANLOG_SLATERprune based on decaying functions (experts only!).Рекомендуемая схема
НАДЕЖНЫЙ.
Тип : строка
По умолчанию : НЕТ
DFT_RADIAL_POINTS
Количество радиальных точек.
Тип : целое число
По умолчанию : 75
ДПФ_РАДИАЛЬНАЯ_СХЕМА
Радиальная схема.
Тип : строка
Возможные значения : TREUTLER, BECKE, MULTIEXP, EM, MURA
По умолчанию : TREUTLER
DFT_SPHERICAL_POINTS
Количество сферических точек (число точек Лебедева).
Тип : целое число
По умолчанию : 302
ДПФ_СФЕРИЧЕСКАЯ_СХЕМА
Сферическая схема.
ДФТ_V2_RHO_CUTOFF
Минимальная отсечка для второй производной
Тип : двойной
По умолчанию : 1.e-6
ДФТ_ВВ10_Б
Определить параметр VV10 b
Тип : двойной
По умолчанию : 0,0
ДФТ_ВВ10_С
Определение параметра VV10 C
Тип : двойной
По умолчанию : 0,0
ДФТ_ВВ10_ПОСТСКФ
коррекция post-scf VV10
Тип : логический
По умолчанию : ложь
ДПФ_ВВ10_РАДИАЛЬНЫЕ_ТОЧКИ
Количество радиальных точек для интегрирования VV10 NL.
Тип : целое число
По умолчанию : 50
DFT_VV10_SPHERICAL_POINTS
Количество сферических точек (количество точек Лебедева) для интегрирования VV10 NL.
Тип : целое число
По умолчанию : 146
ЛОКАЛЬНОЕ_СХОДЕНИЕ
Схождение по процедуре орбитальной локализации
Тип : conv double
По умолчанию : 1e-12
ЛОКАЛЬНЫЙ_МАКСИТЕР
Макситер по процедуре орбитальной локализации
Тип : целое число
По умолчанию : 200
NL_DISPERSION_PARAMETERS
Параметры, определяющие поправку на дисперсию -NL/-V.
Сначала b, затем C
Тип : массив
По умолчанию : нет по умолчанию
СОХРАНИТЬ_УВЧ_НОС
Сохранение NOs УВЧ
Тип : логический
По умолчанию : ложь
UHF_NOONS
Количество ПОЛДЕНИЙ для печати в УВЧ расчете
Тип : строка
По умолчанию : 3
ТДСКФ
TDSCF_COEFF_CUTOFF
Отсечка для печати возбуждений и девозбуждений, влияющих на каждое возбужденное состояние
Тип : двойной
По умолчанию : 0,1
TDSCF_GUESS
Тип предположения, в настоящее время поддерживаются только «знаменатели»
TDSCF_MAXITER
Максимальное количество итераций решателя TDSCF
Тип : целое число
По умолчанию : 60
TDSCF_PRINT
Уровень детализации в TDSCF
Тип : целое число
По умолчанию : 1
TDSCF_R_CONVERGENCE
Порог сходимости для нормы вектора невязки.
Если не установлено, по умолчанию используется D_CONVERGENCE
Тип : conv double
По умолчанию : 1e-4
TDSCF_STATES
Количество корней (возбужденных состояний), к которым мы должны стремиться. Это может быть либо целое число (общее количество состояний для поиска), либо список (количество состояний за один повтор). Последнее справедливо только в том случае, если система обладает симметрией. Кроме того, при использовании симметрии общее количество состояний будет перераспределяться между невозвратами.
Тип : массив
По умолчанию : Нет по умолчанию
ТДСКФ_ТДА
Работа с приближением Тамма-Данкова (TDA), использует приближение со случайной фазой (RPA), если оно ложно
По умолчанию : ложь
Какие переходные дипольные моменты распечатать: - E_TDM_LEN : электрические переходные дипольные моменты, представление длины - E_TDM_VEL : электрические переходные дипольные моменты, представление скорости - M_TDM : магнитные переходные дипольные моменты
Тип : массив
По умолчанию : Нет по умолчанию
Управляет включением триплетных состояний, что допустимо только для ограниченных ссылок. Допустимые варианты: - none : триплеты не вычисляются (по умолчанию) - также : включаются триплеты и синглеты с наименьшей энергией в соотношении 50-50. Обратите внимание, что синглеты являются привилегированными, т. Е. Если вы стремитесь сойтись всего в 5 состояниях, 3 будут синглетами, а 2 будут триплетами. - only : вычисляются только триплетные состояния
Допустимые варианты: - none : триплеты не вычисляются (по умолчанию) - также : включаются триплеты и синглеты с наименьшей энергией в соотношении 50-50. Обратите внимание, что синглеты являются привилегированными, т. Е. Если вы стремитесь сойтись всего в 5 состояниях, 3 будут синглетами, а 2 будут триплетами. - only : вычисляются только триплетные состояния
объединить омега-обмен и обмен Хартри-Фока в одну матрицу для повышения эффективности? Отключено, пока не исправлено.
Тип : логический
По умолчанию : ложь
Выберите алгоритм PK для использования. В целях отладки выбор будет автоматизирован позже.
Все плотности считаются несимметричными, только для отладки.
Тип : логический
По умолчанию : ложь
Максимальное количество пакетов для чтения суперматрицы PK.
Тип : целое число
По умолчанию : 500
Деактивировать в основном алгоритме. В целях отладки.
Тип : логический
По умолчанию : ложь
Тип волновой функции
При использовании STABILITY_ANALYSIS = FOLLOW приращение для изменения значения FOLLOW_STEP_SCALE, если мы окажемся в одном и том же решении SCF.
Тип : двойной
По умолчанию : 0,2
При использовании STABILITY_ANALYSIS FOLLOW , на сколько масштабировать шаг вдоль собственного вектора.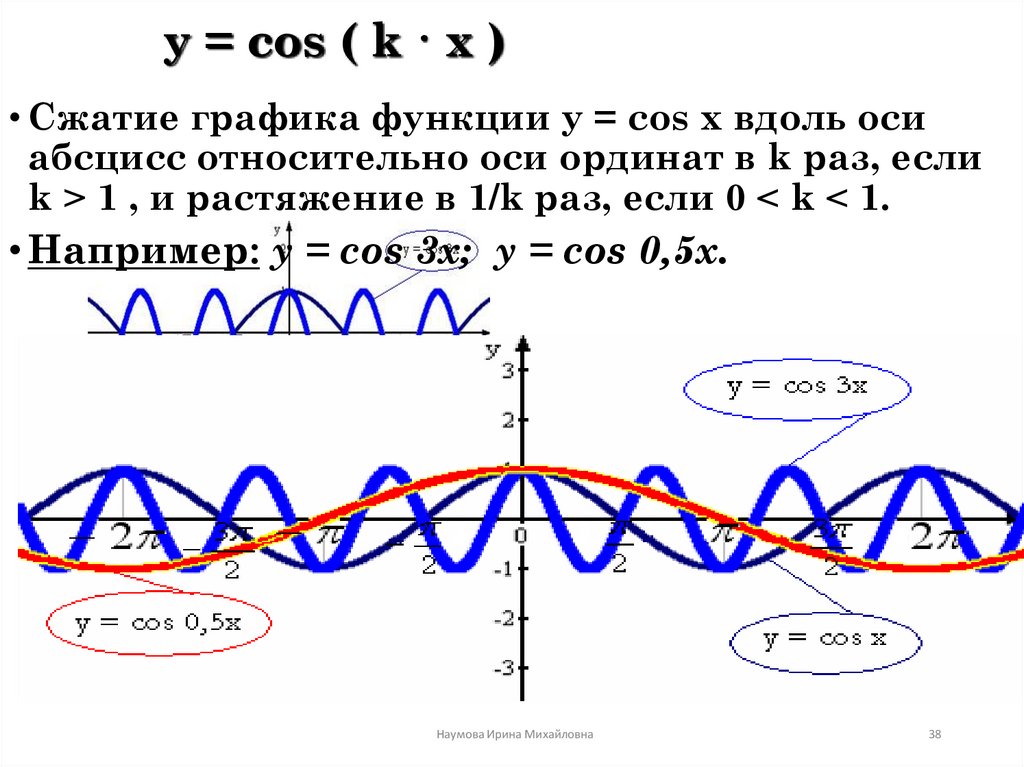 Полный шаг \(pi/2\) соответствует значению 1,0.
Полный шаг \(pi/2\) соответствует значению 1,0.
Тип : двойной
По умолчанию : 0,5
При использовании STABILITY_ANALYSIS FOLLOW , максимальное количество попыток орбитальной оптимизации, чтобы сделать волновую функцию стабильной.
Тип : целое число
По умолчанию : 1
Размеры размерности распределенной матрицы
Тип : массив
По умолчанию : Нет По умолчанию
Запускать параллельно?
Тип : логический
По умолчанию : ложь
Размеры процессорной сетки
Тип : массив
По умолчанию : Нет по умолчанию
Размер плитки для распределенных матриц
Тип : целое число
По умолчанию : 512
Собираетесь делать SAPT? Если да, то какая часть?
Тип : строка
По умолчанию : ЛОЖЬ
Условие подбора, т. е. пороговое значение собственного значения для RI. Аналогично S_TOLERANCE
Тип : двойной
По умолчанию : 1.0e-10
Кэширование ввода-вывода для поправок CP и т. д.
Критерии отбора значений базовой функции в сетках COSX
Тип : conv double
По умолчанию : 1.0e-10
Критерии отбора плотности пар оболочек в COSX
Тип : conv double
По умолчанию : 1.
 0e-10
0e-10
Можно ли повысить эффективность скрининга COSX путем постепенного построения матрицы Фока?
Тип : логический
По умолчанию : ложь
Уменьшить числовые ошибки COSX с помощью подгонки внахлестку?
Тип : логический
По умолчанию : правда
Схема обрезки для сетей COSX
Тип : строка
По умолчанию : НАДЕЖНЫЙ
Основа фитинга плотности, используемая в SAD
SAD порог разложения по плотности приближения
Тип : conv double
По умолчанию : 1e-7
Принуждать к равномерному распределению занятий по последней частично занятой орбитальной оболочке?
Тип : логический
По умолчанию : правда
Максимальное количество атомарных итераций SCF в рамках SAD
Тип : целое число
По умолчанию : 50
Количество информации SAD для печати на выходе
Тип : целое число
По умолчанию : 0
Тип SCF, используемый для атомарных расчетов в SAD-догадке
Тип : строка
Возможные значения : DIRECT, DF, MEM_DF, DISK_DF, PK, OUT_OF_CORE, CD, GTFOCK
По умолчанию : DF
Использовать усредненные по спину заселенности вместо основного спинового состояния атома в дробном SAD?
Тип : логический
По умолчанию : правда
Максимальное количество точек сетки на блок оценки.
Тип : целое число
По умолчанию : 256
Максимальный радиус для завершения подразделения блока октодерева [au].
Тип : двойной
По умолчанию : 3.0
Минимальное количество точек сетки на блок оценки.
Тип : целое число
По умолчанию : 100
Схема блокировки для ДПФ.
для LibXC. Отрицательное значение отключает эту функцию и используются значения по умолчанию LibXC.
Тип : двойной
По умолчанию : -1,0
Градиентная регуляризованная форма функционала асимптотической коррекции корр.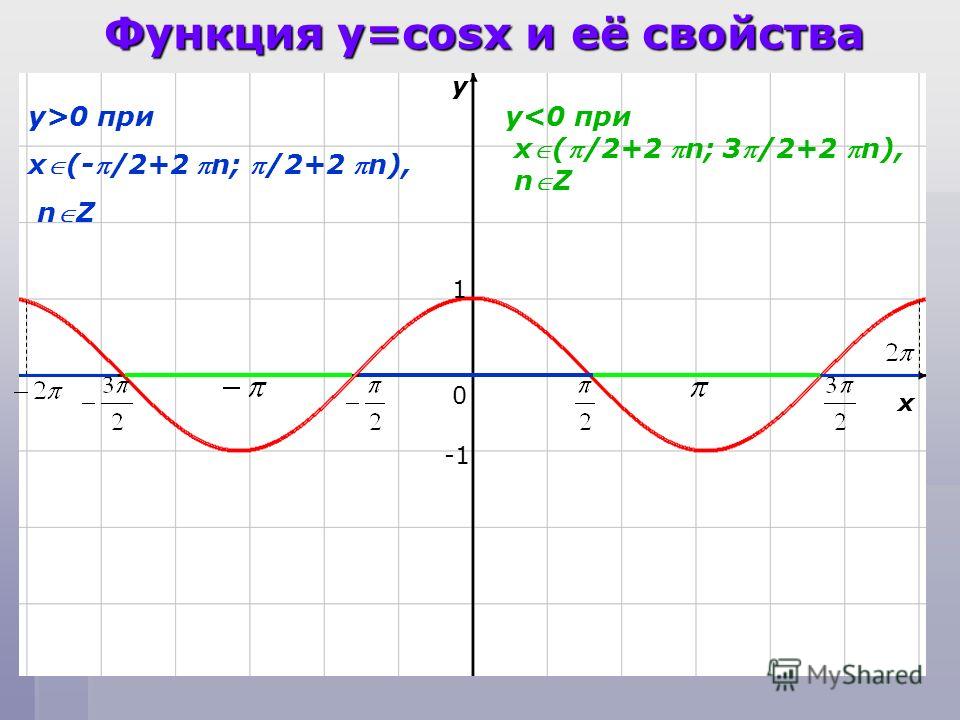
Градиентная регуляризованная форма функционала асимптотической коррекции.
Спецификация сетки ДПФ, например SG1.
Распространение альфа-канала для логарифмической обрезки.
Тип : двойной
По умолчанию : 1,0
Удалить из квадратурной сетки точки, превышающие пространственную протяженность базисных функций.
Тип : логическое значение
По умолчанию : правда
Отсечка Rho для интеграции VV10 NL.
Тип : двойной
По умолчанию : 1.
 e-8
e-8
отсечка по весу сетки. Отключить с -1.0.
Тип : двойной
По умолчанию : 1.0e-15
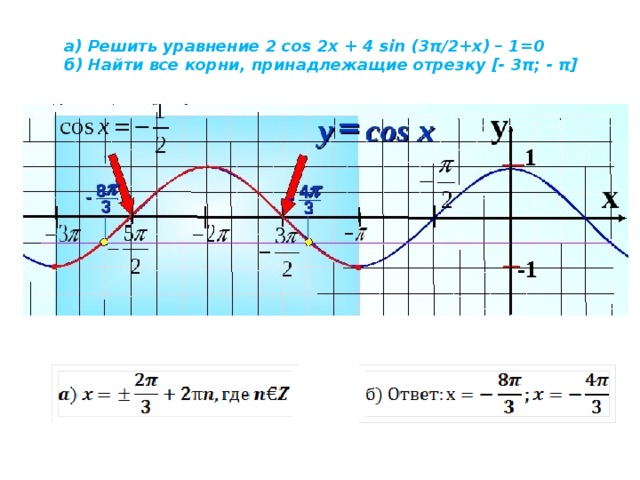
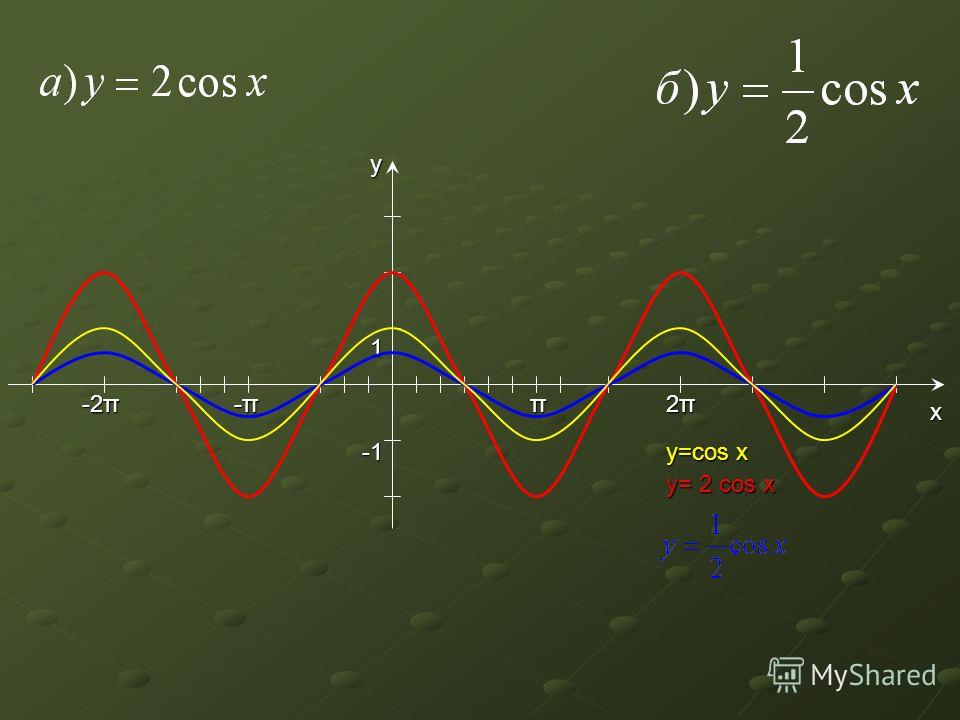 См. также постоянство аналитических отношений.
См. также постоянство аналитических отношений.
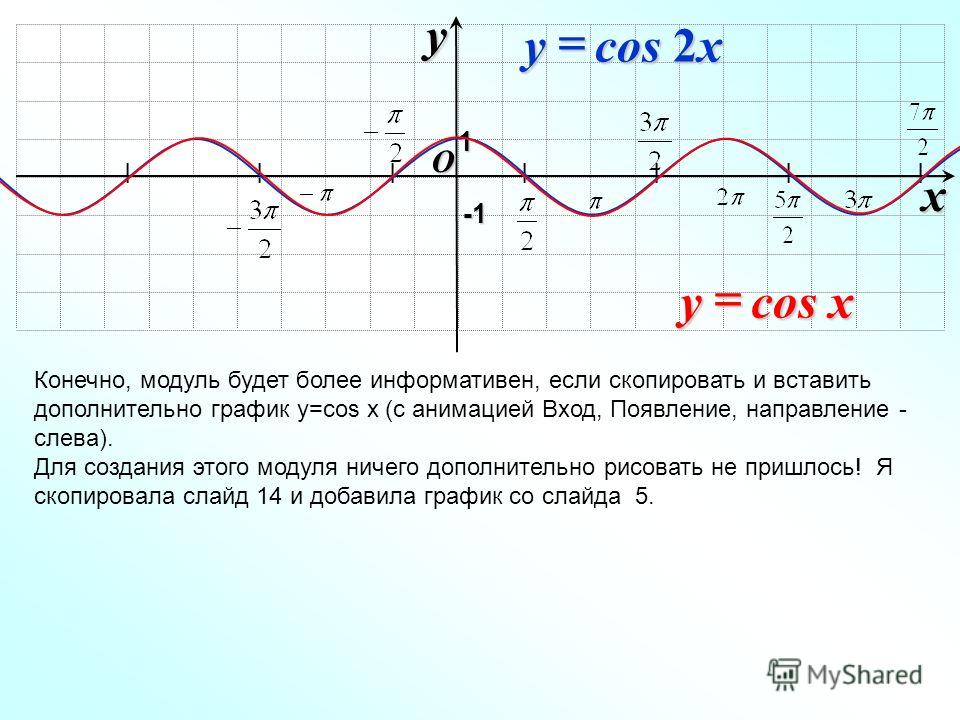 03.2013 14:45:25
03.2013 14:45:25эта страница посвящена той, которая используется в комплексных числах)
79
9 i π + 1 = 0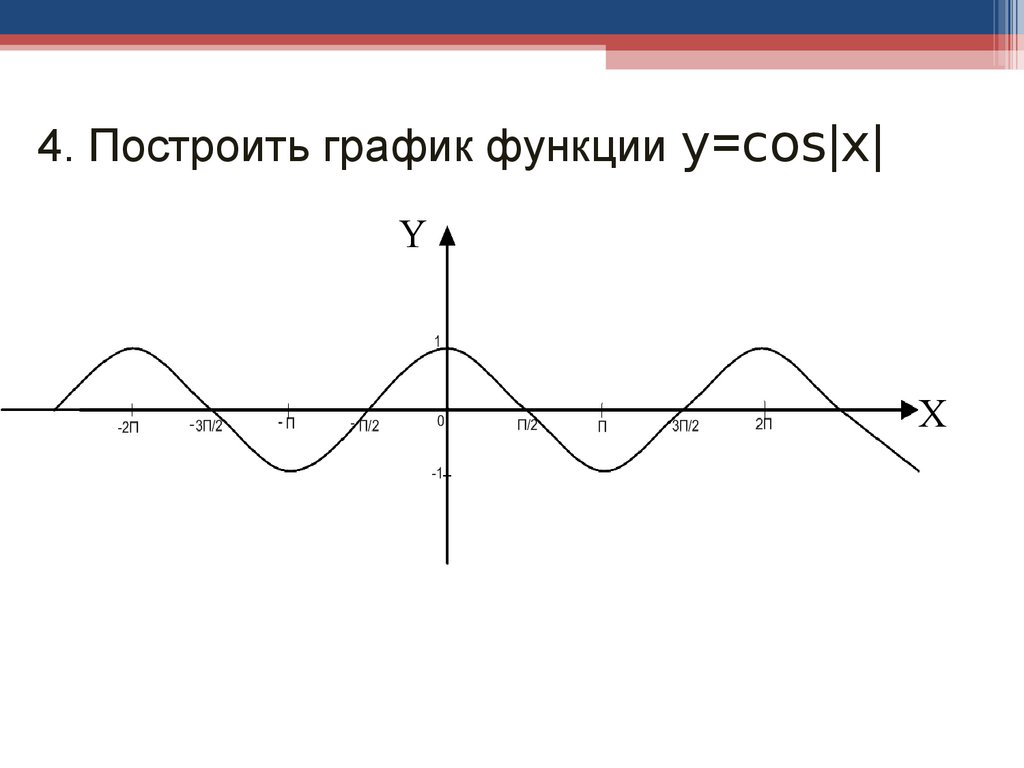
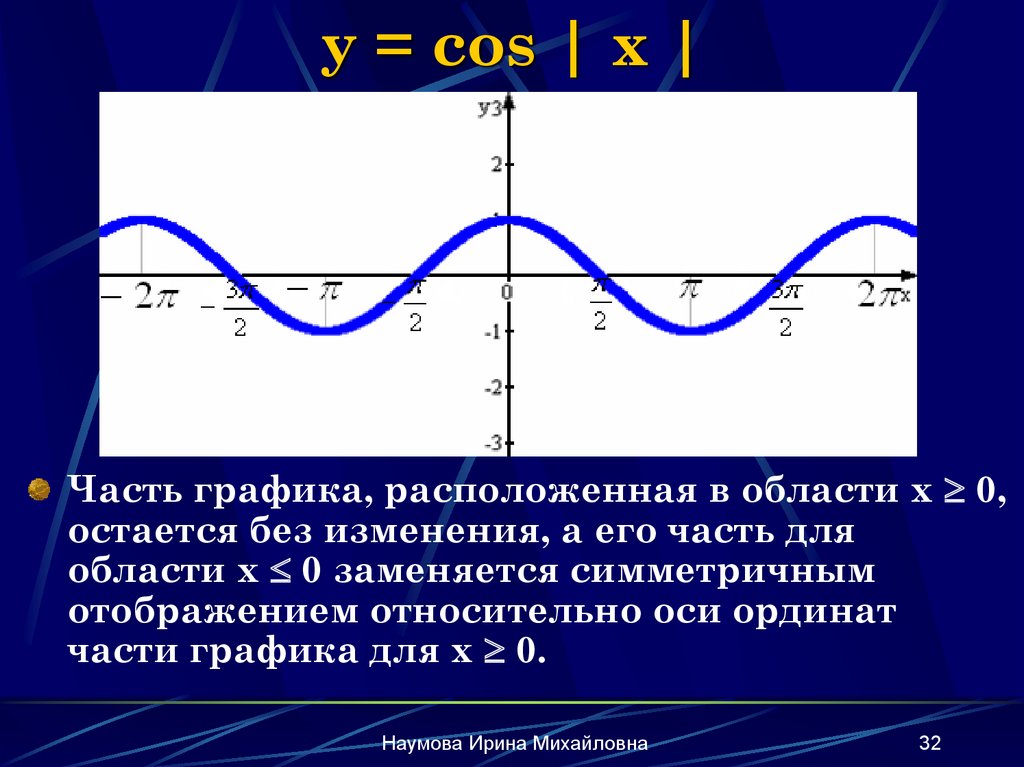 ..
..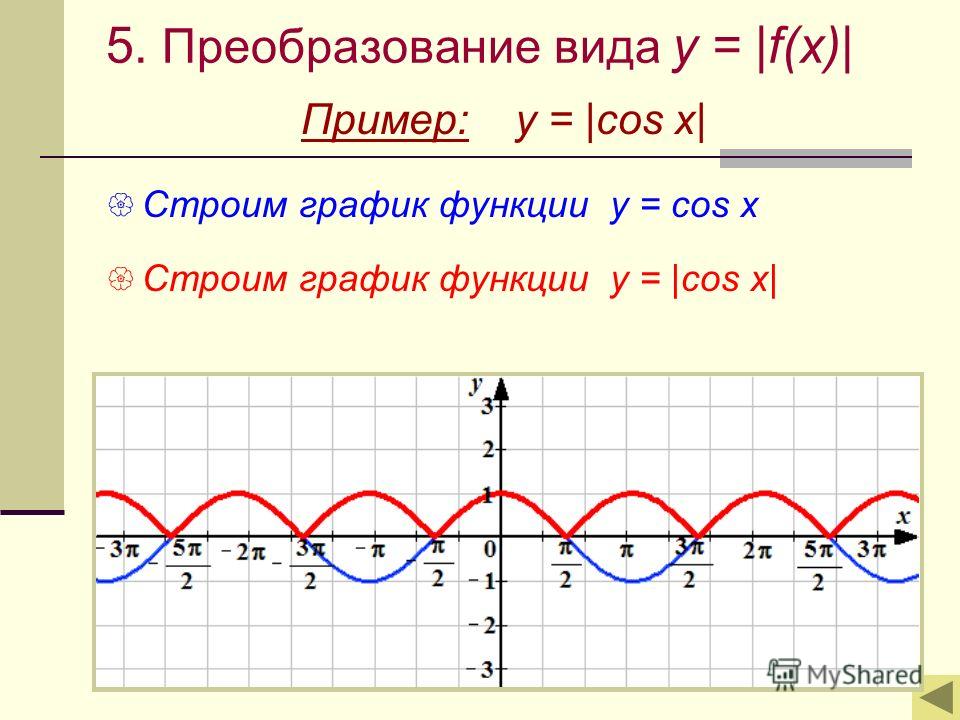 4! x 3 3! + x 5 5! − ... )
4! x 3 3! + x 5 5! − ... )Здесь мы показываем число 0,45 + 0,89 i
E I x создает круг Radius 1
_5.jpg) мы можем превратить любую точку (например, 3 + 4i ) в re i x form by finding the correct value of x and r :
мы можем превратить любую точку (например, 3 + 4i ) в re i x form by finding the correct value of x and r :10110110110110110110111.


 Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.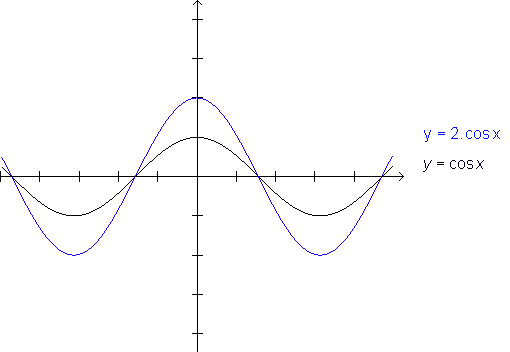 02.19
02.19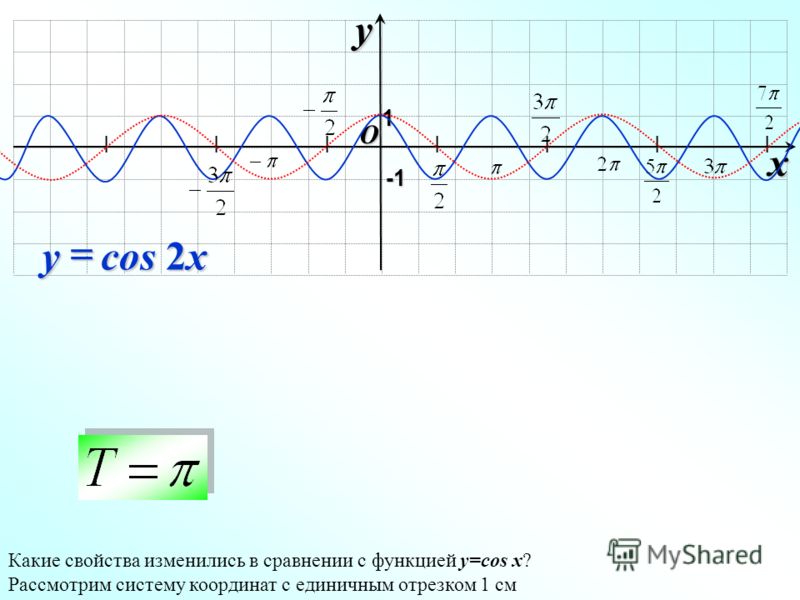 2 xsinx+cosx+tan2x по заданному числу градусов xx.
2 xsinx+cosx+tan2x по заданному числу градусов xx. 2 + bx + c = 0.ax2+bx+c=0.Формат входных данных
2 + bx + c = 0.ax2+bx+c=0.Формат входных данных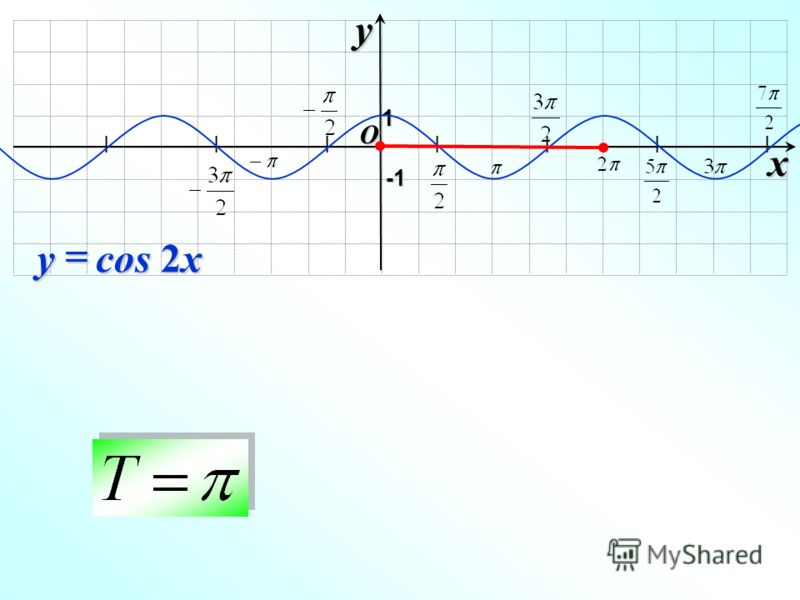 2}{4\tg \left(\dfrac{\pi}{n}\right)}S=4tg(nπ)n⋅a2Даны два числа: натуральное число nn и вещественное число aa. Напишите программу, которая находит площадь указанного правильного многоугольника.
2}{4\tg \left(\dfrac{\pi}{n}\right)}S=4tg(nπ)n⋅a2Даны два числа: натуральное число nn и вещественное число aa. Напишите программу, которая находит площадь указанного правильного многоугольника.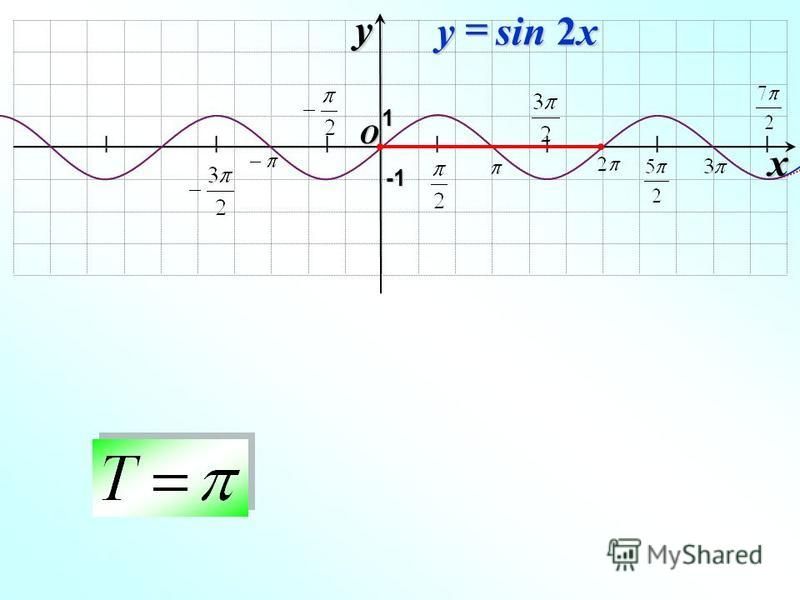 Не используйте его для непроверенного ввода.
Не используйте его для непроверенного ввода.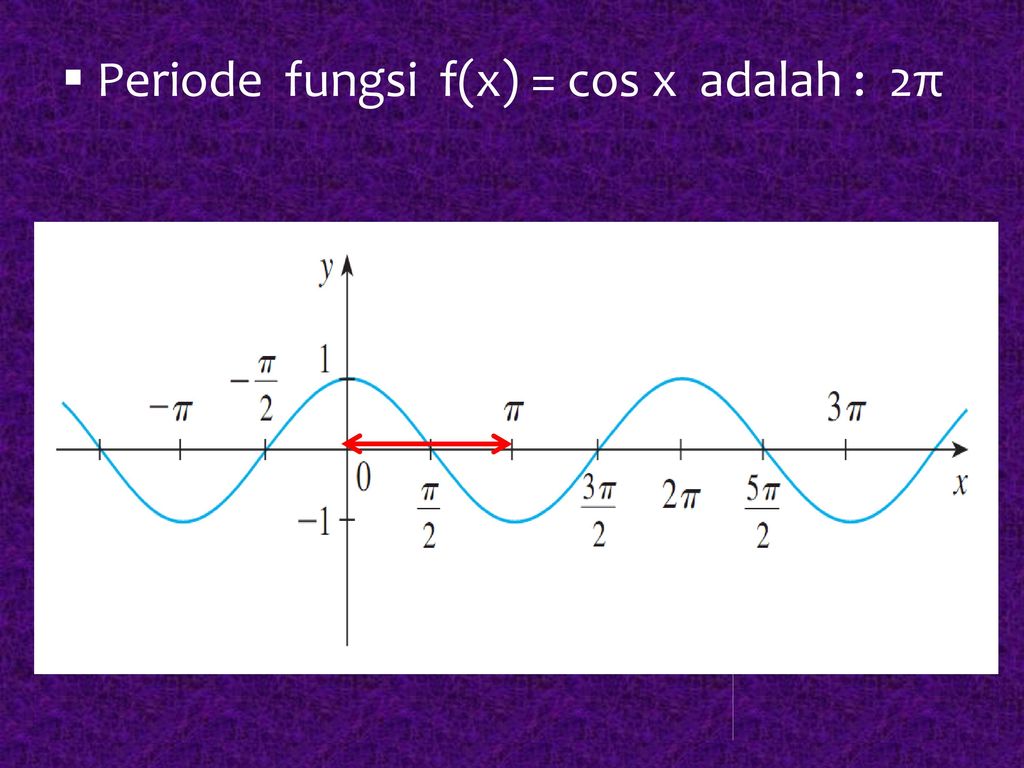
 2.1.1. Использование SymPy в качестве калькулятора
2.1.1. Использование SymPy в качестве калькулятора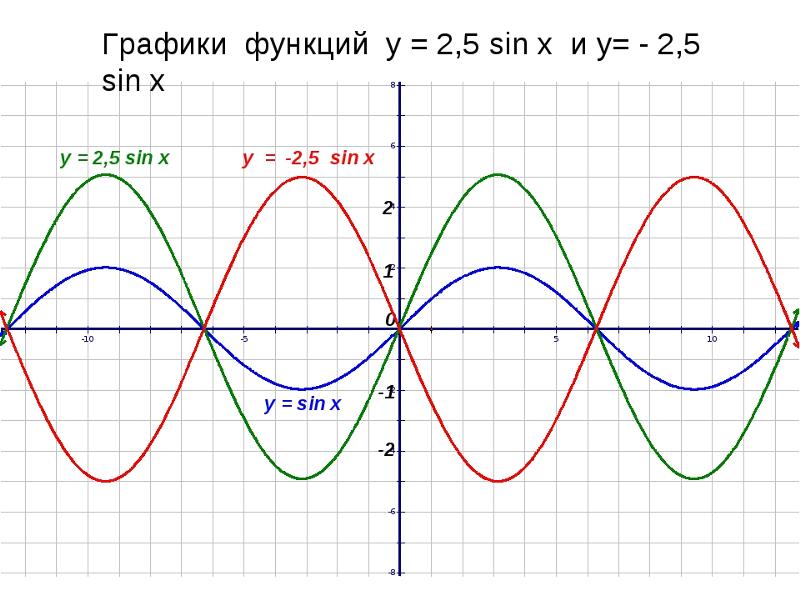 оо > 99999
Истинный
>>> сим.оо + 1
оо
оо > 99999
Истинный
>>> сим.оо + 1
оо
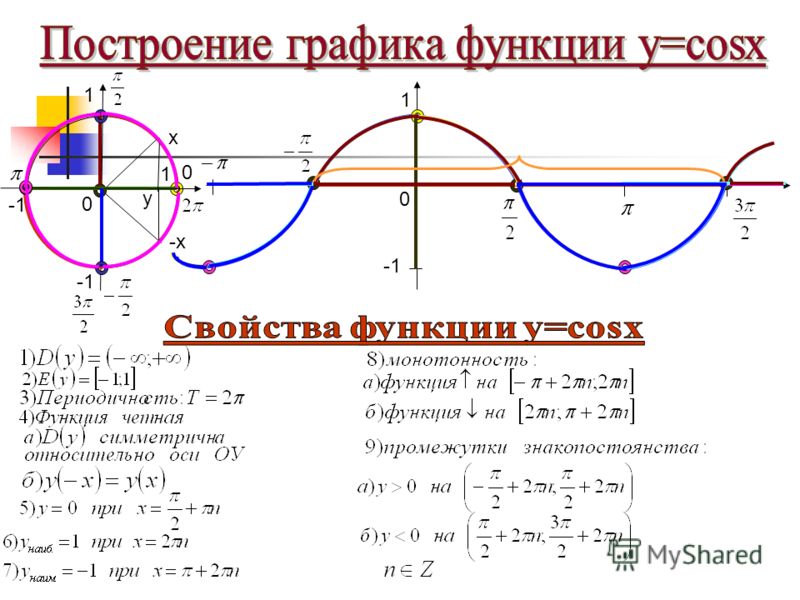
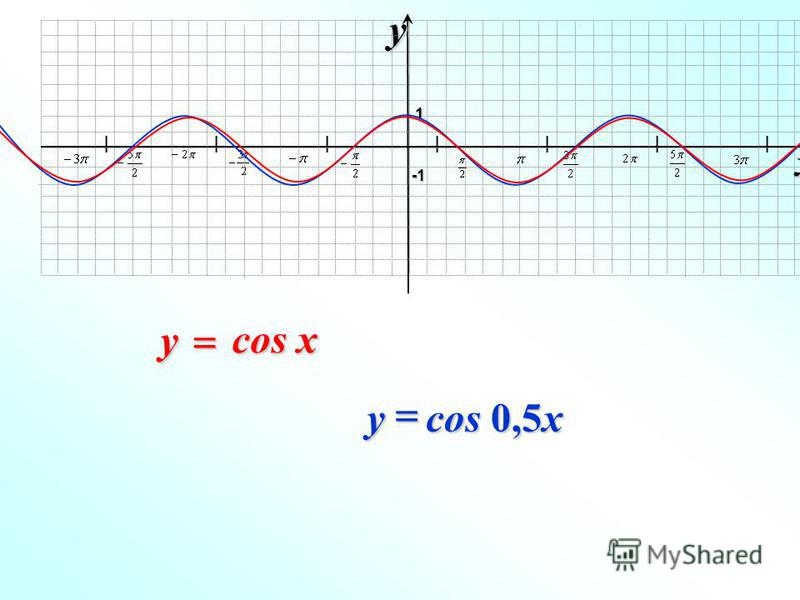 diff(sym.sin(2 * x), x, 1)
2*кос(2*х)
>>> sym.diff(sym.sin(2 * x), x, 2)
-4*грех(2*х)
>>> sym.diff(sym.sin(2 * x), x, 3)
-8*cos(2*x)
diff(sym.sin(2 * x), x, 1)
2*кос(2*х)
>>> sym.diff(sym.sin(2 * x), x, 2)
-4*грех(2*х)
>>> sym.diff(sym.sin(2 * x), x, 3)
-8*cos(2*x)
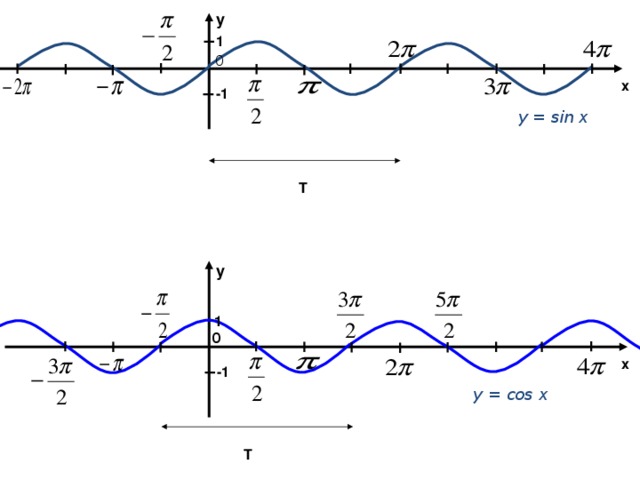 sin(x), x)
-кос(х)
>>> sym.integrate(sym.log(x), x)
х * журнал (х) - х
>>> sym.integrate(2 * x + sym.sinh(x), x)
2
х + кош(х)
sin(x), x)
-кос(х)
>>> sym.integrate(sym.log(x), x)
х * журнал (х) - х
>>> sym.integrate(2 * x + sym.sinh(x), x)
2
х + кош(х)
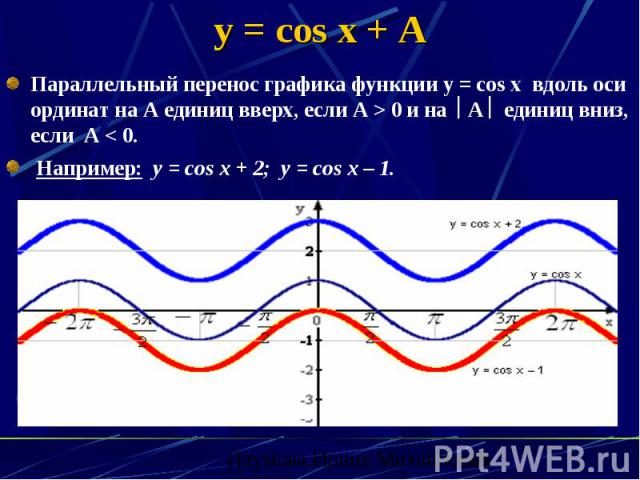 solveset(sym.exp(x) + 1, x)
{I*(2*n*pi + pi) | n в целых числах}
solveset(sym.exp(x) + 1, x)
{I*(2*n*pi + pi) | n в целых числах}
 Для этого мы используем
выполнимая функция:
Для этого мы используем
выполнимая функция: 2.5.2. Дифференциальные уравнения
2.5.2. Дифференциальные уравнения cos(f(x)) + sym.cos(x) * sym.sin(f( x)) * f(x).diff(x), f(x), hint='разделяемый')
/С1\/С1\
[f(x) = - acos|------| + 2*pi, f(x) = acos|------|]
\cos(x)/ \cos(x)/
cos(f(x)) + sym.cos(x) * sym.sin(f( x)) * f(x).diff(x), f(x), hint='разделяемый')
/С1\/С1\
[f(x) = - acos|------| + 2*pi, f(x) = acos|------|]
\cos(x)/ \cos(x)/
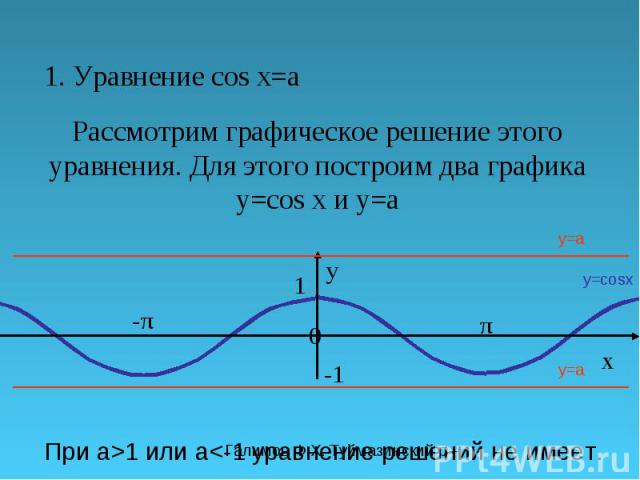 По умолчанию используется JKFIT.
По умолчанию используется JKFIT.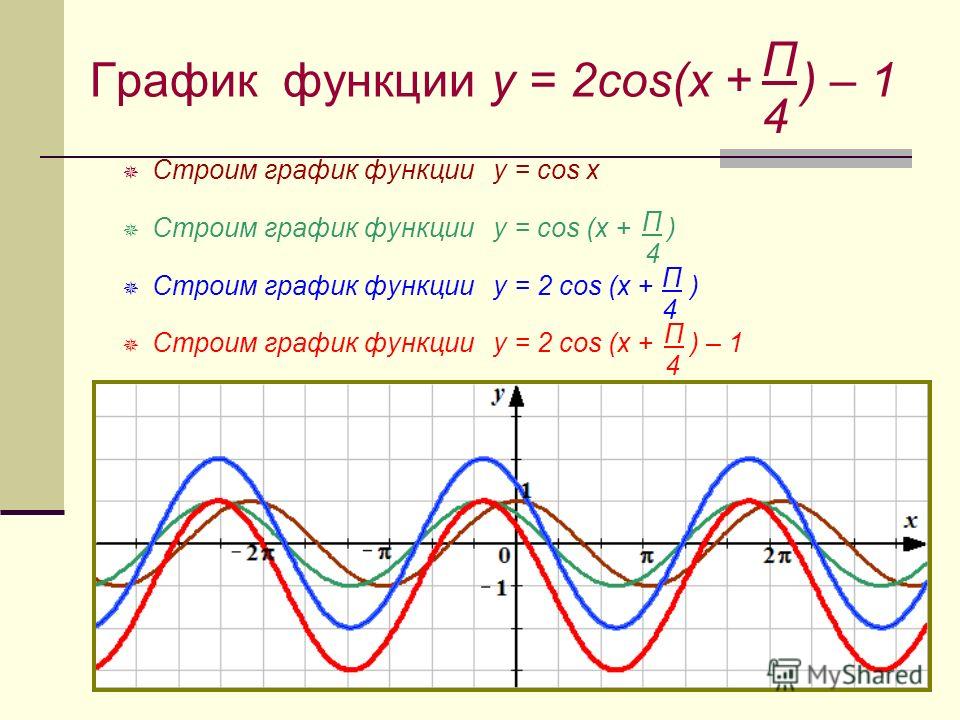 Полезно для создания неограниченных решений с нарушенной симметрией. Обратите внимание, что эта процедура определена только для вычислений в симметрии C1.
Полезно для создания неограниченных решений с нарушенной симметрией. Обратите внимание, что эта процедура определена только для вычислений в симметрии C1. molden, а префикс определяется WRITER_FILE_LABEL (если он установлен) или именем выходного файла плюс имя текущей молекулы.
molden, а префикс определяется WRITER_FILE_LABEL (если он установлен) или именем выходного файла плюс имя текущей молекулы.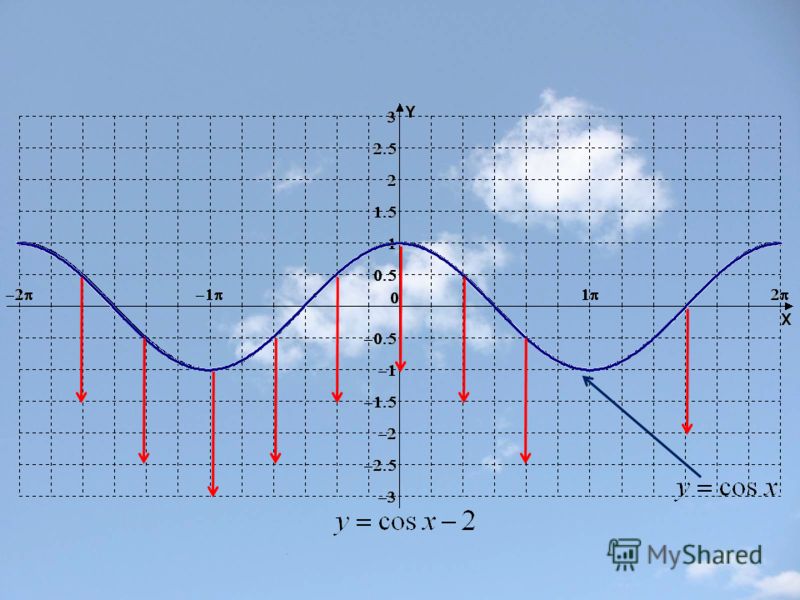 Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_REFERENCE
Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_REFERENCE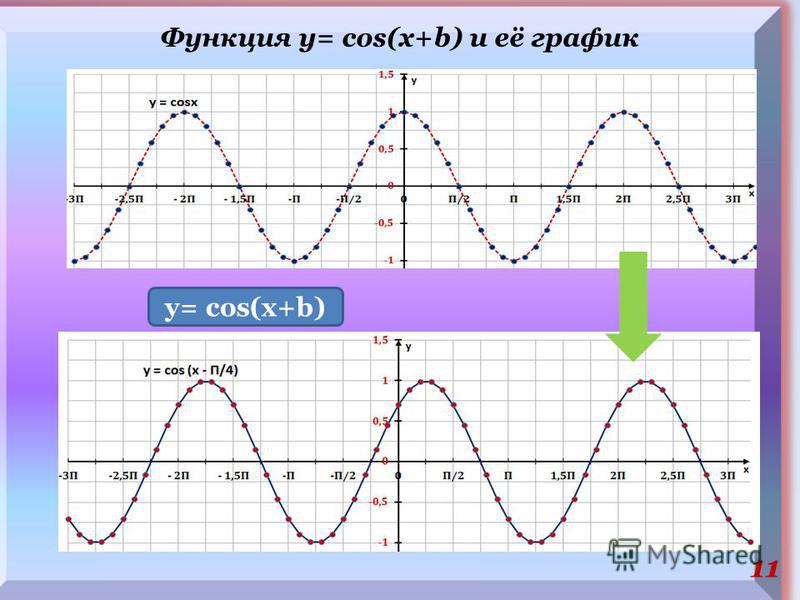
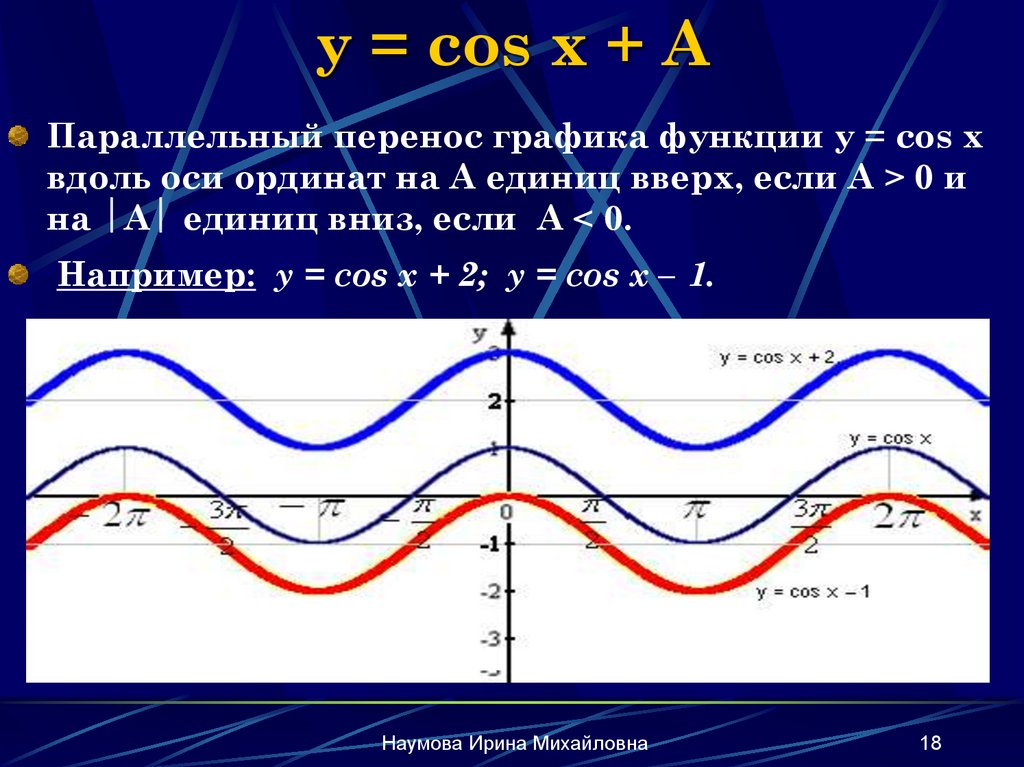 Рекомендуется оставить демпфирование включенным до сходимости, что является значением по умолчанию. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_DAMPING
Рекомендуется оставить демпфирование включенным до сходимости, что является значением по умолчанию. Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_DAMPING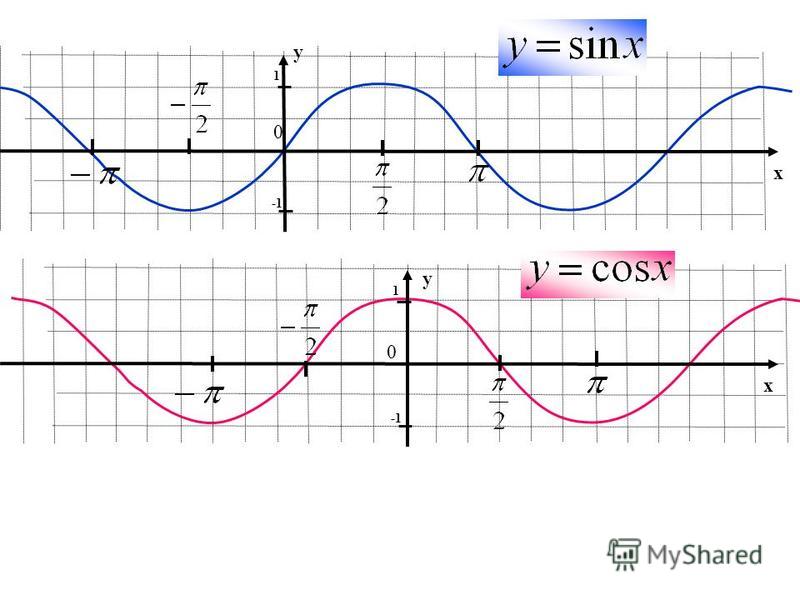 Значение
Значение 
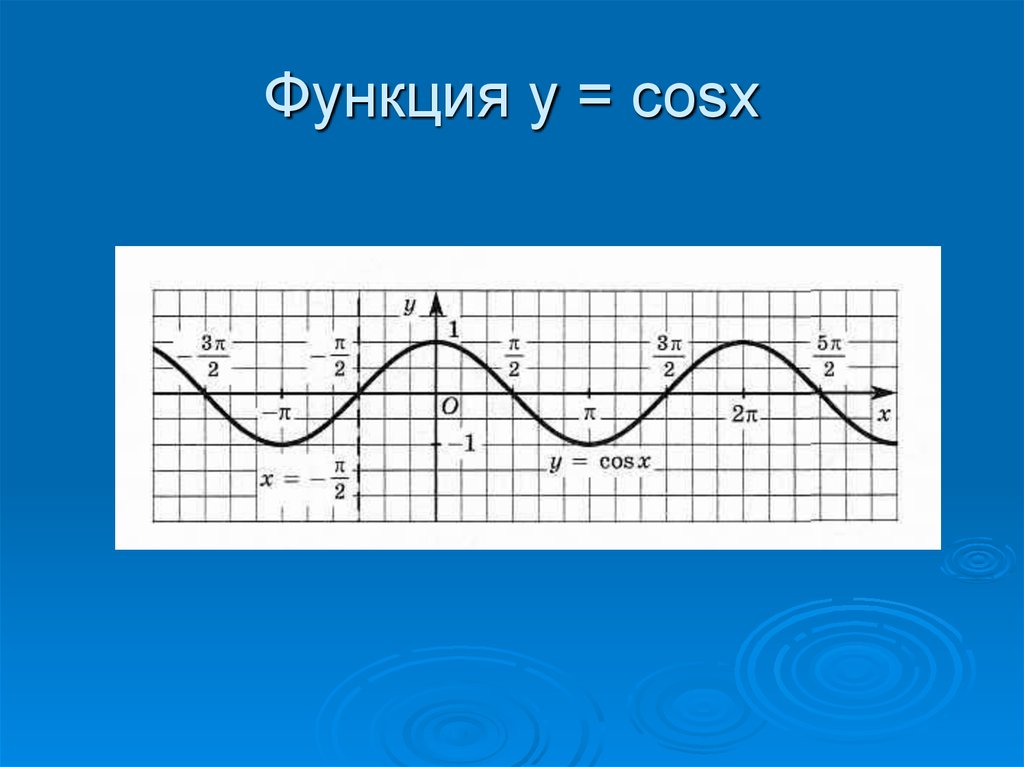 См. Таблицу SCF Convergence & Algorithm для критериев сходимости по умолчанию для различных типов расчета.
См. Таблицу SCF Convergence & Algorithm для критериев сходимости по умолчанию для различных типов расчета.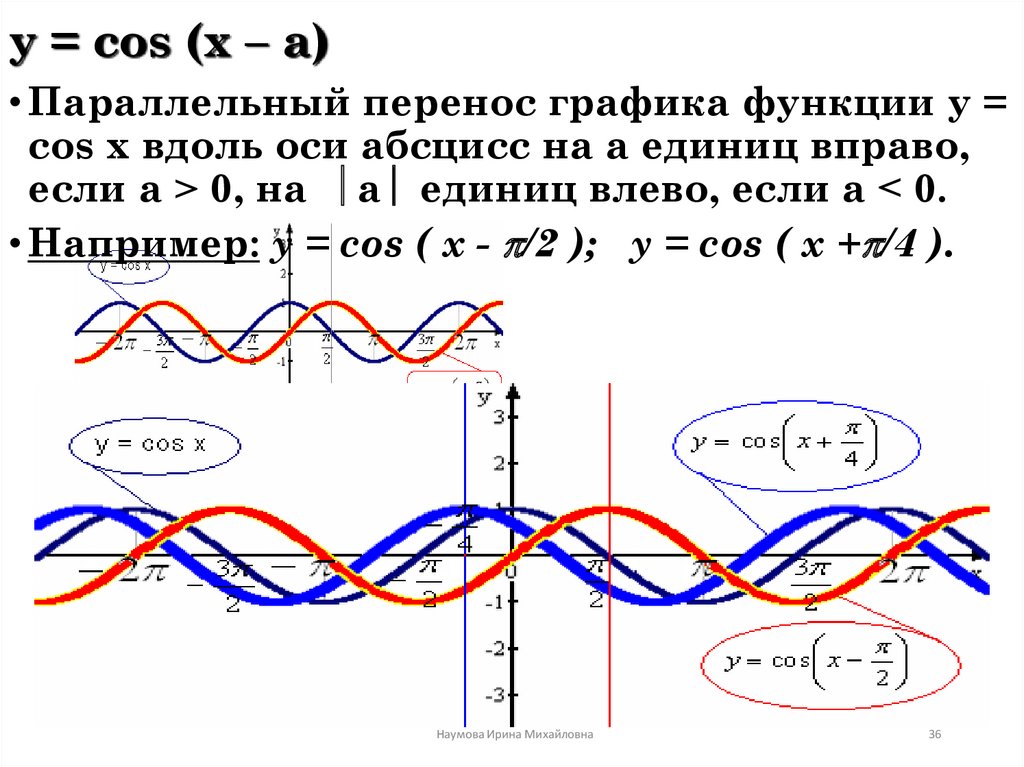 N означает перестраивать каждые N итераций SCF, чтобы избежать накопления ошибок из-за инкрементной процедуры.
N означает перестраивать каждые N итераций SCF, чтобы избежать накопления ошибок из-за инкрементной процедуры.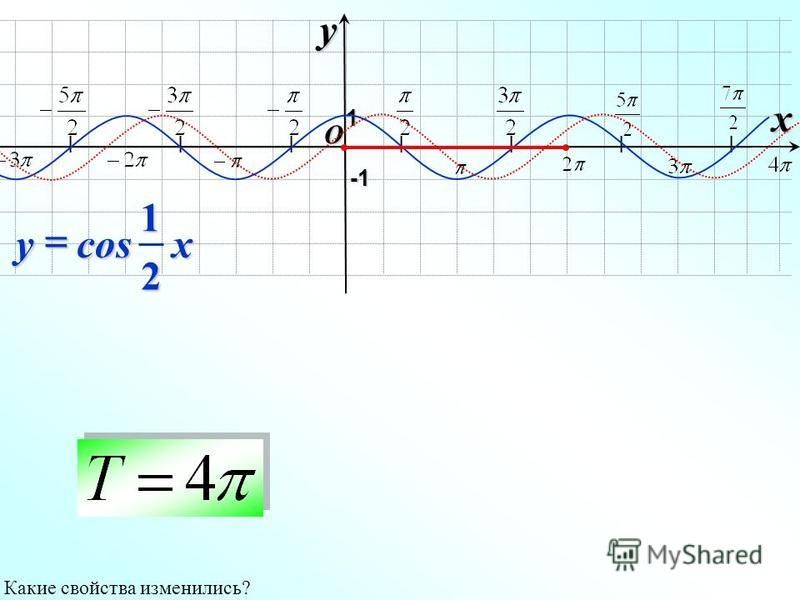 Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_MAXCYC
Интерфейс Cfour: Ключевое слово преобразуется в CFOUR_SCF_MAXCYC Для ссылок с ограниченным доступом
Для ссылок с ограниченным доступом 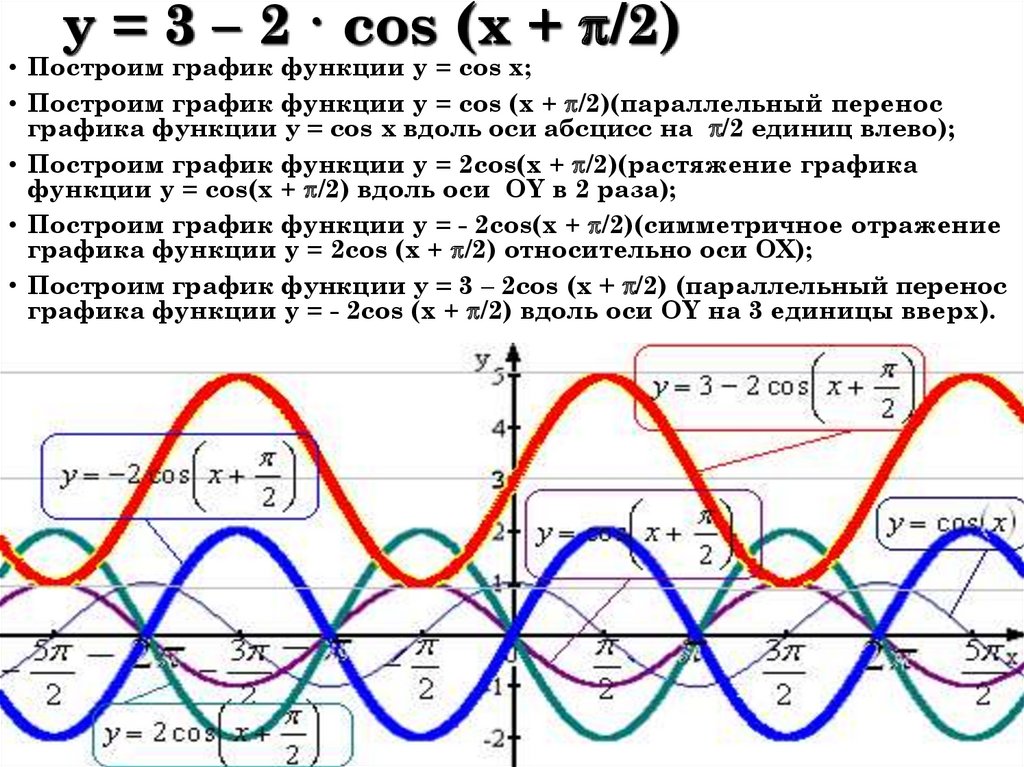 Прекратите микроитерацию на этом значении.
Прекратите микроитерацию на этом значении.
 0\le {\rm occ} \le 1.0\))
0\le {\rm occ} \le 1.0\)) Устарело — вместо этого используйте PERTURB_DIPOLE
Устарело — вместо этого используйте PERTURB_DIPOLE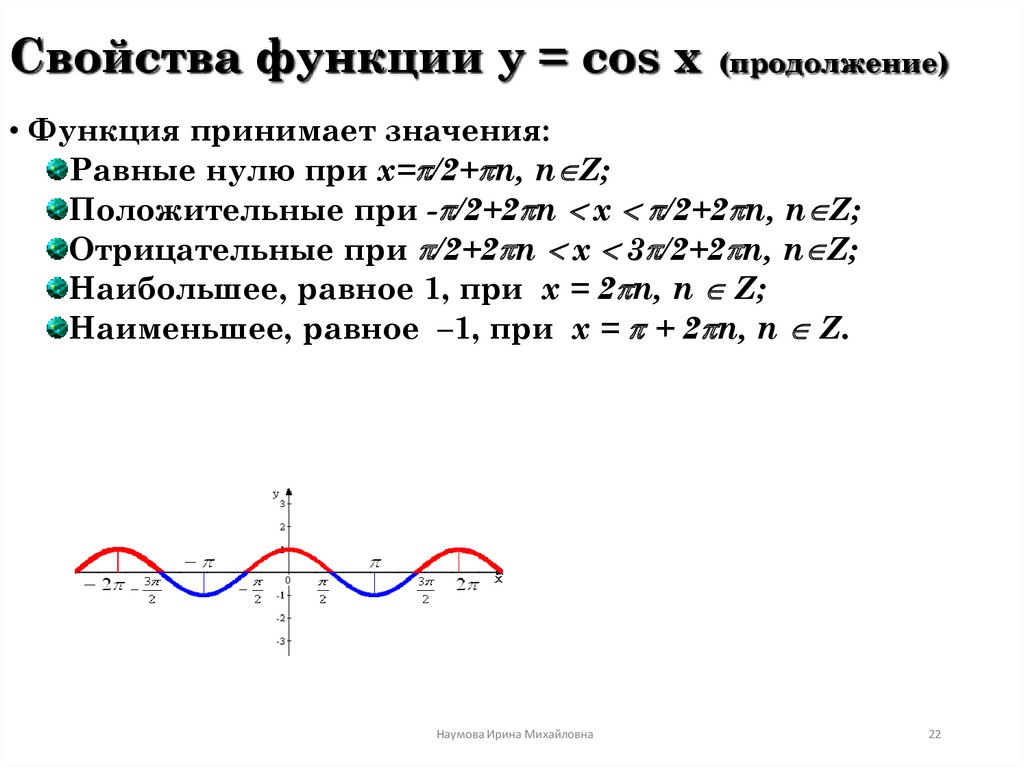 радиус
радиус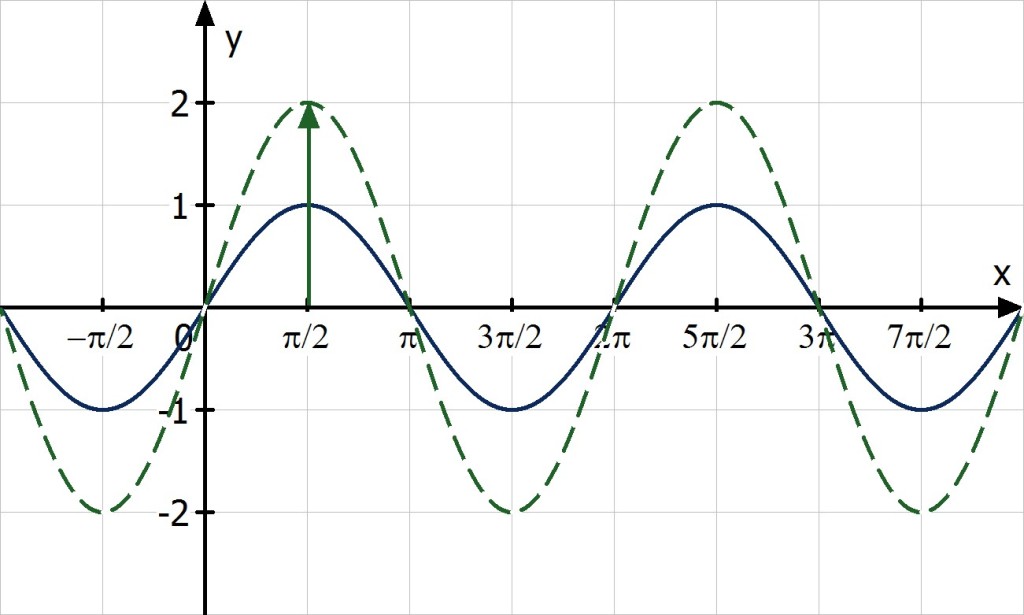 0e-11
0e-11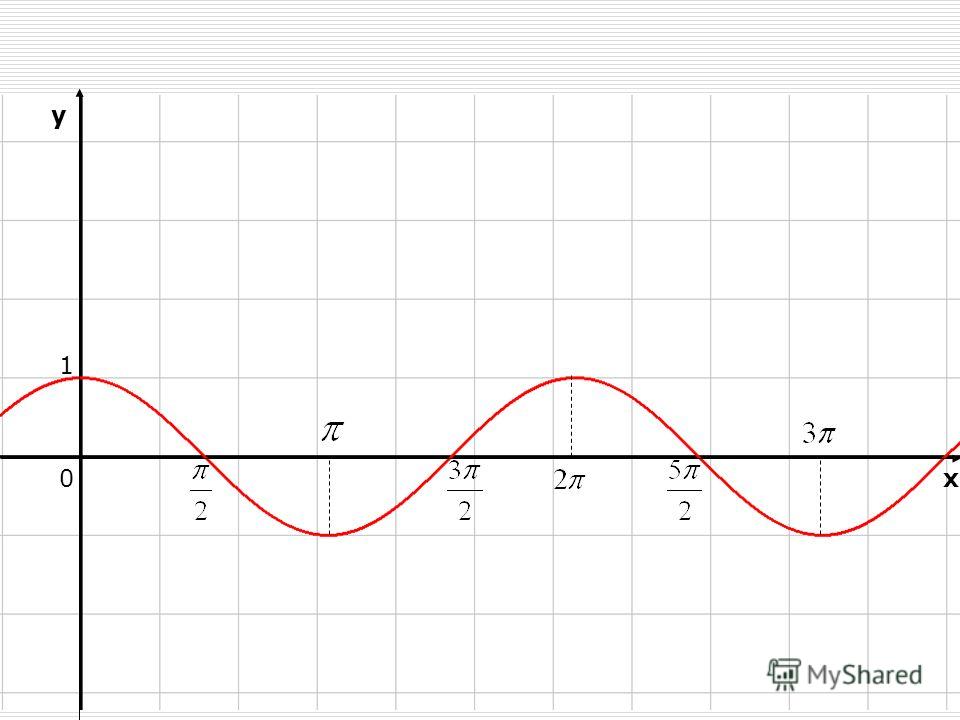
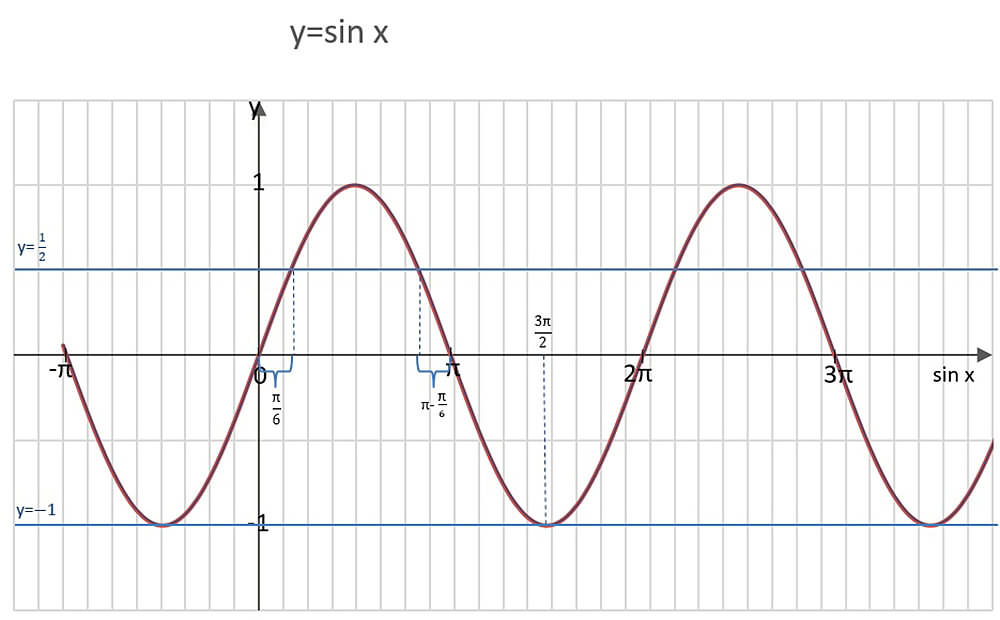
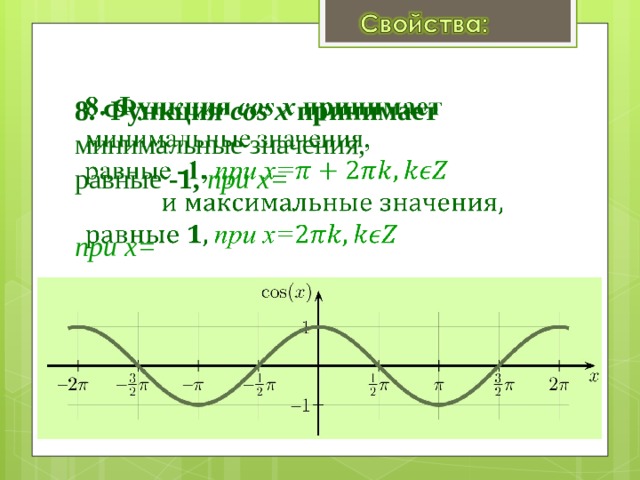 Рекомендуемая схема
Рекомендуемая схема 

 Сначала b, затем C
Сначала b, затем C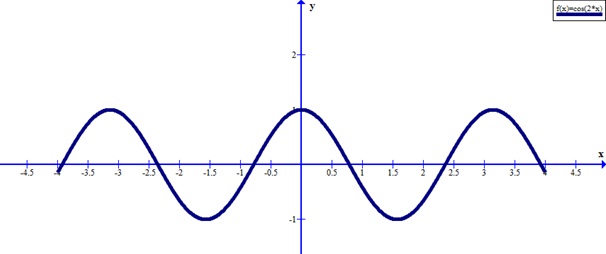 Если не установлено, по умолчанию используется D_CONVERGENCE
Если не установлено, по умолчанию используется D_CONVERGENCE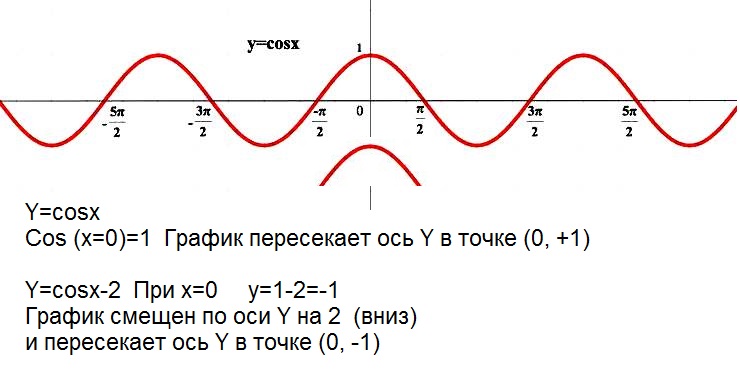
 0e-10
0e-10 e-8
e-8 1i = COS 1,1 + I SIN 1.1
1i = COS 1,1 + I SIN 1.1