от 0 до 360 градусов
Таблица тангенсов – это рассчитанные значения тангенсов от 0 до 360 градусов. Данная информация может выручить, если вдруг потребуется сделать расчеты, содержащие тангенс какого-то угла, а калькулятора рядом не окажется.
Просто находим требуемый градус в таблице, и в колонке справа в той же строке будет представлено значение тангенса – в виде десятичной дроби с округлением до 6 знаков после запятой. Для удобства информация разделена на две части.
- Таблица тангенсов от 0° до 180°
- Таблица тангенсов от 181° до 360°
Таблица тангенсов от 0° до 180°
| tg (0°) | 0 | ||||
| tg (1°) | 0,017455 | tg (61°) | 1,804048 | tg (121°) | -1,664279 |
| tg (2°) | 0,034921 | tg (62°) | 1,880726 | tg (122°) | -1,600335 |
| tg (3°) | 0,052408 | tg (63°) | 1,962611 | tg (123°) | -1,539865 |
| tg (4°) | 0,069927 | tg (64°) | 2,050304 | tg (124°) | -1,482561 |
| tg (5°) | 0,087489 | tg (65°) | 2,144507 | tg (125°) | -1,428148 |
| tg (6°) | 0,105104 | tg (66°) | 2,246037 | tg (126°) | -1,376382 |
| tg (7°) | 0,122785 | tg (67°) | 2,355852 | tg (127°) | -1,327045 |
| tg (8°) | 0,140541 | tg (68°) | 2,475087 | tg (128°) | -1,279942 |
| tg (9°) | 0,158384 | tg (69°) | 2,605089 | tg (129°) | -1,234897 |
| tg (10°) | 0,176327 | tg (70°) | 2,747477 | tg (130°) | -1,191754 |
| tg (11°) | 0,19438 | tg (71°) | 2,904211 | tg (131°) | -1,150368 |
| tg (12°) | 0,212557 | tg (72°) | 3,077684 | tg (132°) | -1,110613 |
| tg (13°) | 0,230868 | tg (73°) | 3,270853 | tg (133°) | -1,072369 |
| tg (14°) | 0,249328 | tg (74°) | 3,487414 | tg (134°) | -1,03553 |
| tg (15°) | 0,267949 | tg (75°) | 3,732051 | tg (135°) | -1 |
| tg (16°) | 0,286745 | tg (76°) | 4,010781 | tg (136°) | -0,965689 |
| tg (17°) | 0,305731 | tg (77°) | 4,331476 | tg (137°) | -0,932515 |
| tg (18°) | 0,32492 | tg (78°) | 4,70463 | tg (138°) | -0,900404 |
| tg (19°) | 0,344328 | tg (79°) | 5,144554 | tg (139°) | -0,869287 |
| tg (20°) | 0,36397 | tg (80°) | 5,671282 | tg (140°) | -0,8391 |
| tg (21°) | 0,383864 | tg (81°) | 6,313752 | tg (141°) | -0,809784 |
| tg (22°) | 0,404026 | tg (82°) | 7,11537 | tg (142°) | -0,781286 |
| tg (23°) | 0,424475 | tg (83°) | 8,144346 | tg (143°) | -0,753554 |
| tg (24°) | 0,445229 | tg (84°) | 9,514364 | tg (144°) | -0,726543 |
| tg (25°) | 0,466308 | tg (85°) | 11,430052 | tg (145°) | -0,700208 |
| tg (26°) | 0,487733 | tg (86°) | 14,300666 | tg (146°) | -0,674509 |
| tg (27°) | 0,509525 | tg (87°) | 19,081137 | tg (147°) | -0,649408 |
| tg (28°) | 0,531709 | tg (88°) | 28,636253 | tg (148°) | -0,624869 |
| tg (29°) | 0,554309 | tg (89°) | 57,289962 | tg (149°) | -0,600861 |
| tg (30°) | 0,57735 | tg (90°) | ∞ | tg (150°) | -0,57735 |
| tg (31°) | 0,600861 | tg (91°) | -57,289962 | tg (151°) | -0,554309 |
| tg (32°) | 0,624869 | tg (92°) | -28,636253 | tg (152°) | -0,531709 |
| tg (33°) | 0,649408 | tg (93°) | -19,081137 | tg (153°) | -0,509525 |
| tg (34°) | 0,674509 | tg (94°) | -14,300666 | tg (154°) | -0,487733 |
| tg (35°) | 0,700208 | tg (95°) | -11,430052 | tg (155°) | -0,466308 |
| tg (36°) | 0,726543 | tg (96°) | -9,514364 | tg (156°) | -0,445229 |
| tg (37°) | 0,753554 | tg (97°) | -8,144346 | tg (157°) | -0,424475 |
| tg (38°) | 0,781286 | tg (98°) | -7,11537 | tg (158°) | -0,404026 |
| tg (39°) | 0,809784 | tg (99°) | -6,313752 | tg (159°) | -0,383864 |
| tg (40°) | 0,8391 | tg (100°) | -5,671282 | tg (160°) | -0,36397 |
| tg (41°) | 0,869287 | tg (101°) | -5,144554 | tg (161°) | -0,344328 |
| tg (42°) | 0,900404 | tg (102°) | -4,70463 | tg (162°) | -0,32492 |
| tg (43°) | 0,932515 | tg (103°) | -4,331476 | tg (163°) | -0,305731 |
| tg (44°) | 0,965689 | tg (104°) | -4,010781 | tg (164°) | -0,286745 |
| tg (45°) | 1 | tg (105°) | -3,732051 | tg (165°) | -0,267949 |
| tg (46°) | 1,03553 | tg (106°) | -3,487414 | tg (166°) | -0,249328 |
| tg (47°) | 1,072369 | tg (107°) | -3,270853 | tg (167°) | -0,230868 |
| tg (48°) | 1,110613 | tg (108°) | -3,077684 | tg (168°) | -0,212557 |
| tg (49°) | 1,150368 | tg (109°) | -2,904211 | tg (169°) | -0,19438 |
| tg (50°) | 1,191754 | tg (110°) | -2,747477 | tg (170°) | -0,176327 |
| tg (51°) | 1,234897 | tg (111°) | -2,605089 | tg (171°) | -0,158384 |
| tg (52°) | 1,279942 | tg (112°) | -2,475087 | tg (172°) | -0,140541 |
| tg (53°) | 1,327045 | tg (113°) | -2,355852 | tg (173°) | -0,122785 |
| tg (54°) | 1,376382 | tg (114°) | -2,246037 | tg (174°) | -0,105104 |
| tg (55°) | 1,428148 | tg (115°) | -2,144507 | tg (175°) | -0,087489 |
| tg (56°) | 1,482561 | tg (116°) | -2,050304 | tg (176°) | -0,069927 |
| tg (57°) | 1,539865 | tg (117°) | -1,962611 | tg (177°) | -0,052408 |
| tg (58°) | 1,600335 | tg (118°) | -1,880726 | tg (178°) | -0,034921 |
| tg (59°) | 1,664279 | tg (119°) | -1,804048 | tg (179°) | -0,017455 |
| tg (60°) | 1,732051 | tg (120°) | -1,732051 | tg (180°) | 0 |
Таблица тангенсов от 181° до 360°
Таблица тангенсов, тангенс угла | Главный механик
- Тригонометрические функции, что это такое и их значение в изучении геометрии
- Онлайн калькулятор расчета тангенса угла
- Применение функции тангенса для решения задач
- Таблица тангенсов Брадиса для углов от 0 до 75 градусов
- Таблица тангенсов Брадиса для углов близких к 90 градусов
Из четырёх наиболее используемых тригонометрических таблиц в справочнике Брадиса является ТАБЛИЦА ТАНГЕНСОВ.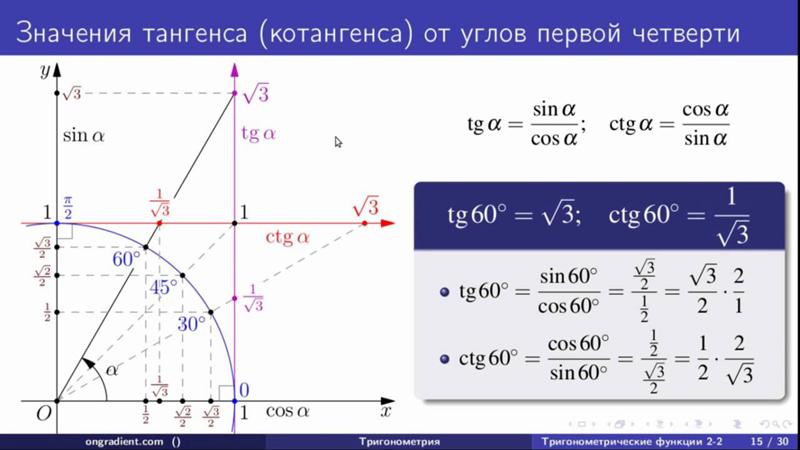 И тангенс и котангенс – это производные от синуса и косинуса и очень удобно, когда есть готовые рассчитанные значения для этих величин
И тангенс и котангенс – это производные от синуса и косинуса и очень удобно, когда есть готовые рассчитанные значения для этих величин
Тригонометрические функции, что это такое и их значение в изучении геометрии
В геометрии особую роль имеют тригонометрические функции, при помощи которых определяют, как относятся между собой стороны и углы прямоугольного треугольника. Конечно, тригонометрия не стоит на месте и со времен Евклида она намного шагнула вперёд и теперь может эти функции могут выражаться через решение дифференциальных уравнений.
В данный момент используются
шесть обозначений для основных тригонометрических функций, причем четыре функции из шести, они стоят в ряду последними, можно определять не только с помощью геометрии.Синус (sin)
Косинус (cos)
Тангенс (tg/tan)
Секанс (sec)
Косеканс (cosec/csc) .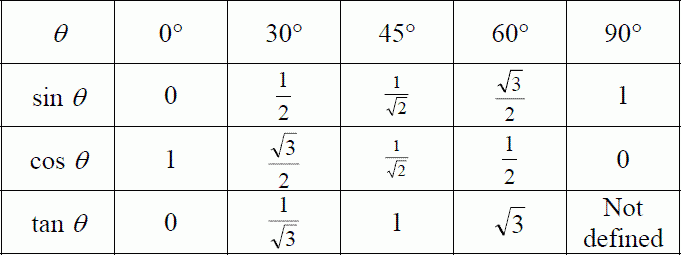
Рассмотрим сам прямоугольный треугольник, обозначения его сторон и углов во всех справочниках, как обычно, стандартные, какой бы стороной он не лежал бы на плоскости.
В этом треугольнике различают три угла, обозначаемые α, β, γ, при этом γ всегда 90°. Сторона, лежащая напротив прямого угла γ, называется гипотенузой, она обозначается буквой С. Угол α, с него начинаются все расчеты, находится напротив стороны а / ВС/, называемой противолежащей к этому углу, и сторона b /АС/, которая находится рядом, подлежит к этому углу и называется прилежащей.
По Евклидовой теории, которая верна до сих пор (и будет верна всегда), суммы углов такого треугольника, который находится в одной плоскости, будет равна 180 или числу π. И значение любого угла будут находиться в пределах между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.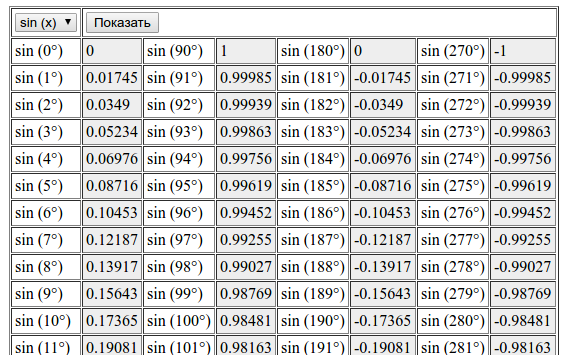
- Синус α выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть sin α = а: с.
- Косинус α выражается через отношение катета, который прилежит к углу α, и гипотенузы с, cos α = b: с. Кстати, sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α.
- Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
- Котангенс угла α
- Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b.
- Косеканс угла α составляет отношение гипотенузы треугольника к катету, который противостоит углу, cosecα = с : a.
Эти функции можно выразить и через окружность путем задания системы координат.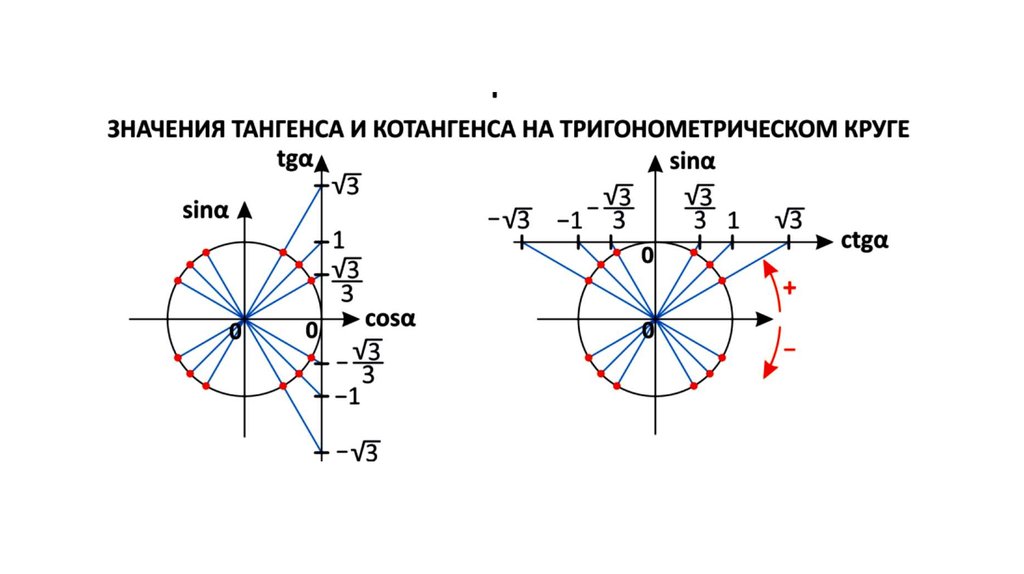 Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
Тогда тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Следовательно, если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Онлайн калькулятор расчета тангенса угла
Применение функции тангенса для решения задач
Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.
Пример: есть два катета ВС = 7 см и АС = 12 см. Нам нужно узнать все остальные данные о треугольнике.
Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.
Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.
Нам осталось найти гипотенузу с.
Можем найти её через sin α, который равен а: с, тогда с = а : sin α.
Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.
Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.
Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875. Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π.
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.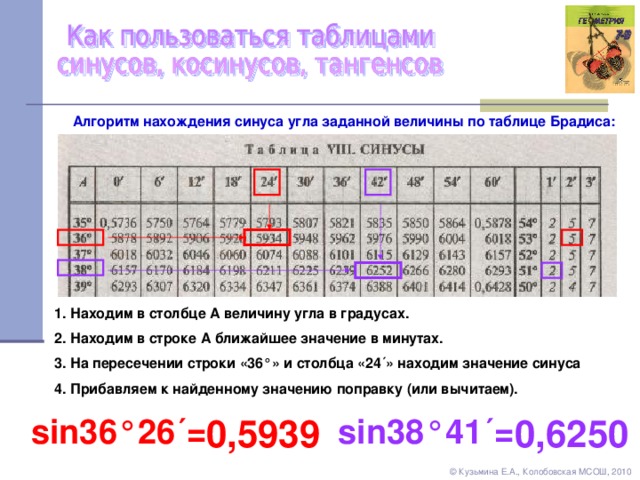 1445 1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | — |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1.7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | — |
| Тангенс 360 | 2π | 0 |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.
Таблица тангенсов Брадиса для углов от 0 до 75 градусов
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 74° | 3.487 | 3.511 | 3.534 | 3.558 | 3.582 | 3.606 | 4 | 8 | 12 | |||||
| 73° | 3.271 | 3.291 | 3.312 | 3.333 | 3.354 | 3.376 | — | — | — | — | — | 3 | 7 | 10 |
| 75° | 3.732 | 3.758 | 3.785 | 3.812 | 3.839 | 3.867 | — | — | — | — | — | 4 | 9 | 13 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 6 | 11 | 17 | |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0. 9657 9657 | 6 | 11 | 17 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 6 | 11 | 16 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 5 | 10 | 16 |
| 40° | 0.8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0.8693 | 5 | 10 | 15 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0.8391 | 5 | 10 | 15 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 5 | 9 | 14 |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 5 | 9 | 14 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 5 | 9 | 14° |
| 35° | 0.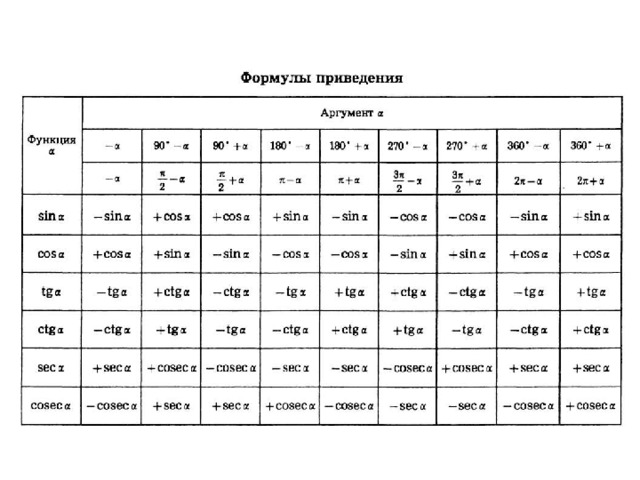 7002 7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7265 | 4 | 8 | 13 | |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1.7321 | 11 | 23 | 34 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0.7002 | 4 | 9 | 13 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 4 | 8 | 13 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 11 | 21 | 32 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 4 | 8 | 12 |
| 30° | 0.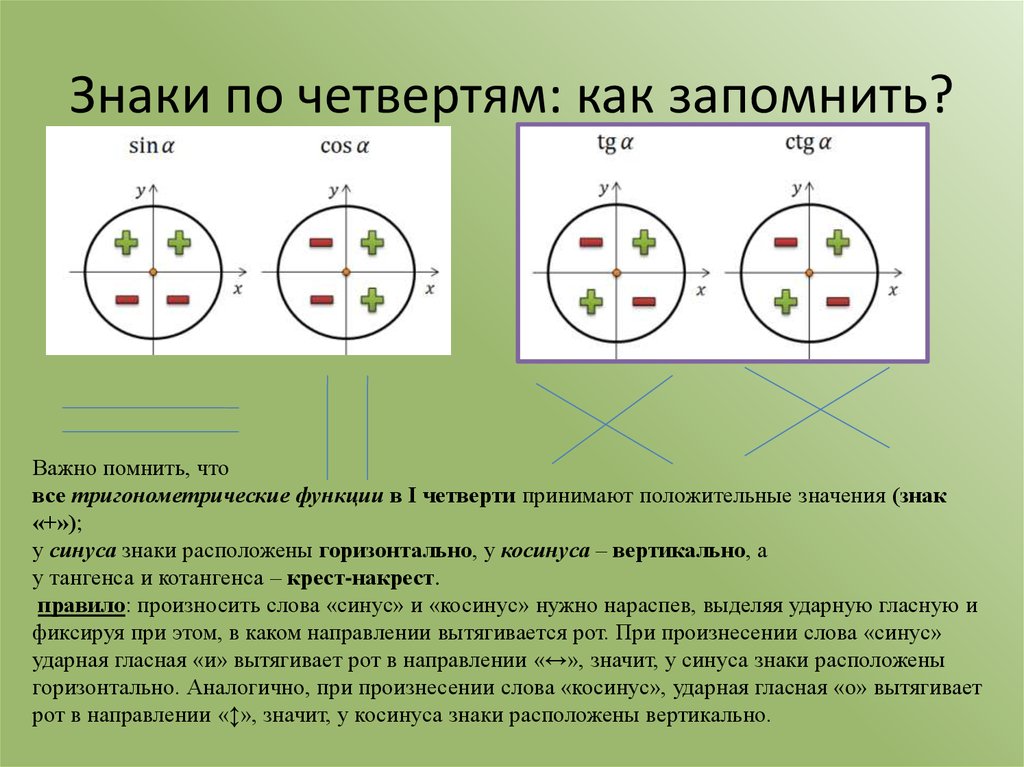 5774 5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 4 | 8 | 12 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 10 | 20 | 30 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0.5774 | 4 | 8 | 12 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 4 | 8 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 4 | 7 | 11 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 10 | 19 | 29 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 4 | 7 | 11 |
| 25° | 0. 4663 4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 4 | 7 | 11 |
| 55° | 1.4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 9 | 18 | 27 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0.4663 | 4 | 7 | 11 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 3 | 7 | 10 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1. 4281 4281 | 9 | 17 | 26 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 3 | 7 | 10 |
| 20° | 0.364 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 3 | 7 | 10 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 8 | 16 | 25 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0.364 | 3 | 7 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 3 | 6 | 10 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 3 | 6 | 10 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 8 | 16 | 24 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 3 | 6 | 9 |
| 15° | 0.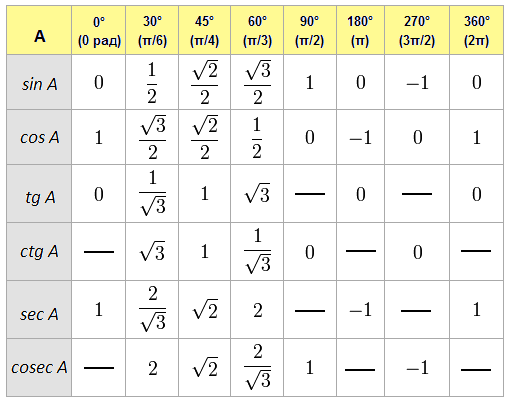 2679 2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 3 | 6 | 9 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 8 | 15 | 23 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0.2679 | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 3 | 6 | 9 |
| 50° | 1.1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 7 | 14 | 22 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 3 | 6 | 9 |
| 10° | 0. 1763 1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 3 | 6 | 9 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1.1918 | 7 | 14 | 21 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0.1763 | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 3 | 6 | 9 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 7 | 13 | 20 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 3 | 6 | 9 |
| 5° | 0.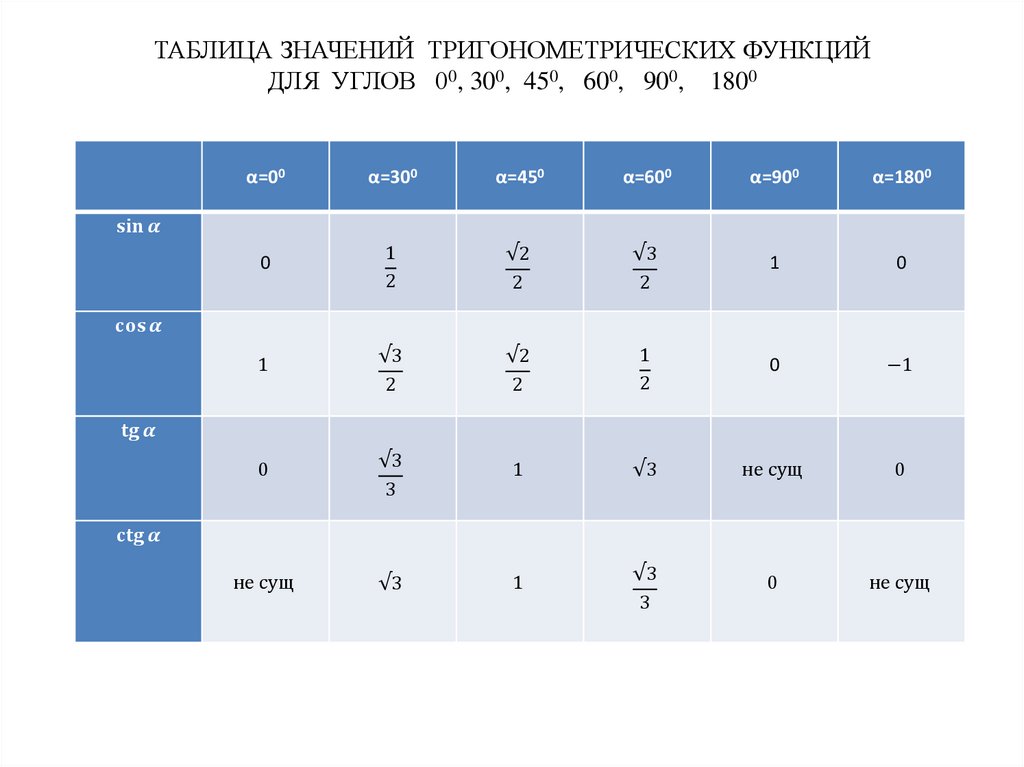 0875 0875 | 892 | 910 | 928 | 945 | 963 | 981 | 998 | 1016 | 1033 | 1051 | 3 | 6 | 9 |
| 47° | 724 | 761 | 799 | 837 | 875 | 913 | 951 | 990 | 1028 | 1067 | 1106 | 6 | 13 | 19 |
| 4° | 699 | 717 | 734 | 752 | 769 | 787 | 805 | 822 | 840 | 857 | 0.0875 | 3 | 6 | 9 |
| 3° | 524 | 542 | 559 | 577 | 594 | 612 | 629 | 647 | 664 | 682 | 699 | 3 | 6 | 9 |
| 46° | 355 | 392 | 428 | 464 | 501 | 538 | 575 | 612 | 649 | 686 | 724 | 6 | 12 | 18 |
| 2° | 349 | 367 | 384 | 402 | 419 | 437 | 454 | 472 | 489 | 507 | 524 | 3 | 6 | 9 |
| 1° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 |
| 45° | 1 | 35 | 70 | 105 | 141 | 176 | 212 | 247 | 283 | 319 | 355 | 6 | 12 | 18 |
| 0° | 0 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 |
| tg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | 1′ | 2′ | 3′ |
| — | — | — | — | — | — | 3. 895 895 | 3.923 | 3.952 | 3.981 | 4.011 | 5 | 10 | 14 | |
| — | — | — | — | — | — | 3.63 | 3.655 | 3.681 | 3.706 | 3.732 | 4 | 8 | 13 | |
| — | — | — | — | — | — | 3.398 | 3.42 | 3.442 | 3.465 | 3.487 | 4 | 7 | 11 | |
| 72° | 3.078 | 3.096 | 3.115 | 3.133 | 3.152 | 3.172 | 3.191 | 3.211 | 3.23 | 3.251 | 3.271 | 3 | 6 | 10 |
| 71° | 2.904 | 2.921 | 2.937 | 2.954 | 2.971 | 2.989 | 3.006 | 3.024 | 3.042 | 3.06 | 3.078 | 3 | 6 | 9 |
| 70° | 2.747 | 2.762 | 2.778 | 2.793 | 2.808 | 2.824 | 2.84 | 2.856 | 2.872 | 2. 888 888 | 2.904 | 3 | 5 | 8 |
| 69° | 2.605 | 2.619 | 2.633 | 2.646 | 2.66 | 2.675 | 2.689 | 2.703 | 2.718 | 2.733 | 2.747 | 2 | 5 | 7 |
| 68° | 2.475 | 2.488 | 2.5 | 2.513 | 2.526 | 2.539 | 2.552 | 2.565 | 2.578 | 2.592 | 2.605 | 2 | 4 | 6 |
| 67° | 2.356 | 2.367 | 2.379 | 2.391 | 2.402 | 2.414 | 2.426 | 2.438 | 2.45 | 2.463 | 2.475 | 2 | 4 | 6 |
| 66° | 2.246 | 2.257 | 2.267 | 2.278 | 2.289 | 2.3 | 2.311 | 2.322 | 2.333 | 2.344 | 2.356 | 2 | 4 | 5 |
| 65° | 2.145 | 2.154 | 2.164 | 2.174 | 2.184 | 2.194 | 2.204 | 2.215 | 2.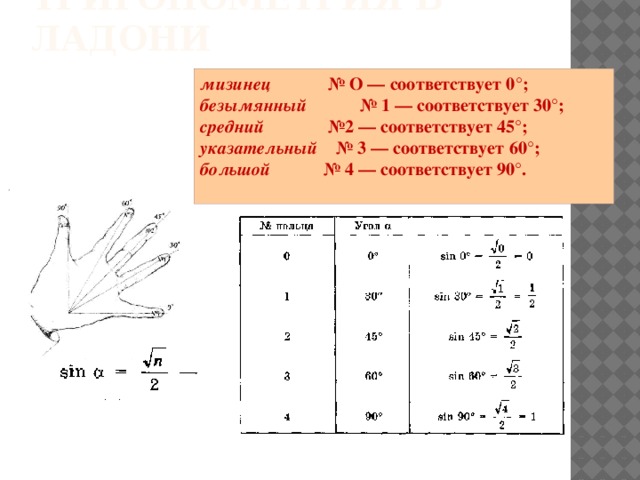 225 225 | 2.236 | 2.246 | 2 | 3 | 5 |
| 64° | 2.05 | 2.059 | 2.069 | 2.078 | 2.087 | 2.097 | 2.106 | 2.116 | 2.125 | 2.135 | 2.145 | 2 | 3 | 5 |
| 63° | 1.963 | 1.971 | 1.98 | 1.988 | 1.997 | 2.006 | 2.014 | 2.023 | 2.032 | 2.041 | 2.05 | 1 | 3 | 4 |
| 62° | 1.881 | 1.889 | 1.897 | 1.905 | 1.913 | 1.921 | 1.929 | 1.937 | 1.946 | 1.954 | 1.963 | 1 | 3 | 4 |
| 61° | 1.804 | 1.811 | 1.819 | 1.827 | 1.834 | 1.842 | 1.849 | 1.857 | 1.865 | 1.873 | 1.881 | 1 | 3 | 4 |
| 60° | 1.732 | 1.739 | 1.746 | 1.753 | 1.76 | 1.767 | 1.775 | 1. 782 782 | 1.789 | 1.797 | 1.804 | 1 | 2 | 4 |
| 0 | 90° |
Таблица тангенсов Брадиса для углов близких к 90 градусов
| tg | 0′ | 1′ | 2′ | 3′ | 4′ | 5′ | 6′ | 7′ | 8′ | 9′ | 10′ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| tg | 10′ | 9′ | 8′ | 7′ | 6′ | 5′ | 4′ | 3′ | 2′ | 1′ | 0′ |
| 76°00′ | 4.011 | 4.016 | 4.021 | 4.026 | 4.031 | 4.036 | 4.041 | 4.046 | 4.051 | 4.056 | 4.061 |
| 10′ | 4.061 | 4.066 | 4.071 | 4.076 | 4.082 | 4.087 | 4.092 | 4.097 | 4.102 | 4.107 | 4.113 |
| 20′ | 4.113 | 4.118 | 4.123 | 4. 128 128 | 4.134 | 4.139 | 4.144 | 4.149 | 4.155 | 4.16 | 4.165 |
| 30′ | 4.165 | 4.171 | 4.176 | 4.181 | 4.187 | 4.192 | 4.198 | 4.203 | 4.208 | 4.214 | 4.219 |
| 40′ | 4.219 | 4.225 | 4.23 | 4.236 | 4.241 | 4.247 | 4.252 | 4.258 | 4.264 | 4.269 | 4.275 |
| 50′ | 4.275 | 4.28 | 4.286 | 4.292 | 4.297 | 4.303 | 4.309 | 4.314 | 4.32 | 4.326 | 4.331 |
| 77°00′ | 4.331 | 4.337 | 4.343 | 4.349 | 4.355 | 4.36 | 4.366 | 4.372 | 4.378 | 4.384 | 4.39 |
| 10′ | 4.39 | 4.396 | 4.402 | 4.407 | 4.413 | 4.419 | 4.425 | 4.431 | 4.437 | 4.443 | 4.449 |
| 20′ | 4. 449 449 | 4.455 | 4.462 | 4.468 | 4.474 | 4.48 | 4.486 | 4.492 | 4.498 | 4.505 | 4.511 |
| 30′ | 4.511 | 4.517 | 4.523 | 4.529 | 4.536 | 4.542 | 4.548 | 4.555 | 4.561 | 4.567 | 4.574 |
| 40′ | 4.574 | 4.58 | 4.586 | 4.593 | 4.599 | 4.606 | 4.612 | 4.619 | 4.625 | 4.632 | 4.638 |
| 50′ | 4.638 | 4.645 | 4.651 | 4.658 | 4.665 | 4.671 | 4.678 | 4.685 | 4.691 | 4.698 | 4.705 |
| 78°00′ | 4.705 | 4.711 | 4.718 | 4.725 | 4.732 | 4.739 | 4.745 | 4.752 | 4.759 | 4.766 | 4.773 |
| 10′ | 4.773 | 4.78 | 4.787 | 4.794 | 4.801 | 4.808 | 4.815 | 4.822 | 4.829 | 4. 836 836 | 4.843 |
| 20′ | 4.843 | 4.85 | 4.857 | 4.864 | 4.872 | 4.879 | 4.886 | 4.893 | 4.901 | 4.908 | 4.915 |
| 30′ | 4.915 | 4.922 | 4.93 | 4.937 | 4.945 | 4.952 | 4.959 | 4.967 | 4.974 | 4.982 | 4.989 |
| 40′ | 4.989 | 4.997 | 5.005 | 5.012 | 5.02 | 5.027 | 5.035 | 5.043 | 5.05 | 5.058 | 5.066 |
| 50′ | 5.066 | 5.074 | 5.081 | 5.089 | 5.097 | 5.105 | 5.113 | 5.121 | 5.129 | 5.137 | 5.145 |
| 79°00′ | 5.145 | 5.153 | 5.161 | 5.169 | 5.177 | 5.185 | 5.193 | 5.201 | 5.209 | 5.217 | 5.226 |
| 10′ | 5.226 | 5.234 | 5.242 | 5.25 | 5.259 | 5.267 | 5.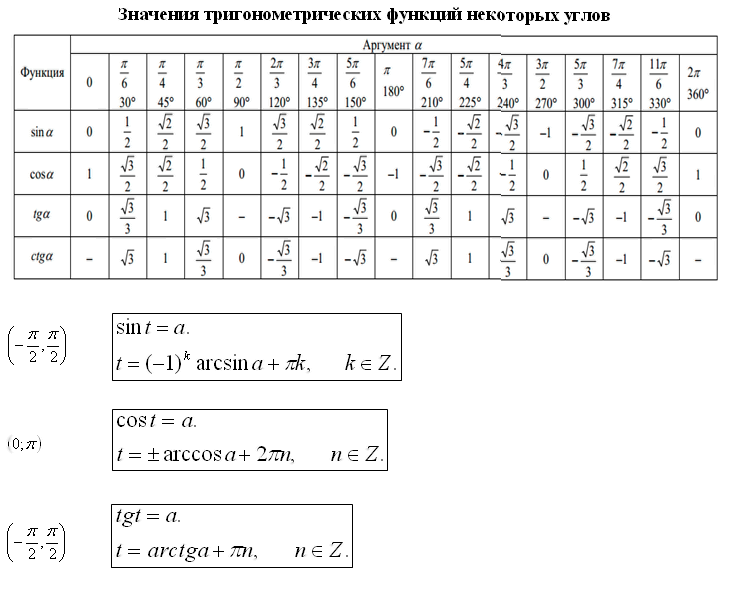 276 276 | 5.284 | 5.292 | 5.301 | 5.309 |
| 20′ | 5.309 | 5.318 | 5.326 | 5.335 | 5.343 | 5.352 | 5.361 | 5.369 | 5.378 | 5.387 | 5.396 |
| 30′ | 5.396 | 5.404 | 5.413 | 5.422 | 5.431 | 5.44 | 5.449 | 5.458 | 5.466 | 5.475 | 5.485 |
| 40′ | 5.485 | 5.494 | 5.503 | 5.512 | 5.521 | 5.53 | 5.539 | 5.549 | 5.558 | 5.567 | 5.576 |
| 50′ | 5.576 | 5.586 | 5.595 | 5.605 | 5.614 | 5.623 | 5.633 | 5.642 | 5.652 | 5.662 | 5.671 |
| 80°00′ | 5.671 | 5.681 | 5.691 | 5.7 | 5.71 | 5.72 | 5.73 | 5.74 | 5.749 | 5.759 | 5.769 |
| 10′ | 5.769 | 5.779 | 5.789 | 5. 799 799 | 5.81 | 5.82 | 5.83 | 5.84 | 5.85 | 5.861 | 5.871 |
| 20′ | 5.871 | 5.881 | 5.892 | 5.902 | 5.912 | 5.923 | 5.933 | 5.944 | 5.954 | 5.965 | 5.976 |
| 30′ | 5.976 | 5.986 | 5.997 | 6.008 | 6.019 | 6.03 | 6.041 | 6.051 | 6.062 | 6.073 | 6.084 |
| 40′ | 6.084 | 6.096 | 6.107 | 6.118 | 6.129 | 6.14 | 6.152 | 6.163 | 6.174 | 6.186 | 6.197 |
| 50′ | 6.197 | 6.209 | 6.22 | 6.232 | 6.243 | 6.255 | 6.267 | 6.278 | 6.29 | 6.302 | 6.314 |
| 81°00′ | 6.314 | 6.326 | 6.338 | 6.35 | 6.362 | 6.374 | 6.386 | 6.398 | 6.41 | 6.423 | 6.435 |
| 10′ | 6.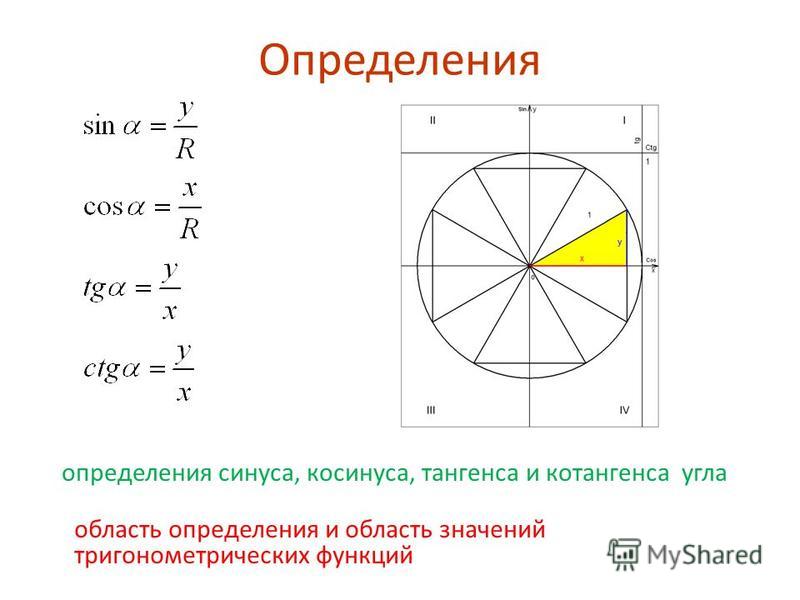 435 435 | 6.447 | 6.46 | 6.472 | 6.485 | 6.497 | 6.51 | 6.522 | 6.535 | 6.548 | 6.561 |
| 20′ | 6.561 | 6.573 | 6.586 | 6.599 | 6.612 | 6.625 | 6.638 | 6.651 | 6.665 | 6.678 | 6.691 |
| 30′ | 6.691 | 6.704 | 6.718 | 6.731 | 6.745 | 6.758 | 6.772 | 6.786 | 6.799 | 6.813 | 6.827 |
| 40′ | 6.827 | 6.841 | 6.855 | 6.869 | 6.883 | 6.897 | 6.911 | 6.925 | 6.94 | 6.954 | 6.968 |
| 50′ | 6.968 | 6.983 | 6.997 | 7.012 | 7.026 | 7.041 | 7.056 | 7.071 | 7.085 | 7.1 | 7.115 |
| 82°00′ | 7.115 | 7.13 | 7.146 | 7.161 | 7.176 | 7.191 | 7.207 | 7.222 | 7.238 | 7. 253 253 | 7.269 |
| 10′ | 7.269 | 7.284 | 7.3 | 7.316 | 7.332 | 7.348 | 7.363 | 7.38 | 7.396 | 7.412 | 7.429 |
| 20′ | 7.429 | 7.445 | 7.462 | 7.478 | 7.495 | 7.511 | 7.528 | 7.545 | 7.562 | 7.579 | 7.596 |
| 30′ | 7.596 | 7.613 | 7.63 | 7.647 | 7.665 | 7.682 | 7.7 | 7.717 | 7.735 | 7.753 | 7.77 |
| 40′ | 7.77 | 7.788 | 7.806 | 7.824 | 7.842 | 7.861 | 7.879 | 7.897 | 7.916 | 7.934 | 7.953 |
| 50′ | 7.953 | 7.972 | 7.991 | 8.009 | 8.028 | 8.048 | 8.067 | 8.086 | 8.105 | 8.125 | 8.144 |
| 83°00′ | 8.144 | 8.164 | 8.184 | 8.204 | 8.223 | 8.243 | 8.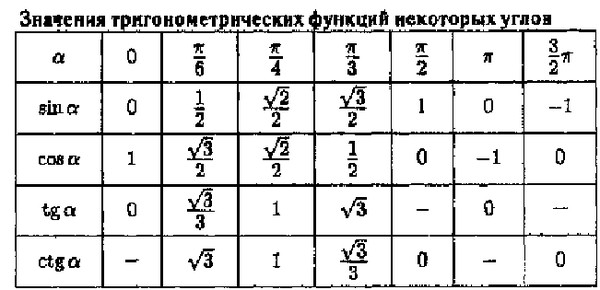 264 264 | 8.284 | 8.304 | 8.324 | 8.345 |
| 10′ | 8.345 | 8.366 | 8.386 | 8.407 | 8.428 | 8.449 | 8.47 | 8.491 | 8.513 | 8.534 | 8.556 |
| 20′ | 8.556 | 8.577 | 8.599 | 8.621 | 8.643 | 8.665 | 8.687 | 8.709 | 8.732 | 8.754 | 8.777 |
| 30′ | 8.777 | 8.8 | 8.823 | 8.846 | 8.869 | 8.892 | 8.915 | 8.939 | 8.962 | 8.986 | 9.01 |
| 40′ | 9.01 | 9.034 | 9.058 | 9.082 | 9.106 | 9.131 | 9.156 | 9.18 | 9.205 | 9.23 | 9.255 |
| 50′ | 9.255 | 9.281 | 9.306 | 9.332 | 9.357 | 9.383 | 9.409 | 9.435 | 9.461 | 9.488 | 9.514 |
| 84°00′ | 9.514 | 9.541 | 9.568 | 9. 595 595 | 9.622 | 9.649 | 9.677 | 9.704 | 9.732 | 9.76 | 9.788 |
| 10′ | 9.788 | 9.816 | 9.845 | 9.873 | 9.902 | 9.931 | 9.96 | 9.989 | 10.02 | 10.05 | 10.08 |
| 20′ | 10.08 | 10.11 | 10.14 | 10.17 | 10.2 | 10.23 | 10.26 | 10.29 | 10.32 | 10.35 | 10.39 |
| 30′ | 10.39 | 10.42 | 10.45 | 10.48 | 10.51 | 10.55 | 10.58 | 10.61 | 10.64 | 10.68 | 10.71 |
| 40′ | 10.71 | 10.75 | 10.78 | 10.81 | 10.85 | 10.88 | 10.92 | 10.95 | 10.99 | 11.02 | 11.06 |
| 50′ | 11.06 | 11.1 | 11.13 | 11.17 | 11.2 | 11.24 | 11.28 | 11.32 | 11.35 | 11.39 | 11.43 |
| 85°00′ | 11. 43 43 | 11.47 | 11.51 | 11.55 | 11.59 | 11.62 | 11.66 | 11.7 | 11.74 | 11.79 | 11.83 |
| 10′ | 11.83 | 11.87 | 11.91 | 11.95 | 11.99 | 12.03 | 12.08 | 12.12 | 12.16 | 12.21 | 12.25 |
| 20′ | 12.25 | 12.29 | 12.34 | 12.38 | 12.43 | 12.47 | 12.52 | 12.57 | 12.61 | 12.66 | 12.71 |
| 30′ | 12.71 | 12.75 | 12.8 | 12.85 | 12.9 | 12.95 | 13 | 13.05 | 13.1 | 13.15 | 13.2 |
| 40′ | 13.2 | 13.25 | 13.3 | 13.35 | 13.4 | 13.46 | 13.51 | 13.56 | 13.62 | 13.67 | 13.73 |
| 50′ | 13.73 | 13.78 | 13.84 | 13.89 | 13.95 | 14.01 | 14.07 | 14.12 | 14.18 | 14.24 | 14. 3 3 |
| 86°00′ | 14.3 | 14.36 | 14.42 | 14.48 | 14.54 | 14.61 | 14.67 | 14.73 | 14.8 | 14.86 | 14.92 |
| 10′ | 14.92 | 14.99 | 15.06 | 15.12 | 15.19 | 15.26 | 15.33 | 15.39 | 15.46 | 15.53 | 15.6 |
| 20′ | 15.6 | 15.68 | 15.75 | 15.82 | 15.89 | 15.97 | 16.04 | 16.12 | 16.2 | 16.27 | 16.35 |
| 30′ | 16.35 | 16.43 | 16.51 | 16.59 | 16.67 | 16.75 | 16.83 | 16.92 | 17 | 17.08 | 17.17 |
| 40′ | 17.17 | 17.26 | 17.34 | 17.43 | 17.52 | 17.61 | 17.7 | 17.79 | 17.89 | 17.98 | 18.07 |
| 50′ | 18.07 | 18.17 | 18.27 | 18.37 | 18.46 | 18.56 | 18.67 | 18. 77 77 | 18.87 | 18.98 | 19.08 |
| 87°00′ | 19.08 | 19.19 | 19.3 | 19.41 | 19.52 | 19.63 | 19.74 | 19.85 | 19.97 | 20.09 | 20.21 |
| 10′ | 20.21 | 20.33 | 20.45 | 20.57 | 20.69 | 20.82 | 20.95 | 21.07 | 21.2 | 21.34 | 21.47 |
| 20′ | 21.47 | 21.61 | 21.74 | 21.88 | 22.02 | 22.16 | 22.31 | 22.45 | 22.6 | 22.75 | 22.9 |
| 30′ | 22.9 | 23.06 | 23.21 | 23.37 | 23.53 | 23.69 | 23.86 | 24.03 | 24.2 | 24.37 | 24.54 |
| 40′ | 24.54 | 24.72 | 24.9 | 25.08 | 25.26 | 25.45 | 25.64 | 25.83 | 26.03 | 26.23 | 26.43 |
| 50′ | 26.43 | 26.64 | 26.84 | 27.06 | 27. 27 27 | 27.49 | 27.71 | 27.94 | 28.17 | 28.4 | 28.64 |
| 88°00′ | 28.64 | 28.88 | 29.12 | 29.37 | 29.62 | 29.88 | 30.14 | 30.41 | 30.68 | 30.96 | 31.24 |
| 10′ | 31.24 | 31.53 | 31.82 | 32.12 | 32.42 | 32.73 | 33.05 | 33.37 | 33.69 | 34.03 | 34.37 |
| 20′ | 34.37 | 34.72 | 35.07 | 35.43 | 35.8 | 36.18 | 36.56 | 36.96 | 37.36 | 37.77 | 38.19 |
| 30′ | 38.19 | 38.62 | 39.06 | 39.51 | 39.97 | 40.44 | 40.92 | 41.41 | 41.92 | 42.43 | 42.96 |
| 40′ | 42.96 | 43.51 | 44.07 | 44.64 | 45.23 | 45.83 | 46.45 | 47.09 | 47.74 | 48.41 | 49.1 |
| 50′ | 49.1 | 49. 82 82 | 50.55 | 51.3 | 52.08 | 52.88 | 53.71 | 54.56 | 55.44 | 56.35 | 57.29 |
| 89°00′ | 57.29 | 58.26 | 59.27 | 60.31 | 61.38 | 62.5 | 63.66 | 64.86 | 66.11 | 67.4 | 68.75 |
| 10′ | 68.75 | 70.15 | 71.62 | 73.14 | 74.73 | 76.39 | 78.13 | 79.94 | 81.85 | 83.84 | 85.94 |
| 20′ | 85.94 | 88.14 | 90.46 | 92.91 | 95.49 | 98.22 | 101.1 | 104.2 | 107.4 | 110.9 | 114.6 |
| 30′ | 114.6 | 118.5 | 122.8 | 127.3 | 132.2 | 137.5 | 143.2 | 149.5 | 156.3 | 163.7 | 171.9 |
| 40′ | 171.9 | 180.9 | 191 | 202.2 | 214.9 | 229.2 | 245.6 | 264.4 | 286.5 | 312.5 | 343. 8 8 |
| 50′ | 343.8 | 382 | 429.7 | 491.1 | 573 | 687.5 | 859.4 | 1146 | 1719 | 3438 |
Интересные статьи
Таблица тангенсов, полная таблица значений тангенсов для студентов
Содержание:
- Таблица тангенсов 0° — 180°
- Таблица тангенсов 180° — 360°
Тангенс — равен отношению синуса к косинусу (tg(x) = Sin(x)/Cos(x)), тоесть таблицу тангенсов можно получить просто поделив значения из таблицы синусов на значения из таблицы косинусов. Таблица тангенсов применяется не часто, но так как из всех таблиц тригонометрических функций значения таблицы тангенсов получить сложнее всего, то эти значения как минимум надо иметь по близости. Для лучшего понимания тригонометрии советуем изучить тригонометрические формулы. Пользуйтесь таблицей тангенсов на здоровье.
Таблица тангенсов 0° — 180°
|
|
|
Таблица тангенсов 180° — 360°
|
|
|
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Значения тангенса на окружности таблица. Понятия в тригонометрии
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.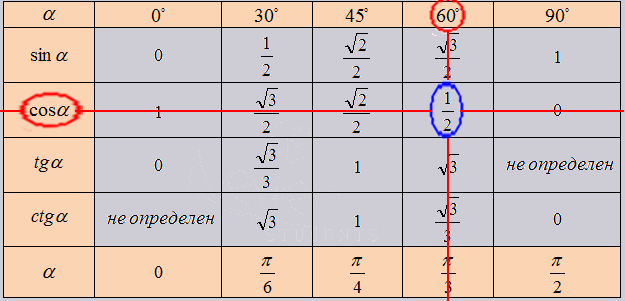
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора.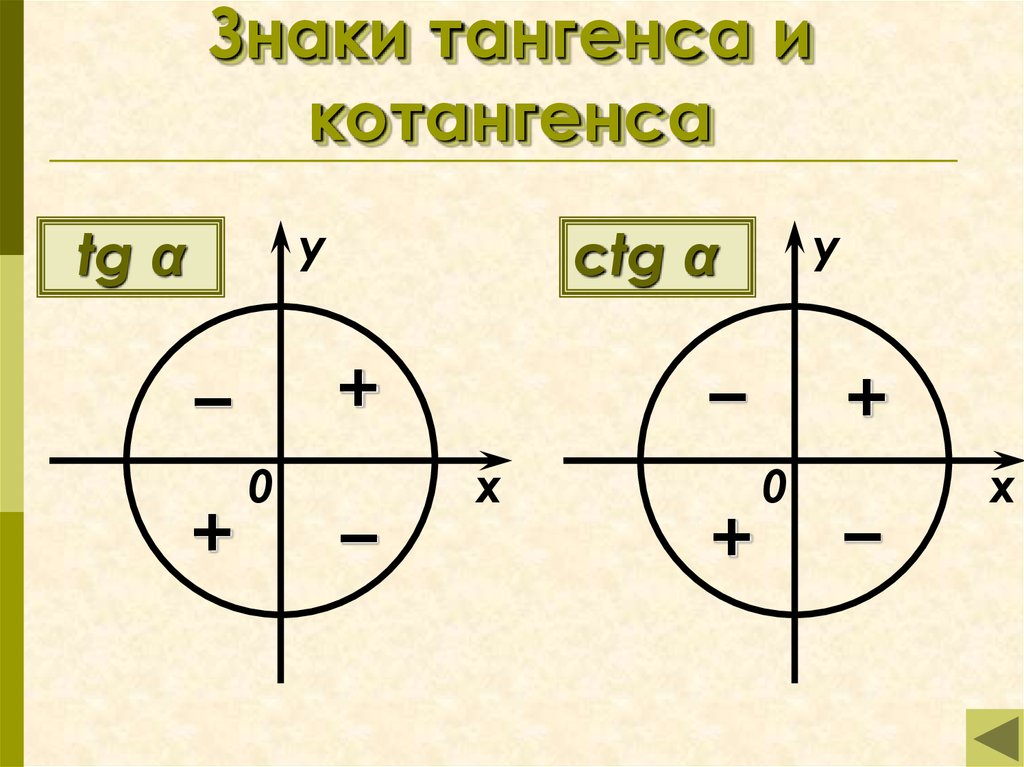 Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.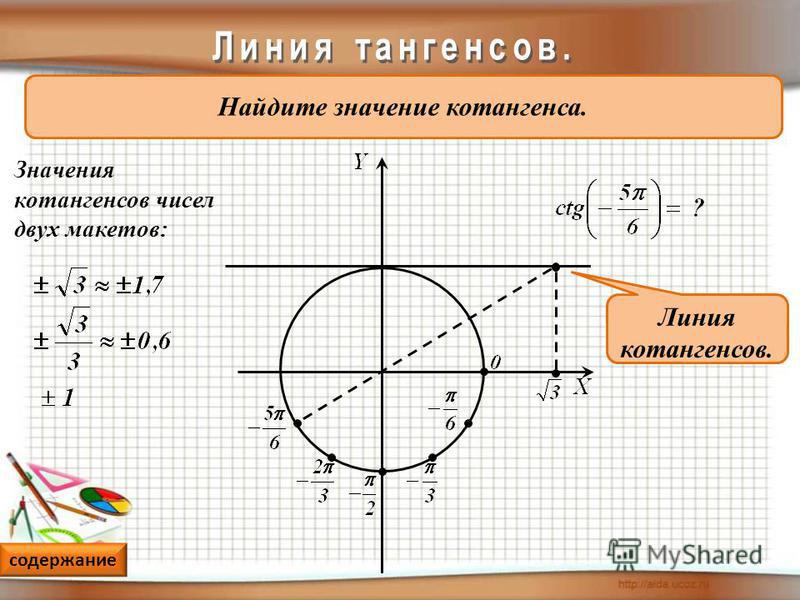
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом.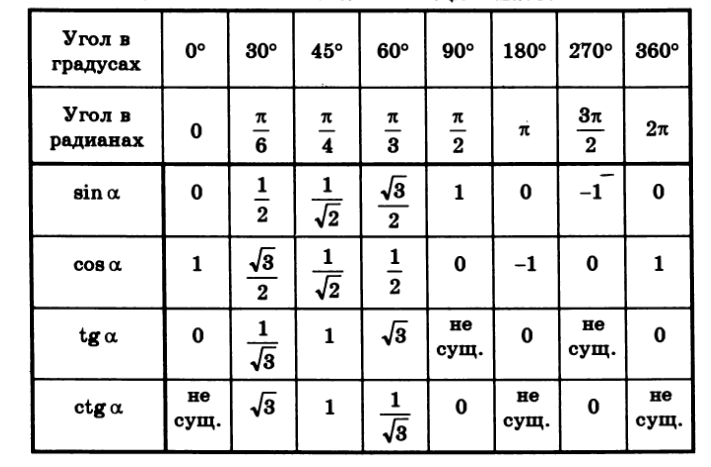 Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа.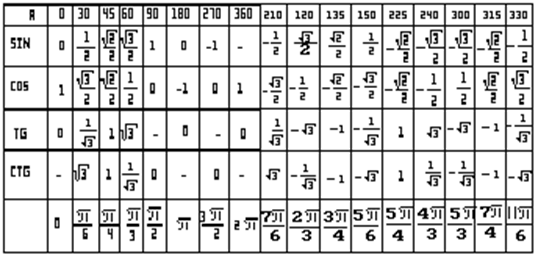 Рассмотрим его подробнее.
Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t .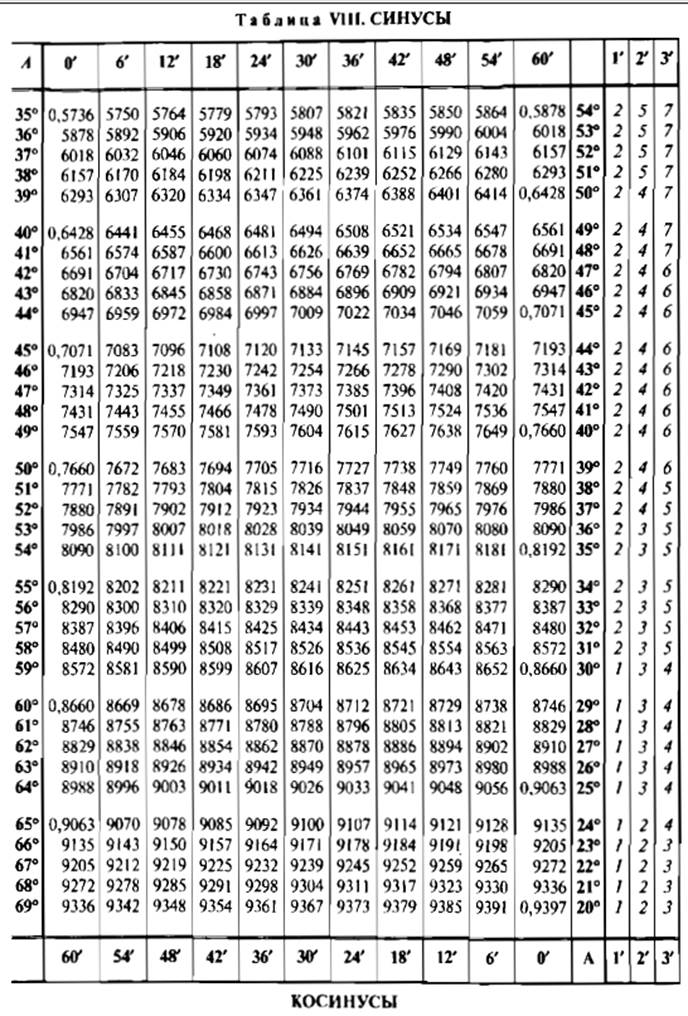 Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) .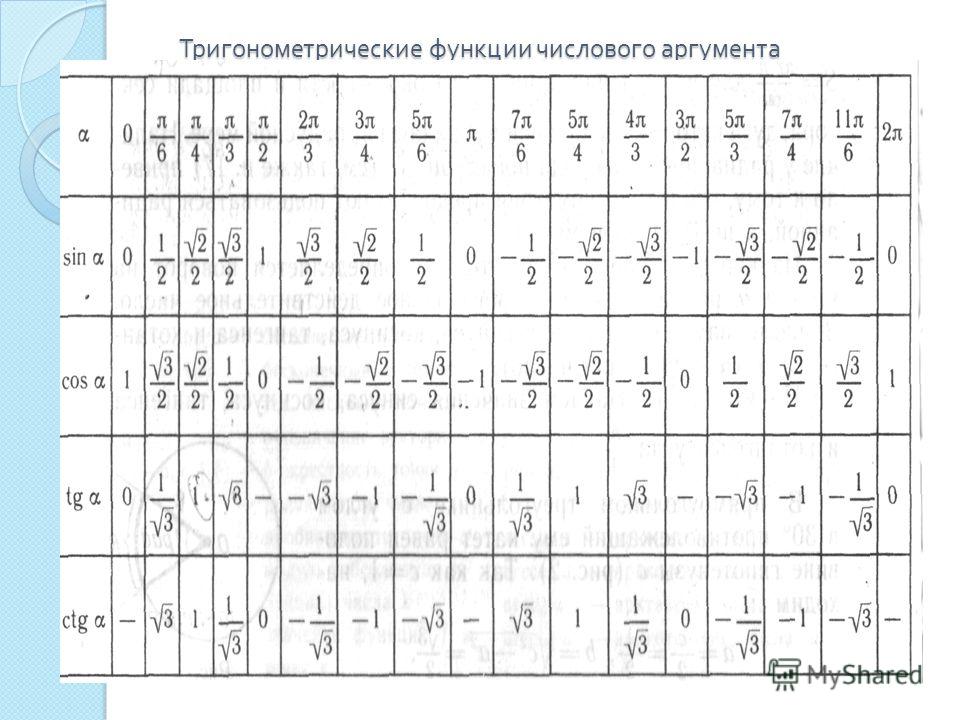 Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Понятия синуса, косинуса, тангенса и котангенса являются основными категориями тригонометрии — раздела математики, и неразрывно связаны с определением угла. Владение этой математической наукой требует запоминания и понимания формул и теорем, а также развитого пространственного мышления. Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности.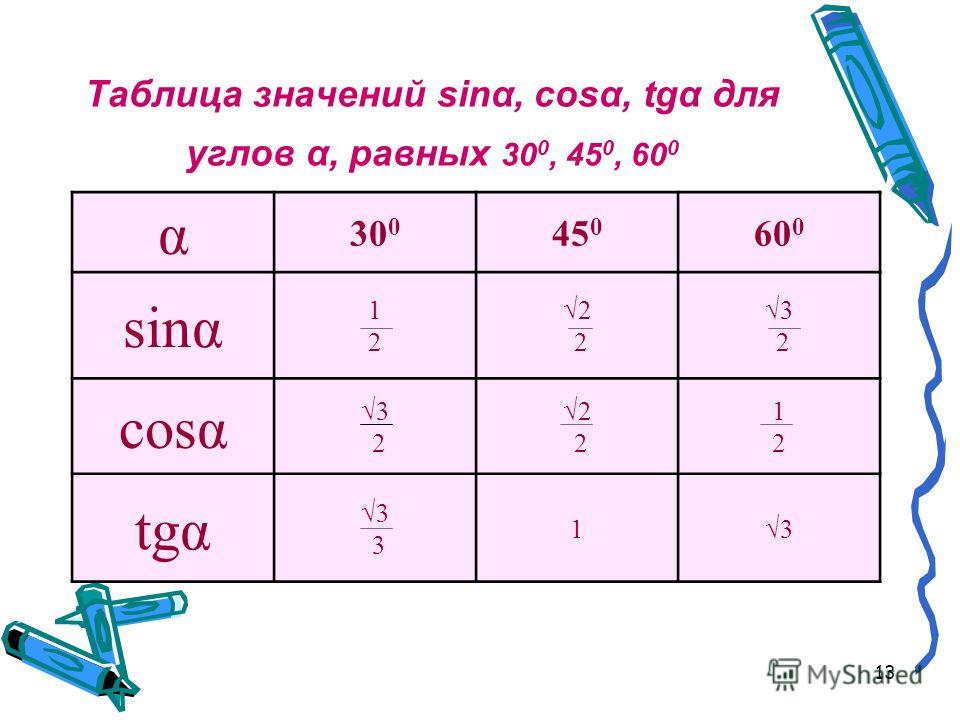 Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Понятия в тригонометрии
Чтобы разобраться в базовых понятиях тригонометрии, следует сначала определиться с тем, что такое прямоугольный треугольник и угол в окружности, и почему именно с ними связаны все основные тригонометрические вычисления. Треугольник, в котором один из углов имеет величину 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, навигации, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Основные категории, связанные с прямоугольными треугольниками — гипотенуза и катеты. Гипотенуза — сторона треугольника, лежащая против прямого угла. Катеты, соответственно, это остальные две стороны. Сумма углов любых треугольников всегда равна 180 градусам.
Сферическая тригонометрия — раздел тригонометрии, который не изучается в школе, однако в прикладных науках типа астрономии и геодезии, учёные пользуются именно им.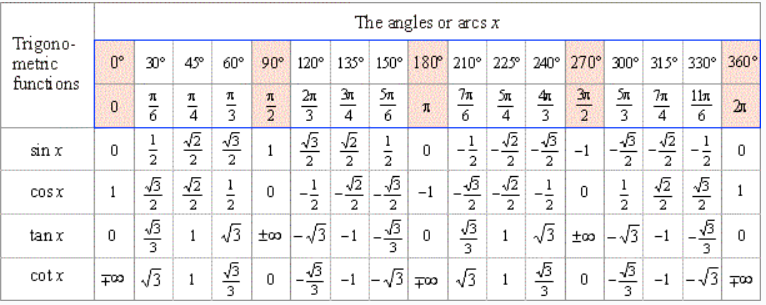 Особенность треугольника в сферической тригонометрии в том, что он всегда имеет сумму углов более 180 градусов.
Особенность треугольника в сферической тригонометрии в том, что он всегда имеет сумму углов более 180 градусов.
Углы треугольника
В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Тангенс угла — величина, равная отношению противолежащего катета к прилежащему катету искомого угла, или же синуса к косинусу. Котангенс, в свою очередь, это отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла можно также получить, разделив единицу на значение тангенса.
Единичная окружность
Единичная окружность в геометрии — окружность, радиус которой равен единице. Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс).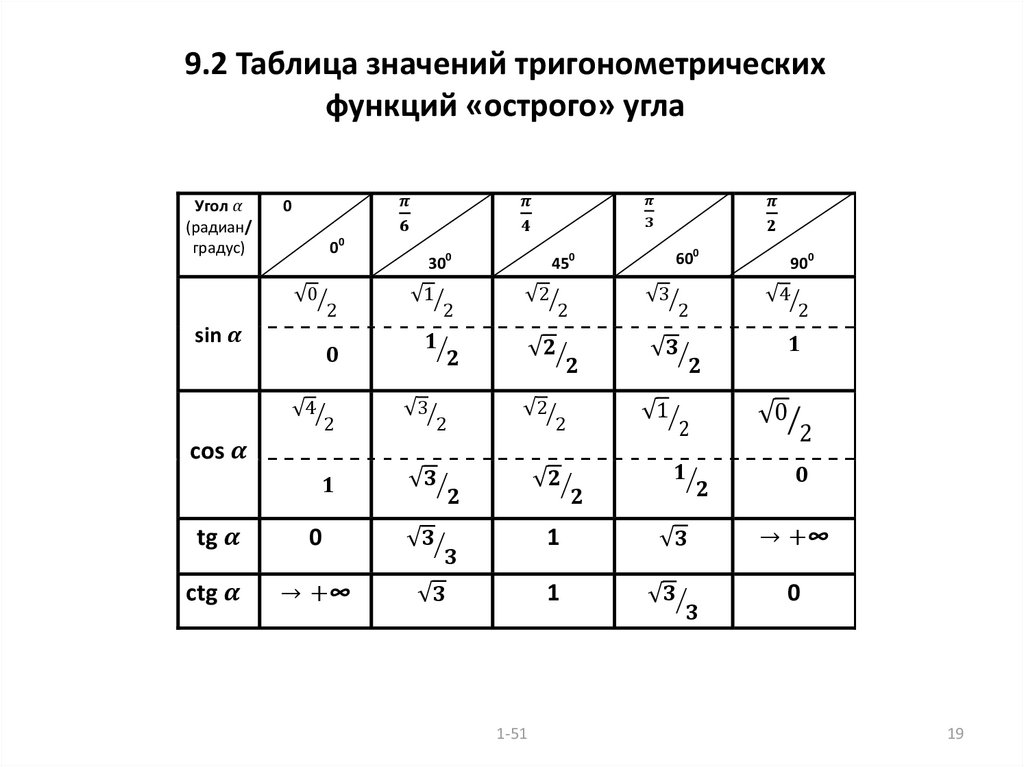 Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Кроме того, зная эти данные, можно определить координату точки С на окружности, так как cos α=AG, а sin α=CG, значит, точка С имеет заданные координаты (cos α;sin α).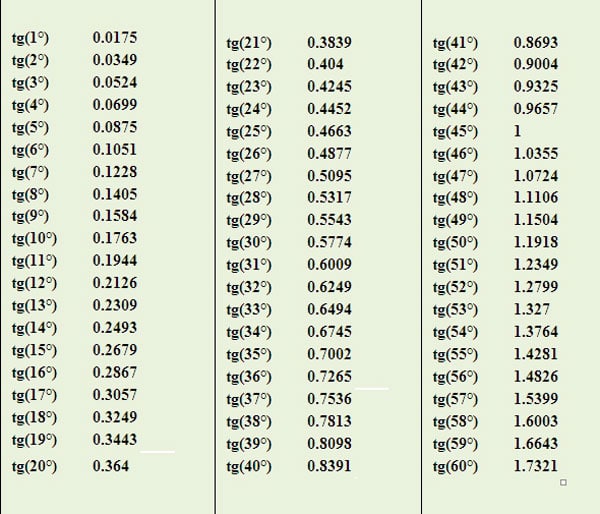 k * arcsin α + πk.
k * arcsin α + πk.
Тождества со значением cos х = а, где k — любое целое число:
- cos х = 0, х = π/2 + πk.
- cos х = 1, х = 2πk.
- cos х = -1, х = π + 2πk.
- cos х = а, |a| > 1, нет решений.
- cos х = а, |a| ≦ 1, х = ±arccos α + 2πk.
Тождества со значением tg х = а, где k — любое целое число:
- tg х = 0, х = π/2 + πk.
- tg х = а, х = arctg α + πk.
Тождества со значением ctg х = а, где k — любое целое число:
- ctg х = 0, х = π/2 + πk.
- ctg х = а, х = arcctg α + πk.
Формулы приведения
Эта категория постоянных формул обозначает методы, с помощью которых можно перейти от тригонометрических функций вида к функциям аргумента, то есть привести синус, косинус, тангенс и котангенс угла любого значения к соответствующим показателям угла интервала от 0 до 90 градусов для большего удобства вычислений.
Формулы приведения функций для синуса угла выглядят таким образом:
- sin(900 — α) = α;
- sin(900 + α) = cos α;
- sin(1800 — α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 — α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 — α) = -sin α;
- sin(3600 + α) = sin α.

Для косинуса угла:
- cos(900 — α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 — α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 — α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 — α) = cos α;
- cos(3600 + α) = cos α.
Использование вышеуказанных формул возможно при соблюдении двух правил. Во-первых, если угол можно представить как значение (π/2 ± a) или (3π/2 ± a), значение функции меняется:
- с sin на cos;
- с cos на sin;
- с tg на ctg;
- с ctg на tg.
Значение функции остаётся неизменным, если угол может быть представлен как (π ± a) или (2π ± a).
Во-вторых, знак приведенной функции не изменяется: если он изначально был положительным, таким и остаётся. Аналогично с отрицательными функциями.
Формулы сложения
Эти формулы выражают величины синуса, косинуса, тангенса и котангенса суммы и разности двух углов поворота через их тригонометрические функции.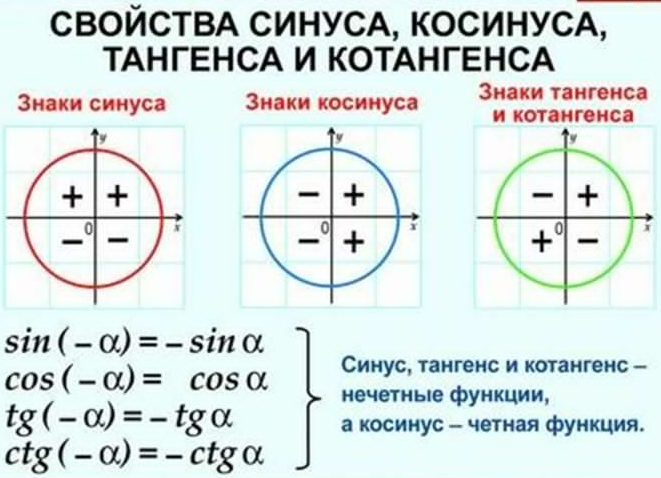 2 x/2) / (2tgx/2), при этом х = π + 2πn.
2 x/2) / (2tgx/2), при этом х = π + 2πn.
Частные случаи
Частные случаи простейших тригонометрических уравнений приведены ниже (k — любое целое число).
Частные для синуса:
| Значение sin x | Значение x |
|---|---|
| 0 | πk |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk или 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk или -5π/6 + 2πk |
| √2/2 | π/4 + 2πk или 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk или -3π/4 + 2πk |
| √3/2 | π/3 + 2πk или 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk или -2π/3 + 2πk |
Частные для косинуса:
| Значение cos x | Значение х |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Частные для тангенса:
| Значение tg x | Значение х |
|---|---|
| 0 | πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Частные для котангенса:
| Значение ctg x | Значение x |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Теоремы
Теорема синусов
Существует два варианта теоремы — простой и расширенный.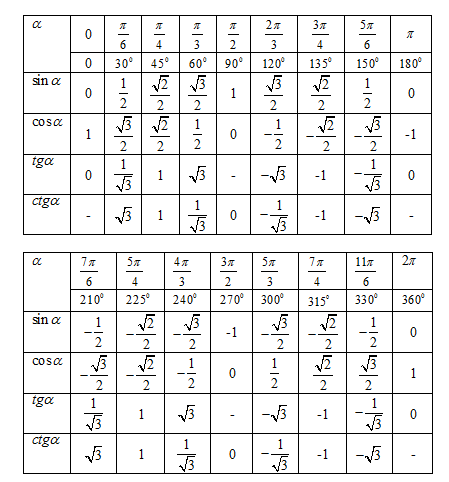 2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
Теорема тангенсов
Формула выражает связь между тангенсами двух углов, и длиной сторон, им противолежащих. Стороны обозначены как a, b, c, а соответствующие противолежащие углы — α, β, γ. Формула теоремы тангенсов: (a — b) / (a+b) = tg((α — β)/2) / tg((α + β)/2).
Теорема котангенсов
Связывает радиус вписанной в треугольник окружности с длиной его сторон. Если a, b, c — стороны треугольника, и А, В, С, соответственно, противолежащие им углы, r — радиус вписанной окружности, и p — полупериметр треугольника, справедливы такие тождества:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.
Прикладное применение
Тригонометрия — не только теоретическая наука, связанная с математическими формулами. Её свойствами, теоремами и правилами пользуются на практике разные отрасли человеческой деятельности — астрономия, воздушная и морская навигация, теория музыки, геодезия, химия, акустика, оптика, электроника, архитектура, экономика, машиностроение, измерительные работы, компьютерная графика, картография, океанография, и многие другие.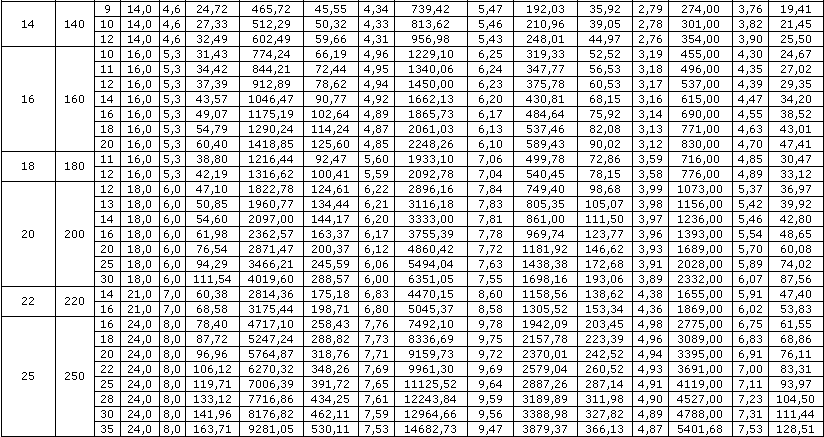
Синус, косинус, тангенс и котангенс — основные понятия тригонометрии, с помощью которых математически можно выразить соотношения между углами и длинами сторон в треугольнике, и найти искомые величины через тождества, теоремы и правила.
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние.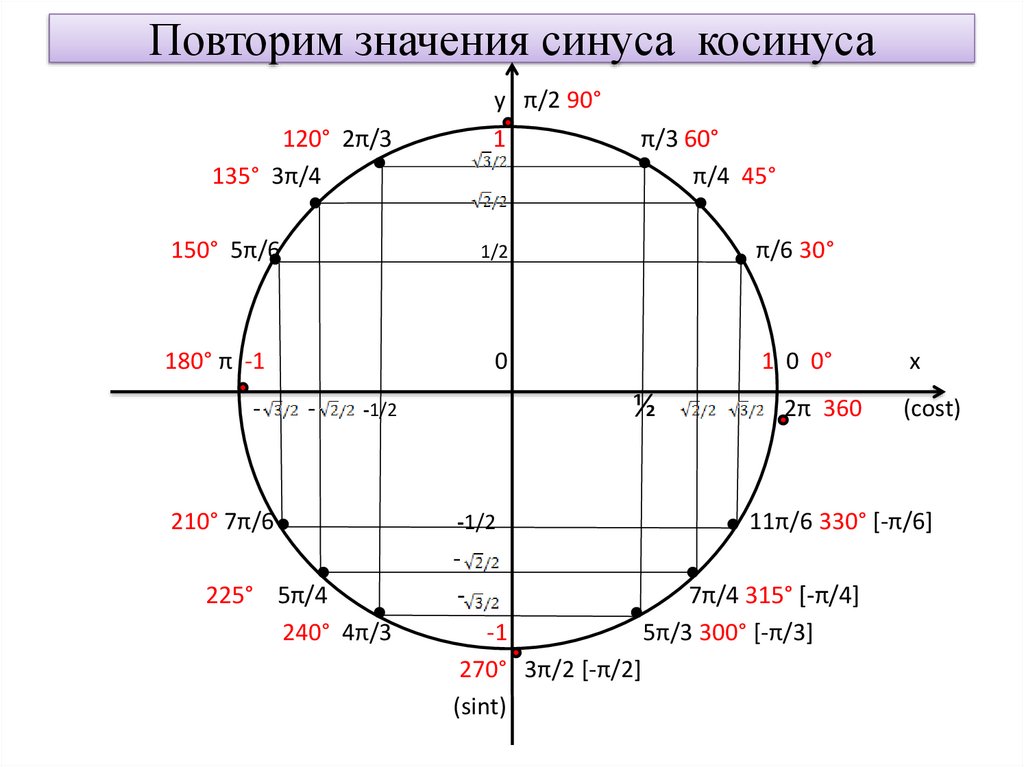 Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
среда, 4 июля 2018 г.
Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.
Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.
Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Вот здесь начнется самое интересное.
В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.
Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».
воскресенье, 18 марта 2018 г.
Сумма цифр числа — это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.
Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа». Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.
1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.
2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки — это не математическое действие.
3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.
4. Складываем полученные числа. Вот это уже математика.
Сумма цифр числа 12345 равна 15. Вот такие вот «курсы кройки и шитья» от шаманов применяют математики. Но это ещё не всё.
С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.
Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.
Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.
Открывает дверь и говорит:
Ой! А это разве не женский туалет?
— Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх. Какой еще туалет?
Какой еще туалет?
Женский… Нимб сверху и стрелочка вниз — это мужской.
Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,
Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:
Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
1А — это не «минус четыре градуса» или «один а». Это «какающий человек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Тангенс и котангенс. Формулы и определение. Тангенс угла это отношение чего? Основы тригонометрии
Содержание
- Как пользоваться таблицей Брадиса.
- Решение уравнения tg x = a
- Тангенс угла
- Тригонометрические функции и их значение в изучении геометрии
- Тангенс — это отношение…
- Применение функции тангенса для решения задач
- Найти тангенс угла tg(α), в прямоугольном треугольнике
- График тангенса
- Определение
- Таблица Брадиса tg, ctg
- Свойства
- Решение уравнения ctg x = a
- Таблица Брадиса – синусы и косинусы.

- Как найти тангенс угла (формулы)
- Обратная к тангенсу функция
- Как связаны тангенс с котангенсом?
Как пользоваться таблицей Брадиса.
На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса.
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.
sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.
Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.
Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654
Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо
cos 80°27′=80°30′−3′=0.1650−(-0.0009)=0.1659
Решение уравнения tg x = a
| Обычная форма записи решения: | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.
Рис. 3
Частные случаи решения уравнений tg x = a
| Уравнение | Решение |
| tg x = – 1 | |
| tg x = 0 | |
| tg x = 1 | |
Уравнение: Решение: |
Уравнение: tg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 0 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 1 Решение: |
Уравнение: Решение: |
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тригонометрические функции и их значение в изучении геометрии
В геометрии особую роль имеют тригонометрические функции, при помощи которых определяют, как относятся между собой стороны и углы прямоугольного треугольника. Конечно, тригонометрия не стоит на месте и со времен Евклида она намного шагнула вперёд и теперь может эти функции могут выражаться через решение дифференциальных уравнений.
В данный момент используются шесть обозначений для основных тригонометрических функций, причем четыре функции из шести, они стоят в ряду последними, можно определять не только с помощью геометрии.
Синус (sin)
Косинус (cos)
Тангенс (tg/tan)
Котангенс (ctg/cot)
Секанс (sec)
Косеканс (cosec/csc) .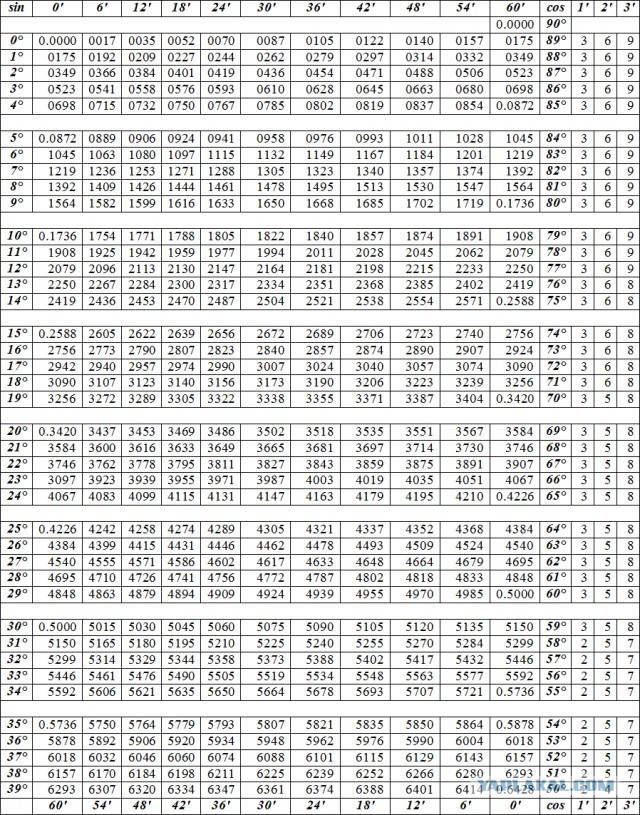
Рассмотрим сам прямоугольный треугольник, обозначения его сторон и углов во всех справочниках, как обычно, стандартные, какой бы стороной он не лежал бы на плоскости.
В этом треугольнике различают три угла, обозначаемые α, β, γ, при этом γ всегда 90°. Сторона, лежащая напротив прямого угла γ, называется гипотенузой, она обозначается буквой С. Угол α, с него начинаются все расчеты, находится напротив стороны а / ВС/, называемой противолежащей к этому углу, и сторона b /АС/, которая находится рядом, подлежит к этому углу и называется прилежащей.
По Евклидовой теории, которая верна до сих пор (и будет верна всегда), суммы углов такого треугольника, который находится в одной плоскости, будет равна 180 или числу π. И значение любого угла будут находиться в пределах между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.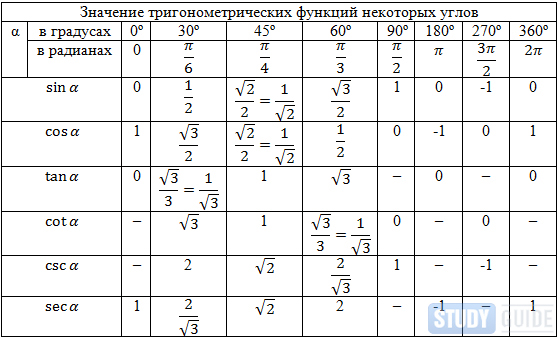
- Синус α выражается через отношение катета, который лежит напротив этого угла, к гипотенузе нашего треугольника, то есть sin α = а: с.
- Косинус α выражается через отношение катета, который прилежит к углу α, и гипотенузы с, cos α = b: с. Кстати, sin β = α: с, что позволяет принять то, что sin α равен cos β и следовательно sin β равен cos α.
- Тангенс α равен частному от отношения противолежащего катета а к катету прилежащему b: tg α = а : b.
- Котангенс угла α в соответствии равен ctg α = b : а.
- Секанс угла α составляет отношение гипотенузы треугольника к катету, прилежащему к этому углу sec α = c : b.
- Косеканс угла α составляет отношение гипотенузы треугольника к катету, который противостоит углу, cosecα = с : a.
Эти функции можно выразить и через окружность путем задания системы координат. Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
Тогда тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Следовательно, если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Тангенс — это отношение…
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

Приняты обозначения:
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Применение функции тангенса для решения задач
Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.
Пример: есть два катета ВС = 7 см и АС = 12 см. Нам нужно узнать все остальные данные о треугольнике.
Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.
Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.
Нам осталось найти гипотенузу с.
Можем найти её через sin α, который равен а: с, тогда с = а : sin α.
Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.
Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875.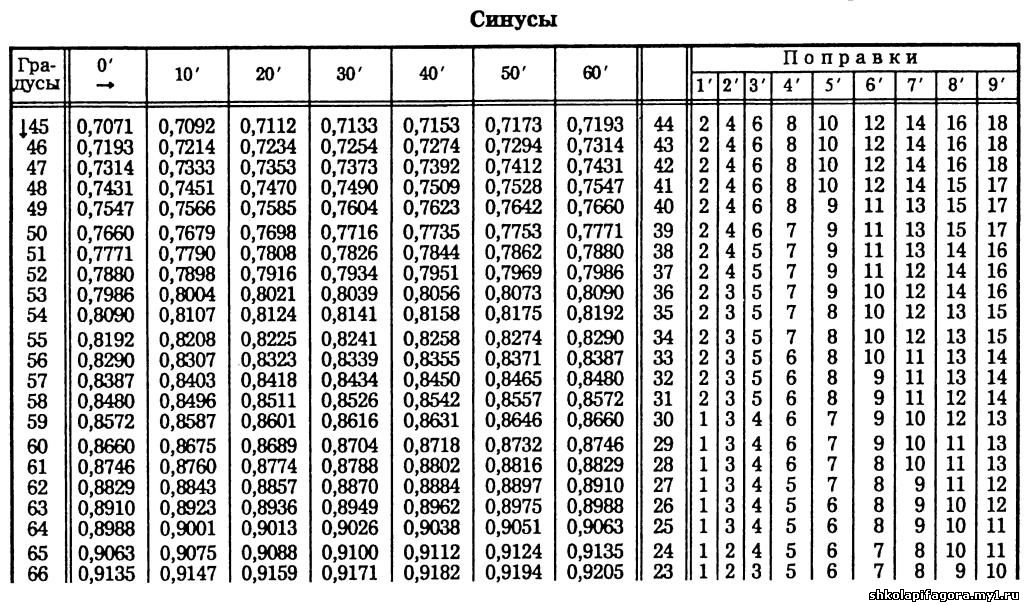 Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.
Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π.
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | – |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1. 7321 7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | – |
| Тангенс 360 | 2π | 0 |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.
Найти тангенс угла tg(α), в прямоугольном треугольнике
Противолежащий катет a
Прилежащий катет b
График тангенса
Функция тангенса пишется как y = tg (x).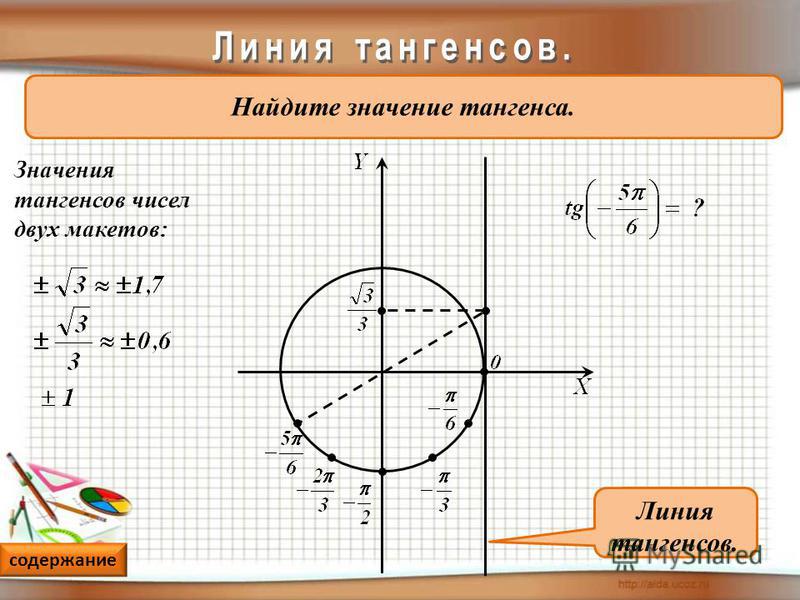 График в общем виде выглядит следующим образом:
График в общем виде выглядит следующим образом:
Определение
Геометрический смысл понятия таков: в контексте прямоугольного треугольника тангенс угла – это отношение катета противолежащего к катету прилежащему. Рассмотрим это отношение на конкретной фигуре для удобства понимания.
В данном треугольнике тангенс угла альфа – это отношение С к А. Теперь рассмотрим другой острый угол – β (бета). Для бета тангенс угла – это отношение А к С.
Теперь перейдем к определению тангенса, которое несет алгебраический смысл, для этого нам понадобится единичная окружность.
Для того чтобы отметить в декартовой системе координат численное значение тангенса необходимо для начала провести прямую х = 1, которая будет перпендикулярна оси абсцисс и параллельна оси ординат. После чего отложим от оси абсцисс угол альфа и продлим его сторону до пересечения с прямой х = 1. Ордината точки пересечения в конкретной ситуации будет являться численным значением тангенса отложенного угла.
С точки зрения алгебры, определение тангенса имеет следующий вид: тангенс угла – это отношение синуса данного угла к его косинусу.
Таблица Брадиса tg, ctg
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
Свойства
Тангенс угла tg(α) — есть отношение противолежащего катета a к прилежащему катету b.
Решение уравнения ctg x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.
Рис. 4
Частные случаи решения уравнений ctg x = a
| Уравнение | Решение |
| ctg x = – 1 | |
| ctg x = 0 | |
| ctg x = 1 | |
Уравнение: Решение: |
Уравнение: ctg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: ctg x = 0 Решение: |
Решение: |
Уравнение: ctg x = 1 Решение: |
Уравнение: Решение: |
Таблица Брадиса – синусы и косинусы.
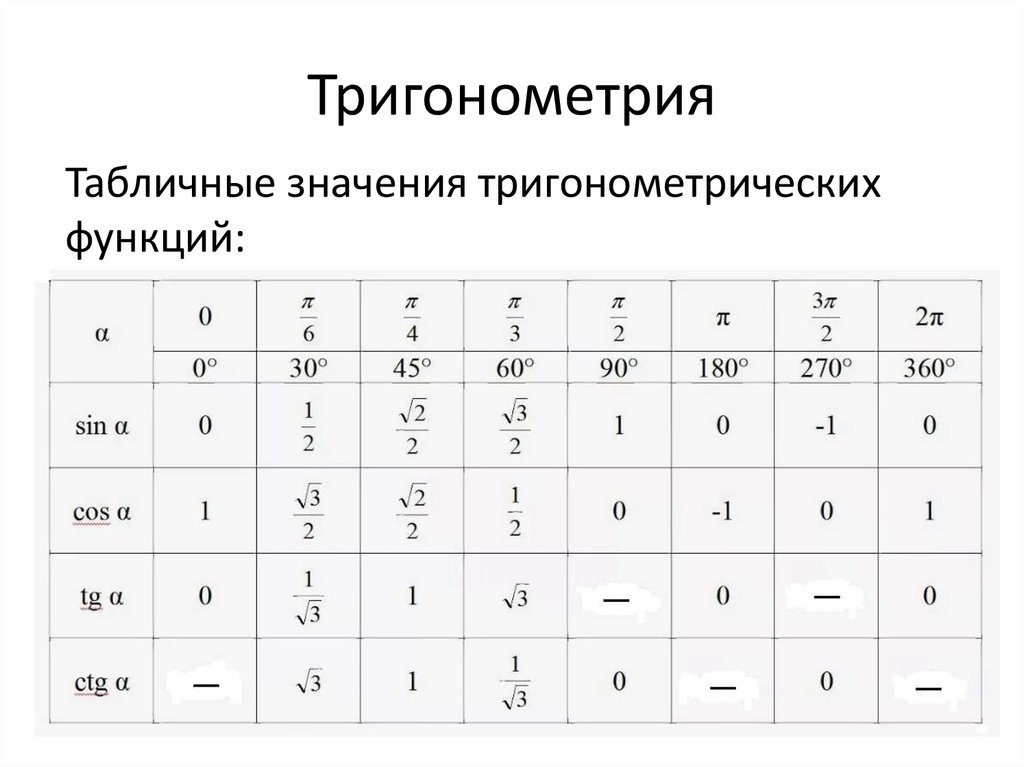
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Получается, что
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
В частности,
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Обратная к тангенсу функция
Арктангенс x – это обратная функция к тангенсу x, где x – любое число (x∈ℝ).
Если тангенс угла у равняется х (tg y = x), значит арктангенс x равен у:
arctg x = tg-1 x = y
Например:
arctg 1 = tg-1 1 = 45° = π/4 рад
Как связаны тангенс с котангенсом?
Тангенс является обратной функцией от котангенса, а это значит что: tg = 1/ctg. Таким образом, отношение тангенса к котангенсу является равным единице: tg/ctg = 1.
Источники
- https://www.calc.ru/Tablitsa-Bradisa-Tangensy-I-Kotangensy.html
- https://www.resolventa.ru/spr/trig/equation.htm
- https://KtoNaNovenkogo.ru/voprosy-i-otvety/tangens-chto-ehto-takoe-otnoshenie-najti-formulam-kletochkam.html
- https://themechanic.ru/bradis/tablica-tangensov
- https://geleot.
 ru/education/math/geometry/angle/tangent
ru/education/math/geometry/angle/tangent - https://MicroExcel.ru/tangens/
- https://1Ku.ru/obrazovanie/56899-tangens-ugla-jeto-otnoshenie-chego-osnovy-trigonometrii/
- https://www.mozgan.ru/Table/TableBradis
Электронный справочник по математике для школьников таблица значений тригонометрических функций синуса косинуса тангенса котангенса примеры вычисления значений
| Справочник по математике | Тригонометрия |
Содержание
| Таблица значений тригонометрических функций часто используемых углов |
| Вычисление значений тригонометрических функций |
Таблица значений тригонометрических функций часто используемых углов
| I четверть | |||||
| α (рад) | α (град) | sin α | cos α | tg α | ctg α |
| 0 | 0° | 0 | 1 | 0 | не существует |
| – 2π | – 360° | ||||
| 30° | – 330° | ||||
| 1 | 1 | ||||
| 45° | – 315° | ||||
| 60° | – 300° | ||||
| 1 | 0 | не существует | 0 | ||
| 90° | – 270° | ||||
| II четверть | |||||
| α (рад) | α (град) | sin α | cos α | tg α | ctg α |
| 120° | – 240° | ||||
| – 1 | – 1 | ||||
| 135° | – 225° | ||||
| 150° | – 210° | ||||
| π | – π | 0 | – 1 | 0 | не существует |
| 180° | – 180° | ||||
| III четверть | |||||
| α (рад) | α (град) | sin α | cos α | tg α | ctg α |
| 210° | – 150° | ||||
| 1 | 1 | ||||
| 225° | – 135° | ||||
| 240° | – 120° | ||||
| – 1 | 0 | не существует | 0 | ||
| 270° | – 90° | ||||
| IV четверть | |||||
| α (рад) | α (град) | sin α | cos α | tg α | ctg α |
| 300° | – 60° | ||||
| – 1 | – 1 | ||||
| 315° | – 45° | ||||
| 330° | – 30° | ||||
| 2π | 0 | 0 | 1 | 0 | не существует |
| 360° | 0° | ||||
| I четверть | |
| α (рад): 0, – 2π α (град): 0°, – 360° | |
| sin α | 0 |
| cos α | 1 |
| tg α | 0 |
| ctg α | не существует |
| α (рад): , α (град): 30°, – 330° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 45°, – 315° | |
| sin α | |
| cos α | |
| tg α | 1 |
| ctg α | 1 |
| α (рад): , α (град): 60°, – 300° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 90°, – 270° | |
| sin α | 1 |
| cos α | 0 |
| tg α | не существует |
| ctg α | 0 |
| II четверть | |
| α (рад): , α (град): 120°, – 240° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 135°, – 225° | |
| sin α | |
| cos α | |
| tg α | – 1 |
| ctg α | – 1 |
| α (рад): , α (град): 150°, – 210° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): π, – π α (град): 180°, – 180° | |
| sin α | 0 |
| cos α | – 1 |
| tg α | 0 |
| ctg α | не существует |
| III четверть | |
| α (рад): , α (град): 210°, – 150° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 225°, – 135° | |
| sin α | |
| cos α | |
| tg α | 1 |
| ctg α | 1 |
| α (рад): , α (град): 240°, –120° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 270°, – 90° | |
| sin α | – 1 |
| cos α | 0 |
| tg α | не существует |
| ctg α | 0 |
| IV четверть | |
| α (рад): , α (град): 300°, – 60° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 315°, – 45° | |
| sin α | |
| cos α | |
| tg α | – 1 |
| ctg α | – 1 |
| α (рад): , α (град): 330°, –30° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): 2π, 0 α (град): 360°, 0° | |
| sin α | 0 |
| cos α | 1 |
| tg α | 0 |
| ctg α | не существует |
Примеры вычисления значений тригонометрических функций
ПРИМЕР 1. Найти sin 15°.
Найти sin 15°.
РЕШЕНИЕ. Воспользовавшись формулой «Синус разности», получаем:
ПРИМЕР 2. Найти cos 22,5°.
РЕШЕНИЕ. Воспользовавшись формулой «Косинус двойного угла», получаем:
ПРИМЕР 3. Найти sin 18°.
РЕШЕНИЕ. Поскольку
то, с помощью формул «Синус тройного угла» и «Косинус двойного угла», отсюда получаем:
Теперь, если ввести обозначение
sin 18° = t ,
то возникает кубическое уравнение
4t3 – 2t2 – 3t + 1 = 0 .
Решим это уравнение, раскладывая его левую часть на множители:
Поскольку
0 < sin 18° < 1 ,
то первый и второй корни должны быть отброшены. Следовательно,
Таблица касательных.
Таблица тангенсов – подсчитанные значения тангенсов углов, отмеченных в таблице от 0° до 360°.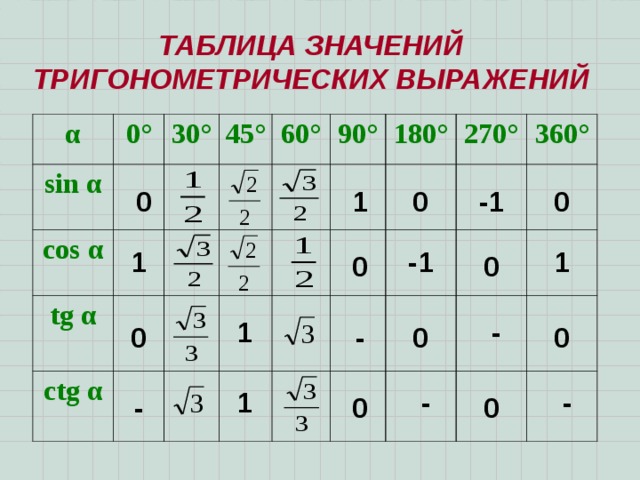 С помощью таблицы тангенсов можно производить расчеты, даже если под рукой не окажется научного калькулятора. Для нахождения тангенсов угла достаточно найти значение в таблице.
С помощью таблицы тангенсов можно производить расчеты, даже если под рукой не окажется научного калькулятора. Для нахождения тангенсов угла достаточно найти значение в таблице.
Вычислить тангенс угла
Таблица тангенса в радианах
| α | 0 | №6 | №4 | №3 | №2 | № | 3π2 | 2π |
| желтовато-коричневый α | 0 | √33 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Таблица касательных углов от 0° до 180°
| тангенс (0°) = 0 тангенс (1°) = 0,01746 тангенс (2°) = 0,03492 тангенс (3°) = 0,05241 тангенс (4°) = 0,06993 тангенс (5) 0,08749 тангенс (6°) = 0,1051 тангенс (7°) = 0,12278 тангенс (8°) = 0,14054 тангенс (9°) = 0,15838 тангенс (10°) = 0,17633 7 тангенс (0,119) 3 = 8 тангенс (119) tan(12°) = 0,21256 tan(13°) = 0,23087 tan(14°) = 0,24933 tan(15°) = 0,26795 tan(16°) = 0,28675 tan(17°) = 0, 3 tan 18°) = 0,32492 тангенс(19°) = 0,34433 тангенс (20°) = 0,36397 тангенс (21°) = 0,38386 тангенс (22°) = 0,40403 тангенс (23°) = 0,42447 тангенс (24°) = 0,44523 тангенс = 0,46631 тангенс (26°) = 0,48773 тангенс (27°) = 0,50953 тангенс (28°) = 0,53171 тангенс (29°) = 0,55431 тангенс (30°) = 0,57735 8 ( 7) тангенс tan(32°) = 0,62487 tan(33°) = 0,64941 tan(34°) = 0,67451 tan(35°) = 0,70021 tan(36°) = 0,72654 tan(37°)3 = 0,79067 tan(37°)3 = 0,7905 (38°) = 0,78129 тангенс (39°) = 0,80978 тангенс (40°) = 0,8391 тангенс (41°) = 0,86929 тангенс (42°) = 0,9004 тангенс (43°) = 0, | тангенс (61°) = 1,80405 тангенс (62°) = 1,88073 тангенс (63°) = 1, тангенс (64°) = 2,0503 тангенс (65°) = 2,14451 тангенс тангенс (67°) = 2,35585 тангенс (68°) = 2,47509 тангенс (69°) = 2,60509 тангенс (70°) = 2,74748 тангенс (71°) = 2, тангенс (72°) = 8 3, тангенс (72°) = 8 3, тангенс (72°) (73°) = 3,27085 тангенс (74°) = 3,48741 тангенс (75°) = 3,73205 тангенс (76°) = 4,01078 тангенс (77°) = 4,33148 тангенс (78°) = 4,7067 9067 °) = 5,14455 | тангенс (121°) = -1,66428 тангенс (122°) = -1,60033 тангенс (123°) = -1,53986 тангенс (124°) = -1, 6 тангенс (1,480676) 125°) = -1,42815 тангенс (126°) = -1,37638 тангенс (127°) = -1,32704 тангенс (128°) = -1,27994 тангенс (129°) = -1,2349 тангенс (130°) = — 1,19175 тангенс (131°) = -1,15037 тангенс (132°) = -1,11061 тангенс (133°) = -1,07237 тангенс (134°) = -1,03553 тангенс (135°) = -1 тангенс °) = -0, | 7 тангенс °) = -0,72654 tan(145°) = -0,70021 tan(146°) = -0,67451 tan(147°) = -0,64941 tan(148°) = -0,62487 tan(149°) = -0,60086 tan(150°) = -0,57735 tan(151°) = -0,55431 tan(152°) = -0,53171 tan(153°) = -0,50953 tan(154°) = -0,48773 tan(15567) ) = -0,46631 тангенс (156°) = -0,44523 тангенс (157°) = -0,42447 tan(158°) = -0,40403 tan(159°) = -0,38386 tan(160°) = -0,36397 tan(161°) = -0,34433 tan(162°) = -0,32492 tan(163° ) = -0,30573 тангенс (164°) = -0,28675 тангенс (165°) = -0,26795 тангенс (166°) = -0,24933 тангенс (167°) = -0,23087 тангенс (168°) = -0,201256 tan(169°) = -0,19438 tan(170°) = -0,17633 tan(171°) = -0,15838 tan(172°) = -0,14054 tan(173°) = -0,12278 tan(174°) = -0,1051 тангенс (175°) = -0,08749 тангенс (176°) = -0,06993 tan(177°) = -0,05241 tan(178°) = -0,03492 tan(179°) = -0,01746 tan(180°) = 0 |
Таблица касательных углов от 181° до 360°
| тангенс (181°) = 0,01746 тангенс (182°) = 0,03492 тангенс (183°) = 0,05241 тангенс (184°) = 0,06993 тангенс (185°) 18 = 0,06993 тангенс (185°) 18 = 0,06993 0,1051 тангенс (187°) = 0,12278 тангенс (188°) = 0,14054 тангенс (189°) = 0,15838 тангенс (190°) = 0,17633 тангенс (191°) = 0,19438 тангенс (192°) = 0,21256 тангенс (193°) = 0,23087 тангенс (194°) = 0,24933 тангенс (195°) = 0,26795 6 7 7 тангенс (19628) (197°) = 0,30573 тангенс (198°) = 0,32492 тангенс (199°) = 0,34433 тангенс (200°) = 0,36397 тангенс (201°) = 0,38386 тангенс (202°) 3 06 0,404 0,4004 °) = 0,42447 тангенс (204°) = 0,44523 тангенс (205°) = 0,46631 тангенс (206°) = 0,48773 тангенс (207°) = 0,50953 тангенс (208°) = 0,502671 ° = 0,55431 тангенс (210°) = 0,57735 тангенс (211°) = 0,60086 тангенс (212°) = 0,62487 тангенс (213°) = 0,64941 тангенс (214°) = 0,67451 тангенс (215°) = 0,70021 5 тангенс (216067) (217°) = 0,75355 тангенс (218°) = 0,78129 тангенс (219°) = 0,80978 тангенс (220°) = 0,8391 тангенс (221°) = 0,86929 тангенс (227°) 4 тангенс (222°) = 0,9000 °) = 0, | тангенс = 1,15037 тангенс (230°) = 1,19175 тангенс (231°) = 1,2349 тангенс (232°) = 1,27994 тангенс (233°) = 1,32704 тангенс (234°) = 1,37638 тангенс (235°) = 1,428915 | 0 0 6 (200368) 0 Tan (237 °) = 1,53986 TAN (238 °) = 1,60033 TAN (239 °) = 1,66428 TAN (240 °) = 1,73205 | TAN (241 °) = 1,80405 TAN (2420. 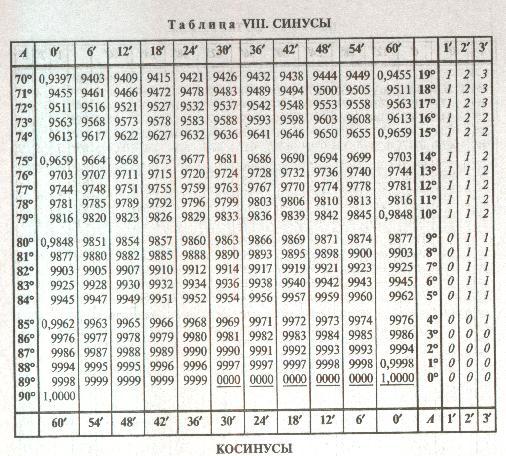 ) = 1,88073 = ) = 1,88073 = 3973 = 1,88073 = 1,88073 = 1,8077 | 7773977 гг. tan(243°) = 1, tan(301°) = -1,66428 tan(302°) = -1,60033 tan(303°) = -1,53986 tan(304°) = -1,48256 tan( ) °) = -1,42815 тангенс (306°) = -1,37638 тангенс (307°) = -1,32704 tan(308°) = -1,27994 tan(309°) = -1,2349 tan(310°) = -1,19175 tan(311°) = -1,15037 tan(312°) = -1,11061 tan(313°) ) = -1,07237 tan(314°) = -1,03553 tan(315°) = -1 tan(316°) = -0, |
Таблицы значений тригонометрических функций Таблица синуса Таблица косинусов Таблица котангенсов Таблица тригонометрических функций (синусы, косинусы, тангенсы, котангенсы)
Формулы тригонометрии
Все таблицы и формулы
Таблица касательных | Кубенс
Таблица тангенсов В таблицу заносятся расчетные значения тангенсов углов от 0° до 360°. С помощью таблицы тангенсов можно производить расчеты, даже если под рукой не окажется научного калькулятора. Чтобы узнать значение тангенса искомого угла, достаточно найти его в таблице.
С помощью таблицы тангенсов можно производить расчеты, даже если под рукой не окажется научного калькулятора. Чтобы узнать значение тангенса искомого угла, достаточно найти его в таблице.
Используя таблицу тангенсов, можно произвести расчет, даже если под рукой не окажется научного калькулятора.
Чтобы найти значение тангенса угла достаточно воспользоваться этой таблицей.
Таблица тангенсов в радианах
| α | 0 | №/6 | №/4 | №/3 | №/2 | № | 3π/2 | 2π |
| тг α |
Таблица тангенсов вместе с таблицей косинусов и таблицей синусов изучается в начале тригонометрии. Без понимания таблицы тангенсов будет очень сложно изучать тригонометрию и применять тригонометрические формулы.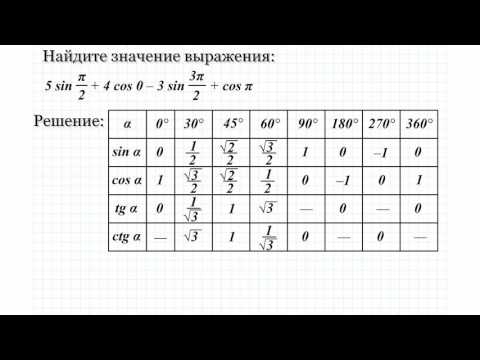
Тригонометрические функции имеют большое практическое значение в геометрии. По сути это только показатели отношения различных сторон прямоугольного треугольника друг к другу, они могут помочь в решении большинства задач, результат которых сводится к решениям прямоугольных треугольников.
Одна из основных тригонометрических функций тангенс. Поэтому в этой таблице тангенсов вы сможете найти любое значение тангенса.
Таблица тангенсов углов от 0° до 180°
Таблица тангенсов углов от 0° до 180°
| tg(0°) = 0 7070 tg(1°) (2°) = 0,03492 tg(3°) = 0,05241 tg(4°) = 0,06993 tg(5°) = 0,08749 tg(6°) = 0,1051 tg(7°) = 0,12278 9008 °) = 0,14054 tg(9°) = 0,15838 tg(10°) = 0,17633 tg(11°) = 0,19438 tg(12°) = 0,21256 tg(13°) = 0,23087 7 tg(14°) (15°) = 0,26795 tg(16°) = 0,28675 tg(17°) = 0,30573 tg(18°) = 0,32492 tg(19°) = 0,34433 tg(20°) = 7,0633 tg(20°) °) = 0,38386 tg(22°) = 0,40403 tg(23°) = 0,42447 tg(24°) = 0,44523 tg(25°) = 0,46631 tg(26°) = 0,400677° = 0,50953 tg(28°) = 0,53171 tg(29°) = 0,55431 tg(30°) = 0,57735 tg(31°) = 0,60086 tg(32°) = 0,62487 tg(33°) = 0,64941 tg(34°) = 0,67451 0,7 tg(350) (36°) = 0,72654 tg(37°) = 0,75355 tg(38°) = 0,78129 tg(39°) = 0,80978 tg(40°) = 0,8391 tg(41°) = 0, °) = 0,9004 tg(43°) = 0, | tg(61°) = 1,80405 tg(62°) = 1,88073 tg(63°) = 1, tg(64°) = 2,0503 tg(65°) = 2,14451 0,72067 tg(6204) (67°) = 2,35585 тг(68°) = 2,47509 тг(69°) = 2,60509 тг(70°) = 2,74748 тг(71°) = 2, TG (72 °) = 3,07768 TG (73 °) = 3,27085 TG (74 °) = 3,48741 TG (75 °) = 3,73205 TG (76 °) = 4,01078 TG (7773.  4773 = 4,01078 4773 = 4,01078 TG (7773. 4773 = 4,01078 TG (7773. 4773 = 4,01078 TG (7773. 4,314 = 4,01078 TG (7773. 4,333 = 4,01078 TG (7773. 4,333 = 4,01078 TG (7773333 = 4.01078 TG (7773. 4,314. tg(78°) = 4,70463 tg(79°) = 5,14455 tg(80°) = 5,67128 tg(81°) = 6,31375 tg(82°) = 7,11537 tg(81°)4 = 8,11537 tg(81°)4 = 8,11537 tg(80°) 84 °) = 9,51436 TG (85 °) = 11,43005 TG (86 °) = 14,30067 TG (87 °) = 19,08114 TG (88 °) = 28,63625 TG (89 °) = 57,9, | 66666666666666666666666666 гг. °) = ∞ tg(91°) = -57,28996 tg(92°) = -28,63625 tg(93°) = -19,08114 tg(94°) = -14,30067 tg(95°) = -11,43005 tg(96°) = -9,51436 ° tg ) = -8,14435 tg(98°) = -7,11537 tg(99°) = -6,31375 tg(100°) = -5,67128 tg(101°) = -5,14455 tg(102°) = -7,0046 tg(103°) = -4,33148 tg(104°) = -4,01078 tg(105°) = -3,73205 tg(106°) = -3,48741 tg(107°) = -3,27085 ° = -3,07768 тг(109°) = -2, тг(110°) = -2,74748 тг(111°) = -2,60509 tg(112°) = -2,47509 tg(113°) = -2,35585 tg(114°) = -2,24604 tg(115°) = -2,14451 tg(116°) = -2,0503 | tg(121°) = -1,66428 tg(122°) = -1,60033 tg(123°) = -1,53986 tg(124°) = -1,48256 tg(125°) = -1,42815 | 6 tg ) = -1,37638
Тангенс 0 (нулевой тангенс)
равен (равен нулю)
1 тангенс (тангенс единиц)
равен
Тангенс 3 (три тангенса)
равен
90 тангенс (тангенс 90 градусов)
(до бесконечности)
тангенс 30 (тангенс 30 градусов)
равен
равен
9030 9030
градусов ( градусов)The tangent of 60 (the tangent of 60 degrees)
equal
Table of tangents of angles from 181° to 360°
tg(181°) = 0.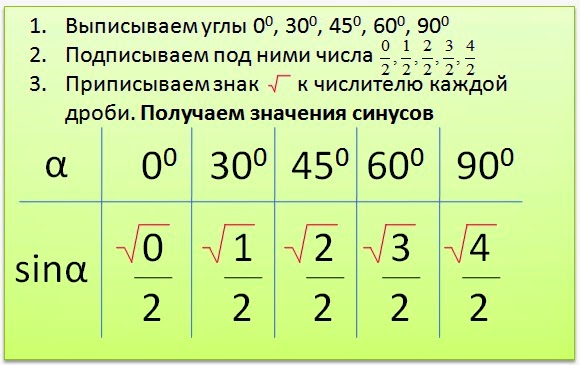 01746 01746 tg(182°) = 0.03492 tg (183°) = 0,05241 tg(184°) = 0,06993 TG (185 °) = 0,08749 TG (186 °) = 0,1051 TG (187 °) = 0,12278 TG (188 °) = 0,14054 TG (189 °) = 0,15838 TG (19066) = 0,1763333333 гг. tg(191°) = 0,19438 tg(192°) = 0,21256 tg(193°) = 0,23087 tg(194°) = 0,24933 tg(195°) = 0,26795° 0 79 tg(19,6 8) 197°) = 0.30573 tg(198°) = 0.32492 tg(199°) = 0.34433 tg(200°) = 0.36397 tg(201°) = 0.38386 tg(202°) = 0.40403 tg(203° ) = 0,42447 tg(204°) = 0,44523 TG (205 °) = 0,46631 TG (206 °) = 0,48773 TG (207 °) = 0,50953 TG (208 °) = 0,53171 TG (209 °) = 0,55431 TG (210673 = 0,5773 = 0,55431 TG (210673 = 0,5773 = 0,55431 TG) = 0,5773 = 0,55431 TG) = 0,55431 TG) = 0,55431. (211°) = 0,60086 tg(212°) = 0,62487 tg(213°) = 0,64941 tg(214°) = 0,67451 tg(215°) = 0,70021 tg(216°) = 0,70021 tg(216°) 2(4 0,72)06 °) = 0,75355 tg(218°) = 0,78129 tg(219°) = 0,80978 tg(220°) = 0,8391 tg(221°) = 0,86929 tg(222°) = 3°7604 0,904 = 0, | тг(241°) = 1,80405 тг(242°) = 1,88073 тг(243°) = 1, тг(244°) = 2,0503 TG (245 °) = 2,14451 TG (246 °) = 2,24604 TG (247 °) = 2,35585 TG (248 °) = 2,47509 TG (249 °) = 2,60509 TG (250 °) = 2,7474347448474747447474747474 гг. (251°) = 2, tg(252°) = 3,07768 tg(253°) = 3,27085 tg(254°) = 3,48741 tg(255°) = 3,73205 tg(24061)0 = 8 5777 tg(24061)02 °) = 4,33148 tg(258°) = 4,70463 tg(259°) = 5,14455 tg(260°) = 5,67128 tg(261°) = 6,31375 tg(262°)5 6 7 7,1 03 = 8,14435 tg(264°) = 9,51436 tg(265°) = 11,43005 tg(266°) = 14,30067 tg(267°) = 19,08114 tg(268°) = 28,63625 tg(269°) = 57,28996 tg(270°) = 47 ∞1 90 0 57,28996 tg(272°) = -28,63625 tg(273°) = -19,08114 tg(274°) = -14,30067 tg(275°) = -11,43005 tg(275°)4 = -7,43005 tg(2751°)4 = -7,43005 tg(2751°)3 °) = -8,14435 tg(278°) = -7,11537 tg(279°) = -6,31375 tg(280°) = -5,67128 tg(281°) = -5,14455 tg(282°)4 = -4,706 tg(283°) = -4,33148 tg(284°) = -4,01078 tg(285°) = -3,73205 tg(286°) = -3,48741 tg(287°) = -3,27085 tg(288°) = -3,07768 tg(289°) = -2, | 0 tg° ) = -2,74748 тг(301°) = -1,66428 тг(302°) = -1,60033 тг(303°) = -1,53986 tg(304°) = -1,48256 tg(305°) = -1,42815 tg(306°) = -1,37638 tg(307°) = -1,32704 tg(308°) = -1,27997 tg(307°) °) = -1,2349 tg(310°) = -1,19175 tg(311°) = -1,15037 tg(312°) = -1,11061 tg(313°) = -1,07237 tg(314°)5 = -1,033 тг(315°) = -1 тг(316°) = -0, |
Помимо таблицы тангенсов , на нашем сайте вы можете просмотреть таблицу косинусов, таблицу котангенсов, таблицу синусов.
Тригонометрическая (Sin Cos Tan) таблица 0-360 градусов (загружаемая) и как извлечь из нее уроки 360 градусов (доступно для скачивания) и как извлечь из этого уроки
В этой статье Compute Expert вы сможете увидеть полные тригонометрические (sin cos tan) таблицы от 0 до 360 градусов. Вы можете скачать таблицы в формате Excel или PDF, если хотите, по ссылкам для скачивания, которые мы предоставляем.
Здесь мы также немного обсудим тригонометрическую таблицу и то, как по ней учиться. Здесь есть раздел, в котором рассказывается о том, как создать и изменить таблицу в Excel, если вам это интересно.
Здесь есть раздел, в котором рассказывается о том, как создать и изменить таблицу в Excel, если вам это интересно.
Excel — это гибкое программное обеспечение, которое мы можем использовать для создания многих вещей. Одной из таких вещей является тригонометрическая таблица. Эта таблица может быть очень полезна, если мы хотим выполнить некоторые арифметические операции с имеющимися у нас числами степеней.
Хотите узнать больше о тригонометрической таблице и научиться создавать ее самостоятельно в Excel? Читайте нашу статью до последней ее части!
Отказ от ответственности : Этот пост может содержать партнерские ссылки, по которым мы получаем комиссию от соответствующих покупок/действий без каких-либо дополнительных затрат для вас. Учить больше
Содержание :
- Содержание нашей тригонометрической таблицы (специальные углы (градусы))
- Содержимое нашей тригонометрической таблицы (все углы (градусы) от 0° до 360°)
- Скачать тригонометрическую таблицу (excel xlsx/PDF)
- Определение тригонометрии
- Определение тригонометрической таблицы
- Определение греха, косы и загара
- Советы по изучению наших тригонометрических таблиц
- Как создать тригонометрическую таблицу в excel
- Как изменить наши тригонометрические таблицы в их шаблонах Excel
- Упражнение/игра на умножение
- Дополнительное примечание
Содержание нашей тригонометрической таблицы (специальные углы (градусы))
Есть два типа тригонометрических таблиц, которые часто используют люди: тригонометрическая таблица специальных углов и тригонометрическая таблица всех углов. Вы можете выбрать, какой из них вы предпочитаете использовать, из таблиц, которые мы создали для вас здесь.
Вы можете выбрать, какой из них вы предпочитаете использовать, из таблиц, которые мы создали для вас здесь.
Первая — специальная тригонометрическая таблица углов. Вот содержание тригонометрической таблицы специальных углов, которую мы включаем в нашу таблицу, начиная с 0 до 90 градусов.
от 0 до 90 градусов, тригонометрическая таблица специальных углов
| Градус (°) | sin | cos | tan |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 30 | 1/2 | 1/2√3 | 1/2√3 |
| 45 | 1/2√2 | 1/2√2 | 1 |
| 60 | 1/2√3 | 1/2 | √3 |
| 90 | 1 | 0 | ∞ |
90-180 градусов, тригонометрическая таблица специальных углов
| Градус (°) | sin | cos | tan |
|---|---|---|---|
| 90 | 1 | 0 | ∞ |
| 120 | 1/2√3 | -1/2 | -√3 |
| 135 | 1/2√2 | -1/2√2 | -1 |
| 150 | 1/2 | -1/2√3 | -1/2√3 |
| 180 | 0 | -1 | 0 |
180-270 градусов, тригонометрическая таблица специальных углов
| Градус (°) | sin | cos | tan |
|---|---|---|---|
| 180 | 0 | -1 | 0 |
| 210 | -1/2 | -1/2√3 | 1/3√3 |
| 225 | -1/2√2 | -1/2√2 | 1 |
| 240 | -1/2√3 | -1/2 | √3 |
| 270 | -1 | 0 | ∞ |
270-360 градусов, тригонометрическая таблица специальных углов
| Градус (°) | sin | cos | желто-коричневый |
|---|---|---|---|
| 270 | -1 | 0 | ∞ |
| 300 | -1/2√3 | 1/2 | -√3 |
| 315 | -1/2√2 | 1/2√2 | -1 |
| 330 | -1/2 | -1/2√3 | -1/3√3 |
| 360 | 0 | 1 | 0 |
А вот так выглядит наша тригонометрическая таблица специальных углов.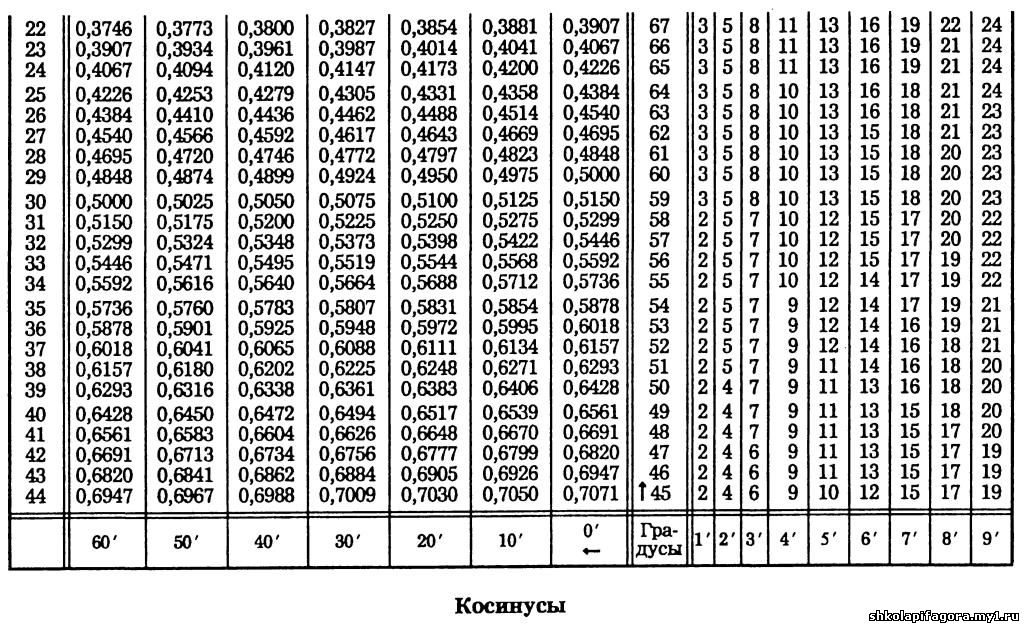
Содержание нашей тригонометрической таблицы (все углы (градусы) от 0 до 360)
Хотите получить значение sin, cos или tan из степеней, отличных от указанных выше специальных степеней? Вы можете взглянуть на нашу тригонометрическую таблицу для всех углов (от 0 до 360 градусов), если это так!
Вот что мы поместили в нашу таблицу.
| Градус (°) | sin | cos | tan |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 1 | 0,0175 | 0,9998 | 0,0175 |
| 2 | 0,0349 | 0,9994 | 0,0349 |
| 3 | 0,0523 | 0,9986 | 0,0524 |
| 4 | 0,0698 | 0,9976 | 0,0699 |
| 5 | 0,0872 | 0,9962 | 0,0875 |
| 6 | 0,1045 | 0,9945 | 0,1051 |
| 7 | 0,1219 | 0,9925 | 0,1228 |
| 8 | 0,1392 | 0,9903 | 0,1405 |
| 9 | 0,1564 | 0,9877 | 0,1584 |
| 10 | 0,1736 | 0,9848 | 0,1763 |
| 11 | 0,1908 | 0,9816 | 0,1944 |
| 12 | 0,2079 | 0,9781 | 0,2126 |
| 13 | 0,225 | 0,9744 | 0,2309 |
| 14 | 0,2419 | 0,9703 | 0,2493 |
| 15 | 0,2588 | 0,9659 | 0,2679 |
| 16 | 0,2756 | 0,9613 | 0,2867 |
| 17 | 0,2924 | 0,9563 | 0,3057 |
| 18 | 0,309 | 0,9511 | 0,3249 |
| 19 | 0,3256 | 0,9455 | 0,3443 |
| 20 | 0,342 | 0,9397 | 0,364 |
| 21 | 0,3584 | 0,9336 | 0,3839 |
| 22 | 0,3746 | 0,9272 | 0,404 |
| 23 | 0,3907 | 0,9205 | 0,4245 |
| 24 | 0,4067 | 0,9135 | 0,4452 |
| 25 | 0,4226 | 0,9063 | 0,4663 |
| 26 | 0,4384 | 0,8988 | 0,4877 |
| 27 | 0,454 | 0,891 | 0,5095 |
| 28 | 0,4695 | 0,8829 | 0,5317 |
| 29 | 0,4848 | 0,8746 | 0,5543 |
| 30 | 0,5 | 0,866 | 0,5774 |
| 31 | 0,515 | 0,8572 | 0,6009 |
| 32 | 0,5299 | 0,848 | 0,6249 |
| 33 | 0,5446 | 0,8387 | 0,6494 |
| 34 | 0,5592 | 0,829 | 0,6745 |
| 35 | 0,5736 | 0,8192 | 0,7002 |
| 36 | 0,5878 | 0,809 | 0,7265 |
| 37 | 0,6018 | 0,7986 | 0,7536 |
| 38 | 0,6157 | 0,788 | 0,7813 |
| 39 | 0,6293 | 0,7771 | 0,8098 |
| 40 | 0,6428 | 0,766 | 0,8391 |
| 41 | 0,6561 | 0,7547 | 0,8693 |
| 42 | 0,6691 | 0,7431 | 0,9004 |
| 43 | 0,682 | 0,7314 | 0,9325 |
| 44 | 0,6947 | 0,7193 | 0,9657 |
| 45 | 0,7071 | 0,7071 | 1 |
| 46 | 0,7193 | 0,6947 | 1,0355 |
| 47 | 0,7314 | 0,682 | 1,0724 |
| 48 | 0,7431 | 0,6691 | 1,1106 |
| 49 | 0,7547 | 0,6561 | 1,1504 |
| 50 | 0,766 | 0,6428 | 1,1918 |
| 51 | 0,7771 | 0,6293 | 1,2349 |
| 52 | 0,788 | 0,6157 | 1,2799 |
| 53 | 0,7986 | 0,6018 | 1.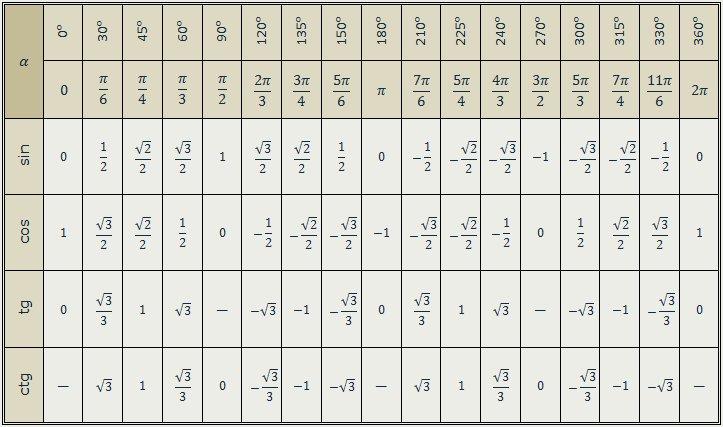 327 327 |
| 54 | 0,809 | 0,5878 | 1,3764 |
| 55 | 0,8192 | 0,5736 | 1,4281 |
| 56 | 0,829 | 0,5592 | 1,4826 |
| 57 | 0,8387 | 0,5446 | 1,5399 |
| 58 | 0,848 | 0,5299 | 1,6003 |
| 59 | 0,8572 | 0,515 | 1,6643 |
| 60 | 0,866 | 0,5 | 1,7321 |
| 61 | 0,8746 | 0,4848 | 1,804 |
| 62 | 0,8829 | 0,4695 | 1,8807 |
| 63 | 0,891 | 0,454 | 1,9626 |
| 64 | 0,8988 | 0,4384 | 2,0503 |
| 65 | 0,9063 | 0,4226 | 2,1445 |
| 66 | 0,9135 | 0,4067 | 2,246 |
| 67 | 0,9205 | 0,3907 | 2,3559 |
| 68 | 0,9272 | 0,3746 | 2,4751 |
| 69 | 0,9336 | 0,3584 | 2,6051 |
| 70 | 0,9397 | 0,342 | 2,7475 |
| 71 | 0,9455 | 0,3256 | 2,9042 |
| 72 | 0,9511 | 0,309 | 3,0777 |
| 73 | 0,9563 | 0,2924 | 3,2709 |
| 74 | 0,9613 | 0,2756 | 3,4874 |
| 75 | 0,9659 | 0,2588 | 3,7321 |
| 76 | 0,9703 | 0,2419 | 4. 0108 0108 |
| 77 | 0,9744 | 0,225 | 4,3315 |
| 78 | 0,9781 | 0,2079 | 4,7046 |
| 79 | 0,9816 | 0,1908 | 5,1446 |
| 80 | 0,9848 | 0,1736 | 5,6713 |
| 81 | 0,9877 | 0,1564 | 6,3138 |
| 82 | 0,9903 | 0,1392 | 7,1154 |
| 83 | 0,9925 | 0,1219 | 8,1443 |
| 84 | 0,9945 | 0,1045 | 9,5144 |
| 85 | 0,9962 | 0,0872 | 11,4301 |
| 86 | 0,9976 | 0,0698 | 14,3007 |
| 87 | 0,9986 | 0,0523 | 19,0811 |
| 88 | 0,9994 | 0,0349 | 28,6363 |
| 89 | 0,9998 | 0,0175 | 57,29 |
| 90 | 1 | 0 | ∞ |
| 91 | 0,9998 | -0,0175 | -57,29 |
| 92 | 0,9994 | -0,0349 | -28,6363 |
| 93 | 0,9986 | -0,0523 | -19,0811 |
| 94 | 0,9976 | -0,0698 | -14,3007 |
| 95 | 0,9962 | -0,0872 | -11,4301 |
| 96 | 0,9945 | -0,1045 | -9,5144 |
| 97 | 0,9925 | -0,1219 | -8,1443 |
| 98 | 0,9903 | -0,1392 | -7,1154 |
| 99 | 0,9877 | -0,1564 | -6,3138 |
| 100 | 0,9848 | -0,1736 | -5,6713 |
| 101 | 0,9816 | -0,1908 | -5,1446 |
| 102 | 0,9781 | -0,2079 | -4,7046 |
| 103 | 0,9744 | -0,225 | -4,3315 |
| 104 | 0,9703 | -0,2419 | -4,0108 |
| 105 | 0,9659 | -0,2588 | -3,7321 |
| 106 | 0,9613 | -0,2756 | -3,4874 |
| 107 | 0,9563 | -0,2924 | -3,2709 |
| 108 | 0,9511 | -0,309 | -3,0777 |
| 109 | 0,9455 | -0,3256 | -2,9042 |
| 110 | 0,9397 | -0,342 | -2,7475 |
| 111 | 0,9336 | -0,3584 | -2,6051 |
| 112 | 0,9272 | -0,3746 | -2,4751 |
| 113 | 0,9205 | -0,3907 | -2,3559 |
| 114 | 0,9135 | -0,4067 | -2,246 |
| 115 | 0,9063 | -0,4226 | -2,1445 |
| 116 | 0,8988 | -0,4384 | -2,0503 |
| 117 | 0,891 | -0,454 | -1,9626 |
| 118 | 0,8829 | -0,4695 | -1,8807 |
| 119 | 0,8746 | -0,4848 | -1,804 |
| 120 | 0,866 | -0,5 | -1,7321 |
| 121 | 0,8572 | -0,515 | -1,6643 |
| 122 | 0,848 | -0,5299 | -1,6003 |
| 123 | 0,8387 | -0,5446 | -1,5399 |
| 124 | 0,829 | -0,5592 | -1,4826 |
| 125 | 0,8192 | -0,5736 | -1,4281 |
| 126 | 0,809 | -0,5878 | -1,3764 |
| 127 | 0,7986 | -0,6018 | -1,327 |
| 128 | 0,788 | -0,6157 | -1,2799 |
| 129 | 0,7771 | -0,6293 | -1,2349 |
| 130 | 0,766 | -0,6428 | -1,1918 |
| 131 | 0,7547 | -0,6561 | -1,1504 |
| 132 | 0,7431 | -0,6691 | -1,1106 |
| 133 | 0,7314 | -0,682 | -1,0724 |
| 134 | 0,7193 | -0,6947 | -1,0355 |
| 135 | 0,7071 | -0,7071 | -1 |
| 136 | 0,6947 | -0,7193 | -0,9657 |
| 137 | 0,682 | -0,7314 | -0,9325 |
| 138 | 0,6691 | -0,7431 | -0,9004 |
| 139 | 0,6561 | -0,7547 | -0,8693 |
| 140 | 0,6428 | -0,766 | -0,8391 |
| 141 | 0,6293 | -0,7771 | -0,8098 |
| 142 | 0,6157 | -0,788 | -0,7813 |
| 143 | 0,6018 | -0,7986 | -0,7536 |
| 144 | 0,5878 | -0,809 | -0,7265 |
| 145 | 0,5736 | -0,8192 | -0,7002 |
| 146 | 0,5592 | -0,829 | -0,6745 |
| 147 | 0,5446 | -0,8387 | -0,6494 |
| 148 | 0,5299 | -0,848 | -0,6249 |
| 149 | 0,515 | -0,8572 | -0,6009 |
| 150 | 0,5 | -0,866 | -0,5774 |
| 151 | 0,4848 | -0,8746 | -0,5543 |
| 152 | 0,4695 | -0,8829 | -0,5317 |
| 153 | 0,454 | -0,891 | -0,5095 |
| 154 | 0,4384 | -0,8988 | -0,4877 |
| 155 | 0,4226 | -0,9063 | -0,4663 |
| 156 | 0,4067 | -0,9135 | -0,4452 |
| 157 | 0,3907 | -0,9205 | -0,4245 |
| 158 | 0,3746 | -0,9272 | -0,404 |
| 159 | 0,3584 | -0,9336 | -0,3839 |
| 160 | 0,342 | -0,9397 | -0,364 |
| 161 | 0,3256 | -0,9455 | -0,3443 |
| 162 | 0,309 | -0,9511 | -0,3249 |
| 163 | 0,2924 | -0,9563 | -0,3057 |
| 164 | 0,2756 | -0,9613 | -0,2867 |
| 165 | 0,2588 | -0,9659 | -0,2679 |
| 166 | 0,2419 | -0,9703 | -0,2493 |
| 167 | 0,225 | -0,9744 | -0,2309 |
| 168 | 0,2079 | -0,9781 | -0,2126 |
| 169 | 0,1908 | -0,9816 | -0,1944 |
| 170 | 0,1736 | -0,9848 | -0,1763 |
| 171 | 0,1564 | -0,9877 | -0,1584 |
| 172 | 0,1392 | -0,9903 | -0,1405 |
| 173 | 0,1219 | -0,9925 | -0,1228 |
| 174 | 0,1045 | -0,9945 | -0,1051 |
| 175 | 0,0872 | -0,9962 | -0,0875 |
| 176 | 0,0698 | -0,9976 | -0,0699 |
| 177 | 0,0523 | -0,9986 | -0,0524 |
| 178 | 0,0349 | -0,9994 | -0,0349 |
| 179 | 0,0175 | -0,9998 | -0,0175 |
| 180 | 0 | -1 | 0 |
| 181 | -0,0175 | -0,9998 | 0,0175 |
| 182 | -0,0349 | -0,9994 | 0,0349 |
| 183 | -0,0523 | -0,9986 | 0,0524 |
| 184 | -0,0698 | -0,9976 | 0,0699 |
| 185 | -0,0872 | -0,9962 | 0,0875 |
| 186 | -0,1045 | -0,9945 | 0,1051 |
| 187 | -0,1219 | -0,9925 | 0,1228 |
| 188 | -0,1392 | -0,9903 | 0,1405 |
| 189 | -0,1564 | -0,9877 | 0,1584 |
| 190 | -0,1736 | -0,9848 | 0,1763 |
| 191 | -0,1908 | -0,9816 | 0,1944 |
| 192 | -0,2079 | -0,9781 | 0,2126 |
| 193 | -0,225 | -0,9744 | 0,2309 |
| 194 | -0,2419 | -0,9703 | 0,2493 |
| 195 | -0,2588 | -0,9659 | 0,2679 |
| 196 | -0,2756 | -0,9613 | 0,2867 |
| 197 | -0,2924 | -0,9563 | 0,3057 |
| 198 | -0,309 | -0,9511 | 0,3249 |
| 199 | -0,3256 | -0,9455 | 0,3443 |
| 200 | -0,342 | -0,9397 | 0,364 |
| 201 | -0,3584 | -0,9336 | 0,3839 |
| 202 | -0,3746 | -0,9272 | 0,404 |
| 203 | -0,3907 | -0,9205 | 0,4245 |
| 204 | -0,4067 | -0,9135 | 0,4452 |
| 205 | -0,4226 | -0,9063 | 0,4663 |
| 206 | -0,4384 | -0,8988 | 0,4877 |
| 207 | -0,454 | -0,891 | 0,5095 |
| 208 | -0,4695 | -0,8829 | 0,5317 |
| 209 | -0,4848 | -0,8746 | 0,5543 |
| 210 | -0,5 | -0,866 | 0,5774 |
| 211 | -0,515 | -0,8572 | 0,6009 |
| 212 | -0,5299 | -0,848 | 0,6249 |
| 213 | -0,5446 | -0,8387 | 0,6494 |
| 214 | -0,5592 | -0,829 | 0,6745 |
| 215 | -0,5736 | -0,8192 | 0,7002 |
| 216 | -0,5878 | -0,809 | 0,7265 |
| 217 | -0,6018 | -0,7986 | 0,7536 |
| 218 | -0,6157 | -0,788 | 0,7813 |
| 219 | -0,6293 | -0,7771 | 0,8098 |
| 220 | -0,6428 | -0,766 | 0,8391 |
| 221 | -0,6561 | -0,7547 | 0,8693 |
| 222 | -0,6691 | -0,7431 | 0,9004 |
| 223 | -0,682 | -0,7314 | 0,9325 |
| 224 | -0,6947 | -0,7193 | 0,9657 |
| 225 | -0,7071 | -0,7071 | 1 |
| 226 | -0,7193 | -0,6947 | 1,0355 |
| 227 | -0,7314 | -0,682 | 1,0724 |
| 228 | -0,7431 | -0,6691 | 1,1106 |
| 229 | -0,7547 | -0,6561 | 1,1504 |
| 230 | -0,766 | -0,6428 | 1,1918 |
| 231 | -0,7771 | -0,6293 | 1,2349 |
| 232 | -0,788 | -0,6157 | 1,2799 |
| 233 | -0,7986 | -0,6018 | 1,327 |
| 234 | -0,809 | -0,5878 | 1,3764 |
| 235 | -0,8192 | -0,5736 | 1,4281 |
| 236 | -0,829 | -0,5592 | 1,4826 |
| 237 | -0,8387 | -0,5446 | 1,5399 |
| 238 | -0,848 | -0,5299 | 1,6003 |
| 239 | -0,8572 | -0,515 | 1,6643 |
| 240 | -0,866 | -0,5 | 1,7321 |
| 241 | -0,8746 | -0,4848 | 1,804 |
| 242 | -0,8829 | -0,4695 | 1,8807 |
| 243 | -0,891 | -0,454 | 1,9626 |
| 244 | -0,8988 | -0,4384 | 2,0503 |
| 245 | -0,9063 | -0,4226 | 2,1445 |
| 246 | -0,9135 | -0,4067 | 2,246 |
| 247 | -0,9205 | -0,3907 | 2,3559 |
| 248 | -0,9272 | -0,3746 | 2,4751 |
| 249 | -0,9336 | -0,3584 | 2,6051 |
| 250 | -0,9397 | -0,342 | 2,7475 |
| 251 | -0,9455 | -0,3256 | 2,9042 |
| 252 | -0,9511 | -0,309 | 3,0777 |
| 253 | -0,9563 | -0,2924 | 3,2709 |
| 254 | -0,9613 | -0,2756 | 3,4874 |
| 255 | -0,9659 | -0,2588 | 3,7321 |
| 256 | -0,9703 | -0,2419 | 4,0108 |
| 257 | -0,9744 | -0,225 | 4,3315 |
| 258 | -0,9781 | -0,2079 | 4,7046 |
| 259 | -0,9816 | -0,1908 | 5,1446 |
| 260 | -0,9848 | -0,1736 | 5,6713 |
| 261 | -0,9877 | -0,1564 | 6,3138 |
| 262 | -0,9903 | -0,1392 | 7,1154 |
| 263 | -0,9925 | -0,1219 | 8,1443 |
| 264 | -0,9945 | -0,1045 | 9,5144 |
| 265 | -0,9962 | -0,0872 | 11,4301 |
| 266 | -0,9976 | -0,0698 | 14,3007 |
| 267 | -0,9986 | -0,0523 | 19,0811 |
| 268 | -0,9994 | -0,0349 | 28,6363 |
| 269 | -0,9998 | -0,0175 | 57,29 |
| 270 | -1 | 0 | ∞ |
| 271 | -0,9998 | 0,0175 | -57,29 |
| 272 | -0,9994 | 0,0349 | -28,6363 |
| 273 | -0,9986 | 0,0523 | -19,0811 |
| 274 | -0,9976 | 0,0698 | -14,3007 |
| 275 | -0,9962 | 0,0872 | -11,4301 |
| 276 | -0,9945 | 0,1045 | -9,5144 |
| 277 | -0,9925 | 0,1219 | -8,1443 |
| 278 | -0,9903 | 0,1392 | -7,1154 |
| 279 | -0,9877 | 0,1564 | -6,3138 |
| 280 | -0,9848 | 0,1736 | -5,6713 |
| 281 | -0,9816 | 0,1908 | -5,1446 |
| 282 | -0,9781 | 0,2079 | -4,7046 |
| 283 | -0,9744 | 0,225 | -4,3315 |
| 284 | -0,9703 | 0,2419 | -4,0108 |
| 285 | -0,9659 | 0,2588 | -3,7321 |
| 286 | -0,9613 | 0,2756 | -3,4874 |
| 287 | -0,9563 | 0,2924 | -3,2709 |
| 288 | -0,9511 | 0,309 | -3,0777 |
| 289 | -0,9455 | 0,3256 | -2,9042 |
| 290 | -0,9397 | 0,342 | -2,7475 |
| 291 | -0,9336 | 0,3584 | -2,6051 |
| 292 | -0,9272 | 0,3746 | -2,4751 |
| 293 | -0,9205 | 0,3907 | -2,3559 |
| 294 | -0,9135 | 0,4067 | -2,246 |
| 295 | -0,9063 | 0,4226 | -2,1445 |
| 296 | -0,8988 | 0,4384 | -2,0503 |
| 297 | -0,891 | 0,454 | -1,9626 |
| 298 | -0,8829 | 0,4695 | -1,8807 |
| 299 | -0,8746 | 0,4848 | -1,804 |
| 300 | -0,866 | 0,5 | -1,7321 |
| 301 | -0,8572 | 0,515 | -1,6643 |
| 302 | -0,848 | 0,5299 | -1,6003 |
| 303 | -0,8387 | 0,5446 | -1,5399 |
| 304 | -0,829 | 0,5592 | -1,4826 |
| 305 | -0,8192 | 0,5736 | -1,4281 |
| 306 | -0,809 | 0,5878 | -1,3764 |
| 307 | -0,7986 | 0,6018 | -1,327 |
| 308 | -0,788 | 0,6157 | -1,2799 |
| 309 | -0,7771 | 0,6293 | -1,2349 |
| 310 | -0,766 | 0,6428 | -1,1918 |
| 311 | -0,7547 | 0,6561 | -1,1504 |
| 312 | -0,7431 | 0,6691 | -1,1106 |
| 313 | -0,7314 | 0,682 | -1,0724 |
| 314 | -0,7193 | 0,6947 | -1,0355 |
| 315 | -0,7071 | 0,7071 | -1 |
| 316 | -0,6947 | 0,7193 | -0,9657 |
| 317 | -0,682 | 0,7314 | -0,9325 |
| 318 | -0,6691 | 0,7431 | -0,9004 |
| 319 | -0,6561 | 0,7547 | -0,8693 |
| 320 | -0,6428 | 0,766 | -0,8391 |
| 321 | -0,6293 | 0,7771 | -0,8098 |
| 322 | -0,6157 | 0,788 | -0,7813 |
| 323 | -0,6018 | 0,7986 | -0,7536 |
| 324 | -0,5878 | 0,809 | -0,7265 |
| 325 | -0,5736 | 0,8192 | -0,7002 |
| 326 | -0,5592 | 0,829 | -0,6745 |
| 327 | -0,5446 | 0,8387 | -0,6494 |
| 328 | -0,5299 | 0,848 | -0,6249 |
| 329 | -0,515 | 0,8572 | -0,6009 |
| 330 | -0,5 | 0,866 | -0,5774 |
| 331 | -0,4848 | 0,8746 | -0,5543 |
| 332 | -0,4695 | 0,8829 | -0,5317 |
| 333 | -0,454 | 0,891 | -0,5095 |
| 334 | -0,4384 | 0,8988 | -0,4877 |
| 335 | -0,4226 | 0,9063 | -0,4663 |
| 336 | -0,4067 | 0,9135 | -0,4452 |
| 337 | -0,3907 | 0,9205 | -0,4245 |
| 338 | -0,3746 | 0,9272 | -0,404 |
| 339 | -0,3584 | 0,9336 | -0,3839 |
| 340 | -0,342 | 0,9397 | -0,364 |
| 341 | -0,3256 | 0,9455 | -0,3443 |
| 342 | -0,309 | 0,9511 | -0,3249 |
| 343 | -0,2924 | 0,9563 | -0,3057 |
| 344 | -0,2756 | 0,9613 | -0,2867 |
| 345 | -0,2588 | 0,9659 | -0,2679 |
| 346 | -0,2419 | 0,9703 | -0,2493 |
| 347 | -0,225 | 0,9744 | -0,2309 |
| 348 | -0,2079 | 0,9781 | -0,2126 |
| 349 | -0,1908 | 0,9816 | -0,1944 |
| 350 | -0,1736 | 0,9848 | -0,1763 |
| 351 | -0,1564 | 0,9877 | -0,1584 |
| 352 | -0,1392 | 0,9903 | -0,1405 |
| 353 | -0,1219 | 0,9925 | -0,1228 |
| 354 | -0,1045 | 0,9945 | -0,1051 |
| 355 | -0,0872 | 0,9962 | -0,0875 |
| 356 | -0,0698 | 0,9976 | -0,0699 |
| 357 | -0,0523 | 0,9986 | -0,0524 |
| 358 | -0,0349 | 0,9994 | -0,0349 |
| 359 | -0,0175 | 0,9998 | -0,0175 |
| 360 | 0 | 1 | 0 |
Мы превращаем это в нечто подобное в Excel.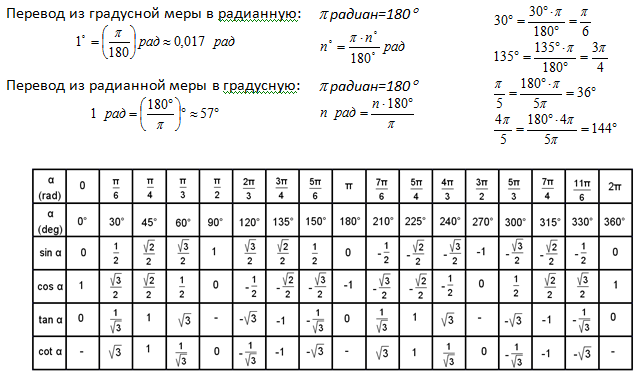
Загрузите нашу специальную тригонометрическую таблицу углов и/или всех углов в следующей части этой статьи!
Загрузка тригонометрической таблицы (Excel xlsx/PDF)
Вам нужна тригонометрическая таблица? Вы можете скачать наши тригонометрические таблицы, перейдя по ссылкам ниже. Таблицы, которые мы подготовили для вас, представлены в файлах Excel и PDF.
Файл Excel:
Эксель xlsx
Тригонометрическая таблица специальных углов:
PDF (A3)
PDF (А4)
Тригонометрическая таблица всех углов:
PDF (A3)
PDF (А4)
Если вы хотите распечатать тригонометрическую таблицу, вы должны загрузить файл PDF с нужным размером бумаги (A3 или A4).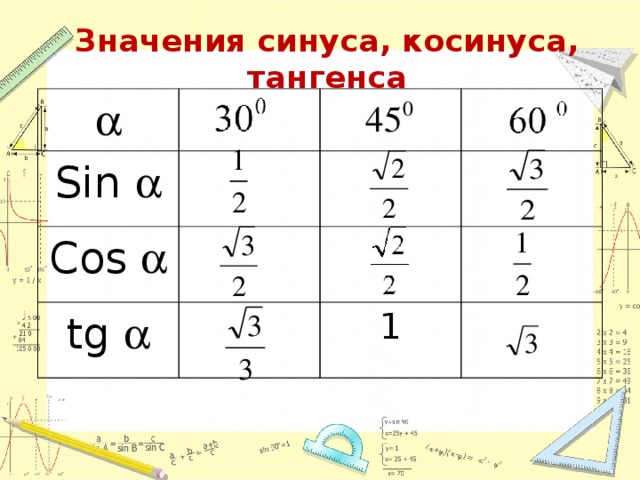 Однако, если вы хотите сначала немного отредактировать таблицу, вам следует загрузить файл Excel.
Однако, если вы хотите сначала немного отредактировать таблицу, вам следует загрузить файл Excel.
Определение тригонометрии
Тригонометрия — это раздел математики, изучающий отношения между сторонами и углами треугольников.
Шесть отношений становятся основной темой расчета тригонометрии. Эти отношения сравнивают длины сторон треугольника, имеющего определенный угол.
Мы называем эти шесть отношений синус (sin), косинус (cos), тангенс (tan), косеканс (cosec), секанс (sec) и котангенс (cot). Однако, когда мы говорим о тригонометрии, люди обращают внимание в основном только на три соотношения: sin, cos и tan.
Определение тригонометрической таблицы
Тригонометрическая таблица — это таблица, в которой сведены тригонометрические отношения различных углов треугольника.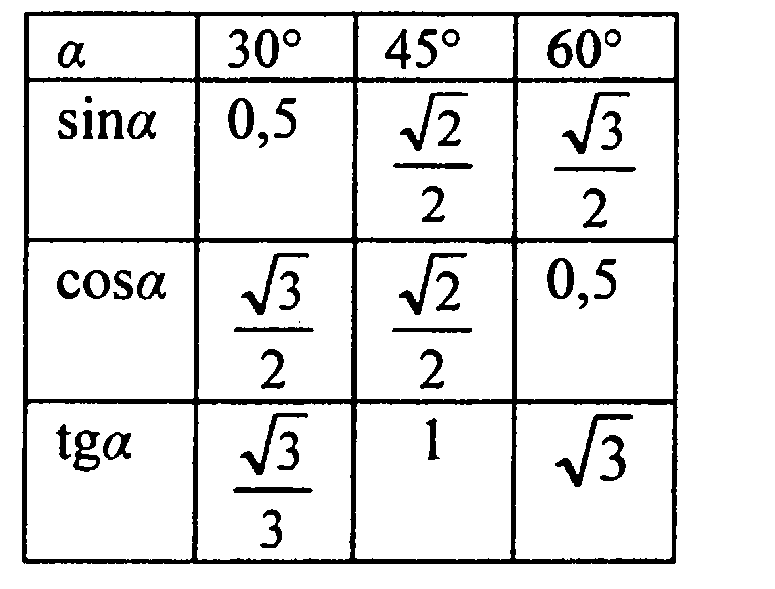 Глядя на эту таблицу, мы можем легко получить тригонометрическое соотношение, необходимое нам для нашего результата расчета/дальнейшей обработки данных.
Глядя на эту таблицу, мы можем легко получить тригонометрическое соотношение, необходимое нам для нашего результата расчета/дальнейшей обработки данных.
Обычно существует два типа тригонометрических таблиц: таблица специальных степеней и таблица всех степеней. Таблица специальных степеней содержит тригонометрические отношения для треугольных степеней, которые обеспечивают точные тригонометрические отношения. Эти специальные градусы: 0°, 30°, 45°, 60° и 9.0° и их эквиваленты в других квадрантах градусов.
Между тем, таблица всех градусов содержит тригонометрические соотношения для всех чисел степени треугольника от 0° до 360°.
Sin, Cos и Tan Определение
Как мы упоминали ранее, отношения sin, cos и tan — это сравнение длин сторон треугольника. Длины сторон, которые мы сравниваем в каждом отношении, зависят от того, отношения каких углов мы вычисляем в треугольнике.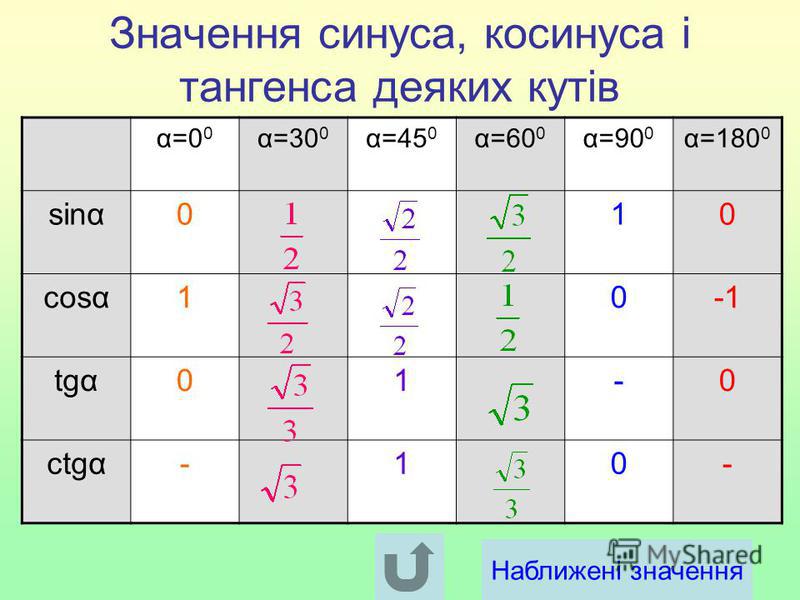
Вот изображение, иллюстрирующее определение коэффициентов sin, cos и tan.
Вот описание того, что вычисляет каждое отношение, если мы объясним приведенную выше иллюстрацию словами.
- sin = делит длину противоположной стороны от угла нашего треугольника на длину стороны гипотенузы треугольника
- cos = делит длину прилежащей стороны от угла нашего треугольника на длину стороны гипотенузы треугольника
- tan = делит длину стороны, противоположной нашему углу треугольника, на длину прилежащей стороны
Советы по использованию наших тригонометрических таблиц
Теперь, когда вы поняли, что такое тригонометрия и отношения sin cotan, давайте изучим тригонометрическую таблицу!
Может быть трудно уложить в голове все значения sin cos tan из таблицы.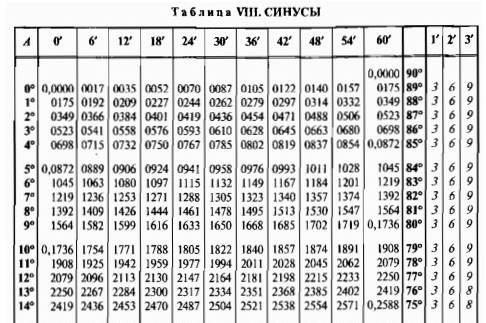 Тем не менее, вот несколько советов, которые помогут вам извлечь больше пользы из процесса обучения.
Тем не менее, вот несколько советов, которые помогут вам извлечь больше пользы из процесса обучения.
Надеемся, что наши советы помогут вам более продуктивно изучить тригонометрическую таблицу!
Как создать тригонометрическую таблицу в Excel
Хотите самостоятельно создать тригонометрическую таблицу в excel? Вы можете сделать это легко, если вы понимаете основы того, как манипулировать отображением рабочих листов Excel!
Когда мы создаем наши тригонометрические таблицы, мы в основном работаем над тем, как мы отображаем наши таблицы на листах Excel. Мы меняем цвета ячеек наших рабочих листов, отображение шрифта, ширину столбцов и строк, а также границы. Вы должны научиться делать это, чтобы создавать тригонометрические таблицы, подобные нашей!
Для значений степени и отношения в тригонометрической таблице специальных степеней мы вводим их вручную. Мы используем меню символов в Excel, чтобы вставить корневой и бесконечный символы, которые мы туда вводим.
Мы используем меню символов в Excel, чтобы вставить корневой и бесконечный символы, которые мы туда вводим.
Тригонометрическую таблицу всех степеней мы разделили на четыре (по 90 градусов в каждой), чтобы значения в таблице было легче читать. Сначала мы создаем одну часть, пока не закончим ее, чтобы мы могли скопировать ее в качестве шаблона для других частей.
Мы вводим значения градусов в тригонометрическую таблицу всех градусов, используя автозаполнение, чтобы сделать это намного быстрее. Чтобы использовать автозаполнение, мы вводим два значения градусов в верхней части каждого столбца градусов. Затем мы выделяем их ячейки и копируем их вниз, чтобы иметь все значения степени, которые нам нужны, в наших столбцах степени.
Значения sin, cos и tan мы получаем, комбинируя функции ROUND, SIN/COS/TAN и RADIANS. Вот общая формула для комбинации этих функций в нашем Excel.
= КРУГЛЫЙ (SIN/COS/TAN (РАДИАНЫ (значение_градуса)) , 4 )
Сначала мы применяем РАДИАНЫ к нашим значениям градусов, прежде чем применять SIN/COS/TAN.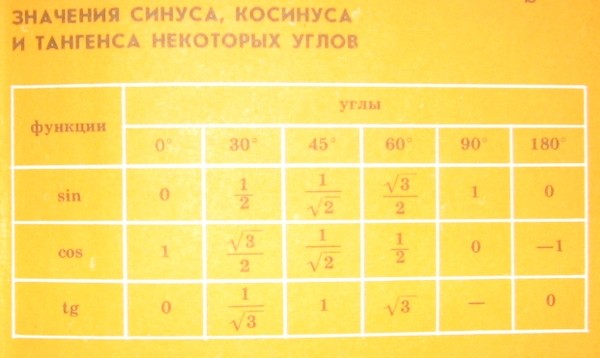 Это связано с тем, что SIN/COS/TAN может получить значения sin, cos и tan наших значений градусов только из их радиан. После того, как мы получим его результат, мы применяем ОКРУГЛ, потому что мы хотим округлить результат до 4 знаков после запятой.
Это связано с тем, что SIN/COS/TAN может получить значения sin, cos и tan наших значений градусов только из их радиан. После того, как мы получим его результат, мы применяем ОКРУГЛ, потому что мы хотим округлить результат до 4 знаков после запятой.
Нам просто нужно написать приведенную выше формулу один раз для каждого столбца sin/cos/tan. После этого мы копируем запись формулы, чтобы получить все необходимые отношения sin, cos и tan!
После того, как мы скопировали первый лист для создания других частей таблицы, нам просто нужно изменить значения градусов. Просто выполните автозаполнение еще раз, чтобы мы могли вводить нужные значения градусов намного быстрее.
Как изменить эту таблицу в ее шаблоне Excel
Хотите изменить имеющиеся здесь тригонометрические таблицы, чтобы они больше соответствовали вашим предпочтениям? Загрузите их файл Excel, чтобы начать!
Если вам нужно изменить отображение таблиц, вы можете использовать для этого основные функции отображения Excel. Функции, которые вам нужно использовать, скорее всего, связаны с цветами ячеек, границей, шириной столбца и шрифтом.
Функции, которые вам нужно использовать, скорее всего, связаны с цветами ячеек, границей, шириной столбца и шрифтом.
Вы также можете добавить и уменьшить количество значений градусов, которые у нас есть, или переместить их на другой лист. Чтобы сделать это, вы должны запустить операции копирования, вырезания и вставки.
Если вам нужно получить коэффициенты sin, cos и tan значения градуса, просто используйте наш метод формулы. Объедините ROUND, SIN/COS/TAN и RADIANS в одной формуле, чтобы получить отношения легко!
Упражнение с тригонометрической таблицей
После того, как вы ознакомились с нашими тригонометрическими таблицами и узнали больше о тригонометрии из этой статьи, давайте сделаем упражнение. Это сделано для того, чтобы вы могли углубить свое понимание тригонометрических соотношений.
Загрузите файл упражнения и заполните его. Вы можете заполнить их непосредственно в файле Excel или распечатать PDF-файл и написать на пустых местах на бумажном носителе. Не смотрите в тригонометрические таблицы и не используйте формулы Excel, когда выполняете упражнение!
Вы можете заполнить их непосредственно в файле Excel или распечатать PDF-файл и написать на пустых местах на бумажном носителе. Не смотрите в тригонометрические таблицы и не используйте формулы Excel, когда выполняете упражнение!
После выполнения упражнения проверьте свои ответы, просмотрев тригонометрические таблицы или загрузив файл с ключами ответов.
Ссылка на файл упражнения:
Эксель xlsx
PDF (A3)
PDF (А4)
Ссылка на файл ключа ответов:
Эксель xlsx
PDF (A3)
PDF (А4)
Если вам нужно больше упражнений, вы можете изменить значения градусов в нашем файле Excel с упражнениями!
Дополнительное примечание
Значения отношения косеканса, секанса и котангенса являются обратными величинами отношения sin, cos и tan. Способ расчета их по отношению к этим взаимным отношениям заключается в следующем.
Способ расчета их по отношению к этим взаимным отношениям заключается в следующем.
- Косеканс = 1/sin
- секанс = 1/cos
- Контангенс = 1/тангенс
Должно быть легко получить косеканс, секанс и котангенс, если вы знаете sin, cos и tan!
Учебники по Excel, которые вы должны изучить:
способа оптимального изучения Excel
Хотите узнать, как быстрее освоить Excel? Прочтите эту статью от Compute Expert!
Таблица Excel
Используя функцию таблицы Excel, вы можете группировать и обрабатывать свои данные намного проще. Хотите узнать больше об этой функции и о том, как ее использовать оптимально? Узнайте из этого руководства Compute Expert!
СУММЕСЛИМН
Хотите суммировать числа из ваших записей данных, которые соответствуют определенным критериям? Используйте СУММЕСЛИМН! Узнайте, как использовать эту формулу, прочитав этот урок!
Тригонометрическая таблица, формула, диаграмма, функции и значения
Тригонометрическая таблица
Тригонометрическая таблица представляет собой набор значений тригонометрических функций для обычно используемых стандартных углов 0°, 30°, 45°, 60°, 90° и нестандартные углы 180°, 270° и 360° .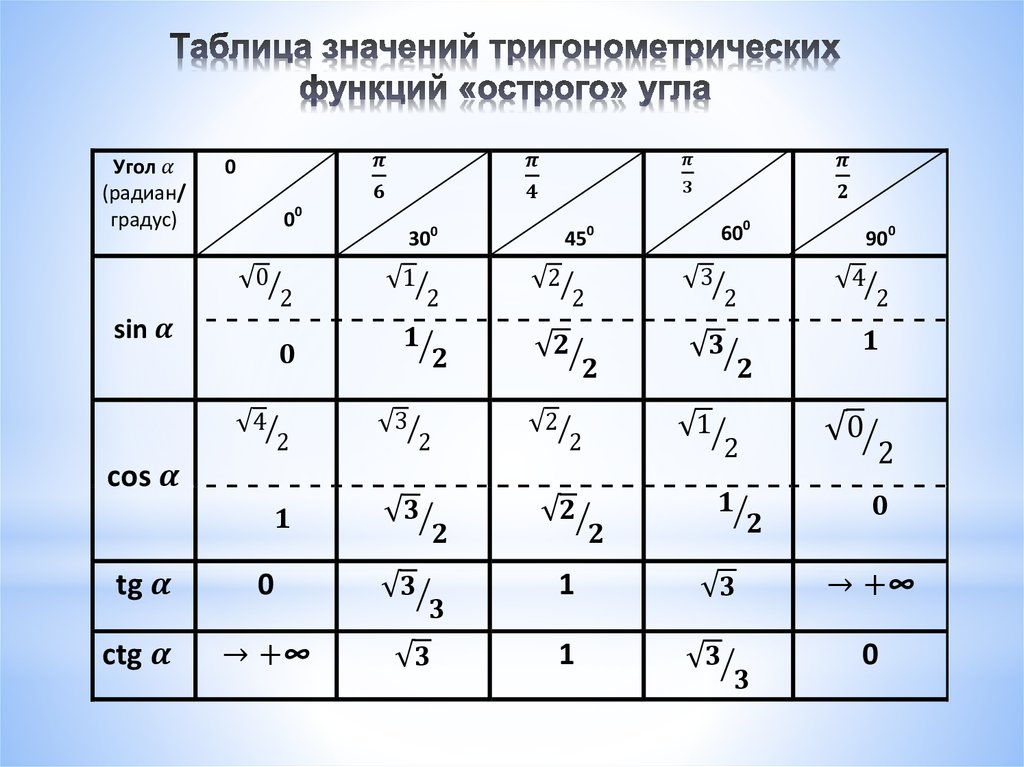 Тригонометрия — это тема и глава математики, которая включает в себя изучение отношений между длиной и углами треугольника. Тригонометрия играет важную роль в предметах математики классов 10, 11 и 12, и на многих конкурсных экзаменах некоторые вопросы задаются из тригонометрии . Прежде чем приступить к изучению тригонометрии, вы должны запомнить таблицу тригонометрии, которая обсуждается ниже.
Тригонометрия — это тема и глава математики, которая включает в себя изучение отношений между длиной и углами треугольника. Тригонометрия играет важную роль в предметах математики классов 10, 11 и 12, и на многих конкурсных экзаменах некоторые вопросы задаются из тригонометрии . Прежде чем приступить к изучению тригонометрии, вы должны запомнить таблицу тригонометрии, которая обсуждается ниже.
Тригонометрический стол от 0° до 360°
Таблица тригонометрических соотношений помогает найти значения обычных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°, а также необычных углов, таких как 180°, 270° и 360°. Он состоит из тригонометрических соотношений. Шесть тригонометрических соотношений: синус, косинус, тангенс, котангенс, косеканс и секанс. Эти отношения могут быть записаны кратко как sin, cos, tan, cosec, sec и cot. Значения тригонометрических отношений стандартных углов необходимы для решения задач по тригонометрии в 10, 11, 12 классах и на любых конкурсных экзаменах.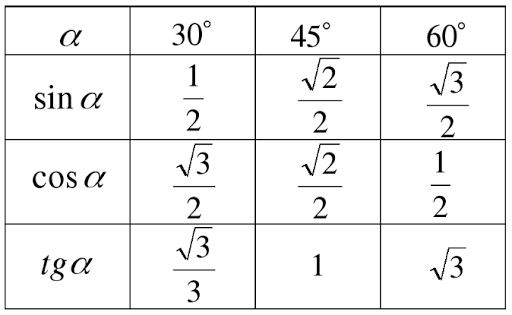 Поэтому необходимо запомнить значения тригонометрических соотношений от 0° до 360°. Давайте посмотрим на таблицу тригонометрии и значения функций от 0° до 360°.
Поэтому необходимо запомнить значения тригонометрических соотношений от 0° до 360°. Давайте посмотрим на таблицу тригонометрии и значения функций от 0° до 360°.
| Trigonometry Table | ||||||||
|---|---|---|---|---|---|---|---|---|
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| Trigonometry Table | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Angles (In Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | ||||||||||
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 | ||||||||||
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 | ||||||||||
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 | ||||||||||
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ | ||||||||||
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ | ||||||||||
| СЕС | 1 | 2/√3 | √2 | 2/√3 | √2 | 2/√3 | √2 | 2/√3 | √2 | 2/√3 | √2 | 2/√3 | √2 | 2/√3 | √2 | 2/√3 | a | 1 |
Уловки с таблицей тригонометрии
Запоминание таблицы тригонометрии поможет вам решить вопросы по тригонометрии, а очень легко запомнить таблицу тригонометрии для стандартных углов от 0° до 90° .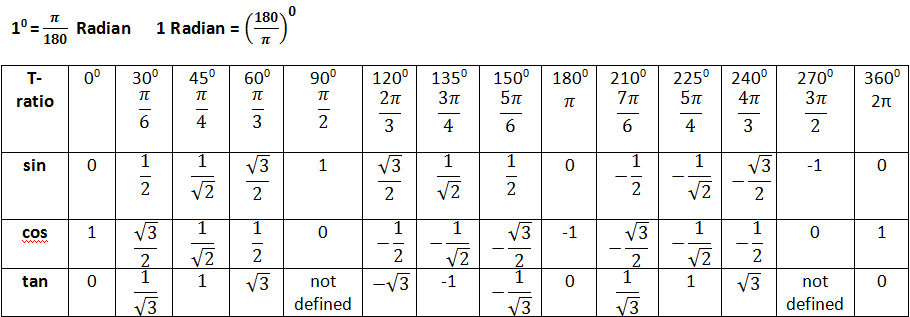 Если вы знаете формулы тригонометрии, то запомнить таблицу тригонометрии очень легко. Таблица соотношений тригонометрии зависит от формул тригонометрии. Здесь мы предлагаем некоторые приемы и формулы тригонометрической таблицы, которые обсуждаются ниже.
Если вы знаете формулы тригонометрии, то запомнить таблицу тригонометрии очень легко. Таблица соотношений тригонометрии зависит от формул тригонометрии. Здесь мы предлагаем некоторые приемы и формулы тригонометрической таблицы, которые обсуждаются ниже.
- sin (90°− θ) = cos θ
- cos (90°− θ) = sin θ
- tan (90°− θ) = cot θ
- cot (90°− θ) = tan θ
- cosec (90°− θ) = sec θ
- sec (90°− θ) = cosec θ
- 1/sin θ = cosec θ
- 1/cos θ = sec θ
- 1/tan θ = cot θ
Таблица таблицы тригонометрии
Значения тригонометрических функций для углов 0°, 30°, 45°, 60° и 90° в таблице тригонометрии обычно используются для решения задач и вопросов по тригонометрии. Таким образом, 0°, 30°, 45°, 60° и 90° называются стандартными углами. Таблица таблицы тригонометрии для стандартных ангелов приведена ниже. вы можете скачать таблицу тригонометрической таблицы для будущего использования и изучения значений тригонометрической таблицы.
Тригонометрическая таблица для тригонометрических функций
В тригонометрии есть шесть тригонометрических функций – это синус, косинус, тангенс, секанс, косеканс и котангенс . Он также известен как sin, cos, tan, cosec, sec и cot. Таблица тригонометрии для каждой тригонометрической функции обсуждается ниже.
Таблица тригонометрии для функции sin
Таблица тригонометрии для функции sin приведена ниже. Значение sin0° равно 0, а значение sin 90° равно 1. Значение sin 30° равно 1/2, а значение sin 45° равно 1/√2.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
Таблица тригонометрии для cos
Ниже приведена таблица тригонометрической функции для cos
. Значение cos 0° равно 1, а значение cos 90° равно 0. Это прямо противоположно функции sin от 0° до 90°.
Значение cos 0° равно 1, а значение cos 90° равно 0. Это прямо противоположно функции sin от 0° до 90°.
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
Trigonometry Table for tan
Таблица тригонометрии для функции тангенса приведена ниже. Значение тангенса 30° равно 1/√3, а значение тангенса 60° равно √3.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Таблица тригонометрии для детской кроватки
Таблица тригонометрии для функции детской кроватки приведена ниже. Значение раскладушки 30° равно √3, а значение раскладушки 60° равно 1/√3.
Значение раскладушки 30° равно √3, а значение раскладушки 60° равно 1/√3.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
Таблица тригонометрии для функции cosec
Таблица тригонометрии для функции cosec обсуждается ниже. Значение cosec 45° равно √2, а значение cosec 30° равно 2.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cosec | ∞ | 2 | √2 | 2 /√3 | 1 | ∞ | -1 | ∞ |
Таблица тригонометрии для sec
Таблица тригонометрии для функции sec обсуждается ниже. Значение секунды 45° равно √2, а значение секунды 30° равно 2. Значение секунды 0° равно 1,9.0005
Значение секунды 45° равно √2, а значение секунды 30° равно 2. Значение секунды 0° равно 1,9.0005
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
000000.
- Главная
- Таблицы
- Тригонометрический
В математике тригонометрические функции (также называемые круговыми функциями, угловыми функциями или гониометрическими функциями) являются функциями угла. Они связывают углы треугольника с длинами его сторон. Тригонометрические функции важны при изучении треугольников и моделировании периодических явлений, а также во многих других приложениях.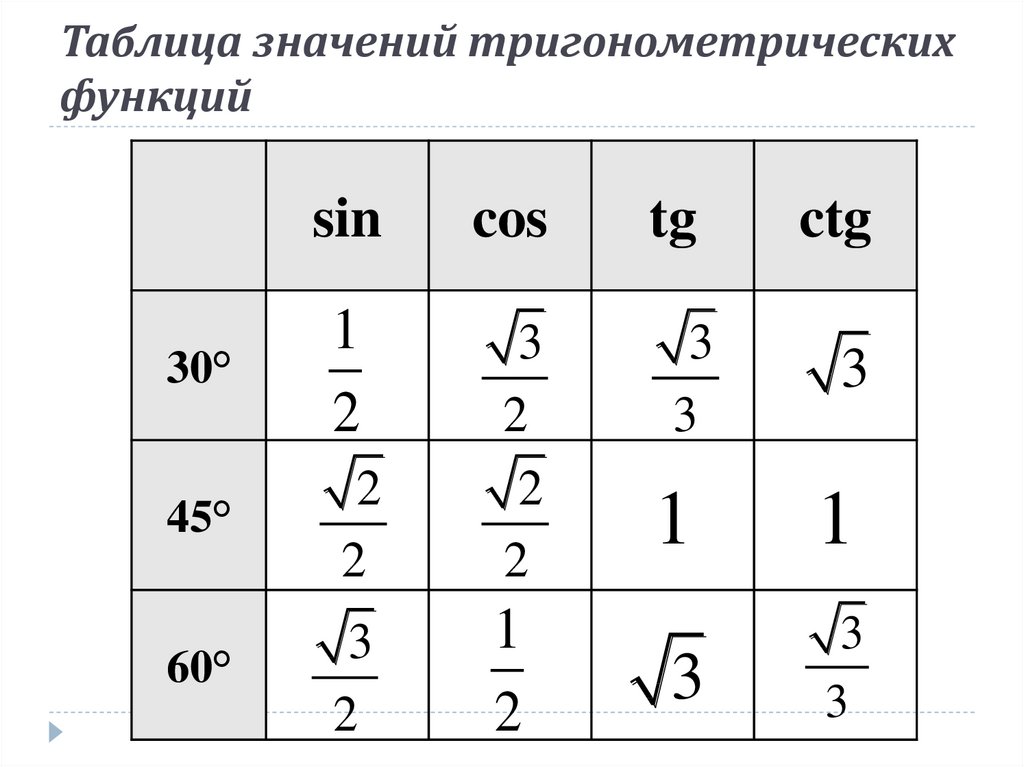
Другие связанные страницы тригонометрии
- Тригонометрические формулы
- Скачать таблицы тригонометрии (PDF)
В математике единичная окружность — это окружность с радиусом, равным единице. Часто, особенно в тригонометрии, единичная окружность представляет собой окружность радиуса один с центром в начале координат (0, 0) в декартовой системе координат на евклидовой плоскости. Используя единичный круг, значения любой тригонометрической функции для многих углов, кроме отмеченных, можно вычислить без использования калькулятора, используя формулы суммы и разности углов.
Изображение предоставлено Википедией
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 0,000000 | 0,000000 | 1.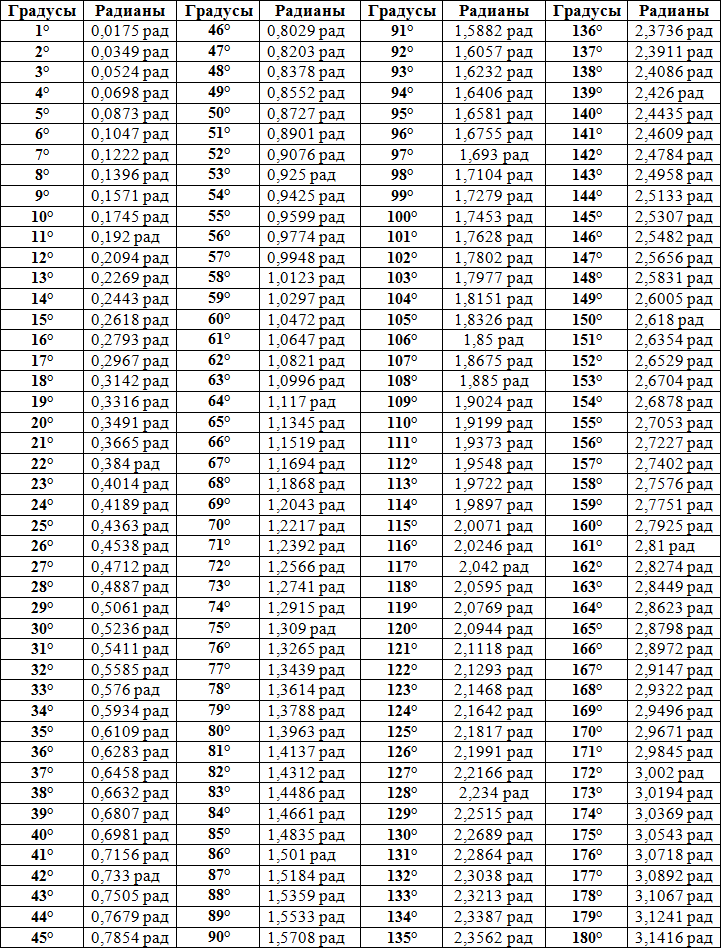 000000 000000 | 0,000000 | 1.000000 | ИНФ | ИНФ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1° | 0,017460 | 0,017459 | 0,9 | 0,017462 | 1.000152 | 57.275637 | 57.266907 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2° | 0,034921 | 0,034914 | 0,9 | 0,034935 | 1.000610 | 28.642185 | 28.624722 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3° | 0,052381 | 0,052357 | 0,9 | 0,052429 | 1.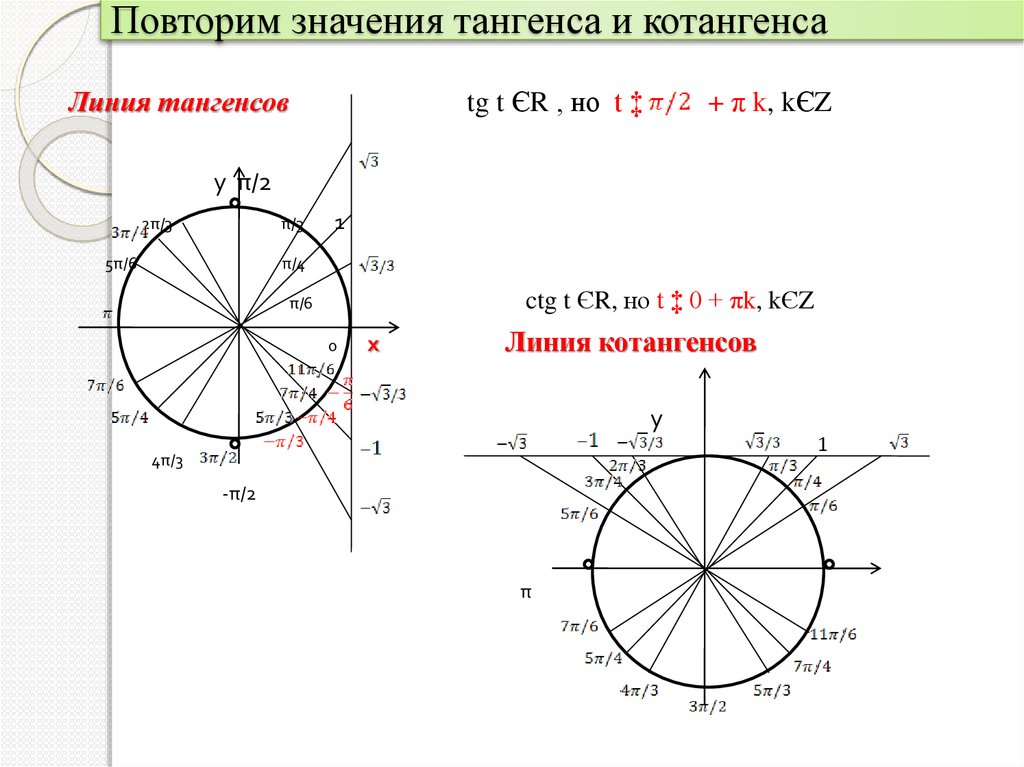 001373 001373 | 19.0 | 19.073446 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4° | 0,069841 | 0,069785 | 0,9 | 0,069955 | 1.002444 | 14.329829 | 14.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5° | 0,087302 | 0,087191 | 0,9 | 0,087524 | 1.003823 | 11.469109 | 11.425430 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6° | 0,104762 | 0,104570 | 0,9 | 0,105147 | 1. 005513 005513 | 9.562937 | 9.510508 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7° | 0,122222 | 0,121918 | 0,9 | 0,122834 | 1.007516 | 8.202224 | 8.141037 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8° | 0,139683 | 0,139229 | 0,9
| 0,051726 | 19.306901 | 19.332782 | 1.001340 | 0,051795 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88° | 1.536508 | 0,9 | 0,034282 | 29.152960 | 29.170106 | 1.000588 | 0,034302 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89° | 1. 553968 553968 | 0,9 | 0,016827 | 59.418902 | 59.427316 | 1.000142 | 0,016830 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90° | 1.571429 | 1.000000 | -0,000632 | -1581.666041 | -1581.666357 | 1.000000 | -0,000632 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | |
|---|---|---|---|---|---|---|---|---|
| 90° | 1. 571429 571429 | 1.000000 | -0,000632 | -1581.666041 | -1581.666357 | 1.000000 | -0,000632 | |
| 91° | 1.588889 | 0,9 | -0,018092 | -55.265301 | -55.274347 | 1.000164 | -0,018095 | |
| 92° | 1.606349 | 0,9 | -0,035545 | -28.115265 | -28.133043 | 1.000632 | -0,035568 | |
| 93° | 1. 623810 623810 | 0,9 | -0,052988 | -18.845553 | -18.872066 | 1.001407 | -0,053063 | |
| 94° | 1.641270 | 0,9 | -0,070415 | -14.166229 | -14.201480 | 1.002488 | -0,070590 | |
| 95° | 1.658730 | 0,9 | -0,087821 | -11.342861 | -11.386856 | 1.003879 | -0,088161 | |
| 96° | 1. 676190 676190 | 0,9 | -0,105199 | -9.453035 | -9.505781 | 1.005580 | -0,105786 | |
| 97° | 1.6 | 0,9 | -0,122546 | -8.0 | ||||
| -8.160224 | 1.007594 | -0,123476 | ||||||
| 98° | 1.711111 | 0,9 | -0,139855 | -7.080000 | -7.150272 | 1.009926 | -0,141243 | |
| 99° | 1. 728571 728571 | 0, | 9-0,157121 | -6.285456 | -6.364508 | 1.012577 | -0,159097 | |
| 100° | 1.746032 | 0, | 6 | -0,174340 | -5.648077 | -5.735920 | 1.015553 | -0,177051 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | ||
|---|---|---|---|---|---|---|---|---|---|
| 100° | 1. 746032 746032 | 0, | 6 | -0,174340 | -5.648077 | -5.735920 | 1.015553 | -0,177051 | |
| 101° | 1.763492 | 0, | |||||||
| -0,1 | -5.125137 | -5.221784 | 1.018857 | -0,1 | |||||
| 102° | 1.780952 | 0,8 | -0,208613 | -4.688110 | -4,7 | ||||
| 1.022497 | -0,213306 | ||||||||
| 103° | 1. 7 7 | 0, | 7 | -0,225656 | -4.317222 | -4.431524 | 1.026476 | -0,231630 | |
| 104° | 1.815873 | 0, | 9-0,242631 | -3,9 | -4.121490 | 1.030802 | -0,250104 | ||
| 105° | 1.833333 | 0, | |||||||
| -0,259531 | -3.721070 | -3,853097 | 1.035481 | -0,268740 | |||||
| 106° | 1. 850794 850794 | 0, | 6-0,276353 | -3,477639 | -3,618559 | 1.040522 | -0,287551 | ||
| 107° | 1.868254 | 0, | 5 | -0,2 | -3.262081 | -3.411916 | 1.045932 | -0,306553 | |
| 108° | 1.885714 | 0,2 | -0,309738 | -3.069757 | -3.228530 | 1.051722 | -0,325759 | ||
| 109° | 1. 5 | 0, | |||||||
| -0,326292 | -2.8 | -3,064739 | 1.057900 | -0,345184 | |||||
| 110° | 1. | 5 | 0, | 8-0,342746 | -2.740886 | -2, | 1 | 1.064477 | -0,364846 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | ||
|---|---|---|---|---|---|---|---|---|---|
| 110° | 1. | 5 | 0, | 8-0,342746 | -2.740886 | -2, | 1 | 1.064477 | -0,364846 |
| 111° | 1. | 5 | 0, | 1-0,359096 | -2,5 | -2,784772 | 1.071466 | -0,384759 | |
| 112° | 1. | 60, | 9-0,375336 | -2,469491 | -2,664280 | 1.078878 | -0,404942 | ||
| 113° | 1. | 60, | 4 | -0,3 | -2.350663 | -2,554528 | 1.086727 | -0,425412 | |
| 114° | 1.9 | 0, | 9 | -0,407468 | -2.241205 | -2.454180 | 1.0 | -0,446189 | |
| 115° | 2.007937 | 0, 6 | -0,423350 | -2.139992 | -2.362110 | 1. | -0,467292 | ||
| 116° | 2. 025397 025397 | 0,8 | -0,439103 | -2.046070 | -2.277368 | 1.113045 | -0,488742 | ||
| 117° | 2.042857 | 0,8 | -0,454723 | -1, | 9 | -2.1 | 1.122797 | -0,510561 | |
| 118° | 2.060317 | 0,882558 | -0,470203 | -1,876971 | -2.126740 | 1.133070 | -0,532773 | ||
| 119° | 2. 077778 077778 | 0,874214 | -0,485541 | -1.800496 | -2.059560 | 1.143885 | -0,555402 | ||
| 120° | 2.0 | ||||||||
| 0,865604 | -0,500730 | -1,728684 | -1,9 | ||||||
| 1.155263 | -0,578475 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | |
|---|---|---|---|---|---|---|---|---|
| 120° | 2. 0 0 | |||||||
| 0,865604 | -0,500730 | -1,728684 | -1,9 | |||||
| 1.155263 | -0,578475 | |||||||
| 121° | 2.112698 | 0,856729 | -0,515766 | -1,661080 | -1, | |||
| 1.167230 | -0,602018 | |||||||
| 122° | 2.130159 | 0,847594 | -0,530646 | -1,5 | ||||
| -1,884496 | 1.179811 | -0,626062 | ||||||
| 123° | 2. 147619 147619 | 0,838200 | -0,545363 | -1,536956 | -1,833639 | 1.1 | -0,650637 | |
| 124° | 2.165079 | 0,828550 | -0,559915 | -1,479779 | -1,785986 | 1.206928 | -0,675777 | |
| 125° | 2.182540 | 0,818648 | -0,574296 | -1.425482 | -1,741264 | 1.221526 | -0,701517 | |
| 126° | 2. 200000 200000 | 0,808496 | -0,588501 | -1,373823 | -1,6 | 1.236864 | -0,727896 | |
| 127° | 2.217460 | 0,7 | -0,602527 | -1.324584 | -1,659676 | 1.252979 | -0,754954 | |
| 128° | 2.234921 | 0,787457 | -0,616370 | -1,277572 | -1.622403 | 1.269911 | -0,782735 | |
| 129° | 2. 252381 252381 | 0,776575 | -0,630024 | -1.232612 | -1,587240 | 1.287705 | -0,811286 | |
| 130° | 2.269841 | 0,765457 | -0,643487 | -1.189546 | -1,554033 | 1.306409 | -0,840657 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | ||
|---|---|---|---|---|---|---|---|---|---|
| 130° | 2. 269841 269841 | 0,765457 | -0,643487 | -1.189546 | -1,554033 | 1.306409 | -0,840657 | ||
| 131° | 2.287302 | 0,754106 | -0,656753 | -1.148233 | -1,522642 | 1.326074 | -0,870904 | ||
| 132° | 2.304762 | 0,742524 | -0,669819 | -1.108544 | -1,4 | 1.346758 | -0, 5 | ||
| 133° | 2. 322222 322222 | 0,730716 | -0,682681 | -1.070362 | -1,464812 | 1.368520 | -0, | ||
| 134° | 2.339683 | 0,718686 | -0,6 | -1.033581 | -1.438155 | 1.3 | -0, | 0||
| 135° | 2.357143 | 0,706436 | -0,707777 | -0,9 | -1.412874 | 1.415557 | -1.001899 | ||
| 136° | 2. 374603 374603 | 0,6 | -0,720003 | -0, | 4 | -1,388883 | 1.440983 | -1.037512 | |
| 137° | 2.3 | 0,681294 | -0,732010 | -0, | 7 | -1.366102 | 1.467795 | -1.074440 | |
| 138° | 2.409524 | 0,668410 | -0,743793 | -0,8 | -1.344460 | 1.4 | -1.112780 | ||
| 139° | 2. 426984 426984 | 0,655322 | -0,755350 | -0,867574 | -1.323890 | 1.525968 | -1.152640 | ||
| 140° | 2.444444 | 0,642034 | -0,766676 | -0,837425 | -1.304332 | 1.557550 | -1.1 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | |
|---|---|---|---|---|---|---|---|---|
| 140° | 2. 444444 444444 | 0,642034 | -0,766676 | -0,837425 | -1.304332 | 1.557550 | -1.1 | |
| 141° | 2.461905 | 0,628550 | -0,777769 | -0,808145 | -1,285729 | 1.5 |
 282577
282577 745988
745988 178413
178413| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | ||
|---|---|---|---|---|---|---|---|---|---|
| 150° | 2. 619048 619048 | 0,4 | -0,866552 | -0,575946 | -1,153999 | 2.003658 | -1,736273 | ||
| 151° | 2.636508 | 0,483882 | -0,875133 | -0,552923 | -1.142683 | 2.066621 | -1.808570 | ||
| 152° | 2,653968 | 0,468528 | -0,883448 | -0,530341 | -1.131928 | 2.134342 | -1,885581 | ||
| 153° | 2. 671429 671429 | 0,453033 | -0,8 | -0,508172 | -1.121713 | 2.207347 | -1, | 6||
| 154° | 2.688889 | 0,437399 | -0,8 | -0,486394 | -1.112016 | 2.286244 | -2.055946 | ||
| 155° | 2.706349 | 0,421631 | -0, 7 | -0,464983 | -1. | 2.371741 | -2.150618 | ||
| 156° | 2. 723810 723810 | 0,405735 | -0, | 1 | -0,443916 | -1.0 | 2.464661 | -2,252677 | |
| 157° | 2.741270 | 0,389716 | -0, | 5 | -0,423174 | -1.085853 | 2,565973 | -2.363095 | |
| 158° | 2.758730 | 0,373577 | -0, | 9 | -0,402736 | -1.078052 | 2.676823 | -2.483018 | |
| 159° | 2. 776190 776190 | 0,357325 | -0, | 0-0,382583 | -1.070687 | 2.7 | -2,613812 | ||
| 160° | 2.7 | 0,340964 | -0, | 6 | -0,362698 | -1.063743 | 2. | ||
| -2,757116 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | |
|---|---|---|---|---|---|---|---|---|
| 160° | 2. 7 7 | 0,340964 | -0, | 6 | -0,362698 | -1,063743 | 2. | |
| -2,757116 | ||||||||
| 161° | 2.811111 | 0,324499 | -0, | 6-0,343063 | -1.057210 | 3.081678 | -2, | 7 |
| 162° | 2.828571 | 0,307934 | -0, | 8-0,323662 | -1.051074 | 3.247444 | -3. 089643 089643 | |
| 163° | 2.846032 | 0,2 | -0, | 9-0,304479 | -1.045326 | 3.433164 | -3.284299 | |
| 164° | 2.863492 | 0,274530 | -0, | 9-0,285499 | -1,039957 | 3.642593 | -3,502640 | |
| 165° | 2.880952 | 0,257699 | -0, | 5 | -0,266707 | -1.034955 | 3. 880492 880492 | -3,749430 |
| 166° | 2.8 | 0,240790 | -0, | 7-0,248090 | -1.030315 | 4.152992 | -4.030800 | |
| 167° | 2. | 3 | 0,223808 | -0, | 3-0,229633 | -1.026027 | 4.468119 | -4.354778 |
| 168° | 2. | 3 | 0,206757 | -0, | ||||
| -0,211323 | -1. 022085 022085 | 4.836592 | -4.732085 | |||||
| 169° | 2. | |||||||
| 0,189643 | -0, | |||||||
| -0,1 | -1.018482 | 5.273053 | -5.177363 | |||||
| 170° | 2, | 40,172472 | -0, | 4-0,175096 | -1.015214 | 5.7 | -5.711157 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | ||
|---|---|---|---|---|---|---|---|---|---|
| 170° | 2, | 40,172472 | -0, | 4-0,175096 | -1. 015214 015214 | 5.7 | -5.711157 | ||
| 171° | 2. | ||||||||
| 0,155248 | -0, | 6-0,157153 | -1.012273 | 6.441312 | -6.363215 | ||||
| 172° | 3.003175 | 0,137976 | -0,9 | -0,139309 | -1,009657 | 7.247613 | -7.178293 | ||
| 173° | 3.020635 | 0,120663 | -0,9 | -0,121551 | -1,007360 | 8. 287545 287545 | -8.226992 | ||
| 174° | 3.038095 | 0, | -0,9 | -0, | -1,005380 | 9.679348 | -9,627553 | ||
| 175° | 3.055556 | 0,085931 | -0,9 | -0,086250 | -1,003713 | 11.637245 | -11.5 | ||
| 176° | 3.073016 | 0,068523 | -0,9 | -0,068684 | -1. 002356 002356 | 14.5 | -14.559329 | ||
| 177° | 3.0 | 0,051094 | -0,9 | -0,051161 | -1.001308 | 19.571691 | -19,546127 | ||
| 178° | 3.107937 | 0,033650 | -0,9 | -0,033669 | -1.000567 | 29.717866 | -29.701036 | ||
| 179° | 3.125397 | 0,016195 | -0,9 | -0,016197 | -1. 000131 000131 | 61.746995 | -61,738897 | ||
| 180° | 3.142857 | -0,001264 | -0,9 | 0,001264 | -1.000001 | -790,833337 | 790.832704 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | |
|---|---|---|---|---|---|---|---|---|
| 180° | 3. 142857 142857 | -0,001264 | -0,9 | 0,001264 | -1.000001 | -790,833337 | 790.832704 | |
| 181° | 3.160317 | -0,018724 | -0,9 | 0,018727 | -1.000175 | -53.408212 | 53.3 | |
| 182° | 3.177778 | -0,036177 | -0,9 | 0,036201 | -1.000655 | -27,641698 | 27.623603 | |
| 183° | 3. 1 1 | |||||||
| -0,053620 | -0,9 | 0,053697 | -1.001441 | -18.649857 | 18.623028 | |||
| 184° | 3.212698 | -0,071046 | -0,9 | 0,071226 | -1,002533 | -14.075416 | 14.039849 | |
| 185° | 3.230159 | -0,088450 | -0,9 | 0,088798 | -1,003935 | -11.305779 | 11.261467 | |
| 186° | 3. 247619 247619 | -0,105828 | -0,9 | 0,106425 | -1,005647 | -9.449308 | 9.3 | |
| 187° | 3.265079 | -0,123173 | -0,9 | 0,124118 | -1,007673 | -8.118655 | 8.056833 | |
| 188° | 3.282540 | -0,140481 | -0,9 | 0,141888 | -1.010016 | -7.118410 | 7.047819 | |
| 189° | 3. 300000 300000 | -0,157746 | -0, | 0 | 0,159746 | -1,012679 | -6.339317 | 6.259948 |
| 190° | 3.317460 | -0,174962 | -0,5 | 0,177704 | -1.015667 | -5.715511 | 5.627350 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(x) | ||
|---|---|---|---|---|---|---|---|---|---|
| 190° | 3. 317460 317460 | -0,174962 | -0,5 | 0,177704 | -1,015667 | -5.715511 | 5.627350 | ||
| 191° | 3.334921 | -0,1 | |||||||
| -0, | 00,1 | -1.018983 | -5.204919 | 5.107953 | |||||
| 192° | 3.352381 | -0,209231 | -0, | 6 | 0,213967 | -1.022635 | -4.779411 | 4.673625 | |
| 193° | 3. 369841 369841 | -0,226272 | -0, | 4 | 0,232297 | -1,026626 | -4.419461 | 4.304839 | |
| 194° | 3.387302 | -0,243244 | -0, | 5 | 0,250776 | -1.030965 | -4.111098 | 3, | 2 |
| 195° | 3.404762 | -0,260142 | -0, | 00,269418 | -1.035657 | -3.844055 | 3.711705 | ||
| 196° | 3. 422222 422222 | -0,276961 | -0, | 1 | 0,288236 | -1.040711 | -3.610621 | 3.469378 | |
| 197° | 3.439683 | -0,2 | -0, | 90,307245 | -1.046135 | -3.404894 | 3.254736 | ||
| 198° | 3.457143 | -0,310340 | -0,6 | 0,326458 | -1.051939 | -3.222277 | 3.063180 | ||
| 199° | 3. 474603 474603 | -0,326890 | -0, | ||||||
| 0,345892 | -1.058131 | -3.059136 | 2.8 | ||||||
| 200° | 3.4 | -0,343340 | -0, | 1 | 0,365562 | -1.064723 | -2. | 42.735513 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(х) | ||
|---|---|---|---|---|---|---|---|---|---|
| 200° | 3. 4 4 | -0,343340 | -0, | 1 | 0,365562 | -1.064723 | -2. | 42.735513 | |
| 201° | 3.509524 | -0,359686 | -0, | 3 | 0,385485 | -1.071727 | -2.780204 | 2,5 | |
| 202° | 3,526984 | -0,375922 | -0, | 0,405678 | -1.079155 | -2.660127 | 2. 465010 465010 | ||
| 203° | 3,544444 | -0,3 | -0, | 70,426159 | -1.087019 | -2,550738 | 2.346543 | ||
| 204° | 3,561905 | -0,408045 | -0, | ||||||
| 0,446947 | -1.0 | -2.450708 | 2.237402 | ||||||
| 205° | 3.579365 | -0,423923 | -0, 8 | 0,468062 | -1.104121 | -2,358919 | 2. 136469 136469 | ||
| 206° | 3,5 | -0,439671 | -0,8 | 0,489525 | -1.113389 | -2,274426 | 2.042796 | ||
| 207° | 3.614286 | -0,455286 | -0,8 | 0,511358 | -1.123160 | -2.1 | 1. | 5||
| 208° | 3.631746 | -0,470761 | -0,882261 | 0,533585 | -1.133452 | -2. 124219 124219 | 1.874115 | ||
| 209° | 3.649206 | -0,486093 | -0,873907 | 0,556230 | -1.144287 | -2.057219 | 1.7 | ||
| 210° | 3,666667 | -0,501277 | -0,865287 | 0,579319 | -1.155686 | -1,9 | 1.726165 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(х) | |
|---|---|---|---|---|---|---|---|---|
| 210° | 3,666667 | -0,501277 | -0,865287 | 0,579319 | -1,155686 | -1,9 | 1. 726165 726165 | |
| 211° | 3.684127 | -0,516308 | -0,856403 | 0,602880 | -1,167675 | -1, | 81.658705 | |
| 212° | 3.701587 | -0,531182 | -0,847258 | 0,626942 | -1.180278 | -1,882595 | 1.5 | |
| 213° | 3.719048 | -0,545893 | -0,837855 | 0,651537 | -1.1 | -1,831860 | 1. 534832 534832 | |
| 214° | 3.736508 | -0,560439 | -0,828196 | 0,676698 | -1.207444 | -1,784317 | 1.477764 | |
| 215° | 3,753968 | -0,574813 | -0,818285 | 0,702461 | -1.222068 | -1,739696 | 1.423567 | |
| 216° | 3.771429 | -0,589012 | -0,808124 | 0,728863 | -1.237434 | -1,6 | 1. 371999 371999 | |
| 217° | 3.788889 | -0,603032 | -0,7 | 0,755947 | -1,253577 | -1,658287 | 1.322844 | |
| 218° | 3.806349 | -0,616868 | -0,787067 | 0,783755 | -1.270540 | -1.621094 | 1.275909 | |
| 219° | 3.823810 | -0,630515 | -0,776177 | 0,812335 | -1,288366 | -1,586004 | 1. 231020 231020 | |
| 220° | 3.841270 | -0,643971 | -0,765050 | 0,841737 | -1.307104 | -1,552866 | 1.188020 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(х) | ||
|---|---|---|---|---|---|---|---|---|---|
| 220° | 3.841270 | -0,643971 | -0,765050 | 0,841737 | -1. 307104 307104 | -1,552866 | 1.188020 | ||
| 221° | 3.858730 | -0,657230 | -0,753690 | 0,872016 | -1.326805 | -1,521538 | 1.146768 | ||
| 222° | 3.876190 | -0,670289 | -0,742100 | 0, 2 | -1.347527 | -1,4 | 1.107135 | ||
| 223° | 3.8 | -0,683143 | -0,730284 | 0, | 8 -1. 369330 369330 | -1,463822 | 1.069006 | ||
| 224° | 3. | 1 | -0,6 | -0,718246 | 0, | 4-1.3 | -1.437216 | 1.032275 | |
| 225° | 3. | 1 | -0,708224 | -0,705988 | 1.003166 | -1.416454 | -1.411984 | 0,9 | |
| 226° | 3. | 2 | -0,720442 | -0,6 | 1. 038826 038826 | -1,441929 | -1.388037 | 0,5 | |
| 227° | 3, | 2-0,732440 | -0,680831 | 1.075803 | -1,468793 | -1,365299 | 0, | 8 | |
| 228° | 3. | ||||||||
| -0,744216 | -0,667939 | 1.114196 | -1.4 | -1,343697 | 0,8 | ||||
| 229° | 3,9 | -0,755764 | -0,654844 | 1. 154113 154113 | -1,527081 | -1.323164 | 0,866466 | ||
| 230° | 4.015873 | -0,767082 | -0,641549 | 1.1 | -1,558727 | -1.303642 | 0,836350 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(х) | |
|---|---|---|---|---|---|---|---|---|
| 230° | 4. 015873 015873 | -0,767082 | -0,641549 | 1.1 | -1,558727 | -1.303642 | 0,836350 | |
| 231° | 4.033333 | -0,778166 | -0,628058 | 1.239003 | -1,5 | -1.285073 | 0,807101 | |
| 232° | 4.050794 | -0,789013 | -0,614376 | 1.284250 | -1,627667 | -1,267406 | 0,778664 | |
| 233° | 4. 068254 068254 | -0,7 | -0,600507 | 1.331574 | -1,665260 | -1.250595 | 0,750991 | |
| 234° | 4.085714 | -0,809982 | -0,586455 | 1.381151 | -1.705162 | -1.234595 | 0,724034 | |
| 235° | 4. | -0,820098 | -0,572223 | 1.433178 | -1,747569 | -1.219367 | 0,6 | |
| 236° | 4. 120635 120635 | -0,829964 | -0,557818 | 1.487876 | -1,7 | -1.204872 | 0,672099 | |
| 237° | 4.138095 | -0,839576 | -0,543242 | 1.545492 | -1,840800 | -1.1 | 0,647043 | |
| 238° | 4.155556 | -0,848933 | -0,528501 | 1.606304 | -1,8 | -1,177949 | 0,622547 | |
| 239° | 4. 173016 173016 | -0,858031 | -0,513598 | 1.670627 | -1, | 7-1,165459 | 0,5 | |
| 240° | 4.1 | -0,866867 | -0,4 | 1.738815 | -2,005860 | -1.153579 | 0,575104 |
| Угол(х) | Радиан | грех(х) | кос(х) | рыжевато-коричневый(х) | сек(х) / секанс | csc(x)/косеканс | детская кроватка(х) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 240° | 4. 1 1 | -0,866867 | -0,4 | 1.738815 | -2,005860 | -1.153579 | 0,575104 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 241° | 4.207937 | -0,875439 | -0,483328 | 1.811273 | -2,068988 | -1.142284 | 0,552098 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 242° | 4.225397 | -0,883744 | -0,467970 | 1.888464 | -2.136890 | -1.131549 | 0,529531 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 243° | 4. 242857 242857 | -0,8 | -0,452469 | 1. | 1 | -2.210097 | -1.121353 | 0,507377 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 244° | 4.260317 | -0,8
|


 0175
0175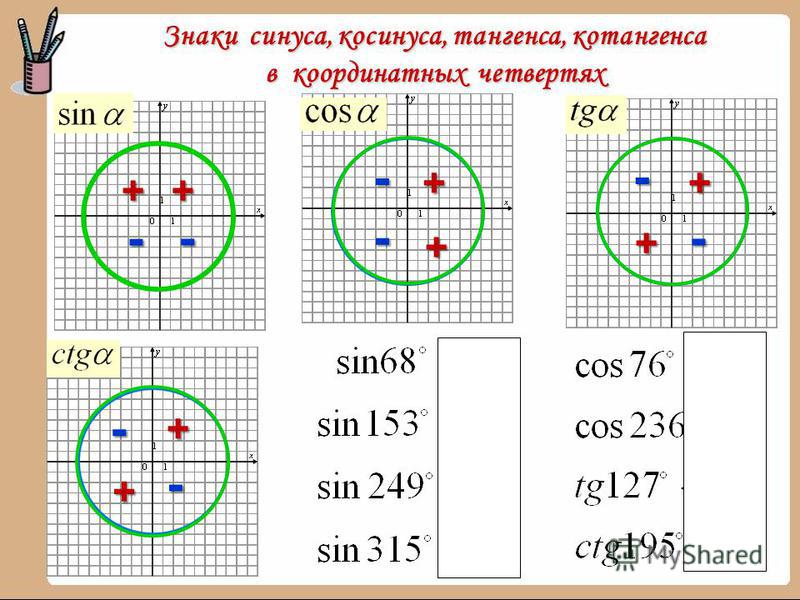 4877
4877 1918
1918 4874
4874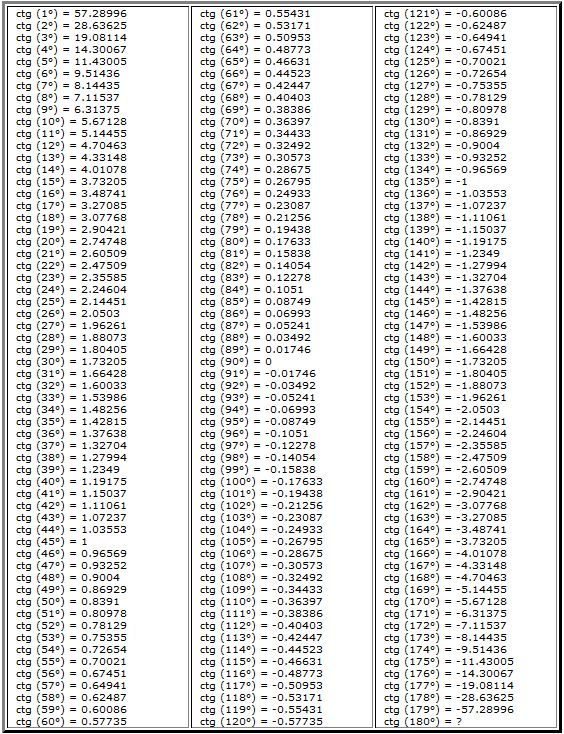 1154
1154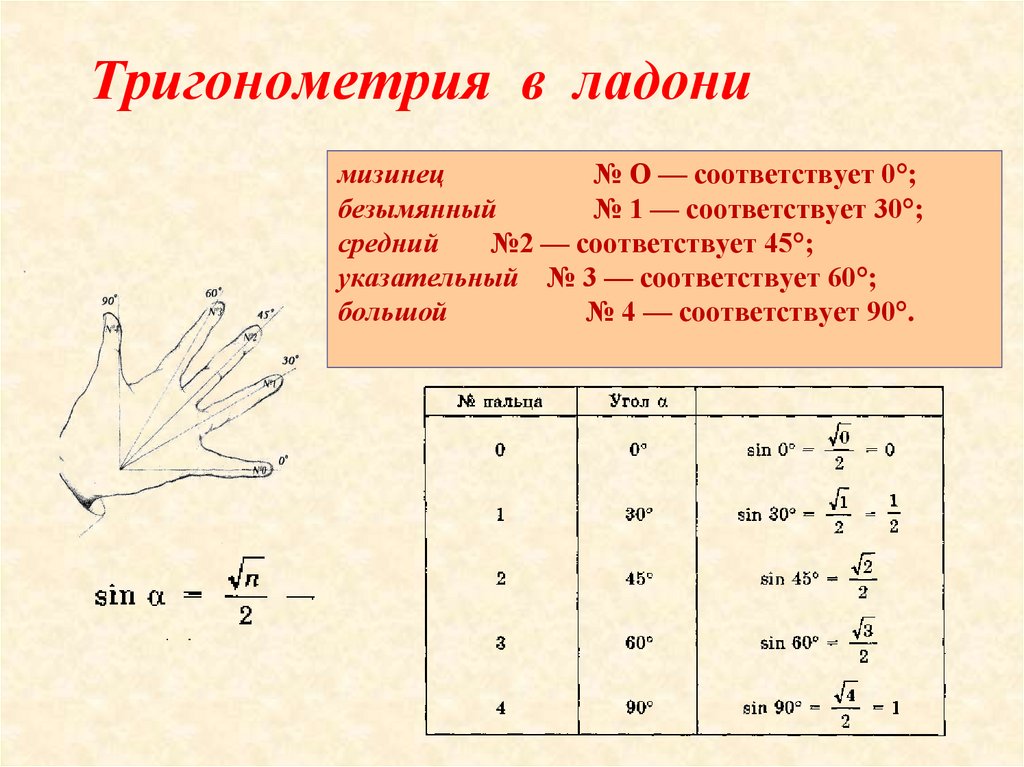 6643
6643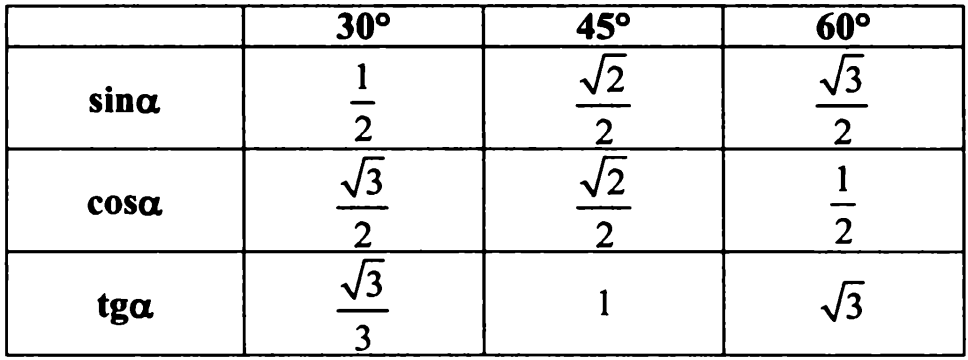 7265
7265 2309
2309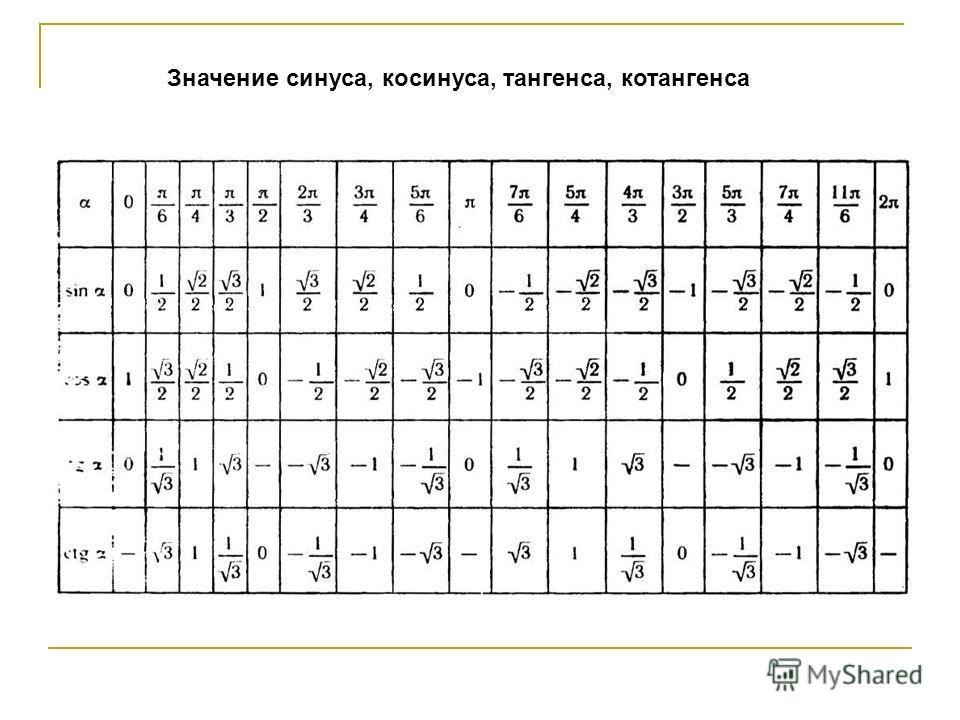 1405
1405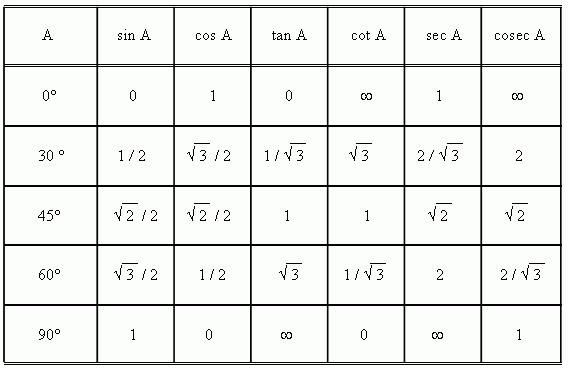 6249
6249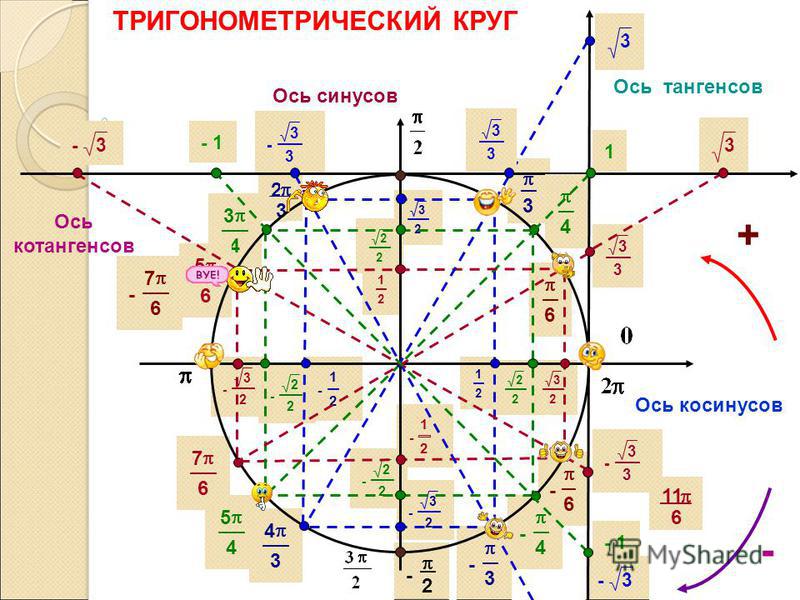 4826
4826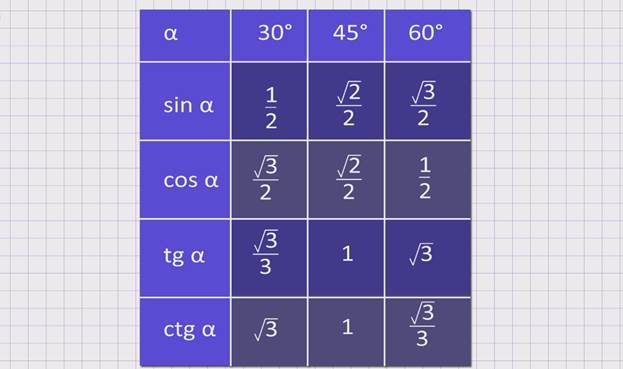 1446
1446 7046
7046 4826
4826 6494
6494 1763
1763


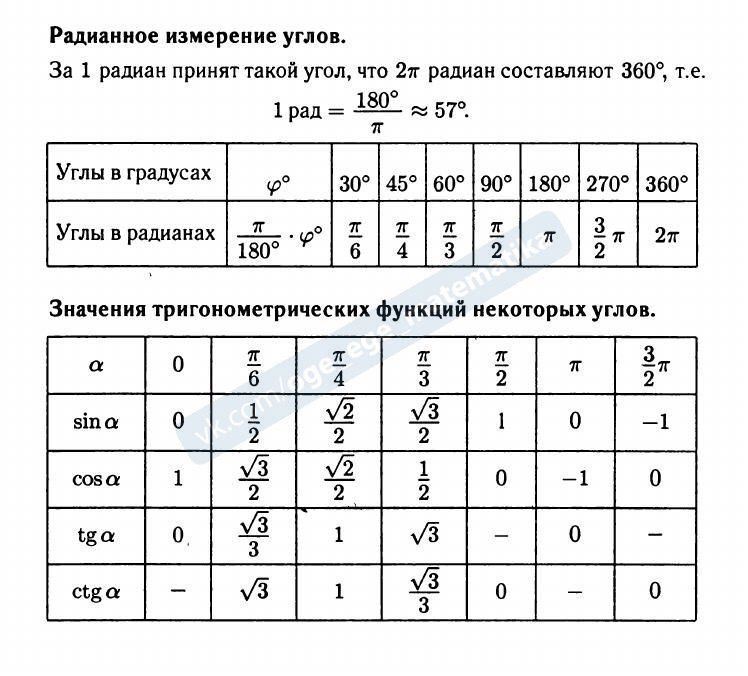

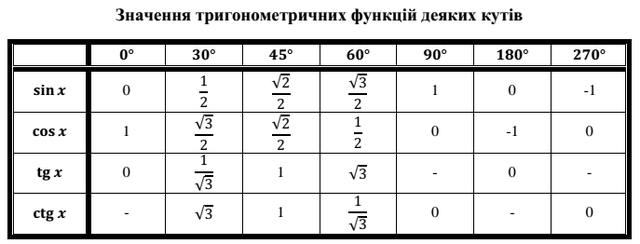

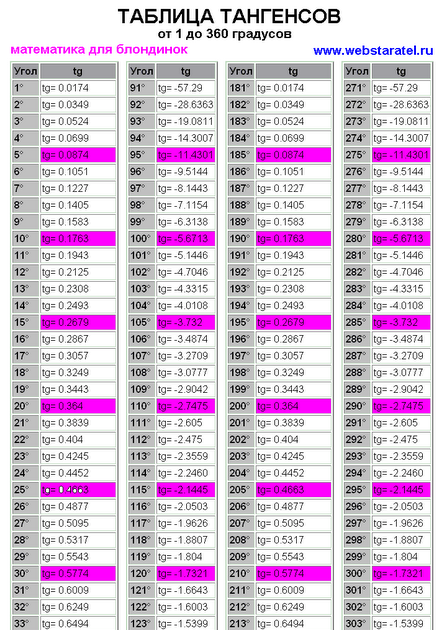
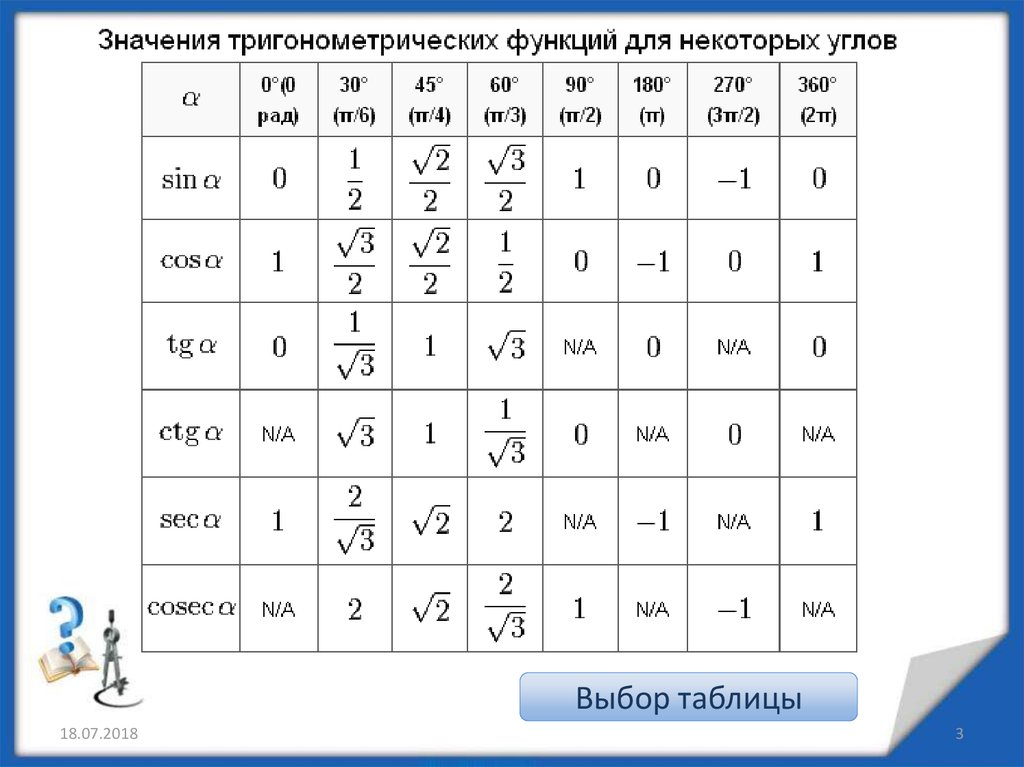
 ru/education/math/geometry/angle/tangent
ru/education/math/geometry/angle/tangent (87°) = 19,08114
(87°) = 19,08114  tg(231°) = 1,2349
tg(231°) = 1,2349  21256
21256  012475
012475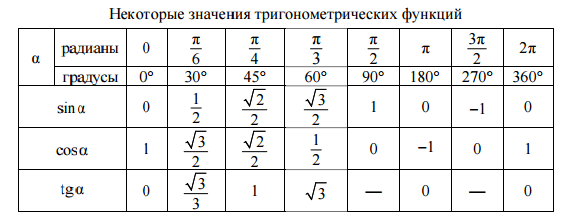 015439
015439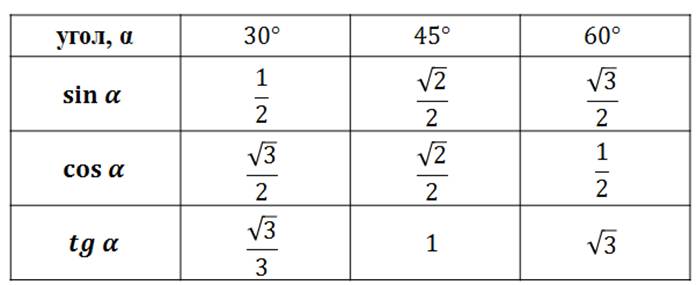 026326
026326 040333
040333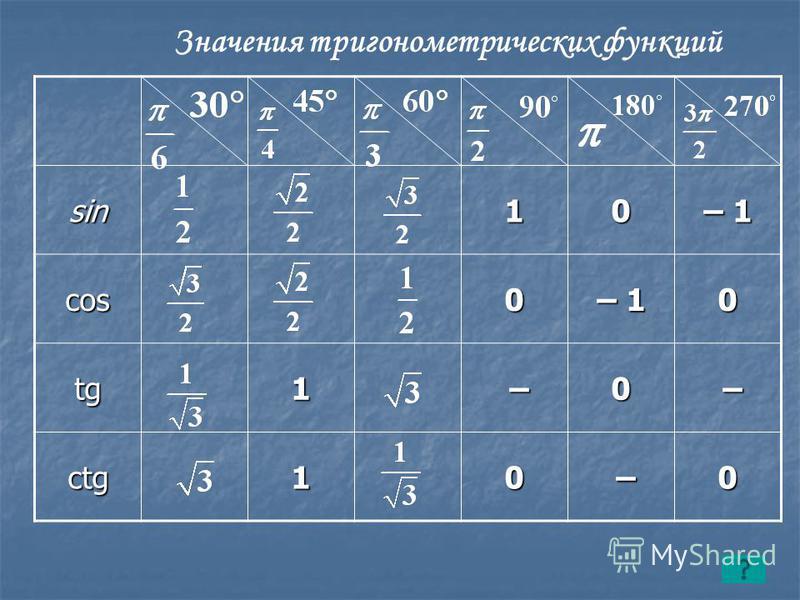 057669
057669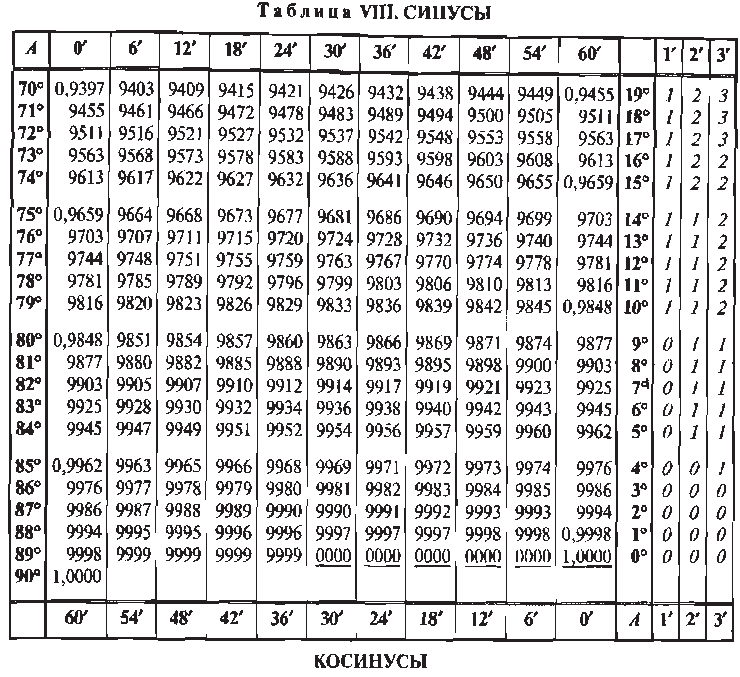 064232
064232 086435
086435 112701
112701 143483
143483 154841
154841 1
1 236295
236295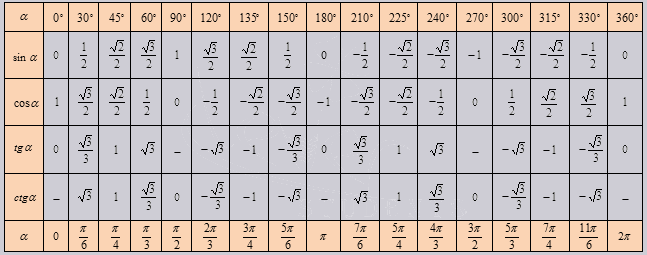 287045
287045 305715
305715 367713
367713 036200
036200 151168
151168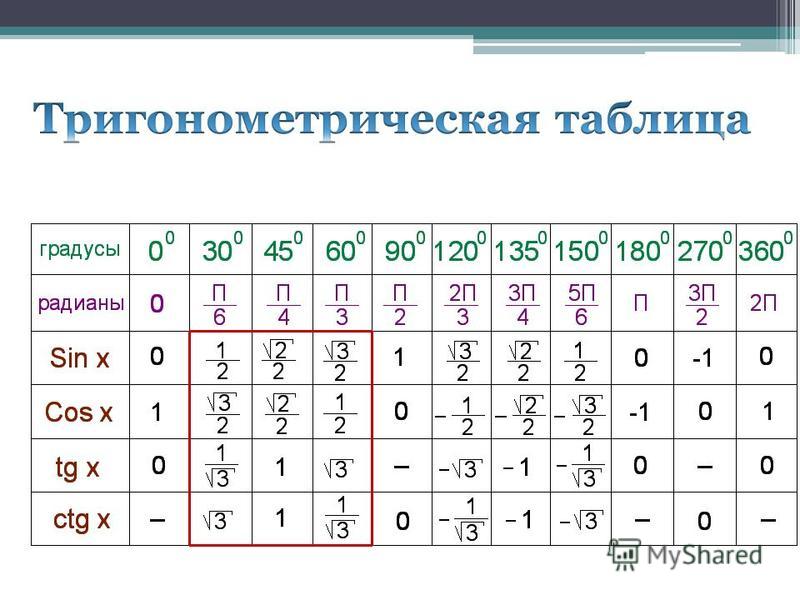 1
1 328073
328073 483820
483820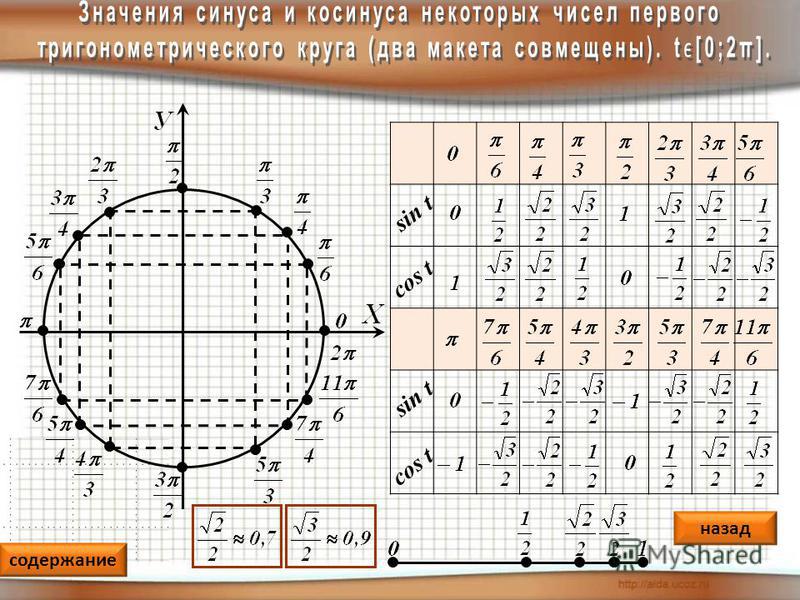 665843
665843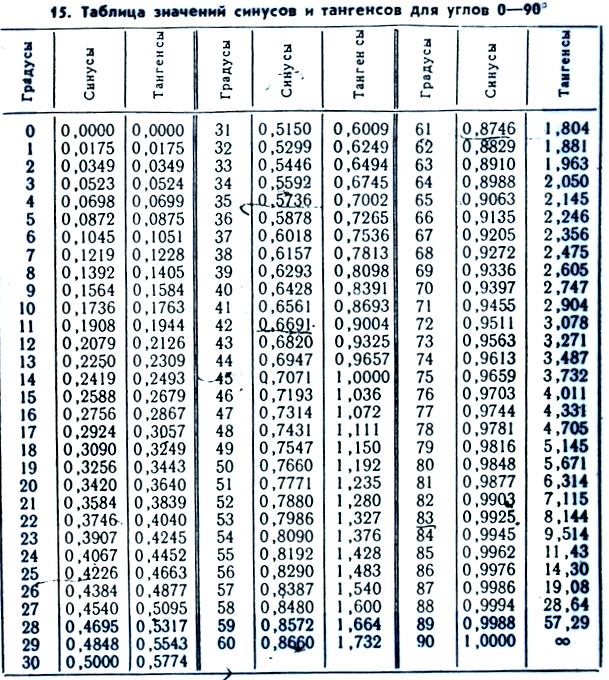 047619
047619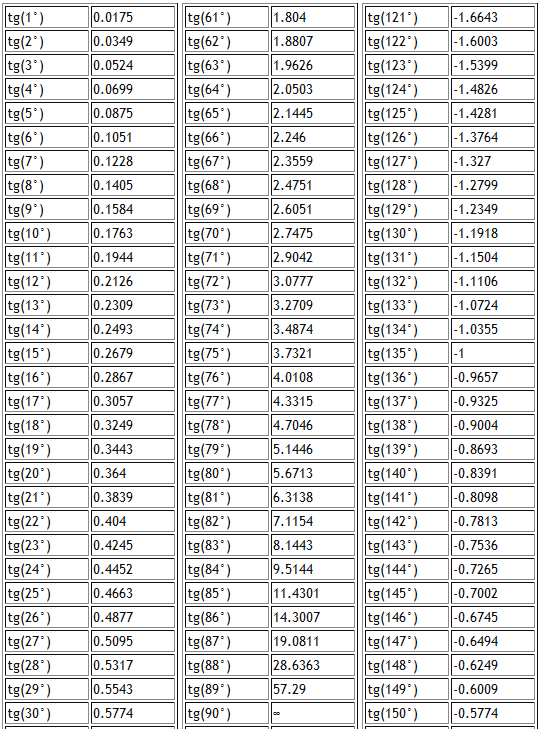
 152381
152381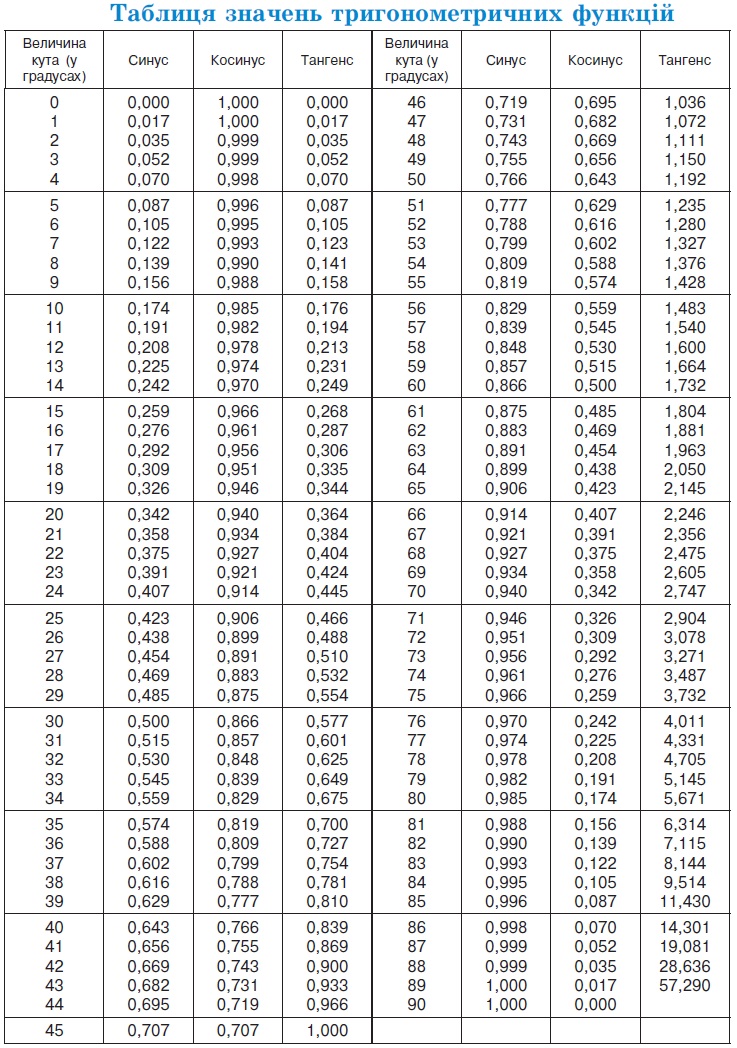 204762
204762 222222
222222 274603
274603 326984
326984 379365
379365 3
3 449206
449206 501587
501587