ПРОИЗВОДНАЯ
— это скорость!
ФСП
|
\S S(t1 ) — S(t)
Vср = ¾¾ = ¾¾¾¾¾
\t t1 — t
при t1 ® t , \t ® 0
тогда Vср
Вывод: Пусть V(t) — мгновенная скорость:
S(t1 ) — S(t)
V(t) = lim ¾¾¾¾¾
t1®t t1 — t
ГСП
\y y(x1 ) — y(x)
tgj1 = ¾¾ = ¾¾¾¾¾
\x x1 — x
при x1 ® x , \x ® 0
тогда j1 ® j
— угол наклона касательной
Вывод: Пусть k(x) — тангенс угла наклона касательной:
y(x1 ) — y(x)
k(x) = lim ¾¾¾¾¾
x1®x x1 — x
О: Производной функции f в точке x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю:
f(x +\x) — f(x )
f ‘(x) = lim ¾¾¾¾¾¾¾
\x®0
План вычисления производной:
1). f(x)
f(x)
2). f(x + \x)
3). \y = f(x + \x) — f(x)
4). \y /\x
5). \y
f ‘(x) = lim ¾¾
\x®0 \x
Правила вычисления производной:
1). (u ± v)’ = u’ ± v’
2). (u · v)’ = u’ v + u v’
(c· u)’ = c· u’
3). (u / v)’ = (u’ v — u v’) / v 2
4). (f(g(x)))’ = g'(x) · f ‘(g(x))
Формулы для вычисления производной:
|
1).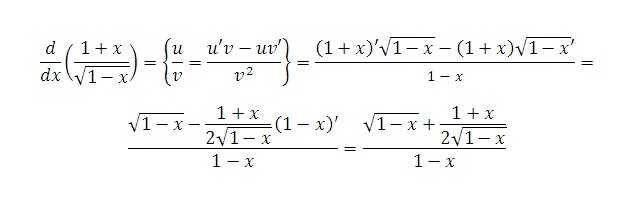 (x n)’ = n· x n — 1
(x n)’ = n· x n — 1
c’ = 0
x’
(ax + b)’ = a
(Ö x )’ = 1 / 2Ö x
(1 / x)’ = — 1 / x2
2). (sin x)’ = cos x
(cos x)’ = — sin x
(tg x)’ = 1 / cos2 x
(ctg x)’ = — 1 / sin2 x
Уравнение касательной к данной функции f(x) в данной точке x0 :
|
План: 1. f (x0)
2. f ‘(x)
3. f ‘(x0)
4. y = f(x0 ) + f ‘(x0 )(x — x0 )
Приближённые вычисления:
Ö 1 +
1 / (1+ x) » 1 — x + x2
nÖ 1+ x » 1+ x ¤ n
( 1+ x)k» 1+ k x
1.
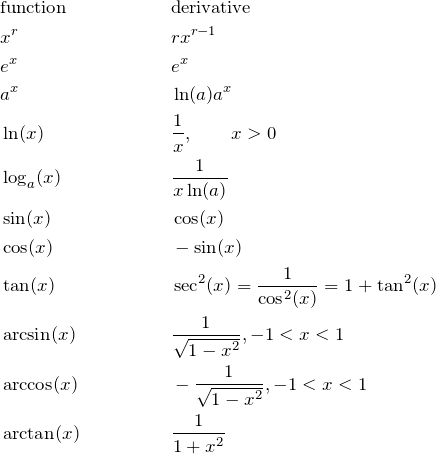 Производная функции y = cos (1 + 2×3) имеет вид 1 страница 1. Производная функции y = cos (1 + 2×3) имеет вид 1 страница
Производная функции y = cos (1 + 2×3) имеет вид 1 страница 1. Производная функции y = cos (1 + 2×3) имеет вид 1 страница
|
Стр 1 из 5Следующая ⇒
Вариант 1
1.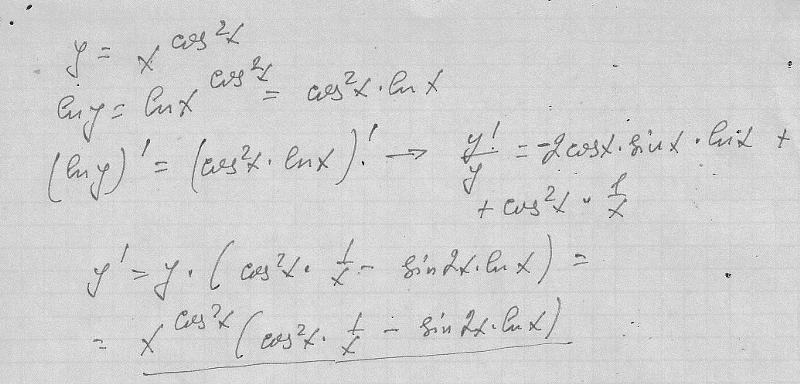 Производная функции y = cos (1 + 2x3) имеет вид…
Производная функции y = cos (1 + 2x3) имеет вид…
1) − 2x3 sin (1 + 2x3) 2) − 6x sin (1 + 2x3) 3) − 6x sin x 4) − sin (1 + 2x3)
2. Множество первообразных функции f(x) = имеет вид…
1) ln 3x2 + C 2) 3x2 + C 3) ln |1 + x3| + C 4) 3ln |1 + x3 | + C 5) 6ln |1 + x3| + C
3. Общим решением дифференциального уравнения является функция
1) y = (x3 + C)x 2) y = x2 + Cx 3) y = + C 4) y = (x2 + C)x2
4. Дано дифференциальное уравнение y« + 3y` + 2y = 0. Тогда его общее решение имеет вид
1) C e + C e 2) C e + C e 3) C e + C e 4) C e + C e
5. Укажите правильное утверждение относительно сходимости числовых рядов
A) и B)
1) A — сходится, B — расходится 3) A — расходится, B — сходится
2) A и B расходятся 4) A и B сходятся
6.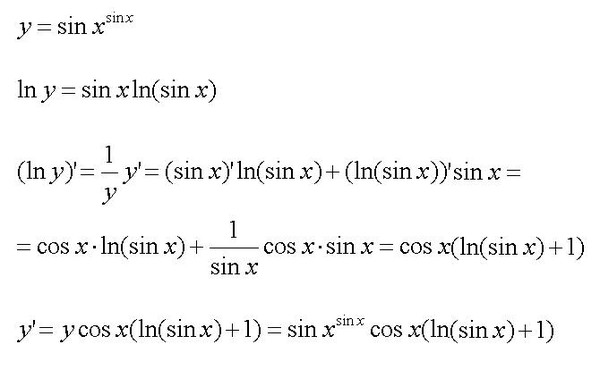
1) 0,0985 2) 0,0054 3) 0,8564 4) 0,8554
Вариант 2
1. Производная функции y = sin (1 + 3x2 ) имеет вид…
1) cos x 2) x2 cos(1 + 3x2 ) 3) 6x cos(1 + 3x2 ) 4) 3x2 cos (1 + 3x2 ) 5) 3xcos (1 + 3x2 )
2. Множество первообразных функции имеет вид…
1) ln 4x3 + C 2) 3x4 + C 3) ln (1 + x4 ) + C 4) 4ln (1 + x4 ) + C 5) 1 + x4 + C
3. Дано дифференциальное уравнение y` = (2k − 1)x , тогда функция y = является его решением при k равном…
1) 0,5 2) 1,5 3) 2,5 4) 3,5
1) C e + C e 2) C e + C e 3) C e + C e 4) C e + C e
5. Укажите правильное утверждение относительно сходимости числовых рядов
Укажите правильное утверждение относительно сходимости числовых рядов
A) и B)
1) A — сходится, B — расходится 3) A — расходится, B — сходится
2) A и B расходятся 4) A и B сходятся
6. Найти дисперсию ДСВ X с рядом распределения
− 2 | ||||
? | 0,2 | 0,1 | 0,4 |
1) 1,78 2) 2,65 3) 4,56 4) 0,5
Вариант 3
1. Производная функции имеет вид…
1) 2) 3) 4) 5)
2. Множество первообразных функции f(x) = sin2 x·cosx имеет вид…
1) sin3 x + C 2) + C 3) + C 4) sin2 x − cosx + C 5) sin2 x·cosx + C
3. Общим решением дифференциального уравнения является функция
1) y = (x3 + C) 2) y = Cx2 + 3) y = (x2 + C) 4) y = (x +C)
4. Дано дифференциальное уравнение y« − 3y` + 2y = 0. Тогда его общее решение имеет вид
Дано дифференциальное уравнение y« − 3y` + 2y = 0. Тогда его общее решение имеет вид
1) C e + C e 2) C e + C e 3) C e + C e 4) C e + C e
5. Укажите правильное утверждение относительно сходимости числовых рядов
A) и B)
1) A — сходится, B — расходится 3) A — расходится, B — сходится
2) A и B расходятся 4) A и B сходятся
6. Известно, что математическое ожидание случайной величины X равно 1. Найти математическое ожидание случайной величины 1 + 2X.
1) 2 2) 3 3) 4 4) 5
Вариант 4
1. Производная функции y = cos (x2 + x) имеет вид…
1) − (2x + 1) sin( x2 + x) 2) − 2x sin( x2 + x) 3) − sin( x2 + x)
4) (x2 + x) sin( x2 + x) 5) − 2x2 sin( x2 + x)
2. Множество первообразных функции имеет вид…
1) ln 3x2 + C 2) 3x2 + C 3) 3ln (5 + x3 ) + C 4) ln (5 + x3 ) + C 5) 3x2 ln (5 + x3 ) + C
3. Найти частное решение дифференциального уравнения, если указаны начальные условия:
Найти частное решение дифференциального уравнения, если указаны начальные условия:
, y(4) = 1
1) 2) 3) 4)
4. Дано дифференциальное уравнение y« + 7y` + 10y = 0. Тогда его общее решение имеет вид
1) C e + C e 2) C e + C e 3) C e + C e 4) C e + C e
5. Найти верный ответ относительно сходимости рядов: A) и B)
1) A — сходится, B — расходится 3) A — расходится, B — сходится
2) A и B расходятся 4) A и B сходятся
6. Найти дисперсию ДСВ X с рядом распределения
0,1 | ? | 0,2 | 0,4 |
1) 1,61 2) 1,25 3) 1,52 4) 3,11
Вариант 5
1. Производная функции y = 2arcsin ( x + x3 ) имеет вид…
1) 2) 3) 4) 5)
2. Множество первообразных функции имеет вид…
Множество первообразных функции имеет вид…
1) ln 8x3 + C 2) 8x3 + C 3) ln (4 + x4 ) + C 4) 2ln (4 + x4 ) + C 5) ln (1 + x4 ) + C
3. Общим решением дифференциального уравнения является функция
1) y = 2) y = Cx2 + 3 3) y = Cx + 3 4) y = + 3
4. Дано дифференциальное уравнение y« − 4y` + 3y = 0. Тогда его общее решение имеет вид
1) C e + C e 2) C e + C e 3) C e + C e 4) C e + C e
5. Укажите правильное утверждение относительно сходимости числовых рядов
A) и B)
1) A — сходится, B — расходится 3) A — расходится, B — сходится
2) A и B расходятся 4) A и B сходятся
6. Найти вероятность того, что из трех наудачу выбранных карт из колоды в 36 карт все три окажутся дамами.
1) 1/946 2) 1/1785 3) 3/595 4) 1/2386
Вариант 6
1. Производная функции y = sin (5x2 − 4x3) имеет вид…
1) (10x − 12x2 ) cos( 5x2 − 4x3 ) 2) cos( 5x2 − 4x3 ) 3) (10x − 12x2 ) cos x
4) 5x2 − 4x3 5) 5x2 cos( 5x2 − 4x3 )
2.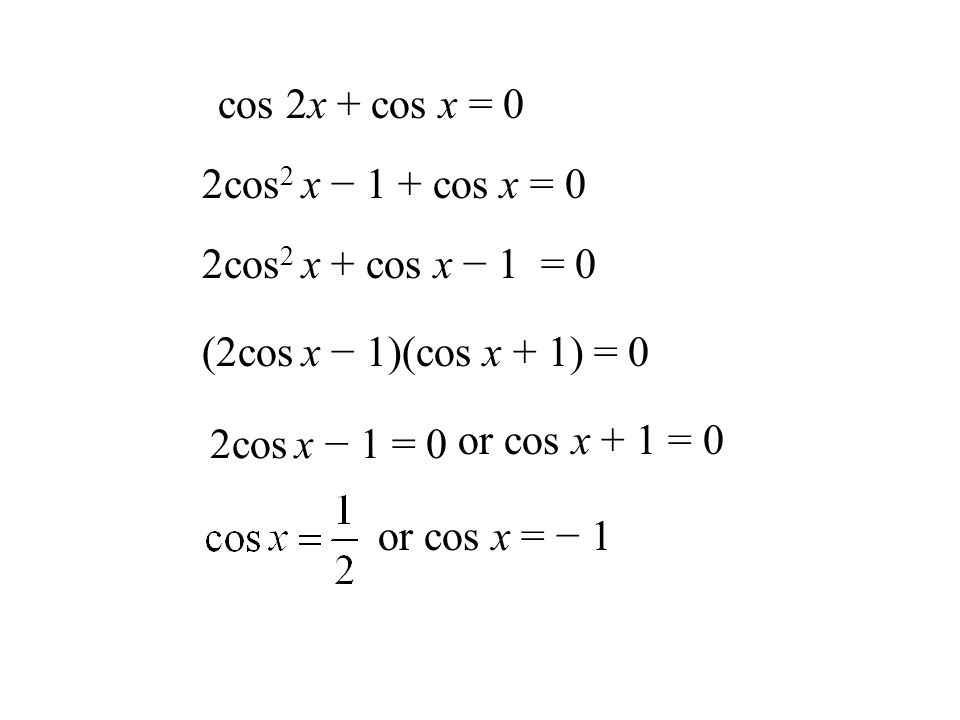 Множество первообразных функции имеет вид…
Множество первообразных функции имеет вид…
1) + C 2) + C 3) + C 4) + C 5) + C
3.Дано дифференциальное уравнение y` = (2k − 1)x , тогда функция y = является его решением при k равном… 1) 2 2) 1 3) 0 4) 3
4. Дано дифференциальное уравнение y« − 6y` + 8y = 0. Тогда его общее решение имеет вид
1) C e + C e 2) C e + C e 3) C e + C e 4) C e + C e
5. Укажите правильное утверждение относительно сходимости числовых рядов
A) и B)
1) A — сходится, B — расходится 3) A — расходится, B — сходится
2) A и B расходятся 4) A и B сходятся
6. Игральная кость бросается один раз. Найти вероятность того, что на верхней грани выпадет не более семи очков.
1) 4/6 2) 1/6 3) 5/6 4) 1
Вариант 7
1. Производная функции y = 3cos x3 имеет вид…
1) − 3x2 sin x 2) cos x3 3) − 3 sin x34) − x2 sin x3 5) − 9x2 sin x3
2. Множество первообразных функции имеет вид…
Множество первообразных функции имеет вид…
1) ln |3 + x3| + C 2) ln x2 + C 3) 3ln |3 + x3| + C 4) x2 ln |3 + x3| + С 5) ln |3 + x3| + С
3. Общим решением дифференциального уравнения является функция
1) y = Ce − e 2) y = e − Ce 3) y = e + Ce 4) y = e + Ce
4. Дано дифференциальное уравнение y« − 2y` − 8y = 0. Тогда его общее решение имеет вид
1) C e + C e 2) C e + C e 3) C e + C e 4) C e + C e
5. Укажите правильное утверждение относительно сходимости числовых рядов
A) и B)
1) A — сходится, B — расходится 3) A — расходится, B — сходится
2) A и B расходятся 4) A и B сходятся
6. Игральная кость бросается один раз. Найти вероятность того, что на верхней грани выпадет не более 2-х очков. 1) 4/6 2) 5/6 3) 1/6 4) 1/3
Вариант 8
1. Производная функции y = sin2 4x имеет вид…
1) 4cos2 4x 2) 2sin 8 x3) cos2 4x 4) cos 4x 5) 4sin 8x
( Указание: вспомнить школьную формулу sin 2x = 2sin x·cos x)
2. Множество первообразных функции имеет вид…
Множество первообразных функции имеет вид…
1) − cos 3x + sin 5x + C 2) + C 3) − 3cos 3x + 5sin 5x + C
4) + С 5) + С
3.Дано дифференциальное уравнение y` = (2 + k)sin x, тогда функция y = 3cos x является его решением при k равном… 1) − 3 2) − 5 3) 3 4) − 4
4. Дано дифференциальное уравнение y« − 4y = 0. Тогда его общее решение имеет вид
1) C cos 2x + C sin 2x 2) C cos (− 2x) + C sin (− 2x)
3) C e + C e 4) e (C cos 2x + C sin 2x)
5. Укажите правильное утверждение относительно сходимости числовых рядов
A) и B)
1) A — сходится, B — расходится 3) A — расходится, B — сходится
2) A и B расходятся 4) A и B сходятся
6. В группе из 18 студентов имеется 5 отличников. Выбирается наудачу 2 студента. Найти вероятность того, что оба они отличники.
1) 4/163 2) 15/73 3) 10/153 4) 3/613
Вариант 9
1. Производная функции имеет вид…
1) 2) 3) 4) 5)
2. Множество первообразных функции имеет вид…
Множество первообразных функции имеет вид…
1) 2) 3) 4) 5)
3. Общим решением дифференциального уравнения является функция
1) y = x2(e + C) 2) y = x(e + C) 3) y = x(e + C) 4) y =
4. Дано дифференциальное уравнение y« + 8y` + 15y = 0. Тогда его общее решение
1) C e + C e 2) C e + C e 3) C e + C e 4) C e + C e
Дата добавления: 2015-08-28; просмотров: 79 | Нарушение авторских прав
| | | следующая лекция ==> | |
Электронный учебник по математическому анализу
Задачи.
1. В круговой конус высоты $H$ с радиусом основания $R$ вписан цилиндр (образующая цилиндра при этом полагается параллельной оси конуса). Определить площадь боковой поверхности и объем цилиндра как функции радиуса цилиндра $r$.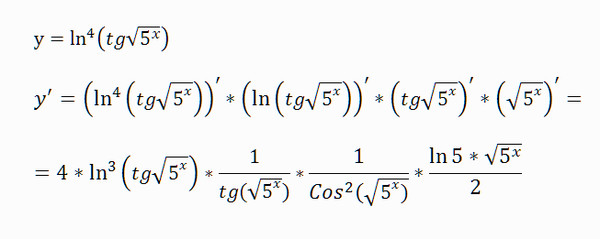 2$ и $y=0$.
2$ и $y=0$.
1. Найти кооординаты центра масс (полагая распределение масс равномерным)
а) симметричного параболического сегмента с основанием $a$ и высоты $h$;
б) дуги окружности радиуса $R$, стягивающей центральный угол $\alpha $.
2. Найти момент инерции (полагая распределение масс равномерным)
а) полукруга радиуса $R$ относительно его диаметра;
б) конуса с радиусом основания $R$, высоты $H$, относительно его оси;
в) шара радиуса $R$ относительно его диаметра.
Производная сложной функции. Производная обратной функции. Производная функции, заданной неявно. Теорема. (Семинар 8)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Семинар 8. Производная сложной функции. Производная обратной функции.
Производная функции, заданной неявно
Производная сложной функции
Теорема
)
Если y f ( z ), z ( xдифференцируемые
функции от своих аргументов, то
производная сложной функции y f [ ( x )]существует и равна производной данной
функции y по промежуточному аргументу z, умноженной на производную самого
промежуточного аргумента z по независимой переменной х
.
y x’ y z’ z x’
Производная обратной функции
Пусть y=f(x) — дифференцируемая функция от аргумента х в некотором интервале
(a,b). Рассмотрим x ( y ) где f [ ( y)] y -обратная функция .
y
Задача Зная производную y x’ lim x 0
функции y=f(x) найти производную
x
x
обратной функции x ( y )
x ‘y lim y 0
y
предполагая, что обратная функция существует и непрерывна в соответствующем
интервале.
Теорема
Для дифференцируемой функции с производной не равной нулю, производная
обратной функции равна обратной величине производной данной функции, то есть
x ‘y
1
y x’
Производная функции заданной неявно
Рассмотрим способы нахождения производных функций заданных неявно.
Пример. Найти 2производную
функции y(y>0), определенную уравнением (уравнение
x
y2
эллипса) 2 2 1 Разрешая это уравнение относительно y и, выбирая знак
a
b
плюс в силу начального условия получаем функцию в явном виде
y
b 2
b
x
a x 2 y’
a
a a2 x2
Однако в некоторых случаях уравнение элементарными средствами нельзя разрешить
относительно y и приходится рассматривать y как неявную функцию от x.
Существует другой способ нахождения производной.
Предполагая, что в уравнение подставлено вместо y явное выражение получим
тождество: x 2 y 2
причем y функция от x. Очевидно, если две функции
1
тождественно
a 2 равны
b 2 друг другу, то равны и их производные. Поэтому, взяв
Поэтому, взяв
производные от левой и правой частей тождества и применяя правило
дифференцирования сложной функции, получаем 2 x 2 y
b2 x
a2
Примеры с решениями
1. Найти производные сложных функций
b2
y’ 0 y’
a2 y
1) y (2 x 3 5) 4
Решение. Обозначим 2 x 3 5 u y u 4 По правилу дифференцирования сложной функции
имеем y’ (u 4 ) u’ (2 x 3 5) ‘x 4u 3 (6 x 2 ) 24 x 2 (2 x 3 5) 3
2) y tg ln x
Решение
3) y ln tg
Решение
y ‘ (tg ln x)’
1
1
cos 2 ln x x
x
2
x
1
1
1
1
y ‘ (ln tg )’
(tg ( x / 2))’
( x / 2)’
2
2
tg ( x / 2)
2 sin( x / 2) cos( x / 2) sin x
tg ( x / 2) cos ( x / 2)
4) y ln( x x 2 1)
Решение
y’ (ln( x x 2 1))’
1
x x2 1
( x x 2 1) )’
1
x x2 1
(1
2x
2 x2 1
)
1
x x2 1
5) y e x arctgx ln 1 e 2 x
Решение
1
1
y ‘ (e x arctgx ln 1 e 2 x )’ (e x arctgx ln( 1 e 2 x )’ e x arctgx e x
2
1 x2
1 2e 2 x
1
ex
x
e (arctgx
)
2 1 e2x
1 x 2 1 e2x
x x2 1
x2 1
1
x2 1
6) y
sin x
1 sin x
ln
2
cos x
cos x
Решение. Преобразуем функцию
Преобразуем функцию
y
sin x
1 sin x
sin x
ln
ln( 1 sin x) ln cos x
2
cos x
cos x
cos 2 x
cos x cos 2 x sin x 2 cos x( sin x)
cos x
sin x cos 2 x 2 sin 2 x cos 2 x sin 2 x sin x
y’
1 sin x cos x
cos x(1 sin x)
cos 4 x
cos 3 x
1 sin 2 x
1
2
3
cos x cos 3 x
cos x
2. Для функции y x 2 5x 3 найти
Решение x ‘ 1 x ‘ 1
y
y x’
y
x ‘y
2x 5
3. Найти производные для функций заданных неявно
1) x 3 y 3 3xy 0
Решение ( x 3 y 3 3xy)’ 0
3x 2 3 y 2 y ‘ 3 y 3xy’ 0 y ‘
2)e x e y 2 xy 1 0
y x2
y2 x
Решение (e x e y 2 xy 1)’ 0 e x e y y’ 2 xy ln 2( y xy’ ) 0
(e y x 2 xy ln 2) y’ y 2 xy ln 2 e x y’
3) x y y x 0
y 2 xy ln 2 e x
e y x 2 xy ln 2
Решение
x y y x 0 x y y x y ln x x ln y ( y ln x)’ ( x ln y)’ y’ ln x y / x ln y ( xy’ ) / y
(ln x x / y ) y ‘ ln y y / x y ‘
ln y y / x
ln x x / y
Примеры для самостоятельного решения.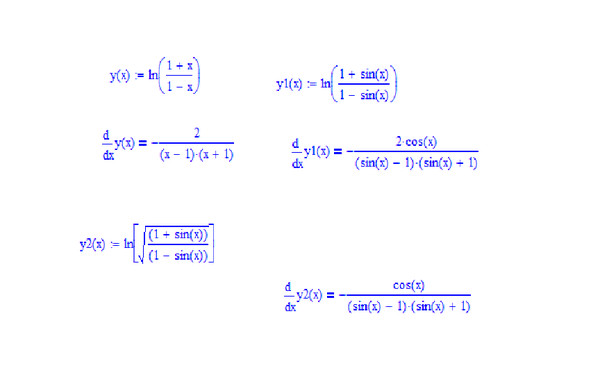
1.
Продифференцировать функции
1. y x ( x 3 x 1) 2. y 3 1 3. y 1 tg( x 1 ) 4.
1 x
5.
9.
2
x 3
y ln arctg 1 x 6. y ln sin
4
10.
y th(ln x)
1 x
y arctg
1 x
2
3
x
7.
y 2
x
ln x
y
8.
14
arcsin
2
y ln sin 3 arctge 3 x
2. Найти производную обратной функции
4
1. y 1 x 4 …Выразить.. dx ..через..х; через.. y 2. x y 3 4 y 1.Найти.. dx
dy
dy
1 x
3. Найти производные от функций y, заданных неявно
1. y 1 xe y 2. x sin y cos y cos 2 y 0 3. tg y 1 k tg x
2
1 k
x 2 2x
2
4. y x arctgy
English Русский Правила
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | 92)|||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная от cos x – формула, доказательство, примеры
Дифференцирование cos x – это процесс вычисления производной от cos x или определения скорости изменения cos x относительно переменной x. Производная функции косинуса записывается как (cos x)’ = -sin x, то есть производная от cos x равна -sin x. Другими словами, скорость изменения cos x под определенным углом определяется выражением -sin x.
Производная функции косинуса записывается как (cos x)’ = -sin x, то есть производная от cos x равна -sin x. Другими словами, скорость изменения cos x под определенным углом определяется выражением -sin x.
Теперь производную от cos x можно вычислить разными методами. Его можно получить с помощью определения пределов, цепного правила и частного правила. В этой статье мы вычислим производную от cos x, а также обсудим антипроизводную от cos x, которая представляет собой не что иное, как интеграл от cos x.
| 1. | Что такое производная Cos x? |
| 2. | График производной Cos x |
| 3. | Производная Cos x с использованием первого принципа |
| 4. | Производная от Cos x с использованием цепного правила |
| 5. | Производная от Cos x с использованием правила отношения |
| 6. | Антипроизводное Cos x |
7. | Часто задаваемые вопросы о производной Cos x |
г. Что такое производная от cos x?
Производная от cos x является отрицательной функцией синуса, то есть -sin x. Производные всех тригонометрических функций можно вычислить, используя производную от cos x и производную от sin x. Производная функции характеризует скорость изменения функции в некоторой точке. Процесс нахождения производной называется дифференцированием. Дифференцировать cos x можно по-разному, и его можно получить, используя определение предела и правило частных. Поскольку производная cos x равна -sin x, поэтому график производной cos x будет графиком отрицательного значения -sin x.
Производная от Cos x — Формула
Теперь мы математически запишем производную от cos x. Производная функции — это наклон касательной к функции в точке касания. Следовательно, -sin x представляет собой функцию наклона касательной к графику cos x в точке касания. В основном мы запоминаем производную от cos x. Простой способ сделать это — знать тот факт, что производная от cos x отрицательна от sin x, а производная от sin x является положительным значением cos x. Выражение для записи дифференцирования cos x:
Простой способ сделать это — знать тот факт, что производная от cos x отрицательна от sin x, а производная от sin x является положительным значением cos x. Выражение для записи дифференцирования cos x:
d(cos x )/ dx = -sin x
График производной cos x
Поскольку производная cos x от sin x отрицательна, то график производной cos x подобен графику тригонометрической функции sin x с отрицательными значениями, где sin x имеет положительные значения. Во-первых, давайте посмотрим, как выглядят графики cos x и производной cos x. Поскольку sin x является периодической функцией, график дифференцирования cos x также является периодическим и его период равен 2π.
Производная от cos x с использованием первого принципа производных
Производная — это просто мера скорости изменения. Теперь выведем производную от cos x по первому принципу производных, то есть по определению пределов. Чтобы найти производную от cos x, мы берем предельное значение, когда x приближается к x + h. Чтобы упростить это, мы устанавливаем x = x + h и хотим взять предельное значение, когда h приближается к 0. Мы собираемся использовать определенные формулы тригонометрии для определения производной cos x. Формулы:
Чтобы упростить это, мы устанавливаем x = x + h и хотим взять предельное значение, когда h приближается к 0. Мы собираемся использовать определенные формулы тригонометрии для определения производной cos x. Формулы:
- cos (A + B) = cos A cos B — sin A sin B
- \(\lim_{x\стрелка вправо 0} \dfrac{\cos x -1}{x} = 0\)
- \(\lim_{x\стрелка вправо 0} \dfrac{\sin x}{x} = 1\)
Таким образом, мы имеем
\(\begin{align}\frac{\mathrm{d} (\cos x)}{\mathrm{d} x} &= \lim_{h\rightarrow 0} \dfrac{ \cos (x + h)-\cos x}{(x+h)-x} \\&= \lim_{h\rightarrow 0} \dfrac{\cos x \cos h -\sin x \sin h- \ cos x} {h} \\ & = \ lim_ {h \ rightarrow 0} \ dfrac {\ cos h -1 } {h} \ cos x — \ dfrac {\ sin h} {h} \ sin x \\ &=(0)\cos x — (1)\sin x\\&=-\sin x\end{align}\)
Следовательно, производная от cos x доказана с использованием первого принципа дифференцирования.
Производная от cos x с использованием цепного правила
Цепное правило дифференцирования: (f(g(x)))’ = f’(g(x)) . г’(х). Теперь, чтобы вычислить производную cos x с помощью цепного правила, мы будем использовать некоторые тригонометрические свойства и тождества, такие как:
г’(х). Теперь, чтобы вычислить производную cos x с помощью цепного правила, мы будем использовать некоторые тригонометрические свойства и тождества, такие как:
- \(\cos (\dfrac{\pi}{2} — \theta) = \sin \ тета\)
- \(\sin (\dfrac{\pi}{2} — \theta) = \cos \theta\) г.
- d(sin x)/dx = cos x
Используя три приведенных выше тригонометрических свойства, мы можем записать производную от cos x как производную от sin (π/2 — x), то есть d(cos x)/dx = d (sin (π/2 — x ))/дх. Используя цепное правило, мы имеем
\(\begin{align} \frac{\mathrm{d} \cos x}{\mathrm{d} x} &=\frac{\mathrm{d} \sin(\ dfrac{\pi}{2}-x)}{\mathrm{d} x}\\&=\cos(\dfrac{\pi}{2}-x).(-1)\\&=-\ cos(\dfrac{\pi}{2}-x)\\&= -\sin x\end{align}\)
Следовательно, мы получили производную cos x как -sin x, используя цепное правило.
Производная от cos x по правилу частных
Факторное правило для дифференцирования: (f/g)’ = (f’g — fg’)/g 2 . Чтобы получить производную от cos x, мы будем использовать следующие формулы:
Чтобы получить производную от cos x, мы будем использовать следующие формулы:
- cos x = 1/сек x
- сек х = 1/cos х
- d(сек x)/dx = сек x тангенс x
- тангенс x = sin x/cos x
Используя приведенные выше тригонометрические формулы, мы можем записать производную cos x и производную 1/sec x, то есть d(cos x)/dx = d(1/sec x)/dx, и применить факторное правило дифференцирования. 92x}\\&=\dfrac{-\tan x}{\sec x}\\&=\dfrac{\frac{-\sin x}{\cos x}}{\frac{1}{\cos x }}\\&=-\sin x\end{align}\)
Следовательно, мы получили производную от cos x, используя правило дифференцирования.
Антипроизводная cos x
Первообразная от cos x есть не что иное, как интеграл от cos x. Как следует из названия, антипроизводная — это процесс, обратный дифференцировке. Производная от cos x равна -sin x, а производная от sin x равна cos x. Таким образом, первообразная cos x равна sin x + C, а первообразная sin x равна -cos x + C, где C — постоянная интегрирования. Таким образом, мы получили первообразную cos x как sin x + C.
Таким образом, мы получили первообразную cos x как sin x + C.
\(\int \cos x = \sin x + C\)
Важные примечания о производной от cos x
- Производная от cos x равна -sin x
- Первообразная cos x равна sin x + C
- Производная от cos x может быть получена с использованием определения предела, цепного правила и частного правила.
Связанные темы по производной от cos x
- Применение производных
- Цепное правило Формула г.
- Ограничения
- Формулы косинуса
Часто задаваемые вопросы о производной cos x
Что такое производная Cos x в исчислении?
Производная от cos x является отрицательной функцией синуса, то есть -sin x. Производная функции — это наклон касательной к функции в точке касания. Производную от cos x можно вычислить разными способами.
Что такое производная от cos x.sin x?
Производная от cos x. sin x можно вычислить, используя правило дифференцирования произведения. d(cos x. sin x)/dx = (cos x)’ sin x + cos x (sin x)’ = -sin x.sin x + cos x. cos x = cos 2 x — sin 2 x = cos 2x. Следовательно, производная от cos x.sin x = cos 2x
sin x можно вычислить, используя правило дифференцирования произведения. d(cos x. sin x)/dx = (cos x)’ sin x + cos x (sin x)’ = -sin x.sin x + cos x. cos x = cos 2 x — sin 2 x = cos 2x. Следовательно, производная от cos x.sin x = cos 2x
Что такое вторая производная от Cos x?
Первая производная от cos x равна -sin x. Вторая производная cos x получается дифференцированием первой производной cos x, то есть -sin x. Производная от -sin x равна -cos x. Следовательно, вторая производная от cos x равна -cos x.
Как найти производную от Cos x?
Производная от cos x может быть получена различными методами, такими как определение предела, цепное правило дифференцирования и частное правило дифференцирования. Чтобы определить производную от cos x, нам нужно знать некоторые формулы тригонометрии и тождества.
Производные функции запуска
Производные функции запуска| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
Дано : lim(d->0) sin(d)/d = 1. грех(х) = lim (d->0) (sin(x+d) — sin(x)) / d = lim ( sin(x)cos(d) + cos(x)sin(d) — sin(x)) / d92 (d) / ( d(cos(d) + 1) + cos(x) lim sin(d)/d = sin(x) lim (-sin(d)) * lim sin(d)/d * lim 1/(cos(d)+1) + cos(x) lim sin(d)/d = sin(x) * 0 * 1 * 1/2 + cos(x) * 1 = cos(x) КЭД Доказательство cos(x) : из производной синуса Можно получить так же, как sin(x) было получено или проще из результата sin(x) Дано : грех (х) = потому что (х); Правило цепи. cos(x) = sin(x + PI/2) кос(х) = грех (х + PI / 2) = грех(и) * (x + PI/2) (Установить и = х + PI/2) = cos(u) * 1 = cos(x + PI/2) = -sin(x) КЭД Доказательство tan(x) : из производных синуса и косинуса Дано : sin(x) = cos(x); потому что (х) = -sin (х); частное Правило. tan(x) = sin(x) / cos(x)92 (х) КЭД Взаимные отношения Доказательство csc(x), сек(x), детская кроватка(х) : от производные их обратных функций Дано : sin(x) = cos(x); потому что (х) = -sin (х); загар (х) = детская кроватка (х); частное Правило. | ||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический
Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью
Политика. |
Производная от Cos(x) Доказательство Обзор
Вычисление производной от cos(x) является одним из наиболее важных вопросов в исчислении с одной переменной, потому что производные других тригонометрических функций могут быть получены из производной от cos(x) с помощью правила дифференцирования. В этом обзоре исчисления мы исследуем свойства функции cos(x) и способы ее дифференцирования. Мы также показываем, как эта производная может быть получена из производной sin(x). Этот пост отвечает на все ваши вопросы о производной cos(x).
В исчислении углы удобнее всего измерять в радианах, а не в градусах. Угол x в радианах определяется как длина дуги единичной окружности (с радиусом, равным единице). Поскольку окружность радиуса один имеет длину окружности 2 \pi , мы можем выразить x следующим образом:
x = \dfrac{2\pi}{360, \text{степени}}, \theta
где \theta — тот же самый угол в градусах. Преобразование радианов в градусы показано на изображении ниже:
Преобразование радианов в градусы показано на изображении ниже:
Теперь рассмотрим функцию
f(x) = cos (x)
Теперь мы применим методы исчисления одной переменной для исследования производной cos(x) и докажем, что
\dfrac{d}{dx}, cos(x) = -, sin (x)
Вывод производной из основного определения
На изображении ниже показан процесс нахождения производной функции f(x) на основе определения производной:
Предельный хордовый процесс дифференцировки. Источник изображения: Wikimedia CommonsA и B — две точки, расположенные очень близко друг к другу на кривой y = f(x) . По мере того, как разница h между координатами x точек A и B становится меньше, хорда AB (красная линия) приближается к касательной в точке A (зеленая линия). По определению производная функции f(x) является пределом:
f'(x) =\dfrac{d}{d x},f(x) = \lim\limits_{h \rightarrow 0} \dfrac { е(х+ч) — е(х)}{ч}
Применяя это общее правило к функции f(x) = cos (x), мы получаем
\dfrac{d}{d x}, cos(x) = \lim\limits_{h \rightarrow 0} \dfrac{cos ( х + ч ) — потому что х} {ч}
Мы можем продолжить, используя тригонометрическое тождество для косинуса суммы двух углов:
cos (x + h) = cos(x) cos(h) — sin(x) sin(h)
В результате получается следующее:
\dfrac{d}{d x}, cos(x) = \lim\limits_{h \rightarrow 0} \dfrac{ cos(x) cos(h) — sin(x) грех(ч) — cos(х)}{ч} 92 \left( \dfrac{h}{2} \right) }{ \dfrac{h}{2} } \right]- ,sin x \left[ \lim\limits_{h \rightarrow 0} \dfrac{sin (ч) {ч} \справа]
Чтобы оценить представленные здесь пределы, давайте посмотрим на геометрическое представление основных тригонометрических функций в терминах единичного круга:
Тригонометрические функции на единичном круге. Источник изображения: Wikimedia Commons
Источник изображения: Wikimedia Commons Как видно из этого изображения, если угол измеряется в радианах (помните, что угол x в этом случае равен длине дуги на единичной окружности), выполняется следующее неравенство:
sin (x) < x < tan (x)
Разделив это неравенство на sin (x) , получим
1 < \dfrac{x}{sin (x)} < \dfrac{1}{cos (x)}
или, что то же самое:
cos (x) < \dfrac{sin (x)}{x} < 1
Но при стремлении х к нулю cos х, очевидно, стремится к единице, т. е. функция sin(x)/x всегда лежит между единицей и величиной, стремящейся к единице. Следовательно,
,\lim\limits_{x \rightarrow 0},\dfrac{ sin (x)}{ x } = 1
92 \left( \dfrac{h}{2} \right) }{\dfrac{h}{2}} \right]- sin x \left[ \lim\limits_{h \rightarrow 0} \dfrac{sin ( h) }{h} \right] =-,cos (x) \cdot 0 — sin (x) \cdot 1 = — sin (x)Это искомый результат для производной cos(x).
Доказательство, основанное на производной от Sin(x)
В исчислении с одной переменной производные всех тригонометрических функций могут быть получены из производной от cos(x) с использованием правил дифференцирования.
Эквивалентно, мы можем доказать производную cos(x) от производной sin(x). Давайте посмотрим, как это можно сделать.
Мы знаем, что производная от sin(x) определяется следующим выражением:
\dfrac{d}{d x},sin (x) = cos (x)
Мы также знаем, что при смещении тригонометрических функций на угол 90 градусов (что равно \pi/2 в радианах) выполняется следующее тождество:
cos \left( \dfrac{\pi}{2} — у\справа) = sin(у)
Дифференцируя левую часть этого тождества, получаем
\dfrac{d}{d y},cos \left( \dfrac{\pi}{2} — y \right) = \dfrac{d x}{d y } \cdot \dfrac{d}{d x},cos (x)
Где x — новая переменная, определенная как
x = \dfrac{\pi}{2} — y
Очевидно,
\dfrac{d x}{d y} = — 1
Итак, мы имеем
\dfrac{d}{d y},cos \left( \dfrac{\pi}{2} — y \right) = -, \dfrac{d}{d x} ,cos (x)
С другой стороны, на основе тригонометрического тождества, приведенного выше, мы можем написать
\dfrac{d}{d y},cos \left( \dfrac{\pi}{2} — y \right) = \dfrac {d}{d y} ,sin (y) = cos (y)
, где мы также использовали закон дифференцирования для sin(x).
Таким образом, имеем
\dfrac{d}{d x},cos (x) = -,cos (y) = -, cos \left( \dfrac{\pi}{2} — x \right) = -, грех (х)
Естественно, что оба представленных нами метода доказательства производной от cos(x) дают один и тот же результат.
Завершая вывод производной от Cos(x)
В этой обзорной статье мы рассмотрели различные способы доказательства производной от cos(x). Теперь вы сможете доказать производную от cos(x), используя фундаментальные определения или производную от sin(x). Мы надеемся, что эта статья придаст вам большей уверенности в ваших знаниях правил дифференцирования и облегчит изучение исчисления с одной переменной.
Давайте применим все на практике. Попробуйте этот практический вопрос по исчислению одной переменной: Ищете больше практики исчисления с одной переменной? Вы можете найти тысячи практических вопросов на Albert.io. Albert.io позволяет вам настроить свой учебный процесс так, чтобы он ориентировался на практику, в которой вам больше всего нужна помощь. Мы дадим вам сложные практические вопросы, которые помогут вам достичь мастерства в исчислении с одной переменной.
Мы дадим вам сложные практические вопросы, которые помогут вам достичь мастерства в исчислении с одной переменной.
Начните тренироваться здесь .
Вы учитель или администратор, заинтересованный в повышении успеваемости учащихся по исчислению с одной переменной?
Узнайте больше о наших школьных лицензиях здесь .
Научное предложение
Научное предложение| Научный Приговор | Научный Калькуляторы | Решения за Уравнения |
|
|
|
|
| |||||||||||||||||||||||||||||



 линейный | Лес граф | Астрономия
линейный | Лес граф | Астрономия 