|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 2 Найдём число возможных исходов, переберём все варианты бросков. В подобных задачах составляйте таблицу, так считать на много удобней.
Всего возможных исходов восемь. Первые два броска одинаково могут окончится в четырёх случаях это 1,2,5,6 варианты, то есть благоприятных исходов 4. Искомая вероятность равна 4/8=0,5. Обратите внимание, что если в условие добавить одно только слово, смысл задачи изменится, многие из-за невнимательности решают неверно. Итак: Монету бросают трижды. Найдите вероятность того, что только первые два броска окончатся одинаково. Благоприятных исходов будет 2, это 2-й и 6-й варианты, первый и пятый варианты исключаются из-за этого «только». В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу. В данной задаче составляется та же таблица, что и предыдущей. Орёл не выпадет ни разу только в одном варианте из восьми (пятый вариант). Искомая вероятность равна 1 к 8 или 0,125. Ответ: 0,125 В среднем на 150 карманных фонариков приходится три неисправных. Какова вероятность купить исправный фонарик. Количество возможных исходов 150. Количество благоприятных исходов 150-3=147 (на 150 приходится 147 исправных). Вероятность купить исправный фонарик 147 к 150 или 147/150=49/50=0,98 Ответ: 0,98
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. В подобных задачах для удобства следует составить таблицу сумм для двух костей (все варианты сумм, которые могут выпасть): Всего исходов 36 (6 на 6). Благоприятных исходов 5 (легко подсчитать в таблице). Вероятность того, что в сумме выпадет 8 очков, равна 5 к 36 или 0,13888888…. Округляем до сотых, получаем 0,14. Ответ: 0.14
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Ответ: 0,25
Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Выясним, как распределятся выступления по дням: 1 день – 8 выступлений, остальные поровну, значит по 18 выступлений в день. Вероятность, что выступление представителя России состоится в третий день конкурса, равна 18 к 80 или 18/80=0,225. Ответ: 0,225
На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России. Восьмым может оказаться любой учёный, значит возможных исходов 10 (их всего 10). Ответ: 0,3
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? В данном случае нужно поставить себя на место Руслана Орлова. Он будет играть кем-то из 25 спортсменов (на чемпионат приехали Руслан и ещё 25 спортсменов), значит возможных исходов 25. Из них осталось 9 спортсменов из России. Это и есть число благоприятных исходов. Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России 9 к 25 или 0,36. Ответ: 0,36 ⇐ Предыдущая12 Читайте также: Как правильно слушать собеседникаТипичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Симметричная математическая монета — вероятность выпадения одной стороны
В качестве предисловия. Все знают, что монета имеет две стороны — орёл и решку. Нумизматы считают, что монета имеет три стороны — аверс, реверс и гурт. И среди тех, и среди других, мало кто знает, что такое симметричная или математическая монета. Зато об этом знают (ну, или должны знать :), те, кто готовится сдавать ЕГЭ. В общем, в этой статье речь пойдёт о необычной монете, которая, к нумизматике никакого отношения не имеет, но, при этом, является самой популярной монетой среди школьников.
Итак.
Симметричная монета — это воображаемая математически идеальная монета без размера, веса
и диаметра. Как следствие, гурта у такой монеты тоже нет, то есть вот она-то действительно имеет только две стороны. Главное свойство симметричной монеты в том, что при таких условиях вероятность выпадения орла или решки абсолютно одинакова. А придумали симметричную
математическую монету для проведения мысленных экспериментов.
Как следствие, гурта у такой монеты тоже нет, то есть вот она-то действительно имеет только две стороны. Главное свойство симметричной монеты в том, что при таких условиях вероятность выпадения орла или решки абсолютно одинакова. А придумали симметричную
математическую монету для проведения мысленных экспериментов.
Понятно, что в результате броска математическая монета упадёт либо орлом, либо решкой. Сколько раз — зависит от того, сколько бросков совершить. Вероятность выпадения орла или решки вычисляется делением количества удовлетворяющих условию исходов на общее количество возможных исходов. Рассмотрим решение данной задачи на конкретных примерах.
В случайном эксперименте симметричную монету бросают один раз
Здесь всё просто.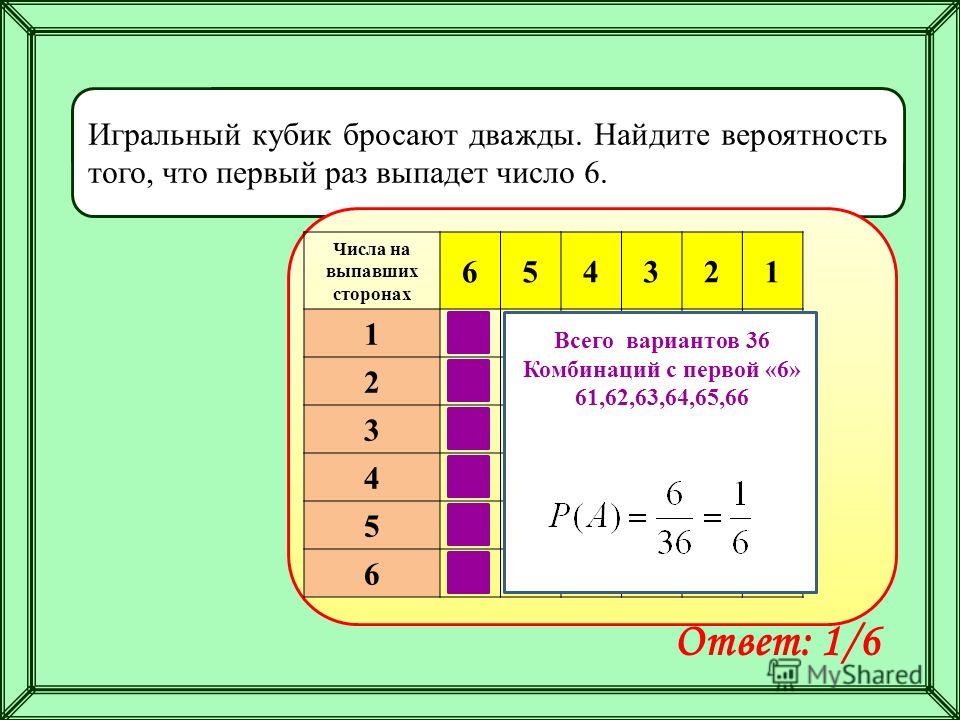 Выпадет либо орёл, либо решка. То есть, имеем
два возможных исхода, один из которых нас удовлетворяет
Выпадет либо орёл, либо решка. То есть, имеем
два возможных исхода, один из которых нас удовлетворяет
— 1/2=50%
В случайном эксперименте симметричную монету бросают дважды
За два броска могут выпасть:
- два орла
- две решки
- орёл, затем решка
- решка, затем орёл
Итак, возможны всего четыре варианта. Задачи с более, чем одним броском, проще всего решать составлением таблицы возможных вариантов. Для простоты, обозначим орла цифрой «0», а решку цифрой «1».
Тогда таблица возможных исходов будет выглядеть так:
00
01
10
11
Если, например, нужно найти вероятность того, что орёл выпадет один раз, требуется просто подсчитать количество подходящих вариантов в таблице —
то есть тех строк, где орёл встречается один раз. Таких строк две (вторая и
третья). Значит, вероятность выпадения одного орла в двух бросках симметричной монеты равна 2/4=50%
Значит, вероятность выпадения одного орла в двух бросках симметричной монеты равна 2/4=50%
Вероятность того, что орёл в двух бросках выпадет дважды равна 1/4=25%, так
как два орла встречаются в таблице один раз (первая строка).
В случайном эксперименте симметричную монету бросают трижды
Составляем таблицу вариантов:
000
001
010
011
100
101
110
111
Те, кто знаком с двоичным исчислением, понимают, к чему мы пришли. 🙂 Да, это двоичные
числа от «0» до «7». Так проще не запутаться с вариантами, поскольку строки
таблицы вариантов представляют собой логическую последовательность.
Решим задачу из предыдущего пункта — вычислим вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется три. Значит, вероятность выпадения одного орла в трёх бросках симметричной монеты равна
трём из восьми — 3/8=37,5%
Вероятность того, что орёл в трёх бросках выпадет дважды тоже равна 3/8=37,5%, то
есть абсолютно такая же.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 1/8=12,5%.
В случайном эксперименте симметричную монету бросают четырежды
Составляем таблицу вариантов:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется всего три, так же, как и в случае трёх бросков. Но, вариантов уже шестнадцать. Значит, вероятность выпадения одного орла в четырёх бросках симметричной монеты равна три из шестнадцати — 3/16=18,75%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 6/8=75%.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 4/8=50%.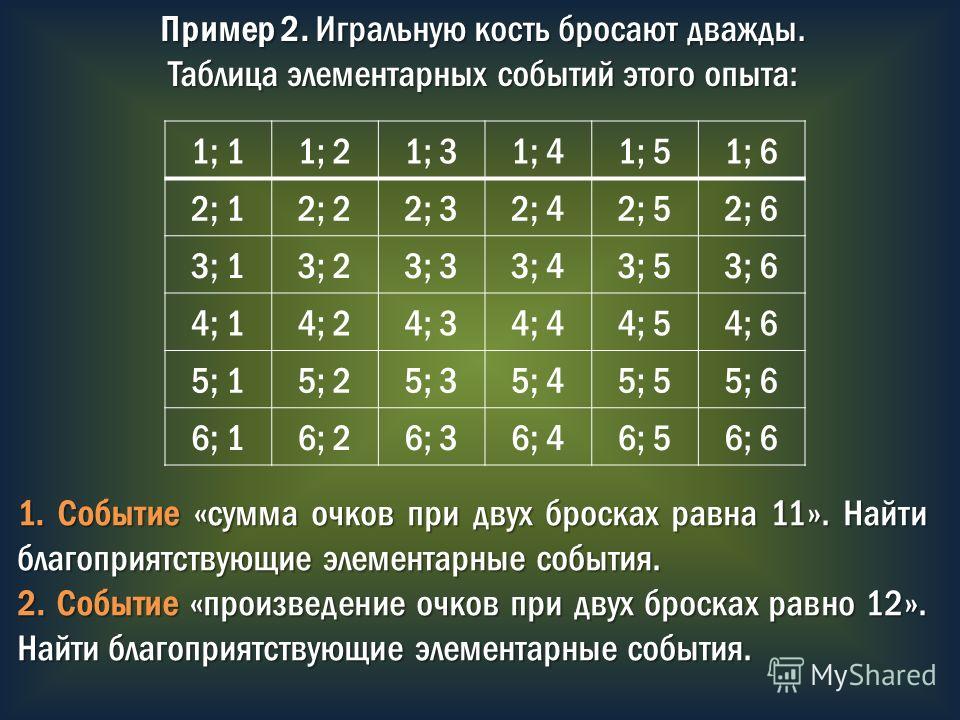
В случайном эксперименте симметричную монету бросают более четырёх раз
С увеличением количества бросков, принцип решения задачи
совершенно не меняется — только, в соответствующей прогрессии,
увеличивается количество вариантов. Принцип тот же — составляем
таблицу вариантов и подсчитываем количество требуемых
результатов. Делением количества удовлетворяющих нас результатов
на общее количество попыток получаем вероятность выпадения
нужного результата.
Даже, если например, симметричную монету бросают 10 раз. Таблица
получится очень большая, но составить её несложно. А в принципе
и делать это самому необязательно, можно найти в интернете. Для
подсчёта нулей и единиц тоже нет необходимости водить по бумаге
или экрану карандашом — для этого можно использовать, например,
Excel. Да, компьютер очень нужная
вещь, если научится им пользоваться. 🙂
🙂
Математика и мы. В случайном эксперименте симметричную монету бросают дважды 1200 в случайном эксперименте симметричную монету
Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:
где p — искомая вероятность, k — число устраивающих нас событий, n — общее число возможных событий.
Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n . В этом и состоит вся сложность.
Тем не менее, существует как минимум два принципиально различных метода решения:
- Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
- Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.

Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!
Метод перебора комбинаций
Этот метод еще называется «решение напролом». Состоит из трех шагов:
- Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n ;
- Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k ;
- Осталось найти вероятность: p = k : n .
К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:
Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):
Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:
Таких вариантов оказалось k = 2. Находим вероятность:
Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем все возможные комбинации орлов и решек:
OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP
Всего получилось n = 16 вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:
Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.
Специальная формула вероятности
Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:
Где C n k — число сочетаний из n элементов по k , которое считается по формуле:
Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.
Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:
Задача.
Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем числа n и k . Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:
Напомню, что 0! = 1 по определению. Поэтому C 3 0 = 1.
Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.
Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.
Пусть p 1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем:
Теперь найдем p 2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем:
Чтобы получить ответ, осталось сложить вероятности p
1 и p
2 . Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:
Имеем:
p = p 1 + p 2 = 0,25 + 0,0625 = 0,3125
В задачах по теории вероятностей, которые представлены в ЕГЭ номером №4, кроме , встречаются задачи на подбрасывание монеты и о бросках кубика. Их сегодня мы и разберем.
Задачи о подбрасывании монеты
Задача 1. Симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.
В таких задачах удобно выписать все возможные исходы, записывая их при помощи букв Р (решка) и О (орел). Так, исход ОР означает, что при первом броске выпал орел, а при втором – решка. В рассматриваемой задаче возможны 4 исхода: РР, РО, ОР, ОО. Благоприятствуют событию «решка выпадет ровно один раз» 2 исхода: РО и ОР. Искомая вероятность равна .
Ответ: 0,5.
Задача 2. Симметричную монету бросают трижды, Найдите вероятность того, что орел выпадет ровно два раза.
Всего возможны 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоприятствуют событию «орёл выпадет ровно два раза» 3 исхода: РОО, ОРО, ООР. Искомая вероятность равна .
Благоприятствуют событию «орёл выпадет ровно два раза» 3 исхода: РОО, ОРО, ООР. Искомая вероятность равна .
Ответ: 0,375.
Задача 3. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно один раз.
Эта задача аналогична предыдущей. Пусть каждый раз выпадение решки означает выигрыш жребия «Изумрудом» (такое предположение не влияет на вычисление вероятностей). Тогда возможны 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоприятствуют событию «решка выпадет ровно один раз» 3 исхода: РОО,ОРО,ООР. Искомая вероятность равна .
Ответ: 0,375.
Задача 4 . Симметричную монету бросают трижды. Найдите вероятность того, что наступит исход РОО (в первый раз выпадает решка, во второй и третий — орёл).
Как и в предыдущих задачах, здесь имеется 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Вероятность наступления исхода РОО равна .
Вероятность наступления исхода РОО равна .
Ответ: 0,125.
Задачи о бросках кубикаЗадача 5. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «сумма очков равна 8»?
Задача 6 . Одновременно бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.
Вообще, если бросают игральных костей (кубиков), то имеется равновозможных исходов. Столько же исходов получается, если один и тот же кубик бросают раз подряд.
Событию «в сумме выпало 4» благоприятствуют следующие исходы: 1 – 3, 2 – 2, 3 – 1. Их количество равно 3. Искомая вероятность равна .
Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Таким образом, приблизительно равна 0,083…, округлив до сотых имеем 0,08.
Ответ: 0,08
Задача 7 . Одновременно бросают три игральные кости.
Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
Исходом будем считать тройку чисел: очки, выпавшие на первой, второй и третьей игральной кости. Всего имеется равновозможных исходов. Событию «в сумме выпало 5» благоприятствуют следующие исходы: 1–1–3, 1–3–1, 3–1–1, 1–2–2, 2–1–2, 2–2–1. Их количество равно 6. Искомая вероятность равна . Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Приблизительно получаем 0,027…, округлив до сотых, имеем 0,03.Источник “Подготовка к ЕГЭ. Математика. Теория вероятностей”. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и наглядно представлять предлагаемую ситуацию. Такими задачами является большинство задач с подбрасыванием монеты и задачи с бросанием игрального кубика. Напомним классическое определение вероятности.
Вероятность события А (объективная возможность наступления события в числовом выражении) равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов: Р(А)=m/n , где:
- m – число элементарных исходов испытания, благоприятствующих появлению события А;
- n – общее число всех возможных элементарных исходов испытания.

Число возможных элементарных исходов испытания и число благоприятных исходов в рассматриваемых задачах удобно определять перебором всех возможных вариантов (комбинаций) и непосредственным подсчетом.
Из таблицы видим, что число возможных элементарных исходов n=4. Благоприятные
исходы события А = {орел выпадает 1 раз} соответствуют варианту №2 и №3 эксперимента, таких
вариантов два m=2.
Находим вероятность события Р(А)=m/n=2/4=0,5
Задача 2 . В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел не выпадет ни разу.
Решение . Поскольку монету бросают дважды, то, как и в задаче 1, число
возможных элементарных исходов n=4. Благоприятные исходы события А = {орел не выпадет ни разу}
соответствуют варианту №4 эксперимента (см. таблицу в задаче 1). Такой вариант один, значит m=1.
Находим вероятность события Р(А)=m/n=1/4=0,25
Задача 3 . В случайном эксперименте симметричную
монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.
Найдите вероятность того, что орёл выпадет ровно 2 раза.
Решение . Возможные варианты трех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
Из таблицы видим, что число возможных элементарных исходов n=8. Благоприятные
исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента.
Таких вариантов три, значит m=3.
Находим вероятность события Р(А)=m/n=3/8=0,375
Задача 4 . В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орёл выпадет ровно 3 раза.
Решение . Возможные варианты четырех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
| № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок | № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок |
| 1 | Орел | Орел | Орел | Орел | 9 | Решка | Орел | Решка | Орел |
| 2 | Орел | Решка | Решка | Решка | 10 | Орел | Решка | Орел | Решка |
| 3 | Решка | Орел | Решка | Решка | 11 | Орел | Решка | Решка | Орел |
| 4 | Решка | Решка | Орел | Решка | 12 | Орел | Орел | Орел | Решка |
| 5 | Решка | Решка | Решка | Орел | 13 | Решка | Орел | Орел | Орел |
| 6 | Орел | Орел | Решка | Решка | 14 | Орел | Решка | Орел | Орел |
| 7 | Решка | Орел | Орел | Решка | 15 | Орел | Орел | Решка | Орел |
| 8 | Решка | Решка | Орел | Орел | 16 | Решка | Решка | Решка | Решка |
Из таблицы видим, что число возможных элементарных исходов n=16. Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Находим вероятность события Р(А)=m/n=4/16=0,25
Задача 5 . Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 3 очков.
Решение . При бросании игрального кубика (правильной кости) может
выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение
от 1 до 6 точек (очков). Значит число возможных элементарных исходов n=6.
Событие А = {выпало более 3 очков} означает, что выпало 4, 5 или 6 точек (очков). Значит
число благоприятных исходов m=3.
Вероятность события Р(А)=m/n=3/6=0,5
Задача 6 . Определите вероятность того, что при бросании игрального
кубика выпало число очков, не большее 4. Результат округлите до тысячных.
Результат округлите до тысячных.
Решение . При бросании игрального кубика может выпасть любая из шести
его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 точек (очков). Значит
число возможных элементарных исходов n=6.
Событие А = {выпало не более 4 очков} означает, что выпало 4, 3, 2 или 1 точка (очко).
Значит число благоприятных исходов m=4.
Вероятность события Р(А)=m/n=4/6=0,6666…≈0,667
Задача 7 . Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.
Решение . Так как игральную кость (игральный кубик) бросают дважды, то будем рассуждать следующим образом: если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6. Получаем пары (1;1), (1;2), (1;3), (1;4), (1;5), (1;6) и так с каждой гранью. Все случаи представим в виде таблицы из 6-ти строк и 6-ти столбцов:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Благоприятные исходы события А = {оба раза выпало число, меньшее 4} (они выделены жирным)
подсчитаем и получим m=9.
Находим вероятность события Р(А)=m/n=9/36=0,25
Задача 8 . Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до тысячных.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Благоприятные исходы события А = {наибольшее из двух выпавших чисел равно 5} (они выделены жирным)
подсчитаем и получим m=8.
Находим вероятность события Р(А)=m/n=8/36=0,2222…≈0,222
Задача 9 . Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Фраза «хотя бы раз выпало число, меньшее 4» означает «число меньшее 4 выпало один раз или два раза»,
тогда число благоприятных исходов события А = {хотя бы раз выпало число, меньшее 4} (они выделены жирным)
m=27.
Находим вероятность события Р(А)=m/n=27/36=0,75
В качестве предисловия.
Все знают, что монета имеет две стороны — орёл и решку.
Нумизматы считают, что монета имеет три стороны — аверс, реверс и гурт.
И среди тех, и среди других, мало кто знает, что такое симметричная монета. Зато об этом знают (ну, или должны знать:), те, кто готовится сдавать ЕГЭ.
В общем, в этой статье речь пойдёт о необычной монете, которая, к нумизматике никакого отношения не имеет, но, при этом, является самой популярной монетой среди школьников.
Итак.
Симметричная монета — это воображаемая математически идеальная монета без размера, веса, диаметра и пр. Как следствие, гурта у такой монеты тоже нет, то есть вот она-то действительно имеет только две стороны. Главное свойство симметричной монеты в том, что при таких условиях вероятность выпадения орла или решки абсолютно одинакова. А придумали симметричную монету для проведения мысленных экспериментов.
Главное свойство симметричной монеты в том, что при таких условиях вероятность выпадения орла или решки абсолютно одинакова. А придумали симметричную монету для проведения мысленных экспериментов.
Самая популярная задача с симметричной монетой звучит так — «В случайном эксперименте симметричную монету бросают дважды (трижды, четырежды и т.д.). Требуется определить вероятность того, что одна из сторон выпадет определённое количество раз.
Ршение задачи с симметричной монетой
Понятно, что в результате броска монета упадёт либо орлом, либо решкой. Сколько раз — зависит от того, сколько бросков совершить. Вероятность выпадения орла или решки вычисляется делением количества удовлетворяющих условию исходов на общее количество возможных исходов.
Одн бросок
Здесь всё просто. Выпадет либо орёл, либо решка. Т.е. имеем два возможных исхода, один из которых нас удовлетворяет — 1/2=50%
Дваброска
За два броска могут выпасть:
два орла
две решки
орёл, затем решка
решка, затем орёл
Т. е. возможны всего четыре варианта. Задачи с более, чем одним броском, проще всего решать составлением таблицы возможных вариантов. Для простоты, обозначим орла цифрой «0», а решку цифрой «1». Тогда таблица возможных исходов будет выглядеть так:
е. возможны всего четыре варианта. Задачи с более, чем одним броском, проще всего решать составлением таблицы возможных вариантов. Для простоты, обозначим орла цифрой «0», а решку цифрой «1». Тогда таблица возможных исходов будет выглядеть так:
00
01
10
11
Если, например, нужно найти вероятность того, что орёл выпадет один раз, требуется просто подсчитать количество подходящих вариантов в таблице — т.е. тех строк, где орёл встречается один раз. Таких строк две. Значит, вероятность выпадения одного орла в двух бросках симметричной монеты равна 2/4=50%
Вероятность того, что орёл в двух бросках выпадет дважды равна 1/4=25%
Три роска
Составляем таблицу вариантов:
000
001
010
011
100
101
110
111
Те, кто знаком с двоичным исчислением, понимают, к чему мы пришли. 🙂 Да, это двоичные цифры от «0» до «7». Так проще не запутаться с вариантами.
Решим задачу из предыдущего пункта — вычислим вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется три. Значит, вероятность выпадения одного орла в трёх бросках симметричной монеты равна 3/8=37,5%
Строк, где «0» встречается один раз имеется три. Значит, вероятность выпадения одного орла в трёх бросках симметричной монеты равна 3/8=37,5%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 3/8=37,5%, т.е. абсолютно такая же.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 1/8=12,5%.
Четыр броска
Составляем таблицу вариантов:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется всего три, так же, как и в случае трёх бросков. Но, вариантов уже шестнадцать. Значит, вероятность выпадения одного орла в четырёх бросках симметричной монеты равна 3/16=18,75%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 6/8=75%,.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 4/8=50%.
Итак с увеличением количества бросков, принцип решения задачи совершенно не меняется — только, в соответствующей прогрессии, увеличивается количество вариантов.
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:
Решение задач по теории вероятностей. Учитель математики МБОУ Нивнянская СОШ, Нечаева Тамара Ивановна
2 слайд
Описание слайда:
Цели урока: рассмотреть разные виды задач по теории вероятностей и методы их решения. Задачи урока: обучить распознавать различные разновидности задач по теории вероятностей и совершенствовать логическое мышление школьников.
3 слайд
Описание слайда:
Задача 1.В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
4 слайд
Описание слайда:
Задача 2.Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
5 слайд
Описание слайда:
Задача 3.В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение: Для того чтобы найти вероятность указанного события, необходимо рассмотреть все возможные исходы эксперимента, а затем из них выбрать благоприятные исходы (благоприятные исходы – это исходы удовлетворяющие требованиям задачи). В нашем случае, благоприятными будут те исходы, в которых при двух бросаниях симметричной монеты, орел выпадет только один раз. Вероятность события вычисляется как отношение количества благоприятных исходов к общему количеству исходов. Следовательно, вероятность того, что при двух кратном бросании симметричной монеты орел выпадет только один раз, равна: Р=2/4=0,5=50% Ответ: вероятность того, что в результате проведения вышеописанного эксперимента орел выпадет только один раз равна 50%. Номер эксперимента 1-ый бросок 2-ой бросок Сколько раз выпал орел 1 Орел Орел 2 2 Решка Решка 0 3 Орел Решка 1 4 Решка Орел 1
Найдите вероятность того, что орел выпадет ровно один раз. Решение: Для того чтобы найти вероятность указанного события, необходимо рассмотреть все возможные исходы эксперимента, а затем из них выбрать благоприятные исходы (благоприятные исходы – это исходы удовлетворяющие требованиям задачи). В нашем случае, благоприятными будут те исходы, в которых при двух бросаниях симметричной монеты, орел выпадет только один раз. Вероятность события вычисляется как отношение количества благоприятных исходов к общему количеству исходов. Следовательно, вероятность того, что при двух кратном бросании симметричной монеты орел выпадет только один раз, равна: Р=2/4=0,5=50% Ответ: вероятность того, что в результате проведения вышеописанного эксперимента орел выпадет только один раз равна 50%. Номер эксперимента 1-ый бросок 2-ой бросок Сколько раз выпал орел 1 Орел Орел 2 2 Решка Решка 0 3 Орел Решка 1 4 Решка Орел 1
6 слайд
Описание слайда:
Задача 4. Игральный кубик бросили один раз. Какова вероятность того, что выпало число очков, большее чем 4. Решение: Случайный эксперимент – бросание кубика. Элементарное событие – число на выпавшей грани. Ответ:1/3 Всего граней: 1, 2, 3, 4, 5, 6 Элементарные события: N=6 N(A)=2
Какова вероятность того, что выпало число очков, большее чем 4. Решение: Случайный эксперимент – бросание кубика. Элементарное событие – число на выпавшей грани. Ответ:1/3 Всего граней: 1, 2, 3, 4, 5, 6 Элементарные события: N=6 N(A)=2
7 слайд
Описание слайда:
Задача 5. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых. Решение: Вероятность попадания = 0,8 Вероятность промаха = 1 — 0,8 = 0,2 А={попал, попал, попал, промахнулся, промахнулся} По формуле умножения вероятностей Р(А)= 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 Р(А)= 0,512 ∙ 0,04 = 0,02048 ≈ 0,02 Ответ: 0,02
8 слайд
Описание слайда:
Задача 6.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Ответ округлите до сотых Решение: Элементарный исход в этом опыте – упорядоченная пара чисел. Первое число выпадет на первом кубике, второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют количеству очков на первом кубике, столбцы –на втором кубике. Всего элементарных событий п = 36. Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6. Таких ячеек 5. Значит, событию А = {сумма выпавших очков равна 6} благоприятствует 5 элементарных исходов. Следовательно, т = 5. Поэтому, Р(А) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
Первое число выпадет на первом кубике, второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют количеству очков на первом кубике, столбцы –на втором кубике. Всего элементарных событий п = 36. Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6. Таких ячеек 5. Значит, событию А = {сумма выпавших очков равна 6} благоприятствует 5 элементарных исходов. Следовательно, т = 5. Поэтому, Р(А) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
9 слайд
Описание слайда:
Формула вероятности Теорема Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле: Где Cnk — число сочетаний из n элементов по k, которое считается по формуле:
10 слайд
Описание слайда:
Задача 7. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза. Решение По условию задачи, всего бросков было n =4. Требуемое число орлов: k =3. Подставляем n и k в формулу: С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же. Ответ: 0,25
Решение По условию задачи, всего бросков было n =4. Требуемое число орлов: k =3. Подставляем n и k в формулу: С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же. Ответ: 0,25
11 слайд
Описание слайда:
Задача 8. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу. Решение Снова выписываем числа n и k. Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу: Напомню, что 0! = 1 по определению. Поэтому C30 = 1. Ответ: 0,125
12 слайд
Описание слайда:
Задача 9.В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка. Решение: Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий. Пусть p1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем: Теперь найдем p2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем: Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
Тогда n = 4, k = 3. Имеем: Теперь найдем p2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем: Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
13 слайд
Описание слайда:
Задача 10.Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры. Решение. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда нахо дим: 0,5·0,5·0,5 = 0,125. Ответ: 0,125.
Вероятность каждого из них равна 0,5, откуда нахо дим: 0,5·0,5·0,5 = 0,125. Ответ: 0,125.
Использование предлога in в английском языке
Употребление и произношение in
|
В случайном эксперте симметричную монету бросают дважды.
 Математика и мы
Математика и мыВ задачах по теории вероятностей, которые представлены в ЕГЭ номером №4, кроме , встречаются задачи на подбрасывание монеты и о бросках кубика. Их сегодня мы и разберем.
Задачи о подбрасывании монеты
Задача 1. Симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.
В таких задачах удобно выписать все возможные исходы, записывая их при помощи букв Р (решка) и О (орел). Так, исход ОР означает, что при первом броске выпал орел, а при втором – решка. В рассматриваемой задаче возможны 4 исхода: РР, РО, ОР, ОО. Благоприятствуют событию «решка выпадет ровно один раз» 2 исхода: РО и ОР. Искомая вероятность равна .
Ответ: 0,5.
Задача 2. Симметричную монету бросают трижды, Найдите вероятность того, что орел выпадет ровно два раза.
Всего возможны 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоприятствуют событию «орёл выпадет ровно два раза» 3 исхода: РОО, ОРО, ООР. Искомая вероятность равна .
Искомая вероятность равна .
Ответ: 0,375.
Задача 3. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно один раз.
Эта задача аналогична предыдущей. Пусть каждый раз выпадение решки означает выигрыш жребия «Изумрудом» (такое предположение не влияет на вычисление вероятностей). Тогда возможны 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоприятствуют событию «решка выпадет ровно один раз» 3 исхода: РОО,ОРО,ООР. Искомая вероятность равна .
Ответ: 0,375.
Задача 4 . Симметричную монету бросают трижды. Найдите вероятность того, что наступит исход РОО (в первый раз выпадает решка, во второй и третий — орёл).
Как и в предыдущих задачах, здесь имеется 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Вероятность наступления исхода РОО равна .
Вероятность наступления исхода РОО равна .
Ответ: 0,125.
Задачи о бросках кубикаЗадача 5. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «сумма очков равна 8»?
Задача 6 . Одновременно бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.
Вообще, если бросают игральных костей (кубиков), то имеется равновозможных исходов. Столько же исходов получается, если один и тот же кубик бросают раз подряд.
Событию «в сумме выпало 4» благоприятствуют следующие исходы: 1 – 3, 2 – 2, 3 – 1. Их количество равно 3. Искомая вероятность равна .
Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Таким образом, приблизительно равна 0,083…, округлив до сотых имеем 0,08.
Ответ: 0,08
Задача 7 . Одновременно бросают три игральные кости.
Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
Исходом будем считать тройку чисел: очки, выпавшие на первой, второй и третьей игральной кости. Всего имеется равновозможных исходов. Событию «в сумме выпало 5» благоприятствуют следующие исходы: 1–1–3, 1–3–1, 3–1–1, 1–2–2, 2–1–2, 2–2–1. Их количество равно 6. Искомая вероятность равна . Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Приблизительно получаем 0,027…, округлив до сотых, имеем 0,03.Источник “Подготовка к ЕГЭ. Математика. Теория вероятностей”. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
Формулировка задачи: В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл (решка) не выпадет ни разу (выпадет ровно/хотя бы 1, 2 раза).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 10 (Классическое определение вероятности).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых нет ни одного орла. Такая комбинация всего одна (РР).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 2:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно два раза.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадает ровно 2 раза. Такая комбинация всего одна (ОО).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 3:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпал ровно 1 раз. Таких комбинаций всего две (ОР и РО).
Ответ: 0.5
Пример задачи 4:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадет хотя бы 1 раз. Таких комбинаций всего три (ОО, ОР и РО).
P = 3 / 4 = 0.75
В качестве предисловия.
Все знают, что монета имеет две стороны — орёл и решку.
Нумизматы считают, что монета имеет три стороны — аверс, реверс и гурт.
И среди тех, и среди других, мало кто знает, что такое симметричная монета. Зато об этом знают (ну, или должны знать:), те, кто готовится сдавать ЕГЭ.
В общем, в этой статье речь пойдёт о необычной монете, которая, к нумизматике никакого отношения не имеет, но, при этом, является самой популярной монетой среди школьников.
Итак.
Симметричная монета — это воображаемая математически идеальная монета без размера, веса, диаметра и пр. Как следствие, гурта у такой монеты тоже нет, то есть вот она-то действительно имеет только две стороны. Главное свойство симметричной монеты в том, что при таких условиях вероятность выпадения орла или решки абсолютно одинакова. А придумали симметричную монету для проведения мысленных экспериментов.
Самая популярная задача с симметричной монетой звучит так — «В случайном эксперименте симметричную монету бросают дважды (трижды, четырежды и т.д.). Требуется определить вероятность того, что одна из сторон выпадет определённое количество раз.
Ршение задачи с симметричной монетой
Понятно, что в результате броска монета упадёт либо орлом, либо решкой. Сколько раз — зависит от того, сколько бросков совершить. Вероятность выпадения орла или решки вычисляется делением количества удовлетворяющих условию исходов на общее количество возможных исходов.
Одн бросок
Здесь всё просто. Выпадет либо орёл, либо решка. Т.е. имеем два возможных исхода, один из которых нас удовлетворяет — 1/2=50%
Дваброска
За два броска могут выпасть:
два орла
две решки
орёл, затем решка
решка, затем орёл
Т.е. возможны всего четыре варианта. Задачи с более, чем одним броском, проще всего решать составлением таблицы возможных вариантов. Для простоты, обозначим орла цифрой «0», а решку цифрой «1». Тогда таблица возможных исходов будет выглядеть так:
00
01
10
11
Если, например, нужно найти вероятность того, что орёл выпадет один раз, требуется просто подсчитать количество подходящих вариантов в таблице — т. е. тех строк, где орёл встречается один раз. Таких строк две. Значит, вероятность выпадения одного орла в двух бросках симметричной монеты равна 2/4=50%
е. тех строк, где орёл встречается один раз. Таких строк две. Значит, вероятность выпадения одного орла в двух бросках симметричной монеты равна 2/4=50%
Вероятность того, что орёл в двух бросках выпадет дважды равна 1/4=25%
Три роска
Составляем таблицу вариантов:
000
001
010
011
100
101
110
111
Те, кто знаком с двоичным исчислением, понимают, к чему мы пришли. 🙂 Да, это двоичные цифры от «0» до «7». Так проще не запутаться с вариантами.
Решим задачу из предыдущего пункта — вычислим вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется три. Значит, вероятность выпадения одного орла в трёх бросках симметричной монеты равна 3/8=37,5%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 3/8=37,5%, т.е. абсолютно такая же.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 1/8=12,5%.
Четыр броска
Составляем таблицу вариантов:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется всего три, так же, как и в случае трёх бросков. Но, вариантов уже шестнадцать. Значит, вероятность выпадения одного орла в четырёх бросках симметричной монеты равна 3/16=18,75%
Строк, где «0» встречается один раз имеется всего три, так же, как и в случае трёх бросков. Но, вариантов уже шестнадцать. Значит, вероятность выпадения одного орла в четырёх бросках симметричной монеты равна 3/16=18,75%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 6/8=75%,.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 4/8=50%.
Итак с увеличением количества бросков, принцип решения задачи совершенно не меняется — только, в соответствующей прогрессии, увеличивается количество вариантов.
В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и наглядно представлять предлагаемую ситуацию. Такими задачами является большинство задач с подбрасыванием монеты и задачи с бросанием игрального кубика. Напомним классическое определение вероятности.
Вероятность события А (объективная возможность наступления события в числовом выражении) равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов: Р(А)=m/n , где:
- m – число элементарных исходов испытания, благоприятствующих появлению события А;
- n – общее число всех возможных элементарных исходов испытания.

Число возможных элементарных исходов испытания и число благоприятных исходов в рассматриваемых задачах удобно определять перебором всех возможных вариантов (комбинаций) и непосредственным подсчетом.
Из таблицы видим, что число возможных элементарных исходов n=4. Благоприятные
исходы события А = {орел выпадает 1 раз} соответствуют варианту №2 и №3 эксперимента, таких
вариантов два m=2.
Находим вероятность события Р(А)=m/n=2/4=0,5
Задача 2 . В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел не выпадет ни разу.
Решение . Поскольку монету бросают дважды, то, как и в задаче 1, число
возможных элементарных исходов n=4. Благоприятные исходы события А = {орел не выпадет ни разу}
соответствуют варианту №4 эксперимента (см. таблицу в задаче 1). Такой вариант один, значит m=1.
Находим вероятность события Р(А)=m/n=1/4=0,25
Задача 3 . В случайном эксперименте симметричную
монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.
Найдите вероятность того, что орёл выпадет ровно 2 раза.
Решение . Возможные варианты трех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
Из таблицы видим, что число возможных элементарных исходов n=8. Благоприятные
исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента.
Таких вариантов три, значит m=3.
Находим вероятность события Р(А)=m/n=3/8=0,375
Задача 4 . В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орёл выпадет ровно 3 раза.
Решение . Возможные варианты четырех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
| № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок | № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок |
| 1 | Орел | Орел | Орел | Орел | 9 | Решка | Орел | Решка | Орел |
| 2 | Орел | Решка | Решка | Решка | 10 | Орел | Решка | Орел | Решка |
| 3 | Решка | Орел | Решка | Решка | 11 | Орел | Решка | Решка | Орел |
| 4 | Решка | Решка | Орел | Решка | 12 | Орел | Орел | Орел | Решка |
| 5 | Решка | Решка | Решка | Орел | 13 | Решка | Орел | Орел | Орел |
| 6 | Орел | Орел | Решка | Решка | 14 | Орел | Решка | Орел | Орел |
| 7 | Решка | Орел | Орел | Решка | 15 | Орел | Орел | Решка | Орел |
| 8 | Решка | Решка | Орел | Орел | 16 | Решка | Решка | Решка | Решка |
Из таблицы видим, что число возможных элементарных исходов n=16. Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Находим вероятность события Р(А)=m/n=4/16=0,25
Задача 5 . Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 3 очков.
Решение . При бросании игрального кубика (правильной кости) может
выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение
от 1 до 6 точек (очков). Значит число возможных элементарных исходов n=6.
Событие А = {выпало более 3 очков} означает, что выпало 4, 5 или 6 точек (очков). Значит
число благоприятных исходов m=3.
Вероятность события Р(А)=m/n=3/6=0,5
Задача 6 . Определите вероятность того, что при бросании игрального
кубика выпало число очков, не большее 4. Результат округлите до тысячных.
Результат округлите до тысячных.
Решение . При бросании игрального кубика может выпасть любая из шести
его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 точек (очков). Значит
число возможных элементарных исходов n=6.
Событие А = {выпало не более 4 очков} означает, что выпало 4, 3, 2 или 1 точка (очко).
Значит число благоприятных исходов m=4.
Вероятность события Р(А)=m/n=4/6=0,6666…≈0,667
Задача 7 . Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.
Решение . Так как игральную кость (игральный кубик) бросают дважды, то будем рассуждать следующим образом: если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6. Получаем пары (1;1), (1;2), (1;3), (1;4), (1;5), (1;6) и так с каждой гранью. Все случаи представим в виде таблицы из 6-ти строк и 6-ти столбцов:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Благоприятные исходы события А = {оба раза выпало число, меньшее 4} (они выделены жирным)
подсчитаем и получим m=9.
Находим вероятность события Р(А)=m/n=9/36=0,25
Задача 8 . Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до тысячных.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Благоприятные исходы события А = {наибольшее из двух выпавших чисел равно 5} (они выделены жирным)
подсчитаем и получим m=8.
Находим вероятность события Р(А)=m/n=8/36=0,2222…≈0,222
Задача 9 . Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Фраза «хотя бы раз выпало число, меньшее 4» означает «число меньшее 4 выпало один раз или два раза»,
тогда число благоприятных исходов события А = {хотя бы раз выпало число, меньшее 4} (они выделены жирным)
m=27.
Находим вероятность события Р(А)=m/n=27/36=0,75
Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:
где p — искомая вероятность, k — число устраивающих нас событий, n — общее число возможных событий.
Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n . В этом и состоит вся сложность.
Тем не менее, существует как минимум два принципиально различных метода решения:
- Метод перебора комбинаций — стандартный алгоритм.
 Выписываются все комбинации орлов и решек, после чего выбираются нужные;
Выписываются все комбинации орлов и решек, после чего выбираются нужные; - Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.
Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!
Метод перебора комбинаций
Этот метод еще называется «решение напролом». Состоит из трех шагов:
- Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n ;
- Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k ;
- Осталось найти вероятность: p = k : n .
К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации.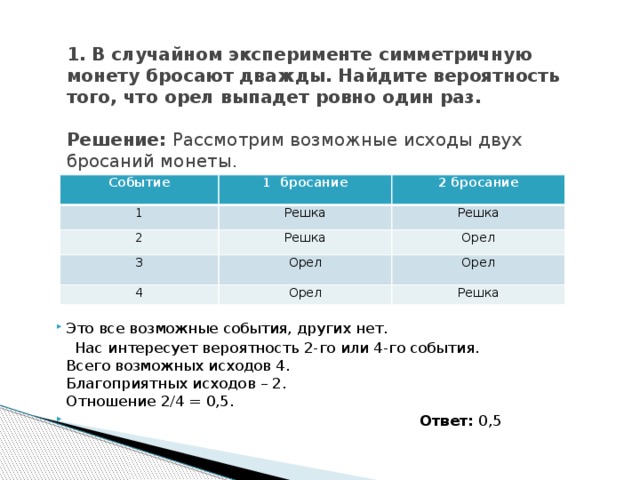 Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:
Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:
Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):
Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:
Таких вариантов оказалось k = 2. Находим вероятность:
Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем все возможные комбинации орлов и решек:
OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP
Всего получилось n = 16 вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:
Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.
Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.
Специальная формула вероятности
Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:
Где C n k — число сочетаний из n элементов по k , которое считается по формуле:
Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.
Задача.
Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:
Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем числа n и k . Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:
Напомню, что 0! = 1 по определению. Поэтому C 3 0 = 1.
Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.
Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.
Пусть p 1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем:
Теперь найдем p
2 — вероятность того, что орел выпадет все 4 раза. В этом случае n
= 4, k
= 4. Имеем:
В этом случае n
= 4, k
= 4. Имеем:
Чтобы получить ответ, осталось сложить вероятности p 1 и p 2 . Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:
p = p 1 + p 2 = 0,25 + 0,0625 = 0,3125
Понравилась статья? Поделись с друзьями:
11 класс контрольная работы по математике на тему Элементы теории вероятностей 14 вариантов
Вариант 1
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно один раз.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 130 качественных сумок приходится пять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45 этих стекол, вторая — 55 . Первая фабрика выпускает 1 бракованных стекол, а вторая — 5 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Первая фабрика выпускает 45 этих стекол, вторая — 55 . Первая фабрика выпускает 1 бракованных стекол, а вторая — 5 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В аэропорте два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 2
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 110 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70 этих стекол, вторая — 30 . Первая фабрика выпускает 3 бракованных стекол, а вторая — 1 Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В аэропорту два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 3
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 110 качественных сумок приходится пять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45 этих стекол, вторая — 55 . Первая фабрика выпускает 1 бракованных стекол, а вторая — 3 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 4
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 120 качественных сумок приходится девять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70 этих стекол, вторая — 30 . Первая фабрика выпускает 5 бракованных стекол, а вторая — 4 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Первая фабрика выпускает 70 этих стекол, вторая — 30 . Первая фабрика выпускает 5 бракованных стекол, а вторая — 4 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В аэропорте два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,37. Вероятность того, что чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 5
В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что орел выпадет ровно 4 раза.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 14 очков. Результат округлите до сотых.
Найдите вероятность того, что в сумме выпадет 14 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 200 качественных сумок приходится четыре сумки со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 65 этих стекол, вторая — 35 . Первая фабрика выпускает 5 бракованных стекол, а вторая — 3 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,3. Вероятность того, что чай закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 6
В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что орел выпадет все 5 раз.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 15 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 60 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,98. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
0,02 0,98
0,98 0,04
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,23. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 7
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что наступит исход РРР (все три раза выпадает решка).
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 12 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится одна сумка со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
В среднем на 80 качественных сумок приходится одна сумка со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,01. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 8
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно один раз.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 130 качественных сумок приходится пять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45 этих стекол, вторая — 55 . Первая фабрика выпускает 1 бракованных стекол, а вторая — 5 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 9
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что решка выпадет два раза.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 110 качественных сумок приходится пять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45 этих стекол, вторая — 55 . Первая фабрика выпускает 1 бракованных стекол, а вторая — 3 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 10
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет два раза.
Найдите вероятность того, что орел выпадет два раза.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 11 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 120 качественных сумок приходится девять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70 этих стекол, вторая — 30 . Первая фабрика выпускает 6 бракованных стекол, а вторая — 4 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В аэропорту два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,33. Вероятность того, что чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 11
В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что орел выпадет ровно 3 раза.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 14 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 210 качественных сумок приходится четыре сумки со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,01. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,02. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,02. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 12
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет два раза.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 11 очков. Результат округлите до сотых.
Найдите вероятность того, что в сумме выпадет 11 очков. Результат округлите до сотых.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,95. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 66 теннисистов, среди которых 14 участников из России, в том числе Антон Переделкин. Найдите вероятность того, что в первом туре Антон Переделкин будет играть с каким-либо теннисистом из России?
Вероятность того, что авторучка бракованная, равна 0,04. Покупатель в магазине выбирает случайную упаковку, в которой две таких авторучки. Найдите вероятность того, что обе авторучки окажутся исправными.
Найдите вероятность того, что обе авторучки окажутся исправными.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 13
В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орел выпадет два раза.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 120 качественных сумок приходится девять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70 этих стекол, вторая — 30 . Первая фабрика выпускает 5 бракованных стекол, а вторая — 6 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Первая фабрика выпускает 5 бракованных стекол, а вторая — 6 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 шахматистов, среди которых 4 участника из России, в том числе Александр Ефимов. Найдите вероятность того, что в первом туре Александр Ефимов будет играть с каким-либо шахматистом из России?
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Вариант 14
В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что решка выпадет ровно 4 раза.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 15 очков. Результат округлите до сотых.
Найдите вероятность того, что в сумме выпадет 15 очков. Результат округлите до сотых.
Фабрика выпускает сумки. В среднем на 190 качественных сумок приходится четыре сумки со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 65 этих стекол, вторая — 35 . Первая фабрика выпускает 4 бракованных стекол, а вторая — 3 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,31. Вероятность того, что чай закончится в обоих автоматах, равна 0,11. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
Нормальную монету подбрасывают три раза, какова вероятность того, что выпадет три орла?
2112 просмотровЧестную монету подбрасывают три раза, какова вероятность того, что выпадет три орла?
- монета
- подбрасывание
- вероятность
- голов
- решки
- последовательно
- событий
1 Ответ
0 нравится 0 не нравится
Возможные результаты: S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Независимые события, поэтому P(H H H) = P(H).P(H).P(H) = ½ x ½ х ½ = (1/8)
ответил по ♦КТ Алмаз (49 174 балла)Похожие вопросы
Предположим, вы взяли чистую монету и подбросили ее пять раз. Если выпало пять орлов, более вероятно, что при следующем броске выпадет орел или решка? Объяснять.
спросил 23 июня 2020 г. в науке о данных и статистике по Джошуа Мванза Алмаз (53 024 балла) | 395 просмотров
- вероятность
- монета
- результатов
- голов
- решки
- ярмарка
- тест
Какова выборочная площадь $S$, когда мы бросаем монету 3 раза?
спросил 22 мая 2021 г. в науке о данных и статистике по Томас | 290 просмотров
- пробел
- образец
- голов
- решки
- подбрасывание
- монета
- вероятность
Монету подбрасывают дважды, найдите вероятность того, что выпадет два орла.
спросил
6 марта 2019 г. в науке о данных и статистике
по
♦МатематикаГи
Платина
(136 794 балла)
|
1552 просмотра
в науке о данных и статистике
по
♦МатематикаГи
Платина
(136 794 балла)
|
1552 просмотра
- головок
- решки
- монета
- бросить
- вероятность
Роза дважды подбросит правильную монету. Если вы знаете, что при первом подбрасывании монеты выпал орел, какова вероятность того, что обе монеты выпадут орлом?
спросил 23 сент. 2020 г. в науке о данных и статистике по Ученик Серебряный статус (11 226 баллов) | 632 просмотра
- вероятность
- результатов
- голов
- монета
- решки
- ярмарка
- тест
Предположим, что монету подбрасывают 3 раза. Какова вероятность получить ровно одну голову?
спросил 16 января в науке о данных и статистике по ♦Гаусс Алмаз (64 437 баллов) | 223 просмотра
- вероятность
- результатов
- монета
- голов
- решки
- ярмарка
- тест
Монета подбрасывается 3 раза. Какова вероятность того, что броски будут одинаковыми?
Какова вероятность того, что броски будут одинаковыми?
спросил 16 января в науке о данных и статистике по ♦Гаусс Алмаз (64 437 баллов) | 581 просмотр
- вероятность
- монета
- результатов
- ярмарка
- решки
- голов
- тест
В коробке три монеты: две обычные монеты и одна фальшивая монета с обеими сторонами, отмеченными решкой. Если монету взять наугад и подбросить, какова вероятность того, что выпадет решка?
спросил 11 августа по математике по ♦МатематикаГи Платина (136 794 балла) | 57 просмотров
- вероятность
- голов
- ярмарка
- вычислить
- результатов
- монета
- решки
Каково пространство выборки при подбрасывании монеты?
спросил 22 июля в науке о данных и статистике по ♦Гаусс Алмаз (64 437 баллов) | 31 просмотр
- образец
- пробел
- голов
- решки
- подбрасывание
- вероятность
Учитывая, что вы видите 10 решек, какова вероятность того, что при следующем подбрасывании этой монеты тоже выпадет решка?
спросил
28 июля 2020 г. в науке о данных и статистике
по
♦МатематикаГи
Платина
(136 794 балла)
|
239 просмотров
в науке о данных и статистике
по
♦МатематикаГи
Платина
(136 794 балла)
|
239 просмотров
- вероятность
- голов
- результатов
- монета
- решки
- ярмарка
- тест
Подбрасывается монета. Скажи мне, что такое пространство выборки?
спросил 22 июня 2020 г. в науке о данных и статистике по Джошуа Мванза Алмаз (53 024 балла) | 175 просмотров
- образец
- пробел
- с
- голов
- решки
- подбрасывание
Три монеты подброшены 200 раз. Количество раз, когда выпадет 2 орла, равно 72. Тогда вероятность того, что выпадет 2 орла, равна:
спросил 13 мая 2021 г. в науке о данных и статистике по ♦МатематикаГи Платина (136 794 балла) | 387 просмотров
- монет
- бросил
- вероятность
- голов
- событий
Монета подбрасывается 1000 раз, и 560 раз выпадает орёл. Считаете ли вы монету необъективной?
Считаете ли вы монету необъективной?
спросил 11 марта 2019 г. в науке о данных и статистике по Эдзай Звонво Бронзовый статус (9488 баллов) | 1893 просмотра
- монета
- флип
- голов
- вероятность
- смещение
Монета подбрасывается 10 раз, выпадает 2 решки и 8 решек. Как вы будете анализировать, честная монета или нет? Каково значение p для того же самого?
спросил 11 марта 2019 г. в науке о данных и статистике по Эдзай Звонво Бронзовый статус (9488 баллов) | 1252 просмотра
- р-значение
- монета
- вероятность
- раздача
Подбрасываются три беспристрастные монеты. Какова вероятность того, что выпадет не более двух орлов?
спросил 6 марта 2019 г. в науке о данных и статистике по ♦МатематикаГи Платина (136 794 балла) | 1382 просмотра
- беспристрастный
- монет
- вероятность
- голов
- статистика
Монета подбрасывается 3 раза. Найдите вероятность того, что выпадет: (а) все орлы (б) 2 орла и 1 решка
Найдите вероятность того, что выпадет: (а) все орлы (б) 2 орла и 1 решка
спросил 22 июня 2020 г. в науке о данных и статистике по Джошуа Мванза Алмаз (53 024 балла) | 7054 просмотра
- вероятность
- монета
- результатов
- взаимоисключающие
- зависимый
- независимый
Просто подбрось монетку! Мгновенный бросок монеты 50/50. Орел или решка?
С 2010 года Just Flip A Coin является оригинальным веб-симулятором подбрасывания монеты. Этот быстрый и простой в использовании инструмент использует код, который генерирует истинные случайные результаты 50/50. Чтобы играть, просто нажмите / коснитесь монеты. После того, как вы перевернете, проверьте свой номер переворота! Нажмите / коснитесь цветных полей, чтобы выбрать свою любимую цветовую схему. Давай, листай сколько душе угодно!
- Выбор между двумя вариантами
- Играем в орёл или решку с друзьями
- Принятие решений «да» или «нет»
- Определение того, какая команда ходит первой в игре
- Разрешение спора между двумя игроками
- Определение победителя ничьей
- Выбор делать что-то или нет
- Альтернатива игре «Камень, ножницы, бумага»
- Решить, какой из двух фильмов или сериалов посмотреть
- Обучение детей и студентов природе вероятности
- Делать выбор в фэнтезийных лигах
Назад к монете!
История подбрасывания монеты
Металлические монеты были впервые изготовлены еще в 7 веке до нашей эры, однако первые упоминания о практике подбрасывания монет можно найти в Древнем Риме. В этот период римляне называли игру «navia aut caput», что переводится как «корабль или голова». Это связано с тем, что на некоторых римских монетах с одной стороны был изображен корабль, а с другой — голова (или «бюст») императора. Сам Юлий Цезарь одобрил подбрасывание монеты в 49 г.до н.э., когда он начал чеканить монеты с изображением его имени. В это время флипы использовались для принятия очень серьезных решений, в том числе связанных с преступностью, собственностью и браком. Результаты этих бросков считались юридически обязательными.
В этот период римляне называли игру «navia aut caput», что переводится как «корабль или голова». Это связано с тем, что на некоторых римских монетах с одной стороны был изображен корабль, а с другой — голова (или «бюст») императора. Сам Юлий Цезарь одобрил подбрасывание монеты в 49 г.до н.э., когда он начал чеканить монеты с изображением его имени. В это время флипы использовались для принятия очень серьезных решений, в том числе связанных с преступностью, собственностью и браком. Результаты этих бросков считались юридически обязательными.
Позже в истории британцы назвали игру «крест и куча». В то время на многих монетах с одной стороны был изображен крест. «Куча» происходит от среднеанглийского термина, означающего «реверс монеты». В Перу игра до сих пор называется «морда или тюлень»! В Древнем Китае игра была известна как «корабль или голова». Это потому, что древние китайские монеты чеканились с кораблем на одной стороне и головой на другой.
Хотя фактическое происхождение подбрасывания монеты является предметом споров, многие историки считают, что оно возникло в Древней Греции. Считается, что игроки покрывали одну сторону раковины черным или очень темно-коричневым веществом, называемым «черная смола» — смолистой слизью, которую получают из деревьев. Другая сторона скорлупы сохранит свой первоначальный цвет. Затем игроки подбрасывали снаряд в воздухе и называли правильную сторону, как мы делаем сейчас!
Считается, что игроки покрывали одну сторону раковины черным или очень темно-коричневым веществом, называемым «черная смола» — смолистой слизью, которую получают из деревьев. Другая сторона скорлупы сохранит свой первоначальный цвет. Затем игроки подбрасывали снаряд в воздухе и называли правильную сторону, как мы делаем сейчас!
Сегодня практику подбрасывания монет можно встретить во всем мире. Многие виды спорта, такие как футбол (как американский, так и неамериканский варианты), киберспорт, крикет, теннис и фехтование, подбрасывают монету, чтобы определить, какая команда идет первой в матче, или определить победителя в случае ничьей. В политике флип иногда используется для определения результатов выборов в случае, если два кандидата получают одинаковое количество голосов. Иногда даже ученые подбрасывают монетку, чтобы определить порядок перечисления авторов для использования в академических публикациях.
Вернуться к монете!
Психология подбрасывания монеты
Люди часто сталкиваются с трудным выбором между двумя вариантами. Бросание монеты может быть очень полезным в таких ситуациях. Однако иногда вы можете обнаружить, что разочарованы результатом. В этом сценарии, вместо того, чтобы позволить монете решать, вы можете выбрать тот вариант, который, как вы теперь понимаете, вы действительно хотели.
Бросание монеты может быть очень полезным в таких ситуациях. Однако иногда вы можете обнаружить, что разочарованы результатом. В этом сценарии, вместо того, чтобы позволить монете решать, вы можете выбрать тот вариант, который, как вы теперь понимаете, вы действительно хотели.
На самом деле, говорят, что сам Зигмунд Фрейд осознал это явление и использовал его в своих интересах. Столкнувшись с кем-то, кто изо всех сил пытался принять решение, Фрейд иногда предлагал подбросить монетку. Якобы тогда Фрейд сказал: «Посмотрите на свои собственные реакции. Спросите себя: доволен ли я? Я разочарован?» Этот метод подбрасывания иногда называют подбрасыванием монеты по Фрейду. Анализируя свою реакцию, вы можете понять, что действительно знали, какой выбор хотели сделать!
В свою книгу под названием Grooks датский поэт Пит Хейн включил стихотворение под названием «Психологический совет», которое относится к фрейдистскому подбрасыванию монеты. Стихотворение звучит так:
Всякий раз, когда вас призывают принять решение,
И вам мешает его отсутствие,
Лучший способ решить дилемму, вы найдете,
Просто крутить пенни.
Нет, не так, чтобы случай решил дело.
Пока ты пассивно стоишь и хандришь;
Но в тот момент, когда пенни висит в воздухе,
Вы вдруг понимаете, на что надеетесь.
Вернуться к монете!
Известные броски монет
Название Портленд, штат Орегон
Один из самых известных бросков в истории произошел в 1845 году с монетой в один цент. Два основателя города Портленда, Фрэнсис Петтигроув и Аса Лавджой, оба хотели назвать территорию площадью 640 акров, которая в то время называлась Клиринг. Они решили оставить права на название на волю случая, подбрасывая монету по принципу «лучший из трех». Петтигроув победил и назвал город Портленд в честь своего родного города Портленд, штат Мэн. Историческая монета позже была названа Портлендским пенни.
Выбор первого летного пилота
14 декабря 1903 года братья Райт (Уилбур и Орвилл) готовились к первому в мире полету на аппарате тяжелее воздуха. Чтобы определить, кто первым поведет самолет, Уилбур вытащил из кармана монету и подбросил ее в воздух. Он приземлился в пользу Уилбура, дав ему первый шанс летать. К несчастью для Уилбура, эта первая попытка закончилась аварией после полета всего 3,5 секунды. Через три дня настала очередь Орвилла, и наконец-то был совершен первый успешный полет.
Он приземлился в пользу Уилбура, дав ему первый шанс летать. К несчастью для Уилбура, эта первая попытка закончилась аварией после полета всего 3,5 секунды. Через три дня настала очередь Орвилла, и наконец-то был совершен первый успешный полет.
1966-1984 драфты НБА
До того, как в 1985 году была введена система лотереи, подбрасывание монеты между худшими командами в каждой конференции определяло, кто получит первый выбор на драфте. Карьеры многих самых известных игроков лиги навсегда изменились после жеребьевки, включая Карима Абдул-Джаббара, Майкла Джордана и Мэджика Джонсона среди других легенд.
День, когда умерла музыка
3 февраля 1959 года Бадди Холли, Ричи Валенс и Дж. П. Ричардсон попали в авиакатастрофу, которая стоила им жизни. Если бы не подбрасывание монеты, жизнь Валента была бы сохранена. Перед полетом гитарист Валенса и Холли (Томми Оллсап) подбросил монетку, чтобы определить, кто полетит на самолете, зафрахтованном Холли. Валент победил, а все остальное — печальная история. В 1971-летний Дон Маклин увековечил этот день как «День, когда умерла музыка» в своем хите «Американский пирог».
В 1971-летний Дон Маклин увековечил этот день как «День, когда умерла музыка» в своем хите «Американский пирог».
Секретариат, лошадь Тройной Короны
В 1969 году, за четыре года до того, как Секретариат претендовал на Тройную Корону, Пенни Ченери и Огден Фиппс подбросили монетку, чтобы получить первого жеребенка от знаменитой скаковой лошади Смелого Рулера. Фиппс выиграл жеребьевку, отказался от Секретариата и выбрал другого жеребенка, решение, которое дорого обошлось. Секретариат Ченери впоследствии стал одной из самых известных лошадей в истории, установив несколько рекордов, которые стоят до сих пор.
Вернуться к монете!
Часто задаваемые вопросы
Что такое подбрасывание монеты?
Подбрасывание монеты (также известное как подбрасывание монеты, подбрасывание монеты или «орел или решка») — это игра, в которой монета подбрасывается в воздух движением большого пальца, заставляя ее вращаться ребро за ребро быстро. Как правило, пока монета находится в воздухе, кто-то (либо флиппер, либо другой игрок) выкрикивает «Орел» или «Решка» до того, как она приземлится. Монета упадет орлом или решкой вверх, и победит тот, кто назовет правильную сторону!
Монета упадет орлом или решкой вверх, и победит тот, кто назовет правильную сторону!
Действительно ли подбрасывание монетки дает результаты 50/50?
Да. Just Flip A Coin использует код javascript, который генерирует настоящие случайные результаты 50/50.
Что такое подбрасывание монеты втроем?
Подбрасывание втроем отлично подходит для принятия решения «два из трех» или «один из трех». Вот как:
- Два из трех: подбросьте монету три раза. Если два броска приводят к одному и тому же результату, тот, который отличается, проигрывает. Если все три броска одинаковые, игра повторяется до тех пор, пока результаты не будут различаться.
- Один из трех: Как и в случае подбрасывания монеты два из трех, подбросьте монету три раза. Какой бы флип ни был другим, тот и выиграл!
Что представляет собой австралийская версия подбрасывания монеты «двойка»?
В Австралии существует версия игры, которая называется «Two Up», иногда пишется как «Two-Up». В этой игре монета подбрасывается два раза. Цель состоит в том, чтобы угадать, приведут ли два броска к одному из следующих результатов:
В этой игре монета подбрасывается два раза. Цель состоит в том, чтобы угадать, приведут ли два броска к одному из следующих результатов:
- Оба броска приземляются с орлом вверх
- Оба броска приземляются решкой вверх
- Один бросок приземляется орлом вверх, а другой — решкой вверх
Почему Just Flip A Coin выглядит так, как будто он был разработан в 1997 году?
Потому что в 1997 году интернет был крутым! Серьезно, ты должен был быть там. Кроме того, в 2010 году, когда был запущен justflipacoin.com, сайты с разовым обслуживанием были популярны. Они все еще горячие, на наш взгляд.
Кто сделал Просто подбрось монетку?
Этот плавник был создан и поддерживается My Tech Tailor. Мы создаем с нуля веб-сайты с индивидуальным дизайном, уделяя большое внимание SEO (поисковая оптимизация), удобству для пользователей, скорости и простоте управления контентом. Для получения дополнительной информации, пожалуйста, посетите mytechtailor. com!
com!
Вернуться к монете!
сообщить об этом объявлении
Как узнать вероятность подбрасывания монеты? — Гикс для гиков
ĐẦU TƯ TÀI CHÍNH трангвики &пуля; 21.09.2022 &пуля;
Вероятность — это раздел математики, изучающий возникновение подробного события. Это в основном указывает, насколько вероятно, что что-то произойдет. Упражнение: Какова вероятность дождя при чистом флипе? Диапазон вероятности лежит между 0 и 1. Вероятность невозможного последствия равна 0, а вероятность неоспоримого события равна 1. Кроме того, вероятность может быть выражена через долю. Термины, связанные с вероятностью
- Эксперимент: Любая операция, дающая четко определенные результаты, называется экспериментом. Например: Бросание монеты или бросание игральной кости — это эксперимент.
- Случайный эксперимент: В любых экспериментах возможны все возможные результаты, но неизвестно, какой именно результат произойдет.
 Это называется случайным экспериментом. Например: при подбрасывании монеты выпадает либо орел, либо решка, но нельзя быть уверенным, что выпадет только орел или выпадет решка.
Это называется случайным экспериментом. Например: при подбрасывании монеты выпадает либо орел, либо решка, но нельзя быть уверенным, что выпадет только орел или выпадет решка. - Пространство выборки: Пространство выборки — это набор всех возможных результатов. Пример: При бросании монеты у нас есть 2 исхода: орел и решка.
- Испытание: Это процесс, посредством которого проводится эксперимент и фиксируется его результат. Например: Взять карту из колоды из 52 карт.
- Событие: Каждый результат эксперимента называется событием. Например: Получение орла при бросании монеты — это событие.
- Независимых событий: Когда возникновение одного события не зависит от возникновения другого события, это называется независимыми событиями. Например, можно одновременно подбрасывать монету и бросать кости, так как это разные события.
- Исчерпывающие события: Два события называются исчерпывающими, если их объединение равно выборочному пространству.

- Эксклюзивные события: Когда два события не могут произойти одновременно или два события не пересекаются, они называются эксклюзивными событиями. Например: при подбрасывании монеты может выпасть либо орел, либо решка, но не то и другое одновременно.
Формула вероятности
Формула вероятности: Вероятность = количество благоприятных исходов/общее число исходов Как узнать вероятность броска монеты?
Известно, что у монеты две стороны: Орел и Решка. Неизвестно, какое последствие произойдет, но известно, что есть 2 шанса: один проход, а другой хвост. Это случайный эксперимент. Предположим, есть беспристрастная монета. Таким образом, полное количество результатов = 2 (так как 1 опережающий и 1 решка), и нужно, чтобы точка произошла. Какова вероятность того, что произойдет подруливание? Так как на 1 монете изображена 1 решка, а общее количество исходов равно 2, то вероятность выпадения орла = 1/2, а вероятность выпадения дока = 1/2 Нахождение вероятности для нескольких монет Найдена вероятность 1 монеты, но как насчет 2 монет или более.
Давайте проверим это. Для 2 монет есть четыре чистых результата {HH, TH, HT, TT}, поскольку на первой монете может произойти решка или погоня. Аналогично для второй монеты. поэтому из приведенной выше оболочки нужно узнать вероятность правила
- 2 головки
- 1 хвост.
Для начального испытуемого благоприятные исходы = {ЧЧ} = 1 вероятность выпадения 2 орлов = 1/4 Для второго шрифта благоприятные исходы = {ПН, НТ} = 2 (здесь специально указано, что нужно найти вероятность выпадения 1 док, поэтому 2 решки не учитываются } Вероятность выпадения 1 решки = 2/4 = 1/2 Но так как общее количество монет увеличивается, кроме увеличения последствий, невозможно найти дружественные исходы. используйте биномиальное распределение. Формула для биномиального распределения, P(X) = nCx × px × (1 – p)n – x Где нормальность – это сумма числа испытаний, десять – благоприятное испытание, фосфор – вероятность золотого следствия. 1 – p – вероятность неблагоприятного последствия.
Найдем вероятность выпадения 1 решки при использовании 2 монет вероятность погони = 0,5 общее количество попыток = 2 вероятность угнать = 0,5 Таким образом, вероятность равна = 2C1 × (0,5) 1 × (1 – 0,5) 1 =0,5 Найдем вероятность получения 1 корма при использовании 3 монет. всего испытаний 3, благоприятный тест 1
Вероятность = 3C1 × (0,5) 1 × (1 – 0,5) 3 – 1 = {3/(1! 2!) } × 0,5 × 0,52 = 3 × (1/2) × (1/2) × (1 /2 ) = 3/8, что и является нашим ответом. Так что подбрасывание монет совсем не сбивает с толку. Честное запоминание рецепта и понимание концепции помогут.
Примеры задач
Вопрос 1: Монету подбрасывают 3 раза. Какова вероятность того, что на каждой монете выпадет одно и то же лицо? (Подсказка: благоприятными событиями являются HHH, TTT) Решение:
Пространство выборки: HTH, HHT, HHH, HTT, TTH, THT, TTT, THT общее количество событий расстояния выборки = 8 благоприятных событий = HHH, TTT Количество благоприятных событий = 2 вероятность получения одинакового лица на трех монетах = 2/8 = 1/4 = 0,25
Вопрос 2: Есть 10 монет, все подбрасываются одновременно.
Найдите вероятность выпадения 5 орлов. Решение:
Вероятность выпадения орла на 1 монете ( p ) = 0,50 Вероятность выпадения орла на 1 монете ( q ) = 0,5 Количество монет ( север ) = 10 Количество орлов ( r ) = 5 Использование правило биномиального распределения, nCrprqn – r 10C5 (0,5) 5 (0,5) 10 – 5 = [(10!) / (5! × 5!)] × (0,5) 10 = 63/256 = 0,2461
Вопрос 3: Два монеты подбрасываются одновременно. Какова вероятность выпадения орла и решки? Решение:
Пространство распределения выборки: TT, HH, TH, HT Количество пространств выборки = 2 золотых события = HT, TH Количество благоприятных событий = 2 вероятность получения 1 орла и 1 решки = 2/4 = 1/2 = 0,5
arrow_drop_up
генератор: https://trangwiki.com
Категория: ĐẦU TƯ TÀI CHÍNHПохожие сообщения
ĐẦU TƯ TÀI CHÍNH 21.09.2022 &пуля;
Что такое NEM (XEM)? NEM, который является аббревиатурой от «Движение за новую экономику», представляет собой одноранговую (P2P…
ĐẦU TƯ TÀI CHÍNH 21.
09.2022 &пуля;
$ 0.0002199 +0 % ( 1D ) Чтение: Лобби (LBY) Цена, График и Новости | Binance: цена лобби, цена LBY,…
ĐẦU TƯ TÀI CHÍNH 21/09/2022 &пуля;
Swipe — это экосистема цифрового кошелька, которая позволяет пользователям покупать цифровые активы и тратить декретные деньги и цифровые…
ĐẦU TƯ TÀI CHÍNH 21.09.2022 &пуля;
Криптовалюта сейчас повсюду. Кажется, все понимают важность и следуют направлению инвестирования в криптовалюту. Есть…
ĐẦU TƯ TÀI CHÍNH 21.09.2022 &пуля;
Большинство людей могут назвать по крайней мере одну криптовалюту, и, скорее всего, это биткойн или эфириум. С…
ĐẦU TƯ TÀI CHÍNH 21.09.2022 &пуля;
Главная » Журнал Клевер Прогноз цен 2022 – 2025 – 2030 | Прогноз цен KLVJournalPredictions Прогноз цен Klever 2022 –…
ĐẦU TƯ TÀI CHÍNH 21.09.2022 &пуля;
Британская недесятичная пенни монета, сокращенно 1d (от «denarius» — римская монета, из которой…
ĐẦU TƯ TÀI CHÍNH 21.
09.2022 &пуля;
Стирая грань между валютой и изготовленными на заказ монетами Этот монетный двор был разработан для участников Лос-Анджелесского отдела по борьбе с мошенничеством…
ĐẦU TƯ TÀI CHÍNH 21.09.2022 &пуля;
В середине 1950-х, когда я действительно начал хорошо разбираться в коллекционировании монет, я проводил много вечеров…
ĐẦU TƯ TÀI CHÍNH 21.09.2022 &пуля;
Оценка MS 61 соответствует монете Монетного двора штата со слабой или средней пробой, без следов покрышки…
Решения NCERT для математики класса 10 Глава 15 Вероятность Ex 15.1
Получите бесплатно Решения NCERT для математики класса 10 Глава 15 Ex 15.1 PDF. Математика класса вероятности 10 Решения NCERT чрезвычайно полезны при выполнении домашних заданий. Упражнение 15.1 Решения NCERT по математике для 10 класса были подготовлены опытными учителями LearnCBSE.in. Подробные ответы на все вопросы в Главе 15 Математика Класс 10 Вероятность Упражнение 15.
1 приведено в учебнике NCERT.
Темы и подтемы в 10 классе Математика Глава 15 Вероятность:
Название раздела Название темы 15 Вероятность 15,1 Введение 15,2 Теоретический подход 15,3 Резюме
- Класс вероятности 10 Ex 15.1
- प्रश्नावली 15.1 का हल हिंदी में
- Класс вероятности 10 Ex 15.2
- प्रश्नावली 15.2 का हल हिंदी में
- Класс вероятности 10 дополнительных вопросов
Решения NCERT для математики класса 10 Глава 15 Вероятность Ex 15.1 являются частью решений NCERT для математики класса 10. Здесь мы дали решения NCERT для математики класса 10, глава 15, вероятность, пример 15.1.
Доска CBSE Учебник NCERT Класс Класс 10 Субъект Математика Глава Глава 15 Название главы Вероятность Упражнение Ex 15. 1
Количество решенных вопросов 20 Категория Решения NCERT Упр. 15.1 Класс 10 Математика Вопрос 1.
Дополните следующие утверждения:
(i) Вероятность события E + Вероятность события «не E» = ………
(ii) Вероятность события, которое не может произойти это ……… Такое событие называется ………
(iii) Вероятность события, которое обязательно произойдет, это ………. Такое событие называется ………
(iv) Сумма вероятностей всех элементарных событий эксперимента равна ………..
(v) Вероятность события больше или равна …………. и меньше или равно ………..
Решение:Вы также можете скачать бесплатный PDF-файл Ex 15.
1 Class 10 Probability Solutions NCERT или сохранить изображения решения и взять распечатку, чтобы держать ее под рукой. подготовка к экзамену.
Загрузить Решения NCERT для математики класса 10 Глава 15 Вероятность PDF
Пример 15.1 Математика для 10 класса. Вопрос 2.
Какие из следующих экспериментов имеют равновероятные результаты? Объяснять.
(i) Водитель пытается завести автомобиль. Машина заводится или не заводится.
(ii) Игрок пытается бросить баскетбольный мяч. Она/он стреляет или промахивается.
(iii) Проба проводится для ответа на вопрос «верно-ложно». Ответ правильный или неправильный.
(iv) Рождение ребенка. Это мальчик или девочка.
Решение:
- Класс вероятности 10 Пример 15.1
- Класс вероятности 10 Ex 15.2
Пример 15.1 Математика класса 10 Вопрос 3.
Почему подбрасывание монеты считается справедливым способом решить, какая команда должна получить залог в начале футбольного матча?
Решение:Упр.
15.1 Класс 10 Математика Вопрос 4.
Что из следующего не может быть вероятностью события?
(A) \(\frac { 2 }{ 3 }\)
(B) -1,5
(C) 15%
(D) 0,7
Решение:Пример 15.1 Класс 10 Математика Вопрос 5.
Если P (E) = 0,05, какова вероятность «не E»?
Решение:Пример 15.1 Класс 10 Математика Вопрос 6.
Пакет содержит только леденцы со вкусом лимона. Малини достает одну конфету, не заглядывая в сумку. Какова вероятность того, что она достанет
(i) конфету со вкусом апельсина?
(ii) леденец со вкусом лимона?
Решение:Пример 15.1. Математика 10 класса, вопрос 7.
Известно, что в группе из 3 учащихся вероятность того, что у 2 учащихся разные дни рождения, равна 0,9.92. Какова вероятность того, что у двух учеников день рождения в один день?
Решение:Упражнение 15.1 Класс 10 Математика Вопрос 8.
В мешочке 3 красных и 5 черных шаров. Из мешка случайным образом вынимают шар.Какова вероятность того, что извлеченный шар
(i) красный?
(ii) не красный?
Решение:Пример 15.1 Класс 10 Математика Вопрос 9.
В коробке 5 красных, 8 белых и 4 зеленых шарика. Из коробки наугад достают один шарик. Какова вероятность того, что вынутый шарик будет 9?0326 (и) красный?
(ii) белый?
(iii) не зеленый?
Решение:Пример 15.1 Класс 10 Математика Вопрос 10.
Копилка содержит сто монет по 50 p, пятьдесят монет по 1 ₹, двадцать монет по 2 ₹ и десять монет по 5 ₹. Если равновероятно, что одна из монет выпадет, когда банку перевернут вверх дном, какова вероятность того, что монета
(i) будет монетой в 50 пенсов?
(ii) не будет монетой номиналом 5 ₹?
Решение:Пример 15.1 Класс 10 Математика Вопрос 11. 903:26 Гопи покупает в магазине рыбку для своего аквариума. Продавец наугад достает одну рыбу из аквариума, в котором 5 самцов и 8 самок (см. рисунок). Какова вероятность того, что вынутая рыба — самец?
Решение:Пример 15.
1 Класс 10 Математика Вопрос 12.
Азартная игра заключается в вращении стрелки, которая останавливается и указывает на одно из чисел 1, 2, 3, 4, 5, 6, 7, 8. (см. рис.), и это равновероятные исходы. Какова вероятность того, что он укажет на
(и) 8?
(ii) нечетное число?
(iii) число больше 2?
(iv) число меньше 9?
Решение:Упражнение 15.1 Класс 10 Математика Вопрос 13.
Кость подбрасывается один раз. Найдите вероятность того, что
(i) простое число
(ii) число от 2 до 6
(ill) нечетное число
Решение:Упр. хорошо перетасованная колода из 52 карт. Найдите вероятность того, что выпадет
(i) король красного цвета
(ii) лицевая карта
(iii) красная лицевая карта
(iv) червовый валет
(v) пиковая
(vi) бубновая дама
Решение:Пример 15.1 Класс 10 Математика Вопрос 15.
Пять карт – десятка, валет, дама, король и бубновый туз – хорошо перетасованы лицевой стороной вниз.Затем случайным образом выбирается одна карта.
(i) Какова вероятность того, что это дама?
(ii) Если дама вытянута и отложена в сторону, какова вероятность того, что вторая взятая карта равна
(а) туз?
(б) королева?
Решение:Пример 15.1 Класс 10 Математика Вопрос 16.
12 дефектных ручек случайно смешаны со 132 хорошими. Невозможно просто посмотреть на ручку и сказать, неисправна она или нет. Из этой партии случайным образом берут одну ручку. Определить вероятность того, что вынутая ручка исправна.
Решение:Пример 15.1 Класс 10 Математика Вопрос 17.
(i) В партии из 20 лампочек есть 4 бракованные. Из партии случайным образом выбирается одна луковица. Какова вероятность того, что эта лампочка бракованная?
(ii) Предположим, что лампочка, показанная в (i), не дефектна и не заменена. Теперь одна лампочка вытягивается наугад из остальных. Какова вероятность того, что эта лампочка исправна?
Решение:Пример 15.
1 Класс 10 Математика Вопрос 18.
В коробке 90 дисков, пронумерованных от 1 до 90. Если из коробки наугад вынуть один диск, найдите вероятность того, что на нем
(i) a двузначное число.
(ii) совершенное квадратное число.
(iii) число, кратное 5.
Решение:Пример 15.1 Математика для 10 класса. Вопрос 19.
У ребенка есть кубик, на шести гранях которого изображены буквы, указанные ниже:
Кубик подбрасывается один раз. Какова вероятность получить
(i)A?
(ii) Д?
Решение:Упражнение 15.1 Класс 10 по математике Вопрос 20.
Предположим, вы бросаете кубик наугад в прямоугольную область, показанную на рисунке. Какова вероятность того, что он попадет внутрь круга диаметром 1 м?
Решение:Пример 15.1 Класс 10 Математика Вопрос 21.
Партия состоит из 144 шариковых ручек, из которых 20 неисправны, а остальные исправны. Нури купит ручку, если она хорошая, но не купит неисправную.Продавец наугад берет одну ручку и дает ей. Какова вероятность того, что
(i) она его купит?
(ii) она не купит?
Решение:Упражнение 15.1 Класс 10 по математике Вопрос 22.
Две игральные кости, синяя и серая, подбрасываются одновременно. Сейчас
(i) Заполните следующую таблицу:
(ii) Учащийся утверждает, что существует 11 возможных исходов 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12. Следовательно, каждый из их имеет вероятность \(\frac { 1 }{ 11 }\). Вы согласны с этим аргументом? Обосновать ответ.
Решение:Упражнение 15.1 Класс 10 Математика Вопрос 23.
Игра состоит из подбрасывания монеты в одну рупию 3 раза и каждый раз запоминания результата. Ханиф выигрывает, если все броски дают одинаковый результат, то есть три орла или три решки, и проигрывает в противном случае. Вычислите вероятность того, что Ханиф проиграет.
Решение:Пример 15.1 Математика для 10 класса. Вопрос 24.
Кость бросают дважды.Какова вероятность того, что
(i) 5 не выпадет ни в том, ни в другом случае?
(ii) 5 выпадет хотя бы раз?
[Подсказка: бросание кубика дважды и одновременное бросание двух кубиков рассматриваются как один и тот же эксперимент.]
Решение:Упражнение 15.1, класс 10, математика, вопрос 25.
Какие из следующих аргументов верны, а какие нет? Обоснуйте свой ответ.
(i) Если одновременно подбрасываются две монеты, возможны три исхода: два орла, две решки или по одному каждому из них. Следовательно, для каждого из этих исходов вероятность равна \(\frac { 1 }{ 3 }\).
(ii) При бросании игральной кости возможны два исхода: четное или нечетное число. Следовательно, вероятность получения нечетного числа равна \(\frac { 1 }{ 2 }\).
Решение:Класс 10 Математика Вероятность Интеллект-карты
Вероятность — экспериментальный (эмпирический) подход
Пусть n будет общим количеством трасс. Эмпирическая вероятность события E определяется как
(i) Эксперимент: Операция, которая может привести к некоторым четко определенным результатам, известна как эксперимент.

(ii) След: Проведение эксперимента называется испытанием.
(iii) Равновероятные исходы: Исходы испытания равновероятны, если нет причин отдавать предпочтение одному из них по сравнению с другими.
(iv) Пространство выборки. Множество всех возможных результатов эксперимента называется пространством выборки.
(v) Элементарное событие: событие, имеющее только один исход
Обратите внимание, что сумма вероятностей всех элементарных событий эксперимента равна 1.Вероятность – теоретический подход (классическая вероятность)
Если событие «А» может произойти m способами и не может произойти n способами, то вероятность наступления события A, обозначаемого P(A), равна
Число благоприятных исходов mВероятность невозможного и гарантированного События
Вероятность события, которое невозможно произойти, равна 0, и такое событие называется невозможным событием, т.е. для невозможного события T P(I) = 0
Вероятность события, которое обязательно или несомненно произойдет, равна 1, и такое событие называется определенным событием или определенным событием.
т.е.; для определенного события или определенного события ‘s’, P(s) = 1Диапазон вероятности события
Из определения вероятности P(E) мы видим, что числитель (количество исходов, благоприятных для событие E) всегда равно или больше 0, но меньше или равно знаменателю (количеству всех возможных исходов). Следовательно,
0 ≤ P(E) ≤ 1Дополнительные события
Событие, представляющее («не E»), называется дополнением события «E», и мы говорим, что события E и \(\overline{E}\) являются дополнительными событиями,
Решения NCERT для Class 10 Maths Chapter 15 Probability (Hindi Medium) Ex 15.1
Мы надеемся, что решения NCERT для класса 10 по математике, глава 15, вероятностный пример 15.1, помогут вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 10, главы 15, вероятностного упражнения 15.
1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
Packers Snap Counts: Амари Роджерс не существует, а Уотсон и Даубс бегут Новости Висконсина
перейти к содержанию
Автор: Митч Видмайер, Bally Sports Wisconsin
11 сентября 2022 г .; Миннеаполис, Миннесота, США; Ресивер «Грин Бэй Пэкерс» Ромео Дубс (87) ловит пас против «Миннесота Викингз» в третьей четверти на стадионе «Ю.С. Бэнк». Обязательный кредит: Брэд Ремпел-USA TODAY Sports
Дверь была широко открыта в начале недели 1, чтобы один или два широких приемника из Green Bay Packers пробежали прямо и взяли бразды правления вместе с товарищем по широкому кругу Алленом Лазардом. После первой игры эта дверь все еще открыта и кажется заброшенной.
Нападение Грин-Бея было беспорядком против «Миннесотских викингов», набрав всего семь очков и упустив другие возможности, такие как четвертый гол с ярдовой линии и ставшее вирусным падение Кристиана Уотсона в первом нападении, которое могло бы совершил тачдаун на 75 ярдов.
Одним из странных событий стало то, что второкурсник Амари Роджерс не сделал ни единого щелчка в нападении. С другой стороны, новички Уотсон и Ромео Даубс зафиксировали 40 и 35 снэпов из возможных 61.
Упущение Роджерса странно, учитывая, что Грин-Бей карабкался на любой широкий выход, чтобы создать разделение, и напрашивается вопрос: или нет, он будет продолжать быть снаружи, смотрящим вперед.
Главный тренер Мэтт ЛаФлер осыпал Роджерса похвалой в межсезонье, и после ужасного сезона новичка, который невероятно разочаровал, невозможно было представить, что второй сезон Роджерса будет хуже.
«Амари давно присутствует в игре. Можно сказать, что он сын тренера. Он очень усердно учится.
Мы много на него накидали. Мы не сдерживаемся с точки зрения того, что у нас есть он в нескольких разных ролях. В первую очередь, я думаю, что он будет больше на месте, а затем я думаю, что мы будем использовать его в струйных вещах… Я в восторге от того, куда он может пойти».
Исчезновение акта на первой неделе и отсутствие у Packers даже возможности пробежаться, когда игра оказалась вне досягаемости, говорит о другом.
Грин Бэй заигрывал с Роджерсом в предсезонке, и после того, как в окончательном списке из 53 человек остались только два раннингбека, идея сделать Роджерса игроком-гаджетом, которого можно было бы использовать в бэкфилде, была еще более реалистичной.
Ничего из этого не осуществилось и даже не имело пульса против Миннесоты.
Вызывает тревогу тот факт, что второкурсник, которого «Пэкерс» выбрали в третьем раунде, не смог даже понюхать атакующую свалку в первом матче. На данный момент это проливает свет на иерархию, но если Роджерс не сможет даже сделать попытку, эта иерархия не изменится, поскольку № 8 останется снаружи и заглянет внутрь.
Уотсон и Даубс, с другой стороны, были брошены прямо в микс, и мы все знаем, как прошла первая игра для Уотсона, но готовность Грин-Бей открыть одну игру новичку показала уровень уверенности, которого не было замечено в Грин-Бее. в сторону новичков.
Ни Уотсон, ни Даубс не выделялись, но это относится ко всему нападению, за исключением Эй Джей Диллона. Уотсон закончил двумя приемами на 34 ярда, а Дубс сделал четыре приема на 37 ярдов.
Если эта тенденция сохранится, два новичка вместе с Лазардом, Рэндаллом Коббом и Сэмми Уоткинсом будут пережевывать повторения для нападения на широкий ресивер, оставив Роджерса чесать, чтобы получить хоть какое-то сцепление.
Нет другого способа выразить это, кроме как отметить, насколько тревожным было начало для Роджерса, когда он не вышел на поле с нападением. Одно дело, если Роджерс не станет мишенью или у него не будет приема, но даже если его номер телефона не будет назван для снэпа, это открывает еще одну банку червей.
Это нападение, которому не хватает стабильного производства в широких масштабах, и бывший продукт Clemson смотрит в тяжелую битву.
Другие заметки по воскресным подсчетам снэпов:
— Роберт Тоньян не получил травму на первой неделе из-за разрыва передней крестообразной связки в прошлом сезоне, но сыграл лишь 36% снэпов «Грин Бэй» в нападении. Ожидайте, что это число будет продолжать расти, и воспринимайте это как то, что Packers просто возвращают свой тайт-энд обратно в фолд.
— Новичок внутреннего полузащитника Куэй Уокер сделал 38 снэпов из 62 возможных (61%), и их было бы гораздо больше, если бы он не получил травму плеча в третьей четверти, из-за которой он покинул игру и не вернулся. Уокер летал по полю в обороне и зарегистрировал семь одиночных отборов мяча. Хороший старт для новичка.
— При всей неуверенности в широком приемнике именно Уоткинс сделал больше всего снимков (41) в группе, едва обойдя Уотсона (40). Ветеран Уоткинс попал в цель только три раза, но поймал все три на 18 ярдов.
Как только Лазар вернется, корона будет передана № 13.
— Новичок Зак Том вошел в охрану после того, как Джону Раньяну пришлось уйти с симптомами сотрясения мозга, а Том зарегистрировал 30 щелчков (49%). Линия нападения была в руинах большую часть дня с правым защитником Джейком Хэнсоном и правым тэклом Ройсом Ньюманом, допустившим семь из 11 разрешенных прессингов, и будет интересно посмотреть, получит ли Том старт на неделе 2, и если Дэвид Бахтиари и / или Элгтон Дженкинс возвращается.
Правонарушение ИГРОК ПРОГРАММ (61) % Хэнсон 61 100% Майерс 61 100% Ньюман 61 100% Нейман 61 100% Роджерс 56 92% Уоткинс 41 67% Ватсон 40 66% Джонс 37 61% Кобб 37 61% Дуб 35 57% Диллон 31 51% Рунян 31 51% Том 30 49% Льюис 23 38% Тонян 22 36% Дэвис 15 25% Дегуара 15 25% Уинфри 9 15% Любовь 5 8%
Защита ИГРОК ИГРЫ (62) % Стоукс 62 100% Кэмпбелл 62 100% Амос 62 100% Дикарь 62 100% Александр 62 100% Смит 53 85% Гэри 49 79% Кларк 43 69% Рид 42 68% Дуглас 41 66% Лоури 38 61% Уокер 38 61% Слейтон 18 29% Гарвин 12 19% Энагбаре 10 16% Барнс 9 15% Макдаффи 6 10% Никсон 1 2% Вам также может понравиться
Packers Snap Counts: возвращение Дженкинса помогает Грин Бэй навязать свою волю
Грин Бэй вел свои дела против Чикагских Медведей в воскресенье вечером.
Там ничего удивительного. После этого тренер Packers Мэтт Лафлер похвалил одного из своих игроков. Он не был направлен ни на кого предсказуемого — ни на Аарона Джонса, который набрал 170 ярдов от схватки, ни на конкретного парня.
Возвращение Дженкинса придает уверенности Packers в линии нападения
ГРИН-БЕЙ, Висконсин. Элгтон Дженкинс неоднозначно отозвался о своем возвращении в атакующую линию «Грин-Бей Пэкерс». «В основном просто ржавый», — сказал Дженкинс в воскресенье вечером, сыграв свою первую игру с ноября прошлого года. «Я должен отточить свою технику, выйти из стойки, зафиксировать их».
При дальнейшем рассмотрении: упаковщики делают правильный выбор, набирая номер Showtyme в прайм-тайм
Грин Бэй позвонил кому-то, на кого, как он знал, он мог рассчитывать в воскресной победе со счетом 27-10 над соперником NFC North Чикаго.
Через неделю после того, как Аарон Джонс отошел на второй план в плане игры Packers, выбор в пятом раунде 2017 года напомнил остальной части НФЛ, что, несмотря на потерю одного суперзвездного игрока, этот
Читать Далее
МИННЕАПОЛИС. Смело заявив перед началом сезона о своей цели стать лучшим принимающим в лиге, Джастин Джефферсон из Миннесоты уже может претендовать на этот субъективный, но желанный статус. Аарон Роджерс может только желать, чтобы Джефферсон был на его стороне. Джефферсон разгромил соперника Грин Бэй за 184, получив
Вернуться к началу страницыПакистан против Шри-Ланки. Основные моменты финала Кубка Азии 2022: SL обыгрывает ПАК с разницей в 23 раунда, выигрывает титул Дубай в воскресенье.

ШРИ-ЛАНКА ПОБЕДИЛА ПАКИСТАН НА 23 ПРОБЕГА
Ваши NEWWWWWWWW Чемпионы Азии🏆
Шри-Ланка вышла в лидеры и ошеломила азиатский субконтинент! #AsiaCup2022Final#SLvsPAKpic.twitter.com/8cI8HoDpjQ
— Sportstar (@sportstarweb) 11 сентября 2022 г.ПАК 147/10 ЗА 20 ОВЕРОВ
Карунаратне забьет последним. Медленный вышибала, Рауф промахивается. Пакистану нужно 32 из пяти мячей. Сингл в глубоком мидвикете для сингла. Еще один, более медленный, и Хаснайн тренирует его до еще одного. Мяч более медленной длины снаружи, и Рауф замахивается и промахивается. ШЕСТЬ! Полный снаружи, и Рауф забирается под него и долбит его по максимуму. ВНЕ! И символическое завершение турнира, когда Карунаратне разбивает культи Рауфа. Шри-Ланка выигрывает с разницей в 23 очка и поднимает свой шестой титул Кубка Азии и первый с 2014 года.
ПАК 139/9 В 19 ОВЕРСАХ
Заходит Насим. Пакистану нужно 51 ран, чтобы выиграть с 12 мячей.
Первый мяч широкой опущенной ногой. ЧЕТЫРЕ! Насим идет на удар по ноге и получает мощный внешний край, который убегает к границе третьего человека. ВНЕ! Насим отрабатывает этот полный бросок прямо на дальнего полевого игрока. Более медленный снаружи, и Хаснайн побежден. Он попадает в цель с синглом, когда он очищает переднюю ногу и забивает ее в дальний удар. ЧЕТЫРЕ! Харис Рауф разбивает это до предела. Полевой игрок в глубине пробежал слишком много, чтобы поймать мяч, и в итоге пропустил четыре попытки. Это также не мяч, так как срабатывает зуммер. Приближается бесплатный удар, и вышибала из Мадушана и Уайда заколлировали. ШЕСТЬ! Мяч более медленной длины, и Хаснайн выжидает и отбивает его по максимуму.
ПАК 120/8 В 18 ОВЕРСАХ
ЧЕТЫРЕ! Толстый внешний край для Шадаба, когда он идет на слог, и он убегает мимо вратаря за границу. Отбивающие сильно размахивают битой, но не в реальном времени. Шадаб берет тайтовую двойку, а Тикшана не может забрать мяч, и это упущение для Пакистана.
ВНЕ! Шадаб летает по воздуху и над укрытиями, и его забирает Гунатилака.
ПАК 112/7 В 17 ОВЕРСАХ
КОНЕЦ! Выброшенный наружу, Ризван слог подметает это прямо в руки глубокого мидвикета. Это игра здесь? Асиф и Кушдил на складе. ВНЕ! Асиф Али забивает первый мяч и идет за золотой уткой. Шадаб сейчас дома. Щелкает с передней ноги для сингла. ВНЕ! Еще один повержен в прах. Кхушдил борется с вращением и в конечном итоге разрезает его высоко в воздухе. Три калитки для Хасаранги в овере.
PAK 110/4 IN 16 OVERS
Rizwan делает глубокую квадратную ногу для сингла. ВНЕ! Наваз тянет это, но находит глубокую заднюю квадратную ногу, и Пакистан теряет свою четвертую калитку. Более медленная, уходящая под углом наружу, и Кушдила бьют, когда он пытается открыть морду летучей мыши. Оторвался от него за одиночный на глубокой квадратной ноге следующий мяч. ШЕСТЬ! Полный выход наружу, и Ризван встает на одно колено и максимально тяжело проносится через глубокую середину калитки.
На этот раз снова медленнее, Ризван выходит раньше и просто успевает щелкнуть ногой на один раз.
ПАК 101/3 ЗА 15 ОВЕРСОВ
Дхананджайя де Сильва сейчас будет подавать. Наваз пробивает первый по земле, а сенсационный сейв на дальней дистанции удерживает его до пары. Еще парочку, пока Наваз сбрасывает кожу с этого полного броска в глубокую точку. Де Сильва держит Наваза на привязи. Всего четыре пробега от конца. Запрашиваемая ставка теперь 14 и Шри-Ланка является фаворитом, чтобы поднять трофей отсюда сейчас.
ПАК 97/3 В 14 ОВЕРСАХ
Мадушан с мячом. Медленно и коротко и делается это ногой и будет широкая. ВНЕ! Ифтихар идет к большому и заканчивает тем, что разрезает его высоко в воздухе, и его берут на глубокой квадратной ноге. Пакистан сейчас в беде. Наваз следующий. Три сингла после падения калитки. Ризван перемещается на 47. Наваз берет последний мяч и продолжает наносить удары.
ПАК 91/2 В 13 ОВЕРСАХ
Теекшана возвращается. Ризван начинает с пары.
Отличный бросок с офф-спиннера, так как от него отрывается всего три прогона. Давление на Пакистан нарастает, поскольку процентная ставка превышает 11,4.
ПАК 88/2 ЗА 12 ОВЕРСОВ
Хасаранга в своем третьем овере. ШЕСТЬ! Наконец-то есть повод порадоваться за Пакистан. Ифтихар усердно подметает и отправляет мяч максимально глубоко в середину калитки. ЧЕТЫРЕ! Это вбито в землю для четверки с одним отскоком. Направляемый позади на пару в глубокой трети. Этот держится низко, и Ифтихар пробивает его глубоко в мидвикет для сингла. Обошел Ризван за один мяч после последнего мяча.
ПАК 74/2 В 11 ОВЕРСАХ
Карунаратне продолжится после перерыва. Длина на пнях и Ризван попадает за мяч надежно защищается. Сорвал подушечки за один-единственный следующий мяч. Медленнее на пнях, еще один в глубоком мидвикете. Серия более медленных мячей в овере и всего шесть пробежек.
ПАК 68/2 В 10 ОВЕРСАХ
Хасаранга вернулся. Ризван сметает это от широкой внешней стороны до глубокой квадратной ноги для сингла.
Еще один для Ифтихар следующий мяч. У Гугли Ризвана проблемы, поскольку он бьет его по внутреннему краю, прежде чем врезаться в его подушечку. Крик LBW отключен, но Шанака идет наверх. Ризван выживет, поскольку это задело внутренний край, как подтверждают повторы. Шри-Ланка теряет обзор. Четыре сингла с конца. Сделайте пять, когда Ризван опустится и пронесется за квадрат для сингла.
ПАК 63/2 В 9 ОВЕРСАХ
Текшана возвращается на второй овер. ЧЕТЫРЕ! Деликатно сделано Ризваном. Короткий, и он остается позади и направляет его к границе третьего человека. Еще пара плотных пробежек, и он мог бы быть близок, если бы бросок не нападающего был лучше. Ризван сбрасывает последнюю пластинку со своих пэдов для сингла.
ПАК 53/2 В 8 ОВЕРСАХ
Чамика Карунаратне в атаку. ЧЕТЫРЕ! Длинный мяч, Ризван шаркает по пню и бьет летучими мышами по прямоугольному забору на протяжении четырех проходов. Пара следующих мячей и хорошая игра отбивающих. Slower on off, и Ризван мягко постукивает по нему и заяц для сингла.
Еще три сингла, чтобы закончить. Пакистан, наконец, набирает обороты.
ПАК 43/2 В 7 ОВЕРСАХ
Хасаранга в атаку. ЧЕТЫРЕ! Вылетел на улицу, и Ифтикар оторвался от своей передней ноги и ударил ею по укрытию в поисках границы. Шесть пробегов с конца, несмотря на границу.
ПАК 37/2 В 6 ОВЕРСАХ
Мадушан продолжает. Ифтикар поднимает это над кругом со стороны ног на пару. Ризван делает еще одну длинную площадку. Толстый внешний край лезвия Итихара, и он получает одиночный удар между укрытием и острием.
ПАК 32/2 В 5 ОВЕРСАХ
Мадушанка выбивает третий бросок. Длина задней части посередине и ноге, и Ризван тянет ее через квадратную ногу пару раз. Ифтихар избит, когда собирается выехать на улицу. Хорошо направленный короткий мяч и Ифтихар спешит на пулл и просто получает сингл. ЧЕТЫРЕ! Задняя часть длины снаружи снова, и на этот раз Ризван хорошо разрезает его и проходит мимо полевого игрока на границе.
ПАК 24/2 В 4 ОВЕРСАХ
КОНЕЦ! Бабар падает на культю ноги.
Длинный мяч летит вниз по ноге, и он бросает его короткой тонкой ноге, которая очень хорошо цепляется за эту ногу. Следующим идет Фахар Заман. ВНЕ! Факхар выходит на улицу, получает внутреннее преимущество и продолжает рубить. Фахар идет за золотой уткой. Две калитки в два мяча для Мадушана. Мяч для хет-трика лежит на лонжероне на подушечках, и Ифтихар толкает его ногой на раз. Ризван толкает последний мяч в овере для быстрого сингла в середине.
ПАК 20/0 В 3 ОВЕРСА
Мадушанка продолжает. Снаружи вылетает широкий йоркер, и Ризван не может его выкопать. ЧЕТЫРЕ! Это полузалп снаружи, и Ризван мягко продвигает его за середину для границы. Немного короче и шире снаружи от этого, и Ризван побежден! Ризван точно рассчитывал мяч и идеально подбирал полевых игроков. Всего четыре пробега от конца.
ПАК 16/0 В 2 ОВЕРСА
Текшана с другого конца со своим офф-спином. Спускающаяся нога и широкий называется. Ризвану трудно его увести, так как он играет тремя точками подряд.
Наконец, он получает одиночный удар от пятого мяча, когда он становится ниже, чтобы перейти к квадратной ноге. Пара для Бабара, чтобы закончить окончание.
PAK 12/0 IN 1 OVER
Бабар Азам и Мохаммад Ризван отправятся в погоню за Пакистаном. Мадушанка с новым мячом для Шри-Ланки. Длинный мяч над пнями на пне, и Ризван отстает, чтобы защитить его. Однако нет мяча, когда срабатывает зуммер. Пакистан на высоте. Короткий мяч и это называется широким. Еще один дополнительный прогон, и свободный удар продолжается. Третий дополнительный подряд, так как это вниз по ноге. И страдание продолжается, когда его бьют по ноге, а замах уносит его дальше на пять ширин. Восемь пробежек на доске без подброшенного мяча. Сделайте девять дополнений сейчас, так как это тоже идет вниз. ПАК 9/0 в 0,0 оверов. И, наконец, легальная подача, так как это хорошая длина мяча, и Ризван прокручивает линию для сингла. Широко снаружи, и Бабар избит, отъезжая от своего тела. Полные щитки, и Бабар пропускает бросок позади вратаря.
Длинный мяч, уходящий под углом наружу, и Бабар не попадает в цель с одним, когда он направляет его третьему игроку. Полный снаружи, и Ризван ведет это к дополнительному укрытию для точечного мяча. Полные пэды, и Бабар доводит это до середины для быстрого сингла. Двенадцать пробегов с конца. Хороший камбэк от боулера после того, как он пропустил девятку, не забив шар.
ШРИ-ЛАНКА 170/6 ИН 20 оверов
SL 170/6 ИН 20 оверов
Насим выбивает финальный овер. Мяч более медленной длины на подушечках, и Карунаратне размахивает им до глубокой квадратной ноги для сингла. Раджапакса получает верхнее преимущество, когда он пытается выбить заднюю квадратную ногу, и получает пару, когда мяч приземляется далеко от глубокого полевого игрока. Еще два для него следующий мяч. Две шестерки подряд из Раджапакса завершают подачу, и Шри-Ланка получает 170 очков.
SL 155/6 IN 19 OVERS
Добрый день из Хаснаина. Всего два сингла от первых четырех мячей. ШЕСТЬ! Раджапакша сильно ударяет по ноге.
Это высоко в воздухе, и Асиф Али и Шадаб Хан сталкиваются, когда они идут за добычей в глубоком мидвикете. Мяч выскакивает из руки полевого игрока из-за столкновения и максимум перелетает через канат, а Шадаб падает на землю и, кажется, поранился.
SL 147/6 IN 18 OVERS
Рауф выбивает. Раджапакса сокращает это более медленное отставание на один балл. ЧЕТЫРЕ! Карунаратне немного шаркает, и мяч отскакивает от его бедра на четыре фут-бай. Управляемый Karunaratne для быстрого сингла в дополнительном укрытии. Раджапакса в конечном итоге взлетает так высоко в ночное небо, и Шадаб бросает этого лыжника на дальней дистанции, позволяя отбивающим вернуться на три. Раджапакса поднимает свои 35 мячей на 50 с одним последним мячом.
SL 136/6 IN 17 OVERS
Длинный мяч попадает под углом в подушечки, Карунаратне пропускает бросок и собирает одну ногу. ШЕСТЬ! Более медленная длина мяча на ноге, и Раджапакса возмутительно поднимает его над глубокой задней квадратной ногой.
ШЕСТЬ! Karunaratne теперь присоединяется к партии, забивая полный один над длинным до максимума, чтобы закончить овер.
SL 120/6 В 16 ОВЕРСАХ
Наваз в атаку. Он держит его ровно в основном в этом. Три сингла с конца.
SL 117/6 IN 15 ВЕРХОВ
Рауф возвращается. Пара для Хасаранги, когда он бесстрашно пятится внешней ногой, обнажая свои культи и шлепки через одеяло. ЧЕТЫРЕ! Чудо из Ванинду! Снова освобождает место, отступая на ногу, и опускается на землю еще на четыре. ЧЕТЫРЕ! Рауф делает три пня, поскольку Хасаранга снова освобождает место в офсайде и нарезает мяч через заднюю точку для еще одной границы. Снова освобождает место, промахивается и вот выдается застигнутый сзади. Хасаранга ходит без обзора, и это большой удар для Шри-Ланки. Карунаратне находится в следующем. Полные и отодвинутые колодки для сингла при длительном включении.
SL 106/5 IN 14 OVERS
Шадаб выбывает. Хасаранга продвигает один к дальнему за сингл, и это на 100 больше для SL за 13,1 овера.
ЧЕТЫРЕ! Раджапакса выходит и вбивает это в землю, чтобы установить границу. Плотный одиночный следующий мяч, но Хасаранга ныряет вперед. Шадаб заканчивается цифрами один из 28 из своих четырех оверов.
SL 99/5 В 13 ОВЕРСАХ
Хаснейн возвращается в атаку. Он бьет Раджапакса коротким ударом по культе ноги, который попадает отбивающему в тело, прежде чем перейти к третьему игроку на одну ногу. ЧЕТЫРЕ! Хасаранга с несколькими важными пробегами здесь. Держится низко и одним ударом отбрасывает этого йоркера сквозь укрытия. Он отбрасывает следующий мяч внешней ногой и снимает с этого покрытия еще два. ШЕСТЬ! Сенсационный выстрел. Хасаранга режет это в темпе через точку глубокого отставания по максимуму. Одноместный, чтобы закончить.
SL 85/5 В 12 ОВЕРСАХ
Еще один овер для Ифтикара. Раджапакса живет здесь опасно. Идет на усердный подсечка, получает внутренний край по своим подушечкам, и мяч закручивается, но не долетает до боулера. На этот раз Хасаранга замахивается и получает сингл в глубоком мидвикете.
ЧЕТЫРЕ! Очень дерзко сделано Хасарангой. Открывает лицо биты и очень точно пропускает ее мимо перчаток вратаря к границе позади в течение четырех проходов.
SL 77/5 IN 11 OVERS
Shadab делает третий овер. ЧЕТЫРЕ! Раджапакса выходит наизнанку после выхода и находит границу укрытия. Он щелкает следующий для сингла. ЧЕТЫРЕ! Аккуратно отрежьте Хасарангой до границы точки. Немного короче, и Хасаранга остался низким. Он все еще короткий и соскальзывает с поверхности, прежде чем попасть в Хасарангу, который пробивает его до середины для сингла. Десять пробежек с конца.
SL 67/5 IN 10 OVERS
Раджапакса ключ здесь и сейчас для Шри-Ланки. Ифтихар продолжает. Раджапакса резко обрезает одну пару. Следующим шаром он чуть не шлепнул мяч обратно в боулер, так как тот получил преимущество. Небольшая путаница в середине, когда Хасаранга ведет одного с задней ноги в середину и заяц для сингла, но отправляется обратно на полпути вниз по полю.
SL 62/5 В 9 ОВЕРСАХ
Шадаб продолжает.
Пара синглов после первых двух мячей. ВНЕ! Шанака проходит через линию мяча, промахивается и путает свои культи. Шри-Ланка пять вниз и в абсолютном беспорядке. ЧЕТЫРЕ! Хасаранга не попадает в цель, забив четыре мяча. Он остается позади и рулит этой задней точки.
SL 55/4 IN 8 OVERS
Ифтихар выходит с мячом. ЧЕТЫРЕ! Небольшой внешний край для Раджапакса мимо вратаря и к границе. ВНЕ! де Сильва возвращает улов Ифтихару, который пытается поднять его над головой боулера.
SL 47/3 В 7 ОВЕРСАХ
Шадаб с мячом после PowerPlay. Пять синглов с конца.
SL 42/3 В 6 ОВЕРСАХ
Рауф продолжает. ВЫЙТИ! Гунатхилака видит, как его культи разбиваются вдребезги. Наклонил и он движется в левша, чтобы разбить его защиту и грохот в пни. ЧЕТЫРЕ! Этот уходит, толстый внешний край для Раджапакса и убегает к границе третьего человека. Серьезный темп тут у Рауфа — метнулся в 153 км/ч. Следующим взламывает йоркера, и Раджапакса рассказывает об этом полевому игроку с обложки.
Это в длину по середине, и Раджапакса защищает его назад. LBW кричит другому Рауфу йоркеру. Судья невозмутим, но Бабар идет на проверку. Не повезло Пакистану, поскольку культя ноги отрезана ровно настолько, чтобы это можно было назвать решением судьи, а Раджапакса выживает.
SL 36/2 В 5 ОВЕРСАХ
Хаснайн возвращается. ЧЕТЫРЕ! де Сильва поднимает это над кругом для другой границы. Длина мяча, отдаляется и де Сильва выходит наизнанку. Убраны колодки для одного следующего мяча. Гунатилака не попадает в цель с единственным мячом, с которым он столкнулся.
SL 28/2 В 4 ОВЕРСА
Харис Рауф в атаке. Ниссанка получает небольшое внутреннее преимущество, защищая этот длинный мяч от котелка. ВНЕ! Ниссанка поднимает это над головой боулера и не засекает время, и Бабар безошибочно кладет это в мешочек. Удивительный замах на выезде, и де Сильва терпит поражение, когда он выходит на улицу. Гунатилака — следующий отбивающий под номером 4. ЧЕТЫРЕ! де Сильва пробивает мяч этой длины между укрытием и точкой за границей.
де Сильва продолжает наносить удар одним ударом.
SL 23/1 В 3 ОВЕРСАХ
Насим побеждает Ниссанку тем, кто держится низко. Огромный LBW кричит следующий мяч, но Ниссанка выживает, так как это выглядело как поражение ноги. ЧЕТЫРЕ! Теперь Ниссанка пускает в ход прикрытие за рубеж. Три сингла, чтобы закончить овер.
SL 16/1 IN 2 OVERS
Hasnain с другого конца. Ниссанка тычет длинным мячом в канал ориентировочно для сингла. ЧЕТЫРЕ! де Сильва хрустит полным снаружи сквозь обложки с восхитительным кавер-драйвом. Мяч удалялся, но де Силва держался уверенно и набрал отличную форму. Идет вниз по ноге, но мяч отскакивает от бедра отбивающего и все еще коллируется мимо. ЧЕТЫРЕ! Еще четыре для де Сильвы. Скинул колодки на пару с последнего мяча.
SL 4/1 IN 1 OVER
У Насима Шаха новый мяч. Насим Ниссанке подходит к первому мячу. Широкая нога с мячом для начала. Опускается нога и уходит дальше с замахом. Длинный мячик на подушечках и ниссанка постукивает по ноге сбоку.
Ниссанка получает сильное внутреннее преимущество, когда мяч резко влетает и убегает в штрафную ногу для одиночного удара. ВНЕ! Мендис идет первым мячом. Замахивается резко и поздно и гремит культями Мендиса. Золотая уточка для Мендиса. Дхананджайя де Сильва входит и забирает пару с последнего мяча в овере, чтобы не попасть в цель.
Пакистанские игроки ссорятся. Ниссанка и Мендис уходят, чтобы открыть ватин.
Команды выходят на национальные гимны. Пакистан на первом месте. С гимнами покончено.
ПАКИСТАН ИГРАЕТ XI: Мохаммад Ризван (жк), Бабар Азам (к), Фахар Заман, Ифтихар Ахмед, Хушдил Шах, Мохаммад Наваз, Шадаб Хан, Асиф Али, Харис Рауф, Насим Шах, Мохаммад Хаснейн.
ШРИ-ЛАНКА ИГРАЕТ XI: Патхум Ниссанка, Кусал Мендис (жк), Данушка Гунатхилака, Дхананджая де Сильва, Бханука Раджапакса, Дасун Шанака (с), Ванинду Хасаранга, Чамика Карунаратне, Прамод Мадушан, Махиш Теекшана, Дилшан Мадушанка.
ЖЕСТОК: Пакистан выигрывает жеребьевку и выбирает чашу.
Шадаб Хан и Насим Шах вернулись в Пакистан, а Шри-Ланка осталась без изменений.
6:51 IST
Шри-Ланке до сих пор везло с жеребьевками на турнире, выиграв четыре из пяти. Тем временем Пакистан выиграл три из пяти бросков в этом выпуске Кубка Азии.
Поддержка болельщиков 🇵🇰
Все готово к финалу Кубка Азии 👊#AsiaCup2022 | #SLvPAKpic.twitter.com/iUXiurjG2x
— Пакистанский крикет (@TheRealPCB) 11 сентября 2022 г.Шри-Ланка и Пакистан трижды встречались в финале Кубка Азии (1986, 2000, 2014). Шри-Ланка выиграла две из этих встреч, а Пакистан выиграл одну.
В последний раз Шри-Ланка и Пакистан встречались в финале Кубка Азии еще в 2014 году. Шри-Ланка выиграла схватку на высшем уровне с разницей в пять калиток в Мирпуре и завоевала свой пятый континентальный титул.
18:30 IST
В воскресенье Шри-Ланка завоюет шестой титул Кубка Азии, приближаясь к рекордным семи титулам Индии. Тем временем Пакистан надеется занять третье место.
Шри-Ланка в Кубке Азии
👉11-кратный Финалист
👉5-кратный Чемпион6-й титул ███░░⏳#RoaringForGlory#SLvPAKpic.twitter.com/raLPS9bzHd
— Шри-Ланка Крикет 11, 2022Идет подготовка к #AsiaCup2022Final. pic.twitter.com/hspLNbIts5
— Аян (@ayan_acharya13) 11 сентября 2022 г.ШРИ-ЛАНКА ПРОТИВ ПАКИСТАНА DREAM11 FANTASY TEAM
Калитки: Кусал Мендис, Мохаммад Ризван
Боттеры: Бханука Раджапакса, Бабар Азам, Патхум Ниссанка
Универсалы: Ванинду Хасаранга (к), Шадаб Хан (вк), Мохаммад Наваз
Боулеры, Махеш Рауфша6, Насим Шаххна 9146
17:57 IST
ШРИ-ЛАНКА ПРОГНОЗ XI: Патхум Ниссанка, Кусал Мендис (рабочий), Чарит Асаланка/Дхананджая де Силва, Данушка Гунатилака, Бханука Раджапакса, Дасун Шанака (с), Ванинду Хасаранга, Чамика Каруна Махиш Тикшана, Прамод Мадушан/Асита Фернандо, Дилшан Мадушанка.
ПАКИСТАН ПРОГНОЗ XI: Мохаммад Ризван (жк), Бабар Азам (с), Фахар Заман, Ифтихар Ахмед, Шадаб Хан, Мохаммад Наваз, Асиф Али, Хушдил Шах, Харис Рауф, Насим Шах, Мохаммад Хаснайн.
ФИНАЛ КУБКА АЗИИ 2022 ТАКТИЧЕСКИЙ ОБЗОР
Пакистан сыграет со Шри-Ланкой в финале Кубка Азии 2022 года на Дубайском международном крикетном стадионе в воскресенье. Две команды встретились в последней игре Super 4 в одном и том же месте в пятницу и поделились тактикой, которая может повлиять на сегодняшний финал. Вот четыре тактических хода, которые могут оказать существенное влияние на результат.
ЧИТАЙТЕ ТАКЖЕ | Шри-Ланка против Пакистана Жеребьевка в прямом эфире Финал Кубка Азии 2022: выиграет ли при подбрасывании монеты Бабар Азам или Дасун Шанака?
Подобно прошлогоднему чемпионату мира T20, который проходил в Объединенных Арабских Эмиратах, команды, гонявшиеся в ночных матчах в Дубае на Кубке Азии, одержали верх, выиграв шесть из восьми матчей.
У погони в ОАЭ есть явное преимущество, где роса, как правило, облегчает отбивание второй возможности. В последнем матче, сыгранном в Дубае, Пакистан бил первым и изо всех сил пытался вырваться на изнашиваемой поверхности, которая использовалась во второй раз за столько же ночей. Но воскресный финал будет на свежей калитке. Команда, отбивающая здесь первой, должна отказаться от осторожного отбивания первой возможности.
Кого вы выберете, чтобы поднять трофей #AsiaCup2022? 🏆#SLvPAK#AsiaCup
— Sportstar (@sportstarweb) 11 сентября 2022 г.Пакистан выиграл один и проиграл два матча, забив первым, набрав 7,3 балла в PowerPlay и проиграв четыре калитки. Шри-Ланка, с другой стороны, предпочла погоню и била первой только один раз в первом матче турнира против Афганистана, который она проиграла. Показатель пробега Шри-Ланки в PowerPlay в этом матче составил 6,83, и она потеряла три калитки в первых шести оверах. Таким образом, то, как люди Дасуна Шанаки реагируют на вызов отбить первыми, если они будут вставлены, может стать решающим фактором.
С 2021 года среднее количество выигрышей в первом иннинге в Дубае превышает 19.0. Команды, отбивающие первыми, будут стремиться к чему-то в диапазоне 180-200, чтобы чувствовать себя комфортно.
ЧИТАЙТЕ ТАКЖЕ | Пакистан — Шри-Ланка. Кубок Азии 2022. Финал: личные встречи PAK и SL, статистика он был лучшим отбивающим своей команды и ее самым результативным игроком на данный момент — 226 пробежек в пяти матчах. Если Ризван будет бить глубоко, он либо очень выгодно сравняется с офф-спиннером из Шри-Ланки Махишем Тексаной, которого обычно сдерживали для средних оверов и смерти, либо Дханаджайя де Сильва. Это будет иметь решающее значение, потому что, если шри-ланкийцы не вытащат Ризвана раньше, он может навредить им смертью, когда он набирает более 180 фунтов на этом Кубке Азии. Против Шри-Ланки, в последнем матче Super 4, Ризван был пойман в четвертом овере, и возможности Пакистана так и не взлетели.
И Пакистан, и Шри-Ланка будут предлагать здоровую диету в виде боулинга в финале.
Тем не менее, оба набора отбивающих имеют довольно обычные средние показатели и количество ударов по сравнению с твикерами на этом Кубке Азии. Пакистан и Шри-Ланка потеряли 13 и 16 калиток соответственно, в среднем 26,07 и 21,81. Что делает эту дуэль более заманчивой, так это распределение левых и правых отбивающих в первой семерке обеих команд. Чарит Асаланка был исключен из игры в последнем матче Super 4 против Пакистана, но с ним в составе обе команды будут иметь по три отбивающих-левши в своей семерке лучших, что побудит обоих шкиперов использовать варианты перерыва и перелома ноги. с умом.
Насим Шах вернется в финал, отдохнув перед последним матчем Super 4. Харис Рауф и Насим делят между собой семь калиток в PowerPlay этого Кубка Азии, при этом набирая менее восьми очков за овер. Первые игроки Кусал Мендис и Патхум Ниссанка сыграли решающую роль в быстром старте Шри-Ланки в PowerPlay на этом турнире. На данный момент они достигли уровня 143 забастовок и в среднем 41,6 при четырех пятидесятых.


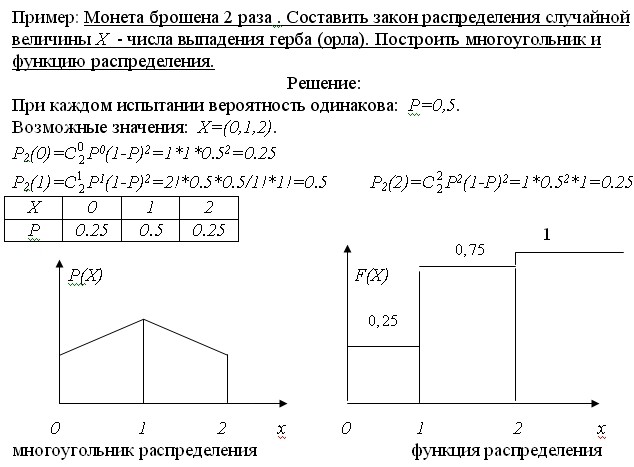
 Кому-то из них достанется первый номер. Вероятность того, что его вытянет китайская спортсменка равна 5 к 20, то есть 5/20 (поскольку из Китая — 5 спортсменок).
Кому-то из них достанется первый номер. Вероятность того, что его вытянет китайская спортсменка равна 5 к 20, то есть 5/20 (поскольку из Китая — 5 спортсменок). Из России приехало трое, значит благоприятных исходов три. Вероятность того, что восьмым окажется доклад ученого из России 3 к 10 или 0,3.
Из России приехало трое, значит благоприятных исходов три. Вероятность того, что восьмым окажется доклад ученого из России 3 к 10 или 0,3. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.009 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.009 с.)

 Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.





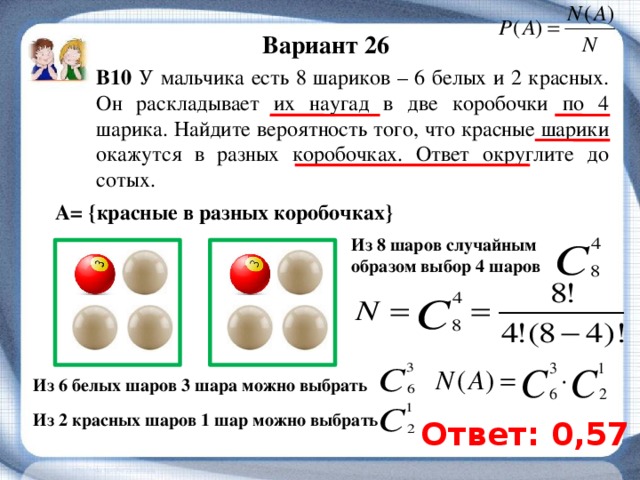




 Ответ: 0, 14.
Ответ: 0, 14.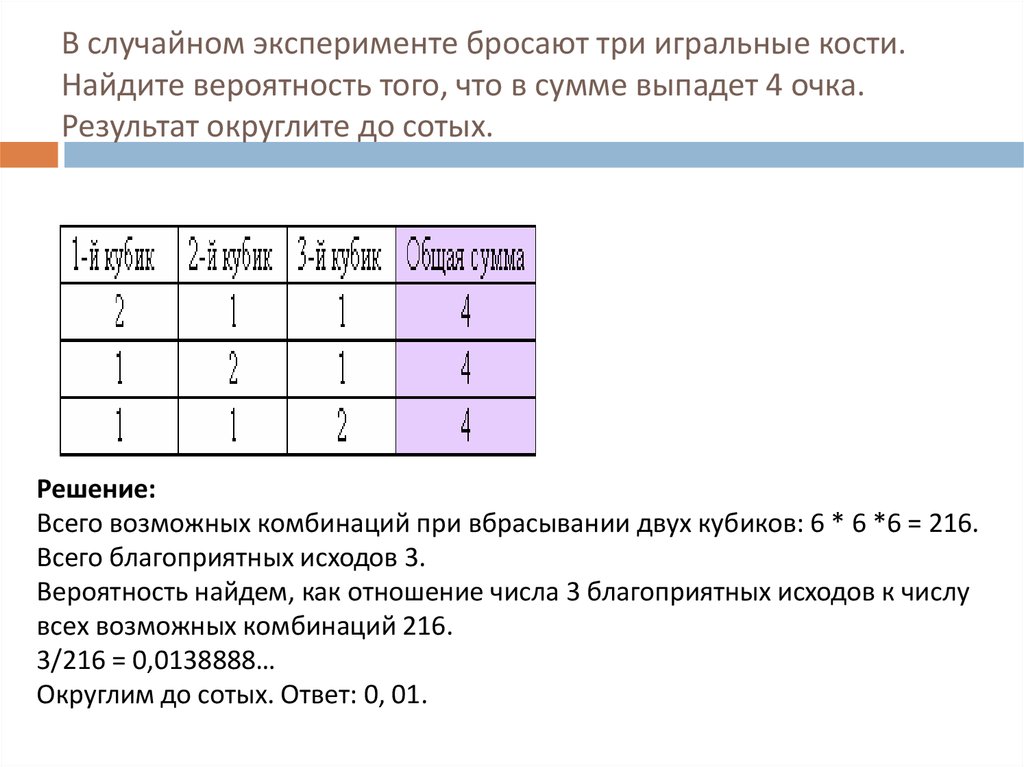

 Определите вероятность того, что при двух бросках выпадет разное количество очков. Результат округлите до сотых.
Определите вероятность того, что при двух бросках выпадет разное количество очков. Результат округлите до сотых. Всего исходов 36.
Всего исходов 36. 
 Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.

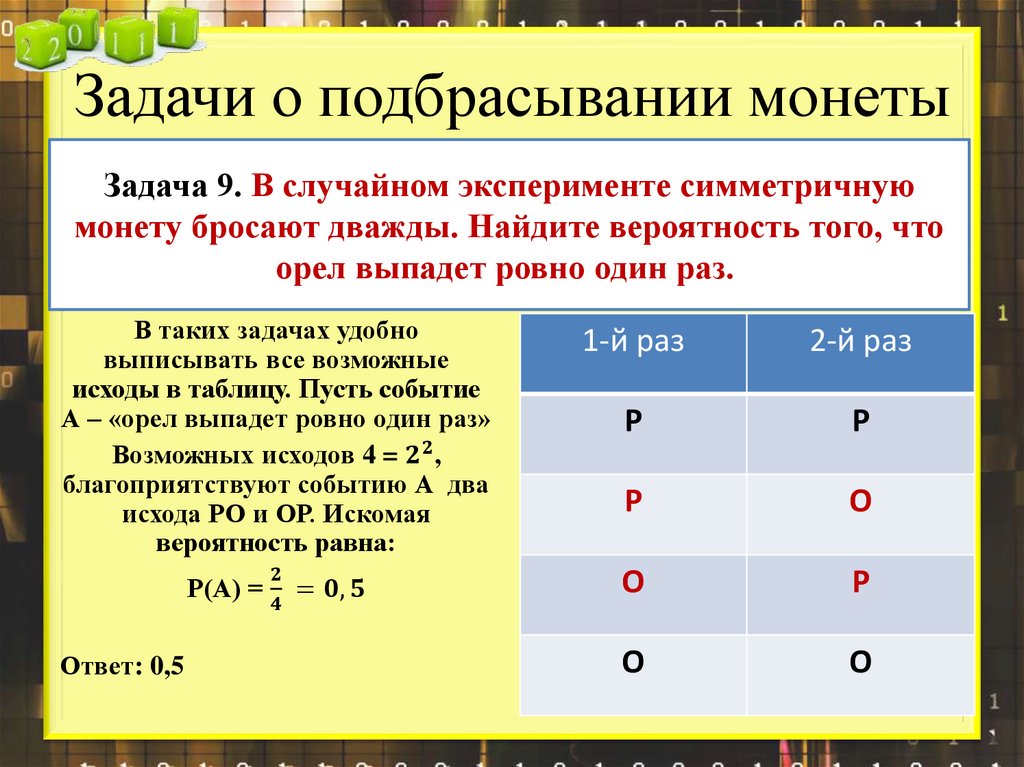


 Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
 Выписываются все комбинации орлов и решек, после чего выбираются нужные;
Выписываются все комбинации орлов и решек, после чего выбираются нужные; Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
 Это называется случайным экспериментом. Например: при подбрасывании монеты выпадает либо орел, либо решка, но нельзя быть уверенным, что выпадет только орел или выпадет решка.
Это называется случайным экспериментом. Например: при подбрасывании монеты выпадает либо орел, либо решка, но нельзя быть уверенным, что выпадет только орел или выпадет решка.
 Давайте проверим это. Для 2 монет есть четыре чистых результата {HH, TH, HT, TT}, поскольку на первой монете может произойти решка или погоня. Аналогично для второй монеты. поэтому из приведенной выше оболочки нужно узнать вероятность правила
Давайте проверим это. Для 2 монет есть четыре чистых результата {HH, TH, HT, TT}, поскольку на первой монете может произойти решка или погоня. Аналогично для второй монеты. поэтому из приведенной выше оболочки нужно узнать вероятность правила Найдем вероятность выпадения 1 решки при использовании 2 монет вероятность погони = 0,5 общее количество попыток = 2 вероятность угнать = 0,5 Таким образом, вероятность равна = 2C1 × (0,5) 1 × (1 – 0,5) 1 =0,5 Найдем вероятность получения 1 корма при использовании 3 монет. всего испытаний 3, благоприятный тест 1
Найдем вероятность выпадения 1 решки при использовании 2 монет вероятность погони = 0,5 общее количество попыток = 2 вероятность угнать = 0,5 Таким образом, вероятность равна = 2C1 × (0,5) 1 × (1 – 0,5) 1 =0,5 Найдем вероятность получения 1 корма при использовании 3 монет. всего испытаний 3, благоприятный тест 1 Найдите вероятность выпадения 5 орлов. Решение:
Найдите вероятность выпадения 5 орлов. Решение:  09.2022
&пуля;
09.2022
&пуля; 09.2022
&пуля;
09.2022
&пуля; 1 приведено в учебнике NCERT.
1 приведено в учебнике NCERT. 1
1 1 Class 10 Probability Solutions NCERT или сохранить изображения решения и взять распечатку, чтобы держать ее под рукой. подготовка к экзамену.
1 Class 10 Probability Solutions NCERT или сохранить изображения решения и взять распечатку, чтобы держать ее под рукой. подготовка к экзамену. 15.1 Класс 10 Математика Вопрос 4.
15.1 Класс 10 Математика Вопрос 4.  Какова вероятность того, что извлеченный шар
Какова вероятность того, что извлеченный шар  1 Класс 10 Математика Вопрос 12.
1 Класс 10 Математика Вопрос 12.  Затем случайным образом выбирается одна карта.
Затем случайным образом выбирается одна карта.  1 Класс 10 Математика Вопрос 18.
1 Класс 10 Математика Вопрос 18.  Продавец наугад берет одну ручку и дает ей. Какова вероятность того, что
Продавец наугад берет одну ручку и дает ей. Какова вероятность того, что  Какова вероятность того, что
Какова вероятность того, что 

 1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
 Мы много на него накидали. Мы не сдерживаемся с точки зрения того, что у нас есть он в нескольких разных ролях. В первую очередь, я думаю, что он будет больше на месте, а затем я думаю, что мы будем использовать его в струйных вещах… Я в восторге от того, куда он может пойти».
Мы много на него накидали. Мы не сдерживаемся с точки зрения того, что у нас есть он в нескольких разных ролях. В первую очередь, я думаю, что он будет больше на месте, а затем я думаю, что мы будем использовать его в струйных вещах… Я в восторге от того, куда он может пойти».
 Это нападение, которому не хватает стабильного производства в широких масштабах, и бывший продукт Clemson смотрит в тяжелую битву.
Это нападение, которому не хватает стабильного производства в широких масштабах, и бывший продукт Clemson смотрит в тяжелую битву. Как только Лазар вернется, корона будет передана № 13.
Как только Лазар вернется, корона будет передана № 13. Там ничего удивительного.
После этого тренер Packers Мэтт Лафлер похвалил одного из своих игроков. Он не был направлен ни на кого предсказуемого — ни на Аарона Джонса, который набрал 170 ярдов от схватки, ни на конкретного парня.
Там ничего удивительного.
После этого тренер Packers Мэтт Лафлер похвалил одного из своих игроков. Он не был направлен ни на кого предсказуемого — ни на Аарона Джонса, который набрал 170 ярдов от схватки, ни на конкретного парня. Через неделю после того, как Аарон Джонс отошел на второй план в плане игры Packers, выбор в пятом раунде 2017 года напомнил остальной части НФЛ, что, несмотря на потерю одного суперзвездного игрока, этот
Через неделю после того, как Аарон Джонс отошел на второй план в плане игры Packers, выбор в пятом раунде 2017 года напомнил остальной части НФЛ, что, несмотря на потерю одного суперзвездного игрока, этот
 Первый мяч широкой опущенной ногой. ЧЕТЫРЕ! Насим идет на удар по ноге и получает мощный внешний край, который убегает к границе третьего человека. ВНЕ! Насим отрабатывает этот полный бросок прямо на дальнего полевого игрока. Более медленный снаружи, и Хаснайн побежден. Он попадает в цель с синглом, когда он очищает переднюю ногу и забивает ее в дальний удар. ЧЕТЫРЕ! Харис Рауф разбивает это до предела. Полевой игрок в глубине пробежал слишком много, чтобы поймать мяч, и в итоге пропустил четыре попытки. Это также не мяч, так как срабатывает зуммер. Приближается бесплатный удар, и вышибала из Мадушана и Уайда заколлировали. ШЕСТЬ! Мяч более медленной длины, и Хаснайн выжидает и отбивает его по максимуму.
Первый мяч широкой опущенной ногой. ЧЕТЫРЕ! Насим идет на удар по ноге и получает мощный внешний край, который убегает к границе третьего человека. ВНЕ! Насим отрабатывает этот полный бросок прямо на дальнего полевого игрока. Более медленный снаружи, и Хаснайн побежден. Он попадает в цель с синглом, когда он очищает переднюю ногу и забивает ее в дальний удар. ЧЕТЫРЕ! Харис Рауф разбивает это до предела. Полевой игрок в глубине пробежал слишком много, чтобы поймать мяч, и в итоге пропустил четыре попытки. Это также не мяч, так как срабатывает зуммер. Приближается бесплатный удар, и вышибала из Мадушана и Уайда заколлировали. ШЕСТЬ! Мяч более медленной длины, и Хаснайн выжидает и отбивает его по максимуму. ВНЕ! Шадаб летает по воздуху и над укрытиями, и его забирает Гунатилака.
ВНЕ! Шадаб летает по воздуху и над укрытиями, и его забирает Гунатилака. На этот раз снова медленнее, Ризван выходит раньше и просто успевает щелкнуть ногой на один раз.
На этот раз снова медленнее, Ризван выходит раньше и просто успевает щелкнуть ногой на один раз. Отличный бросок с офф-спиннера, так как от него отрывается всего три прогона. Давление на Пакистан нарастает, поскольку процентная ставка превышает 11,4.
Отличный бросок с офф-спиннера, так как от него отрывается всего три прогона. Давление на Пакистан нарастает, поскольку процентная ставка превышает 11,4.