Умножение чисел с отрицательными степенями: Свойства отрицательных степеней. Как умножать отрицательные степени. Деление отрицательных степеней. Степени чисел

3 = 8 .

Примеры для решения:

Содержание

Возведение в степень презентация

Презентация по возведению в степень, рассчитанную на семиклассников. Презентация может разъяснить некоторые непонятные моменты, но, вероятно, таких моментов не будет благодаря нашей статье.

Итог

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:

Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.

Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.

С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.

Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».

Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам.

На языке Зенона это выглядит так:

За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.

Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.

Другая интересная апория Зенона повествует о летящей стреле:

Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.

В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.

среда, 4 июля 2018 г.

Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.

Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.

Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.

Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.

Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…

А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.

Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.

Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».

воскресенье, 18 марта 2018 г.

Сумма цифр числа — это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.

Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа». Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.

Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.

1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.

2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки — это не математическое действие.

3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.

4. Складываем полученные числа. Вот это уже математика.

Сумма цифр числа 12345 равна 15. Вот такие вот «курсы кройки и шитья» от шаманов применяют математики. Но это ещё не всё.

С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.

Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.

Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.

Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.

Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.

Табличка на двери Открывает дверь и говорит:

Ой! А это разве не женский туалет?
— Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх. Какой еще туалет?

Женский… Нимб сверху и стрелочка вниз — это мужской.

Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,

Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:

Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.

1А — это не «минус четыре градуса» или «один а». Это «какающий человек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.

Со школы всем нам известно правило о возведении в степень: любое число с показателем N равно результату перемножения данного числа на самого себя N-ное количество раз. Иными словами, 7 в степени 3 — это 7, умноженное на себя три раза, то есть 343. Еще одно правило — возведение любой величины в степень 0 дает единицу, а возведение отрицательной величины представляет собой результат обычного возведения в степень, если она четная, и такой же результат со знаком «минус», если она нечетная.

Правила же дают и ответ, как возводить число в отрицательную степень. Для этого нужно возвести обычным способом нужную величину на модуль показателя, а потом единицу поделить на результат.

Из этих правил становится понятно, что выполнение реальных задач с оперированием большими величинами потребует наличия технических средств. Вручную получится перемножить на самого себя максимум диапазон чисел до двадцати-тридцати, и то не более трех-четырех раз. Это не говоря уж о том, чтобы потом еще и единицу разделить на результат. Поэтому тем, у кого нет под рукой специального инженерного калькулятора, мы расскажем, как возвести число в отрицательную степень в Excel.

Решение задач в Excel

Для разрешения задач с возведением в степень Excel позволяет пользоваться одним из двух вариантов. -C2.

Второй вариант — использование готовой функции «Степень», принимающей два обязательных аргумента — число и показатель. Чтобы приступить к ее использованию, достаточно в любой свободной ячейке поставить знак «равно» (=), указывающий на начало формулы, и ввести вышеприведенные слова. Осталось выбрать две ячейки, которые будут участвовать в операции (или указать конкретные числа вручную), и нажать на клавишу Enter. Посмотрим на нескольких простых примерах.

Формула

Результат

СТЕПЕНЬ(B2;C2)

СТЕПЕНЬ(B3;C3)

0,002915

Как видим, нет ничего сложного в том, как возводить число в отрицательную степень и в обычную с помощью Excel. Ведь для решения данной задачи можно пользоваться как привычным всем символом «крышечка», так и удобной для запоминания встроенной функцией программы. Это несомненный плюс!

Перейдем к более сложным примерам. Вспомним правило о том, как возводить число в отрицательную степень дробного характера, и увидим, что эта задача очень просто решается в Excel.

Дробные показатели

Если кратко, то алгоритм вычисления числа с дробным показателем следующий.

Преобразовать дробный показатель в правильную или неправильную дробь.
Возвести наше число в числитель полученной преобразованной дроби.
Из полученного в предыдущем пункте числа вычислить корень, с условием, что показателем корня будет знаменатель дроби, полученной на первом этапе.

Согласитесь, что даже при оперировании малыми числами и правильными дробями подобные вычисления могут занять немало времени. Хорошо, что табличному процессору Excel без разницы, какое число и в какую степень возводить. C$3».

Число / Степень

Обратите внимание, что положительные числа (даже нецелые) без проблем вычисляются при любых показателях.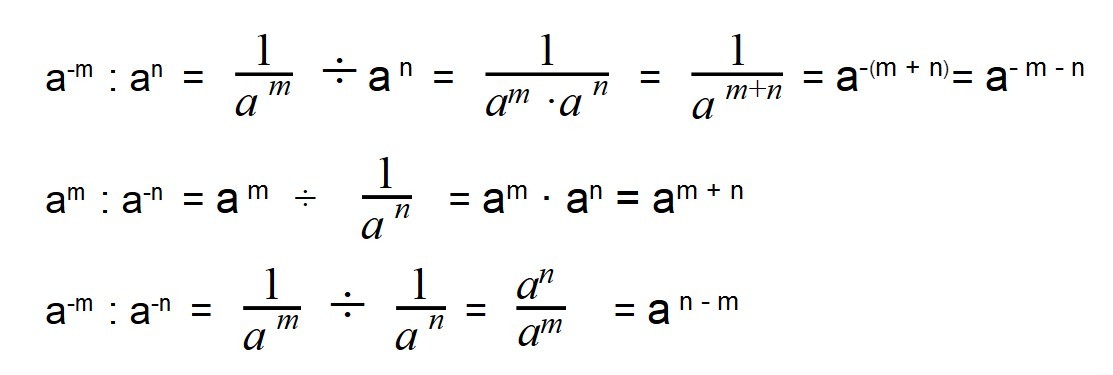 {a}ix=cosax+isinax} , где i = (− 1) {\displaystyle i={\sqrt {(}}-1)} ; е — константа, примерно равная 2,7; а — произвольная постоянная. Доказательство этого равенства можно найти в любом учебнике по высшей математике.

Предупреждения

При увеличении показателя степени ее значение сильно возрастает. Поэтому если ответ кажется вам неправильным, на самом деле он может оказаться верным. Вы можете проверить это, построив график любой показательной функции, например, 2 x .

Что делать с отрицательными степенями при умножении. Отрицательная степень числа: правила возведения и примеры

Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c является n -ной степенью числа a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

(a/b) n = a n /b n .

5. Возводя степень в степень, показатели степеней перемножают:

(a m) n = a m n .

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:

Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .

Например . a 4:a 7 = a 4 — 7 = a -3 .

Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.

Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а . 5 = 40*40*40*40*40/(-29)*(-29)*(-29)*(-29)*(-29) = 102400000/(-20511149) = -4,9924.

В данном случае, мы видим, что модуль продолжает расти , а вот знак зависит от чётности или нечётности показателя.

Следует заметить, если мы возводим единицу, то она всегда останется сама собой. В случае, если нужно возвести число минус один, то при чётном показателе степени она превратится в единицу, при нечётном останется минус единицей.

Возведение в целую отрицательную степень если модуль больше единицы

Для цифр, чей модуль больше единицы, есть свои особенности действий. Прежде всего, нужно целую часть дроби перевести в числитель, то есть перевести в неправильную дробь. Если у нас имеется десятичная дробь, то её необходимо перевести в обычную. Делается это следующим образом:

6 целых 7/17 = 109/17;
2,54 = 254/100.

Теперь рассмотрим, как возвести число в отрицательную степень в данных условиях. Уже из вышеизложенного, мы можем предположить, чего нам ждать от результата вычислений. 3) = 1/rad64 = 1/8.

В этом случае, нужно иметь в виду, что извлечение корней высокого уровня возможно только в специально подобранном виде и, скорее всего, избавиться от знака радикала (корня квадратного, кубического и так далее) при точных вычислениях вам не удастся.

Все же, подробно изучив предыдущие главы, сложностей в школьных вычислениях ожидать не стоит.

Следует заметить, что под описание данной главы подходит и возведение с заведомо иррациональным показателем , например, если показатель равен минус ПИ. Действовать нужно по вышеописанным принципам. Однако, вычисления в подобных случаях становятся настолько сложными, что под силу только мощным электронно-вычислительным машинам.

Заключение

Действие, которое мы изучали, является одной из самых сложнейших задач в математике (особенно в случае дробно-рационального или иррационального его значения). Однако, подробно и пошагово изучив данную инструкцию, можно научиться без особых проблем проделывать это на полном автомате.

В одной из предыдущих статей мы уже упоминали о степени числа. Сегодня мы постараемся сориентироваться в процессе нахождения ее значения. Научно говоря, мы будем выяснять, как правильно возводить в степень. Мы разберемся, как производится этот процесс, одновременно затронем все вероятные показатели степени: натуральный, иррациональный, рациональный, целый.

Итак, давайте подробно рассмотрим решения примеров и выясним, что значит:

Определение понятия.
Возведение в отрицательную ст.
Целый показатель.
Возведение числа в иррациональную степень.

Вот точно отражающее смысл определение: «Возведением в степень называют определение значения степени числа».

Соответственно, возведение числа a в ст. r и процесс нахождения значения степени a с показателем r — это идентичные понятия. К примеру, если стоит задача вычислить значение степени (0,6)6″, то ее можно упростить до выражения «Возвести число 0,6 в степень 6».

После этого можно приступать напрямую к правилам возведения.

Возведение в отрицательную степень

Для наглядности следует обратить внимание на такую цепочку выражений:

110=0,1=1* 10 в минус 1 ст.,

1100=0,01=1*10 в минус 2 степ.,

11000=0,0001=1*10 в минус 3 ст.,

110000=0,00001=1*10 в минус 4 степeни.

Благодаря данным примерам можно четко просмотреть возможность моментально вычислить 10 в любой минусовой степени. Для этой цели достаточно банально сдвигать десятичную составляющую:

10 в -1 степeни — перед единицей 1 ноль;
в -3 — три нуля перед единицей;
в -9 — это 9 нулей и проч.

Так же легко понять по данной схеме, сколько будет составлять 10 в минус 5 ст. —

1100000=0,000001=(1*10)-5.

Как возвести число в натуральную степeнь

Вспоминая определение, учитываем, что натуральное число a в ст. n равняется произведению из n множителей, при этом каждый из них равняется a. Проиллюстрируем: (а*а*…а)n, где n — это количество чисел, которые умножаются. Соответственно, чтобы a возвести в n, необходимо рассчитать произведение следующего вида: а*а*…а разделить на n раз.

Отсюда становится очевидно, что возведение в натуральную ст. опирается на умение осуществлять умножение (этот материал освещен в разделе про умножение действительных чисел). Давайте рассмотрим задачу:

Возведите -2 в 4-ю ст.

Мы имеем дело с натуральным показателем. Соответственно, ход решения будет следующим: (-2) в cт. 4 = (-2)*(-2)*(-2)*(-2). Теперь осталось только осуществить умножение целых численностей:(-2)*(-2)*(-2)*(-2). Получаем 16.

Ответ на задачу:

(-2) в ст. 4=16.

Пример:

Вычислите значение: три целых две седьмых в квадрате.

Данный пример равняется следующему произведению: три целых две седьмых умножить на три целых две седьмых. Припомнив, как осуществляется умножение смешанных чисел, завершаем возведение:

3 целых 2 седьмых умножить на самих себя;
равно 23 седьмых умножить на 23 седьмых;
равно 529 сорок девятых;
сокращаем и получаем 10 тридцать девять сорок девятых.

Ответ: 10 39/49

Касаемо вопроса возведения в иррациональный показатель, следует отметить что расчеты начинают проводить после завершения предварительного округления основы степени до какого-либо разряда, который позволил бы получить величину с заданной точностью. К примеру, нам необходимо возвести число П (пи) в квадрат.

Начинаем с того, что округляем П до сотых и получаем:

П в квадрате = (3,14)2=9,8596. Однако если сократить П до десятитысячных, получим П=3,14159. Тогда возведение в квадрат получает совсем другое чиcло: 9,8695877281.

Здесь следует отметить, что во многих задачах нет надобности возводить иррациональные числа в cтeпeнь. Как правило, ответ вписывается или в виде, собственно, степени, к примеру, корень из 6 в степени 3, либо, если позволит выражение, проводится его преобразование: корень из 5 в 7 cтепeни = 125 корень из 5.

Как возвести чиcло в целую степень

Эту алгебраическую манипуляцию уместно принимать во внимание для следующих случаев:

для целых чисел;
для нулевого показателя;
для целого положительного показателя.

Поскольку практически все целые положительные числа совпадают с массой чисел натуральных, то постановка в положительную целую степень — это тот же процесс, что и постановка в ст. натуральную. Данный процесс мы описали в предшествующем пункте.

Теперь поговорим о вычислении ст. нулевой. Мы уже выяснили выше, что нулевую степень числа a можно определить для любого отличного от нуля a (действительного), при этом a в ст. 0 будет равно 1.

Соответственно, возведение какого угодно действительного числа в нулевую ст. будет давать единицу.

К примеру, 10 в ст.0=1, (-3,65)0=1, а 0 в ст. 0 нельзя определить.

Для того чтобы завершить возведение в целую степень, остается определиться с вариантами целых отрицательных значений. Мы помним, что ст. от a с целым показателем -z будет определяться как дробь. В знаменателе дроби располагается ст. с целым положительным значением, значение которой мы уже научились находить. Теперь остается лишь рассмотреть пример возведения.

Пример:

Вычислить значение числа 2 в кубе с целым отрицательным показателем.

Процесс решения:

Согласно определению стeпeни с отрицательным показателем обозначаем: два в минус 3 ст. равняется один к двум в третьей cтепeни.

Знаменатель рассчитывается просто: два в кубе;

3 = 2*2*2=8.

Ответ: два в минус 3-й ст. = одна восьмая.

Возведение в отрицательную степень – один из основных элементов математики, который часто встречается при решении алгебраических задач. Ниже приведена подробная инструкция.

Как возводить в отрицательную степень – теория

Когда мы число в обычную степень, мы умножаем его значение несколько раз. Например, 3 3 = 3×3×3 = 27. С отрицательной дробью все наоборот. Общий вид по формуле будет иметь следующий вид: a -n = 1/a n . Таким образом, чтобы возвести число в отрицательную степень, нужно единицу поделить на данное число, но уже в положительной степени.

Как возводить в отрицательную степень – примеры на обычных числах

Держа вышеприведенное правило на уме, решим несколько примеров.

4 -2 = 1/4 2 = 1/16
Ответ: 4 -2 = 1/16

4 -2 = 1/-4 2 = 1/16.
Ответ -4 -2 = 1/16.

Но почему ответ в первом и втором примерах одинаковый? Дело в том, что при возведении отрицательного числа в четную степень (2, 4, 6 и т.д.), знак становится положительным. Если бы степень была четной, то минус сохранился:

4 -3 = 1/(-4) 3 = 1/(-64)

Как возводить в отрицательную степень – числа от 0 до 1

Вспомним, что при возведении числа в промежутке от 0 до 1 в положительную степень, значение уменьшается с возрастанием степени. Так например, 0,5 2 = 0,25. 0,25

Пример 3: Вычислить 0,5 -2
Решение: 0,5 -2 = 1/1/2 -2 = 1/1/4 = 1×4/1 = 4.
Ответ: 0,5 -2 = 4

Разбор (последовательность действий):

Переводим десятичную дробь 0,5 в дробную 1/2. Так легче.
Возводим 1/2 в отрицательную степень. 1/(2) -2 . Делим 1 на 1/(2) 2 , получаем 1/(1/2) 2 => 1/1/4 = 4

Пример 4: Вычислить 0,5 -3
Решение: 0,5 -3 = (1/2) -3 = 1/(1/2) 3 = 1/(1/8) = 8

Пример 5: Вычислить -0,5 -3
Решение: -0,5 -3 = (-1/2) -3 = 1/(-1/2) 3 = 1/(-1/8) = -8
Ответ: -0,5 -3 = -8

Исходя из 4-го и 5-ого примеров, сделаем несколько выводов:

Для положительного числа в промежутке от 0 до 1 (пример 4), возводимого в отрицательную степень, четность или нечетность степени не важна, значение выражения будет положительным. При этом, чем больше степень, тем больше значение.
Для отрицательного числа в промежутке от 0 до 1 (пример 5), возводимого в отрицательную степень, четность или нечетность степени неважна, значение выражения будет отрицательным. При этом, чем больше степень, тем меньше значение.

Как возводить в отрицательную степень – степень в виде дробного числа

Выражения данного типа имеют следующий вид: a -m/n , где a – обычное число, m – числитель степени, n – знаменатель степени.

Рассмотрим пример:
Вычислить: 8 -1/3

Решение (последовательность действий):

Вспоминаем правило возведения числа в отрицательную степень. Получим: 8 -1/3 = 1/(8) 1/3 .
Заметьте, в знаменателе число 8 в дробной степени. Общий вид вычисления дробной степени таков: a m/n = n √8 m .
Таким образом, 1/(8) 1/3 = 1/(3 √8 1). Получаем кубический корень из восьми, который равен 2. Исходя отсюда, 1/(8) 1/3 = 1/(1/2) = 2.
Ответ: 8 -1/3 = 2

Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:

Другая интересная апория Зенона повествует о летящей стреле:

среда, 4 июля 2018 г.

Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.

воскресенье, 18 марта 2018 г.

3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.

4. Складываем полученные числа. Вот это уже математика.

Открывает дверь и говорит:

Женский… Нимб сверху и стрелочка вниз — это мужской.

Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,

Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:

Табличка на двери

Сравнение чисел с отрицательными степенями: Сравнение стандартных чисел с отрицательными степенями. Отрицательная степень числа: правила возведения и примеры — ЭкоДом: Дом своими руками

Содержание

правило, примеры, сравнение положительных и отрицательных чисел

В статье ниже озвучим принцип сравнения отрицательных чисел: сформулируем правило и применим его в решении практических задач.

Правило сравнения отрицательных чисел

В основе правила – сравнение модулей исходных данных. По сути, сравнить два отрицательных числа – значит сравнить положительные числа, равные модулям сравниваемых отрицательных чисел.

Определение 1

При сравнении двух отрицательных чисел меньшим является то число, модуль которого больше; бОльшим является то число, модуль которого меньше. Заданные отрицательные числа являются равными, если их модули равны.

Сформулированное правило применимо как к отрицательным целым числам, так и к рациональным и действительным.

Геометрическое толкование подтверждает принцип, озвученный в указанном правиле: на координатной прямой отрицательное число, которое является меньшим, находится левее, чем большее отрицательное. Это утверждение, в общем, верно для любых чисел.

Примеры сравнения отрицательных чисел

Самым простым примером сравнения отрицательных чисел является сравнение целых чисел. С подобной задачи и начнем.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 1

Необходимо сравнить отрицательные числа -65 и -23.

Решение

Согласно правилу, для осуществления действия сравнения отрицательных чисел сначала необходимо определить их модули. |-65| = 65 и |-23| = 23. Теперь сравним положительные числа, равные модулям заданных: 65 > 23. Применим вновь правило, гласящее, что больше то отрицательное число, модуль которого меньше. Таким образом, получим: -65 < -23.

Ответ: -65 < -23.

Чуть сложнее сравнивать отрицательные рациональные числа: действие в конечном счете приводит к сравнению обыкновенных или десятичных дробей.

Пример 2

Необходимо определить, какое из заданных чисел больше: -4314или-4,7.

Решение

Определим модули сравниваемых чисел. -4314=4314 и |-4,7| = 4,7. Теперь сравним полученные модули. Целые части дробей равны, так что приступим к сравнению дробных частей: 314 и 0,7. Осуществим перевод десятичной дроби 0,7 в обыкновенную: 710, найдем общие знаменатели сравниваемых дробей, получим: 1570и4970. Тогда результатом сравнения станет: 1570<4970 или 314<0,7. Таким образом, 4314<4,7.fff Применив правило сравнения отрицательных чисел, имеем: -4314<-4,7

Также можно было осуществить сравнение путем перевода обыкновенной дроби в десятичную. Разница – лишь в удобстве вычисления.

Ответ: -4314<-4,7

Сравнение отрицательных действительных чисел производится согласно тому же правилу.

6 класс. Математика. Сравнение чисел — Сравнение чисел

Комментарии преподавателя

Положительные числа мы используем для обозначения разных количеств – целых и дробных. Например, три яблока, полтора литра молока.

Отрицательных количеств не существует. Отрицательные числа – это инструмент для упрощения расчетов.

Например, таких:

Ключ имеет одну функцию – открывать или закрывать замок. Если нет замка, то ключ практически бесполезен, ему трудно найти применение.

Так и отрицательные числа – без самого «замка», без различных математических расчетов они используются не очень много.

Тем не менее есть и прямое применение отрицательным числам. Вы можете пройти по ссылке, где мы обсуждаем использование отрицательных чисел в окружающем мире.

Как мы понимали, что одно положительное число больше другого?

Из 8 яблок можно взять 5 яблок. 5 – это часть восьми. Поэтому мы с вами и знаем, что 5 меньше 8.

Но про числа -8 и -5 нельзя сказать, что одно – часть другого. Отрицательного количества не существует.

Но что же такое тогда отрицательное число?

Отрицательное число – это и число, и знак вычитания.

Что значит к 10 добавить -8?

Это значит вычесть 8.

А добавить -5 – означает вычесть 5.

Мы к одному и тому же числу 10 добавили два разных отрицательных. Во втором случае результат был больше. Естественно считать, что второе отрицательное число было больше.

То есть чем большее число мы вычитаем, тем меньше будет результат. Это очевидно, но если это записать на языке отрицательных чисел, то мы и получим правила их сравнения.

Сформулируем теперь правила, как сравнивать отрицательные числа друг с другом или с положительными.

1. Все отрицательные числа меньше всех положительных. Между ними находится ноль. То есть ноль меньше любого положительного числа, но больше любого отрицательного.

Почему это так?

Если мы к числу прибавляем положительное число, то число увеличится; если ноль, то не изменится; если вычтем положительное, то число уменьшится. Но добавление отрицательного числа и означает вычитание.

2. Чем больше положительное число, тем меньше противоположное ему отрицательное число.

Например, , поэтому .

Это и понятно, ведь если отнять 20, то результат будет меньше, чем если отнять 10.

Если у числа не обращать внимания на знак, то получающееся число мы называем модулем.

У числа -23 и у 23 одинаковые модули, 23.

Тогда про отрицательные числа можно сказать и так.

Из двух отрицательных чисел меньше то, у которого больше модуль.

Вернемся к такой функции чисел, как порядок.

Когда мы едем по дороге, то через равные промежутки нам встречаются километровые столбы с обозначением пройденного расстояния. В математике мы сделали аналог такой дороги – числовой луч. Числа на луче соответствуют точкам, и наоборот.

«Одно число больше другого» теперь означает, что «одна точка правее другой». Чем правее точка, тем больше соответствующее ей число, мы это число называем координатой (см. рис. 1).

Рис. 1. Числовой луч

Теперь, когда у нас есть отрицательные числа, мы можем расширить нашу модель. Вместо луча мы уже берем целую прямую и влево от нуля откладываем отрицательные числа.

Правило «чем правее точка, тем больше число» сохраняется и для левой части прямой.

Точка с координатой -5 правее точки с координатой -8. Это эквивалентно тому, что .

Шкала уличного термометра – пример, как такую числовую прямую можно применить в жизни (см. рис. 2).

Рис. 2. Термометр

Потренируемся сравнивать числа.

1. 25 641 и -25 642

Тут все просто: отрицательное число всегда меньше положительного.

2. -25 641 и -25 642

Оба числа отрицательны. Значит, нужно сравнить их модули. У второго числа модуль больше, значит, само число меньше.

3. -75,47 и -75,53

4. и

Сначала сравним модули этих чисел:

Разложим на множители оба знаменателя. Общий знаменатель – это три тройки и одна пятерка. Домножим у первой дроби числитель и знаменатель на две тройки, а у второй – на 5.

Получаем две дроби с одинаковыми знаменателями. Считать их не будем. Но числитель первой дроби больше второго.

Первая дробь больше.

Значит:

И тогда:

Итак, подведем итог.

Отрицательные числа появляются как инструмент, упрощающий вычисления.
Договоренность про сравнение этих чисел следующая:

1) Любое отрицательное число меньше любого положительного.

2) Ноль находится между всеми отрицательными и всеми положительными числами (больше любого отрицательного и меньше любого положительного).

3) Из двух отрицательных чисел больше то, у которого меньше модуль.

Кроме того, что отрицательные числа упрощают вычисления, в обычной жизни им тоже нашли применение. Например, для упорядочивания, для обозначения температуры по шкале Цельсия, этажей ниже первого

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/polozhitelnye-i-otricatelnye-chisla/sravnenie-chisel-2?seconds=0&chapter_id=1825

источник видео — http://www.youtube.com/watch?v=y2fR98kHaAM

источник презентации — http://5klass. net/zip/matematika/Sravnenie-chisel-6-klass.zip

Как сравнивать степени | Логарифмы

Как сравнивать степени с одинаковыми основаниями? С одинаковыми показателями? Можно ли сравнить степени, если и основания, и показатели различны?

Как и сравнение логарифмов, сравнение степеней основано на свойстве показательной функции.

Сравнение степеней с одинаковыми основаниями

Если основание степени больше единицы (a>1), показательная функция возрастает, большему значению аргумента соответствует большее значение функции, соответственно, знак неравенства между показателями степеней и между степенями одинаковый.

Если основание степени меньше единицы (0<a<1), функция убывает, большему значению аргумента соответствует меньшее значение функции, знак неравенства между показателями степеней противоположен знаку между степенями.

С помощью схемы сравнение степеней с равными основаниями можно изобразить так:

Примеры.

№1. Сравнить значения выражений:

Решение:

Сравниваем показатели степеней: 1,5<1,9.

Основание a=2/7 меньше единицы, функция убывает, знак неравенства между степенями меняется на противоположный:

Решение:

Сравниваем показатели степеней:

Основание a=5,2 больше единицы, функция возрастает, знак неравенства между степенями не меняется:

№2. Сравнить показатели m и n, если известно, что для степеней выполняется неравенство:

Решение:

Основание a=0,21<1, функция убывает, поэтому знак неравенства между показателя степеней нужно изменить на противоположный: m>n.

Решение:

Основание

функция возрастает, поэтому знак неравенства между показателями степеней не изменяется: m<n.

Сравнение степеней с одинаковыми показателями.

1) Для возрастающих функций ( x>0):

Пример.

Для положительных значений аргумента

например,

Для отрицательных значений аргумента

например,

2) Для убывающих функций:

Пример.

Для положительных значений аргумента

например,

Для отрицательных значений аргумента:

например,

Как сравнивать степени, если и основания, и показатели различны?

Можно попробовать, например, сравнить каждую из степеней с единицей. Любая степень с основанием, большим единицы, при положительных значениях аргумента принимает значения, большие единицы:

при отрицательных — меньшие 1:

Если основание меньше единицы — соответственно,

Пример.

Сравнить

Решение:

В алгебре сравнивать степени чаще всего приходится при решении показательных неравенств.

Как решать показательные неравенства, мы рассмотрим позже.

Задание 6 ОГЭ по математике. Числа и вычисления.

Задача 6 ОГЭ по математике называется «Числа и вычисления». Это действия с обыкновенными и с десятичными дробями. Действия со степенями. Сравнение чисел.

Приступим к решению задач.

Пример 1. Найдите значение выражения

Решение. Вспоминаем, что при вычитании дробей нужно их привести к общему знаменателю, а при делении дробей первую из них умножаем на перевёрнутую вторую.

Посчитаем, чему равен знаменатель.

Получим:

Ответ: 0,9.

Пример 2. Соотнесите обыкновенные дроби с равными им десятичными дробями.

А.	Б.	В.	Г.
1) 0,5	2) 0,02	3) 0,12	4) 0,625

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Решение.Каждую из данных обыкновенных дробей можно представить в виде десятичной, например, используя деление в столбик.

Итак, деление выполнено. Сопоставим полученные результаты:

Ответ: 4312.

Замечание 1. Преобразование обыкновенных дробей в десятичные можно произвести и без деления в столбик. Т. к. любая десятичная дробь записывается как обыкновенная со знаменателем 10, 100, 1000 и т. д., то данные обыкновенные дроби можно «доделать» до десятичных. Для этого используем основное свойство дроби: дробь не изменится, если её числитель и знаменатель домножить на одно и тоже число.

Замечание 2. В этой задаче можно было, наоборот, преобразовывать заданные десятичные дроби в обыкновенные путём упрощения, т. е. сокращения числителя и знаменателя.

Выбирайте любой способ. Здесь важен правильный результат!

Для выполнения следующих заданий нам потребуются свойства степеней. Напомним основные из них.

Степенью называется выражение вида

Здесь a — основание степени, c — показатель степени.
По определению,

Возвести число в квадрат — значит умножить его само на себя:

Возвести число в куб — значит умножить его само на себя три раза:

Возвести число в натуральную степень n — значит умножить его само на себя n раз:

По определению,

Это верно для Выражение не определено.

Определим, что такое степень с целым отрицательным показателем.

Конечно, все это верно для поскольку на ноль делить нельзя.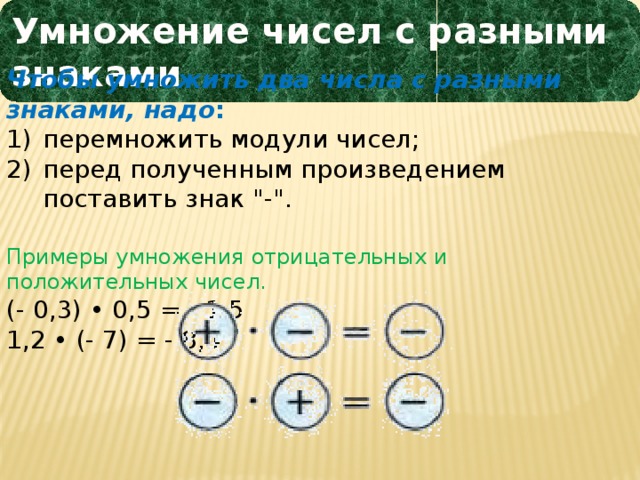

Соберем свойства степеней и основные формулы в одной таблице.

Пример 3. Найдите значение выражения

Решение. Вычислим, используя свойства степеней:

Ответ: 3328.

Пример 4. Найдите значение выражения

Решение.Вычислим, используя свойства степеней:

Ответ: 0,5604.

Пример 5. Найдите значение выражения

Решение. Вычислим, используя свойства степеней:

Ответ: 81.

Математический калькулятор. Подробный онлайн калькулятор всех математических операции.

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

С ← ( ) ±

7 8 9 ÷ %

4 5 6 х √

1 2 3 — x²

0 . = + ¹/_x

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x²	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
¹/_x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Пример:

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Пример:

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Пример:

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Пример:

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Пример:

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Пример:

Возведение в квадрат целого числа { (3) ² = 9 }

Возведение в квадрат десятичных дробей { (2,2) ² = 4,84 }

Перевод в десятичные дроби.

Пример:

{ 1/3 = 0,33 }

{ ½ = 0,5 }

Вычисление процентов от числа

Пример:

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Алгебра.

Урок 1. Числа и вычисления

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Действия с дробями

Действия со степенями

Примеры решений заданий из ОГЭ

Понятие обыкновенной, десятичной, смешанной дроби.

Обыкновенная дробь – дробь вида

где число a – числитель дроби, число b – знаменатель.
Примеры:

12;65;31;715.

Обыкновенная дробь может быть правильной или неправильной, сократимой или несократимой:

Дробь называется правильной, если числитель (a) меньше знаменателя (b).
Примеры:

56;34.

Дробь называется неправильной, если числитель (a) больше знаменателя (b).
Примеры:

65;31.

Основное свойство обыкновенной дроби:

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число (натуральные числа – числа, которые используются при счете: 1, 2, 3, …), то получится дробь, равная данной.

Дробь называется сократимой, если числитель и знаменатель имеют общие множители (числитель и знаменатель можно поделить на одно и то же число).
Примеры сократимых дробей:

1216=3?44?4=34

2114=3?72?7=32

Дробь называется несократимой, если числитель и знаменатель дроби не имеют общих множителей.
Примеры несократимых дробей:

25;911;125126.

Дробь называется смешанной, если у нее есть целая часть. То есть саму дробь можно представить в виде суммы целого числа и обыкновенной дроби.
Примеры смешанных дробей:

312;278;901277.

Смешанную дробь всегда можно перевести в неправильную обыкновенную дробь.

312=3⋅2+12=72

278=2⋅8+78=238

901277=90⋅77+1277=694277

Дробь называется десятичной, если она представлена в десятичной записи.
Примеры десятичных дробей:

56,002; 4,125; 12,3; 0,01.

Десятичную дробь всегда можно перевести в смешанную дробь или в обыкновенную дробь с числителем и знаменателем. Так поступают, когда необходимо совершить действие между обыкновенной дробью и десятичной.

Перевод в смешанные дроби:

56,002=5621000=561500

Перевод в обыкновенные дроби:

12,3=12310=12⋅10+310=123100,01=1100

Сложение и вычитание дробей.

Для того, чтобы складывать и вычитать смешанные дроби между собой, необходимо действовать следующим образом:

превратить дроби из смешанных в неправильные, если такие дроби есть,
например: \[2\frac{7}{8} = \frac{{2 \cdot 8 + 7}}{8} = \frac{{23}}{8}\]
найти наименьший общий знаменатель у полученных дробей и домножить числители на недостающие множители;
произвести сложение или вычитание числителей дробей, подписав под суммой или разностью общий знаменатель.

Примеры:

(1)216+178=2⋅6+16+1⋅8+78=136+158=13⋅46⋅4+15⋅38⋅3=52+4524=9724=4124

(2)3712−2316=3⋅12+712−2⋅16+316=4312−3516=43⋅412⋅4−35⋅316⋅3=172−10548=6748=11948

(3)2314−0,6=2⋅14+314−610=3114−35=31⋅514⋅5−3⋅145⋅14=155−4270=11370=14370

Умножение и деление дробей.

При умножении двух дробей числитель первой дроби умножается на числитель второй дроби, знаменатель первой дроби умножается на знаменатель второй:

\[\frac{a}{b} \cdot \frac{c}{d} = \frac{{a \cdot c}}{{b \cdot d}}\]

Чтобы умножить дробь на число, необходимо представить это число в виде дроби со знаменателем-единицей:

\[\frac{a}{b} \cdot c = \frac{a}{b} \cdot \frac{c}{1} = \frac{{a \cdot c}}{{b \cdot 1}} = \frac{{a \cdot c}}{b}\]

При делении двух дробей необходимо первую дробь умножить на «перевёрнутую» предыдущую, то есть у дроби-делителя поменять местами числитель и знаменатель и поставить операцию умножения вместо операции деления между этими дробями:

\[\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{{a \cdot d}}{{b \cdot c}}\]

Чтобы разделить дробь на число, необходимо представить это число в виде дроби со знаменателем-единицей:

\[\frac{a}{b} \div c = \frac{a}{b} \div \frac{c}{1} = \frac{a}{b} \cdot \frac{1}{c} = \frac{{a \cdot 1}}{{b \cdot c}} = \frac{a}{{b \cdot c}}\]

Примеры:

(1)234⋅811÷0,5=11141⋅82111÷51102=2÷12=2⋅21=4

(2)6÷2,25⋅1,5=61÷214⋅151102=61÷94⋅32=631⋅493⋅3121=4

Сравнение дробей.

Для того, чтобы сравнивать две дроби между собой, нужно уметь выполнять действия с дробями (сложение, вычитание, умножение, деление). При сравнении дробей, особенно в заданиях, где требуется расположить дроби в порядке возрастания или убывания, удобно приводить обыкновенную дробь к виду десятичной.

Сравнение дробей с одинаковыми знаменателями

Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Примеры:

\[\frac{4}{7} \frac{1}{{14}};\;\;\;\; \frac{2}{3} Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.
Примеры:

\[\frac{2}{7} \frac{7}{{11}};\;\;\;\; \frac{5}{4} > \frac{5}{5}.\]Сравнение дробей с разными числителями и знаменателями

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.
Пример 1:

\[\frac{2}{5}?\frac{3}{7}\]

Приводим дроби к общему знаменателю:

\[\mathop {\frac{{{2^{\backslash 7}}}}{5}?\frac{{{3^{\backslash 5}}}}{7}}\limits_{35} \Leftrightarrow \frac{{14}}{{35}}

Приходим к выводу, что:

\[\frac{2}{5}

Пример 2:

\[\frac{5}{6}?\frac{7}{9}\]

Приводим дроби к общему знаменателю:

\[\mathop {\frac{{{5^{\backslash 3}}}}{6}?\frac{{{7^{\backslash 2}}}}{9}}\limits_{18} \Leftrightarrow \frac{{15}}{{18}} > \frac{{14}}{{18}}\]

Приходим к выводу, что:

\[\frac{5}{6} > \frac{7}{9}\]

$a^n$ — степень числа $a$ с натуральным показателем $n$. 6} = 1000000.\]

Скачать домашнее задание к уроку 1.

Что такое степень числа Возведение в степень отрицательного…

Привет, мой друг, тебе интересно узнать все про что такое степень числа возведение в степень отрицательного числа порядок действий в ах со степенями, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
что такое степень числа возведение в степень отрицательного числа порядок действий в ах со степенями , настоятельно рекомендую прочитать все из категории Арифметика

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулем.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберемся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращенное обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 4⁶ и произносят «четыре в шестой степени».

4 • 4 • 4 • 4 • 4 • 4 = 4⁶

Выражение 4⁶ называют степенью числа, где:

4 — основание степени;
6 — показатель степени.

В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения :

Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».

Запись aⁿ читается так: «а в степени n» или «n-ая степень числа a».

Исключение составляют записи:

a² — ее можно произносить как «а в квадрате»;
a³ — ее можно произносить как «а в кубе».

Конечно, выражения выше можно читать и по определению степени:

a² — «а во второй степени»;
a³ — «а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).

Степенью числа «а» с показателем n = 1 является само это число :

a¹ = a

Любое число в нулевой степени равно единице.

a⁰ = 1

Ноль в любой натуральной степени равен нулю.

0ⁿ = 0

Единица в любой степени равна 1.

1ⁿ = 1

Выражение 0⁰ (ноль в нулевой степени) считают лишенным смыслом.

(-32)⁰ = 1
0²⁵³ = 0
1⁴ = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.

Пример . Об этом говорит сайт https://intellect.icu . Возвести в степень.

5³ = 5 • 5 • 5 = 125
2.5² = 2.5 • 2.5 = 6.25
(

)⁴ =

•

•

•

=
3 • 3 • 3 • 3
4 • 4 • 4 • 4

=

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулем.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того четным или нечетным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечетную степень, то получается отрицательное число. Так как произведение нечетного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в четную степень, то получается положительное число. Так как произведение четного количество отрицательных сомножителей положительно.

Отрицательное число, возведенное в четную степень, есть число положительное.

Отрицательное число, возведенное в нечетнуюстепень, — число отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть:

a² ≥ 0 при любом a.

2 • (- 3)² = 2 • (- 3) • (- 3) = 2 • 9 = 18
— 5 • (- 2)³ = — 5 • (- 8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (- 5)⁴ и -5⁴ это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (- 5)⁴ означает найти значение четвертой степени отрицательного числа.

(- 5)⁴ = (- 5) • (- 5) • (- 5) • (- 5) = 625

В то время как найти -5⁴ означает, что пример нужно решать в 2 действия:

Возвести в четвертую степень положительное число 5.
5⁴ = 5 • 5 • 5 • 5 = 625
Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание ).
-5⁴ = — 625

Пример. Вычислить: — 6² — (- 1)⁴

— 6² — (- 1)⁴ = — 37

6² = 6 • 6 = 36
-6² = — 36
(- 1)⁴ = (- 1) • (- 1) • (- 1) • (- 1) = 1
— (- 1)⁴ = — 1
— 36 — 1 = — 37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление , а в конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример. Вычислить:

Для облегчения решения примеров полезно знать и пользоватьсятаблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про что такое степень числа возведение в степень отрицательного числа порядок действий в ах со степенями Надеюсь, что теперь ты понял что такое что такое степень числа возведение в степень отрицательного числа порядок действий в ах со степенями
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика

{-7} [/ латекс]

При отрицательных показателях степени: чем больше отрицательная экспонента, тем меньше число.

Преобразование между научным и десятичным представлением

S научная нотация используется учеными, математиками и инженерами, когда они работают с очень большими или очень маленькими числами. Используя экспоненциальную запись, можно записывать большие и маленькие числа таким образом, чтобы их было легче читать.

Когда число записано в экспоненциальной записи, показатель степени сообщает вам, является ли член большим или малым числом.{n} [/ latex], где коэффициент a равен [latex] 1 \ leq {a} n является целым числом.

Теперь давайте сравним некоторые числа, выраженные как в научной, так и в стандартной десятичной системе счисления, чтобы понять, как преобразовать одну форму в другую. Взгляните на таблицы ниже. Обратите особое внимание на показатель степени в экспоненциальном представлении и положение десятичной точки в десятичном представлении.

Большие числа

Маленькие числа

Десятичное представление

Научная запись

Десятичное представление

Научная запись

500.{5} \ end {array} [/ latex]

Обратите внимание, что десятичная запятая была перемещена на 5 позиций влево, а показатель степени равен 5.

Пример

Запишите следующие числа в экспоненциальном представлении.

[латекс] 920 000 000 [/ латекс]
[латекс] 10,200,000 [/ латекс]
[латекс] 100000000000 [/ латекс]

Показать решение

[latex] \ underset {\ longleftarrow} {920,000,000} [/ latex] Мы переместим десятичную запятую влево, это поможет поместить ее в конец числа, а затем посчитать, сколько раз вы переместите ее, чтобы получить одно число перед ним от 1 до 10.

{-5} \ end {array} [/ latex]

Вы можете заметить, что десятичная точка была перемещена на пять позиций вправо , пока вы не добрались до числа 4, которое находится между 1 и 10. Показатель степени [латекс] −5 [/ латекс].

Пример

Запишите следующие числа в экспоненциальном представлении.

[латекс] 0,0000000000035 [/ латекс]
[латекс] 0,0000000102 [/ латекс]
[латекс] 0,00000000000000793 [/ латекс]

Показать решение

[латекс] \ underset {\ longrightarrow} {0.{-8} = \ underset {\ longleftarrow} {0,00000005.} = 0,00000005 \ end {array} [/ latex]

Для каждой степени 10 вы перемещаете десятичную запятую на одну позицию. Будьте осторожны и не увлекайтесь нулями — количество нулей после десятичной запятой всегда будет на 1 меньше , чем показатель степени, потому что требуется одна степень 10, чтобы сдвинуть это первое число влево от десятичной запятой. .

Пример

Запишите следующее в десятичной системе счисления.

[латекс] 4,8 \ times10 {-4} [/ латекс]

[латекс] 3.{-7} [/ латекс]

В десятичной форме сравнивая 0,05 с 0,00000043, легче сразу определить, какое из них больше, но полезнее сравнивать числа в том виде, в котором они были представлены изначально. Для небольших чисел, записанных в экспоненциальной форме, чем больше отрицательная экспонента, тем меньше число.

Умножение и деление чисел, выраженных в научной записи

Числа, записанные в экспоненциальном представлении, можно довольно просто умножать и делить, пользуясь свойствами чисел и правилами экспонент, которые вы, возможно, помните.{-2}} [/ латекс]

Обратите внимание, что при делении экспоненциальных членов вы вычитаете показатель степени в знаменателе из показателя степени в числителе.

Решение проблем приложений

Правила обучения для экспонентов могут показаться бессмысленными без контекста, поэтому давайте рассмотрим несколько примеров использования научных обозначений, которые связаны с реальными проблемами. Во-первых, давайте рассмотрим пример того, как научные обозначения могут использоваться для описания реальных измерений.

Красные кровяные тельца

Одна из наиболее важных частей решения «реальной» проблемы — это перевод слов в соответствующие математические термины и определение того, когда хорошо известная формула может помочь.3 [/ латекс]. Биологи недавно обнаружили, как использовать плотность некоторых типов клеток, чтобы указать на наличие таких заболеваний, как серповидноклеточная анемия или лейкоз. Плотность рассчитывается как отношение [латекс] \ frac {\ text {mass}} {\ text {volume}} [/ latex]. Рассчитайте плотность средней клетки человека.

Показать решение

Прочтите и поймите: Нам дана средняя клеточная масса и объем, а также формула для плотности. Мы ищем плотность средней человеческой клетки.2 = t [/ latex] секунд, или в стандартном обозначении 500 секунд. Это неплохо, учитывая, как далеко нужно проехать!

экспонентов и отрицательные числа | Purplemath

Purplemath

Теперь вы можете перейти к показателям степени, используя свойство умножения с отменой знаков минус.

Напомним, что силы создают повторяющееся умножение.Например, (3) ² = (3) (3) = 9. Таким образом, мы можем использовать кое-что из того, что мы уже узнали об умножении на отрицательные числа (в частности, мы узнали о сокращении пар минус знаков), когда мы находим отрицательные числа внутри экспонент.

Например:

MathHelp.com

Квадрат означает «умноженное на себя с двумя копиями основания».Это означает, что у меня будет два знака «минус», которые я могу отменить:

(–3) ² = (–3) (- 3) = (+3) (+ 3) = 9

Обратите особое внимание и обратите внимание на разницу между приведенным выше упражнением и следующим:

–3 ² = — (3) (3) = –1 (3) (3) = (–1) (9) = –9

Во втором упражнении квадрат («в степени 2») был только на 3; на минусе было , а не . Эти скобки в первом упражнении имеют большое значение! Будьте осторожны с ними, особенно когда вы вводите выражения в программное обеспечение. Разные программы могут трактовать одно и то же выражение по-разному, как очень подробно продемонстрировал один исследователь.

(–3) ³ = (–3) (- 3) (- 3)

= (+3) (+ 3) (- 3)

= (9) (- 3)

= –27

(–3) ⁴ = (–3) (- 3) (- 3) (- 3)

= (+3) (+ 3) (- 3) (- 3)

= (+3) (+ 3) (+ 3) (+ 3)

= (9) (9)

= 81

(–3) ⁵ = (–3) (- 3) (- 3) (- 3) (- 3)

= (+3) (+ 3) (- 3) (- 3) (- 3)

= (+3) (+ 3) (+ 3) (+ 3) (- 3)

= (9) (9) (- 3)

= –243

Обратите внимание на закономерность: отрицательное число, взятое в степени даже при , дает положительный результат (потому что пары отрицаний отменяются), а отрицательное число, взятое в степени нечетности , дает отрицательный результат (потому что, после отмены останется один знак минус). Поэтому, если они дадут вам упражнение, содержащее что-то немного нелепое, например (–1) ¹⁰⁰¹, вы знаете, что ответ будет либо +1, либо –1, а поскольку 1001 — это с нечетным , то ответ должен быть –1 .

Вы также можете делать негативы внутри корней и радикалов, но только если будете осторожны. Вы можете упростить

, потому что есть число, равное 16. То есть

… потому что 4 ² = 16. А как насчет

? Можете ли вы возвести что-нибудь в квадрат и получить 90 455 отрицательных? Нет! Таким образом, вы не можете извлечь квадратный корень (или корень четвертой степени, или корень шестой степени, или корень восьмой степени, или любой другой четный корень) отрицательного числа. С другой стороны, вы можете сделать кубическими корнями из отрицательных чисел. Например:

. .. потому что (–2) ³ = –8. По той же причине вы можете взять любой нечетный корень (третий корень, пятый корень, седьмой корень и т. Д.) отрицательного числа.

URL: https://www.purplemath.com/modules/negative4.htm

отрицательных показателей: 8 вещей, которые нужно знать вашим ученикам

отрицательные показатели: 8 вещей, которые нужно знать вашим ученикам | Prodigy Education

Категория

Стратегии преподавания
Инструменты обучения
Без категорий

Многим ученикам уже трудно понять отрицательные числа, правила экспонент и дроби. Итак, что произойдет, если вы добавите к уравнению отрицательный показатель степени ? Полный хаос. Ну, не совсем. Но понимание отрицательных показателей — это , важный строительный блок для математических курсов в старших классах, и это также концепция, которую многие студенты считают сложной. Постепенно наращивая знания учеников, вы убедитесь, что они готовы решать сложные задачи в классе и за его пределами. Если вы не знаете, с чего начать, этот пост в блоге поможет вам изменить свой блок на негатив в положительный опыт для вас и ваших учеников! Мы рассмотрим:

Правила для отрицательных показателей

Как и все остальное в классе математики, отрицательные показатели должны соответствовать правилам.Если вам нужно напоминание, вот краткое изложение семи правил экспонент:

Произведение степеней : сложение степеней при умножении как оснований
Правило отношения степеней : вычитание степеней при делении как оснований
Правило силы степеней : Умножение степеней вместе при возведении в степень на другой показатель
Правило степени произведения : Распределение мощности на каждую базу при возведении нескольких переменных в степень
Правило степени частного : Распределение мощности к каждой базе при возведении нескольких переменных в степень
Правило нулевой степени : Любое основание, возведенное в степень нуля, становится единицей
Правило отрицательной экспоненты : Чтобы изменить отрицательную экспоненту на положительную, переверните ее в взаимный.

Напомните учащимся, что правила для отрицательных показателей остаются неизменными — возможно, потребуется выполнить несколько дополнительных шагов.

Быстрый просмотр отрицательных чисел

Отрицательные числа требуют определенного абстрактного мышления, которое не всегда бывает естественным. Но без твердого понимания отрицательных чисел учащиеся не будут готовы к работе с отрицательными показателями. Вот краткий обзор: Отрицательное число — это любое число меньше нуля. Отрицательные числа обозначаются отрицательным знаком.Например, -4 на четыре меньше нуля. Полезно думать, что отрицательные числа присутствуют в числовой строке: когда вы складываете и вычитаете отрицательные числа, вы перемещаетесь либо вправо, либо влево от числовой линии. Когда вы вычитаете отрицательное число, вы перемещаетесь влево от числовой строки, потому что это то же самое, что добавить положительное число. Если вы добавляете отрицательное число, вы перемещаетесь вправо, потому что это то же самое, что вычитание положительного числа. Когда вы умножаете отрицательное число на положительное (или наоборот), произведение будет отрицательным.Если вы умножите два отрицательных числа или два положительных числа, результат будет положительным. Умножение разных знаков всегда дает отрицательное произведение, а умножение одних и тех же знаков дает положительное произведение. Всегда считайте, что число положительное, если перед ним нет знака.

Что означают отрицательные показатели?

Мы уже знаем, что положительные показатели — это способ выражения многократного умножения. Например: есть несколько разных способов думать об отрицательных показателях, но в целом отрицательный показатель противоположен положительным.

Все отрицательные показатели степени могут быть выражены как положительные , обратные . Обратное число — это дробь, в которой числитель и знаменатель меняются местами. Как можно что-то превратить в обратную, если вначале это не была дробь? Мы знаем, что числа могут быть выражены более чем одним способом. Например, восемь также можно записать как: Итак, отрицательные показатели могут быть выражены как положительная величина, обратная основанию, умноженному на себя x раз. Чем больше отрицательный показатель степени, тем меньшее число он представляет. В то время как положительные показатели указывают на повторное умножение, отрицательные показатели представляют собой повторяющееся деление. Поэтому 2 ^-3 больше 2 ^-6.

Как решить отрицательные показатели

В большинстве вопросов вам будет предложено решить отрицательные показатели, выразив их в виде положительных уравнений . Вот как: переверните основание и показатель степени в обратную величину, а затем решите знаменатель. Разделите числитель на знаменатель, чтобы найти последний десятичный знак.

Умножение и деление отрицательных показателей

Мы уже рассмотрели умножение показателей показателей, но вот краткий обзор того, как умножать и делить отрицательные показатели.

Умножение отрицательных показателей

Хорошие новости! Правила умножения показателей такие же, даже если показатель отрицательный. Если основания совпадают, добавьте экспоненты. Помните о правилах сложения и вычитания отрицательных чисел. Если основания разные, но экспоненты одинаковые, умножьте основания и оставьте экспоненты такими, какие они есть.Если ничего общего нет, переходите непосредственно к решению уравнения. Переверните экспоненты в их обратные числа, а затем умножьте. Если вам нужно напоминание, посмотрите наш пост о том, как умножать дроби.

Деление отрицательных показателей

Деление отрицательных показателей почти то же самое, что их умножение, за исключением того, что вы делаете обратное: вычитаете, где бы вы добавили, и делите, где вы бы умножили. Если основания совпадают, вычтите показатели степени. Не забудьте перевернуть показатель степени и сделать его положительным, если необходимо.Если показатели такие же, но основания разные, сначала разделите основания. Если между ними нет ничего общего, переходите непосредственно к решению уравнения. Чтобы узнать больше о делении дробей, ознакомьтесь с нашим сообщением в блоге «Как разделить дроби».

Отрицательные числа с показателями степени

Что произойдет, если основание отрицательное, а не показатель степени? Если показатель степени положительный, работайте с ним так же, как и с обычным показателем, но помните две вещи:

Если основание отрицательное, а показатель степени равен четное число, конечным результатом всегда будет положительное число.
Если основание отрицательное, а показатель степени — нечетное число, конечным результатом всегда будет отрицательное число.

Если отрицательное основание заключено в круглые скобки, степень применяется ко всему уравнению, включая отрицательный знак. Если скобок нет, степень применяется только к основанию, а не к отрицательному знаку. Поскольку в первом примере возводится в четное значение, два отрицательных знака отменяются, и вы получаете положительный результат. Если бы показатель степени был нечетной степенью, произведение было бы отрицательным, потому что было бы одно число, которое не могло быть сокращено. Во втором примере положительная степень применяется только к четырем, а не к отрицательному знаку. В этом случае отрицательный знак говорит о том, что продукт будет отрицательным независимо от того, четная или нечетная степень.

Упрощение отрицательных показателей

Умножение, деление и понимание отрицательных показателей — это первый шаг к упрощению выражений с отрицательными показателями. Помните: все шаги, описанные выше, остаются в силе независимо от того, насколько сложным является выражение. Давайте начнем с умножения отрицательных показателей на переменные. В этом примере степень применяется только к основанию x, а не к 4. Чтобы сделать его положительным выражением, переверните x на обратную величину и оставьте 4 сверху. Давайте попробуем что-нибудь посложнее. Переменные здесь такие же, поэтому в соответствии с правилом первой экспоненты мы можем умножать числа, сохранять основание и складывать показатели вместе. Умножив 6 и 4, получим произведение 24. Затем сложим показатели вместе, чтобы получилось умножьте переменные x. А как насчет деления отрицательных показателей на переменные? Начнем с простого примера: чтобы сделать отрицательную экспоненту положительной, переместите ???? в начало уравнения и умножьте. Вот пример отрицательного показателя степени с несколькими переменными: поскольку отрицательный показатель степени применяется только к переменной, переместите 𝑥-4 в конец уравнения, чтобы сделать его положительным, и оставьте 6 на месте. И вот ваше упрощенное уравнение! Давайте попробуем другой. Во-первых, перераспределим мощность внутри скобок, следуя правилу третьей степени.Затем переверните переменные 𝑥 с отрицательными показателями в их обратную величину. Наконец, умножьте переменные by, сложив показатели вместе. Давайте сделаем еще одно. Для начала возведите уравнение в квадрат или сначала переместите скобки. Начнем с того, что возведем верхнюю скобку в квадрат и перераспределим власть. Затем переместите отрицательные показатели вниз или вверх, в зависимости от их положения. Отрицательная экспонента сверху может быть перенесена в нижнюю, так что получается обратная величина, и наоборот. Закончите упрощением. Часто существует несколько способов упростить выражения с отрицательной экспонентой. Поскольку показатели — это повторяющееся умножение, и вы можете умножать числа в любом порядке, разные шаги могут привести к одному и тому же результату.

Дроби с отрицательными показателями

Мы знаем, что делать с целыми числами с отрицательными показателями, но как насчет дробей с отрицательными показателями? Чтобы упростить дроби с отрицательными показателями, переверните их в обратные, умножьте и уменьшите .

Как обучать отрицательным показателям с помощью Prodigy

Студентам понравится практиковать отрицательные показатели с помощью Prodigy: бесплатной математической платформы, соответствующей учебной программе, с экзотическими домашними животными, веселыми задачами и образовательными приключениями. Отрицательные показатели — это важная концепция, которую ученики должны усвоить до того, как они пойдут в старшую школу, но многие учащиеся испытывают трудности с ключевыми концепциями. Используя мощные инструменты отчетности на панели Teacher Dashboard , вы увидите, какие темы усвоили ваши ученики, а где им нужно больше практики. Функции Prodigy’s Assignments, Plan и Test Prep позволяют назначать целевую математическую практику учащимся, которые испытывают трудности на уровне или .Вы будете получать данные в режиме реального времени, пока учащиеся играют, и сможете выполнять дифференцированные задания, соответствующие тому, что вы преподаете в классе. Вы можете использовать Prodigy для: Лучше всего? Эти инструменты абсолютно бесплатны для учителей и студентов. Чтобы узнать больше о согласовании Prodigy с вашим классом, узнайте, как вы можете использовать индивидуальные планы для улучшения содержания вашего урока.

Заключительные мысли об отрицательных показателях

Если вы хотите больше попрактиковаться в показателях показателей в целом, наша таблица правил для показателей показателей дает учащимся возможность лучше узнать, как работают показатели. При работе с отрицательными показателями важно помнить, что все правила экспоненты остаются неизменными. Помимо этого, студентам нужно только знать, как складывать, вычитать, умножать и делить отрицательные числа. Не торопитесь и переходите к более сложным вопросам. Ваши ученики станут мастерами экспонента в кратчайшие сроки!

Начните обучать отрицательных экспонентов с Prodigy уже сегодня. Prodigy — это бесплатная математическая платформа, соответствующая учебному плану, которая побуждает учащихся любить изучение математики. Prodigy с более чем миллионом учителей и 50 миллионами студентов предлагает уникальные решения для вашего класса.-3. Однако на самом деле вы можете преобразовать любое выражение в дробь, поставив 1 над числом. Это основная причина, по которой мы можем перемещать экспоненты и решать следующие вопросы.

Изучение этого урока также поможет вам на один шаг приблизиться к пониманию того, почему любое число с 0 в экспоненте равно 1. В конце этого урока будет ссылка на диаграмму, которая покажет вам, как возникают эти отношения. о. Скоро вы поймете все основные свойства экспонент!

Как найти отрицательные показатели

Давайте попробуем поработать с некоторыми вопросами об отрицательной степени, чтобы увидеть, как мы переместим числа в верхнюю или нижнюю часть дробной черты, чтобы сделать отрицательные показатели положительными.-3)

Решение:

Если вы когда-нибудь увидите отрицательный показатель в верхней части дроби, вы знаете, что если вы перевернете его вниз, он станет положительным. То же самое действительно работает с отрицательными показателями внизу. Если вы переместите его в числитель, его показатель степени также станет положительным. Имея это в виду, давайте проработаем вопрос. Наш первый шаг — просто перевернуть числитель и знаменатель, чтобы избавиться от всех отрицаний в показателях степени. Затем решите, как обычно, с помощью правила мощности.2)

= 64/9

Определенно не так запутанно, как казалось на первый взгляд, правда?

Вот хорошее место, чтобы взглянуть на сравнение отрицательных и положительных показателей и посмотреть, как они ведут себя на графике.

Упражнения по математике

]]>

Матрицы
Алгебра
Геометрия
Функции
Тригонометрия
Координатная геометрия
Комбинаторика

Сумма и ресторан

Продукт на эскаларе

Продукт

Инверса

Мономы	Полиномы	Особые продукты	Уравнения	Квадратные уравнения
Радикальные выражения	Системы уравнений	Последовательности и серии	Внутренний продукт	Экспоненциальные уравнения
Матрицы	Детерминанты	Инверсия матрицы	Логарифмические уравнения	Системы трех переменных уравнений

Двумерные формы

Площади

Теорема Пифагора

Расстояния

Графики	Определение уклона	Положительный или отрицательный наклон	Определить наклон прямой	Ecuación de una recta	Уравнение прямой (из графика)
Квадратичная функция	Posición relativa de dos rectas		Асимптоты	Пределы	Дистанция
	Непрерывность и разрывы

Теорема Пифагора	Синус	Косинус	Касательная	Косеканс	Секант	Котангенс	Тригонометрические идентификаторы
Тригонометрические функции острого угла	Тригонометрические функции связанных углов			Решение прямоугольных треугольников		Закон косинусов	Закон синусов

Ecuación de una recta

Posición relativa de dos rectas

Дистанция

Углы в пространстве

Внутренний продукт

Факториал	Варианты без повторения	Вариации с повторением	Перестановки с повторением	Перестановки без повторов
Упражнения	Круговые перестановки	Биномиальный коэффициент	Комбинации с повторением	Комбинации без повторов

	Среднее арифметическое

Нулевые экспоненты и отрицательные экспоненты — Подготовка к оценке TSI

Отрицательные показатели степени и нулевые показатели степени часто появляются при применении формул или упрощении выражений.

В этом разделе мы определим правило отрицательной экспоненты и правило нулевой экспоненты и рассмотрим несколько примеров.

Правило отрицательной экспоненты:

Другими словами, когда есть отрицательный показатель степени, нам нужно создать дробь и поместить экспоненциальное выражение в знаменатель, а показатель степени сделать положительным. Например,

Но работа с отрицательными показателями — это просто правило экспонент, которое мы должны уметь использовать при работе с экспоненциальными выражениями.

Пример :

Упростить: 3 ^-2

Решение :

3 ^-2 =

Пример :

Упростить:

Решение :

Примените правило отрицательной экспоненты как к числителю, так и к знаменателю.

Пример :

Упростить: 3 ^-1 + 5 ^-1

Решение :

Примените правило отрицательной экспоненты к каждому члену, а затем сложите дроби, найдя общие знаменатели.

Правило нулевой экспоненты: a ⁰ = 1, a не равно 0. Выражение 0 ⁰ является неопределенным или неопределенным.

В следующем примере, когда мы применяем правило произведения для показателей степени , мы получаем показатель степени равный нулю.

x ⁵ x ^-5 = x ^{5 + (-5)} = x ⁰

Чтобы понять назначение нулевой экспоненты, мы также перепишем x ⁵ x ^-5, используя правило отрицательной степени .

x ⁵ x ^-5 =

Нулевой показатель степени указывает, что у числа нет факторов .

Пример :

Упростите каждое из следующих выражений, используя правило нулевого показателя степени. Запишите каждое выражение, используя только положительные показатели.

а) 3 ⁰

б) -3 ⁰ + н. ⁰

Решение :

а) Примените правило нулевой экспоненты.

3 ⁰ = 1

б) Примените правило нулевой экспоненты к каждому члену, а затем упростите. Нулевой показатель в первом члене применяется только к 3, а не к отрицательному значению перед 3.

-3 ⁰ + n ⁰ = — (3 ⁰) + n ⁰ = — 1 + 1 = 0

Сравнение чисел в научной записи

Вы сможете сравнить два числа в экспоненциальном представлении, посмотрев на показатель степени 10.Число с большей степенью 10 будет иметь большее значение. Если два числа имеют одинаковую экспоненту для 10, сравните десятичные числа, чтобы определить большее число.

Иногда вам может потребоваться сравнить два числа, но только одно из них указано в экспоненциальном представлении. В этом случае сначала преобразуйте число, не указанное в научном представлении, в научное представление. Затем сравните два числа.

Пример 1:

Сравните 5,62 x 10 ⁶ и 7.39 х 10 ⁵.

Решение:

Во-первых, обратите внимание на показатель степени 10.

Это 6 и 5.

Здесь экспоненты разные.

Мы знаем, что число с большей степенью больше по значению.

Поскольку 6 больше 5,

5,62 x 10 ⁶ больше

Следовательно,

5,62 x 10 ⁶> 7,39 x 10 ⁵

Пример 2:

Сравнить 4.29 x 10 ^-3 и 5,38 x 10 ^-3.

Решение:

Во-первых, обратите внимание на показатель степени 10.

То есть -3.

Здесь показатели такие же.

Поскольку показатели одинаковы, мы должны сравнить десятичные числа, чтобы определить большее число.

Если сравнивать 4,29 и 5,38, очевидно, что 5,38 — большее число.

Следовательно,

4,29 x 10 ^-3-3

Пример 3:

Сравнить 9.058915 x 10 ³ и 1.01 x 10 ⁴.

Решение:

Во-первых, обратите внимание на показатель степени 10.

Это 3 и 4.

Здесь экспоненты разные.

Мы знаем, что число с большей степенью больше по значению.

Так как 4 больше 3,

1,01 x 10 ⁴ больше

Следовательно,

9,058915 x 10 ³ 4

Пример 4:

Сравнить 4 .67 x 10 ^-2 и 3,0967 x 10 ^-9.

Решение:

Во-первых, обратите внимание на показатель степени 10.

Это -2 и -9.

Здесь показатели разные.

Мы знаем, что число с большей степенью больше по значению.

Поскольку -2 больше -9,

4,67 x 10 ^-2^больше

Следовательно,

4,67 x 10 ^-2> 3,0967 x 10 ^-9

Пример 5 :

Сравнить 8. 64 x 10 ^-7 и 8,64 x 10 ³.

Решение:

Во-первых, обратите внимание на показатель степени 10.

Это -7 и 3.

Здесь экспоненты разные.

Мы знаем, что число с большей степенью больше по значению.

Поскольку 3 больше -7,

8,64 x 10 ³^больше

Следовательно,

8,64 x 10 ^-7 3

Пример 6:

Сравнить 7.02 x 10 ² и 532,21 x 10 ^-3.

Решение:

В данных двух числах второе не в экспоненциальном представлении.

Итак, преобразуем 532,21 x 10 ^-3 в научную нотацию.

532,21 x 10 ^-3 = 5,3221 x 10 ² x 10 ^-3

532,21 x 10 ^-3 = 5,3221 x 10 ^2-³

532,213 x 10 ^{= 5,3221 x 10 ^-1}

Теперь у нас

7.02 x 10 ² и 5,3221 x 10 ^-1

Обратите внимание на показатель степени 10.

Это 2 и -1.

Здесь показатели разные.

Мы знаем, что число с большей степенью больше по значению.

Поскольку 2 больше -1,

7,02 x 10 ²^больше

Следовательно,

7,02 x 10 ²> 5,3221 x 10 ^-1

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Алгебраные задачи со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Word задачи по сравнению ставок

Преобразование общепринятых единиц в текстовые задачи

Преобразование в метрические единицы в текстовых задачах

Проблемы со словами по простым процентам

Проблемы со словами по сложным процентам

Проблемы со словами по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами в тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках

Проблемы со словами

Проблемы со словами с десятичными числами

Проблемы со словами о дробях

Проблемы со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами с линейными неравенствами

задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами в теореме Пифагора

Процент числового слова pr проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибылей и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Область и диапазон рациональных функций

Область и диапазон рациональных функций функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Поиск квадратного корня с помощью long di зрение

L. Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток, когда 2 степени 256 делятся на 17

Остаток при делении 17 степени 23 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

alexxlab

Упрощение выражений с отрицательными степенями. Степень числа: определения, обозначение, примеры.

Как возводить в отрицательную степень

Главная > Двери > Упрощение выражений с отрицательными степенями. Степень числа: определения, обозначение, примеры. Как возводить в отрицательную степень — теория

Степень с отрицательным показателем определение

Пусть число a есть любое действительное число, отличное от нуля. Число m — отрицательное целое число.

Степень с отрицательным показателем определение:

Действительное, отличное от нуля число a, возведенное в отрицательную целую степень -m, равно дроби, в числителе которой 1 и в знаменателе a, возведенное в положительную целую степень m.

Отрицательная степень формула

Для вычислений отрицательных степеней используем формулу:

Эта формула применяется, если имеется отрицательное значение степени.

Положительная и отрицательная степень

Чтоб лучше понять сравним положительные и отрицательные степени.

Пусть число a есть любое действительное число, отличное от нуля. Число m — любое целое число.

Тогда a в положительной степени m равно:

A m = a * a * a * … (m раз)

Теперь a в отрицательной степени -m:

Степень с целым отрицательным показателем

Обратите внимание, что в этой статье речь идет именно о целом отрицательном показателе. Здесь существенным является то, что показатель целый.

Пример степени с целым отрицательным показателем:

Отрицательное основание степени

Отрицательная степень числа и отрицательное основание степени — это разные вещи.

Итак, давайте подробно рассмотрим решения примеров и выясним, что значит:

Определение понятия.
Возведение в отрицательную ст.
Целый показатель.
Возведение числа в иррациональную степень.

Определение понятия

После этого можно приступать напрямую к правилам возведения.

Возведение в отрицательную степень

Для наглядности следует обратить внимание на такую цепочку выражений:

110=0,1=1* 10 в минус 1 ст.,

1100=0,01=1*10 в минус 2 степ.,

11000=0,0001=1*10 в минус 3 ст.,

110000=0,00001=1*10 в минус 4 степeни.

10 в -1 степeни — перед единицей 1 ноль;
в -3 — три нуля перед единицей;
в -9 — это 9 нулей и проч.

Так же легко понять по данной схеме, сколько будет составлять 10 в минус 5 ст. —

1100000=0,000001=(1*10)-5.

Как возвести число в натуральную степeнь

Возведите -2 в 4-ю ст.

Ответ на задачу:

(-2) в ст. 4=16.

Пример:

Вычислите значение: три целых две седьмых в квадрате.

3 целых 2 седьмых умножить на самих себя;
равно 23 седьмых умножить на 23 седьмых;
равно 529 сорок девятых;
сокращаем и получаем 10 тридцать девять сорок девятых.

Ответ: 10 39/49

Начинаем с того, что округляем П до сотых и получаем:

Как возвести чиcло в целую степень

Эту алгебраическую манипуляцию уместно принимать во внимание для следующих случаев:

для целых чисел;
для нулевого показателя;
для целого положительного показателя.

Соответственно, возведение какого угодно действительного числа в нулевую ст. будет давать единицу.

К примеру, 10 в ст.0=1, (-3,65)0=1, а 0 в ст. 0 нельзя определить.

Пример:

Вычислить значение числа 2 в кубе с целым отрицательным показателем.

Процесс решения:

Знаменатель рассчитывается просто: два в кубе;

3 = 2*2*2=8.

Ответ: два в минус 3-й ст. = одна восьмая.

Видео

Из этого видео вы узнаете, что делать, если степень с отрицательным показателем.

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

Выражение 4 6 называют степенью числа, где:

4 — основание степени ;
6 — показатель степени .

В общем виде степень с основанием «a » и показателем «n » записывается с помощью выражения:

Запомните!

Степенью числа «a » с натуральным показателем «n », бóльшим 1 , называется произведение «n » одинаковых множителей, каждый из которых равен числу «a ».

Запись «a n » читается так: «а в степени n » или «n -ая степень числа a ».

Исключение составляют записи:

a 2 — её можно произносить как «а в квадрате»;
a 3 — её можно произносить как «а в кубе».

a 2 — «а во второй степени»;
a 3 — «а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0) .

Запомните!

Степенью числа «а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени ) считают лишённым смыслом.

(−32) 0 = 1
0 253 = 0
1 4 = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

5 3 = 5 · 5 · 5 = 125
2,5 2 = 2,5 · 2,5 = 6,25
( · = =81
256

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

Запомните!

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Запомните!

Отрицательное число, возведённое в чётную степень, есть число положительное .

Отрицательное число, возведённое в нечётную степень, — число отрицательное .

Квадрат любого числа есть положительное число или нуль, то есть:

a 2 ≥ 0 при любом a .

2 · (−3) 2 = 2 · (−3) · (−3) = 2 · 9 = 18
−5 · (−2) 3 = −5 · (−8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

(−5) 4 = (−5) · (−5) · (−5) · (−5) = 625

В то время как найти «−5 4 » означает, что пример нужно решать в 2 действия:

Возвести в четвёртую степень положительное число 5 .
5 4 = 5 · 5 · 5 · 5 = 625
Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).
−5 4 = −625

Пример. Вычислить: −6 2 − (−1) 4

−6 2 − (−1) 4 = −37

6 2 = 6 · 6 = 36
−6 2 = −36
(−1) 4 = (−1) · (−1) · (−1) · (−1) = 1
−(−1) 4 = −1
−36 − 1 = −37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Запомните!

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень , затем умножение и деление , а в конце сложение и вычитание .

Пример. Вычислить:

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней , которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «

Операции со степенями и корнями. Степень с отрицательным ,

нулевым и дробным показателем. О выражениях, не имеющих смысла.

Операции со степенями.

1. При умножении степеней с одинаковым основанием их показатели складываются :

a m · a n = a m + n .

2. При делении степеней с одинаковым основанием их показатели вычитаются .

3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

( abc … ) n = a n · b n · c n …

4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):

( a / b ) n = a n / b n .

5. При возведении степени в степень их показатели перемножаются:

(a m ) n = a m n .

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .

Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:

5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:

Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.

Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:

Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .

П р и м е р . a 4 : a 7 = a 4 — 7 = a — 3 .

Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.

Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.

Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а :

О выражениях, не имеющих смысла. Есть несколько таких выражений. любое число.

В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.

Случай 3.

0 0 — любое число.

Действительно,

Р е ш е н и е. Рассмотрим три основных случая:

1) x = 0 – это значение не удовлетворяет данному уравнению

(Почему?).

2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,

что x – любое число; но принимая во внимание, что в

Нашем случае x > 0 , ответом является x > 0 ;

3) при x x / x = 1, т. e . –1 = 1, следовательно,

В этом случае нет решения.

Таким образом, x > 0.

Как возводить в отрицательную степень – теория

Как возводить в отрицательную степень – примеры на обычных числах

Держа вышеприведенное правило на уме, решим несколько примеров.

4 -2 = 1/4 2 = 1/16
Ответ: 4 -2 = 1/16

4 -2 = 1/-4 2 = 1/16.
Ответ -4 -2 = 1/16.

4 -3 = 1/(-4) 3 = 1/(-64)

Как возводить в отрицательную степень – числа от 0 до 1

Пример 3: Вычислить 0,5 -2
Решение: 0,5 -2 = 1/1/2 -2 = 1/1/4 = 1×4/1 = 4.
Ответ: 0,5 -2 = 4

Разбор (последовательность действий):

Переводим десятичную дробь 0,5 в дробную 1/2. Так легче.
Возводим 1/2 в отрицательную степень. 1/(2) -2 . Делим 1 на 1/(2) 2 , получаем 1/(1/2) 2 => 1/1/4 = 4

Пример 4: Вычислить 0,5 -3
Решение: 0,5 -3 = (1/2) -3 = 1/(1/2) 3 = 1/(1/8) = 8

Пример 5: Вычислить -0,5 -3
Решение: -0,5 -3 = (-1/2) -3 = 1/(-1/2) 3 = 1/(-1/8) = -8
Ответ: -0,5 -3 = -8

Исходя из 4-го и 5-ого примеров, сделаем несколько выводов:

Для положительного числа в промежутке от 0 до 1 (пример 4), возводимого в отрицательную степень, четность или нечетность степени не важна, значение выражения будет положительным. При этом, чем больше степень, тем больше значение.
Для отрицательного числа в промежутке от 0 до 1 (пример 5), возводимого в отрицательную степень, четность или нечетность степени неважна, значение выражения будет отрицательным. При этом, чем больше степень, тем меньше значение.

Как возводить в отрицательную степень – степень в виде дробного числа

Рассмотрим пример:
Вычислить: 8 -1/3

Решение (последовательность действий):

Вспоминаем правило возведения числа в отрицательную степень. Получим: 8 -1/3 = 1/(8) 1/3 .
Заметьте, в знаменателе число 8 в дробной степени. Общий вид вычисления дробной степени таков: a m/n = n √8 m .
Таким образом, 1/(8) 1/3 = 1/(3 √8 1). Получаем кубический корень из восьми, который равен 2. Исходя отсюда, 1/(8) 1/3 = 1/(1/2) = 2.
Ответ: 8 -1/3 = 2

Формирование понятия степень числа в курсе алгебры основной школы

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Принципы изучения степени числа в общеобразовательной школе

2. Методика изучения степени числа с натуральным показателем

3. Изучение степени отрицательного числа и степени с рациональным показателем

Определение 1

Степень числа – это многократное повторение умножения числа на само себя.

Степень числа записывается в виде числового знака, расположенного над числом. Знак имеет меньший размер, чем само число и обозначает количество раз, которое число умножается на само себя. Число операций умножения называется показателем степени числа, а само число выступает основанием степени.

Степень числа изучается в курсе алгебры средней общеобразовательной школы, начиная с седьмого класса.

Принципы изучения степени числа в общеобразовательной школе

Изучение степени числа в курсе алгебры начинается с седьмого класса. Обучение начинается с познания степени с натуральным показателем. Полноценно изучив данную тему, происходит переход к познанию степени отрицательного числа, а затем изучается степень с целым показателем и степень с рациональным показателем. Во время изучения, осуществляется освоение выполнения различных операций с числами и их степенями.

Возведение числа в степень n первоначально основывалось на понимании повторения данного числа некоторое количество раз, а именно n –ое количество. При этом, не рассматривалось операций с отрицательными основании и отрицательными степенями, а также степенями с рациональными показателями. Только в конце XVII Ньютоном было дано определение степени числа, его значение, рассмотрены числа с различными степенями и операции с ними.

Изучение степени числа реализуется на основании соблюдения ряда принципов:

Принцип доступности. В данном случае, огромную роль играет доступность изложения материала. Педагог должен начинать с простых понятий и переходить постепенно к более сложным. Кроме того, необходимо опираться на аналогии и сравнения в объяснении, давать наглядные примеры и демонстрировать практическое использование теории в решении арифметических задач на нахождение степени числа и совершения иных операций со степенями. Как правило, педагог составляет алгоритм решения задач и добивается запоминания учащимися последовательности совершения арифметических действий.
Принцип наглядности. Обучение арифметическим операциям со степенями должно быть реализовано с помощью наглядных примеров действий. Актуально применение графиков и диаграмм, демонстрирующих натуральные числа и их переходы в степень с помощью линий и отрезков или движения изображения переменной величины. Хорошо выстраивать таблицы с числовыми значениями и отображать их переходы в различные степени с помощью графика. Это не только делает объяснение более понятным для учащихся, но и развивает их интерес к совершению математических операций с различными степенями чисел.
Принцип активности. Предполагается, что учащиеся должны проявлять активность в познании степени числа и стремиться совершать различные арифметические действия с числами и степенями. Для этого, используются приемы интересной подачи нового материала.
Принцип концентричности. { ⁿ/ m}$.
Изучение особенностей совершения различных арифметических действий с отрицательными числами и степенями с рациональным показателем. Осваиваются основы их умножения, деления, возведения в степень.
Закрепление теоретической информации выполнением практических арифметических примеров на данные темы.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 15.03.2022

Выполнение любых типов работ по педагогике

Рецензия на методическую разработку педагога на заказ Заказать ВКР по педагогике Эссе на тему моё представление о безопасной образовательной среде Презентация на тему история и современное состояние ДОУ Реферат на тему образ учителя в истории педагогики Эссе на тему книга жалоб учителя Контрольная работа на тему характеристика деятельности педагога Реферат по педагогике на тему технология модульного обучения в школе Реферат на тему язык и речь Реферат на тему образование

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Умножение отрицательных чисел кратко Арифметика

Привет, мой друг, тебе интересно узнать все про умножение отрицательных чисел, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое умножение отрицательных чисел , настоятельно рекомендую прочитать все из категории Арифметика.

Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.

Умножение чисел с одинаковыми знаками

Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.

Чтобы умножить два числа с одинаковыми знаками надо:

перемножить модули чисел;
перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.

(- 3) • (- 6) = + 18 = 18
2 • 3 = 6

Умножение чисел с разными знаками

Второй возможный случай — это умножение чисел с разными знаками.

Чтобы умножить два числа с разными знаками, надо:

перемножить модули чисел;
перед полученным произведением поставить знак «-».

Примеры умножения отрицательных и положительных чисел.

(- 0,3) • 0,5 = — 1,5
1,2 • (- 7) = — 8,4

Правила знаков для умножения

Запомнить правило знаков для умножения очень просто . Об этом говорит сайт https://intellect.icu . Данное правило совпадает с правилом раскрытия скобок.

Минус на минус дает плюс,

Плюс на минус дает минус.

+ • (+) = +	+ • (-) = —
— • (-) = +	— • (+) = —

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.

При четном числе отрицательных множителей результат будет положительным, а при нечетном количестве — отрицательным.

Пример.

(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».

Теперь вычислим произведение модулей, не обращая внимание на знаки.

6 • 3 • 4 • 2 • 12 • 1 = 1728

Конечный результат умножения исходных чисел будет:

(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) = — 1728

Умножение на ноль и единицу

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.

0 • a = 0
a • 0 = 0
a • 1 = a

Примеры:

0 • (- 3) = 0
0,4 • 1 = 0,4

Особую роль при умножении рациональных чисел играет отрицательная единица (- 1).

При умножении на (- 1) число меняется на противоположное.

В буквенном выражении это свойство можно записать:

a • (- 1) = (- 1) • a = — a

При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Пример умножения отрицательных и положительных чисел.

См. также

сложение отрицательных чисел ,
деление отрицательных чисел ,
методы декомпозиции ячеек ,
десятичные дроби ,
умножение в столбик ,
как читать десятичные дроби ,
перевод обыкновенной дроби в десятичную ,
нахождение обыкновенной дроби от числа ,
деление обыкновенных дробей ,
умножение обыкновенных дробей ,
вычитание обыкновенных дробей ,
взаимно обратные числа , взаимно обратные дроби ,
сравнение обыкновенных дробей ,
периодическая дробь ,
сложение обыкновенных дробей , общий знаменатель ,
сокращение обыкновенных дробей ,
смешанные числа , выделение целой части обыкновенной дроби ,
свойства умножения , свойства деления ,

Как ты считаеешь, будет ли теория про умножение отрицательных чисел улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое умножение отрицательных чисел и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика

Из статьи мы узнали кратко, но емко про умножение отрицательных чисел

Умножение показателей — Как умножать показатели

Как умножать показатели.

Умножение показателей степени с одинаковым основанием
Умножение показателей с разными базы
Умножение отрицательных показателей
Умножение дробей с показателями
Умножение дробных степеней
Умножение переменных с показателями степени
Умножение квадратных корней с показателями

Умножение показателей степени с одинаковым основанием

For exponents with the same base, we should add the exponents:

a ⁿ ⋅ a ^m = a ^n+m

Example:

2 ³ ⋅ 2 ⁴ = 2 ³⁺⁴ = 2 ⁷ = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

Умножение показателей степени с разными основаниями

a и b одинаковы, мы можем сначала умножить a и b:

a ⁿ ⋅ b ⁿ = ( a ⋅ b ) ⁿ

Example:

3 ² ⋅ 4 ² = (3⋅4) ² = 12 ² = 12om12 = 144

Когда основания и показатели различны, мы должны рассчитать каждый показатель, а затем умножьте:

A ^N вно B ^{M ^N} вно B ^M M вно B ^M M вно B ^{M ^N}

Пример:

3 ² ⋅ 4 ³ = 9 ⋅ 64 = 576

Умножение отрицательных показателей

Для показателей с той же основанием мы можем добавить экспоненты:

A ^-N ⋅ A ^{—^-N} ⋅ A ^{—^-N} ⋅ A ^{—^-N}. m = a ^-(n+m ⁾ = 1 / A ^N+M

Пример:

2 ^-3 ⋅ 2 ^-4 = 2 ^-(3+4) = 2 ^-7 = 1 /2 ⁷ = 1. / (2⋅2⋅2⋅2⋅2⋅2⋅2) = 1/128 = 0,0078125

Когда основания различны, а показатели степени а и b одинаковы, мы можем сначала умножить а и b: ⋅ B ) ^-N

Пример:

3 ^-2 ⋅ 4 ^-2 = (3 %) ^-2 = 12 ^-2 = 1 /12 ² = 12 ^-2 = 1 /12 ² = 12 ^-2 = 1 /12 ² = = 1 / (12⋅12) = 1 / 144 = 0,0069444

Когда основания и показатели степени различаются, мы должны вычислить каждый показатель степени, а затем умножить:

A ^-N ⋅ B ^-M

Пример:

3 ^-2 ⋅ 4 ^-3 = (1/9) ⋅ (1/64) = 1/576. = 0.0017361

Multiplying fractions with exponents

Multiplying fractions with exponents with same fraction base:

( a / b ) ⁿ ⋅ ( a / b ) ^m = ( a / b ) ^н+м

Пример:

(4/3) ³ ⋅ (4/3) ² = (4/3) ³⁺² = (4/3) ⁵ = 4 ⁵ ⁵ = 4,214

Умножающие фракции с экспонентами с тем же показателем:

( A / B ) ^N ⋅ ( C / D ) ^N = a = = a x / d ) ⁿ x / d ) ⁿ = x / d ). b )⋅( c / d )) ⁿ

Пример:

(4/3) ³ ⋅ (3/5) ³ = ((4/3)⋅(3/5)) ³ = (4/5) ³ = 0,8 ³ = 0,8⋅0,8⋅0,8 = 0,512

Multiplying fractions with exponents with different bases and exponents:

( a / b ) ⁿ ⋅ ( c / d ) ^m

Example:

(4 /3) ³ ⋅ (1/2) ² = 2,37 ⋅ 0,25 = 0,5925

Умножение дробных показателей

Умножение фракционных экспонентов с тем же дробным показателем:

A ^N/M ⋅ B ^N/M = ( A ⋅ B ). ^{6 N/M} ⋅ B ). Пример ^{6 N/M} ⋅ B ). Пример ^{6 N/M} Ϫ B ). Пример ^{66 N/M} ⋅ B ). Пример ^{6 N/M} ⋅ B ).

2 ^3/2 ⋅ 3 ^3/2 = (2⋅3) ^3/2 = 6 ^3/2 = √ ( 6 ³ ) = √ 216 = 14,7

Умножение дробных степеней с одинаковым основанием:

A ^{( N/M )} ⋅ A ^{( K/J )} = A ^{[ Н/М )+( K/J 8).}

Пример:

2 ^(3/2) ⋅ 2 ^(4/3) = 2 ^{[(3/2)+(4/3)]} = 7,127

3 900 разные степени и дроби:

a ^н/м ⋅ b ^к/дж

Пример:

2 ^3/2 ⋅ 2 ^4/3 = √ (2 ³ ) ⋅ ³ √ (2 ⁴ ) = 2,828 ⋅ 2,52 = 7.127

Умножение квадратных корней с показателями

Для экспонентов с той же основанием мы можем добавить экспоненты:

(√ A ) ^N вно ( √а ) ^м = а ^{( н+м} ^)/2

Пример:

(√5) ² ⋅ ( √ 5) ⁴ = 5 ^(2+4)/2 = 5 ^{^6/2} = 5 ^³ = 125

x ^n+m

Пример:

x ² ⋅ x ³ = ( x> x ) ⋅ ( x> x> ) = x ²⁺³ = x ⁵

^{SEE
^{. Показатель степени деления
Добавление экспонетов
Калькулятор экспоненты}
Правила для экспонентов | Начальная алгебра
Цели обучения
Правила произведения и частного Использование правила произведения для умножения экспоненциальных выражений
Используйте правило отношения для деления экспоненциальных выражений
Правило мощности для показателей Используйте правило степени для упрощения выражений, включающих произведения, частные и показатели степени
отрицательных и нулевых показателей Определение и использование правила нулевого порядка
Определение и использование правила отрицательного порядка
Упростите выражения, используя правила экспоненты Упрощение выражений с использованием комбинации правил экспоненты 9{2}[/латекс]
Показать решение
В следующем видео вам предоставлено больше примеров применения экспонент к различным основаниям.
Вычисление выражений
Вычисление выражений, содержащих экспоненты, аналогично вычислению линейных выражений из предыдущего курса. Вы подставляете значение переменной в выражение и упрощаете.
Вы можете использовать порядок операций для вычисления выражений, содержащих показатели степени. Во-первых, оцените что-нибудь в скобках или сгруппируйте символы. Затем найдите Экспоненты, затем Умножение и Деление (читая слева направо) и, наконец, Сложение и Вычитание (опять же, читая слева направо). 9{3}[/latex] если [latex]x=4[/latex], сначала подставьте значение 4 для переменной x . Затем оцените, используя порядок операций.
В приведенном ниже примере обратите внимание на то, как добавление круглых скобок может изменить результат при упрощении терминов с показателями степени.
Добавление круглых скобок имело большое значение! Скобки позволяют применять показатель степени к переменным или числам, которые умножаются, делятся, складываются или вычитаются друг из друга.
Внимание! Включение отрицательного знака в состав основы часто приводит к путанице. Ниже приведен пример, чтобы прояснить, применяется ли отрицательный знак до или после экспоненты. 9{2}\\=\left(-3\right)\cdot\left(-3\right)\\={ 9}\end{array}[/latex]
Ключ к запоминанию этого — следовать Порядок операций. Первое выражение не содержит круглых скобок, поэтому вы сначала примените показатель степени к целому числу 3, а затем примените знак минус. Второе выражение включает круглые скобки, так что, надеюсь, вы помните, что отрицательный знак также возводится в квадрат.
В следующих разделах вы узнаете, как упростить выражения, содержащие показатели степени. Вернитесь на эту страницу, если вы забудете, как применять порядок операций к терму с показателями степени, или забудете, где основание, а где показатель степени!
В следующем видеоролике представлены примеры вычисления экспоненциальных выражений для заданного числа.
<noscript><img loading='lazy' src='' /></noscript> com/embed/pQNz8IpVVg0?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»> Использование правила произведения для умножения экспоненциальных выражений
Экспоненциальное представление было разработано для более эффективного написания многократного умножения. Бывают случаи, когда проще или быстрее оставить выражения в экспоненциальной записи при умножении или делении. Давайте рассмотрим правила, которые позволят вам это сделать.
9{а+б}[/латекс].
Чтобы умножить экспоненциальные члены с одним и тем же основанием, сложите показатели степени.
Внимание! Когда вы читаете математические правила, важно обращать внимание на условия правила. Например, при использовании правила произведения вы можете применять его только в том случае, если умножаемые члены имеют одно и то же основание, а показатели степени являются целыми числами. Условия математических правил часто даются до формулировки правила, как в этом примере оно гласит: «Для любого числа x 9{x}}[/латекс].
Чем это правило отличается от силы, возведенной в силу? Чем оно отличается от правила произведения для показателей на предыдущей странице?
Если у переменной есть показатель степени, используйте правило степени: умножьте показатели степени.
Возведение частного в степень
Теперь давайте посмотрим, что произойдет, если возвести частное в степень. Помните, что частное означает деление. Предположим, у вас есть [латекс] \displaystyle \frac{3}{4}[/latex] и вы увеличиваете его до 3 9{4}}}[/latex], где показатель степени в числителе (вверху) был больше, чем в знаменателе (внизу), поэтому последний показатель степени после упрощения всегда был положительным числом и больше нуля. В этом разделе мы рассмотрим, что происходит, когда мы применяем правило отношения для показателей степени и получаем отрицательную или нулевую степень. {n}}}[/latex], что происходит, когда 9{-2}}[/latex] Напишите свой ответ, используя положительные показатели степени.
Показать решение
В следующем видео вы увидите примеры упрощения выражений с отрицательными показателями.
Упрощение выражений с помощью комбинации правил экспоненты
Как только правила экспоненты будут понятны, вы сможете начать упрощать более сложные выражения. Есть много приложений и формул, которые используют экспоненты, и иногда выражения могут быть довольно загроможденными. Упрощение выражения перед вычислением часто может упростить вычисление, как вы увидите в следующем примере, в котором используется правило отношения для упрощения перед заменой x на 4.
Обратите внимание, что вы могли решить эту задачу, подставив 4 вместо x и 2 вместо y в исходном выражении. Вы все равно получите ответ 96, но вычисления будут намного сложнее. Обратите внимание, что вам даже не нужно было использовать значение y для вычисления приведенного выше выражения.
В следующем видео показаны примеры вычисления экспоненциального выражения для заданных чисел.
Обычно проще упростить выражение перед подстановкой каких-либо значений для ваших переменных, но в любом случае вы получите один и тот же ответ. В следующих примерах вы увидите, как упростить выражения, используя различные комбинации правил для показателей степени.
Следующие примеры требуют использования всех правил экспоненты, которые мы уже изучили. Помните, что правила произведения, мощности и частного применяются, когда ваши термины имеют одну и ту же основу.
Упрощение выражений с отрицательными показателями
Теперь мы добавим последний слой к нашим навыкам упрощения показателей степени и попрактикуемся в упрощении составных выражений, в которых есть отрицательные показатели степени. Стандартным соглашением является записывать показатели как положительные, потому что пользователю легче понять значение, связанное с положительными показателями, а не с отрицательными показателями. 9{-4}}[/latex]
Запишите свой ответ с положительными показателями. В таблице ниже показано, как упростить одно и то же выражение двумя разными способами: сначала преобразовать отрицательные показатели степени в положительные, а затем применить правило произведения для показателей степени. Вы увидите, что для каждого метода есть столбец, описывающий правило экспоненты или другие шаги, предпринятые для упрощения выражения.
9{-1}}[/latex]
Запишите свой ответ с положительными показателями.
Показать решение
В следующем разделе вы узнаете, как записывать очень большие и очень маленькие числа с использованием показателей степени. Эта практика широко используется в науке и технике.
Сводка
Вычисление выражений, содержащих экспоненты, такое же, как и вычисление любого выражения. Вы подставляете значение переменной в выражение и упрощаете.
Правило произведения для показателей степени: для любого числа 9{x}}[/латекс]
Отрицательные показатели — Полный курс алгебры
Навыки
в
A L G E B R A
Содержание | Дом
20
Степень дроби
Делительные степени одного основания
Отрицательные показатели
Секция 2
Показатель степени 0
Научное обозначение
Степень дроби

«Чтобы возвести дробь в степень, возведите числитель
и знаменатель в эту степень.»
Переписать с положительными показателями сначала Описание предпринятых шагов
Пример 1.
Для, согласно значению показателя степени и правилу умножения дробей:
Пример 2.    Применить правила экспоненты:
Решение . Мы должны принять 4-ю силу всего. Но чтобы взять степень степени — умножьте показатели:
Задача 1.   Применить правила экспонент.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
=Сначала решай задачу сам!
  а) = x ²
у ² б) = 8 x ³
27 в) =
г) =
  д) = x ² − 2 x + 1
x ² + 2 x + 1
Трехчлен Perfect Square
Делительные степени одного основания
В следующем уроке мы увидим следующее правило сокращения дроби:
топор
ай = х
у
«И числитель, и знаменатель могут быть разделены
на общий множитель. »
Рассмотрим эти примеры:
2 · 2 · 2 · 2 · 2
     2 · 1 7 2 9 = 2 · 2 · 2
___2 · 2___
2 · 2 · 2 · 2 · 2 = __1__
2 · 2 · 2
Если писать с показателями, то

2 ² = 2 ³
2 ²
2 ⁵ = 1
2 ³
В каждом случае мы вычитаем показателей степени. Но когда показатель степени в знаменателе больше, мы пишем 1 над разницей.
Пример 3.
x ³ = х ⁵

x ⁸ = 1
x ⁵
Вот правило:
Проблема 2.   Упростите следующее. (Не пишите отрицательную степень.)
  а) = х ³ б) x ²
x ⁵ = 1
x ³ в) x
x ⁵ = 1
x ⁴
  г) x ²
x = х д) = − х ⁴ е) = 1
x ²
Проблема 3.    Упростите каждое из следующих действий. Затем вычислите каждое число.
  а) = 2 ³ = 8 б) 2 ²
2 ⁵ = 1
2 ³ = 1
8 в) 2
2 ⁵ = 1
2 ⁴ = 1
16
  г) 2 ²
2 = 2 д) = −2 ⁴ = −16. См. Урок 13.
  е) = 1
2 ² = 1
4
Пример 4.   Упрощение путем сокращения до наименьших членов:
Раствор.   Рассмотрите каждый элемент по очереди:
Проблема 4.   Упростите, приведя к наименьшим терминам. (Не пишите отрицательные степени.
  а) = г ³
5 x ³ б) = − 8 а ³
5 б ³
  в) = –   3 z _
5 x ⁴ г ³ г) = с ³
16
д) ( x + 1) ³ ( x — 1)
( x — 1) ³ ( x + 1) 910 = ( x + 1) ²
( x — 1) ²
Отрицательные показатели степени
Теперь мы собираемся расширить значение экспоненты не только на положительное целое число. Мы сделаем это таким образом, чтобы выполнялись обычные правила экспонент. То есть нам нужно, чтобы для любых показателей степени выполнялись следующие правила: положительные, отрицательные, 0 — четные дроби.
а ^м а ⁿ = а ^{м + п}   То же основание

( аб ) ^п = а ⁿ б ^н   Сила продукта

( a ^м ) ⁿ = а ^мин   Сила силы
Начнем с определения числа с отрицательным показателем степени .
а ^{− п} =   1
а ^п
Это число, обратное этому числу с положительным показателем степени.
a ^{− n} является обратным a ⁿ .
Пример 5.    2 ⁻³ = 1
2 ³ = 1
8
База 2 не меняется. Отрицательная экспонента становится положительной — в знаменателе.
Пример 6.   Сравните следующее. То есть оцените каждый:
3 ⁻² −3 ⁻² (−3) ⁻² (−3) ⁻³
   Ответы. 3 ⁻² = 1
3 ² = 1
9 .
Далее,
−3 ⁻² является минус из 3 ⁻² . (См. Урок 13.) База по-прежнему равна 3.
. −3 ⁻² = − 1
9 .
Что касается (−3) ⁻², скобки указывают, что основание равно −3:
. (−3) ⁻² = 1
(−3) ² = 1
9 .
Наконец,
(−3) ⁻³ = 1
(−3) ³ = – 1
27 .
Таким образом, отрицательная экспонента не дает отрицательного числа. Это может сделать только отрицательное основание. И тогда показатель степени должен быть нечетным
Пример 7.    Упростить а ²
а ⁵ .
Решение . Поскольку мы изобрели отрицательные показатели степени, теперь мы можем вычесть любые показателей степени следующим образом:
²
⁵ = a ^{2 − 5} = a ⁻³
Теперь у нас есть следующее правило для любых показателей m , n :
На самом деле, именно потому, что мы хотели, чтобы это правило выполнялось, мы
определено a ^{− n} как 1
а ^п .
Мы хотим
²
⁵ = а ⁻³
Но
²
⁵ = 1
а ³
. Следовательно, мы определяем a ⁻³ как 1
а ³ .
Пример 8.    а ⁻¹ = 1
а
a ⁻¹ теперь является символом обратной или мультипликативной инверсии числа к любому числу a . Он появляется в следующем правиле (Урок 6):
a · a ⁻¹ = 1
Проблема 5.   Оцените следующее.
. а) ( 2
3 ) ⁻¹ = 3
2 . 3
2 является обратным числом 2
3 .
. б) ( 2
3 ) ⁻⁴ = 81
16 . 81
16 является величиной, обратной 4-й степени числа 2
3 .
Задача 6.   Показать: a ^m · b ^{− n} = а ^м
б ^н .
a ^m · b ^{− n} = a ^m · 1
б ^н = а ^м
б ^н .
Определение подразделения
Пример 9.    Используйте правила экспонент, чтобы вычислить (2 ⁻³ · 10 ⁴ ) ⁻² .
Решение. (2 ⁻³ · 10 ⁴ ) ⁻² = 2 ⁶ · 10 ⁻⁸ Сила силы

= Проблема 6

= _64_
100 000 000
Задача 7.   Оцените следующее.
  а) 2 ⁻⁴ = 1
2 ⁴ = 1
16   б) 5 ⁻² = 1
5 ² = 1
25   в) 10 ⁻¹ = 1
10 ¹ = 1
10
  г) (−2) ⁻³ = 1
(−2) ³ = 1
−8 = – 1
8
  д) (−2) ⁻⁴ = 1
(−2) ⁴ = 1
16 е) −2 ⁻⁴ = – 1
2 ⁴ = – 1
16
г) (½) ⁻¹ =
2. 2 есть , обратное ½.
Задача 8.   Используйте правила экспонент, чтобы оценить следующее.
а) 10 ² · 10 ⁻⁴ = 10 ^{2 − 4} = 10 ⁻² = 1/100.
б) (2 ⁻³ ) ² = 2 ⁻⁶ = 1
2 ⁶ = 1
64
в) (3 ⁻² · 2 ⁴ ) ⁻² = 3 ⁴ · 2 ⁻⁸ = 3 ⁴
2 ⁸ = 81
256
г) 2 ⁻² · 2 = 2 ⁻²⁺¹ = 2 ⁻¹ = 1
2
Задача 9.    Перепишите без знаменателя.
  а) х ²
x ⁵ = x ²⁻⁵ = x ⁻³ б) г
г ⁶ = г ¹⁻⁶ = г ⁻⁵
  в) = x ⁻³ у ⁻⁴ г) = а ⁻¹ б ⁻⁶ в ⁻⁷
  д) 1
х = x ⁻¹ е) 1
x ³ = х ⁻³
ж) ( x + 1)
   x = ( х + 1) х ⁻¹ з) ( x + 2) ²
( x + 2) ⁶ = ( х + 2) ⁻⁴
Пример 10.     Перепишите без знаменателя и оцените:
Ответить . Правило вычитания показателей —
— выполняется, даже если показатель степени отрицателен.
Следовательно,
= 10 ^{−3 + 5 − 2 + 4} = 10 ⁴ = 10 000.
Показатель степени 2 входит в числитель как −2; показатель -4 идет туда как +4.
Задача 10.    Перепишите без знаменателя и оцените.
а) 2 ²
2 ⁻³ = 2 ^{2 + 3} = 2 ⁵ = 32 б) 10 ²
10 ⁻² = 10 ^{2 + 2} = 10 ⁴ = 10 000
в) = 10 ^{2 − 5 − 4 + 6} = 10 ⁻¹ = 1
10
г) = 2 ^{5 − 6 + 9 − 7} = 2 ¹ = 2
Проблема 11.    Можно сдвинуть множители между числителем и знаменателем [Как?]
Путем изменения знака показателя степени.
  Пример 11.   Перепишите без знаменателя:
   Ответ.
Показатель степени 3 входит в числитель как −3; показатель -4 идет туда как +4.
Задача 12.    Перепишите только с положительными показателями.
а) x
y ⁻² = ху ² б) = в) =
г) = д) =
Задача 13.     Примените правила показателей, затем перепишите с положительными показателями.
а) = = б) = =
Раздел 2: показатель степени 0
Следующий урок: Алгебраические дроби
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]

Умножение, деление и степень ｜ Hatsudy
При изучении отрицательных чисел многие люди путаются. Это потому, что когда вы умножаете или делите разные знаки, знаки меняются. Кроме того, при умножении отрицательного на отрицательное знак становится положительным. Почему это происходит?
Мало кто может объяснить эту причину. Однако, чтобы понять математику, нам нужно решить вопрос заранее.
Как только вы поймете знаки умножения, вы сможете решать не только деление и степени, но и сложные вопросы с помощью четырех арифметических действий.
Многим людям сложно вычислять отрицательные числа, потому что они не понимают основных принципов. Итак, объясним, почему меняются знаки при отрицательном умножении и как решать вопросы.
Содержание
1 В зависимости от знака умножение может быть положительным или отрицательным 1.1 Почему возможно умножение на плюс и минус?
1.2 Почему при умножении отрицательного числа на отрицательное число получается положительное
2 Знаки деления также меняются 2.1 Знак меняется в зависимости от того, четное или нечетное отрицательное число
Как делать Вычислить мощность с помощью экспоненты 3.1 Обращайте внимание на разницу в знаках и скобках при вычислении степеней
3. 2 В степенях с дробями следует обращать внимание на скобки
4 Упражнения: математические умножение, деление и степень Умножение и деление
В зависимости от знака умножение может быть положительным или отрицательным
При изучении только положительных чисел нет необходимости рассматривать отрицательные числа. Однако в математике нам приходится иметь дело с отрицательными числами.
В математике есть умножение и деление. При умножении знак ответа будет меняться в зависимости от того, какой знак используется. При умножении получается следующее.
Положительное число $(+)×$ Положительное число $(+)=+$
Отрицательное число $(-)×$ Положительное число $(+)=-$
Положительное число $(+)×$ Отрицательное число $(-)=-$
Отрицательное число $(-)×$ Отрицательное число $(-)=+$
Возможно, вы думаете, что вам нужно запомнить четыре из них. Тем не менее, не нужно помнить о них. Это происходит следующим образом.
Умножение одинаковых знаков дает $+$.
Умножение разных знаков дает $-$.
Например, $4×-3=-12$. Это потому, что это умножение различных знаков. С другой стороны, $-4×-3=12$. Это потому, что это умножение с теми же знаками.
Но почему ответ отрицательный, если мы умножаем положительное число на отрицательное? И почему умножение отрицательного числа на отрицательное число дает положительный ответ? Мало кто может правильно объяснить эту причину, поэтому попробуем ответить на этот вопрос.
Почему возможно умножение на плюс и минус?
Почему при умножении положительные и отрицательные ответы становятся отрицательными? Сначала решим этот вопрос.
В общем, когда мы решаем этот вопрос, мы думаем о скорости, времени и расстоянии. Существует следующая формула.
Скорость $×$ Время $=$ Расстояние
Например, если вы идете со скоростью 1 км/ч и проходите 3 часа, вы пройдете расстояние 3 км. Таким образом, мы видим, что умножение между положительными числами допустимо.
-Почему ответ отрицательный для разных знаков?
Почему использование разных знаков делает ответ отрицательным? 0 (ноль) представляет собой контрольную точку. И если вы используете только положительные знаки, вы думаете только о будущем. Но на самом деле прошлое тоже существует.
Для пройденного расстояния мы можем сделать следующую цифру.
В этом случае, если вы идете со скоростью -1 км/ч и проходите 3 часа, где вы будете? Ходьба со скоростью -1 км/ч означает, что вы идете на запад со скоростью 1 км/ч. Если вы пойдете на запад и пройдете 3 часа, вы окажетесь на -3 км.
-1 км/ч $×$ 3 часа $=$ -3 км
Кроме того, если вы идете со скоростью 1 км/ч и проходит -3 часа, где вы будете? -3 часа прошло, значит 3 часа назад. Если вы идете на восток со скоростью 1 км/ч, 3 часа назад вы были на -3 км.
1 км/ч $×$ -3 часа $=$ -3 км
Если подумать об этом таким образом, то становится понятно, почему умножение положительного числа на отрицательное дает отрицательный ответ.
Почему умножение отрицательного числа на отрицательное число дает положительное число
Почему, напротив, умножение отрицательного числа на отрицательное число дает положительное число? Как и прежде, давайте рассмотрим взаимосвязь между скоростью, временем и расстоянием. Если вы пойдете со скоростью -1 км/ч и пройдете -3 часа, где вы окажетесь?
Ходьба со скоростью -1 км/ч означает, что вы идете на запад. Также — 3 часа прошло означает, что 3 часа назад.
Если вы идете на запад (минус), то 3 часа назад вы были на +3 км (3 км на восток).
-1 км/ч $×$ -3 часа $=$ +3 км
Такой способ мышления позволяет нам понять, почему ответ положительный, если мы умножаем отрицательное значение на отрицательное.
Знаки меняются и для деления
До сих пор мы объясняли умножение. С другой стороны, как насчет деления?
Мы можем думать о делении точно так же, как об умножении. Короче говоря, если два числа имеют одинаковый знак, ответ будет положительным. С другой стороны, если делить по разным знакам, ответ будет отрицательным.
Разделы с одинаковыми знаками дают $+$.
Деление с разными знаками дает $-$.
Причина этого в том, что и умножение, и деление одинаковы. Например, если вы идете со скоростью 1 км/ч в течение 3 часов, вы пройдете 3 км.
1 км/ч $×$ 3 часа $=$ 3 км
Итак, какова скорость в час, если вы пройдете расстояние 3 км за 3 часа? Уравнение и ответ следующие.
3 км $÷$ 3 часа $=$ 1 км/ч
Таким образом, умножение можно преобразовать в деление.
Например, при делении дробей, поменяв местами верх и низ, выражение можно заменить на умножение. Это потому, что деление может быть преобразовано в умножение. Умножение и деление имеют одинаковые свойства. Поэтому смена знака при делении такая же, как и при умножении.
Знак меняется в зависимости от того, является ли отрицательное число четным или нечетным
Однако при выполнении математических расчетов редко удается вычислить только два числа. Часто мы умножаем или делим несколько чисел. Что происходит со знаком при умножении нескольких положительных и отрицательных чисел?
Для этого при умножении (или делении), если отрицательное число четное, знак ответа будет положительным. С другой стороны, если отрицательное число является нечетным при умножении (или делении), то знак ответа будет отрицательным.
×7×9$—1 Number of minuses Equation Answer sign
1 (odd) $+×-$ $-$
2 (even) $- ×-$ $+$
3 (нечетные) $-×-×-$ $-$
4 (четные) $—1 $+$
5 (нечетный) $-×-×-×-×-$ $-$
Как было сказано выше, негатив имеет противоположную природу. Противоположность противоположности положительна. Следовательно, если отрицательное число четное, то знак ответа положительный. Напротив, если отрицательное число нечетное, знак ответа отрицательный.
Этому правилу подчиняются не только целые числа, но также десятичные числа и дроби. Например, верно следующее.
$-1×-1×-\displaystyle\frac{1}{2}=-\displaystyle\frac{1}{2}$
Поскольку существует три отрицательных числа (нечетное число отрицательных чисел ), ответ будет отрицательным. В вычислениях умножения и деления знак ответа меняется в зависимости от того, является ли отрицательное число четным или нечетным числом.
Как вычислить степень с помощью экспоненты
Для положительных и отрицательных чисел понятие степени так же важно, как умножение и деление. Степень — это расчет, который показывает, на сколько умножается одно и то же число. Например, в степенях $3×3$ выражается как 3 ² . Кроме того, $4×4×4$ выражается как 4 ³ .
С точки зрения чтения, 3 ² равно 3 в квадрате. 4 ³ равно 4 в кубе.
3 ² = 3 в квадрате (или 3 во второй степени)
3 ³ = 3 куба (или 3 до 3 -й мощности)
3 ⁴ = 3 к 4 -й мощности
3 ⁵ = 3-5 -й мощности
3 ⁶ = 3 до 3-5 -й мощности
3 ⁶ = 3 до 5 -й мощности 6-я степень
Небольшое число в правом верхнем углу называется показателем степени. Например, для 4 ³ 3 является показателем степени. Проверяя показатель степени, вы можете увидеть, сколько раз нужно умножить одно и то же число.
Вычисляя степени с помощью показателей степени, получаем следующее. 92=-1×-3×-3=9$
Показатель степени (-3) равен 2. Следовательно, мы умножаем -3 дважды. Кроме того, мы должны вычислить -3 и знак (-1) отдельно. Результатом является уравнение, показанное выше.
В степенях с дробями следует обращать внимание на круглые скобки
В зависимости от того, присутствуют круглые скобки или нет, ответ на вопрос сильно различается при вычислении степеней. Важно обращать внимание на круглые скобки даже для степеней с дробями.
94$, $\left(\displaystyle\frac{2}{3}\right)$ в 4-й степени, потому что перед показателем степени стоят круглые скобки.
Если нет круглых скобок, только число перед показателем степени может быть вычислено путем включения питания. С другой стороны, если есть круглые скобки, все числа внутри круглых скобок должны быть рассчитаны путем включения. Важно понимать, что при расчетах с использованием показателей степени метод расчета меняется в зависимости от того, есть скобки или нет.
Упражнения: математические умножение, деление и степень
Q1: Выполните следующие вычисления.
$3×-4$
$-30÷-5$
$-4×-6×-3$
A1: Ответы.
При умножении или делении с использованием положительных и отрицательных чисел важно помнить, что если отрицательное число четное, ответ положительный, а если отрицательное число нечетное, ответ отрицательный. Поэтому ответы следующие. 92$
$=-16×3×\displaystyle\frac{4}{9}$
$=-\displaystyle\frac{192}{9}$
$=-\displaystyle\frac{64} {3}$
Рассчитав каждое по отдельности, мы наконец можем составить уравнение только для умножения.
Вычисление плюса и минуса с помощью умножения и деления
Мы не можем выполнять математические вычисления, если не знаем, как вычислять плюс и минус. Итак, когда вы умножаете и делите, изучите, как работают знаки.
В частности, многие люди путаются при умножении (или делении) отрицательного числа на отрицательное число, потому что не понимают, почему оно становится положительным. Таким образом, мы объяснили, почему ответ положительный при умножении отрицательного числа на отрицательное число.
Также важен тот факт, что если отрицательное число является четным числом, ответ положительный, а если отрицательное число является нечетным числом, ответ отрицательный.
В дополнение к этому вам нужно изучить понятие силы. Скобки важны в степенях, и ответ зависит от того, где они расположены. Это концепция умножения и деления, которую вы должны изучить с положительными и отрицательными числами.
Что такое экспонента? (Видео и практические вопросы)
TranscriptFAQsFact SheetPractice
Возможно, вы слышали, как один или два учителя математики говорят, что математика — это язык. Если это так, то алгебраические правила и обозначения следует считать грамматикой и пунктуацией языка математики!
Некоторые ученики, у которых проблемы с математикой, не понимают, как применять правила и интерпретировать обозначения. В этом видео мы сосредоточимся на обозначениях и интерпретации показателей степени. В этом видео также рассматривается значение показателей степени, которые являются натуральными числами, также называемыми «счетными числами» (например, 1, 2, 3 и т. 3\) является более эффективным способом записи расширенной версии $x \times x \times x$. 92+4х+4\).
Итак, пока вы можете определить основание, умножение этого основания само по себе становится довольно простым. Как уже упоминалось, интерпретация обозначений в математике — это полдела! Практика основ является ключом к тому, чтобы обрести уверенность в более сложном математическом содержании.
Спасибо за просмотр и удачной учебы!
Законы показателей степени

Часто задаваемые вопросы
Q
Что такое показатели степени в математике? 91=8\).
Q
Какие существуют 4 типа показателей?
A
Четыре типа показателей: положительный, отрицательный, нулевой и рациональный. Положительные показатели степени говорят вам, сколько раз нужно умножить основание само на себя. Как правило, это приводит к очень большому числу. Отрицательные показатели степени говорят вам, сколько раз делить основание само по себе. Как правило, это приводит к очень небольшому числу. Показатель степени нуля всегда будет равен единице. А 96\).
Q
В чем разница между степенью и показателем степени?
A
Термины «степень» и «показатель степени» по существу означают одно и то же. Например, «пять в третьей степени » представляет основание числа пять и показатель степени числа числа три. Часто эти два термина используются взаимозаменяемо.
Q
Индексы и показатели одинаковы?
A
Индекс или индекс — это другое название показателя степени. Индекс числа говорит вам, сколько раз нужно умножить основание само на себя. Например, 97\). Степень или экспонента может быть положительной или отрицательной. Положительные показатели степени приведут к большим числам, а отрицательные показатели — к маленьким числам.
Q
Как показатели степени используются в технике?
A
Инженеры используют показатели степени, потому что они часто работают с очень большими или очень маленькими измерениями. Например, инженер-строитель может работать с расчетами веса массивного моста. Эти измерения могут исчисляться десятками тысяч, поэтому часто наиболее эффективно выражать их с помощью положительных показателей степени. С другой стороны, инженеры-химики часто работают с чрезвычайно малыми значениями. Эти значения наиболее эффективно записываются с использованием отрицательных показателей. 92-14x+49\)
Скрыть ответ

Вернуться к видео по комплексным арифметическим вычислениям
600998
Рабочие листы по степеням десяти
есть сила, чтобы изучить этот важный навык! Эта страница включает в себя рабочие листы по математике со степенью десяти с целыми числами и десятичными знаками в форматах запятая/точка и точка/запятая, чтобы учащиеся могли освоить этот важный навык.
Понимание того, как умножать и делить на десять, является одним из тех важных навыков, без которых учащиеся не могут обойтись. Это облегчает использование навыков оценки, это важно для изучения больших и малых чисел и укрепляет понимание разрядного значения и чисел в целом. Эта страница включает в себя множество степеней десяти рабочих листов с целыми числами на них, потому что здесь меньше цифр для работы, а десятичный знак находится в постоянном месте, а это означает, что рабочие листы с целыми числами окажутся хорошей ступенькой к большему сложные десятичные версии далее по странице.
Положительные степени числа десять относятся к 10, 100 и 1000. Отрицательные степени числа десять относятся к 0,1, 0,01 и 0,001. Мы предоставили рабочие листы как в стандартной форме, так и в форме экспоненты. Если это для вас новое, 10 ^-3 = 0,001, 10 ^-2 = 0,01, 10 ^-1 = 0,1, 10 ⁰ = 1, 10 ¹ 2 90, 26 10 ³ = 10000606 598 просмотров на этой неделе )Умножение целых чисел на все степени десяти (стандартная форма) ( 336 просмотров на этой неделе )Умножение и деление десятичных чисел на положительные степени десяти (стандартная форма) ( 246 просмотров на этой неделе )Умножение и Деление десятичных дробей на 10 ( 178 просмотров на этой неделе )Учимся умножать числа (в диапазоне от 10 до 99) на кратные положительных степеней десяти в стандартной форме ( 175 просмотров на этой неделе )
Учимся умножать и делить целые числа на степени из десяти рабочих листов
Рабочие листы для изучения закономерностей, связанных с умножением и делением на степени десяти.
Обучение умножению на десять рабочих листов включает одно и то же число, умноженное на положительные или отрицательные степени десяти. Это позволяет учащимся увидеть закономерности в умножении или делении на набор степеней десяти.
Обучение умножению целых чисел на степени десяти
Лучше всего начать со степеней десяти в стандартной форме. Позже познакомьте учащихся с формой экспоненты, так как они уже будут знать, как умножать или делить со степенями десяти, и могут сосредоточиться на изучении взаимосвязи между экспонентами и количеством нулей, с которыми им нужно работать.
Числа от 1 до 10 × Положительные Степени Десятки (Стандартная Форма) Двузначные Числа × Положительные Степени Десяти (Стандартная Форма)
Числа от 1 до 10 × Отрицательные Степени Десяти (Стандартная Форма) Двузначные Числа × Отрицательные Степени Десяти (Стандартная Форма)
Целое число × Отрицательные степени десяти (результаты целых чисел) (стандартная форма)
Числа от 1 до 10 × Положительный Степени Десяти (Форма Экспонента ) Двузначные Числа × Положительные Степени Десятки (Форма Экспонента )
Числа от 1 до 10 × Отрицательные Степени Десятки (Форма Экспонента ) Двузначные Числа × Отрицательные Степени Десяти (Форма Экспонента )
Числа от 90 606 1 до 10 90 607 × 90 606 Отрицательные 90 607 Степени Десятки (Результаты целых чисел) ( Экспонента Форма)
Умение умножать целых чисел на числа, кратные десяткам
Умножение на числа, кратные десятичной степени, имеет огромные преимущества в ментальной арифметике. Подумайте о длинном умножении, которое, по сути, умножается на степени, кратные десяти. Например, 456 × 4 можно представить как 4 × 400 + 4 × 50 + 4 × 6. Чем удобнее учащимся обращаться со всеми этими лишними нулями, тем реже они будут делать ошибки.
Числа от от 1 до 10 × кратные Положительные Степени десяти (стандартная форма) Двузначные Числа × кратные Положительные Степени Десяти (Стандартная Форма)
Числа от от 1 до 10 × кратные отрицательные степени десяти (стандартная форма) Двузначные Числа × кратные Отрицательные Степени Десяти (Стандартная Форма)
Целое число × число, кратное отрицательным степеням десяти (результаты целых чисел) (стандартная форма)
Числа от От 1 до 10 × Кратные числа Положительные Степени десяти (форма Экспонента ) Двузначные Числа × кратные Положительные Степени Десяти (Форма Экспонента )
Числа от 1 до 10 × Кратные Отрицательные Степени Десятки (Форма Экспонента ) Двузначные Числа × кратные Отрицательные Степени Десяти (Форма Экспонента )
Числа от 1 до 10 × Кратные числа Отрицательные Степени десяти (Результаты целых чисел) (Форма Экспонента )
Обучение делению целых чисел на степени десяти
Обучение делению на десять рабочих листов включает одно и то же число, деленное на положительные или отрицательные степени десяти.
Числа от 1 до 10 ÷ Положительные Степени Десяти (Стандартная Форма) Двузначное число Числа ÷ Положительные Степени Десяти (Стандартная Форма)
Числа от 1 до 10 ÷ Отрицательные Степени Десяти (Стандартная Форма) Двузначные Числа ÷ Отрицательные Степени Десяти (Стандартная Форма)
Целое число ÷ Положительная степень числа десять (результаты целых чисел)
Числа от 1 до 10 ÷ Положительные Степени Десяти (Форма Экспонента ) Двузначные Числа ÷ Положительные Степени Десятки ( Экспонента Форма)
Числа от 1 до 10 ÷ Отрицательные Степени Десятки (Форма Экспонента ) Двузначные Числа ÷ Отрицательные Степени Десяти (Форма Показатель )
Числа от 1 до 10 ÷ Положительные Степени десяти (Результаты целых чисел) (Форма Exponent )
Обучение делению целых чисел на числа, кратные десяткам
Числа ÷ Кратные числа Положительные Степени десяти (Стандартная форма) (Частные от 1 до 10 )
Числа ÷ Кратные Положительные Степени Десяти (Стандартная Форма) (Частные от 10 до 99 )
Числа ÷ Кратные Отрицательные Степени Десяти (Стандартная Форма) (Частные от 1 до 10 )
Числа ÷ Кратные Отрицательные Степени Десяти (Стандартная Форма) (Частные 10 до 99 )
Целое число ÷ число, кратное положительной степени десяти (результаты целых чисел)
Числа от От 1 до 10 ÷ Кратность Положительные Степени Десяти (Форма Экспонента ) Двузначные Числа ÷ Кратные Положительные Степени Десятки (Форма Показатель )
Числа от 1 до 10 ÷ Кратные Отрицательные Степени Десятки (Форма Показатель ) Двузначные Числа ÷ Кратные Отрицательные Степени Десяти ( Экспонента Форма)
Числа от 1 до 10 ÷ Кратные числа Положительные Степени десяти (Результаты целых чисел) (Форма Экспонента )
Умножение и деление целых чисел на степени десяти.
Рабочие листы Рабочие листы для практики умножения и деления целых чисел на степени десяти со смешанными и отдельными степенями десяти, а также в стандартных и экспоненциальных формах.
Умножение целых чисел на степени десяти
Умножение на положительные степени десяти всегда увеличивает абсолютное значение числа. И наоборот, умножение на отрицательные степени десяти всегда уменьшает абсолютное значение числа. Умножение на 10 ⁰ равносильно умножению на 1.
Целое число × Все степени десяти (стандартная форма)
Целое число × Все степени десяти (форма экспоненты)
Целое число × все положительные степени десяти (стандартная форма)
Целое число × все положительные степени десяти (форма экспоненты)
Целое число × все отрицательные степени числа десять (стандартная форма)
Целое число × все отрицательные степени десяти (форма экспоненты)
Целое число × 0,001
Целое число × 10 ^-3 Целое число × 0,01
Целое число × 10 ^-2 Целое число × 0,1
Целое число × 10 ^-1 Целое число × 10
Целое число × 10 ¹ Целое число × 100
Целое число × 10 ² Целое число × 1000
Целое число × 10 ³
Умножение целых чисел на степени десяти (числовой формат точка/запятая)
Целое число × Все степени десяти (стандартная форма)
Целое число × Все степени десяти (форма экспоненты)
Целое число × все положительные степени десяти (стандартная форма)
Целое число × все положительные степени десяти (форма экспоненты)
Целое число × все отрицательные степени числа десять (стандартная форма)
Целое число × все отрицательные степени десяти (форма экспоненты)
Целое число × 0,001
Целое число × 10 ^-3 Целое число × 0,01
Целое число × 10 ^-2 Целое число × 0,1
Целое число × 10 ^-1 Целое число × 10
Целое число × 10 ¹ Целое число × 100
Целое число × 10 ² Целое число × 1. 000
Целое число × 10 ³
Деление целых чисел на степени десяти
Деление на положительные степени десяти всегда уменьшает абсолютное значение числа. И наоборот, деление на отрицательные степени десяти всегда увеличивает абсолютное значение числа. Деление на 10 ⁰ равносильно делению на 1.
Целое число ÷ Все степени десяти (стандартная форма)
Целое число ÷ Все степени десяти (форма экспоненты)
Целое число ÷ все положительные степени числа десять (стандартная форма)
Целое число ÷ все положительные степени десяти (форма экспоненты)
Целое число ÷ Все отрицательные степени числа десять (стандартная форма)
Целое число ÷ все отрицательные степени десяти (форма экспоненты)
Целое число ÷ 0,001
Целый номер ÷ 10 ^-3 Целое число ÷ 0,01
Целое число ÷ 10 ^-2 Целое число ÷ 0,1
Целое число ÷ 10 ^-1 Целое число ÷ 10
Целое число ÷ 10 ¹ Целое число ÷ 100
Целое число ÷ 10 ² Целое число ÷ 1000
Целое число ÷ 10 ³
Деление целых чисел на степени десяти (формат точки/запятая)
Целое число: все степени десяти (стандартная форма)
Целое число: все степени десяти (форма экспоненты)
Целое число: все положительные степени числа десять (стандартная форма)
Целое число: все положительные степени десяти (форма экспоненты)
Целое число: все отрицательные степени десяти (стандартная форма)
Целое число: все отрицательные степени десяти (форма экспоненты)
Целое число: 0,001
Целое число: 10 ^-3 Целое число : 0,01
Целый номер: 10 ^-2 Целое число : 0,1
Целый номер: 10 ^-1 Целое число: 10
Целый номер: 10 ¹ Целое число: 100
Целый номер: 10 ² Целое число: 1. 000
Целый номер: 10 ³
Умножение и деление целых чисел на степени десяти
Эти математические рабочие листы должны помочь немного запутаться. Смешение операций на странице помогает учащимся обращать внимание на детали и побуждает их к доступу к большему количеству процессов, пока они отвечают на вопросы. Первые рабочие листы ниже включают все степени десяти от 0,001 до 1000.
Целое число × или ÷ Все степени десяти (стандартная форма)
Целое число × или ÷ Все степени десяти (форма экспоненты)
Целое число × или ÷ Все положительные степени числа десять (стандартная форма)
Целое число × или ÷ Все положительные степени десяти (форма экспоненты)
Целое число × или ÷ Все отрицательные степени числа десять (стандартная форма)
Целое число × или ÷ Все отрицательные степени десяти (форма экспоненты)
Целое число × или ÷ 0,001
Целое число × или ÷ 10 ^-3 Целое число × или ÷ 0,01
Целое число × или ÷ 10 ^-2 Целое число × или ÷ 0,1
Целое число × или ÷ 10 ^-1 Целое число × или ÷ 10
Целое число × или ÷ 10 ¹ Целое число × или ÷ 100
Целое число × или ÷ 10 ² Целое число × или ÷ 1000
Целое число × или ÷ 10 ³
Умножение и деление целых чисел на степени десяти (формат точки/запятая)
Целое число × или : все степени десяти (стандартная форма)
Целое число × или : все степени десяти (форма экспоненты)
Целое число × или : все положительные степени десяти (стандартная форма)
Целое число × или : все положительные степени десяти (форма экспоненты)
Целое число × или : все отрицательные степени десяти (стандартная форма)
Целое число × или : все отрицательные степени десяти (форма экспоненты)
Целое число × или : 0,001
Целое число × или : 10 ^-3 Целое число × или : 0,01
Целое число × или : 10 ^-2 Целое число × или : 0,1
Целое число × или : 10 ^-1 Целое число × или : 10
Целое число × или : 10 ¹ Целое число × или : 100
Целое число × или : 10 ² Целое число × или : 1. 000
Целое число × или : 10 ³
Умножение и деление десятичных чисел на степени десяти. Рабочие листы
Рабочие листы для практики умножения и деления десятичных чисел на степени десяти со смешанными и отдельными степенями десяти, а также в стандартных и экспоненциальных формах.
В отличие от рабочих листов с целыми числами, приведенных выше, эти рабочие листы, а также следующие за ними версии с делением и смешанными числами содержат больше цифр, требуют большего количества разрядов и, следовательно, являются более сложными. Это, вероятно, не лучшее место для начала, если ваши ученики только учатся умножать и делить на степени десяти. Вместо этого попробуйте листы с целыми числами выше по странице. Если они готовы, эти рабочие листы должны стать прекрасным испытанием и во многом помогут вашим ученикам добиться успеха в изучении математики.
Умножение десятичных чисел на степени десяти
Десятичный × Все степени десяти (стандартная форма)
Десятичный × Все степени десяти (форма экспоненты)
Десятичный × Все положительные степени числа десять (стандартная форма)
Десятичный × Все положительные степени десяти (форма экспоненты)
Десятичный × Все отрицательные степени числа десять (стандартная форма)
Десятичный × Все отрицательные степени десяти (форма экспоненты)
Десятичный × 0,001
Десятичный × 10 ^-3 Десятичный × 0,01
Десятичный × 10 ^-2 Десятичный × 0,1
Десятичный × 10 ^-1 Десятичный × 10
Десятичный × 10 ¹ Десятичный × 100
Десятичный × 10 ² Десятичный × 1000
Десятичный × 10 ³
Умножение десятичных чисел на степени десяти (формат точка/запятая)
Десятичный × Все степени десяти (стандартная форма)
Десятичный × Все степени десяти (форма экспоненты)
Десятичный × Все положительные степени числа десять (стандартная форма)
Десятичный × Все положительные степени десяти (форма экспоненты)
Десятичный × Все отрицательные степени числа десять (стандартная форма)
Десятичный × Все отрицательные степени десяти (форма экспоненты)
Десятичный × 0,001
Десятичный × 10 ^-3 Десятичный × 0,01
Десятичный × 10 ^-2 Десятичный × 0,1
Десятичный × 10 ^-1 Десятичный × 10
Десятичный × 10 ¹ Десятичный × 100
Десятичный × 10 ² Десятичный × 1. 000
Десятичный × 10 ³
Деление десятичных чисел на степени десяти
Иногда учащимся требуется некоторое время, чтобы освоить деление на степени десяти, особенно на отрицательные степени числа десять. Это связано с тем, что студентов обычно учат, что деление уменьшает число, но при делении на отрицательные степени десяти результатом является большее число. Конечно, это относится только к числам, которые изначально были положительными…
Десятичный ÷ Все степени десяти (стандартная форма)
Десятичный ÷ Все степени десяти (форма экспоненты)
Десятичный ÷ Все положительные степени числа десять (стандартная форма)
Десятичный ÷ Все положительные степени числа десять (форма экспоненты)
Десятичный ÷ Все отрицательные степени числа десять (стандартная форма)
Десятичный ÷ Все отрицательные степени числа десять (форма экспоненты)
Десятичный ÷ 0,001
Десятичный ÷ 10 ^-3 Десятичный ÷ 0,01
Десятичный ÷ 10 ^-2 Десятичный ÷ 0,1
Десятичный ÷ 10 ^-1 Десятичный ÷ 10
Десятичный ÷ 10 ¹ Десятичный ÷ 100
Десятичный ÷ 10 ² Десятичный ÷ 1000
Десятичный ÷ 10 ³
Деление десятичных чисел на степени десяти (формат точка/запятая)
Десятичный: все степени десяти (стандартная форма)
Десятичный: все степени десяти (форма экспоненты)
Десятичный: все положительные степени числа десять (стандартная форма)
Десятичный: все положительные степени десяти (форма экспоненты)
Десятичный: все отрицательные степени числа десять (стандартная форма)
Десятичный: все отрицательные степени десяти (форма экспоненты)
Десятичный: 0,001
Десятичный: 10 ^-3 Десятичный: 0,01
Десятичный: 10 ^-2 Десятичный : 0,1
Десятичный: 10 ^-1 Десятичный: 10
Десятичный: 10 ¹ Десятичный : 100
Десятичный: 10 ² Десятичный: 1.
No related posts.}