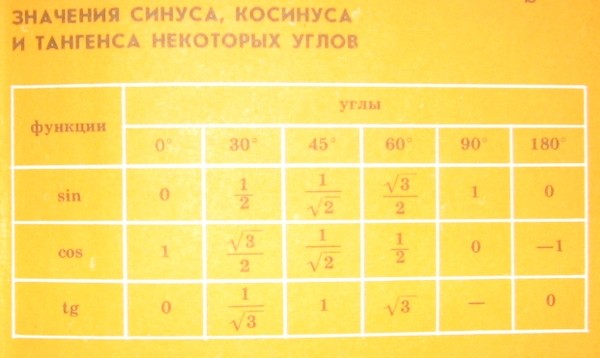
синуса, косинуса, тангенса и котангенса
- Производная синуса
- Производная косинуса
- Производная тангенса и котангенса
- Примеры
п.1. Производная синуса
Найдем производную функции \(f(x)=sinx\) по общему алгоритму.
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=sin(x+\triangle x)-sinx=\\ =2sin\frac{x+\triangle x-x}{2}cos\frac{x+\triangle x+x}{2}=2sin\frac{\triangle x}{2}cos\frac{2x+\triangle x}{2} \end{gather*} Используем первый замечательный предел (см. §39 данного справочника): \begin{gather*} \lim_{x\rightarrow 0}\frac{sinx}{x}=1 \end{gather*} Ищем производную: \begin{gather*} f'(x)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{2sin\frac{\triangle x}{2}cos\frac{2x+\triangle x}{2}}{\triangle x}=\underbrace{\left(\lim_{\triangle x\rightarrow 0}\frac{sin\frac{\triangle x}{2}}{\frac{\triangle x}{2}}\right)}_{=1}\cdot \lim_{\triangle x\rightarrow 0}cos\frac{2x+\triangle x}{2}=\\ =1\cdot cos\frac{2x+0}{2}=cos x \end{gather*} Или: \((sinx)’=cos x\)
Для любого действительного x: $$ (sinx)’=cos x $$
Например:
\((x^2sinx)’=(x^2)’\cdot sinx+x^2\cdot (sinx)’=2xsinx+x^2cosx\)
п.
 2. Производная косинуса
2. Производная косинусаНайдем производную функции \(f(x)=cosx\) по общему алгоритму.
Пусть \(\triangle x\) — некоторое приращение аргумента. Тогда приращение функции: \begin{gather*} \triangle y=f(x+\triangle x)-f(x)=cos(x+\triangle x)-cosx=\\ =-2sin\frac{x+\triangle x-x}{2}sin{x+\triangle x+x}{2}=-2sin\frac{\triangle x}{2}sin\frac{2x+\triangle x}{2} \end{gather*} Как и для производной синуса, используем первый замечательный предел. Ищем производную: \begin{gather*} f'(x)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{-2sin\frac{\triangle x}{2}sin\frac{2x+\triangle x}{2}}{\triangle x}=\underbrace{-\left(\lim_{\triangle x\rightarrow 0}\frac{sin\frac{\triangle x}{2}}{\frac{\triangle x}{2}}\right)}_{=1}\cdot \lim_{\triangle x\rightarrow 0}sin\frac{2x+\triangle x}{2}=\\ =-1\cdot sin\frac{2x+0}{2}=-sinx \end{gather*} Или: \((cosx)’=-sinx\)
Для любого действительного x: $$ (cosx)’=-sinx $$
Например:
\((\sqrt{x}cosx)’=(\sqrt{x})’\cdot cosx+\sqrt{x}\cdot (cosx)’=\frac{1}{2\sqrt{x}}cosx-\sqrt{x}sinx \)
п.
 2x=1\\ 1-2cosx=0\\ cosx=\frac12\\ x=\pm\frac\pi 3+2\pi k \end{gather*} Ответ: \(\left\{\pm\frac\pi 3+2\pi k\right\}\)
2x=1\\ 1-2cosx=0\\ cosx=\frac12\\ x=\pm\frac\pi 3+2\pi k \end{gather*} Ответ: \(\left\{\pm\frac\pi 3+2\pi k\right\}\)| Производная синуса | Производная косинуса | Производная котангенса | Правила нахождения производныхПример 1. Пример 2. Найти производную функции . Пример 3. Найти производную функции Учитывая, что , будем иметь Но , откуда Пример 4. Найти производную функции Общие формулы дифференцирования функцийВ этих формулах u и v — произвольные дифференцируемые функции вещественной переменной, а c — вещественная константа. Этих формул достаточно для дифференцирования любой элементарной функции. (c · u)′ = c · u ′ (u + v)′ = u ′ + v ′ (u · v)′ = u ′ · v + u · v ′
Производная от константыc ′ = 0, где c = const Производная степенной функции(xn )′ = n · xn – 1 Производная показательной функции(ax )′ = ax · ln a Таблица производныхПроизводная степенной функции: Производная логарифмической функции: Производные тригонометрических функций: , , , Производные обратных тригонометрических функций: , , , Производные гиперболических функций: Таблица производных сложных функцийВ следующей таблице приведены формулы для производных сложных функций. В отдельных строках (с желтым фоном) приведены формулы для производных сложных функций в случае, когда внутренняя функция является линейной функцией и имеет вид f (x) = kx + b , где k и b – любые числа, .
Производная и тригонометрические функцииТригонометрические функции неразрывно связаны с производной. K (x0; f (x0)) – произвольная точка, x0 + ∆x – приращение по оси OX, а f (x0 + ∆x) – приращение по оси OY в некой точке L. Проведем прямую через точки K и L и построим прямоугольный треугольник KLN. Если мысленно перемещать отрезок LN по графику Y = f (x), то точки L и N будут стремиться к значениям K (x0; f (x0)). Назовем эту точку условным началом графика — лимитом, если же функция бесконечна, хотя бы на одном из промежутков – это стремление также будет бесконечным, а его предельное значение близким к 0. Характер данного стремления можно описать касательной к выбранной точке y = kx + b или графиком производной первоначальной функции dy – зеленая прямая. Но где же здесь тригонометрия?! Все очень просто рассмотрим прямоугольный треугольник KLN. Значение дифференциала для конкретной точки K есть тангенс угла α или ∠K: Таким образом можно описать геометрический смымсл производной и ее взаимосвязь с тригонометрическими функциями. Таблица производных часто встречающихся функцийВ следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.
ПримерыРассмотрим простые примеры нахождения производных от функций, содержащих синус. Прикладное использование производнойВычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
Вычисление производнойВычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз… Формулы дифференцирования. Правила дифференцирования. |
Формулы производных тригонометрических функций
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Производные тригонометрических функций: формулы
В таблицах ниже представлены формулы производных тригонометрических функций: прямых, производных и обратных.
Содержание
- Прямые и производные функции: sin, cos, tg, ctg
- Обратные функции: arcsin, arccos, arctg, arcctg
Прямые и производные функции: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).

| Действие | Формула |
| Производная синуса | sin’ x = cos x |
| Производная косинуса | cos’ x = -sin x |
| Производная тангенса | tg’ x = 1 / cos2 (x) |
| Производная котангенса | ctg’ x = 1 / sin2 (x) |
microexcel. ru
ru
Обратные функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
| Действие | Формула |
| Производная арксинуса | ru/wp-content/uploads/2020/02/arcsinus-formula-exc-6.png" class="stbSkipLazy aligncenter size-full" width="290" height="546" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arcsinus-formula-exc-6.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arcsinus-formula-exc-6.png" class="stbSkipLazy aligncenter size-full" width="290" height="546" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arcsinus-formula-exc-6.png" />»> |
| Производная арккосинуса | ru/wp-content/uploads/2020/02/arccos-exc-3.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-3.png" class="stbSkipLazy aligncenter size-full" width="290" height="290" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-3.png" />»> |
| Производная арктангенса | ru/wp-content/uploads/2020/02/arktangets-formuly-exc-4.png" class="stbSkipLazy aligncenter size-full" width="290" height="504" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arktangets-formuly-exc-4.png" />»> |
| Производная арккотангенса | ru/wp-content/uploads/2020/02/arcctg-proizvodnaya-exc.png" />»> |
microexcel.ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Производные простых тригонометрических функций
Для нахождения производной тригонометрической функции нужно пользоваться таблицей производных, а именно производными 6-13.
При нахождении производных простых тригонометрических функций во избежание распространённых ошибок следует обращать внимание на следующие моменты:
- в выражении функции часто одно из слагаемых представляет собой синус, косинус или другую тригонометрическую функцию не от аргумента функции, а от числа (константы), поэтому производная этого слагаемого равна нулю;
- почти всегда нужно упростить выражение, полученное в результате дифференцирования, а для этого нужно уверенно пользоваться знаниями по действиям с дробями;
- для упрощения выражения почти всегда нужно знать тригонометрические тождества, например, формулу двойного угла и формулу единицы как сумму квадратов синуса и косинуса.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 1. Найти производную функции
.
Решение. Допустим, с производной косинуса всё понятно, скажут многие, начинающие изучать производные. А как быть с производной синуса двенадцати, делённых на пи? Ответ: считать равной нулю! Здесь синус (функция всё-таки!) — ловушка, потому что аргумент — не переменная икс или любая другая переменная, а просто число. То есть, синус этого числа — тоже число. А производная числа (константы), как мы знаем из таблицы производных, равна нулю. Итак, оставляем только минус синус икса и находим его производную, не забывая про знак:
.
Ответ:
.
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 2. Найти производную функции
.
Решение. Второе слагаемое — тот же случай, что и первое слагаемое
в предыдущем примере. То есть, число, а производная числа равна нулю. Находим производную
второго слагаемого как производную частного:
Находим производную
второго слагаемого как производную частного:
Ответ:
Пример 3. Найти производную функции
.
Решение. Это уже другая задача: здесь в первом слагаемом нет ни арксинуса, ни другой тригонометической функции, но есть икс, а значит, это функция от икса. Следовательно, дифференцируем её как слагаемое в сумме функций:
Здесь потребовались навыки в действиях с дробями, а именно — в ликвидации трёхэтажности дроби.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 4. Найти производную функции
.
Решение. Здесь буква «фи» играет ту же роль, что «икс» в предыдущих
случаях (и в большинстве других, но не во всех) — независимой переменной. Поэтому,
когда будем искать производную произведения функций, не будем спешить объявлять
равной нулю производную корня от «фи». Итак:
Итак:
Но на этом решение не заканчивается. Так как в двух скобках собраны подобные члены, от нас ещё требуется преобразовать (упростить) выражение. Поэтому умножаем скобки на вынесенные за них множители, а далее приводим слагаемые к общему знаменателю и выполняем другие элементарные преобразования:
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 5. Найти производную функции
.
Решение. В этом примере от нас потребуется знание того факта, что существует такая тригонометрическая функция — секанс — и её формулы через косинус. Дифференцируем:
Пример 6. Найти производную функции
.
Решение. В этом примере от нас потребуется помнить из школьного
курса формулу двойного угла. Но сначала дифференцируем:
Но сначала дифференцируем:
Далее применяем следующие тригонометрические тождества:
,
(это и есть формула двойного угла)
и получаем:
.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 7. Найти производную функции
.
Решение. В этом примере от нас потребуется всего-то лишь умение сокращать дроби. И внимание — не забыть, что дробь нужно сократить. Это сделано на последнем шаге решения:
В решении применено тригонометрическое тождество:
.
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
- Пригодится: тригонометрические тождества для преобразования выражений
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
Поделиться с друзьями
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
Тангенс квадрат икс равен
Тангенс представлен степенной функцией, поэтому берем производную по правилу $ (x^p)’ = px^ $, а затем умножаем на производную тангенса:
$$ y’ = (tg^2 x)’ = 2tg x cdot (tg x)’ = $$
Основные формулы тригонометрии – это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α + 1 = 1 sin 2 α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.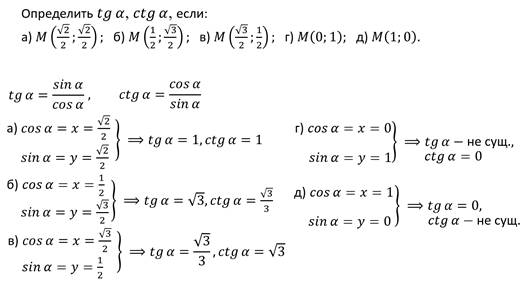
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin – α + 2 π z = – sin α , cos – α + 2 π z = cos α t g – α + 2 π z = – t g α , c t g – α + 2 π z = – c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = – sin α t g π 2 + α + 2 π z = – c t g α , c t g π 2 + α + 2 π z = – t g α sin π 2 – α + 2 π z = cos α , cos π 2 – α + 2 π z = sin α t g π 2 – α + 2 π z = c t g α , c t g π 2 – α + 2 π z = t g α sin π + α + 2 π z = – sin α , cos π + α + 2 π z = – cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π – α + 2 π z = sin α , cos π – α + 2 π z = – cos α t g π – α + 2 π z = – t g α , c t g π – α + 2 π z = – c t g α sin 3 π 2 + α + 2 π z = – cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = – c t g α , c t g 3 π 2 + α + 2 π z = – t g α sin 3 π 2 – α + 2 π z = – cos α , cos 3 π 2 – α + 2 π z = – sin α t g 3 π 2 – α + 2 π z = c t g α , c t g 3 π 2 – α + 2 π z = t g α
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β – sin α · sin β cos α – β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = – 1 ± c t g α · c t g β c t g α ± c t g β
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α – sin 2 α , cos 2 α = 1 – 2 sin 2 α , cos 2 α = 2 cos 2 α – 1 t g 2 α = 2 · t g α 1 – t g 2 α с t g 2 α = с t g 2 α – 1 2 · с t g α sin 3 α = 3 sin α · cos 2 α – sin 3 α , sin 3 α = 3 sin α – 4 sin 3 α cos 3 α = cos 3 α – 3 sin 2 α · cos α , cos 3 α = – 3 cos α + 4 cos 3 α t g 3 α = 3 t g α – t g 3 α 1 – 3 t g 2 α c t g 3 α = c t g 3 α – 3 c t g α 3 c t g 2 α – 1
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
sin 2 α 2 = 1 – cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 – cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 – cos α
Формулы понижения степени
sin 2 α = 1 – cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α – sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 – 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
sin n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 ( – 1 ) n 2 – k · C k n · cos ( ( n – 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 C k n · cos ( ( n – 2 k ) α )
sin n α = 1 2 n – 1 ∑ k = 0 n – 1 2 ( – 1 ) n – 1 2 – k · C k n · sin ( ( n – 2 k ) α ) cos n α = 1 2 n – 1 ∑ k = 0 n – 1 2 C k n · cos ( ( n – 2 k ) α )
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
sin α + sin β = 2 sin α + β 2 · cos α – β 2 sin α – sin β = 2 sin α – β 2 · cos α + β 2 cos α + cos β = 2 cos α + β 2 · cos α – β 2 cos α – cos β = – 2 sin α + β 2 · sin α – β 2 , cos α – cos β = 2 sin α + β 2 · sin β – α 2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход – от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sin α · sin β = 1 2 · ( cos ( α – β ) – cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α – β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α – β ) + sin ( α + β ) )
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции – синус, косинус, тангенс и котангенс, – могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановка
sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 – t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 – t g 2 α 2 c t g α = 1 – t g 2 α 2 2 t g α 2
Таблица производных. Доказательство формул
Приведем сводную таблицу для удобства и наглядности при изучении темы.
Константа y=C (C)’=0 Степенная функция y=xp (xp)’=p·xp-1 | Показательная функция y=ax (ax)’=ax·ln a В частности, при a=e имеем y=ex (ex)’=ex |
Логарифмическая функция (logax)’=1x·ln a В частности, при a=e имеем y=ln x (ln x)’=1x | Тригонометрические функции (sin x)’=cos x(cos x)’=-sin x(tgx)’=1cos2x(ctgx)’=-1sin2x |
Обратные тригонометрические функции (arcsin x)’=11-x2(arccos x)’=-11-x2(arctg x)’=11+x2(arcctg x)’=-11+x2 | Гиперболические функции (shx)’=chx(chx)’=shx(thx)’=1ch3x(cthx)’=-1sh3x |
Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.
Производная постоянной
Доказательство 1Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x0=x, где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f(x)=C. Составим запись предела отношения приращения функции к приращению аргумента при ∆x→0:
lim∆x→0∆f(x)∆x=lim∆x→0C-C∆x=lim∆x→00∆x=0
Обратите внимание, что под знак предела попадает выражение 0∆x. Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.
Итак, производная постоянной функции f(x)=C равна нулю на всей области определения.
Пример 1Даны постоянные функции:
f1(x)=3,f2(x)=a, a∈R,f3(x)=4.13722,f4(x)=0,f5(x)=-87
Необходимо найти их производные.
Решение
Опишем заданные условия. В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от а, где а — любое действительное число. Третий пример задает нам производную иррационального числа 4.13722, четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби -87.
В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от а, где а — любое действительное число. Третий пример задает нам производную иррационального числа 4.13722, четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби -87.
Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)
f1′(x)=(3)’=0,f2′(x)=(a)’=0, a∈R,f3′(x)=4.13722’=0,f4′(x)=0’=0,f5′(x)=-87’=0
Производная степенной функции
Переходим к степенной функции и формуле ее производной, имеющей вид: (xp)’=p·xp-1, где показатель степени p является любым действительным числом.
Доказательство 2Приведем доказательство формулы, когда показатель степени – натуральное число: p=1, 2, 3, …
Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:
(xp)’=lim∆x→0=∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x
Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:
(x+∆x)p-xp=Cp0+xp+Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+. ..++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
..++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
Таким образом:
(xp)’=lim∆x→0∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x==lim∆x→0(Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p)∆x==lim∆x→0(Cp1·xp-1+Cp2·xp-2·∆x+…+Cpp-1·x·(∆x)p-2+Cpp·(∆x)p-1)==Cp1·xp-1+0+0+…+0=p!1!·(p-1)!·xp-1=p·xp-1
Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.
Доказательство 3Чтобы привести доказательство для случая, когда p — любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.
Рассмотрим два случая: когда x положительны и когда x отрицательны.
Итак, x>0. Тогда: xp>0. Логарифмируем равенство y=xp по основанию e и применим свойство логарифма:
y=xpln y=ln xpln y=p·ln x
На данном этапе получили неявно заданную функцию. Определим ее производную:
Определим ее производную:
(ln y)’=(p·ln x)1y·y’=p·1x⇒y’=p·yx=p·xpx=p·xp-1
Теперь рассматриваем случай, когда x – отрицательное число.
Если показатель p есть четное число, то степенная функция определяется и при x<0, причем является четной: y(x)=-y((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Тогда xp<0 и возможно составить доказательство, используя логарифмическую производную.
Если p есть нечетное число, тогда степенная функция определена и при x<0, причем является нечетной: y(x)=-y(-x)=-(-x)p. Тогда xp<0, а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:
y'(x)=(-(-x)p)’=-((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Последний переход возможен в силу того, что если p — нечетное число, то p-1 либо четное число, либо нуль (при p=1), поэтому, при отрицательных x верно равенство (-x)p-1=xp-1.
Итак, мы доказали формулу производной степенной функции при любом действительном p.
Пример 2Даны функции:
f1(x)=1×23,f2(x)=x2-14,f3(x)=1xlog712
Определите их производные.
Решение
Часть заданных функций преобразуем в табличный вид y=xp, опираясь на свойства степени, а затем используем формулу:
f1(x)=1×23=x-23⇒f1′(x)=-23·x-23-1=-23·x-53f2′(x)=x2-14=2-14·x2-14-1=2-14·x2-54f3(x)=1xlog712=x-log712⇒f3′(x)=-log712·x-log712-1=-log712·x-log712-log77=-log712·x-log784
Производная показательной функции
Доказательство 4Выведем формулу производной, взяв за основу определение:
(ax)’=lim∆x→0ax+∆x-ax∆x=lim∆x→0ax(a∆x-1)∆x=ax·lim∆x→0a∆x-1∆x=00
Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z=a∆x-1 (z→0 при ∆x→0). В таком случае a∆x=z+1⇒∆x=loga(z+1)=ln(z+1)ln a. Для последнего перехода использована формула перехода к новому основанию логарифма.
Осуществим подстановку в исходный предел:
(ax)’=ax·lim∆x→0a∆x-1∆x=ax·ln a·lim∆x→011z·ln(z+1)==ax·ln a·lim∆x→01ln(z+1)1z=ax·ln a·1lnlim∆x→0(z+1)1z
Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:
(ax)’=ax·ln a·1lnlimz→0(z+1)1z=ax·ln a·1ln e=ax·ln a
Пример 3Даны показательные функции:
f1(x)=23x,f2(x)=53x,f3(x)=1(e)x
Необходимо найти их производные.
Решение
Используем формулу производной показательной функции и свойства логарифма:
f1′(x)=23x’=23x·ln23=23x·(ln 2-ln 3)f2′(x)=53x’=53x·ln 513=13·53x·ln 5f3′(x)=1(e)x’=1ex’=1ex·ln1e=1ex·ln e-1=-1ex
Производная логарифмической функции
Доказательство 5Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:
(logax)’=lim∆x→0loga(x+∆x)-logax∆x=lim∆x→0logax+∆xx∆x==lim∆x→01∆x·loga1+∆xx=lim∆x→0loga1+∆xx1∆x==lim∆x→0loga1+∆xx1∆x·xx=lim∆x→01x·loga1+∆xxx∆x==1x·logalim∆x→01+∆xxx∆x=1x·logae=1x·ln eln a=1x·ln a
Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim∆x→01+∆xxx∆x=e является верным в соответствии со вторым замечательным пределом.
Пример 4Заданы логарифмические функции:
f1(x)=logln3 x,f2(x)=ln x
Необходимо вычислить их производные.
Решение
Применим выведенную формулу:
f1′(x)=(logln3 x)’=1x·ln(ln 3);f2′(x)=(ln x)’=1x·ln e=1x
Итак, производная натурального логарифма есть единица, деленная на x.
Производные тригонометрических функций
Доказательство 6Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.
Согласно определению производной функции синуса, получим:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x
Формула разности синусов позволит нам произвести следующие действия:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x==lim∆x→02·sin x+∆x-x2·cosx+∆x+x2∆x==lim∆x→0sin ∆x2·cosx+∆x2∆x2==cosx+02·lim∆x→0sin ∆x2∆x2
Наконец, используем первый замечательный предел:
sin’ x=cos x+02·lim∆x→0sin∆x2∆x2=cos x
Итак, производной функции sin x будет cos x.
Совершенно также докажем формулу производной косинуса:
cos’ x=lim∆x→0cos (x+∆x)-cos x∆x==lim∆x→0-2·sin x+∆x-x2·sinx+∆x+x2∆x==-lim∆x→0sin∆x2·sinx+∆x2∆x2==-sinx+02·lim∆x→0sin∆x2∆x2=-sin x
Т.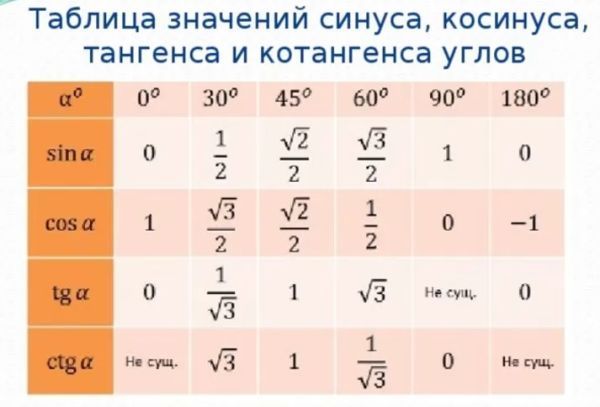 е. производной функции cos x будет –sin x.
е. производной функции cos x будет –sin x.
Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:
tg’x=sin xcos x’=sin’ x·cos x-sin x·cos’ xcos2 x==cos x·cos x-sin x·(-sin x)cos2 x=sin2 x+cos2 xcos2 x=1cos2 xctg’x=cos xsin x’=cos’x·sin x-cos x·sin’xsin2 x==-sin x·sin x-cos x·cos xsin2 x=-sin2 x+cos2 xsin2 x=-1sin2 x
Производные обратных тригонометрических функций
Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.
Производные гиперболических функций
Доказательство 7Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
sh’x=ex-e-x2’=12ex’-e-x’==12ex—e-x=ex+e-x2=chxch’x=ex+e-x2’=12ex’+e-x’==12ex+-e-x=ex-e-x2=shxth’x=shxchx’=sh’x·chx-shx·ch’xch3x=ch3x-sh3xch3x=1ch3xcth’x=chxshx’=ch’x·shx-chx·sh’xsh3x=sh3x-ch3xsh3x=-1sh3x
Рекомендуется выучить формулы из таблицы производных: они не столь сложны для запоминания, но экономят много времени, когда необходимо решать задачи дифференцирования.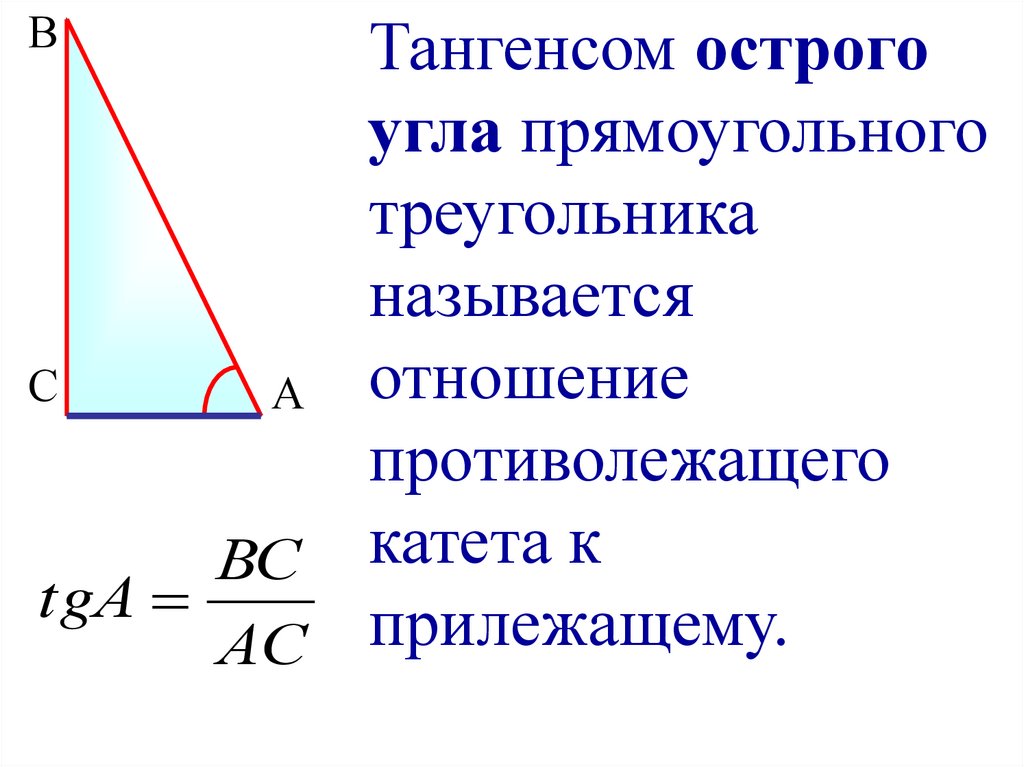
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Дифференцирование тригонометрических функций — тригонометрические производные
Процесс нахождения производных тригонометрических функций известен как дифференцирование тригонометрических функций . Другими словами, дифференцирование тригонометрических функций — это нахождение скорости изменения функции по переменной. Шесть тригонометрических функций имеют формулы дифференцирования, которые можно использовать в различных прикладных задачах производной.
Шесть основных тригонометрических функций включают следующие: синус (sin x), косинус (cos x), тангенс (tan x), котангенс (cot x), секанс (sec x) и косеканс (cosec x). В этой статье мы найдем производные тригонометрических функций и их доказательства. Дифференциация тригонометрических функций имеет приложения в различных областях, таких как электроника, компьютерное программирование и моделирование различных циклических функций.
| 1. | Что такое дифференциация тригонометрических функций? |
| 2. | Доказательства триггерных производных |
| 3. | Приложения дифференцирования тригонометрических функций |
| 4. | Дифференцирование обратных тригонометрических функций |
| 5. | Антидифференцирование тригонометрических функций |
| 6. | Часто задаваемые вопросы о дифференциации тригонометрических функций |
Что такое дифференциация тригонометрических функций?
В тригонометрии дифференцирование тригонометрических функций представляет собой математический процесс определения скорости изменения тригонометрических функций по отношению к переменному углу. Дифференцирование тригонометрических функций может быть выполнено с использованием производных от sin x и cos x с применением правила отношения. формулы дифференцирования шести тригонометрических функций s приведены ниже:
Дифференцирование тригонометрических функций может быть выполнено с использованием производных от sin x и cos x с применением правила отношения. формулы дифференцирования шести тригонометрических функций s приведены ниже:
- Вывод sin x: (sin x)’ = cos x
- Производная от cos x: (cos x)’ = -sin x
- Производная от tan x: (tan x)’ = sec 2 x
- Производная от cot x: (cot x)’ = -cosec 2 x
- Производная от sec x: (sec x)’ = sec x.tan x
- Производная cosec x: (cosec x)’ = -cosec x.cot x
Мы используем d/dx для записи производных. Вот тройные производные, использующие это обозначение.
Доказательства триггерных производных
Теперь, когда у нас есть дифференцирование тригонометрических функций (sin x, cos x, tan x, cot x, sec x, cosec x), мы докажем и выведем тригонометрические производные, используя различные методы, такие как правило первый принцип дифференцирования и цепное правило, а также некоторые предельные формулы.
Производная sin x
Выведем производную от sin x, используя первый принцип дифференцирования, то есть используя определение пределов. Для вывода дифференцирования тригонометрической функции sin x будем использовать следующие предельные и тригонометрические формулы:
- sin (A+B) = sin A cos B + sin B cos A
- \(\lim_{x\стрелка вправо 0} \dfrac{\cos x -1}{x} = 0\)
- \(\lim_{x\стрелка вправо 0} \dfrac{\sin x}{x} = 1\)
Теперь вычислим дифференцирование тригонометрической функции sin x:
\(\begin{align}\frac{\mathrm{d} (\sin x)}{\mathrm{d} x} &= \lim_{h\rightarrow 0} \dfrac{\sin (x + h) )-\sin x}{(x+h)-x} \\&= \lim_{h\rightarrow 0} \dfrac{\sin x \cos h +\cos x \sin h-\sin x}{h }\\&=\lim_{h\стрелка вправо 0} \dfrac{\cos h -1}}{h}\sin x + \dfrac{\sin h}{h}\cos x\\&=(0)\ sin x + (1)\cos x\\&=\cos x\end{align}\)
Следовательно, d(sin x)/dx = cos x
Производная cos x
Выведем производную cos x, используя первый принцип дифференцирования, то есть используя определение пределов. Для вывода дифференцирования тригонометрической функции cos x воспользуемся следующими предельными и тригонометрическими формулами:
Для вывода дифференцирования тригонометрической функции cos x воспользуемся следующими предельными и тригонометрическими формулами:
- cos (A + B) = cos A cos B — sin A sin B
- \(\lim_{x\стрелка вправо 0} \dfrac{\cos x -1}{x} = 0\)
- \(\lim_{x\стрелка вправо 0} \dfrac{\sin x}{x} = 1\)
Таким образом, мы имеем
\(\begin{align}\frac{\mathrm{d} (\cos x)}{\mathrm{d} x} &= \lim_{h\rightarrow 0} \dfrac{ \cos (x + h)-\cos x}{(x+h)-x} \\&= \lim_{h\rightarrow 0} \dfrac{\cos x \cos h -\sin x \sin h- \ cos x} {h} \\ & = \ lim_ {h \ rightarrow 0} \ dfrac {\ cos h -1 } {h} \ cos x — \ dfrac {\ sin h} {h} \ sin x \\ &=(0)\cos x — (1)\sin x\\&=-\sin x\end{align}\)
Следовательно, d(cos x)/dx = -sin x
Производная тангенса х
Определим производную тангенса х, используя правило частных. Для вычисления производной будем использовать следующие формулы и тождества:
- (sin x)’ = cos x
- (cos x)’ = -sin x
- тангенс x = sin x/cos x
- cos 2 х + sin 2 х = 1
- сек х = 1/cos х
(tan x)’ = (sin x/cos x)’
= [(sin x)’ cos x — (cos x)’ sin x]/cos 2 x
= [cos x. cos х — (-sin х). SIN X]/COS 2 X
cos х — (-sin х). SIN X]/COS 2 X
= (COS 2 x + SIN 2 x)/COS 2 x
= 1/COS 2 x
= сек 2 X
Следовательно, d(tan x)/dx = sec 2 x
Производная cot x
Определим производную cot x, используя правило частных. Для вычисления производной будем использовать следующие формулы и тождества:
- (sin x)’ = cos x
- (cos x)’ = -sin x
- раскладушка х = cos х/sin х
- cos 2 х + sin 2 х = 1
- косек х = 1/sin х
(cot x)’ = (cos x/sin x)’
= [(cos x)’ sin x — (sin x)’ cos x]/sin 2 x
= [-sin x. грех х — cos х. cos x]/sin 2 x
= (-sin 2 x — cos 2 x)/sin 2 x
= -1/sin 2 x
= -cosec 2 x
Следовательно, d(cot x)/dx = -cosec 2 x
Производная sec x
Определим производную sec x, используя цепочку правило. Мы будем использовать следующие формулы и тождества для вычисления производной:
Мы будем использовать следующие формулы и тождества для вычисления производной:
- сек х = 1/cos х
- тангенс x = sin x/cos x
- (cos x)’ = -sin x
(сек x)’ = (1/cos x)’ = (-1/cos 2 x).(cos x)’
= (-1/cos 2 x).(-sin x)
= sin x/cos 2 x
= (sin x/cos x).(1/cos x)
= tan x sec x
Следовательно, d(sec x)/dx = tan x sec x
Производная cosec x
Определим производную cosec x с помощью цепного правила. Для вычисления производной будем использовать следующие формулы и тождества:
- cosec x = 1/sin x
- раскладушка x = cos x/sin x
- (sin x)’ = cos x
(cosec x)’ = (1/sin x)’ = (-1/sin 2 x).(sin x)’
= (-1/sin 2 x).(cos x)
= -cos x/sin 2 x
= -(cos x/sin x).(1/sin x)
= -cot x cosec x
Следовательно, d(cosec x)/dx = -кроватка х косек х
Приложения дифференцирования тригонометрических функций
Дифференцирование тригонометрических функций имеет различные приложения в области математики и реальной жизни. Некоторые из них перечислены ниже:
Некоторые из них перечислены ниже:
- Используется для определения наклона касательной к тригонометрической кривой y = f(x).
- Используется для определения наклона нормали к тригонометрической кривой y = f(x).
- Помогает определить уравнение касательной или нормали кривой.
- Дифференциация тригонометрических функций имеет приложения в различных областях, таких как электроника, компьютерное программирование и моделирование различных циклических функций.
- Мы используем производные тригонометрических функций для определения максимальных и минимальных значений конкретных функций.
Дифференцирование обратных тригонометрических функций
Дифференцирование обратных тригонометрических функций выполняется путем установки функции равной y и применения неявного дифференцирования. Перечислим производные обратных тригонометрических функций вместе с их областями определения (arcsin x, arccos x, arctan x, arccot x, arcsec x, arccosec x):
- (угловой синус x)’ = 1/√(1 — x 2 ), -1 < x < 1
- (arccos x)’ = -1/√(1 — x 2 ), -1 < x < 1
- (арктан х)’ = 1/(1 + х 2 ) , -∞ < х < ∞
- (arccot x)’ = -1/(1 + x 2 ) , -∞ < x < ∞
- (угл.
 сек x)’ = 1/|x|√(x 2 — 1) , x ∈ (-∞, -1) ∪ (1, ∞)
сек x)’ = 1/|x|√(x 2 — 1) , x ∈ (-∞, -1) ∪ (1, ∞) - (arccosec x)’ = -1/|x|√(x 2 — 1) , x ∈ (-∞, -1) ∪ (1, ∞)
Антидифференцирование тригонометрических функций
Антидифференцирование тригонометрических функций – процесс, обратный дифференцированию тригонометрических функций. Этот процесс также называют интегрированием тригонометрических функций. Список первообразных тригонометрических функций приведен ниже:
- ∫ sinx dx = -cos x + C
- ∫ cosx dx = sin x + C
- ∫ tanx dx = ln |sec x| + С
- ∫ cotx dx = ln |sin x| + С
- ∫ secx dx = ln |sec x + tan x| + С
- ∫ cosecx dx = -ln |cosec x + cot x| + С
Здесь C — постоянная интегрирования.
☛ Связанные темы:
- Обратные тригонометрические формулы
- грех кост загар
- Тригонометрические тождества
- Синусоидальная функция
Важные замечания по дифференциации тригонометрических функций:
- Вывод sin x: (sin x)’ = cos x
- Производная от cos x: (cos x)’ = -sin x
- Производная от tan x: (tan x)’ = sec 2 x
- Производная от cot x: (cot x)’ = -cosec 2 x
- Производная от sec x: (sec x)’ = sec x.
 tan x
tan x - Производная cosec x: (cosec x)’ = -cosec x.cot x
Часто задаваемые вопросы о дифференциации тригонометрических функций
Что такое дифференциация тригонометрических функций в тригонометрии?
В тригонометрии дифференцирование тригонометрических функций представляет собой математический процесс определения скорости изменения тригонометрических функций по отношению к угловой переменной. Процесс нахождения производных круговых тригонометрических функций известен как дифференцирование тригонометрических функций.
Каковы производные шести триггерных функций?
Формулы дифференцирования шести тригонометрических функций приведены ниже:
- Вывод sin x: (sin x)’ = cos x
- Производная от cos x: (cos x)’ = -sin x
- Производная от tan x: (tan x)’ = sec 2 x
- Производная от cot x: (cot x)’ = -cosec 2 x
- Производная от sec x: (sec x)’ = sec x.
 tan x
tan x - Производная cosec x: (cosec x)’ = -cosec x.cot x
Каково применение
Дифференциация тригонометрических функций ?Дифференцирование тригонометрических функций имеет различные приложения в области математики и реальной жизни.
- Помогает определить уравнение касательной или нормали кривой.
- Дифференциация тригонометрических функций имеет приложения в различных областях, таких как электроника, компьютерное программирование и моделирование различных циклических функций.
- Мы используем дифференцирование тригонометрической функции, чтобы определить максимальное и минимальное значения определенных функций.
Что такое антидифференцирование тригонометрических функций в тригонометрии?
Антидифференцирование тригонометрических функций – процесс, обратный дифференцированию тригонометрических функций. Этот процесс также называют интегрированием тригонометрических функций.
Что такое антипроизводные шести тригонометрических функций?
Список первообразных тригонометрических функций приведен ниже как:
- ∫ sin x dx = -cos x + C
- ∫ cos x dx = sin x + C
- ∫ тангенс x dx = ln |sec x| + С
- ∫ раскладушка x dx = ln |sin x| + С
- ∫ сек х dx = ln | сек х + тангенс х | + С
- ∫ cosec x dx = -ln |cosec x + cot x| + С
Что такое триггерные производные?
Производная тригонометрических функций может быть рассчитана с использованием различных методов, таких как правило частных, первый принцип дифференцирования и цепное правило, а также некоторые предельные формулы. триггерные производные равны
триггерные производные равны
- (sin x)’ = cos x
- (cos x)’ = -sin x
- (тангенс х)’ = сек 2 х
- (кроватка x)’ = -cosec 2 x
- (сек х)’ = сек х.тангенс х
- (косек х)’ = -косек х.кот х
Как вывести производные тригонометрических функций?
Производные тригонометрических функций можно найти с помощью различных методов дифференцирования, таких как первый принцип производных, правило произведения, правило отношения и правило цепочки.
Производные тригонометрических функций
К основным тригонометрическим функциям относятся следующие 6 функций: синус (sin x ), косинус (cos x ), тангенс (tan x ), котангенс (cot x ), секанс (sec x ) и косеканс (csc x ).
Все эти функции непрерывны и дифференцируемы в своих областях определения. Ниже мы составим список производных для этих функций.
Таблица производных тригонометрических функций
В таблице ниже приведены производные \(6\) основных тригонометрических функций:
В приведенных ниже примерах найдите производную заданной функции.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
\[y = \cos 2x — 2\sin x\] 9\prime } = — 2\cos \sin x \cdot \sin \sin x \cdot \cos x.\]
Последнее выражение можно упростить формулой двойного угла:
\[2\cos \sin x \cdot \sin \sin x = \sin \left( {2\sin x} \right).\]
Следовательно, производная равна
\[y’\left( x \right) = — \sin \left( {2\sin x} \right)\cos x.\]
Дополнительные проблемы см. на стр. 2.
AC Производные других тригонометрических функций
Мотивирующие вопросы
Каковы производные функций тангенса, котангенса, секанса и косеканса?
Как сделать производные от \(\tan(x)\text{,}\) \(\cot(x)\text{,}\) \(\sec(x)\text{,}\) и \(\csc(x)\) в сочетании с другими производными правилами, которые мы разработали, чтобы расширить библиотеку функций, которые мы можем быстро дифференцировать?
Одна из важных тем в тригонометрии исходит из очень простой идеи: найти точку на единичной окружности.
Поскольку каждый угол \(\theta\) в стандартном положении соответствует одной и только одной точке \((x,y)\) на единичной окружности, \(x\)- и \(y\)-координаты каждая из этих точек является функцией \(\theta\text{.}\). Фактически, это и есть само определение \(\cos(\theta)\) и \(\sin(\theta)\text{:} \) \(\cos(\theta)\) — это \(x\)-координата точки на единичной окружности, соответствующей углу \(\theta\text{,}\) и \(\sin(\ theta)\) — это \(y\)-координата. На этом простом определении основана вся тригонометрия. Например, фундаментальное тригонометрическое тождество, 92 (\ тета) = 1 \ текст {,} \end{уравнение*}
— это переформулировка теоремы Пифагора, примененная к прямоугольному треугольнику, показанному на рисунке 2.4.1.
Существуют еще четыре тригонометрические функции, каждая из которых определяется через функции синуса и/или косинуса.
Касательная функция определяется как \(\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\text{;}\)
функция котангенса является обратной: \(\cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)}\text{.
 }\)
}\)Функция секанса является обратной функцией косинуса, \(\sec(\theta) = \frac{1}{\cos(\theta)}\text{;}\)
, а функция косеканса является обратной функцией синуса, \(\csc(\theta) = \frac{1}{\sin(\theta)}\text{.}\)
Вместе эти шесть тригонометрических функций дают нам широкий диапазон гибкости в задачах, связанных с прямоугольными треугольниками.
Поскольку мы знаем производные функции синуса и косинуса, теперь мы можем разработать правила быстрого дифференцирования для функций тангенса, котангенса, секанса и косеканса. В предварительном упражнении этого раздела мы выполняем шаги, чтобы найти производную \(y = \tan(x)\text{.}\) 92(х)}\текст{.} \end{уравнение*}
Что такое фундаментальное тригонометрическое тождество? Как можно использовать это тождество, чтобы найти более простую форму для \(f'(x)\text{?}\)
Напомним, что \(\sec(x) = \frac{1}{\cos(x)}\text{.}\) Как мы можем выразить \(f'(x)\) через функцию секущей ?
Для каких значений \(x\) определено \(f'(x)\)? Как этот набор соотносится с доменом \(f\text{?}\)
Подраздел 2.
 4.1 Производные функций котангенса, секанса и косеканса
92(х)\текст{.}
\end{equation*}
4.1 Производные функций котангенса, секанса и косеканса
92(х)\текст{.}
\end{equation*}В следующих двух действиях мы разработаем правила дифференцирования функций секанса и косеканса.
Мероприятие 2.4.2.
Пусть \(h(x) = \sec(x)\) и вспомним, что \(\sec(x) = \frac{1}{\cos(x)}\text{.}\)
Каков домен \(h\text{?}\)
Используйте правило частных для разработки формулы для \(h'(x)\), которая полностью выражается через \(\sin(x)\) и \(\cos(x)\text{.}\ )
Как можно использовать другие отношения между тригонометрическими функциями, чтобы записать \(h'(x)\) только в терминах \(\tan(x)\) и \(\sec(x)\text{?}\)
Что такое домен \(h’\text{?}\) Как это соотносится с доменом \(h\text{?}\)
Мероприятие 2.4.3.
Пусть \(p(x) = \csc(x)\) и вспомним, что \(\csc(x) = \frac{1}{\sin(x)}\text{.}\)
Каков домен \(p\text{?}\)
Используйте правило частных для разработки формулы для \(p'(x)\), которая полностью выражается через \(\sin(x)\) и \(\cos(x)\text{.
 }\)
}\)Как можно использовать другие отношения между тригонометрическими функциями для записи \(p'(x)\) только в терминах \(\cot(x)\) и \(\csc(x)\text{?}\)
Что такое домен \(p’\text{?}\) Как это соотносится с доменом \(p\text{?}\)
Используя правило частных, мы определили производные функций тангенса, котангенса, секанса и косеканса, расширив нашу общую библиотеку функций, которые мы можем дифференцировать. Заметьте, что точно так же, как производная любой полиномиальной функции является полиномом, а производная любой экспоненциальной функции является другой экспоненциальной функцией, так и производная любой базовой тригонометрической функции является другой функцией, состоящей из основных тригонометрических функций. Это имеет смысл, поскольку все тригонометрические функции периодические, а значит, и их производные тоже будут периодическими.
Производная сохраняет все свое основное значение как мгновенная скорость изменения и как наклон касательной к рассматриваемой функции.
Мероприятие 2.4.4.
Ответьте на каждый из следующих вопросов. Если запрашивается производная функция, не забудьте пометить производную функцию ее именем, используя соответствующие обозначения.
Пусть \(f(x) = 5 \sec(x) — 2\csc(x)\text{.}\) Найдите наклон касательной к \(f\) в точке, где \( х = \ гидроразрыва {\ пи} {3} \ текст {.} \) 9т}\текст{.} \end{уравнение*}
Предположим, что \(s\) измеряется в дюймах, а \(t\) — в секундах. Нарисуйте график этой функции для \(t \ge 0\), чтобы увидеть, как она представляет описанную ситуацию. Затем вычислите \(ds/dt\text{,}\) укажите единицы измерения этой функции и объясните, что она говорит вам о движении объекта. Наконец, вычислите и интерпретируйте \(s'(2)\text{.}\)
Подраздел 2.4.2 Резюме
Производные остальных четырех тригонометрических функций равны 92(х)\текст{,} \end{уравнение*}
\begin{уравнение*} \frac{d}{dx}[\sec(x)] = \sec(x)\tan(x), \\text{and} \ \frac{d}{dx}[\csc(x)] = -\csc(x)\cot(x)\text{.
 }
\end{уравнение*}
}
\end{уравнение*}Каждая производная существует и определена в той же области, что и исходная функция. Например, и функция тангенса, и ее производная определены для всех действительных чисел \(x\), таких что \(x \ne \frac{k\pi}{2}\text{,}\), где \(k = \pm 1, \pm 2, \ldots\text{.}\)
Четыре правила для производных тангенса, котангенса, секанса и косеканса можно использовать вместе с правилами для степенных функций, экспоненциальных функций, синуса и косинуса, а также суммы, постоянного кратного, произведения и частные правила, чтобы быстро различать широкий спектр различных функций.
Упражнения 2.4.3 Упражнения
1. Сумма и произведение с участием \(\tan(x)\).
Найдите производную \(h(t) = t \tan t + \cos t\)
\(h'(t) =\)
2. Частное с \(\tan(t)\).
Пусть \(f(x) = \displaystyle \frac{5\tan\!\left(x\right)}{x}\text{.}\) Найдите следующее:
| 1. | \(f'(х)\) | \(=\) | ||||||
2. {2}\tan\!\left(x\right)}{\sec\!\left(x\right)}\text{.}\ ) Найдите следующее: {2}\tan\!\left(x\right)}{\sec\!\left(x\right)}\text{.}\ ) Найдите следующее:
5. Нахождение уравнения касательной.Найдите уравнение касательной к кривой \(y = 3 \tan x\) в точке \(( \pi/4 , 3)\text{.}\) Уравнение этой касательной можно записать в виде \(y = mx+b\), где \(m\) равно: и где \(b\) равно: 6,9т}\текст{.}\)
7.Пусть \(f(x) = \sin(x) \cot(x)\text{.}\)
|

 Найти производную функции
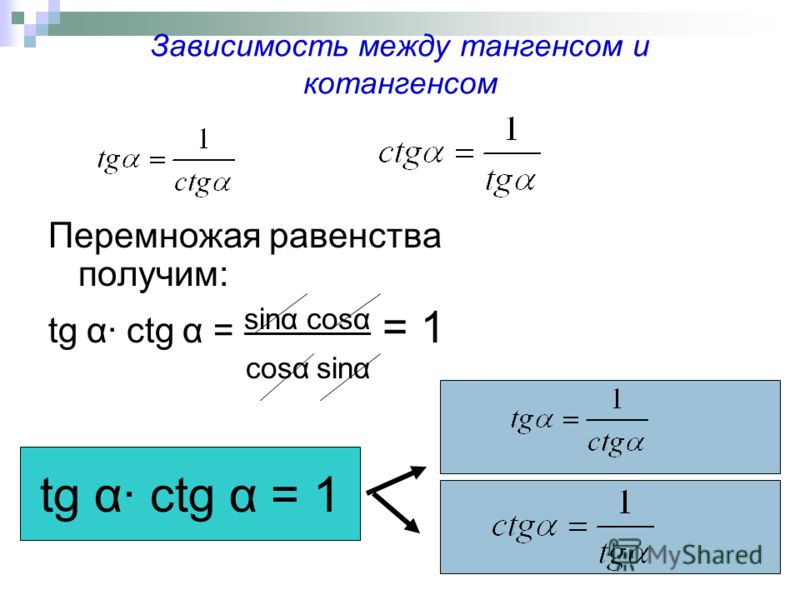
Найти производную функции 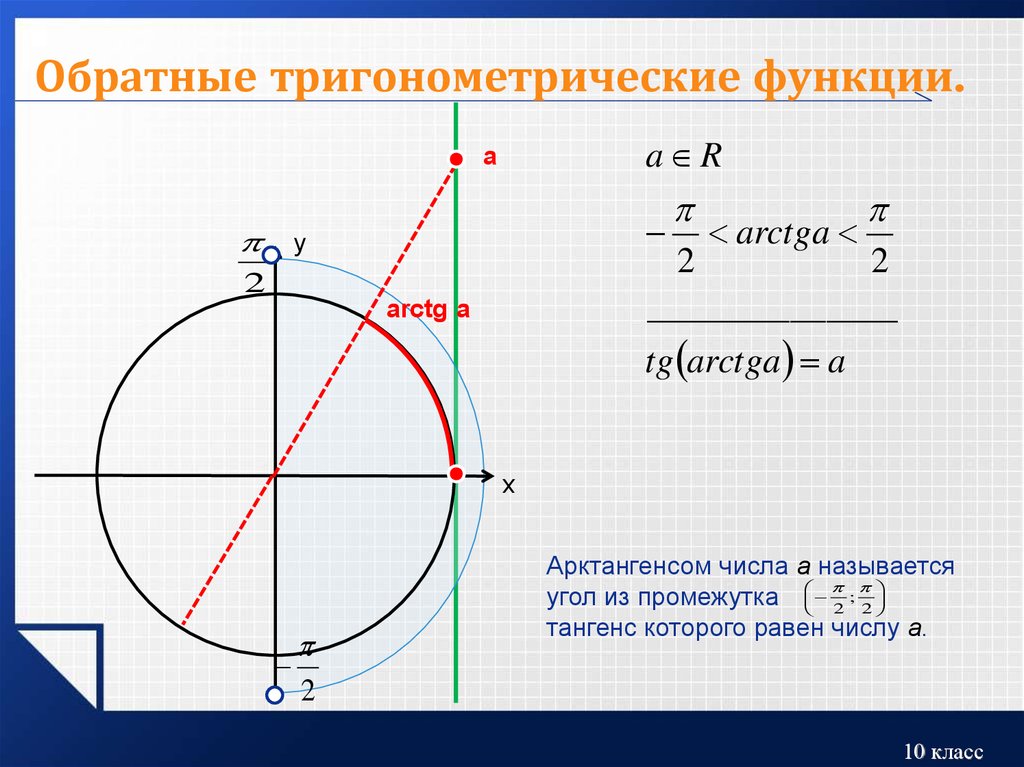

 Понять это можно из следующего чертежа. На рисунке координатной оси изображена функция Y = f (x) – синяя кривая.
Понять это можно из следующего чертежа. На рисунке координатной оси изображена функция Y = f (x) – синяя кривая.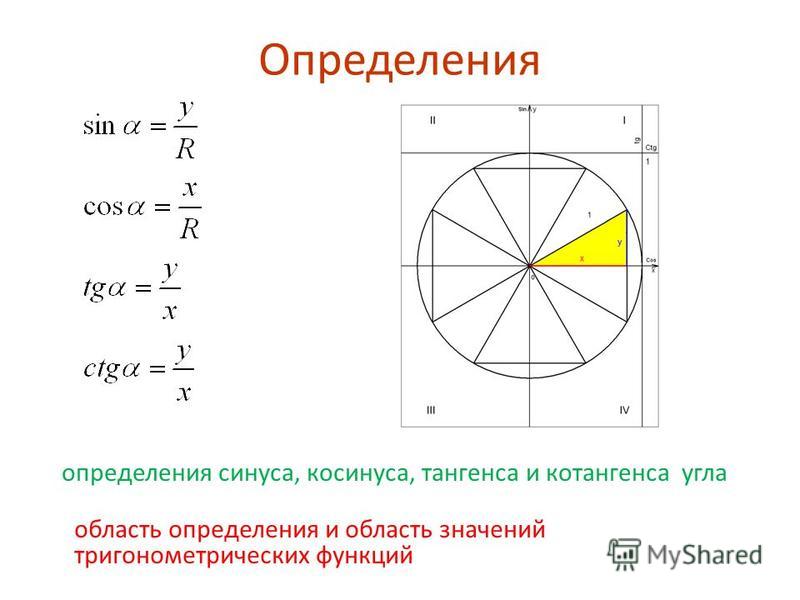 — возведение в степень.
— возведение в степень.
 Мы найдем производные от следующих функций:
Мы найдем производные от следующих функций:
 сек x)’ = 1/|x|√(x 2 — 1) , x ∈ (-∞, -1) ∪ (1, ∞)
сек x)’ = 1/|x|√(x 2 — 1) , x ∈ (-∞, -1) ∪ (1, ∞) tan x
tan x tan x
tan x }\)
}\) }\)
}\) }
\end{уравнение*}
}
\end{уравнение*}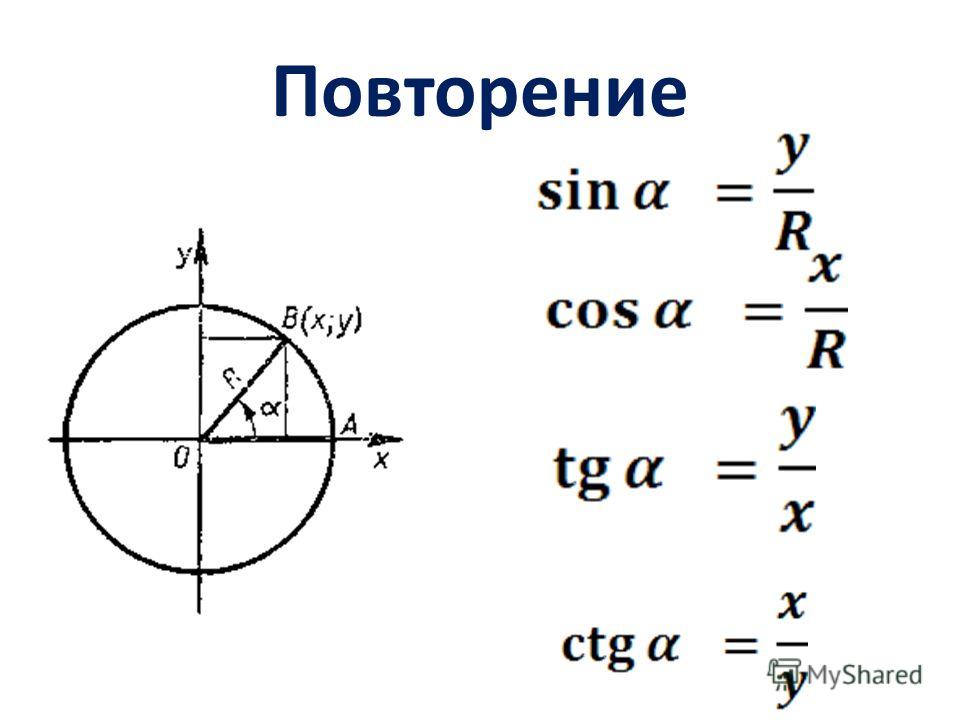 z + 1 \ text {.}
\end{уравнение*}
z + 1 \ text {.}
\end{уравнение*}

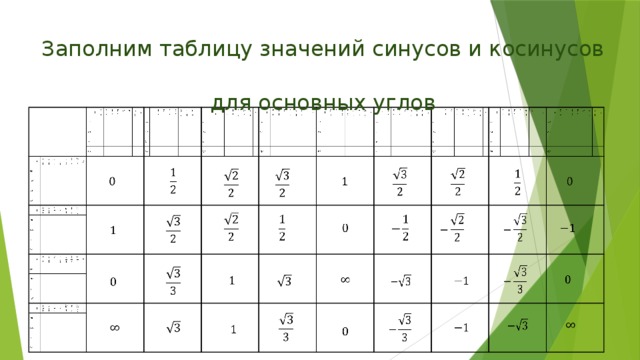
 Для полноты картины давайте углубимся в их доказательство!
Для полноты картины давайте углубимся в их доказательство!
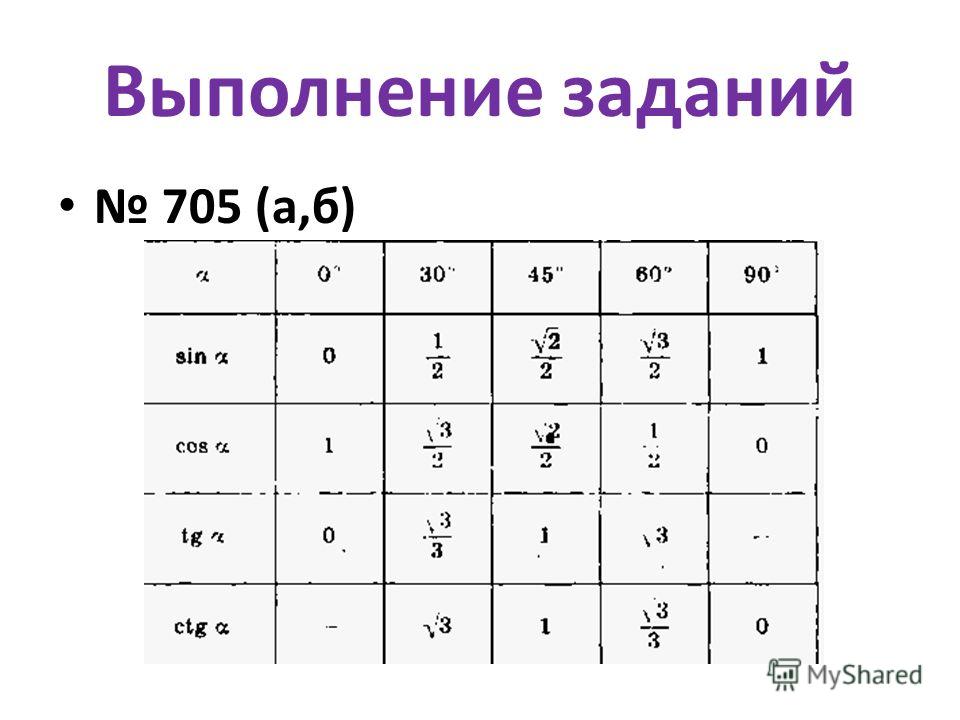 Мы можем использовать производную функции синуса вместе с тригонометрическими тождествами в нашу пользу!
Мы можем использовать производную функции синуса вместе с тригонометрическими тождествами в нашу пользу!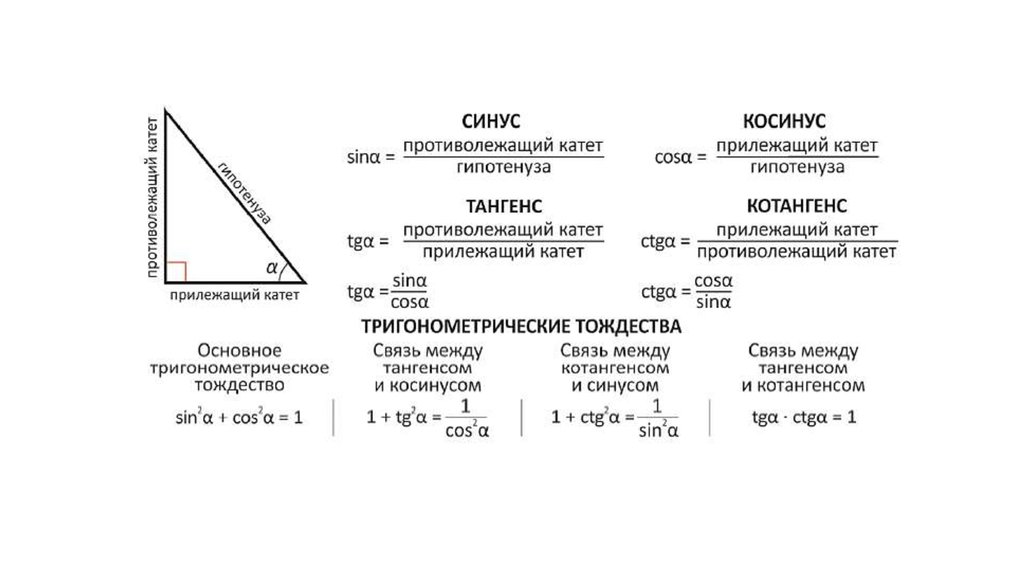 Начнем с того, что запишем функцию тангенса как частное функции синуса и функции косинуса.
Начнем с того, что запишем функцию тангенса как частное функции синуса и функции косинуса.
 Советы по обучению:
Советы по обучению: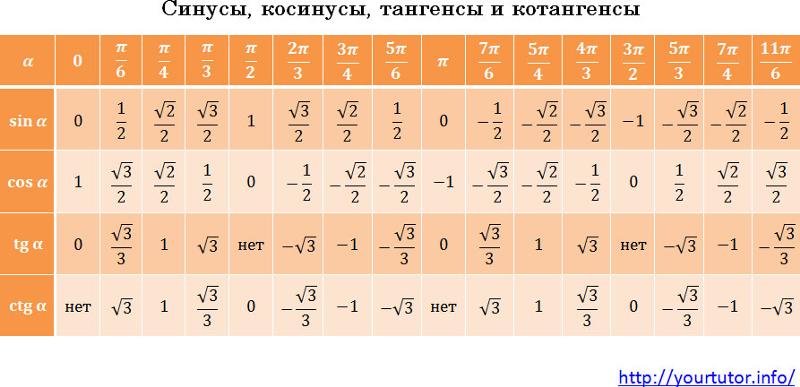 Мы немного увеличиваем его ($dx$), что позволяет разместить вдоль нашей единичной окружности (поскольку радианы — это расстояние, пройденное по периметру).
Мы немного увеличиваем его ($dx$), что позволяет разместить вдоль нашей единичной окружности (поскольку радианы — это расстояние, пройденное по периметру).
 Косинус увеличивается, когда синус отрицательный.)
Косинус увеличивается, когда синус отрицательный.)
 2$
2$
 Соответственно
Соответственно 
