Какие числа называются натуральными приведите примеры: Какие числа называют взаимно простыми? Приведите примеры. Чему равны наибольший общий делитель и на меньшее…

7 класс. Алгебра. Никольский. Учебник. Ответы к стр. 13

Действительные числа

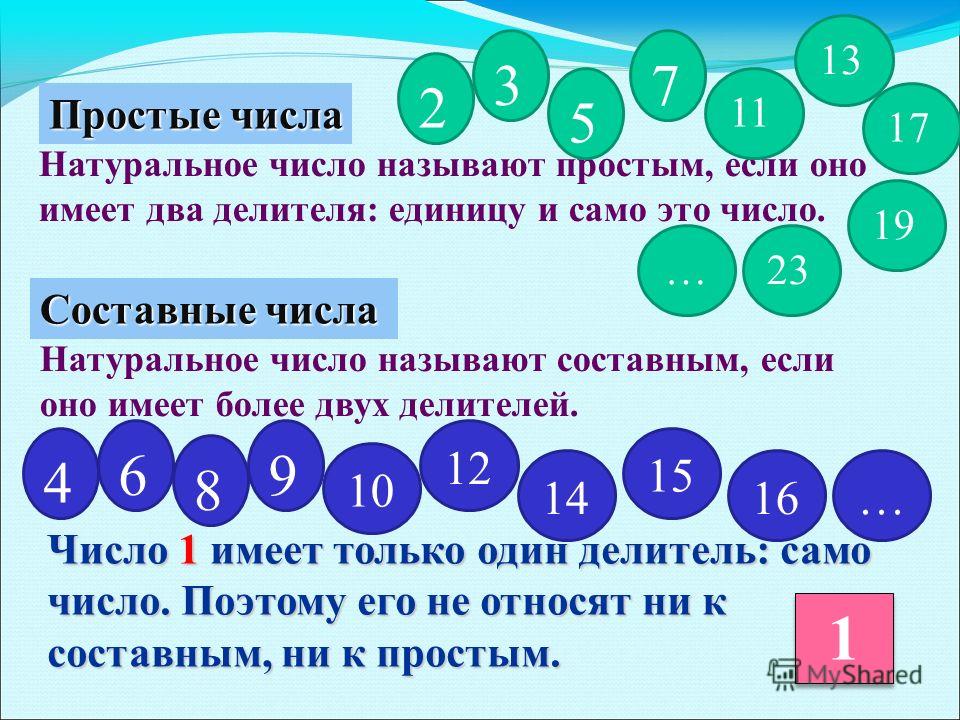
Натуральные числа
Разложение натуральных чисел на множители

Ответы к стр. 13

46. Что называют делителем натурального числа? Назовите делители числа 12.

Делителем натурального числа является такое число, на которое это натуральное число делится без остатка. Делители числа 12: 1, 2, 3, 4, 6, 12.

47. Что называют простым делителем натурального числа? Назовите простые делители числа 12.

Простым делителем натурального числа называют его делитель, который является простым числом. Простые делители числа 12: 2, 3.

48. Назовите все делители числа:
а) 17; б) 45; в) 113; г) 476; д) 32.

а) делители числа 17: 1, 17;
б) делители числа 45: 1, 3, 5, 9, 15, 45;
в) делители числа 113: 1, 113;
г) делители числа 476: 1, 2, 4, 7, 14, 17, 28, 34, 68, 119, 238, 476;
д) делители числа 32: 1, 2, 4, 8, 16, 32.

49. Найдите все простые делители числа:
а) 19; б) 54; в) 112; г) 232.

а) 19 | 19
      1 |
19 = 1 • 19
Простые делители числа 19: 19.

б) 54 | 2
    27 | 3
      9 | 3
      3 | 3
      1 |
54 = 2 • 3 • 3 • 3 = 2 • 3³
Простые делители числа 54: 2, 3.

в) 112 | 2
      56 | 2
      28 | 2
      14 | 2
        7 | 7
        1 |
112 = 2 • 2 • 2 • 2 • 7 = 2⁴ • 7
Простые делители числа 112: 2, 7.

г) 232 | 2
   116 | 2
     58 | 2
     29 | 29
       1 |
232 = 2 • 2 • 2 • 29 = 2³ • 29
Простые делители числа 232: 2, 29.

50. Напишите пять натуральных чисел, не имеющих других простых делителей, кроме 2 и 5, и пять натуральных чисел, не обладающих этим свойством.

Пять натуральных чисел, не имеющих других простых делителей, кроме 2 и 5:
2 • 5 = 10;
2² • 5 = 4 • 5 = 20;
2³ • 5 = 8 • 5 = 40;
2⁵ • 5 = 32 • 5 = 160;
2 • 5³ = 2 • 125 = 250.

Пять натуральных чисел, имеющие другие простые делители 3 и 7:
3 • 7 = 21;
3² • 7 = 9 • 7 = 63;
3 • 7² = 3 • 49 = 147;
3³ • 7 = 27 • 7 = 189;
3² • 7² = 9 • 49 = 441.

51. Приведите примеры натуральных чисел, имеющих делители 3 и 4. Какие делители, кроме указанных, имеют выбранные натуральные числа?

Натуральные числа, имеющие делители 3 и 4: 12, 24, 36.
Число 12 имеет также делители: 1, 2, 6, 12.
Число 24 имеет также делители: 1, 2, 6, 8, 12, 24.
Число 36 имеет также делители: 1, 2, 6, 9, 12, 36.

52. Приведите примеры натуральных чисел, не имеющих других простых делителей, кроме 3 и 5.

3 • 5 = 15;
3² • 5 = 9 • 5 = 45;
3 • 5² = 3 • 25 = 75.

53. Найдите все делители чисел: 2, 6, 12, 28, 48, 100.

2 | 2
1 |
делители числа 2: 1, 2;

6 | 2
3 | 3
1 |
делители числа 6: 1, 2, 3, 6;

12 | 2
  6 | 2
  3 | 3
  1 |
2 • 2 = 4,
2 • 3 = 6
делители числа 12: 1, 2, 3, 4, 6, 12;

28 | 2
14 | 2
  7 | 7
  1 |
2 • 2 = 4,
2 • 7 = 14
делители числа 28: 1, 2, 4, 7, 14, 28;

48 | 2
24 | 2
12 | 2
  6 | 2
  3 | 3
  1 |
2 • 2 = 4,
2 • 3 = 6,
2 • 2 • 2 = 8,
2 • 2 • 3 = 12,
2 • 2 • 2 • 2 = 16,
2 • 2 • 2 • 3 = 24
делители числа 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48;

100 | 2
  50 | 2
  25 | 5
    5 | 5
    1 |
2 • 2 = 4,
2 • 5 = 10,
2 • 2 • 5 = 20,
5 • 5 = 25,
2 • 5 • 5 = 50
делители числа 48: 1, 2, 4, 5, 10, 20, 25, 50, 100.

54. Найдите все простые делители чисел:
а) 4, 9, 15, 10, 24; б) 46, 50, 58, 99, 128;
в) 196, 254, 400, 625, 10 000; г) 7, 77, 777, 7777, 77 777.

а) 4 | 2
    2 | 2
    1 |
простые делители числа 4: 2;

9 | 3
3 | 3
1 |
простые делители числа 9: 3;

15 | 3
  5 | 5
  1 |
простые делители числа 15: 3, 5;

10 | 2
  5 | 5
  1 |
простые делители числа 10: 2, 5;

24 | 2
12 | 2
  6 | 2
  3 | 3
  1 |
простые делители числа 24: 2, 3;

б) 46 | 2
    23 | 23
      1 |
простые делители числа 46: 2, 23;

50 | 2
25 | 5
  5 | 5
  1 |
простые делители числа 50: 2, 5;

58 | 2
29 | 29
  1 |
простые делители числа 58: 2, 29;

99 | 3
33 | 3
11 | 11
  1 |
простые делители числа 99: 3, 11;

128 | 2
  64 | 2
  32 | 2
  16 | 2
    8 | 2
    4 | 2
    2 | 2
    1 |
простые делители числа 128: 2;

в) 196 | 2
      98 | 2
      49 | 7
        7 | 7
        1 |
простые делители числа 196: 2, 7;

254 | 2
127 | 127
    1 |
простые делители числа 254: 2, 127;

400 | 2
200 | 2
100 | 2
  50 | 2
  25 | 5
    5 | 5
    1 |
простые делители числа 400: 2, 5;

625 | 5
125 | 5
  25 | 5
    5 | 5
    1 |
простые делители числа 625: 5;

10 000 | 2
   5000 | 2
   2500 | 2
   1250 | 2
     625 | 5
     125 | 5
       25 | 5
         5 | 5
         1 |
простые делители числа 10 000: 2, 5;

г) 7 | 7
    1 |
простые делители числа 7: 7;

77 | 7
11 | 11
  1 |
простые делители числа 77: 7, 11;

777 | 3
259 | 7
  37 | 37
    1 |
простые делители числа 777: 3, 7, 37;

7777 | 7
1111 | 11
  101 | 101
      1 |
простые делители числа 7777: 7, 11, 101;

77 777 | 7
11 111 | 41
    271 | 271
        1 |
простые делители числа 77 777: 7, 41, 271.

55. Разложите на простые множители числа, т.е. запишите число в виде произведения степеней простых чисел:
а) 16, 18, 26; б) 35, 48, 72;
в) 144, 210, 800; г) 216, 343, 384;
д) 1024, 1728, 1575; е) 9225, 1001, 1739.

а) 16 | 2
      8 | 2
      4 | 2
      2 | 2
      1 |
16 = 2⁴

18 | 2
  9 | 3
  3 | 3
  1 |
18 = 2 • 3²

26 | 2
13 | 13
   1|
26 = 2 • 13

б) 35 | 5
      7 | 7
      1 |
35 = 5 • 7

48 | 2
24 | 2
12 | 2
  6 | 2
  3 | 3
  1 |
48 = 2⁴ • 3

72 | 2
36 | 2
18 | 2
  9 | 3
  3 | 3
  1 |
72 = 2³ • 3²

в) 144 | 2
      72 | 2
      36 | 2
      18 | 2
        9 | 3
        3 | 3
        1 |
144 = 2⁴ • 3²

210 | 2
105 | 3
  35 | 5
    7 | 7
    1 |
210 = 2 • 3 • 5 • 7

800 | 2
400 | 2
200 | 2
100 | 2
  50 | 2
  25 | 5
    5 | 5
    1 |
800 = 2⁵ • 5²

г) 216 | 2
    108 | 2
      54 | 2
      27 | 3
        9 | 3
        3 | 3
        1 |
216 = 2³ • 3³

343 | 7
  49 | 7
    7 | 7
    1 |
343 = 7³

384 | 2
192 | 2
  96 | 2
  48 | 2
  24 | 2
  12 | 2
    6 | 2
    3 | 3
    1 |
384 = 2⁷ • 3

д) 1024 | 2
      512 | 2
      256 | 2
      128 | 2
        64 | 2
        32 | 2
        16 | 2
          8 | 2
          4 | 2
          2 | 2
          1 |
1024 = 2¹⁰

1728 | 2
  864 | 2
  432 | 2
  216 | 2
  108 | 2
    54 | 2
    27 | 3
      9 | 3
      3 | 3
      1 |
1728 = 2⁶ • 3³

1575 | 3
  525 | 3
  175 | 5
    35 | 5
      7 | 7
      1 |
1575 = 3² • 5² • 7

е) 9225 | 3
    3075 | 3
    1025 | 5
      205 | 5
        41 | 41
          1 |
9225 = 3² • 5² • 41

1001 | 7
  143 | 11
    13 | 13
      1 |
1001 = 7 • 11 • 13

1739 | 37
    47 | 47
      1 |
1739 = 37 • 47

56. Сколько чисел от 1 до 100:
а) делится на 2; б) делится на 5;
в) делится на 2 и на 5; г) не делится на 2 и на 5?

а) 100 : 2 = 50 — чисел, делящихся на 2;
б) 100 : 5 = 20 — чисел, делящихся на 5;
в) 100 : (2 • 5) = 100 : 10 = 10 – чисел, делящихся на 2 и на 5;
г) 100 − 100 : (2 • 5) = 100 − 100 : 10 = 100 − 10 = 90 — чисел, не делящихся на 2 и на 5.

57. Сколько чисел от 1 до 100 не делится ни на 2, ни на 3?

100 : 2 = 50 – чисел, делящихся на 2;
100 : 3 = 33 ¹/₃ ≈ 33 – чисел, делящихся на 3;
100 : (2 • 3) = 100 : 6 = 16 ²/₃ ≈ 16 – чисел, делящихся и на 2 и на 3;
50 + 33 – 16 = 67 – всего чисел, делящихся на 2 и на 3
100 − 67 = 33 — числа от 1 до 100, не делящихся ни на 2, ни на 3.

ГДЗ. Ответы по алгебре. 7 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.

Алгебра. 7 класс

Вопросы к зачетам по математике 5 класс Виленкин | Учебно-методическое пособие по алгебре (5 класс) на тему:

Опубликовано 09.11.2014 — 13:17 — Подхватилина Тамара Серафимовна

Вопросы к зачетам по математике 5 класс по учебнику Виленкина

Скачать:

Предварительный просмотр:

Вопросы к зачетам по математике 5 класс

Зачет № 1

1. Какие числа называются натуральными? Назовите все цифры.
2.  Назовите разряды в классе единиц. Назовите по порядку первые четыре класса в записи натуральных чисел.
3.  Что называют отрезком? Как обозначают отрезки? Как сравнивают отрезки?
4.  Перечислите единицы длины.
5.  Что называют плоскостью, прямой, лучом?
6.  Сколько прямых можно провести через две точки?
7.  Дайте определения единичного отрезка, координатного луча, координаты точки.
8.  Перечислите единицы массы.
9.  Как сравнивают натуральные числа?
10.  Какие числа называют слагаемыми? Что называют суммой чисел?
11.  Сформулируйте свойства сложения (переместительное, сочетательное, свойство нуля).
12.  Что такое периметр треугольника?
13.  Какое число называют уменьшаемым, какое — вычитаемым, как называют результат вычитания?
14.  Сформулируйте свойства вычитания суммы из числа, числа из суммы.
15.  Что называют числовым выражением? буквенным выражением?
16.  Буквенная запись свойств сложения и вычитания.
17.  Что называют уравнением? Что значит решить уравнение?
18.  Какое число называют корнем уравнения?
19. Как найти неизвестное слагаемое? вычитаемое? уменьшаемое?
20.  Что значит десятичная система счисления? Позиционная система счисления?
21.  Как называют числа, которые перемножают. Как называют результат умножения?
22.  Сформулируйте свойства умножения (переместительное, сочетательное, свойство нуля). Запишите их с помощью букв.
23.  Что значит «разложить на множители»?
24.  Как называют число, которое делят? Что такое делитель? Как называют результат деления?
25.  Как найти неизвестное делимое? делитель? множитель?
26.  Деление с остатком. Приведите пример. Может ли остаток быть больше делителя?
27.  Сформулируйте распределительное свойство умножения относительно сложения и относительно вычитания. Запишите с помощью букв.]
28.  Что значит упростить выражение?
29.  Какие действия относятся к действиям первой ступени, второй ступени? В каком порядке выполняют действия в выражениях?
30.  Что такое квадрат числа?
31.  Что такое куб числа?
32.  Выучить наизусть таблицу квадратов первых двадцати натуральных чисел и таблицу кубов первых семи натуральных чисел.

Зачет № 2

1. Назовите формулу пути и расскажите, что означают входящие в неё буквы.
2.  Назовите формулу площади прямоугольника? квадрата
3.  Какие фигуры называют равными? равновеликими?
4. Назовите единицы измерения площадей.
5.  Что такое квадратный метр? квадратный дециметр? квадратный километр?
6.  Приведите примеры предметов, имеющих форму прямоугольного параллелепипеда. Что называют кубом?
7.  Сколько граней, рёбер, вершин у прямоугольного параллелепипеда?
8.  Назовите формулу объёма прямоугольного параллелепипеда; куба.
9.  Назовите единицы измерения объёмов.
10.  Что такое кубический сантиметр? кубический метр? кубический дециметр?
11.  Что такое литр? Сколько литров в одном кубическом метре?
12.  Какие ещё единицы измерения объёма вы знаете? (Баррель, бушель, галлон, пинта и др.)
13.  Что такое метрическая система мер? Что такое миля, кабельтов, карат?
14.  Опишите, как строят окружность с помощью циркуля.
15.  Что такое радиус окружности? диаметр? Что называют кругом?
16.  Что называют обыкновенной дробью? Что показывает числитель? Что показывает знаменатель?
17.  Какая часть фигуры закрашена (№ 860)? Как называется… (№ 863)?
18.  Что называют половиной, третью, четвертью?
19.  Какая из двух дробей с одинаковыми знаменателями меньше, а какая больше? Приведите пример двух равных дробей с разными числителями.
20.  Какую дробь называют правильной? неправильной? Какая дробь больше, если одна из них правильная, а другая неправильная?
21.  Как складывают (вычитают) дроби с одинаковыми знаменателями?
22.  Запишите с помощью букв правило сложения (вычитания) дробей с одинаковыми знаменателями.
23.  Как можно понимать черту дроби?
24.  Каким числом является частное, если деление выполняется нацело? не выполняется нацело?
25.  Сформулируйте правило деления суммы на число.
26.  Что называют целой частью числа и что — его дробной частью?
27.  Как из неправильной дроби выделить целую часть?
28.  Как представить смешанное число в виде неправильной дроби?
29.  Как складывают (вычитают) числа смешанного вида?
30.  Что называют десятичной дробью?
31.  Как записывают десятичные дроби?
32.  Сформулируйте правило сравнения десятичных дробей.
33.  Как складывают (вычитают) десятичные дроби?
34. Какое число называют приближённым значением с недостатком? с избытком?
35.  Сформулируйте правило округления чисел.

Зачет № 3

1. Сформулируйте правило умножения десятичной дроби на натуральное число.
2.  Как умножить десятичную дробь на 10, на 100, на 1000?
3.  Как разделить десятичную дробь на натуральное число?
4.  Как разделить десятичную дробь на 10, на 100, на 1000?
5.  Как обратить обыкновенную дробь в десятичную?
6.  Сформулируйте правило умножения на десятичную дробь.
7.  Что надо сделать при умножении на десятичную дробь, если в произведении меньше цифр, чем надо отделить запятой?
8.  Как изменяется число при умножении на неправильную (правильную) десятичную дробь?
9.  Как умножить десятичную дробь на 0,1, на 0,01, на 0,001?
10.  Сформулируйте правило деления десятичной дроби на десятичную дробь.
11.  Сформулируйте правило деления десятичной дроби на 0,1, на 0,01, на 0,001.
12.  Умножением на какое число можно заменить деление на 0,01?
13.  Как найти среднее арифметическое нескольких чисел?
14.  Как найти среднюю скорость движения?
15.  Что такое двоичная система счисления?
16.  Что называют процентом?
17.  Как обратить десятичную дробь в проценты? Как проценты перевести в десятичную дробь?
18.  Как найти процент от числа? число по его проценту?
19.  Какие вам известны более мелкие доли целого?
20.  Что такое угол?
21.  Какой угол называют развёрнутым (прямым, острым, тупым)?
22.  Какие углы называют равными?
23.  Для чего служит транспортир? На сколько делений разделена шкала транспортира?
24.  Что такое градус? минута? секунда? Как их обозначают?
25.  Сколько градусов содержит развёрнутый угол? прямой угол? тупой угол? острый угол?
26.  Какой луч называют биссектрисой угла?
27.  Какие виды треугольников вам известны (по тетради)? Сформулируйте свойство углов треугольника, четырёхугольника).
28.  Что называют круговой диаграммой?

По теме: методические разработки, презентации и конспекты

Вопросы для зачета №1 6 класс

Зачет №1 6 класс (1 полугодие)…

Вопросы для зачета №1 6 класс

Зачет №1 6 класс (1 полугодие)…

Вопросы для зачета №2 6 класс

Зачет №2 6 класс (2 полугодие)…

Вопросы для зачета №2 6 класс

Зачет №2 6 класс (2 полугодие)…

Вопросы к зачету по математике в 5 классе

Материал для самоподготовки к итоговому зачету по математике…

Вопросы к зачету в 5 классе по теме «Десятичные дроби»

Вопросы к зачету по математике в 5 классе по теме «Десятичные дроби»…

Вопросы к зачетам по математике 6 класс Виленкин

Вопросы к зачетам по математике 6 класс по учебнику Виленкина…

Поделиться:

 

Свойства натуральных чисел — определения, примеры и часто задаваемые вопросы.

Свойства натуральных чисел относятся к результату четырех основных арифметических операций над натуральными числами. Натуральные числа — это набор целых чисел, кроме нуля. Эти числа используются в нашей повседневной деятельности и речи. Натуральные числа — это одна из классификаций действительных чисел, которая включает только положительные целые числа, т.е. 1, 2, 3, 4,5,6, ………. кроме нуля, дробей, десятичных и отрицательных чисел. Помните, что множество натуральных чисел не включает в себя отрицательные числа или нуль.

В этой статье вы подробно узнаете о свойствах натуральных чисел.

1.	Каковы свойства натуральных чисел?
2.	Свойство закрытия
3.	Ассоциативное свойство
4.	Коммутативная собственность
5.	Распределительная собственность
6.	Часто задаваемые вопросы о свойствах натуральных чисел

Каковы свойства натуральных чисел?

Натуральные числа — это числа, которые являются целыми положительными числами и включают числа от 1 до бесконечности (∞). Эти числа являются исчисляемыми и обычно используются для расчетов. Множество натуральных чисел в математике — это множество, начинающееся с 1, то есть {1,2,3,…}. Набор натуральных чисел обозначается символом N. Четыре свойства натуральных чисел таковы:

1. Свойство закрытия
2. Ассоциативное свойство
3. Коммутативное свойство
4. Распределительная собственность

Давайте рассмотрим их подробно.

Свойство закрытия

Свойство замыкания натуральных чисел гласит, что сложение и умножение двух или более натуральных чисел всегда дает натуральное число. Проверим все четыре арифметические операции и все a, b ∈ N.

• Сложение: 1 + 5 = 6, 7 + 4 = 11 и т. д. Ясно, что полученное число или сумма является натуральным числом. Таким образом, a + b ∈ N для всех a, b ∈ N.
• Умножение: 2 × 5 = 10, 6 × 4 = 24 и т. д. Ясно, что полученное число или произведение — натуральное число. Таким образом, a × b ∈ N для всех a, b ∈ N.
• Вычитание: 8 – 5 = 3, 7 – 2 = -5 и т. д. Ясно, что результатом может быть натуральное число, а может и не быть. Таким образом, a — b или b — a ∉ N для всех a, b ∈ N.
• Деление: 15 ÷ 5 = 3, 10 ÷ 3 = 3,33 и т. д. Ясно, что полученное число может быть или не быть натуральным числом. Таким образом, a ÷ b или b ÷ a ∉ N для всех a, b ∈ N.

Таким образом, мы можем заключить, что множество натуральных чисел всегда замкнуто относительно сложения и умножения, но не то же самое для вычитания и деления.

Ассоциативное свойство

Ассоциативное свойство натуральных чисел гласит, что сумма или произведение любых трех натуральных чисел остается неизменной, несмотря на изменение группировки чисел. Проверим все четыре арифметические операции и все a, b, c ∈ N.

• Дополнение: а + (b + c) = (a + b) + c. 3 + (15 + 1) = 19 и (3 + 15) + 1 = 19.
• Умножение: a × (b × c) = (a × b) × c. 3 × (15 × 1) = 45 и (3 × 15) × 1 = 45.
• Вычитание: а – (б – в) ≠ (а – б) – в. 2 – (15 – 1) = – 12 и (2 – 15) – 1 = – 14.
• Деление: a ÷ ( b ÷ c ) ≠ ( a ÷ b ) ÷ c. 2 ÷ (3 ÷ 6) = 4 и (2 ÷ 3) ÷ 6 = 0,11.

Таким образом, мы можем заключить, что множество натуральных чисел ассоциативно при сложении и умножении, но не так при вычитании и делении. Итак, ассоциативность N формулируется следующим образом: для всех a, b, c ∈ N, a + (b + c) = (a + b) + c и a × (b × c) = (a × b ) × с

Коммутативное свойство

Коммутативное свойство натуральных чисел гласит, что сумма или произведение двух натуральных чисел остается неизменным даже после изменения порядка чисел. Проверим все четыре арифметических действия и все a, b ∈ N.

• Сложение: a + b = b + a.
• Умножение: a × b = b × a
• Вычитание: а – б ≠ б – а
• Деление: а ÷ b ≠ b ÷ а

Следовательно, мы можем заключить, что множество натуральных чисел коммутативно при сложении и умножении, но не так при вычитании и делении. Итак, коммутативность N формулируется следующим образом: Для всех a, b ∈ N, a + b = b + a и a × b = b × a

Операция	Свойство закрытия	Ассоциативное свойство	Коммутативное свойство
Дополнение	да	да	да
Вычитание	нет	нет	нет
Умножение	да	да	да
Отдел	нет	нет	нет

Распределительная собственность

Распределительное свойство натуральных чисел утверждает, что любое выражение с тремя числами a, b и c, заданное в форме a (b + c), тогда оно разрешается как a × (b + c) = ab + ac или a (b — c) = ab — ca, что означает, что операнд a распределяется между двумя другими операндами, b и c.

• Умножение натуральных чисел всегда дистрибутивнее сложения. а × (б + с) = аб + ас
• Умножение натуральных чисел также является дистрибутивным по отношению к вычитанию. а × (б – в) = аб – ас

Пример: 3 × (2 + 5) = 3 × 2 + 3 × 5

3 × (2 + 5) = 3 × 7 = 21

3 × 2 + 3 × 5 = 6 + 15 = 21

3 × (2 + 5) = 3 × 7 = 21

3 × 2 + 3 × 5 = 6 + 15 = 21

Пример: 3 × (2 − 5) = 3 × 2 − 3 × 5

3 × (2 −5) = 3×(−3) = −9

3 × 2 − 3 × 5 = 6 − 15 = −9

Статьи по теме

Ознакомьтесь с этими интересными статьями, посвященными свойствам натуральных чисел, для более глубокого понимания.

• Распределительное свойство умножения
• Коммутативное свойство
• Ассоциативное свойство
• Калькулятор свойств распределения

Часто задаваемые вопросы о свойствах натуральных чисел

Каковы свойства натуральных чисел в математике?

Свойства натуральных чисел:

1. Свойство замыкания
2. Ассоциативное свойство
3. Коммуникативное имущество
4. Распределительное имущество

Является ли множество натуральных чисел ассоциативным при делении?

Множество натуральных чисел НЕ является ассоциативным при делении. Например, рассмотрим три натуральных числа 6,4 и 2. Тогда: (6÷4)÷2 = 3÷2=1. 6÷(4÷2) = 6÷2 = 3. Таким образом, (6÷4)÷2 ≠ 6÷(4÷2).

Что вы подразумеваете под коммутативным свойством сложения?

Согласно коммутативному свойству сложения, натуральные числа можно складывать в любом порядке, и их ответ останется тем же. Формула для этого свойства такова: a + b = b + a, что верно для любых a, b ∈ N. Например, 1 + 2 или 2 + 1 дадут один и тот же ответ.

Что означает ассоциативное свойство сложения?

Ассоциативное свойство сложения — это свойство натуральных чисел, которое гласит, что сумма трех или более чисел не изменится даже при изменении группировки чисел. Соответствующее уравнение имеет вид a + ( b + c ) = ( a + b ) + c . Здесь группировка относится к тому, как данные числа расположены в скобках.

Какое уравнение показывает коммутативное свойство сложения?

Уравнение, показывающее коммутативность сложения, имеет вид «a + b = b + a». Возьмем пример: 4 + 3 = 3 + 4. Здесь сумма в обеих частях уравнения одинакова, то есть 7,9.0003

Какое уравнение показывает распределительное свойство умножения?

Уравнение, показывающее распределительное свойство умножения, имеет вид «a (b + c) = a b + a c». Здесь термины в круглых скобках не могут быть упрощены из-за одной или нескольких переменных.

Что такое натуральные числа? Определение, свойства и примеры

Определение натуральных чисел

Натуральные числа — это все положительные целые числа от 1 до бесконечности. Их также называют счетными числами, так как они используются для подсчета предметов. Натуральные числа не включают 0 или отрицательные числа.

Числа нужны нам в повседневной жизни, будь то для подсчета предметов, определения времени или нумерации домов. Числа, которые помогают нам в подсчете и представлении величин, называются натуральными числами. К ним относятся 1, 2, 3, 4, 5, 6 и так далее до бесконечности.

Здесь мы видим, что 1 — наименьшее натуральное число и каждое последующее натуральное число ровно на единицу больше предыдущего. Таким образом, числа, находящиеся между этими числами, не являются натуральными числами, такими как дроби, десятичные дроби и т. д. 

История натуральных чисел 

Предполагается, что натуральные числа произошли от слов, используемых для счета предметов, которые начинаются с единицы. Система разряда для числительных 1 (один) и 10 (десять) была впервые разработана вавилонянами.

Типы натуральных чисел

1. Нечетные натуральные числа

Нечетные натуральные числа — это положительные числа, которые не делятся на 2.

Например: 29, 677, 89901 и т. д.

2. Четные натуральные числа

Четные натуральные числа — это положительные числа, которые делятся на 2. 

Например: 28, 456, 6022 и т. д. 

Свойства натуральных чисел 

Вот некоторые важные свойства натуральных чисел.

• Свойство закрытия
• Коммутативное свойство
• Ассоциативное свойство
• Распределительная собственность

1. Свойство замыкания сложения и умножения

При сложении или умножении двух натуральных чисел результатом всегда будет натуральное число.

• Примеры замыкания свойства сложения: 2 + 2 = 4, 3 + 4 = 7, 5 + 5 = 10

В каждом случае результатом сложения натуральных чисел является натуральное число.

• Примеры свойства замыкания умножения: 2 × 2 = 4, 3 × 2 = 6, 5 × 5 = 25

В каждом случае результатом умножения натуральных чисел является натуральное число.

Однако в случае деления и вычитания это свойство не выполняется. Вычитание или деление двух натуральных чисел не всегда дает натуральное число.

• Примеры вычитания: 4 – 6 = –2, 5 – 3 = 2, 6 – 9 = –3

Во втором случае получилось натуральное число, а в первом и третьем нет.

• Примеры деления: 10 ÷ 3 = 3,33, 9 ÷ 3 = 3, 15 ÷ 4 = 3,75 

Первый и третий случаи не привели к натуральным числам.

2. Ассоциативное свойство сложения и умножения  

Сумма или произведение натуральных чисел остается неизменным даже при изменении группировки чисел. Однако это не относится к делению и вычитанию.

• Примеры ассоциативного свойства сложения: 2 + (5 + 6) = 13 и (2 + 5) + 6 = 13
• Примеры ассоциативного свойства умножения: 2 × (3 × 4) = 24 и (2 × 3) × 4 = 24

Давайте теперь посмотрим на природу вычитания и деления с учетом этого свойства.

• Примеры вычитания: 4 – (10 – 2) = –4 и (4 – 10) – 2 = –8
• Примеры деления: 5 ÷ (6 ÷ 3) = 2,5 и (5 ÷ 6) ÷ 3 = 0,27

3. Коммутативное свойство сложения и умножения

Если мы изменим порядок натуральных чисел при умножении и сложении, результат не изменится.

Например,

• 6 + 5 = 11 и 5 + 6 = 11
• 2 × 4 = 8 и 4 × 2 = 8

Свойство коммутативности не распространяется на вычитание и деление натуральных чисел.

Примеры вычитания и деления:

• 5 – 3 = 2 и 3 – 5 = –2
• 6 ÷ 3 = 2 и 3 ÷ 6 = 0,5  

4. Распределительная собственность

В соответствии с распределительным свойством умножения над сложением, если мы умножим сумму двух слагаемых на число или умножим каждое слагаемое по отдельности, а затем сложим их, результат будет таким же.

Пример: 2 × (5 + 3) = (2 x 5) + (2 x 3) = 16

Это свойство справедливо и в случае умножения вместо вычитания.

Пример: 2 x (5 – 3) = (2 x 5) – (2 x 3) = 4

Интересные факты

• Не существует наибольшего натурального числа.
• Просто прибавив 1 к текущему натуральному числу, вы получите еще одно натуральное число.
• Натуральные числа продолжаются вечно.

Решенные примеры

Давайте лучше поймем концепцию на этих примерах.

1. Выберите натуральные числа из следующего списка:

             10, 6/2, 4,66, 22, 1564, –6 

Ответ. Натуральными числами являются 10, 22 и 1564. Отрицательные числа, десятичные числа и дроби не считаются натуральными числами.

2. Перечислите первые десять натуральных чисел.

Ответ. Ответ: 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10, так как натуральные числа начинаются с 1.  

3. В чем разница между любыми двумя последовательными натуральными числами?  

Ответ. Разница между любыми двумя последовательными натуральными числами всегда равна 1.

Практические задачи

1

Между какими двумя натуральными числами лежит дробь 18/3?

10 и 12

5 и 7

7 и 9

12 и 14

Правильный ответ: 5 и 7

2

Если m и m два натуральных числа, то:

m + n = n + m

m – n = n – m

m / n = n / m

Ничего из этого

Правильный ответ: m + n = n + m чисел при умножении и сложении результат не меняется. Это свойство не распространяется на вычитание и деление.

3

Какое свойство натуральных чисел верно для 2 + (5 + 6) = 13 и (2 + 5) + 6 = 13?

ассоциативное свойство умножения

ассоциативность вычитания

ассоциативность сложения

замыкание сложения

Правильный ответ: ассоциативность сложения
Ассоциативность сложения имеет место для данной задачи. Свойство утверждает, что сумма натуральных чисел остается неизменной, даже если их группировка варьируется.

4

Какой из следующих примеров правильно устанавливает коммутативное свойство?

6 + 5 = 11 и 5 + 6 = 11

2 + (5 + 6) = 13 и (2 + 5) + 6 = 13

2 × (5 + 3) = (2 x 5) + (2 x 3) = 16

4 – 6 = –2

Правильный ответ: 6 + 5 = 11 и 5 + 6 = 11
Поскольку свойство коммутативности гласит, что изменение порядка натуральных чисел при умножении и сложении не изменит результат.

Часто задаваемые вопросы

Является ли ноль натуральным числом?

Нет. Ноль не является ни положительным, ни отрицательным. Поскольку натуральные числа включают в себя все положительные целые числа от 1 до бесконечности, ноль в набор не входит.

Являются ли натуральные числа целыми числами?

Все натуральные числа являются целыми числами, но все целые числа не считаются натуральными.