Мерзляк 5 класс — § 11. Угол. Обозначение углов
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какую фигуру называют углом? — Углом называют фигуру, образованную двумя лучами, имеющими общее начало.
2. Какие два угла называют равными? — Два угла называют равными, если они совпадают при наложении.
3. Как называют луч, который делит угол на два равных угла? — биссектриса.
Комментарий: Запомнить это сложное слово поможет шутка: «Биссектриса — это крыса, которая бегает по углам и делит угол пополам».
Решаем устно
1. Каких чисел не хватает в цепочке вычислений?
2. Решите уравнение:
3. Корнем каких из следующих уравнений является число 5:
1) 2х — 3 = 7, если х = 5, то:
2 • 5 — 3 = 7
10 — 3 = 7
7 = 7 — верно, значит число 5 является корнем уравнения 2х — 3 = 7.
2) х + 20 = 20 + х, если х = 5, то:
5 + 20 = 20 + 5
25 = 25 — верно, значит число 5 является корнем уравнения х + 20 = 20 + х.
3) 36 — 3х = 20, если х = 5, то:
36 — 3 • 5 = 20
36 — 15 = 20
21 ≠ 20 — неверно, значит число 5 не является корнем уравнения 36 — 3х = 20.
4) х • х • х + 25 = 150, если х = 5, то:
5 • 5 • 5 + 25 = 150
25 • 5 + 25 = 150
125 + 25 = 150
150 = 150 — верно, значит число 5 является корнем уравнения х • х • х + 25 = 150.
5) 0 • х = 10, если х = 5, то:
0 • 5 = 10
0 = 10 — неверно, значит число 5 не является корнем уравнения 0 • х = 10.
6) х + 12 = 22 — х, если х = 5, то:
5 + 12 = 22 — 5
17 = 17 — верно, значит число 5 является корнем уравнения 36 — 3х = 20.
Ответ: число 5 является корнем уравнений № 1, 2, 4, 6.
4. У Пети и Миши было поровну конфет. Петя отдал Мише 8 конфет. На сколько конфет у Миши стало больше, чем у Пети?
Пусть изначально у Пети и у Миши было по х конфет..jpg)
Тогда после обмена стало:
- у Пети х — 8 конфет
- у Миши х + 8 конфет
Сравним, на сколько конфет у Миши стало больше, чем у Пети:
8 + 8 = 16 (конфет) — у Миши больше, чем у Пети.
Ответ: на 16 конфет.
Упражнения
281. Как можно обозначить угол, изображённый на рисунке 73?
Данный угол можно обозначить как: ∠K, ∠MKN, ∠NKM.
282. На каком из рисунков 74, а, б, в луч ОК является биссектрисой угла АОВ?
Луч ОК является биссектрисой угла АОВ на рисунке 74 б.
283. Назовите все углы, изображённые на рисунке 75.
На рисунке изображено 3 угла:
- ∠BAE (можно обозначить как ∠EAB)
- ∠EAM (можно обозначить как ∠MAE)
- ∠BAM (можно обозначить как ∠MAB)
284. Запишите все углы, изображённые на рисунке 76.
На рисунке изображено 3 угла:
- ∠OTC (можно обозначить как ∠CTO)
- ∠CTF (можно обозначить как ∠FTC)
- ∠OTF (можно обозначить как ∠FTO)
285.
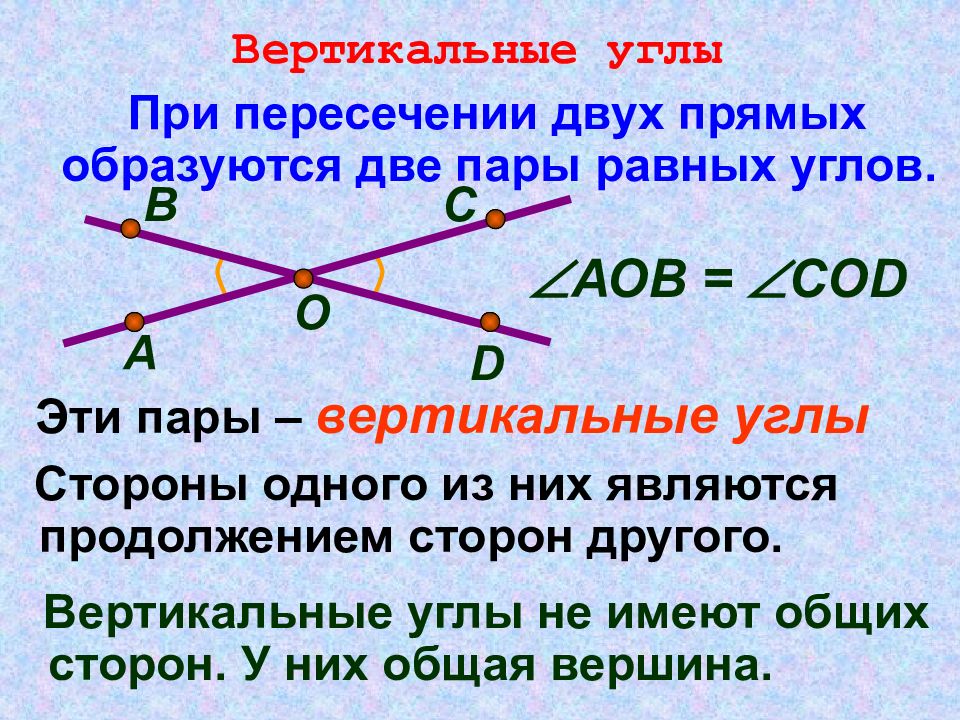Какие из лучей, изображённых на рисунке 77, пересекают сторону угла ВОС?
Сторону угла ВОС пересекают лучи AK, ST.
286. Какие из лучей, изображённых на рисунке 78, пересекают сторону угла ВОС?
Сторону угла ВОС пересекают лучи RP, FE.
287. Начертите ∠MNE и проведите лучи NA и NC между его сторонами. Запишите все образовавшиеся углы.
На рисунке образовалось 6 углов:
- ∠MNA (можно обозначить как ANM)
- ∠MNC (можно обозначить как CNM)
- ∠MNE (можно обозначить как ENM)
- ∠ANC (можно обозначить как CNA)
- ∠ANE (можно обозначить как ENA)
- ∠CNE (можно обозначить как ENC)
288. На рисунке 79 ∠ABE = ∠ СВF. Есть ли ещё на этом рисунке равные углы?
На рисунке изображены следующие равные углы:
- ∠ABE = ∠СВF или ∠EBA = ∠FBC
- ∠ABF = ∠CBE или ∠FBA = ∠EBC
289. На рисунке 80 ∠AOB = ∠DOE, ∠BOC = ∠COD.
Есть ли ещё на этом рисунке равные углы?
На рисунке изображены следующие равные углы:
- ∠AOB = ∠DOE или ∠BOA = ∠EOD
- ∠BOC = ∠COD или ∠COB = ∠DOC
- ∠AOC = ∠EOC или ∠COA = ∠COE
- ∠AOD = ∠EOB или ∠DOA = ∠BOE
290. На рисунке 81 углы FOK и МОЕ равны. Какие ещё углы, изображённые на этом рисунке, равны?
На рисунке изображены следующие равные углы:
- ∠FOK = ∠MOE или ∠KOF = ∠EOM
- ∠FOM = ∠EOK или ∠MOF = ∠KOE
Упражнения для повторения
291. Составьте числовое выражение и найдите его значение:
- произведение суммы чисел 18 и 20 и числа 8: (18 + 20) • 8 = 38 • 8 = 304
- частное от деления разности чисел 128 и 29 на число 11: (128 — 29) : 11 = 99 : 11 = 9
- частное от деления произведения чисел 15 и 6 на их разность: (15 • 6) : (15 — 6) = 90 : 9 = 10
292. Решите уравнение:
293.
На ХХП зимних Олимпийских играх, состоявшихся в 2014 г. в городе Сочи, олимпийская сборная России завоевала 33 медали. Наши спортсмены получили 24 золотых и серебряных медали, а золотых и бронзовых — 22. Сколько медалей каждого вида завоевала на этой Олимпиаде наша сборная?
1) 33 — 22 = 11 (шт.) — медалей — серебряные.
2) 24 — 11 = 13 (шт.) — медалей — золотые.
3) 22 — 13 = 9 (шт.) — медалей — бронзовые.
Ответ: 13 золотых медалей, 11 серебряных медалей и 9 бронзовых медалей.
294. Учащиеся пятых классов ехали на двух автобусах на экскурсию. Когда из одного автобуса, в котором было 42 учащихся, восемь учащихся перешли во второй автобус, то в обоих автобусах учащихся стало поровну. Сколько учащихся было во втором автобусе сначала?
Пусть во втором автобусе сначала было х учащихся. Тогда, после того перешло 8 учащихся из первого автобуса, во втором автобусе стало (х + 8) учащихся.
Мы знаем, что в первом автобусе сначала было 42 учащихся, а после перехода осталось (42 — 8) учащихся — столько же, сколько стало во втором автобусе после перехода.
Составим уравнение:
х + 8 = 42 — 8
х + 8 = 34
х = 34 — 8
х = 26
Значит сначала в первом автобусе было 26 учащихся.
Ответ: 26 учащихся.
Задача от мудрой совы
295. На озере начали распускаться кувшинки. Каждый день количество кувшинок возрастало вдвое. На двадцатый день кувшинками заросла вся поверхность озера. На какой день половина озера была покрыта кувшинками?
Мы знаем, что каждый день количество кувшинок становилось вдвое больше (удваивалось), значит в предыдущий день в озере была половина кувшинок, но сравнению в последующим днём. То есть если на 20-й день озеро полностью заросло кувшинками, то половина от этого числа была в предыдущий день — 19-й.
Ответ: на 19- день.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
8. Какие фигуры называются равными?
1.Отрезок
прямой —
часть прямой,
ограниченная двумя точками.
Отрезок — это часть прямой линии,
которая ограничена двумя точками
(концами отрезка). У отрезка есть и
начало, и конец.
Отрезок
обозначается [A;
B] или отрезок
AB.
Точки A и B называются концами отрезка. Все остальные точки называются внутренними точками отрезка.
Расстояние между концами отрезка называют его длиной и обозначают |AB|.
Все точки отрезка лежат на одной прямой, проходящей через его концы.
2. Через две данные точки находящихся в одной плоскости можно провести одну прямую линию. Через любые две точки можно провести прямую, и притом только одну
3. Если две прямые пересекаются, то они
имеют одну точку, а если прямые
параллельные, то ни одной! Две прямые
пересекаются т.
е., имеют только одну
общую точку,. Определение
точки пересечения прямых:
точка, в которой пересекаются две прямые,
называется точкой пересечения этих
прямых.
4.Что такое луч и что такое полуплоскость? луч это часть прямой ,имеющая начало,но не имеющая конца и имеет направление
Если
провести прямую и отметить на ней точку
О ,то она разделит прямую на две части,
каждая из которых называется лучом,
исходящим из точки О (эти лучи называются
дополнительными). Точка О называется
началом луча. Лучом называется
часть прямой, состоящая из всех точек,
которые лежат по одну сторону от
фиксированной точки прямой,
и самой этой точки, называемой началом
луча.
Разные лучи одной прямой с общим началом
называются дополнительными.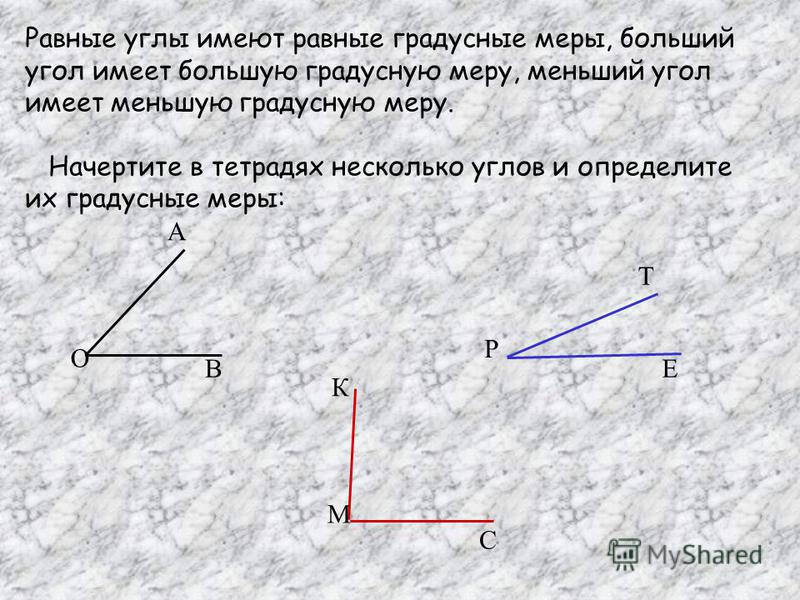
Аксиома
5.
Углом называется часть плоскости ограниченная двумя
лучами.
Сами лучи называются
сторонами угла, а общая точка, из которой
лучи выходят, называется
вершиной угла.
Угол — это геометрическая
фигура, которая образована
двумя лучами, выходящими из одной
точки. Вершина
угла — точка, из которой исходят лучи.
Сторона угла — один из этих лучей 6. Два дополнительных друг другу луча
образуют развернутый угол. Стороны
этого угла вместе составляют прямую
линию, на которой лежит вершина
развернутого угла.
7. Что означают слова: «луч делит угол на два угла»? когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов. Луч ОС делит угол АОВ пополам.
Фигуры, которые совпадают при наложении называются РАВНЫМИ . Две геометрические фигуры называются равными, если их можно совместить при наложении
9.
объясните, как сравнить два отрезка и
как сравнить 2 угла. Один
отрезок накладываешь на другой чтобы
конец первого совместился с концом
второго, если при этом другие два конца
не совместились значит отрезки не равны,
если совместились то равны. Чтобы
сравнить 2 отрезка нужно сравнить их
длины, чтобы сравнить 2 угла надо сравнить
их градусную меру, Два
угла называются равными, если их можно
совместить наложением. Чтобы установить,
равны есть два неразвернутых углы или
нет, необходимо совместить сторону
одного угла со стороной вторым таким
образом, чтобы две другие стороны
оказались по одну сторону от совмещенных
сторон. Наложить
один угол на другой угол таким образом,
чтобы у них совпали вершины и по одной
стороне, а две другие оказались по одну
сторону от совместившихся сторон. Если
вторая сторона одного угла совместиться
со второй стороной другого угла, то
данные углы равны.
(Наложи
углы так чтобы сторона одного совместилась
со стороной др., а две др. оказались по
одну сторон от совместившихся сторон.
если две др стороны совместятся то углы
полностью совместятся а значит они
равны.)
10.Какая точка называется серединой отрезка? Середина отрезка-это точка, которая делит данный отрезок на две равные части. Точка делящая отрезок пополам называется серединой отрезка.
11. Биссектрисой (от лат. bi- «двойное» и sectio «разрезание») угла называется луч, выходящий из вершины угла и проходящий через его внутреннюю область, который образует с его сторонами два равных угла. Или луч исходящий из вершины угла и делящий его на два равных угла называют биссектрисой угла.
12.Как
производится измерение отрезков. Измерить
отрезок, соизмеримый с единицей – это
значит узнать, сколько раз в нем содержится
единица или какая-нибудь доля единицы.
Измерение
отрезка осуществляется
посредством сравнения его с некоторым
отрезком, принятым за единицу.
Измерять длину отрезка
можно с помощью линейки или измерительной
ленты.
Нужно
наложить один отрезок на другой ,который
мы приняли за единицу измерения, чтобы
их концы совместились.
? 13. Как связаны между собой длины отрезков AB и CD, если: а) отрезки AB и CD равны; б) отрезок AB меньше отрезка CD?
А) длины отрезков AB и CD равны. Б) длина отрезка АВ меньше длины отрезка CD.
14.
Точка C делит отрезок AB на
два отрезка. Как связаны между собой
длины отрезков AB, AC и CB? Длина
отрезка АВ равна сумме длин отрезков AC и CB.
Чтобы найти длину отрезка AB надо сложить
длины отрезков AC и CB.
15. Что такое градус? Что показывает градусная мера угла? Углы измеряют в разных единицах измерениях. Это могут быть градусы, радианы. Чаще всего углы измеряют в градусах. (Не следует путать этот градус с мерой измерения температуры, где также используется слово «градус) . Измерение углов основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус — угол, равный 1/180 части развернутого угла . Градус — единица измерения плоских углов в геометрии. (В качестве единицы измерения геометрических углов принят градус – часть развернутого угла.).
Градусная
мера угла показывает,
сколько раз градус и его части — минута
и секунда — укладываются в данном угле,
то есть градусная мера — величина,
отражающая количество градусов, минут
и секунд между сторонами угла.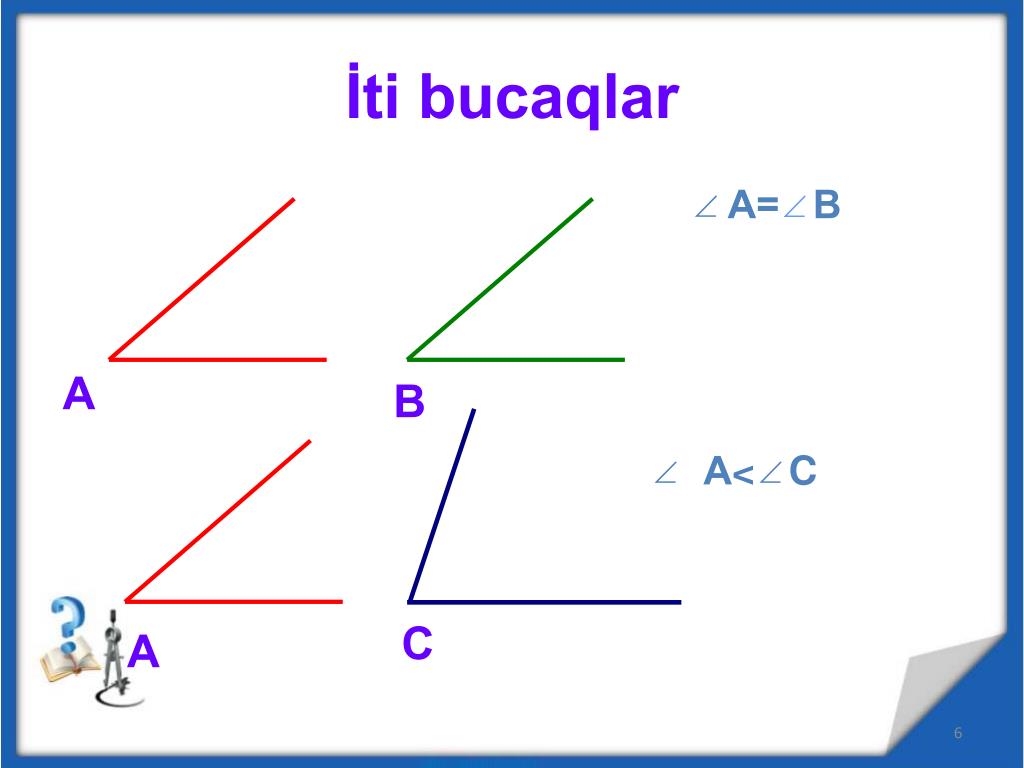
16. Какая часть градуса называется минутой, а какая – секундой? 1/60 часть градуса называется минутой, а 1/60 часть минуты — секундой. Минуты обозначают знаком «′», а секунды — знаком «″»
? 17. Как связаны между собой градусные меры двух углов, если: а) эти углы равны; б) один угол меньше другого? а) градусная мера углов одинакова. б) Градусная мера одного угла меньше градусной меры второго угла.
18. Луч OC делит
угол AOB на два угла. Как связаны
между собой градусные меры углов AOB,
AOC иCOB? Когда луч делит угол на два угла, градусная
мера всего угла равна сумме градусных
мер этих углов. Градусная
мера угла AOB равна сумме градусных мер его частей AOC иCOB.
равных углов | Определения и примеры (видео)
Автор:
Малкольм МакКинси
Проверено
Пол Маццола
Какие площади равны?
Конгруэнтные углы — это два или более угла, которые идентичны друг другу (и самим себе). Конгруэнтные углы могут быть острыми, тупыми, внешними и внутренними углами. Неважно, какой у вас угол; если угол один равен углу два, то они равны.
Конгруэнтность по геометрии означает, что одна фигура, будь то отрезок, многоугольник, угол или трехмерная фигура, идентична другой по форме и размеру. Соответственные углы на конгруэнтных фигурах всегда конгруэнтны.
Определение конгруэнтных углов
Определение конгруэнтных углов — это два или более углов с равными величинами в градусах или радианах. Конгруэнтные углы не обязательно обращены в одну сторону или построены с использованием одних и тех же фигур (лучей, прямых или отрезков).
Если измерения двух углов равны, то углы конгруэнтны.
Если угол B и угол D имеют одинаковую меру, говорят, что они конгруэнтны.
Определение конгруэнтных угловСамый простой способ измерить количество градусов в угле — это транспортир.
Символ конгруэнтных углов
Чтобы говорить и писать об углах или рисовать их, нам нужны общие символы и слова для их описания. У нас есть три символа, которые используют математики:
≅\cong ≅ означает, что одна вещь конгруэнтна другой.
∠\угол ∠ означает угол.
∡\measuredangle ∡ иногда используется для обозначения измеренного угла.
\unicodexb0\unicode{xb0} \unicodexb0, например, 45\unicodexb045\unicode{xb0} 45\unicodexb0 означает градусы.
рад означает радианы, способ измерения углов в метрической системе.
Давайте посмотрим, как мы можем описать эти два угла:
Острые конгруэнтные углы пример Можно сказать, что ∠O\угол \mathrm{O}∠O (угол O) и ∠A\угол \mathrm{A}∠A (угол A) конгруэнтны и оба равны 55°.
Мы могли бы также сказать, что математически:
Поскольку оба угла меньше, чем 90° , они также острые и образованы лучами. Сокращенное описание ∠O\angle \mathrm{O}∠O и ∠A\angle \mathrm{A}∠A определяет вершину каждого угла или точку, где встречаются лучи.
Если вам нужна мера в радианах, напишите 0,959931 рад .
Рефлексивное свойство конгруэнтности
Рефлексивное свойство конгруэнтности говорит нам, что любая геометрическая фигура конгруэнтна самой себе. Отрезок, угол, многоугольник, окружность или другая фигура заданного размера и формы самоконгруэнтны.
Углы имеют измеримую степень открытости, поэтому они имеют определенные формы и размеры. Следовательно, каждый угол равен самому себе.
Примеры конгруэнтных углов
Углы могут быть ориентированы в любом направлении на плоскости и при этом оставаться конгруэнтными. Точно так же, как ∠DOG\angle \mathrm{DOG}∠DOG и ∠CAT\angle \mathrm{CAT}∠CAT выше были конгруэнтны, но не были «выровнены» друг с другом, так и конгруэнтные углы могут появляться каким-либо образом.
на странице.
Вот рисунок с несколькими углами. Какие из этих углов равны?:
Примеры конгруэнтных угловВсе эти углы конгруэнтны.
Направление — расположение двух углов на печатной странице или экране — не имеет значения. То, как построены два угла, не имеет значения. Если меры в градусах или радианах равны, то углы конгруэнтны.
Рисование равных углов
Вы можете нарисовать конгруэнтные углы или сравнить возможные существующие конгруэнтные углы, используя циркуль, линейку и карандаш.
Один из самых простых способов изобразить конгруэнтные углы — провести две параллельные линии, пересеченные секущей. На вашем рисунке соответствующие углы будут равны. У вас будет несколько пар углов с конгруэнтностью.
Построение конгруэнтных углов с помощью параллельных линий и поперечных Еще один простой способ нарисовать конгруэнтные углы — нарисовать прямой угол или прямоугольный треугольник. Затем разделите этот прямой угол с помощью биссектрисы угла.
Если вы разделите угол точно пополам, у вас останется два конгруэнтных острых угла, каждый из которых равен 45° .
Два угла по 45° являются конгруэнтными дополнительными углами. Дополнительные углы равны, только если углы равны 45°.
Но что, если у вас есть заданный угол и вам нужно нарисовать такой же (конгруэнтный) угол рядом с ним: Вот шаги, как нарисовать конгруэнтные углы:
Нарисуйте луч справа от исходного угла, но на некотором расстоянии. Создайте конечную точку для вашего луча и назовите ее. Мы позвоним нашим Точка М .
Откройте циркуль для рисования так, чтобы точка компаса могла быть помещена в вершину существующего угла, но карандаш не проходил за нарисованные отрезки линии или лучи существующего угла.
Не меняя компаса, поместите точку компаса на Точку М на новый чертеж.
Проведите дугу из точки M вверх в пространство над вашим новым лучом.Переместите точку циркуля в точку на одном луче исходного угла, затем отрегулируйте циркуль так, чтобы карандаш касался другой точки. Здесь мы помещаем наш компас на Point K и достигаем с ним Point Y .
Не меняя компаса, переместите точку компаса в точку нового луча, здесь Point U , и поверните дугу, которая пересекается с исходной дугой.
Используйте линейку, чтобы соединить вершину, здесь Point M , с пересечением двух дуг. Вы скопировали существующий угол.
Проведите дугу из точки M вверх в пространство над вашим новым лучом.Если вам нужно сравнить два угла, на которых не указаны их градусы или радианы, вы можете аналогичным образом использовать циркуль, чтобы найти точки на обоих углах и измерить степень их открытости.
Если у вас нет под рукой транспортира, вы можете использовать найденные объекты, чтобы получить представление об измерении угла.
Квадратный край листа бумаги равен 90° . Если вы сложите этот угол так, чтобы две стороны точно выровнялись, у вас получится угол 45° .
Положение или ориентация двух углов не имеет ничего общего с их конгруэнтностью. Углы могут быть равны, если смотреть в разные стороны.
Речевые задачи на равные углы
Предположим, вам сказали, что два угла двух разных треугольников равны. Значит ли это, что треугольники должны быть равны?
Один угол измеряет 91° и состоит из двух лучей. Другой угол имеет размеры 91° , но состоит из двух отрезков. Два угла равны?
Каждый из двух углов 47° , но один из отрезка и луча, а другой из отрезка и прямой. Два угла равны?
Угол измеряет 1,8 r и . Равен ли угол чему-либо?
Точно так же, как любой угол верен себе, будучи конгруэнтным, будьте верны себе, сначала выполняя работу, прежде чем проверять ответы!
Два угла двух разных треугольников могут быть равны, но это не означает, что у вас есть конгруэнтные треугольники; они могли быть разных размеров, и их другие углы могли иметь разные размеры.
Два угла, один из которых имеет размеры 91° и состоит из двух лучей, а другой также имеет размеры 91° , но построенные из двух отрезков, конгруэнтны. Только угол имеет значение.
Два угла, каждый из которых равен 47° , равны независимо от того, как они построены.
Угол, равный 1,8 рад , равен самому себе.
Геометрия: доказательство равенства углов
Два угла равны, если они имеют одинаковую меру. Вы уже знаете, что при пересечении двух прямых образующиеся вертикальные углы равны. Вы также видели, что если A и B дополняют C, то A ~= B. Есть и другие отношения углов, которые нужно исследовать. Когда вы разоблачаете эти угловые отношения, вы устанавливаете их истинность с помощью формального доказательства.
Например, вы познакомились с понятием биссектрисы угла. Итак, получается, что биссектриса угла делит угол на два угла, каждый из которых имеет меру, равную половине меры исходного угла.
Это утверждение очень похоже на теорему 9.1, примененную к углам, а не к отрезкам. Вы можете использовать план игры, аналогичный тому, который вы использовали для доказательства теоремы 9.1, чтобы доказать эту теорему.
- Пример 3 : Докажите, что биссектриса делит угол на два угла, мера каждого из которых равна половине меры исходного угла.
- Решение : Пошагово выполните формальное доказательство.
- 1. Сформулируйте теорему.
- Теорема 9.3 : Биссектриса делит угол на два угла, каждый из которых имеет меру, равную половине меры исходного угла.
- 2. Нарисуй рисунок. Вам нужен угол и его биссектриса. На рис. 9.3 показана линия ABC, разделенная пополам линией BD.
Рисунок 9.3 ABC делится пополам на БД.
- 3. Укажите, что дано в плане вашего рисунка. Вам дана ABC, которая делится пополам на BD.
- 4. Укажите, что вы хотите доказать с помощью вашего рисунка. Вы хотите доказать, что mABD = 1 / 2 mABC.
- 5. Напишите доказательство. Вы должны подумать о том, какие определения, постулаты и теоремы вы можете использовать. Первое, что приходит на ум, это определение биссектрисы угла. Пригодится постулат сложения углов, который утверждает, что если точка D лежит внутри ABC, то mABC + mDBC = mABC. Это большая часть того, что вам нужно, чтобы приготовить это доказательство. Вам понадобится щепотка алгебры, чтобы закончить блюдо.
- 3. Укажите, что дано в плане вашего рисунка. Вам дана ABC, которая делится пополам на BD.
| Выписки | Причины | |
|---|---|---|
| 1. | BD — биссектриса угла ABC | Дано |
| 2. | АБД ~= ДБК | Определение биссектрисы угла |
| 3. | мАБД = мДБК | Определение |
| 4. | mABC + mDBC = mABC | Постулат сложения углов |
5. |