Исследовать на непрерывность функцию онлайн с подробным решением: Точки разрыва функции онлайн

Решение функций | Онлайн калькулятор

Решение функций представляется важным при решении множества инженерных и проектировочных задач по возведению тех или иных строительных объектов, изготовлению деталей, планированию грузоперевозок, технологических и иных процессов. К неотъемлемым основным атрибутам всякой функции относится область определения D(f).

При решении функций требуется выявить соответствие, при котором все числа «X» из массива (множества) области определения будут сопоставляться по определенному Правилу численному значению «Y», находящемуся в некоторой зависимости от числа «X».

Важно знать области определения корня, степенной, показательной, логарифмической, основных тригонометрических и обратных тригонометрических функций.

Калькуляторы для нахождения функций, онлайн

Область определения функции найти область определения функции онлайн	Четность и нечетность функции калькулятор предназначен для определения четности и нечетности функции
Точки пересечения графика функции с осью определения точек пересечения графика функции с осями координат	Асимптоты функции нахождение асимптот графика функции онлайн
Разложить на слагаемые методом неопределенных коэффициентов	Периодичность функции онлайн калькулятор для определения периодичности
Точки перегиба графика функции и интервалы его выпуклости и вогнутости онлайн	Построение графиков кусочно-непрерывных функций
Найти градиент функции u=f(x,y,z)	Полное исследование функции и построение графика
Промежутки знакопостоянства функции найти интервалы знакопостоянства	Найти нули функции они же точки пересечения
Найти критические точки и интервалы монотонности	Оригинал функции по ее изображению обратное преобразования Лапласа онлайн
Найти изображения функций интегральное преобразование Лапласа онлайн	Найти сумму ряда по формуле общего члена ряда
Найти экстремумы функции онлайн калькулятор	Найти максимум функции достаточно задать функцию, чтобы получить значения максимума
Найти минимум функции одно из необходимых условий наличия минимума	Точки разрыва функции функция в этих точках не является непрерывной
Построить график функции провести исследование графика функции	Решение пределов функции решать пределы любых функций онлайн
Уравнение касательной к графику функции составить и решить уравнение касательно	Тригонометрические функции найти как косинусы и синусы угла, так и решить выражения
Значения тригонометрических функций функции относятся к простейшим	Формула прямой, функции график функции
Разложение функции в ряд Тейлора раскладывается в степенной ряд по степеням	Разложение функции в ряд Маклорена любое число раз и в некоторой окрестности
Разложение функции в ряд Фурье абсолютно любую четную функцию можно разложить в ряды Фурье	Формула общего члена последовательности нахождение формулы

Select rating12345

Нет голосов

Сообщить об ошибке

Вам помог этот калькулятор?

Предложения и пожелания пишите на [email protected]

Поделитесь этим калькулятором на форуме или в сети!

Это помогает делать новые

калькуляторы.

НЕТ

Смотрите также

Решение комплексных чисел	Математический анализ	Решение интегралов	Решение неравенств	Решение уравнений
Математика	Производные функции	Графические построения	Решение логарифмов	Решение прогрессии

y x 1 x 2 1 исследовать функцию и построить

y x 1 x 2 1 исследовать функцию и построить

Вы искали y x 1 x 2 1 исследовать функцию и построить? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y x 1 x 2 1 исследовать функцию и построить график, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.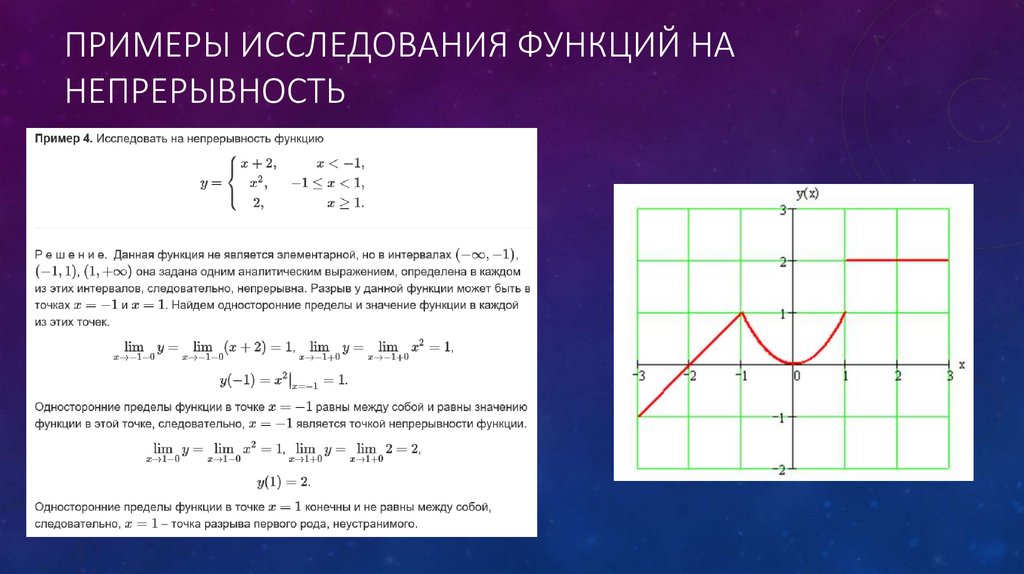

Например, «y x 1 x 2 1 исследовать функцию и построить».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как y x 1 x 2 1 исследовать функцию и построить,y x 1 x 2 1 исследовать функцию и построить график,анализ функции,анализ функции онлайн,график функции для исследования,графики для исследования функций,графики функций для исследования,исследование графика функции,исследование графика функции онлайн,исследование и построение графика функции,исследование и построение графика функции онлайн,исследование и построение графика функции с помощью производной,исследование и построение графика функции с помощью производной онлайн,исследование и построение графиков функции,исследование на непрерывность функции онлайн,исследование на непрерывность функции онлайн калькулятор,исследование функции,исследование функции y 2 x,исследование функции y x 1 x 2,исследование функции y x 2,исследование функции y x 2 x 1,исследование функции и построение графика,исследование функции и построение графика калькулятор онлайн,исследование функции и построение графика онлайн,исследование функции и построение графика онлайн калькулятор,исследование функции и построение графика онлайн с подробным решением,исследование функции и построение графика примеры решения задач,исследование функции и построение графика с помощью производной,исследование функции и построение графика с помощью производной онлайн,исследование функции и построение графика функции с помощью производной,исследование функции и построение графиков,исследование функции и построение графиков функции,исследование функции калькулятор,исследование функции на непрерывность онлайн,исследование функции на непрерывность онлайн калькулятор,исследование функции на непрерывность онлайн с подробным решением,исследование функции онлайн,исследование функции онлайн калькулятор,исследование функции онлайн калькулятор с подробным решением,исследование функции онлайн с подробным решением,исследование функции онлайн с подробным решением онлайн,исследование функции с помощью производной и построение графика,исследование функции с помощью производной и построение графика онлайн,исследование функции с помощью производной онлайн с решением,исследование функции с помощью производной построение графика функции,исследование функции с помощью производной примеры решения,исследование функций,исследование функций и построение графиков,исследование функций онлайн,исследования функции онлайн,исследовать график на непрерывность и построить график онлайн,исследовать график функции,исследовать график функции и построить график,исследовать данные функции на непрерывность и построить их графики онлайн,исследовать и построить график функции,исследовать и построить график функции онлайн с подробным решением,исследовать и построить график функции онлайн с решением,исследовать методами дифференциального исчисления и построить график,исследовать методами дифференциального исчисления и построить график онлайн,исследовать методами дифференциального исчисления функцию,исследовать методом дифференциального исчисления функцию и построить график,исследовать на монотонность функцию онлайн,исследовать на непрерывность и построить график функции онлайн,исследовать на непрерывность функции онлайн,исследовать на непрерывность функцию и построить график онлайн,исследовать на непрерывность функцию онлайн,исследовать на непрерывность функцию онлайн калькулятор,исследовать на непрерывность функцию онлайн с подробным решением,исследовать на ограниченность функцию онлайн,исследовать с помощью производной функцию и построить график,исследовать средствами дифференциального исчисления функцию онлайн,исследовать функции и построить график,исследовать функции и построить график онлайн,исследовать функции на непрерывность онлайн,исследовать функцию,исследовать функцию x y x,исследовать функцию y 2 x 2,исследовать функцию y x 1 x,исследовать функцию y x 2 1 x,исследовать функцию y x 2 1 x 2,исследовать функцию y x 2 x,исследовать функцию y x 3 x 2,исследовать функцию и построить график,исследовать функцию и построить график y x 1 x 2,исследовать функцию и построить график онлайн,исследовать функцию и построить график онлайн решение,исследовать функцию и построить график онлайн с подробным решением,исследовать функцию и построить график онлайн с подробным решением онлайн,исследовать функцию и построить график примеры решения,исследовать функцию и построить график решение онлайн калькулятор,исследовать функцию и построить график с помощью производной,исследовать функцию и построить ее график,исследовать функцию и построить ее график калькулятор онлайн,исследовать функцию и построить ее график онлайн калькулятор,исследовать функцию и построить ее график онлайн с решением,исследовать функцию методами дифференциального исчисления,исследовать функцию методом дифференциального исчисления и построить график,исследовать функцию на монотонность и экстремумы онлайн,исследовать функцию на монотонность онлайн,исследовать функцию на непрерывность и построить график онлайн,исследовать функцию на непрерывность калькулятор онлайн,исследовать функцию на непрерывность онлайн,исследовать функцию на непрерывность онлайн калькулятор,исследовать функцию на непрерывность онлайн с подробным решением,исследовать функцию на ограниченность онлайн,исследовать функцию онлайн,исследовать функцию онлайн с подробным решением,исследовать функцию по графику,исследовать функцию с помощью производной и построить график,исследовать функцию с помощью производной и построить график онлайн,исследовать функцию средствами дифференциального исчисления онлайн,исследовать функцию что значит,исследуйте и постройте график функции,исследуйте и постройте график функции у 3 2х,исследуйте на непрерывность функцию онлайн,исследуйте функции и постройте график,исследуйте функцию,исследуйте функцию y,исследуйте функцию и постройте график,исследуйте функцию и постройте ее график,исследуйте функцию и постройте ее график онлайн,исследуйте функцию на непрерывность онлайн,исследуйте функцию у f x и постройте ее график,как исследовать график функции,как исследовать функцию и построить график,как исследовать функцию и построить ее график,как построить график и исследовать функцию,калькулятор исследование функции,калькулятор исследования функции,калькулятор исследования функции и построения графика,калькулятор онлайн исследование функции на непрерывность,методами дифференциального исчисления исследовать функцию,непрерывность функции онлайн,онлайн анализ функции,онлайн исследование на непрерывность функции онлайн,онлайн исследование функции и построение графика,онлайн исследование функции и построение графика с подробным решением,онлайн исследование функции с помощью производной,онлайн исследования функции,онлайн исследовать функцию на непрерывность и построить график,онлайн калькулятор исследование функции,онлайн калькулятор исследование функции и построение графика,онлайн калькулятор исследование функции на непрерывность,онлайн полное исследование функции и построение графика,периодичность функции онлайн,полное исследование и построение графика функции,полное исследование и построение графика функции онлайн,полное исследование функции,полное исследование функции и построение графика,полное исследование функции и построение графика онлайн,полное исследование функции и построение графика онлайн решение,полное исследование функции и построение графика функции,полное исследование функции онлайн,полное исследование функции онлайн и построение графика,построение графиков и исследование функции,построение графиков функций и исследование,построение и исследование графиков функции,построить график функции используя общую схему исследования функции,построить и исследовать график функции онлайн с подробным решением,примеры исследование функции и построение графика функции,провести исследование и построить график функции,провести исследование и построить график функции онлайн,провести исследование функции и построить график,провести исследование функции и построить график онлайн,провести полное исследование и построить график функции,провести полное исследование и построить график функции онлайн калькулятор,провести полное исследование функции и построить график,провести полное исследование функции и построить график калькулятор онлайн,провести полное исследование функции и построить график онлайн калькулятор,провести полное исследование функции и построить график онлайн решение,провести полное исследование функции и построить график функции,точки пересечения графика функции с осями координат онлайн,функции исследования,что значит исследовать функцию.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и y x 1 x 2 1 исследовать функцию и построить. Просто введите задачу в окошко и нажмите «решить» здесь (например, анализ функции).

Где можно решить любую задачу по математике, а так же y x 1 x 2 1 исследовать функцию и построить Онлайн?

Решить задачу y x 1 x 2 1 исследовать функцию и построить вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Исчисление I — Непрерывность (практические задачи)

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2.9: Непрерывность

1. График \(f\left( x \right)\) приведен ниже. По этому графику определите, где функция является разрывной. Решение
2. График \(f\left( x \right)\) приведен ниже. По этому графику определите, где функция является разрывной. Решение

Для задач 3–7, использующих только свойства 1–9 из раздела «Предельные свойства», односторонние предельные свойства (при необходимости) и определение непрерывности определяют, является ли данная функция непрерывной или разрывной в указанных точках.

1. \(\displaystyle f\left( x \right) = \frac{{4x + 5}}{{92} — 3з — 10}}\)
   1. \(г = — 2\)
   2. \(г = 0\)
   3. \(г = 5\)
   Решение
2. \(g\left( x \right) = \left\{ {\begin{array}{rl}{2x}&{x < 6}\\{x - 1}&{x \ge 6}\end {массив}} \право. 2}} & {t < - 2} \\ {t + 6} & {t \ ge - 2}\end{массив}} \right.\) 9{2t}} = 0\) на \(\left[ {1,3} \right]\) Решение

Исчисление I — Непрерывность

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2.9: Целостность

В последних нескольких разделах мы использовали термин «достаточно хороший» для определения тех функций, пределы которых мы могли бы оценить, просто вычислив функцию в рассматриваемой точке. Пришло время формально определить, что мы подразумеваем под «достаточно хорошим».

Определение

Функция \(f\left( x \right)\) называется непрерывной в точке \(x = a\), если

\[\ mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left(a \right)\]

Функция называется непрерывной на отрезке \(\left[ {a,b} \right]\), если она непрерывна в каждой точке отрезка.

Обратите внимание, что это определение также неявно предполагает, что как \(f\left( a \right)\), так и \(\mathop {\lim }\limits_{x \to a} f\left( x \right)\ ) существовать. Если любой из них не существует, функция не будет непрерывной в \(х = а\).

Это определение можно превратить в следующий факт.

Факт I

Если \(f\left( x \right)\) непрерывна в \(x = a\), то 9+ }} f\left( x \right) = f\left( a \right)\]

Это точно такой же факт, который мы впервые записали, когда начали рассматривать пределы, за исключением того, что мы заменили фразу «достаточно приятно» на «непрерывно».

Приятно, наконец, узнать, что мы подразумеваем под «достаточно хорошим», однако это определение на самом деле не говорит нам, что именно означает, что функция должна быть непрерывной. Давайте рассмотрим пример, который поможет нам понять, что означает непрерывность функции.

Пример 1. Учитывая график \(f\left( x \right)\), показанный ниже, определите, является ли \(f\left( x \right)\) непрерывным в \(x = — 2\), \( х = 0\) и \(х = 3\).

Показать решение

Чтобы ответить на вопрос для каждой точки, нам нужно получить как предел в этой точке, так и значение функции в этой точке. Если они равны, то функция в этой точке непрерывна, а если не равны, то функция в этой точке непрерывна.

Первый \(x = — 2\).

\[f\left( {- 2} \right) = 2\hspace{0.5in}\mathop {\lim }\limits_{x \to — 2} f\left(x \right)\,\,\, {\mbox{не существует}}\]

Значение функции и предел не совпадают, поэтому в этой точке функция не является непрерывной. Этот вид разрыва в графе называется разрывом скачка . Разрывы скачков возникают там, где на графике есть разрыв, как на этом графике, и значения функции по обе стороны от разрыва конечны ( т.е. функция не уходит в бесконечность).

Теперь \(х = 0\).

\ [f \ влево ( 0 \ вправо) = 1 \ hspace {0,5 дюйма} \ mathop {\ lim } \ limit_ {x \ to 0} f \ влево ( x \ вправо) = 1 \]

В этой точке функция непрерывна, так как функция и предел имеют одно и то же значение.

Наконец \(x = 3\).

\ [f \ влево ( 3 \ вправо) = — 1 \ hspace {0,5 дюйма} \ mathop {\ lim } \ limit_ {x \ to 3} f \ влево ( x \ вправо) = 0 \]

В этот момент функция не является непрерывной. Этот вид разрыва называется устранимым разрывом . Устранимые разрывы — это те, где в графе есть дыра, как в данном случае.

Из этого примера мы можем быстро получить «рабочее» определение непрерывности. Функция непрерывна на отрезке, если мы можем нарисовать график от начала до конца, ни разу не взяв в руки карандаш. Граф в последнем примере имеет только два разрыва, так как есть только два места, где нам пришлось бы взяться за карандаш, рисуя его.

Другими словами, функция непрерывна, если на ее графике нет дыр и разрывов.

Для многих функций легко определить, где они не будут непрерывными. Функции не будут непрерывными там, где есть такие вещи, как деление на ноль или логарифмирование нуля. Давайте быстро рассмотрим пример определения того, где функция не является непрерывной. 2} — 2t — 15}}\] 92} — 2t — 15 = \left( {t — 5} \right)\left( {t + 3} \right) = 0\]

Значит, функция не будет непрерывной в точках \(t=-3\) и \(t=5\).

Приятным следствием преемственности является следующий факт.

Факт 2

Если \(f\left( x \right)\) непрерывно в \(x = b\) и \(\mathop {\lim }\limits_{x \to a} g\left( х \справа) = б\) тогда

\[\ mathop {\lim }\limits_{x \to a} f\left({g\left(x\right)} \right) = f\left( {\mathop {\lim }\limits_{x \ к } г\влево( х \вправо)} \вправо)\] 90} = 1\]

Другим очень хорошим следствием непрерывности является теорема о промежуточном значении.

Теорема о промежуточном значении

Предположим, что \(f\left( x \right)\) непрерывно на \(\left[ {a,b} \right]\) и пусть \(M\) будет любым числом между \(f\left( a \right)\) и \(f\left( b \right)\). Тогда существует число \(c\) такое, что

1. \(a < c < b\)
2. \(е\влево(с\вправо) = М\)

Теорема о промежуточном значении на самом деле говорит о том, что непрерывная функция будет принимать все значения между \(f\left( a \right)\) и \(f\left( b \right)\). Ниже приведен график непрерывной функции, иллюстрирующий теорему о промежуточном значении.

Как видно из этого изображения, если мы выберем любое значение \(M\), то есть между значением \(f\left( a \right)\) и значением \(f\left( b \right)\) и проведите из этой точки прямую линию, которая будет пересекаться с графиком хотя бы в одной точке. Другими словами, где-то между \(a\) и \(b\) функция примет значение \(M\). Кроме того, как показано на рисунке, функция может принимать значение более чем в одном месте.

Также важно отметить, что теорема о промежуточном значении говорит только о том, что функция будет принимать значение \(M\) где-то между \(a\) и \(b\). Не сказано, каким именно будет это значение. Это только говорит о том, что он существует.

Итак, теорема о промежуточном значении говорит нам, что функция будет принимать значение \(M\) где-то между \(a\) и \(b\), но она не говорит нам, где она примет значение или говорит ли он нам, сколько раз он будет принимать значение. 2} — 10x + 5\) имеет корень где-то в интервале \(\left[ { — 1, 2} \справа]\).

Показать решение

На самом деле мы спрашиваем здесь, примет ли функция значение

или нет. \[р\влево( х \вправо) = 0\]

где-то между -1 и 2. Другими словами, мы хотим показать, что существует число \(c\) такое, что \(- 1 < c < 2\) и \(p\left( c \right) = 0\). Однако если мы определим \(M = 0\) и признаем, что \(a = -1\) и \(b = 2\), мы увидим, что эти два условия на \(c\) являются в точности выводами промежуточного Теорема о ценности.

Итак, эта задача построена на использовании теоремы о промежуточном значении, и на самом деле все, что нам нужно сделать, это показать, что функция непрерывна и что \(M = 0\) находится между \(p\left( { — 1} \right)\) и \(p\left( 2 \right)\) ( т.е. \(p\left( { — 1} \right) < 0 < p\left( 2 \right)\ ) или \(p\left( 2 \right) < 0 < p\left( { - 1} \right)\) и мы закончим.

Для этого все, что нам нужно сделать, это вычислить,

\[p\left( { — 1} \right) = 8\hspace{0.5in}\hspace{0.25in}p\left( 2 \right) = — 19\]

Итак, имеем

\[ — 19 = p\влево( 2 \вправо) < 0 < p\влево( { - 1} \вправо) = 8\]

Следовательно, \(M = 0\) находится между \(p\left( { — 1} \right)\) и \(p\left( 2 \right)\), а поскольку \(p\left( x \ right)\) — полином, он непрерывен везде и, в частности, непрерывен на отрезке \([-1,2]\). Таким образом, по теореме о промежуточном значении должно существовать число \(-1

\[р\влево( с \вправо) = 0\]

Следовательно, у многочлена есть корень между -1 и 2.

Для полноты картины вот график, показывающий корень, существование которого мы только что доказали. Обратите внимание, что мы использовали компьютерную программу, чтобы фактически найти корень, и что теорема о промежуточном значении не сказала нам, что это за значение.

Давайте рассмотрим еще один пример теоремы о промежуточном значении.

92}}}{2}} \right)\) принимает следующие значения в интервале \([0,5]\).

1. \(f\left( x \right) = 10\)?
2. Соответствует ли \(f\left( x \right) = — 10\)?

Показать все решения Скрыть все решения

Показать обсуждение

Итак, как и в предыдущем примере, нас просят определить, если возможно, принимает ли функция одно из двух значений выше в интервале [0,5]. Во-первых, давайте заметим, что это непрерывная функция, и поэтому мы знаем, что можем использовать теорему о промежуточном значении для решения этой проблемы.

Теперь для каждой части мы допустим, что \(M\) будет заданным значением для этой части, а затем нам нужно будет показать, что \(M\) находится между \(f\left( 0 \right)\) и \(f\left( 5 \right)\). Если это так, то мы можем использовать теорему о промежуточном значении, чтобы доказать, что функция будет принимать заданное значение.

Итак, поскольку нам понадобятся две оценки функций для каждой части, давайте приведем их здесь,

\[f\влево( 0 \вправо) = 2,8224\hspace{0,5 дюйма}\hspace{0,25 дюйма}f\влево( 5 \вправо) = 19.7436\]

Теперь давайте рассмотрим каждую часть.

a Соответствует ли \(f\left( x \right) = 10\)? Показать решение

Хорошо, в этом случае мы определим \(M = 10\) и увидим, что

\[f\влево( 0 \вправо) = 2,8224 < 10 < 19,7436 = f\влево( 5 \вправо)\]

Итак, по теореме о промежуточном значении должно быть число \(0 \le c \le 5\) такое, что

\[е\влево(с\вправо) = 10\]

b Соответствует ли \(f\left( x \right) = — 10\)? Показать решение

В этой части мы определим \(M = — 10\). Теперь у нас есть проблема. В этой части \(M\) не живет между \(f\left( 0 \right)\) и \(f\left( 5 \right)\).