матрица / Сложение матриц разной размерности / Математика
|
Можно ли складывать матрицы 3х3 и 4х4? Если да, то как? матрица задан 16 Янв ’13 21:43 Dikaz изменен 16 Янв ’13 23:10 ХэшКод |
старыеновыеценные
|
Нельзя. ссылка отвечен 16 Янв ’13 21:56 DocentI изменен 16 Янв ’13 21:57 |
В алгебре. Хотя Вы, конечно, можете придумать такое сложение. Например, в статистическом языке R можно складывать векторы (а, значит, и матрицы) разной длины
Формально — нельзя, но практически такая необходимость иногда возникает. В этом случае матрицы приводятся к большей размерности добавлением нулей у матрицы меньшей размерности. T +В ??? ссылка отвечен 11 Сен ’13 13:51 Анннннннннннааа изменен 11 Сен ’13 13:52 |
|
Ребят, если кому нужно есть онлайн сложение матриц https://algebra24.ru/slozhenie-matric ссылка отвечен 8 Мар ’16 0:43  org/Person»>narmada-7 |
Ваш ответ
Если вы не нашли ответ, задайте вопрос.7.1.2. Сложение и вычитание MathCAD 12 руководство
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android.
Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1035 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- База знаний /
- CAD / CAM /
- MathCAD 12
- Линейная алгебра
- 7.1. Простейшие матричные операции
- 7.1.1. Транспонирование
- 7.1.2. Сложение и вычитание
- 7.1.3. Умножение
- 7.2. Векторная алгебра
- 7.2.1. Модуль вектора
- 7.
2.2. Скалярное произведение - 7.2.3. Векторное произведение
- 7.2.4. Векторизация массива
- 7.3. Вычисление определителей и обращение квадратных матриц
- 7.3.1. Определитель квадратной матрицы
- 7.3.2. Ранг матрицы
- 7.3.3. Обращение квадратной матрицы
- 7.3.4. Возведение квадратной матрицы в степень
- 7.3.5. Матричные нормы
- 7.3.6. Число обусловленности квадратной матрицы
- 7.4. Вспомогательные матричные функции
- 7.4.1. Автоматическая генерация матриц
- 7.4.2. Разбиение и слияние матриц
- 7.4.3. Сортировка элементов матриц
- 7.4.4. Вывод размера матрицы
2.2. Скалярное произведениеВ Mathcad можно как складывать матрицы, так и вычитать их друг из друга. Для этих операторов применяются стандартные символы «+» или «—» соответственно. Матрицы должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке.
Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых (листинг 7.2).
Результат унарной операции смены знака матрицы эквивалентен смене знака всех ее элементов. Для того чтобы изменить знак матрицы, достаточно ввести перед ней знак минуса, как перед обычным числом (нижняя строка листинга 7.2).
Листинг 7.2. Сложение, вычитание и смена знака матриц
Кроме сложения матриц Mathcad поддерживает операцию сложения матрицы со скаляром (листинг 7.3). Каждый элемент результирующей матрицы равен сумме соответствующего элемента исходной матрицы и скалярной величины.
Листинг 7.3. Сложение матрицы со скалярной величиной
Иногда бывает нужно вычислить сумму всех элементов вектора или матрицы. Для этого существует вспомогательный оператор (листинг 7.4, первая и вторая строки соответственно), задаваемый кнопкой Vector Sum (Суммирование элементов вектора) на панели
Matrix (Матрица) или сочетанием клавиш <Ctrl>+<4>.
В том же листинге 7.4 (снизу) показано применение операции суммирования диагональных элементов квадратной матрицы. Эту сумму называют следом (trace) матрицы. Данная операция организована в виде встроенной функции
tr:
- tr (А) — след квадратной матрицы А.
Листинг 7.4. Суммирование элементов и вычисление следа матрицы
Нравится
Твитнуть
Теги MathCad САПР
Сюжеты MathCad
Глава 1 Основы работы с системой Mathcad 11
9947 0
Глава 10 Работа с информационными ресурсами Mathcad 11
6966 0
Глава 2 Работа с файлами Mathcad 11
12483 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.
ru обязательна. 0.2167 s
Калькулятор сложения матриц — 2 3 Сумма
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Добавление матрицы
Инструмент для вычисления сложения матриц в компьютерной алгебре. Сумма N матриц обычно получается путем суммирования элементов каждой матрицы.
Результаты
Добавление матрицы — dCode
Метки: Матрица
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах для решения любых задач. день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !
Добавление 2 матриц
Matrix M1 Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Добавление 3-х матриц
Matrix M3 Загрузка.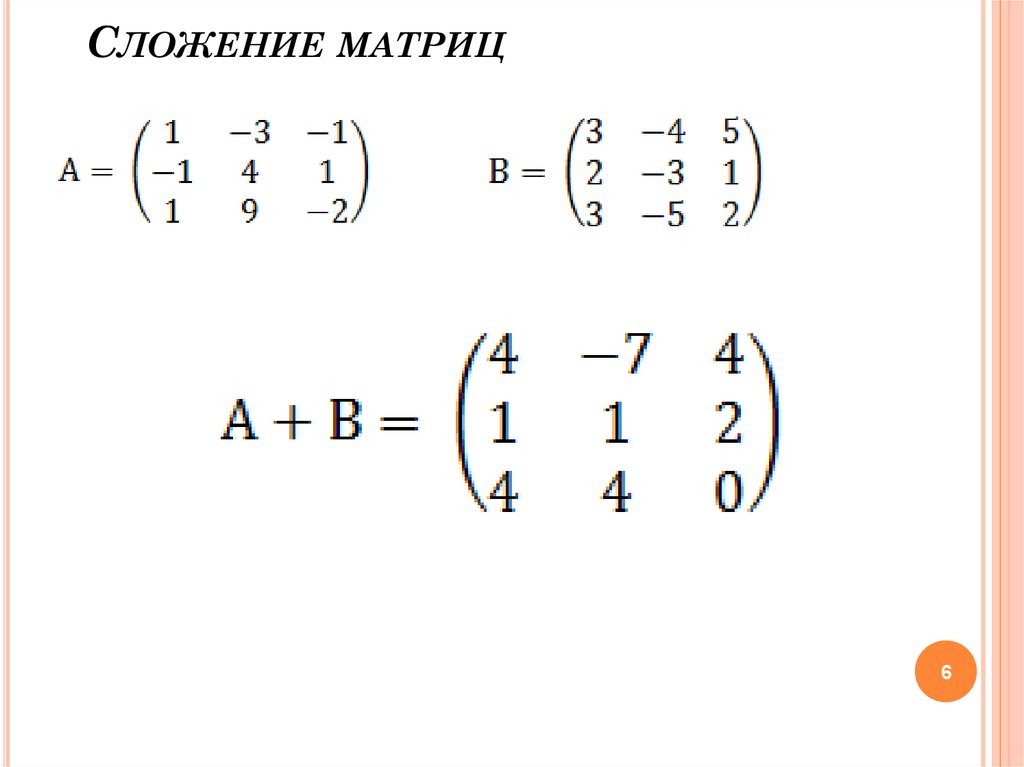
..
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
См. также: Калькулятор матриц — прямая сумма матриц
Ответы на вопросы (FAQ)
Что такое сложение матриц? (Определение)
Добавление 2-х матриц отмечено $ M_1 + M_2 $ с $ M_1=[a_{ij}] $ ($ m $ строк и $ n $ столбцов, с $ m = n $ для квадратной матрицы) и $M_2=[b_{ij}]$ (одинакового размера: $m$ строк и $n$ столбцов).
Сумма этих двух матриц $ M_1 + M_2 = [c_{ij}] $ является матрицей одинакового размера, т.е. $ m $ строк и $ n $ столбцов, где: $$ \forall i, j \quad c_{ij} = a_{ij}+b_{ij} $$
Важное правило: Сложение матриц (матрица A плюс матрица B) может выполняться только с 2 матрицами одинаковой формы/размера/размера (2×2, 2×3, 3×2, 3×3 и т.д.).
Как сложить 2 матрицы?
Добавление матрицы выполняется поэлементно
Пример: $$ \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} + \begin{bmatrix} 7 & 8 \\ 9 и 10 \\ 11 и 12 \end{bmatrix} = \begin{bmatrix} 1+7 и 2+8 \\ 3+9 и 4+10 \\ 5+11 и 6+12 \end{ bmatrix} = \begin{bmatrix} 8 и 10 \\ 12 и 14 \\ 16 и 18 \end{bmatrix} $$
Для всех матриц A и B одинакового размера A+B = B+A.
Как сложить 2 матрицы в Excel?
Сложение матриц в Excel можно осуществить путем добавления элементов с одинаковыми координатами в каждую матрицу.
Как сложить 2 матрицы разного размера?
Операция сложения (или суммирования) для матриц может быть выполнена только с матрицами одинакового размера (возможны все размеры, при условии, что они абсолютно одинаковы: 3×4, 4×3, 4×4, 5×5 и т. д.). Тем не менее, существует прямая операция суммирования, которую можно использовать с матрицами разного размера.
Как добавить скаляр к матрице?
Операция прибавления скалярного числа к матрице $[A]+b$ не определена, но иногда подразумевает операцию $[A]+[I]b$ с $I$ единичной матрицей размера, совместимого с A.
Исходный код
dCode сохраняет за собой право собственности на исходный код Matrix Addition. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Дополнение к матрице», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Дополнение к матрице».
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Добавление матрицы» или любых ее результатов разрешено, если вы цитируете dCode!
Ссылка на источник (библиография):
Matrix Addition на dCode.fr [онлайн-сайт], получено 02 января 2023 г., https://www.dcode.fr/matrix-addition
Сводка
- Сложение двух матриц
- Что такое сложение матриц? (Определение)
- Как сложить 2 матрицы?
- Как сложить 2 матрицы в Excel?
- Как сложить 2 матрицы разного размера?
- Как добавить скаляр к матрице?
Similar pages
- Matrix Direct Sum
- Matrix Calculator
- Matrix Subtraction
- Minors of a Matrix
- Characteristic Polynomial of a Matrix
- Complex Conjugate Matrix
- Transpose of a Matrix
- DCODE’S TOOLS LIST
Опора
- Paypal
- Patreon
- More
Forum/Help
Keywords
addition,sum,plus,matrix,2×2,2×3,3×2,3×3,3×4,4×3,4×4,5×5
Links
▲
Сложение и вычитание матриц — Уроки Византа
Матрицы можно складывать
вместе или вычитать друг из друга, только если они имеют одинаковый размер, что означает
, что они должны иметь одинаковое количество строк и столбцов.
Это потому, что когда
, добавляя или вычитая матрицы, операторы работают с соответствующими элементами матриц
, поэтому необходим одинаковый размер.
Сложение матриц принимает следующую форму, как показано на этих двух матрицах A
и B , обе имеют размер 2 x 2
Каждая запись в матрицах A и B добавляется к соответствующему аналогу
в другой матрице.
Используя обозначение матрицы i,j , упомянутое ранее, вышеприведенное можно обобщить
следующим образом:
То же самое касается вычитания матрицы:
Сложение матриц является коммутативным, что означает, что для двух матриц A и
B :
Лучший способ привыкнуть к матричному сложению и вычитанию — попробовать как можно больше примеров
, как вы можете, и в конечном итоге это станет второй натурой.
Вот несколько проработанных примеров,
начиная с простых.
Примеры сложения и вычитания матриц
Пример 1: Даны матрицы A и B , найти их сумму
решение:
Пример 2: Найдите C + А , учитывая, что
решение:
что математически невозможно, так как матрицы разного размера; A
— это матрица 2 x 3, а C — это матрица 3 x 2, поэтому их нельзя складывать
или вычитать.
Пример 3: Решите для x,y,z , учитывая, что матрица A = матрица B
Этап 1
Мы уже видели, что если A = B , то соответствующие ( i,j )
записи должны быть равны.