Системы менеджмента качества требования. Развитие стандарта ISO 9001
Операционная система. Назначение и основные функции
Adobe Photoshop
AutoCAD история и возможности
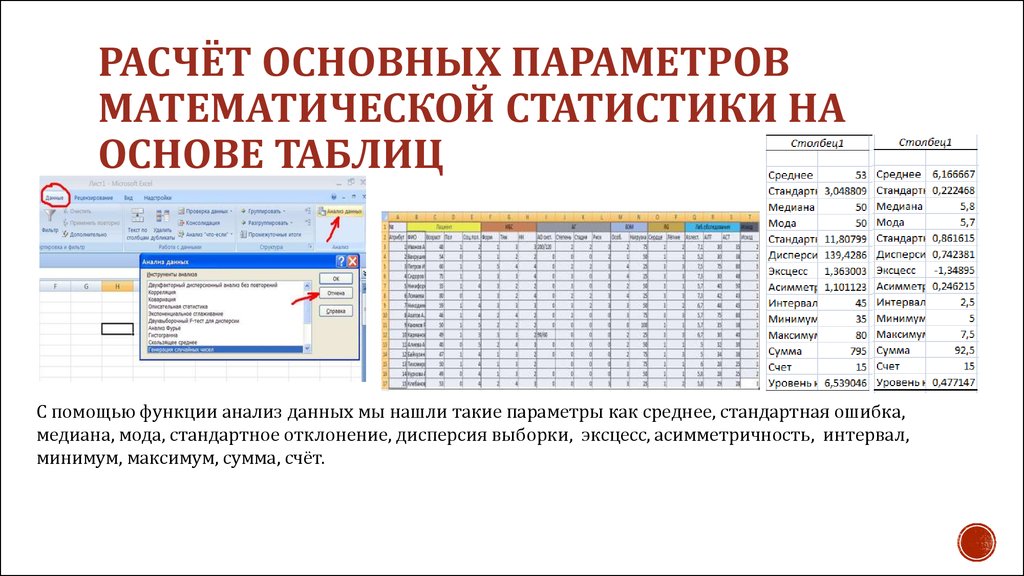
Microsoft Excel
Облачные технологии
Корпорация Microsoft и ее особенности
Веб-дизайн
Тема 2. Пакеты прикладных программ
1. Курсовая работа на тему «Программный продукт «Калькулятор — статистика»
разработчик: студентка группы 4Пз Романова С. А. руководитель: Михайлова Е.А.
2. Актуальность
Для автоматизации процесса расчета статистических данных в современном обществе используют компьютерные средства – программы, которые позволяют одним нажатием клавиши сделать соответствующий расчет. Более популярным и простым инструментарием стали программные приложения: стандартный калькулятор операционной системы Windows в режиме статистика; различные он — лайн калькуляторы в сети интернет; специализированное программное обеспечение (программы Mathcad, Sofa, Excel, OpenEpi и другие). Вследствие вышеизложенного разработка программного приложения «Калькулятор статистика» является актуальной.
3. Цель и задачи
Цель курсовой работы – разработать программное приложение «Калькулятор — статистика». В соответствии с целью были поставлены следующие задачи: анализ предметной области; подбор основной и специализированной литературы; разработка технического задания; построение алгоритма программного приложения; реализация программного приложения на ПК; тестирование приложения; написание инструкции по эксплуатации программного продукта.
4. Объект и предмет исследования
Объектом исследования является программное приложение «Калькулятор — статистика». Предметом – разработка и тестирование программного приложения
5. Этапы работы:
изучение рынка различных программных продуктов; постановка задачи; выбор средств для реализации; создание структуры данных; создание функциональной части программного продукта; подготовка описания программного продукта; презентация программного продукта.
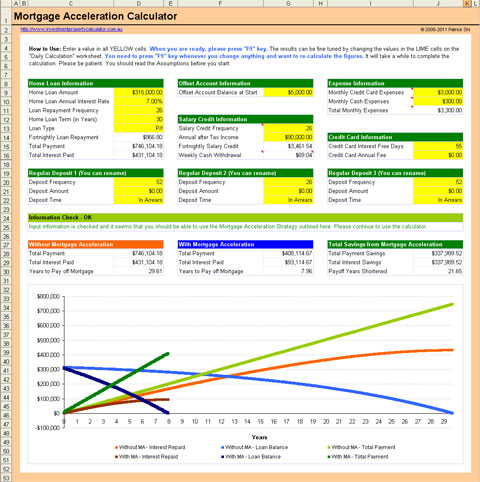
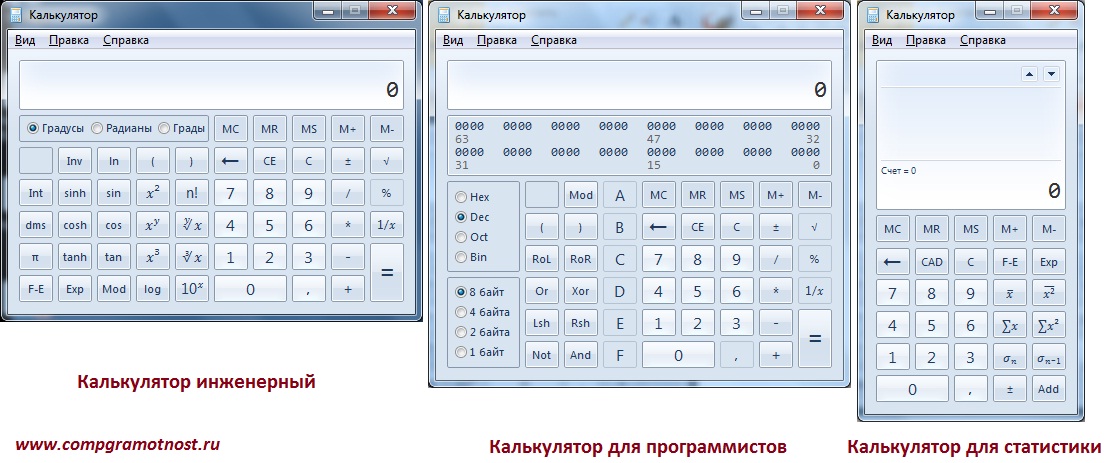
6. Главное окно программного приложения
7. Заключение
В результате выполнения курсовой работы было разработано программное приложение «Калькулятор — статистика», которое выполняет следующие функции: вычисление среднеквадратичного отклонения; заполнение среднеквадратичного отклонения; вычисление суммы значений; вычисление суммы квадратов; значений вычисление среднего значения; вычисление среднеквадратичного значения.
8. Заключение
Интерфейс программы «Калькулятор статистика» дружелюбный и удобный для пользователя. Программа «Калькулятор — статистика» является приложением начального уровня и обладает возможностью дальнейшего
English
Русский
Правила
Риск посчитает калькулятор. Как в Москве изменилась статистика по пожарам | Москва
Инна Алейникова
Примерное время чтения: 3 минуты
466
Еженедельник «Аргументы и Факты» № 29.
Предчувствие еды 20/07/2022
За 5 лет инспекторы Госпожнадзора провели в Москве 7 млн профилактических мероприятий. Вот почему эта команда пожарных выезжала на тушение реже, чем было раньше. АГН Москва
В столице стало меньше пожаров и пострадавших от них горожан. Свою лепту в улучшение статистики вносят пожарные инспекторы.
Штраф за хлам в коридоре
К тому, что прихода инспекторов с проверкой частенько ждут без энтузиазма, начальник отдела ГУ МЧС России по Москве, полковник внутренней службы Александр Бобров относится с пониманием: «Сегодня просто так прийти на объект невозможно: о проверках собственник знает заранее и может подготовиться. Кто-то воспринимает наше посещение с негативной стороны, а кто-то, наоборот, благодарен. Ведь мы помогаем вскрыть нарушения, позволяющие обеспечить безопасность людей».
В надзорной деятельности основным новшеством последнего времени считается риск-ориентированный подход. Иными словами, проведение того или иного контрольно-надзорного мероприятия и периодичность прихода инспекторов планируются, исходя из категории риска, присвоенной зданию. У жилых домов он один. У школ, детских садов, перинатальных центров и прочих объектов социальной направленности – другой и т. д. Любой собственник может сам посмотреть категорию риска, воспользовавшись для этого специальным калькулятором на официальном сайте МЧС.
Многоквартирным домам присваивается средняя или низкая категория риска. «Квартиры инспектор не проверяет, потому что по Конституции РФ они являются неприкосновенными, – объяснил полковник. – Мы смотрим места общего пользования. Оцениваем захламление коридоров, лифтовых холлов, содержание путей эвакуации, работоспособность систем противопожарной защиты, укомплектованность пожарных кранов и т. п. Все проверки проводятся в отношении обслуживающей данный дом организации (например, «Жилищника»), и предписания выписываются ей, а не жителям, потому что за места общего пользования отвечает юрлицо. Соответственно в товариществе собственников жилья предписания оформляются на адрес ТСЖ. Разделение объектов на категории позволило нам уйти от тотальных проверок всех объектов и сосредоточить силы там, где это действительно необходимо, – на объектах чрезвычайно высокого, высокого и значительного риска».
В Москве за последние 5 лет инженерно-инспекторские органы МЧС России, проведя более 41 тыс. проверок, выявили 273 тыс. нарушений требований пожарной безопасности. К административной ответственности привлекли свыше 43 тыс. правонарушителей.
Легче предупредить, чем потушить
В понедельник органы Государственного пожарного надзора МЧС России отметили 95-летие. К системной работе, отражённой в народной мудрости «пожар легче предупредить, чем потушить», в России пришли не сразу. Первые контролирующие органы – местные пожарные комитеты – были созданы в 1918 г. На них возложили составление правил, инструкций пожарной безопасности, надзор за соблюдением требований законов и распоряжений, привлечение к ответственности виновных в нарушениях, ведение пожарной статистики.
Тогда зародились и первые учебные заведения для населения – школы и курсы пожарной охраны. Официальной же датой создания Госпожнадзора считается июль 1927 г.
Штатная численность надзорных органов Москвы составляет более 650 человек. Легендарных сотрудников прошлого и настоящего, моменты их рабочих дней можно увидеть на фотовыставках, которые по 24 июля работают в «Музеоне», Измайловском и Перовском парках. С 2017 по 2021 г. число пожаров в столице снизилось на четверть – до 7413 случаев.
В Госпожнадзор принимают на службу не только окончивших профильный вуз. Приветствуются обладатели дипломов о высшем строительном и юридическом образовании. Необходимые дополнительные знания они получают в учебном центре, а закрепляют их на рабочем месте под руководством наставника.
Госпожнадзор
Следующий материал
Новости СМИ2
Калькуляторы статистических методов
Главная > Калькуляторы статистических методов
Уровень образования
Средняя школа, гимназия и колледж
Назначение программы
Предоставляйте пошаговые решения ваших задач с помощью онлайн-калькуляторов (онлайн-решателей)
Источник проблемы
Ваш учебник и т. д.
1.1 Несгруппированные данные
85,96,76,108,85,80,100,85,70,95
1. Среднее значение, медиана и мода для негруппированных данных 2. Квартили, децили и процентили для негруппированных данных 3. Дисперсия населения, стандартное отклонение и коэффициент вариации для негруппированных данных 4. Выборочная дисперсия, стандартное отклонение и коэффициент вариации для негруппированных данных 5. Асимметрия населения, эксцесс для негруппированных данных 6. Образцовая асимметрия, эксцесс для негруппированных данных 7. Среднее геометрическое, среднее гармоническое для негруппированных данных 8. Среднее отклонение, Квартильное отклонение, Децильное отклонение, Процентильное отклонение для негруппированных данных 9.
Пять цифр для негруппированных данных 10. Графики Box and Whisker для негруппированных данных 11. Построить негруппированную таблицу частотного распределения 12. Построить сгруппированную таблицу частотного распределения 13. Максимум, минимум для разгруппированных данных 14. Сумма, длина для несгруппированных данных 15. Диапазон, средний диапазон для разгруппированных данных 16. График стебля и листа для негруппированных данных 17. По возрастанию, по убыванию для разгруппированных данных
1.2 Сгруппированные данные
Класс
50-55
45-50
40-45
35-40
30-35
35-30
20-25
f
25
30
40
45
80
110
170
1. Среднее значение, медиана и мода для сгруппированных данных 2. Квартили, децили и процентили для сгруппированных данных 3. Дисперсия населения, стандартное отклонение и коэффициент вариации для сгруппированных данных 4. Выборочная дисперсия, стандартное отклонение и коэффициент вариации для сгруппированных данных 5. Асимметрия населения, эксцесс для сгруппированных данных 6. Образцовая асимметрия, эксцесс для сгруппированных данных 7. Среднее геометрическое, среднее гармоническое для сгруппированных данных 8. Среднее отклонение, квартильное отклонение, децильное отклонение, процентильное отклонение для сгруппированных данных 9. Сводка из пяти чисел для сгруппированных данных
10. Графики Box and Whisker для сгруппированных данных 11. Режим с использованием метода группировки для сгруппированных данных
1.3 Смешанные данные
Класс
1
2
5
6-10
10-20
20-30
30-50
50-70
70-1007
9000
F
70-1007
F
7
70-1007
F
70-1007
10110 F.
70-1007
10110.
3
4
10
23
20
20
15
3
2
1. Среднее значение, медиана и мода для смешанных данных 2. Дисперсия населения, стандартное отклонение и коэффициент вариации для смешанных данных 3. Выборочная дисперсия, стандартное отклонение и коэффициент вариации для смешанных данных
2. Отсутствует частота для
1. Разгруппированные данные
Среднее значение наблюдений 18,14,15,19,15,а,12,15,16 равно 16. Найдите недостающую частоту `a`
2. Сгруппированные данные
1. Среднее значение следующего распределения равно 18,1. Найдите 1 недостающую частоту.
Класс
5 — 10
10 — 15
15 — 20
20 — 25
25 — 30
30 — 35
F
11 0007
20 0007
35
20
110007
200007
35
20
110007
200007
35
20
110007
200007
35 9007
20
110007
a
6
2. Среднее значение частотного распределения 40 человек равно 16,5. Найдите 2 недостающие частоты.
Класс
0–5
5–10
10–15
15–20
20 — 25
25 — 30
30 — 35
ф
1
7
11
7 90?
?
4
2
3. Медиана и мода частотного распределения 230 человек составляют 33,50 и 34 соответственно. Найдите 3 недостающие частоты.
Класс
0 — 10
10 — 20
20 — 30
30 — 40
40 — 50
90 -60 9
60 — 70
f
4
16
?
?
?
6
4
3. Проблема со статистикой
Среднее значение 10 наблюдений равно 35 . При вычислении среднего два наблюдения были ошибочно приняты за 35 вместо 25 и за 30 вместо 45 . Найдите правильное среднее.
4. График статистики
1. Гистограмма 2. Многоугольник частот 3. Кривая частоты 4. Совокупная частотная кривая меньше типа 5. Кривая кумулятивной частоты больше, чем тип
Ниже приведено частотное распределение оценок, полученных 100 учащимися за контрольную по математике, набравшей 50 баллов. Нарисуйте гистограмму, полигон частот, кривую частоты, кривую кумулятивной частоты типа «меньше» и кривую кумулятивной частоты «больше» данных.
Найти среднее арифметическое, среднее геометрическое, среднее гармоническое для разгруппированных данных, таких как 2,3,4,5,6
2. Найдите X из среднего арифметического, среднего геометрического, среднего гармонического
Найдите X, где среднее арифметическое = 3,5 для разгруппированных данных 2,3,X,5
3. Найдите среднее значение, медиану или моду из двух других
Найти режим, когда среднее = 3 и медиана = 4
7. Среднее отклонение от среднего для
1. Разгруппированные данные
85,96,76,108,85,80,100,85,70,95
2. Сгруппированные данные
Рассчитайте среднее отклонение от среднего для следующего распределения.
Марк
0-10
10-20
20-30
30-40
40-50
50-60
60-70
№ из студента
60-70
№ из студента
60-70
№ из студента
60-70
.
6
5
8
15
7
6
3
9. Коэффициент ранговой корреляции Спирмена (RHO)
1. Десять участников конкурса оцениваются двумя судьями следующим образом.
x
1
6
5
10
3
2
4
9
7
8
0103
Y
6
4
8
1
2
3
10
5 9007
7
2. Получите коэффициент ранговой корреляции для следующих данных.
X
68
64
75
50
64
80
75
40
55
64
Y
62
58
68
45
81
60
68
48
50
70
10. Уравнения линии регрессии
1. Найдите уравнение двух линий регрессии, также оцените
Найдите уравнение уравнений линии регрессии и коэффициент корреляции из следующих данных.
Х
28
41
40
38
35
33
46
32
36
33
Y
30
34
31
34
30
26
28
31
26
31
2. Найдите коэффициент корреляции из двух уравнений линии регрессии.
Уравнение регрессии двух переменных: 5y = 9х — 22 и 20х = 9у + 350.
Найдите средние x и y. Также найдите значение р.
3. Найдите уравнения линии регрессии, используя среднее значение, стандартное отклонение и корреляционную корреляцию (r)
По результатам экспертизы получена следующая информация
Баллы по статистике
Баллы по математике
Среднее
39,5
47,5 S
9 0,010089 0,010089
10,8
92` = 8822
13. Дисперсионный анализ — дисперсионный анализ
1. Односторонний дисперсионный анализ 2. Двусторонний дисперсионный анализ
Решите с помощью метода One-way ANOVA
Observation
A
B
C
D
1
421
325
320
362
2
118
102
122
56
3
591
518
552
509
4
14
26
20
2
5
116
14
26
46
Поделитесь этим решением или страницей с друзьями.
Калькуляторы — Select Statistical Consultants
Мы собрали несколько бесплатных статистических онлайн-калькуляторов, которые помогут вам самостоятельно выполнять базовые статистические расчеты. Мы решили собрать несколько калькуляторов для типов анализа, которые мы обычно проводим для наших клиентов. Со временем мы добавим к этим онлайн-калькуляторам другие типы статистических расчетов и тестов.
Если у вас есть предложения по новым калькуляторам, которые вы хотели бы, чтобы мы создали, пожалуйста.
Калькуляторы объема выборки
Калькулятор доверительного интервала
Основные статистические тесты
Калькуляторы размера выборки
В Select нас часто просят помочь нашим клиентам рассчитать размеры выборки, необходимые для конкретного опроса или исследования, которое они планируют провести. Для расчета размера выборки часто можно использовать стандартные формулы, но они обычно требуют определенного объема информации, которой вы должны располагать до начала исследования, испытания или опроса.
Во-первых, вы должны знать, как вы собираетесь собирать данные (также известный как план исследования) и что именно вы пытаетесь оценить. Например, вы можете захотеть оценить долю конкретной характеристики в интересующей популяции или оценить разницу в среднем эффекте между экспериментальной и контрольной группами.
Часто вам также потребуется начальная оценка пропорции или средней разницы между двумя группами, которую вы ожидаете увидеть, вместе с оценкой ее изменчивости. Это часто можно получить из предыдущих исследований или путем проведения небольшого пилотного исследования.
Когда у вас есть вся необходимая информация, рассчитать требуемый размер выборки часто бывает довольно просто. Чтобы вы могли сами убедиться, как можно выполнить простые расчеты размера выборки, мы собрали следующую небольшую подборку онлайн-калькуляторов размера выборки. Все это уместно, если вы собрали данные с помощью простой случайной выборки.
Оценка доли населения;
Оценка среднего значения генеральной совокупности;
Оценка отношения шансов;
Сравнение двух пропорций; и
Сравнение двух средних.
Иногда ваше исследование может не соответствовать этим стандартным калькуляторам. Например, если вы оцениваете пропорцию, которая, как вы ожидаете, будет близка к 0 или 1, или если у вас сложный план выборки, например, со стратификацией или кластеризацией. В этом случае есть альтернативные методы, которые можно использовать, и вы можете
Калькуляторы доверительных интервалов
При сообщении точечной оценки по выборке данных (например, при оценке среднего значения генеральной совокупности) обычно рекомендуется указать доверительный интервал, который количественно определяет неопределенность, связанную с оценкой. Интервал рассчитывается на основе выборки данных и представляет собой диапазон значений, в котором мы оцениваем точечную оценку с учетом нашего уровня достоверности.
Для расчета доверительного интервала сначала потребуется точечная оценка и, в некоторых случаях, ее стандартное отклонение. Другой важной частью информации является требуемый уровень достоверности, то есть вероятность того, что доверительный интервал содержит истинную точечную оценку. Например, если мы оцениваем доверительный интервал с учетом оценки среднего значения генеральной совокупности, а уровень достоверности равен 95%, если бы исследование повторялось и каждый раз рассчитывался диапазон, можно было бы ожидать, что истинное значение будет находиться в пределах этих диапазонов в 95% случаев. Чем выше уровень достоверности, тем больше вы можете быть уверены, что интервал содержит истинное среднее значение.
Основные расчеты доверительного интервала остаются неизменными независимо от вашей точечной оценки. Чтобы продемонстрировать это, мы собрали следующую небольшую подборку онлайн-калькуляторов доверительных интервалов. Помните, что вы можете рассчитать доверительные интервалы для многих других оценок, таких как медианы, разности или квантили.
Доля населения;
Средняя численность населения; и
Отношение шансов.
Базовые статистические тесты
Существует огромное количество доступных статистических тестов, и мы разработаем несколько наиболее распространенных из них, которые с небольшим руководством можно легко применять в простых ситуациях.
Иными словами, проведение того или иного контрольно-надзорного мероприятия и периодичность прихода инспекторов планируются, исходя из категории риска, присвоенной зданию. У жилых домов он один. У школ, детских садов, перинатальных центров и прочих объектов социальной направленности – другой и т. д. Любой собственник может сам посмотреть категорию риска, воспользовавшись для этого специальным калькулятором на официальном сайте МЧС.
Соответственно в товариществе собственников жилья предписания оформляются на адрес ТСЖ. Разделение объектов на категории позволило нам уйти от тотальных проверок всех объектов и сосредоточить силы там, где это действительно необходимо, – на объектах чрезвычайно высокого, высокого и значительного риска».
д.
Среднее значение, медиана и мода для сгруппированных данных 
Среднее значение частотного распределения 40 человек равно 16,5. Найдите 2 недостающие частоты.
Проблема со статистикой
Среднее арифметическое, среднее геометрическое, среднее гармоническое 
Сгруппированные данные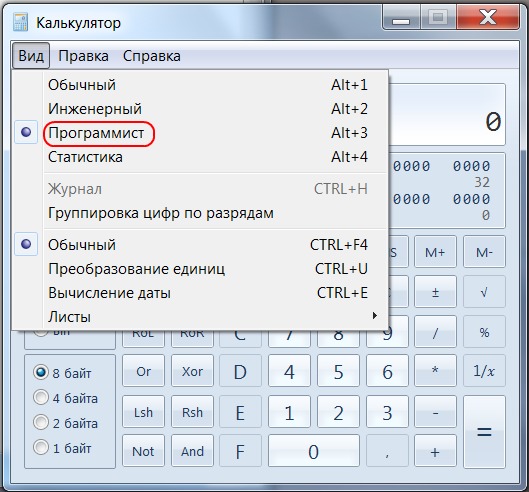
Получите коэффициент ранговой корреляции для следующих данных.
Найдите коэффициент корреляции из двух уравнений линии регрессии.
Например, если мы оцениваем доверительный интервал с учетом оценки среднего значения генеральной совокупности, а уровень достоверности равен 95%, если бы исследование повторялось и каждый раз рассчитывался диапазон, можно было бы ожидать, что истинное значение будет находиться в пределах этих диапазонов в 95% случаев. Чем выше уровень достоверности, тем больше вы можете быть уверены, что интервал содержит истинное среднее значение.