Какие существуют виды множеств: HTTP 429 — too many requests, слишком много запросов

СУНЦ УрФУ

Расписание

Электронный журнал

Поступающим

Олимпиады, турниры, конкурсы

Планы работы

Подготовительные курсы

Новости:

24.10.2022

СУНЦ на конкурсе «Университетская книга»

Издания СУНЦ УрФУ получили высокую оценку на межрегиональном конкурсе.

20.10.2022

УрКОП: шаг вперёд сделан!

Учащийся СУНЦ в составе команды стал победителем командной олимпиады по программированию.

19.10.2022

«Любите общагу!»

Лицеисты, живущие в интернате, поздравили воспитателей.

14.10.2022

СУНЦ как кузница ученых будущего

Лицеист СУНЦ стал победителем международного конкурса в номинации «Математика».

07.10.2022

Все учителя СУНЦ — бриллианты!

Под этим девизом пятого октября в СУНЦ прошел концерт в честь Дня учителя.

29.09.2022

Лицеисты СУНЦ покорили хребет Зюраткуль!

В последние выходные сентября учащиеся СУНЦ побывали в национальном парке «Зюраткуль».

Больше новостей

Видеогалерея:

Концерт к Дню учителя (2022)

Репортаж ТРК «Вести-Урал» о гаджетах у школьника (2022)

Концерт, посвященный Дню Победы (5 мая 2022 года)

Больше видео

О нас:

Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).

В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским  программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.

Иногородние обучающиеся проживают в уютном общежитии.

Прием производится в 8, 9 и 10 классы. Работают подготовительные курсы.

Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22 и в разделе нашего сайта «Поступающим».

Как нас найти:

Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝

Проезд:

• автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
• автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
• троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
• троллейбусами № 4 до остановки «Сулимова», № 12, 19 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.

Элемент множества | это… Что такое Элемент множества?

ТолкованиеПеревод

Элемент множества

Мно́жество — один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением (ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики).

В математической логике и дискретной математике часто употребляемый синоним множества — алфавит.

Содержание 1 Теории 1.1 «Наивная теория множеств» 1.1.1 История определения 1.2 Аксиоматическая теория множеств 2 Элемент множества 3 Некоторые виды множеств 4 Операции над множествами 5 Литература 6 См. также

Теории

Существует два основных подхода к понятию множества — наивная и аксиоматическая теория множеств.

«Наивная теория множеств»

Дать определение какому-нибудь понятию — это значит описать это понятие через понятия, определённые ранее. Если число определений в теории конечно, то первое определение должно быть основано на понятиях, которые являются аксиоматическими, то есть изначально неопределёнными. Множество — как раз одно из таких аксиоматических понятий. В рамках наивной теории множеств множеством считается любой чётко определённый набор объектов (

элементов множества). Вольное использование наивной теории множеств приводит к некоторым парадоксам, возникающим из-за того, что интуитивное понятие «чётко определённый» на самом деле само не определено чётко. Так как теория множеств, фактически, используется как основание и язык всех современных математических теорий, становится очевидной необходимость её строгой аксиоматизации.

Наивная теория множеств была создана Кантором в конце XIX века.

История определения

До XIX века считалось, что точного определения множества нет.

Множеством считалось любое скопление предметов.

В конце XIX века Георг Кантор определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты называются элементами множества. Множество объектов, обладающих свойством A(x), обозначается . Если некое множество , то A(x) называется характеристическим свойством множества Y.

Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.

После этого теория множеств была аксиоматизирована.

Аксиоматическая теория множеств

На сегодняшний день множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).

Элемент множества

Объекты, из которых состоит множество, называют

элементами множества или точками множества. Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а∉А(а не принадлежит А).

Некоторые виды множеств

• Пустое множество
• Упорядоченное множество — множество, на котором задано отношение порядка.
• Набор (в частности, упорядоченная пара). В отличие от просто множества записывается внутри круглых скобок: (x₁, x₂, x₃, …), а элементы могут повторяться.

По иерархии:

Множество множеств

Подмножество

Надмножество

По ограничению:

Основная статья: Операции над множествами

Литература

• Столл Р. Р. Множества. Логика. Аксиоматические теории. — М.: Просвещение, 1968. — 232 с.

См. также

• Круги Эйлера
• Носитель

Wikimedia Foundation. 2010.

Нужно решить контрольную?

• Элемент 118
• Элемент рабочего стола

Полезное

теория множеств | Символы, примеры и формулы

Ключевые люди:

Георг Кантор Пол Эрдёш Джон фон Нейман Сол Крипке Станислав Улам

Похожие темы:

аксиома выбора Диаграмма Венна Лемма Цорна гипотеза континуума Теорема Кантора

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

теория множеств , раздел математики, изучающий свойства четко определенных наборов объектов, которые могут иметь или не иметь математическую природу, например числа или функции. Теория менее ценна в прямом применении к обычному опыту, чем в качестве основы для точной и гибкой терминологии для определения сложных и изощренных математических понятий.

Между 1874 и 1897 годами немецкий математик и логик Георг Кантор создал теорию абстрактных множеств сущностей и превратил ее в математическую дисциплину.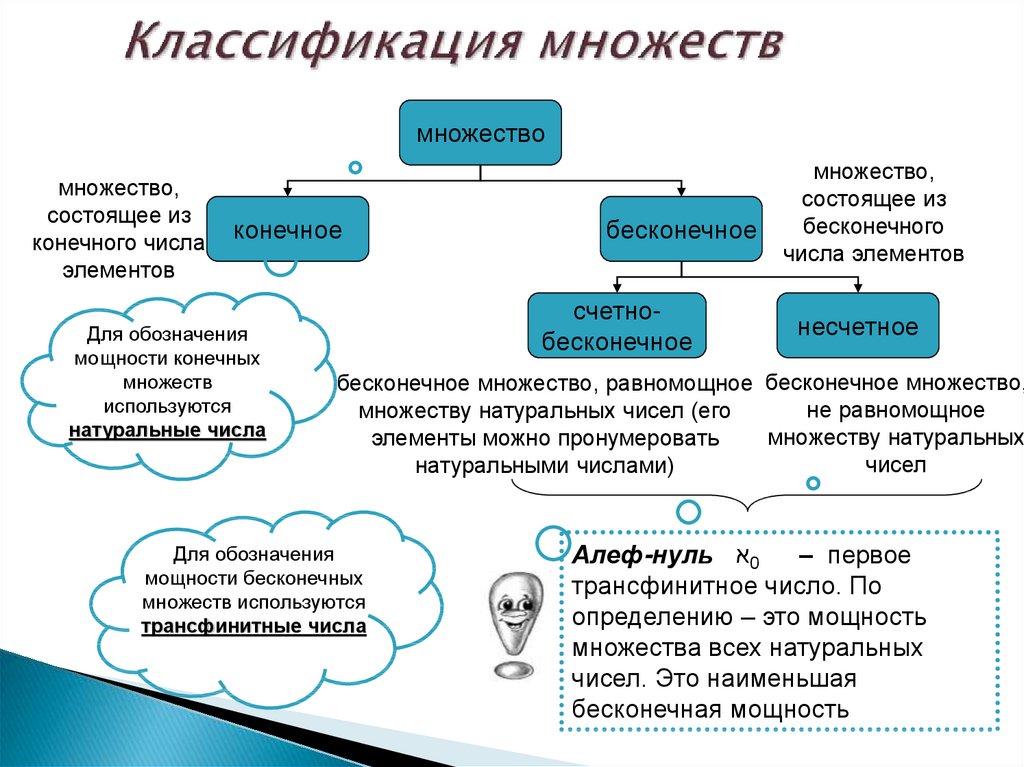 Эта теория выросла из его исследований некоторых конкретных проблем, касающихся определенных типов бесконечных множеств действительных чисел. Множество, писал Кантор, есть совокупность определенных, различимых объектов восприятия или мысли, рассматриваемых как единое целое. Объекты называются элементами или членами множества.

Теория имела революционный аспект, заключающийся в рассмотрении бесконечных множеств как математических объектов, равноправных с теми, которые могут быть построены за конечное число шагов. Со времен античности большинство математиков старательно избегали введения в свои рассуждения актуальной бесконечности (т. е. множеств, содержащих бесконечность объектов, мыслимых как существующие одновременно, по крайней мере, в мыслях). Поскольку такое отношение сохранялось почти до конца XIX века, работы Кантора подвергались многочисленной критике в том смысле, что они касались вымыслов, более того, что они посягали на область философов и нарушали принципы религии. Однако как только начали находить применение анализу, отношение стало меняться, и к 189 г.

Идеи и результаты Кантора получили признание. К 1900 году теория множеств была признана отдельной отраслью математики.

Однако именно тогда были обнаружены некоторые противоречия в так называемой наивной теории множеств. Чтобы устранить такие проблемы, была разработана аксиоматическая основа теории множеств, аналогичная той, которая была разработана для элементарной геометрии. Степень успеха, достигнутого в этом развитии, а также нынешний статус теории множеств хорошо отражены в трудах Николя Бурбаки.0029 Éléments de mathématique

(начало 1939; «Элементы математики»): «В настоящее время известно, что можно, логически говоря, вывести практически всю известную математику из одного источника, Теории множеств».

Britannica Quiz

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Введение в наивную теорию множеств

Фундаментальные концепции множеств

В наивной теории множеств множество представляет собой совокупность объектов (называемых членами или элементами), которые рассматриваются как единый объект.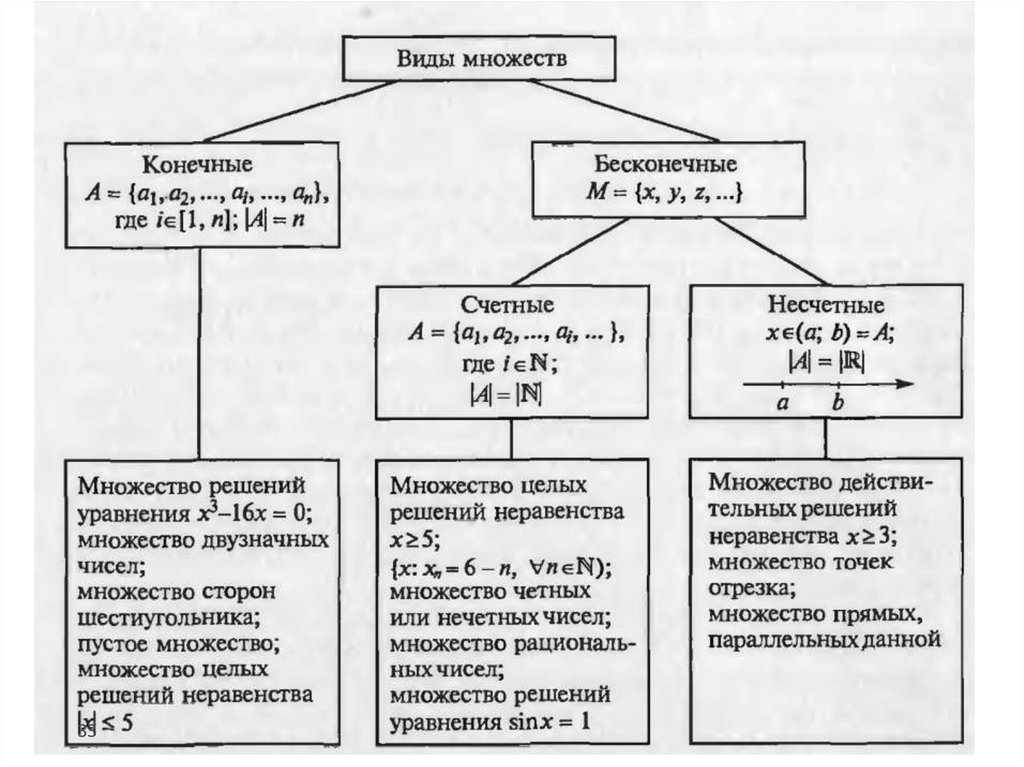

Чтобы указать, что объект x является членом множества A , пишут x ∊ A , тогда как x ∉ A указывает, что x не является членом 39 A . Набор может быть определен правилом членства (формулой) или перечислением его членов в фигурных скобках. Например, множество, заданное правилом «простые числа меньше 10», также может быть задано как {2, 3, 5, 7}. В принципе, любое конечное множество может быть определено явным списком его элементов, но для определения бесконечных множеств требуется правило или шаблон для указания членства; например, многоточие в {0, 1, 2, 3, 4, 5, 6, 7, …} указывает, что список натуральных чисел ℕ можно продолжать бесконечно. Пустой (или недействительный, или нулевой) набор, обозначенный {} или Ø, вообще не содержит элементов. Тем не менее, он имеет статус набора.

Набор A называется подмножеством набора B (обозначается A ⊆ B ), если все элементы A также являются элементами B . Например, любое множество является подмножеством самого себя, а Ø является подмножеством любого множества. Если оба A ⊆ B и B ⊆ A , то A и B имеют точно такие же элементы. Часть концепции множества состоит в том, что в данном случае A = B ; то есть A и B — это один и тот же набор.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

теория множеств | Символы, примеры и формулы

Ключевые люди:

Георг Кантор Пол Эрдёш Джон фон Нейман Сол Крипке Станислав Улам

Похожие темы:

аксиома выбора Диаграмма Венна Лемма Цорна гипотеза континуума Теорема Кантора

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

теория множеств , раздел математики, изучающий свойства четко определенных наборов объектов, которые могут иметь или не иметь математическую природу, например числа или функции. Теория менее ценна в прямом применении к обычному опыту, чем в качестве основы для точной и гибкой терминологии для определения сложных и изощренных математических понятий.

Между 1874 и 1897 годами немецкий математик и логик Георг Кантор создал теорию абстрактных множеств сущностей и превратил ее в математическую дисциплину. Эта теория выросла из его исследований некоторых конкретных проблем, касающихся определенных типов бесконечных множеств действительных чисел. Множество, писал Кантор, есть совокупность определенных, различимых объектов восприятия или мысли, рассматриваемых как единое целое. Объекты называются элементами или членами множества.

Теория имела революционный аспект рассмотрения бесконечных множеств как математических объектов, которые находятся на равной основе с теми, которые могут быть построены за конечное число шагов. Со времен античности большинство математиков старательно избегали введения в свои рассуждения актуальной бесконечности (т. е. множеств, содержащих бесконечность объектов, мыслимых как существующие одновременно, по крайней мере, в мыслях).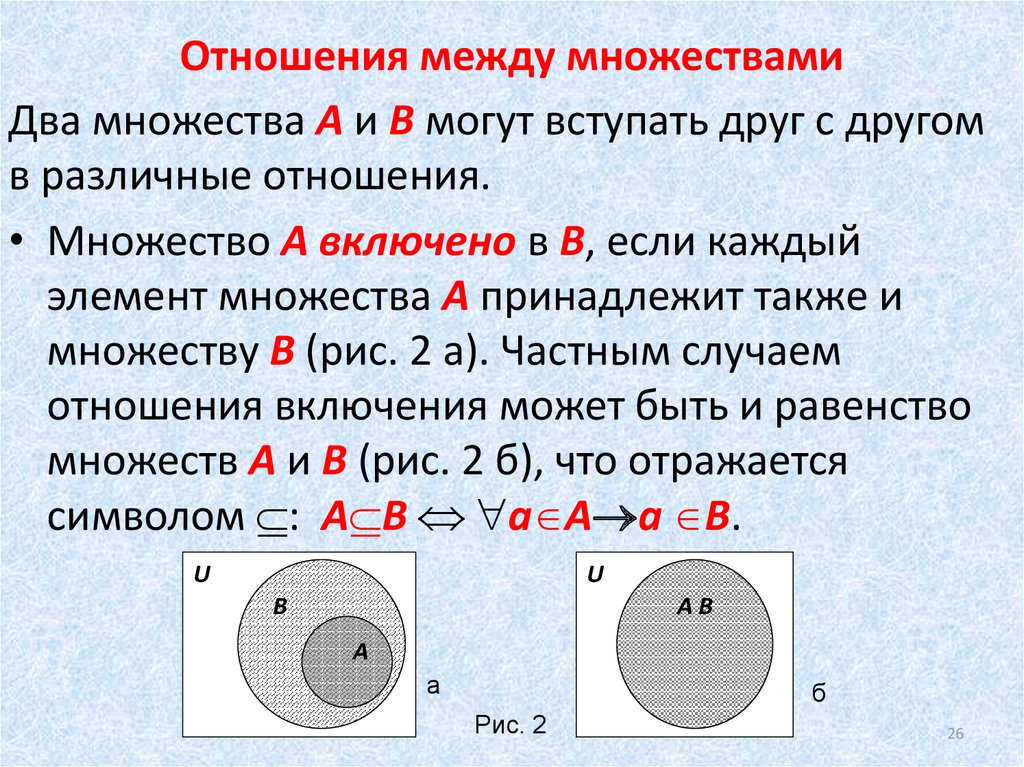 Поскольку такое отношение сохранялось почти до конца XIX в.XX века работы Кантора подверглись многочисленной критике за то, что они касались вымыслов, более того, что они вторгались в область философов и нарушали принципы религии. Однако как только начали находить приложения к анализу, отношение начало меняться, и к 1890-м годам идеи и результаты Кантора получили признание. К 1900 году теория множеств была признана отдельной отраслью математики.

Однако именно тогда были обнаружены некоторые противоречия в так называемой наивной теории множеств. Чтобы устранить такие проблемы, была разработана аксиоматическая основа теории множеств, аналогичная той, которая была разработана для элементарной геометрии. Степень успеха, достигнутого в этом развитии, а также нынешний статус теории множеств хорошо отражены в трудах Николя Бурбаки.0029 Éléments de mathématique (начало 1939; «Элементы математики»): «В настоящее время известно, что можно, логически говоря, вывести практически всю известную математику из одного источника, Теории множеств».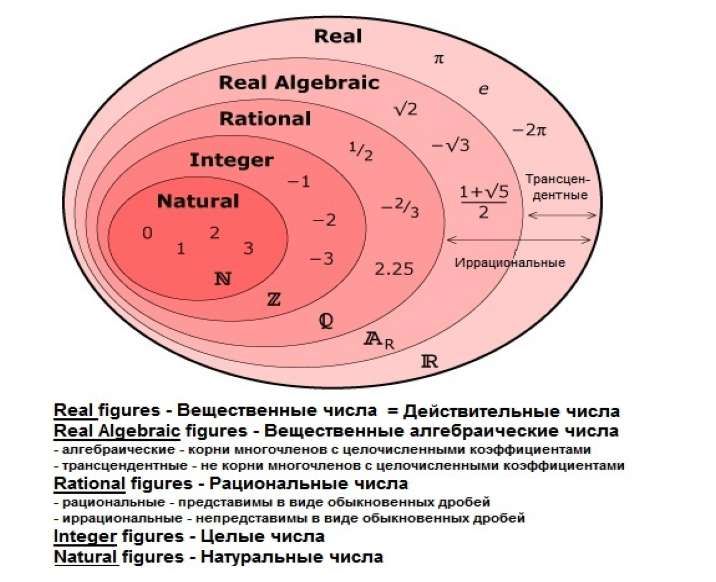

Britannica Quiz

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Введение в наивную теорию множеств

Фундаментальные концепции множеств

В наивной теории множеств множество представляет собой совокупность объектов (называемых членами или элементами), которые рассматриваются как единый объект. Чтобы указать, что объект x является членом множества A , пишут x ∊ A , тогда как x ∉ A указывает, что x не является членом 39 A . Набор может быть определен правилом членства (формулой) или перечислением его членов в фигурных скобках. Например, множество, заданное правилом «простые числа меньше 10», также может быть задано как {2, 3, 5, 7}. В принципе, любое конечное множество может быть определено явным списком его элементов, но для определения бесконечных множеств требуется правило или шаблон для указания членства; например, многоточие в {0, 1, 2, 3, 4, 5, 6, 7, …} указывает, что список натуральных чисел ℕ можно продолжать бесконечно.