Какие углы называют острыми прямыми тупыми: Острые и тупые углы — урок. Математика, 2 класс.

4 класс. Математика. Угол. Виды углов. — Угол. Виды углов.

Комментарии преподавателя

На этом уроке мы рассмотрим угол и виды углов. Вспомним, что такое луч и как он связан с углом, дадим определение этой геометрической фигуре. Далее рассмотрим разные способы обозначения угла и различные виды углов. Узнаем об инструментах, которые применяются для построения углов. Рассмотрим несколько задач на нахождение углов.

 

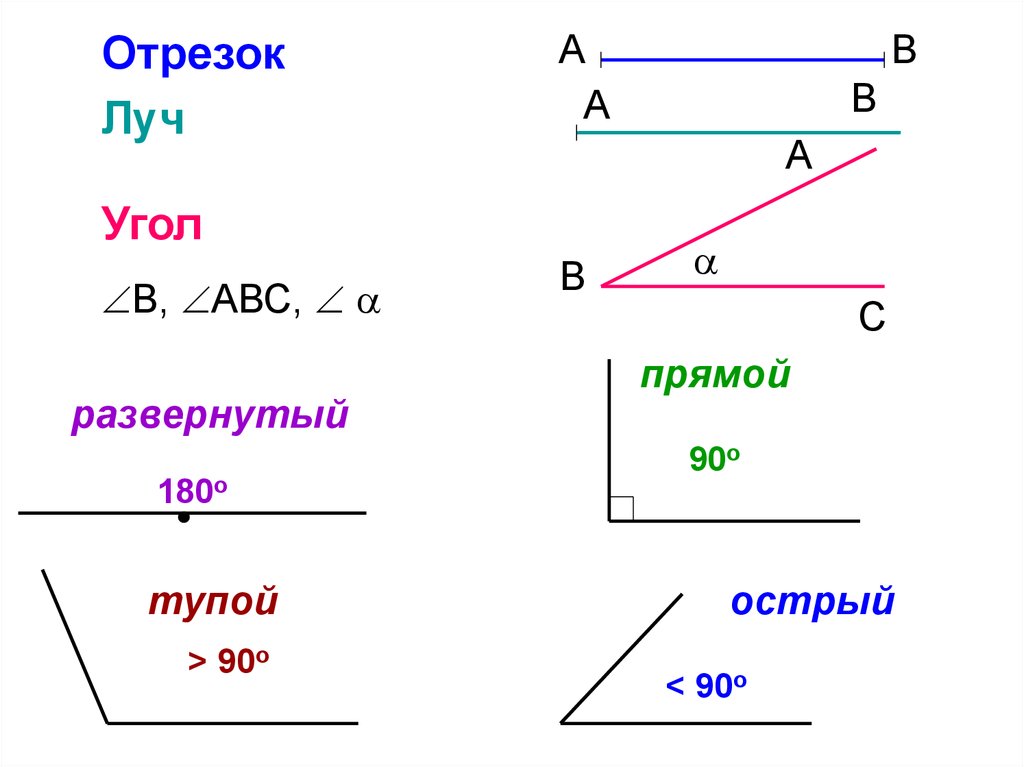
Ранее мы были озна­ком­ле­ны с по­ня­ти­ем «луч». Луч – это часть пря­мой, огра­ни­чен­ная с одной сто­ро­ны точ­кой. На ри­сун­ке можно уви­деть луч с на­ча­лом в точке  и луч с на­ча­лом в точке  (рис. 1).

Рис. 1. Лучи

Фи­гу­ра, об­ра­зо­ван­ная двумя лу­ча­ми с одним и тем же на­ча­лом, на­зы­ва­ет­ся углом. Лучи, об­ра­зу­ю­щие угол, на­зы­ва­ют­ся сто­ро­на­ми угла, а их общее на­ча­ло – вер­ши­ной угла (рис. 2).

Рис. 2. Углы

Угол может быть на­зван одной за­глав­ной ла­тин­ской бук­вой по его вер­шине. На рис. 2 можно уви­деть угол  и угол . Но углы можно обо­зна­чить и дру­гим спо­со­бом.

Угол мно­го­уголь­ни­ка обо­зна­ча­ют тремя за­глав­ны­ми бук­ва­ми. На­зы­вать угол на­чи­на­ют с буквы, сто­я­щей у одной сто­ро­ны, затем на­зы­ва­ют букву у вер­ши­ны, а за­кан­чи­ва­ют бук­вой у дру­гой сто­ро­ны. На­при­мер, в тре­уголь­ни­ке , угол с вер­ши­ной  яв­ля­ет­ся угол  (рис. 3) или в об­рат­ном по­ряд­ке – .

В тре­уголь­ни­ке  угол с вер­ши­ной  – это угол  или .

Рис. 3. Углы в тре­уголь­ни­ке

Необ­хо­ди­мо пом­нить, что в се­ре­дине на­зва­ния угла долж­на сто­ять та буква, ко­то­рой обо­зна­че­на вер­ши­на угла.

Ино­гда угол обо­зна­ча­ют малой бук­вой или циф­рой, ставя их внут­ри угла (рис. 4). Между сто­ро­на­ми угла про­во­дят для яс­но­сти дужку.

Рис. 4. Обо­зна­че­ние угла бук­вой или циф­рой

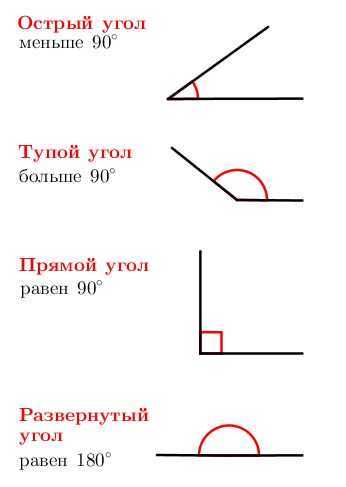
Рис. 5. Виды углов

Су­ще­ству­ют раз­лич­ные виды углов.

1. Если сто­ро­ны угла лежат на одной пря­мой, то такой угол на­зы­ва­ют 

раз­вер­ну­тым.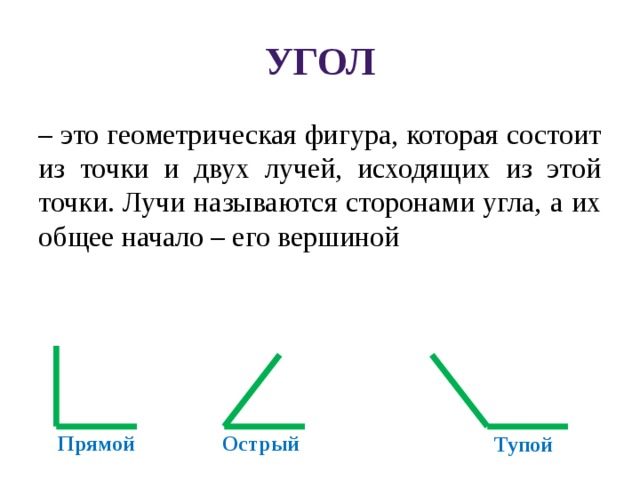  На рис. 6 угол М – раз­вер­ну­тый (умест­но срав­не­ние с раз­вер­ну­тым ве­е­ром).

Рис. 6. Раз­вер­ну­тый угол

2. Пря­мым углом на­зы­ва­ют тот угол, ко­то­рый со­став­ля­ет по­ло­ви­ну раз­вер­ну­то­го угла (рис. 7). На­при­мер, пря­мой угол можно по­лу­чить путем скла­ды­ва­ния бу­ма­ги (если лист сло­жить два­жды).

Рис. 7. Пря­мой угол

Для удоб­ства опре­де­ле­ния, пря­мой угол или нет, есть осо­бый ин­стру­мент – пря­мо­уголь­ный тре­уголь­ник, у ко­то­ро­го один из углов – пря­мой (рис. 8).

Рис. 8. Пря­мо­уголь­ный тре­уголь­ник и его при­ме­не­ние

3. Непря­мые углы де­лят­ся на тупые и ост­рые.

Угол, ко­то­рый мень­ше пря­мо­го, – это ост­рый угол (рис. 9).

Рис. 9. Ост­рый угол
Угол, ко­то­рый боль­ше пря­мо­го, но мень­ше раз­вер­ну­то­го угла, – это 

тупой угол (рис. 10).

Рис. 10. Тупой угол

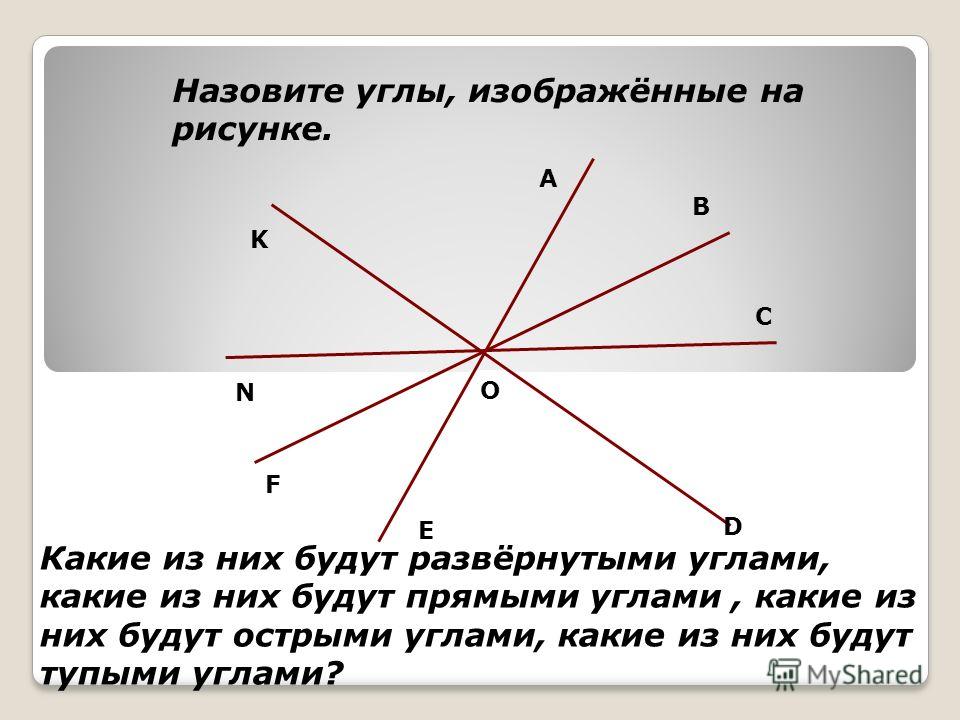
Най­ди­те на чер­те­же пря­мые, тупые и ост­рые углы (рис. 11).

Рис. 11. Ил­лю­стра­ция к за­да­нию

В на­хож­де­нии ре­ше­ния нам по­мо­жет ин­стру­мент – пря­мо­уголь­ный тре­уголь­ник, ко­то­рый будет при­ло­жен к каж­дой из вер­шин тре­уголь­ни­ка путем сов­ме­ще­ния одной из сто­рон. Если он будет сов­па­дать с углом, то этот угол пря­мой. Если угол будет мень­ше пря­мо­го угла ин­стру­мен­та, то этот угол ост­рый. А если же угол боль­ше пря­мо­го угла ин­стру­мен­та – то это тупой угол.

Пря­мые углы:  

Тупые углы: 

Ост­рые углы: , , , 

В по­стро­е­нии 4 пря­мых углов с общей вер­ши­ной на нели­но­ван­ной бу­ма­ге нам по­мо­гут цир­куль и ли­ней­ка.

Сна­ча­ла необ­хо­ди­мо про­ве­сти пря­мую. От­ло­жим на пря­мой про­из­воль­ный от­ре­зок . Про­ве­дем две окруж­но­сти с цен­тра­ми в точке  и  с ра­ди­у­са­ми, рав­ны­ми длине от­рез­ка .

Обо­зна­чим точки пе­ре­се­че­ния окруж­но­стей  и . Про­ве­дем через точки  и  пря­мую. Точку пе­ре­се­че­ния пря­мых обо­зна­чим бук­вой .

Рис. 12. По­стро­е­ние 4 пря­мых углов с общей вер­ши­ной на нели­но­ван­ной бу­ма­ге

С по­мо­щью пря­мо­уголь­но­го тре­уголь­ни­ка можно про­ве­рить, что все 4 угла с вер­ши­ной в точке  – пря­мые. При по­стро­е­нии пря­мых углов на нели­но­ван­ной бу­ма­ге вме­сто окруж­но­стей можно про­во­дить дуги, то есть части окруж­но­сти. При­чем дуги могут быть лю­бо­го ра­ди­у­са, но боль­ше, чем по­ло­ви­на длины от­рез­ка .

На этом уроке мы по­зна­ко­ми­лись с по­ня­ти­ем угла и ви­да­ми углов: раз­вер­ну­тым углом, пря­мым углом, тупым углом и ост­рым углом. На­учи­лись стро­ить пря­мые углы на нели­но­ван­ной бу­ма­ге с по­мо­щью цир­ку­ля и ли­ней­ки.

Источник конспекта: http://interneturok.ru/ru/school/matematika/4-klass/tema-3/ugol-vidy-uglov?konspekt

Источник видео: http://www.youtube.com/watch?v=zoj9YcAz2ws

Угол. Прямой и развернутый угол. Чертежный треугольник | Математика | 5 класс

На этом уроке мы повторим и закрепим знания об углах. Также более подробно разберем такие виды углов, как полный угол, прямой угол и развернутый угол, и вспомним, какие углы называются острыми, а какие – тупыми.

 Полный, развернутый, прямой угол

1. Полный угол (см. Рис. 1)

Рис. 1. Полный угол

Стороны угла совпадают.

Меньший угол не виден. Он называется нулевым углом.

Зато второй угол, больший, захватил плоскость полностью. Такой угол называется полным. Вот он имеет для нас важное значение. Поделив его пополам, а потом еще раз пополам, мы получим еще два типа важных углов.

2. Развернутый угол (см. Рис. 2.)

Рис. 2. Развернутый угол

Если стороны угла будут смотреть в разные стороны, составляя прямую, то два полученных угла будут равны друг другу. При этом вместе они составляют полный угол.

То есть угол, образованный такими лучами, является половиной полного угла.

Сам угол похож на то, как если бы ножки циркуля развернули в разные стороны. Угол так и назвали – развернутым.

3. Прямой угол

Поделим уже развернутый угол пополам. Получим два равных угла (см. Рис. 3).

Рис. 3. Прямой угол

Если столб стоит на земле прямо, то мы видим, что углы с двух сторон равны друг другу. Угол так и называется – прямой. Для него вместо дуги договорились использовать специальную отметку, маленький уголок.

 Способы черчения углов

1. Чтобы начертить полный угол, нужно из точки провести луч, подразумевая, что это два совпадающих луча.

2. Чтобы начертить развернутый угол, нужно провести прямую и поставить на ней точку. Получим два луча, идущих в разные стороны, то есть развернутый угол.

3. Чтобы начертить прямой угол, легче всего воспользоваться готовым деревянным или металлическим прямым углом, который называется чертежным треугольником, или угольником (см. Рис. 4).

Рис. 4. Чертежный треугольник

 Перпендикулярные прямые

Часто уже есть прямая и точка на ней и нужно провести через эту точку вторую прямую под прямым углом к первой.

Совместим угольник одной стороной с имеющейся прямой так, чтобы его вершина совместилась с точкой на прямой. Теперь проведем вторую прямую. Она расположена под прямым углом к первой прямой.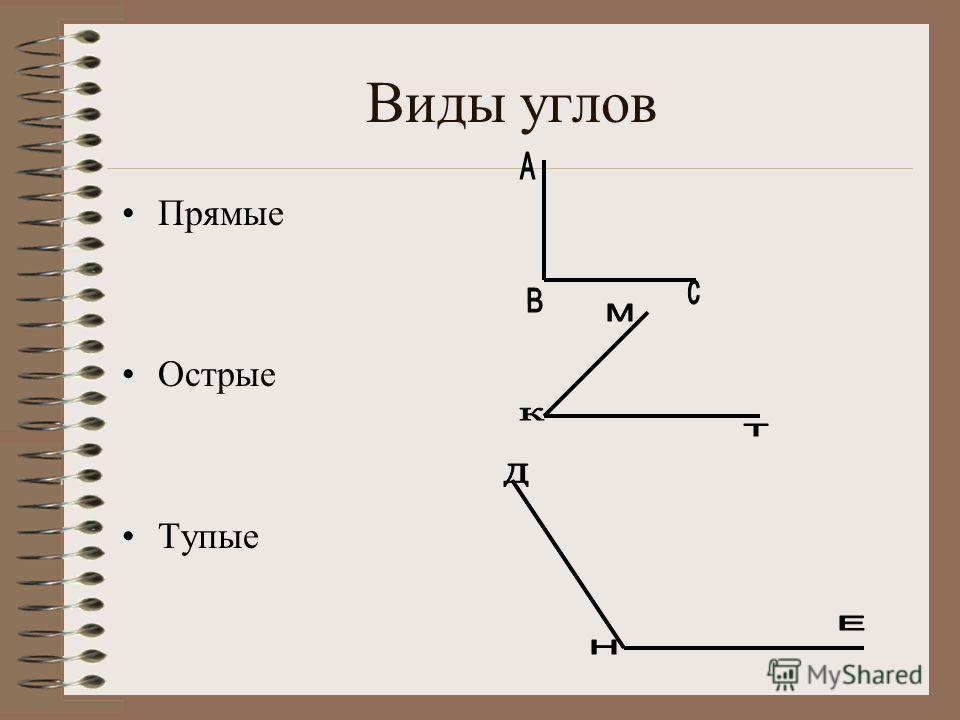 Такие прямые называют перпендикулярными (см. Рис. 5).

Рис. 5. Перпендикулярные прямые и угольник

 Прямой, острый, тупой угол

Дан развернутый угол  (см. Рис. 6).

Рис. 6. Развернутый угол AOB

Поделим его пополам.

Угол  – прямой (см. Рис. 7).

Рис. 7. Прямой угол 

Угол  меньше прямого угла. Такие углы называются острыми (см. Рис. 8).

Рис. 8. Острый угол ЕОВ

Угол  больше прямого угла. Такие углы называются тупыми (см. Рис. 9).

Рис. 9. Тупой угол 

Итак, все это можно сформулировать короткими определениями:

1. Прямой угол – это половина развернутого угла.

2. Острый угол – это угол меньше прямого.

3. Тупой угол – это угол больше прямого и меньше развернутого.

 Различные способы построения прямого угла

Построение прямого угла с помощью циркуля

На листе бумаги можно построить прямой угол, даже если у вас нет угольника.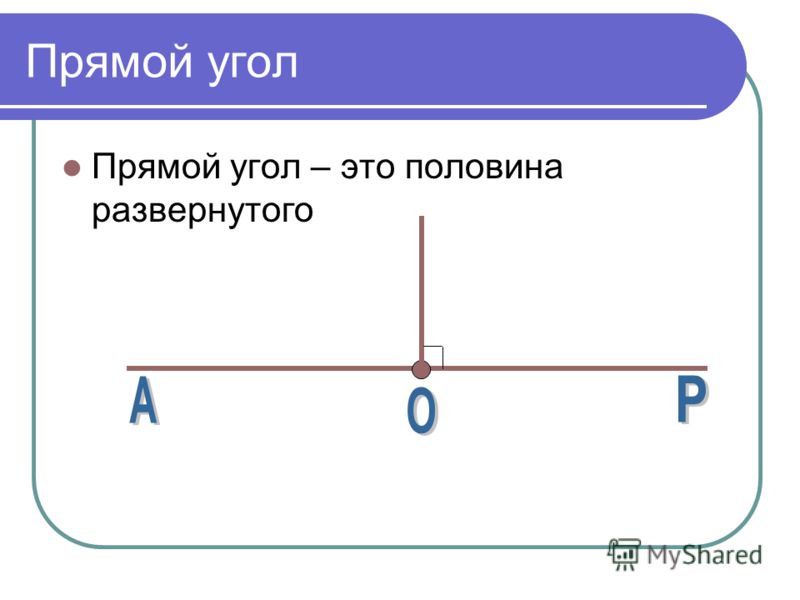

Помните, что прямой угол – это половина развернутого.

Сначала изобразим развернутый угол (см. Рис. 10).

Рис. 10. Построение прямого угла

Теперь поделим его пополам. Для этого возьмем циркуль и от вершины угла  отложим в обе стороны одинаковое расстояние (см. Рис. 11).

Рис. 11. Построение прямого угла (продолжение)

Увеличим чуть-чуть расстояние между ножками циркуля и отложим две дуги с центрами в полученных точках, чтобы они пересеклись над вершиной угла (см. Рис. 12).

Рис. 12. Построение прямого угла (продолжение)

Мы получим новую точку  прямо над вершиной . Соединим точки (см. Рис. 13).

Рис. 13. Построение прямого угла (продолжение)

Мы все делили симметрично, углы получились равными, а значит, прямыми.

 «Египетский треугольник»

Представьте теперь себе землемера в Древнем Египте. Ему нужно разделить поле на прямоугольники, а для этого нужно уметь делать прямые углы. У него нет огромного деревянного угольника. А даже если бы и был, его же тоже нужно уметь сделать.

Египтяне использовали треугольник со сторонами в соотношении 3:4:5. Один угол этого треугольника прямой. Его потом так и назвали – «египетский треугольник».

Чтобы на земле начертить такой треугольник, можно взять веревку 12 метров, отметить на ней три части – 3, 4 и 5 метров. Концы веревки соединить. В отметках привязать колышки. Натянуть за колышки все части веревки и вбить колышки в землю. Получится египетский треугольник, а значит, один прямой угол (см. Рис. 14).

Рис. 14. «Египетский треугольник»

 Отвес

Если у нас ровный пол, то веревка с грузом на конце будет составлять с линией пола прямой угол. Такой инструмент используют строители. Он называется отвес (см. Рис. 15).

Рис. 15. Отвес

 

Список литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013.
2. Виленкин Н.Я. и др. Математика. 5 кл. – М.: Мнемозина, 2013.
3. Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. – М.: Мнемозина, 2013.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Shkolo.ru (Источник).
2. Cleverstudents.ru (Источник).
3. Festival.1september.ru (Источник).

 

Домашнее задание

1. Постройте полный, прямой и развернутый углы.
2. Назовите все углы на рисунке, а также укажите их вид: 

Острый, Прямой, Тупой и Прямой

В этой статье мы хотим предоставить вам информацию об углах и их типах.

Углы создаются всякий раз, когда \(2\) линии перекрываются в одной точке. Тогда мера «расстояния» между этими \(2\) лучами известна как «угол» . Обозначается символом \(∠\). Углы обычно измеряются в градусах и радианах, и это мера округлости или вращения.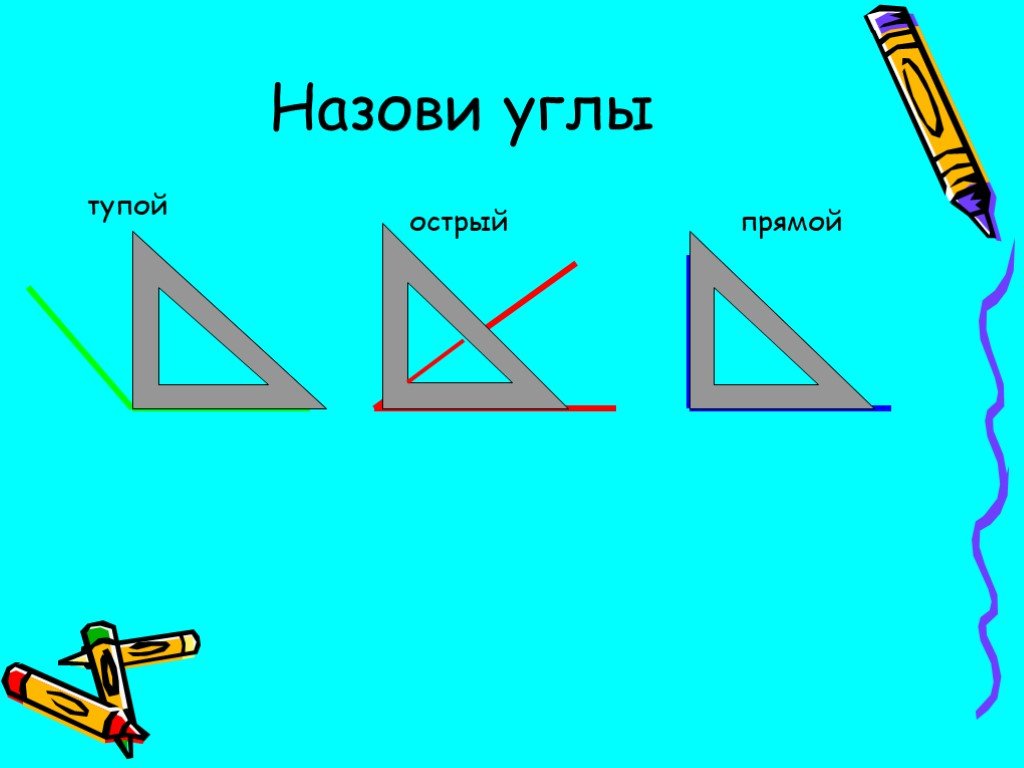 Мы видим углы каждый день, поскольку инженеры, а также архитекторы используют углы для проектирования зданий, дорог и спортивных сооружений.

Есть \(2\) основных компонентов, связанных с углами – ветвей и вершины .

Похожие темы

• Треугольники
• Как найти вертикальные углы?
• Как решить неизвестные углы?
• Как строить треугольники?

Угловые плечи

\(2\) луча, которые соединяются в одной точке и образуют угол, называются угловыми плечами .

Вершина угла

Вершина является общей конечной точкой, разделяемой лучами \(2\).

Измерение углов

Углы измеряются в градусах.  Один полный оборот вокруг точки создает полный угол \(360°\).

Виды углов и свойства

Существует шесть видов углов. Каждый из них имеет свою конкретную идентификацию на источнике измерения угла. Давайте узнаем о каждом из этих видов углов отдельно, а также о свойствах, которыми они обладают.

Острые углы

Острые углы – это углы, размеры которых больше \(0°\) и меньше \(90°\).

Прямые углы

Всякий раз, когда угол равен \(90°\), он называется прямым углом. Прямые углы легко узнать, так как они образуют форму буквы \(L\).

Тупые углы

Всякий раз, когда угол меньше \(180°\), но больше \(90°\), он называется тупым углом.

Прямые углы

Углы, образованные прямыми линиями, называются прямыми углами. Прямые углы состоят из прямых линий, а угол между \(2\) лучами эквивалентен \(180°\). При прямых углах \(2\) лучи противоположны друг другу. Два прямых угла образуют прямой угол. Поскольку измерение прямого угла равно \(180°\), это половина полного оборота окружности.

Углы отражения

Углы отражения — это углы, размер которых больше \(180°\), но меньше \(360°\).

Полные углы

Всякий раз, когда измерение угла эквивалентно \(360°\), это полный угол.

Пропущенные цифры –

Пример 1:

Напишите название угла.

Решение:

Этот угол меньше \(180°\), но больше \(90°\). Значит, это тупой угол.

Пропущенные цифры –

Пример 2:

Напишите название угла.

Решение:

Этот угол больше \(180°\), но меньше \(360°\). Итак, это рефлекторные углы.

Упражнения на пропущенные числа

Напишите названия углов.

1)

2)

1. \(\color{синий}{Острый}\)
2. \(\color{синий}{Правый}\)

Острый, Правый, Тупой, Рефлекторный, Полный Углы

В этой статье вы узнаете о различных типах углов: острый угол, тупой угол, прямой угол, прямой угол, рефлекторный угол, полный угол, дополнительный угол и многое другое.

Что такое угол?

Угол образован двумя лучами с общим концом. Мы измеряем величину угла в ГРАДУСАХ. Стороны и Вершина являются двумя составляющими угла.

Два луча, образующие угол, называются сторонами . Общий конец лучей называется 9.0005 вершина .

Типы углов

Существует в основном ШЕСТЬ типов углов, основанных на их величине угла. Они включают в себя:

1. Острые углы
2. Прямые углы
3. Тупытные углы
4. Углы
5. 9002
   Complete
6. 219009 Complete
. Четырехугольники

1. Острый угол

Острый угол — это угол между 0° и 90°. Это означает, что острый угол больше 0°, но меньше 90°. На изображении выше угол ∠PQR образован пересечением PQ и QR, который составляет 45°. Таким образом, ∠PQR=45° — острый угол.  Обычные примеры острых углов включают 15°, 30°, 45°, 80° и т. д.0°. В основном он образуется, когда две прямые линии перпендикулярны друг другу. ∠MNO = 90°.

3. Тупой угол

Тупой угол – это угол, лежащий в пределах от 90° до 180°. Это означает, что тупой угол больше 90°, но меньше 180° . На приведенном выше рисунке угол ∠RST образован пересечением RS и ST и составляет 110°. Таким образом, ∠RST=110° — тупой угол.   Типичные примеры тупых углов включают 100°, 115°, 145°, 160° и т. д.

4. Прямой угол

Прямой угол – это угол, градусная мера которого равна точно 180°. Это половина целого круга. Прямой угол представляет собой комбинацию острого и тупого угла.

Острый угол = прямой угол – тупой угол
Пример: 180° – 110° = 70° (острый угол)

Тупой угол = прямой угол – острый угол
Пример: 180° – 40° = 140° (тупой угол)

5.

Угол рефлекса

Угол рефлекса — это угол, лежащий в пределах от 180° до 360°. Это означает, что угол рефлекса больше 180°, но меньше 360°. [Между прямым углом (180º) и полным поворотом (360º)]. На приведенном выше рисунке угол ∠RST образован пересечением RS и ST и составляет 220°. Таким образом, ∠RST=220° — это угол рефлекса. Типичные примеры тупых углов: 190°, 215°, 345°, 350° и т. д.

6. Полный угол

Полный угол — это угол, градусная мера которого точно равна 360°. Это один полный оборот, равный 360°. Его также называют полным вращением или полным углом.

Другие типы углов: Как назвать пары углов

Помимо типов углов, упомянутых выше, различные типы углов известны как парные углы. К ним относятся:

Дополнительный угол

Если сумма двух углов равна 90°, то они называются дополнительными углами. Говорят, что один из дополнительных углов является дополнением другого.

No related posts.