Верные цифры числа примеры: 1.3. Значащие цифры и число верных знаков

Верные значащие цифры приближенного числа

Определение 5: Значащими цифрами числа а называют все цифры в его записи, начиная с первой ненулевой слева.

Пример 5: Числа 0,001405и 5,0300 имеют соответственно 4 и 5 значащих цифр. Ноль, записанный в конце десятичной дроби, всегда значащая цифра. В числе 5,0300 последний ноль показывает, что число задано с точностью до десятитысячных.

Определение 6: Значащую цифру числа а  называют верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

Пример 6: Сколько верных значащих цифр содержит приближенное число ?

Решение:

Поскольку , то верными будут цифры 5, 8, 2.

Погрешности математических операций Абсолютная погрешность суммы и разности

Теорема 1

: Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы алгебраических погрешностей этих чисел.

Доказательство: Пусть — алгебраическая сумма точных чисел.

— сумма приближенных значений этих чисел.

Абсолютные погрешности их соответственно равны: . Вычитая из точного значения суммы её приближенное значение, имеем:

или, переходя к модулям:

,

следовательно

,

что требовалось доказать.

Из последней формулы следует, что абсолютная погрешность алгебраической суммы не может быть меньше абсолютной погрешности наименее точного из слагаемых.

Пример 7:

,

где числа 204,4 и 144,2 верны с точностью до 0,1.

Значит, остальные нужно округлить с точностью до 0,01, сложить и округлить результат до 0,1. Итак

Относительная погрешность произведения нескольких приближенных чисел

Теорема 2: Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел.

Доказательство: Пусть (1), где

— положительные приближенные числа и их абсолютные погрешности: .

Логарифмируя (1), получим:

.

По теореме об абсолютной погрешности суммы:

.

Используя то, что

,

получим

,

что требовалось доказать.

Относительная погрешность частного

Теорема 3: Относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.

Доказательство: Пусть — приближенные числа, а — абсолютные погрешности этих чисел. По теореме об абсолютной погрешности алгебраической суммы:

,

что требовалось доказать.

Относительная погрешность натуральной степени и корня

Теорема 4: Относительная погрешность m-й степени приближенного числа (m-натуральное) в m раз больше относительной погрешности самого числа.

Доказательство: Пусть , тогда

,

что требовалось доказать.

Вывод: В результате вычисления степени приближенного числа следует оставить столько верных значащих цифр, сколько верных значащих цифр в основании.

Теорема 5: Относительная погрешность корня m-й степени в m раз меньше предельной относительной погрешности подкоренного числа.

Доказательство: Пусть , тогда

, т.е.

.

Правила подсчета цифр

При массовых вычислениях с приближенными или точными числами, а также с числами, у которых погрешность отсутствует, используют правила подсчета цифр:

• промежуточные вычисления следует получать хотя бы с одной запасной цифрой, по отношению к значащим цифрам чисел, участвующим в промежуточном вычислении,

• окончательный результат вычисления содержит то количество значащих цифр, которое имеет исходное число с наименьшим числом значащих цифр.

Пример 8: Вычислить выражение: Y = 0,125а² (8b-c),

где a = 18; b = 2,75; c = 3,232.

Решение:. Так как погрешность чисел а,b,с отсутствует то вычисления производим в соответствии с правилами подсчета цифр.

Преобразуем исходное выражение к следующему, более рациональному виду :

Y =.0,125а² (8b-c) = a² (b-c/8)

Исходное выражение содержало 5 действий, а окончательное выражение содержит 4 действия.

Далее последовательно производим необходимые вычисления (в соответствии с числом

а = 18, у которого две значащие цифры) и записываем результат в форме с плавающей запятой:

Y = 324 • (2,75 — 0,404) = 324 • 2,346 = 760 = 7,6 • 10².

Запись — приближенное число — Большая Энциклопедия Нефти и Газа, статья, страница 2

Cтраница 2

Какие цифры в записи приближенного числа называются значащими.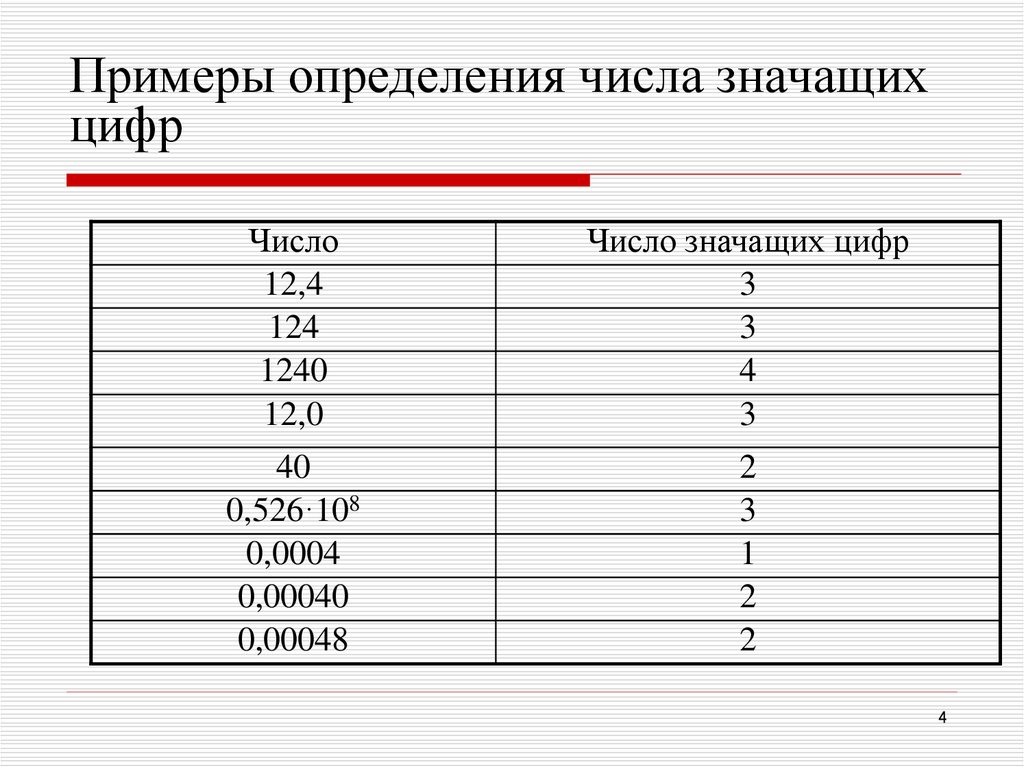  [16]

Какие цифры в записи приближенного числа х являются верными.  [17]

В вычислительной практике рекомендуется оставлять в записи приближенного числа только верные цифры, так как все цифры, следующие за верными, увеличивают объем работы без значительного повышения точности вычислений. В такой записи границу абсолютной погрешности можно и не указывать, так как ясно, что абсолютная погрешность не превосходит единицы последнего сохраняемого разряда числа.  [18]

Используя термин значащая цифра, правило

записи приближенных чисел можно сформулировать так: приближенные числа следует записывать так, чтобы все цифры числа, кроме нулей впереди, если они есть, были значащими и верными цифрами.  [19]

Что касается цифры 0, стоящей в конце записи приближенного числа, то в некоторых случаях нули идут в счет точных цифр, в других — нет.  [20]

Что касается цифры 0, стоящей в конце записи приближенного числа, то в некоторых случаях нули идут в счет точных цифр, в других — нет.  [21]

Здесь следует заметить, что достоверность ( точ ность) результата вычислений в примере 1 такова, что записать его в обычной форме, не нарушив при этом правил записи приближенных чисел, практически невозможно. Действительно, верными здесь являются лишь две значащие цифры результата, однако при обычной записи числа в форме 2800000 право на верность приобретают и нули, стоящие после числа 28, что не соответствует действительности. При записи числа в экспоненциальной форме, его мантисса точно указывает, какие его цифры являются верными, независимо от порядка числа.  [22]

Приближенные числа записывают в нормализованной форме, при этом длина дробной части характеризует точность приближенного числа; пишут только верные цифры, истинность которых не вызывает сомнений. Запись приближенного числа может оканчиваться нулем — это означает, что цифра 0 верная: записи 3 50 — 10 и 3 5 — 10 — имеют различный смысл. Принято считать, что погрешность приближенного числа не превосходит половины единицы разряда последней верной цифры.  [23]

В приближенных числах, как было доказано выше, нецелесообразно сохранять слишком много знаков. Запись приближенных чисел

должна подчиняться определенным правилам, которые связаны с понятием о верных знаках или верных цифрах числа.  [24]

Цифра числа называется верной ( в широком смысле), если абсолютная погрешность числа не превосходит единицы разряда, в котором стоит эта цифра. Значащими цифрами числа, записанного в виде десятичной дроби, называют все его верные цифры, начиная с первой слева, отличной от нуля. Запись приближенного числа только верными знаками принято называть правильной записью.  [25]

Для краткости слово предельная обычно опускается. Если абсолютная погрешность величины а не превышает одной единицы разряда последней цифры числа а, то говорят, что у числа а все знаки верные. Это требование к записи приближенного числа, позволяющее получить представление о его точности, называют принципом академика Крылова.

Если приближенное число содержит лишние или не вполне надежные знаки, его следует округлить, сохранив не более одного ненадежного знака.  [26]

Числа бывают точными и приближенными. Точное число является результатом подсчета небольшого числа предметов или результатом вычисления, в котором применялись только точные числа. В расчетах такие числа встречаются сравнительно редко. Примерами их могут служить числа выполненных определений, взятых навесок, мелких единиц, на которые условно разделена крупная единица ( 1000 мл в 1 л, 60 мин в 1 ч и пр. Приближенное число выражает данную величину не точно, но с некоторой определенной степенью точности, например, результат измерения массы или объема. Результат вычисления, в котором участвуют только приближенные числа или приближенные наряду с точными, есть число тоже приближенное. Верной записью приближенного числа является только такая, которая указывает на его точность.  [27]

Страницы:      1    2

{\beta}$$

$y$ будет приближением к результату $x$, но с правильными только первыми $c$ цифрами.

---

2. Задача

Учитывая приближение ($\alpha$) к $n$ правильных цифр после запятой иррационального числа $a$, И учитывая приближение ($\beta$) к $m$ правильные цифры после запятой иррационального числа $b$ -> Я хочу найти значение $c$, количество цифр после запятой в аппроксимированном результате $y$, которое совпадает с цифрами из реального результата $x$. 9{1.4142}=2.1745637940043789740808552…$$

Помните, я вычислял квадратный корень из 3-5 знаков после запятой? В моей формальной постановке задачи это $n$. И я также аппроксимировал квадратный корень от 2 до 4 цифр, сделав $m$ из моей формальной задачи равным 4.

Теперь, когда мы сравним результат действительного выражения и выражения с аппроксимацией до $n$ цифр иррационального числа $a$ и $m$ цифр иррационального числа $b$, мы видим, что только первые четыре знака после запятой приближенного результата совпадают с реальным результатом.

Количество совпадающих цифр в результате, который использует приближения к реальному результату, определяется как $c$ в моей формальной постановке задачи, и ЭТО то, что я хочу выяснить не только для этого примера, но и для каждое иррациональное число $a$ и $b$, его аппроксимации $\alpha$ и $\beta$ и количество аппроксимируемых цифр, $n$ и $m$ соответственно после запятой, исходных чисел.

В этом примере $c=4$.

---

4. (не знаю как назвать этот раздел)

Теперь, когда я показал пример, я надеюсь, что разделы 1 и 2 этого вопроса будут выглядеть яснее и понятнее. Я ценю любую помощь, и я благодарю заранее.

Что такое цифра в математике? Определение, типы, примеры, факты

Определение цифр в математике

Цифры — это отдельные числа, используемые для представления значений в математике. 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 используются в различных комбинациях и повторениях для представления всех значений в математике.

Любое из десяти чисел от 0 до 9 может быть представлено символом, известным как цифра.

Пример двузначного (2-D) числа — 65. Оно состоит из 6 и 5.  

История

В древние времена у людей не было системы счисления или цифр для измерения или считать вещи. По мере того, как мир расширял свои корни в такие предметы, как наука, и торговля между странами росла, возникла настоятельная потребность в единой системе счисления. Таким образом формировались и объединялись цифры для использования в разных ситуациях.

Мы используем международные цифры, такие как «123» и «65», но римляне использовали римские цифры, и на протяжении всей истории использовалось много других цифр.

Разрядное значение

В математике каждая цифра в числе имеет разрядное значение. Значение места может быть определено как значение, представленное цифрой в числе на основе ее положения в числе.

Например, разряд 7 в числе 3743 равен 7 сотням или 700. Однако разряд 7 в числе 7432 равен 7 тысячам или 7000. Здесь мы видим, что хотя 7 одинакова в обоих числах, его позиционное значение изменяется с изменением его положения.

Номинальная стоимость

Разрядная стоимость и номинальная стоимость не совпадают. Номинальное значение цифры — это значение цифры, а разрядное значение цифры — это ее место в числе. Проще говоря, номинальная стоимость сообщает фактическую стоимость, тогда как стоимость места сообщает стоимость на основе ее положения. Следовательно, номинал цифры никогда не меняется независимо от ее положения в числе, тогда как ее разрядное значение меняется с изменением ее положения.

Например, номинальная стоимость 2 в обоих числах 283 и 823 равна 2. Тогда как разрядная стоимость 2 равна 200 в 283 и 20 в 823. 

Пример цифр:

• Двузначные числа

Двузначные числа начинаются с 10 и заканчиваются на 99. Десятки должны стоять между 1 и 9.

Рассмотрим два числа, 15 и 37. Когда эти два числа складываются, получается новое число 52.

15 + 37 = 52

• Четырехзначные числа

Когда четыре цифры записываются вместе, получается четырехзначное число. Диапазон этих чисел от 1000 до 9999.

Рассмотрим числа 1001, 2001, 5000 и 1040. При сложении этих чисел получается новое четырехзначное число 9042.

1001$ + 2001 + 5000 + 1040 = 9042$ Примеры, упомянутые выше, по мере увеличения цифр в числе увеличивается его значение. Например, 10 000 — это 5-мерное число, значение которого больше всех 4-D натуральных чисел.

Решенные примеры

Пример 1. Сколько цифр в числе 1458?

Решение : Число 1458 состоит из четырех цифр: 1, 4, 5 и 8.

Пример 2. Используя цифры 6, 6, 8, найдите наибольшее $3-$-значное число.

Решение : Наибольшее трехзначное число, которое можно составить из них, равно 866.

Пример 3. Каково разрядное значение цифры 4 в числе 84 527? в 84 527 — 4000 (четыре тысячи).

Практические задачи

1

Какое из этих чисел составляет наибольшее трехзначное число?

1, 0

2

9

9, 1

Правильный ответ: 9
Наибольшее трехзначное число 999 состоит из 9, повторенных трижды.

2

Какой из них стоит на десятитысячном разряде в числе 783 425?

7

4

8

5

Правильный ответ: 8
8 стоит в разряде десятков тысяч.

3

Какое десятичное число в 36,2?

6

8

2

Правильный ответ: 2
В данном числе после запятой стоит 2. Следовательно, это десятичное число.

Часто задаваемые вопросы

В чем разница между десятичными знаками и цифрами?

Термин «цифры» относится к набору действительных чисел, включая ноль и все положительные счетные числа. Дроби, отрицательные целые числа и десятичные дроби не рассматриваются как цифры.

Десятичная дробь — это число, которое ставится справа после точки (.) в числе.

Например, в числе 23,8 8 — десятичное число.

Какие цифры используются для составления чисел?

От 0 до 9 используются в различных комбинациях для образования цифр.

Являются ли дроби частью цифр?

Дроби представляют собой определенные части целой значащей цифры. Они лежат между двумя значащими числами.