Решение задач линейного программирования графическим методом
Похожие презентации:
Симплекс-метод для решения задач линейного программирования
Симплекс-метод решения задач линейного программирования
Предмет, метод и теоретические основы методов линейного программирования
Решение простейших задач линейного программирования графическим методом
Симплексный метод линейного программирования
Задача линейного программирования
Циклы. Методы решения задач
Методы оптимальных решений
Оптимизация методом нелинейного программирования (НЛП)
Методы обработки экспериментальных данных
1. Решение задач линейного программирования графическим методом
Выполнили: студентки ГМУ-11Клдиашвили Кристина,
Кожинова Анастасия
2. ЗАДАЧА Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели
А требуется 2 м тканипервого вида, 1 м ткани второго вида, 2 м ткани третьего вида.
 На
Наизготовление одного платья модели В требуется 3 м ткани первого вида, 1 м
ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида
составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного
изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден.
ед.
РЕШЕНИЕ
Пусть переменные X₁ и X₂ означают количество произведенных
платьев моделей А и В, соответственно.
Тогда количество израсходованной ткани первого вида составит:
2X₁+3X₂ (м)
Количество израсходованной ткани второго вида составит:
X₁+X₂ (м)
Количество израсходованной ткани третьего вида составит:
2X₁+2X₂ (м)
Поскольку произведенное количество платьев не может быть
отрицательным, то X₁ ⩾0 и X₂ ⩾0
Доход от произведенных платьев составит: 400X₁+300X₂ (ден.ед.)
Тогда экономико-математическая модель задачи имеет вид:
F(X)=400X₁+300X₂→ max
2X₁+3X₂ ⩽21
X₁+X₂ ⩽10
2X₁+2X₂ ⩽16
X₁ ⩾0 ; X₂ ⩾0
Решаем графическим методом.

Проводим оси координат X₁ и X₂.
Строим прямую 2X₁+3X₂=21
При X₁=0, X₂=21/3=7
При X₂=0, X₁=21/2=10,5
Проводим прямую через точки (0;7) и (10,5;0)
Строим прямую X₁+X₂=10
При X₁=0, X₂=10
При X₂=0, X₁=10
Проводим прямую через
точки (0;10) и (10;0)
Строим прямую 2X₁+2X₂=16
При X₁=0, X₂=16/2=8
При X₂=0, X₁=16/2=8
Проводим прямую через
точки (0;8) и (8;0)
Прямые X₁=0 и X₂=0 являются
осями координат.
5. 2X₁+3X₂=2*2+3*2=10 ⩽21 X₁+X₂=2+2=4 ⩽10 2X₁+2X₂=2*2+2*2=8 ⩽16 X₁=2 ⩾0; X₂ ⩾0
Область допустимых решений (ОДР) ограничена построеннымипрямыми и осями координат. Чтобы узнать, с какой стороны, замечаем,
что точка X₁=2, X₂=0 принадлежит ОДР, поскольку удовлетворяет системе
неравенств:
2X₁+3X₂=2*2+3*2=10 ⩽21
X₁+X₂=2+2=4 ⩽10
2X₁+2X₂=2*2+2*2=8 ⩽16
X₁=2 ⩾0; X₂ ⩾0
Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную
Строим произвольную линию уровня целевой функции,
например , F=400X₁+300X₂1200
Проводим прямую через точки (0; 4) и (3; 0).

Далее замечаем, что поскольку коэффициенты при X₁и
X₂ целевой функции положительны (400 и 300), то она возрастает
при увеличении X₁и X₂. Проводим прямую, параллельную прямой
(П1.1), максимально удаленную от нее в сторону возрастания
X₁ ,X₂ и проходящую хотя бы через одну точку четырехугольника
OABC. Такая прямая проходит через точку C.
Из построения определяем ее координаты.
X₁=8; X₂=0
Решение задачи: X₁=8; X₂=0
Fmax= 400x₁+300x₂=400*8+300*0=3200
Ответ:
X₁=8;X₂=0;Fmax=3200
То есть, для получения наибольшего дохода,
необходимо изготовить 8 платьев модели А.
Доход при этом составит 3200 ден. ед.
Спасибо за внимание!
English Русский Правила
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении. Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Интересное: Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 17Следующая ⇒ Задача с двумя переменными Графическим методом могут быть решены задачи линейного программирования с двумя переменными и некоторые задачи с большим числом переменных при выполнении определенных условий. Задача линейного программирования с двумя переменными должна иметь систему ограничений, представляющую собой систему неравенств. Неравенства могут быть как вида » £ «, так и » ³ «. Условия неотрицательности могут отсутствовать. Математическая модель должна иметь вид (2.1) (2.2) . Метод решения данной задачи основывается на возможности графического изображения области допустимых решений (ОДР) и нахождения в этой области оптимального решения. Для обоснования метода докажем две теоремы. Теорема 2.1. О виде области решений линейного неравенства. Областью решений линейного неравенства является одна из двух полуплоскостей, на которые разбивает всю координатную плоскость прямая , соответствующая этому неравенству. Доказательство. В системе координат О построим прямую (L) и ее нормаль (рис. 2.1). Рис. 2.1 Прямая (L) разбивает плоскость О на две полуплоскости: верхнюю ( ), соответствующую направлению нормали , и нижнюю ( ). Отсюда следует, что если l>0, т. е. M Î( ), то и тогда . Если же l<0, M Î( ), то и . Пример 2.1. Найти область решений неравенства . Решение. Строим прямую (рис. 2.2).
Чтобы определить какая из двух полуплоскостей является областью решений, выбираем произвольно «пробную» точку, не лежащую на прямой, и подставляем ее координаты в неравенство. Если неравенство выполняется, то область, содержащая эту «пробную» точку, является областью решений. Если же неравенство не выполняется, то областью решений будет полуплоскость, не содержащая «пробную» точку. В рассматриваемом примере в качестве «пробной» точки возьмем О(0, 0). Подставляем координаты этой точки в неравенство, получаем 2 × 0 + 3 × 0 £ 6 Û 0 £ 6, следовательно, областью решений является полуплоскость, содержащая начало координат. Этот факт отмечаем на рисунке стрелками. В общем случае, когда система ограничений состоит из нескольких неравенств, область допустимых решений (ОДР) находят как пересечение полуплоскостей – решений каждого из неравенств-ограничений. ОДР может быть пустым множеством, многоугольником и многоугольным множеством (многоугольником, неограниченным с одной из сторон). Для нахождения среди допустимых решений оптимального используют линии уровня. Линией уровня называется прямая, в точках которой целевая функция постоянна Z(X) = . Уравнение линий уровня , с = const. Теорема 2.2. Об изменении значений функции. Значения целевой функции в точках линий уровня возрастают, если линии уровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении. Рис. 2.3 Доказательство. Пусть целевая функция задачи линейного программирования имеет вид Z(X) = . В системе координат О построим две линии уровня (L ) и (L ) (рис. 2.3). Их общая нормаль . Пусть точка М( ) Î (L ), а точка Î(L ) является проекцией М на (L ). Вектор , = ( ), . Так как коллинеарен вектору , то вектор = ×l, где l число. Скалярное произведение . Используя координаты векторов и , можно записать . Так как , , то . Отсюда получаем следующие выводы: 1) если линия уровня перемещается в направлении нормали из положения (L ) к (L ), то l > 0 и, следовательно, ; 2) если же линия уровня перемещается в направлении противоположном направлению нормали из положения ( Таким образом, если задача линейного программирования на максимум, то для нахождения оптимального решения линии уровня надо перемещать по ОДР в направлении нормали, а в задаче на минимум наоборот – в противоположном направлении. Опорной прямой называется линия уровня, относительно которой ОДР находится в одной из полуплоскостей и которая имеет хотя бы одну общую точку с ОДР. Если ОДР является замкнутым многоугольником, то независимо от вида целевой функции имеется две опорных прямых. Если же ОДР – многоугольное множество (незамкнутый многоугольник), то в зависимости от направления нормали линий уровня ОДР может иметь как две, так и одну опорную прямую. Алгоритм графического метода решения задач линейного программирования с двумя переменными заключается в следующем. 1. Строится область допустимых решений. 2. Если область допустимых решений является пустым множеством, то ввиду несовместности системы ограничений задача не имеет решения. 3. Если область допустимых решений – это непустое множество, то строится нормаль линий уровня и одна из линий уровня, имеющая общие точки с этой областью. 4. Линия уровня перемещается до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум – в противоположном. 5. Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции. 6. Если задача линейного программирования имеет оптимальное решение, то для его нахождения решаются совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычисляется значение целевой функции на этих решениях. Пример 2.2. Решить задачу линейного программирования Рис. 2. Решение. Изобразим на плоскости систему координат (рис. 2.4) и построим граничные прямые области допустимых решений. Прямые, ограничивающие ОДР: Область допустимых решений определяется многоугольником ОАВСD. Для линий уровня (с = const) строим нормальный вектор . Перпендикулярно вектору построим одну из линий уровня (на рисунке она проходит через начало координат). Так как задача на максимум, то перемещаем ее в направлении вектора до опорной прямой. На рисунке видно, что опорная прямая проходит через точку B, являющуюся точкой пересечения первой и второй граничных прямых, . Для определения координат точки В решаем систему уравнений Получаем = 3, = 6. Данному оптимальному решению Ответ: max Z(X) = 30 при X = (3; 6). Пример 2.3 Решить задачу линейного программирования.
Рис. 2.5 Решение. Строим область допустимых решений, нормаль линий уровня и одну из линий уровня, имеющую общие точки с этой областью (рис. 2.5). Перемещаем линию уровня в направлении противоположном направлению нормали , так как решается задача на отыскание минимума функции. Нормаль линии уровня и нормаль = (2; 1) второй граничной прямой, в направлении которой перемещаются линии уровня, параллельны, так как их координаты пропорциональны 4/2 = 2/1. Следовательно, опорная прямая совпадает со второй граничной прямой области допустимых решений, проходит через две угловые точки этой области и . Задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка . Находим точки , , решая соответствующие системы уравнений. Вычисляем Ответ: при Пример 2.4. Решить задачу линейного программирования. Рис. 2.6 Прямые, ограничивающие ОДР: Решение. Ответ: . Пример 2.5. Решить задачу линейного программирования. Рис. 2.7 Решение. Строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств (рис. 2.7). Область допустимых решений задачи – пустое множество. Задача не имеет решения ввиду несовместности системы ограничений. Ответ: система ограничений несовместна. Лекция №3 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Графический метод решения задач линейного Данным методом решаются задачи линейного программирования, имеющие каноническую форму и удовлетворяющие условию , где n – число неизвестных системы, r – ранг системы векторов-условий (число линейно независимых уравнений системы). Рассмотрим алгоритм метода на конкретном примере. Пример 2.6. Решить графическим методом. , . Решение. 1. Проверяем условие применимости графического метода. Нетрудно видеть, что любые два из векторов-столбцов системы ограничений, например, , являются линейно независимыми, так как их координаты непропорциональны, поэтому ранг системы векторов-условий r = 2. Находим n — r = 4 — 2 =2 £ 2. Следовательно, метод применим. 2. Приведем систему ограничений-уравнений к равносильной, разрешенной с помощью метода Жордана – Гаусса. Одновременно исключим разрешенные неизвестные из целевой функции. Для этого Т а б л и ц а 2.1
запишем коэффициенты целевой функции в последней (третьей) строке таблицы, под матрицей системы. 3. Отбросим в уравнениях-ограничениях неотрицательные разрешенные неизвестные и и заменим знаки равенства знаками » «, получим эквивалентную задачу линейного программирования с двумя переменными которая решается графическим методом (рис. 2.8).
Рис. 2.8 Оптимальное решение ; = (2; 0). Значение целевой функции = 4 × 2 + 0 + 5 = 13. 4. Используем систему ограничений исходной задачи, приведенную к каноническому виду, и оптимальное решение задачи с двумя переменными = (2; 0) для нахождения оптимального решения исходной задачи ; . Записываем оптимальное решение исходной задачи Ответ: max Z(X) = 13 при = (3; 0; 2; 0). Задания для самостоятельного решения Решить задачи линейного программирования графическим методом. Пример 2.7. , Пример 2.8. , Пример 2.9. , Пример 2.10. ,
Пример 2.11. ,
Пример 2.12. ,
Лекция№4. СВОЙСТВА РЕШЕНИЙ ЗАДАЧ ЛИНЕЙНОГО ⇐ Предыдущая12345678910Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
Графический метод решения LPP
Простые задачи линейного программирования с двумя переменными легко решаются графическим методом. Схема графического метода решения lpp следующая:
Схема графического метода решения lpp следующая:
Шаг 1:
Рассмотрим каждое ограничение-неравенство как уравнение.
Шаг 2:
Нарисуйте график каждого уравнения, потому что каждое из них геометрически представляет собой прямую линию.
Шаг 3:
Затенение допустимой области. Каждая точка на прямой будет удовлетворять уравнению прямой.
- Если ограничение-неравенство, соответствующее этой линии, равно «≤», то область ниже линии , лежащей в первом квадранте, заштрихована.
- Если ограничение-неравенство, соответствующее этой линии, равно «≥», то область над линией , лежащей в первом квадранте, заштрихована.
- Все точки в общей области будут удовлетворять всем ограничениям одновременно.
- Полученная таким образом общая область известна как возможная область.
Шаг 4:
Найдите оптимальное решение в допустимой области.
- Чтобы определить оптимальную точку, сначала найдите угловые точки на графике или найдите их, решая соответствующие линейные уравнения, взятые по два за раз.
- Затем вычислите значение целевой функции в каждой угловой точке.
- Угол, при котором целевая функция оптимальна (максимум или минимум), даст оптимальное решение ЗПП.
Утилита графического метода для решения LPP:
1. Если есть только две переменные, мы можем использовать графический метод для решения LPP.
2. Когда в задаче две переменные, мы можем называть их x 1 и x 2 , и мы можем провести большую часть анализа на двумерном графике.
3. Еще одним преимуществом графического подхода является его визуальная природа.
4. Графические методы дают нам представление об алгебре линейного программирования, и оно может закрепить наше понимание основных определений и возможностей.
По этим причинам графический подход служит отличной основой для работы с концепциями линейного программирования.
Пример:
Решите следующую LPP графическим методом:
Максимизируйте Z = 40x + 30y
При условии
2x + y ≤ 16
x + y ≤ 10
и,
x, y ≥ 0.
Решение:
. шаги:
ШАГ 1: Нарисуйте систему неравенств.
- Ограничения x ≥ 0 означают от оси y вправо, а y ≥ 0 означают от оси x вверх, поэтому заштрихован только первый квадрант.
- Сначала нарисуйте линию: 2x + y = 16, чтобы нарисовать график 2x + y ≤ 16.
Положите x=0 в 2x + y = 16 и найдите y. Итак, мы получаем y=16 при x=0, то есть точка (x, y) = (0, 16).
Положите y=0 в 2x + y = 16 и найдите x. Итак, мы получаем x=8 при y=0, то есть точка (x, y) = (8, 0).
Участок (0, 16) и (8, 0). Нарисуйте прямую, проходящую через эти точки. Эта линия представляет 2x + y = 16, как показано красным цветом на следующем рисунке.
Нарисуйте прямую, проходящую через эти точки. Эта линия представляет 2x + y = 16, как показано красным цветом на следующем рисунке.
Ограничение 2x + y ≤ 16 имеет «≤», затем закрасьте область ниже линии 2x + y = 16, лежащей в первом квадранте.
- Затем нарисуйте линию: x + y = 10, чтобы нарисовать график x + y ≤ 10.
Поместите x=0 в x + y = 10 и найдите y. Итак, мы получаем y=10 при x=0, то есть точка (x, y) = (0, 10).
Положите y=0 в x + y = 10 и найдите x. Итак, мы получаем x=10 при y=0, то есть точка (x, y) = (10, 0).
Участок (0, 10) и (10, 0). Нарисуйте прямую, проходящую через эти точки. Эта линия представляет x + y = 10, как показано синим цветом на следующем рисунке.
Ограничение x + y ≤ 10 имеет значение «≤», затем заштрихуйте область ниже линии x + y = 10, лежащей в первом квадранте.
Далее добавляем стрелки на оси. Эти стрелки указывают требуемую заштрихованную область или допустимую область, которая представляет график исходной системы неравенств.
ШАГ 2: Далее перечислите все вершины.
Вершины являются угловыми точками допустимой области. Имеется четыре угла допустимой области. На приведенном выше рисунке три угла равны (0,0), (8,0) и (0,10). Единственная неочевидная вершина на графике — это пересечение 2x+y=16 и x+y=10. Найдите точку пересечения следующим образом:
Вычтем уравнение: x+y=10 из уравнения 2x+y=16, получим
(2x+y)−(x+y) = 16−10
x = 6
Подставим x=6 в x +y=10 и найти y, это дает y=4. Следовательно, точка пересечения, то есть четвертая вершина, есть (6, 4).
Таким образом, вершин четыре; (0,0), (8,0), (0,10) и (6,4).
ШАГ 3: Далее находим максимальное значение целевой функции: Z = 40x + 30y для данного региона.
Оценить целевую функцию; Z = 40x + 30y для каждой вершины, как показано ниже:
Обратите внимание, что в этой таблице наибольшее значение целевой функции Z = 40x + 30y равно 360 и находится в вершине (6,4).
Таким образом, максимальное значение Z = 40x + 30y равно 360, что происходит при x=6 и y=4.
(Источник – различные книги из библиотеки колледжа)
Нажмите здесь, чтобы узнать больше о LPP графический метод, решить следующие lpp графическим методом, как решить lpp графическим методом, решение lpp графическим методом, ограничения графического метода в lpp, задача линейного программирования графическим методом, задача линейного программирования графическим методом задачи, задача линейного программирования графическая методические вопросы, решить задачу линейного программирования графическим методом, решить следующую задачу линейного программирования графическим методом, как решить задачу линейного программирования графическим методом, решить задачу линейного программирования графическим методом, ограничения графического метода в задаче линейного программирования
Решите следующую задачу линейного программирования (LPP) с помощью графического метода
спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 700 раз
$\begingroup$
Решите эту задачу линейного программирования (LPP) с помощью графического метода:
$F=2x_1-x_2-2x_3+6x_4$
$x_1+x_2+x_3+3x_4=16$
$-x_1+x_2+3x_3-x_4=8$
$x_1\geq0 ;x_2\geq0 ;x_2\geq0 ;x_3\geq0;x_4\geq0$
Max $F=?$
Я искал и узнал, что графический метод можно использовать, когда у нас есть две переменные, в противном случае, если у нас есть 4 переменные, как в моем примере, предпочтительнее использовать симплекс-метод. Но Задача просит решить ее Графическим методом.
Но Задача просит решить ее Графическим методом.
P.s. Я знаю, как решить, если бы у нас было бы 2 переменные. Нужна небольшая помощь с 4.
Заранее спасибо 🙂
- линейное программирование
$\endgroup$
1
$\begingroup$
$x_1+x_2+x_3+3x_4=16 \tag{1}$
$-x_1+x_2+3x_3-x_4=8 \tag{2}$
Сложение и вычитание (1) и (2) дает :
$$x_1=x_3-2x_4+4\tag{3}$$
$$x_2=-2x_3-x_4+12\tag{4}$$
Теперь подключите (3)+(4) к функция $F$, которая становится:
$$F=2x_1-x_2-2x_3+6x_4=2(x_3-2x_4+4)-(-2x_3-x_4+12)-2x_3+6x_4$$
$$F=2x_3+3x_4-4$$
Теперь вам нужно решить (графически) задачу линейного программирования с двумя переменными $x_3,x_4$ :
Максимизировать $F=2x_3+3x_4-4$ при ограничениях:
$$\left\{\begin{ array}{llll}используя \ (3): \ & \ \ x_3-2x_4+4& \ge& 0\\используя \ (4): \ &-2x_3-x_4+12&\ge&0\\& x_3& \ge &0\\ &x_4 &\ge&0\end{массив}\right.

 ..
..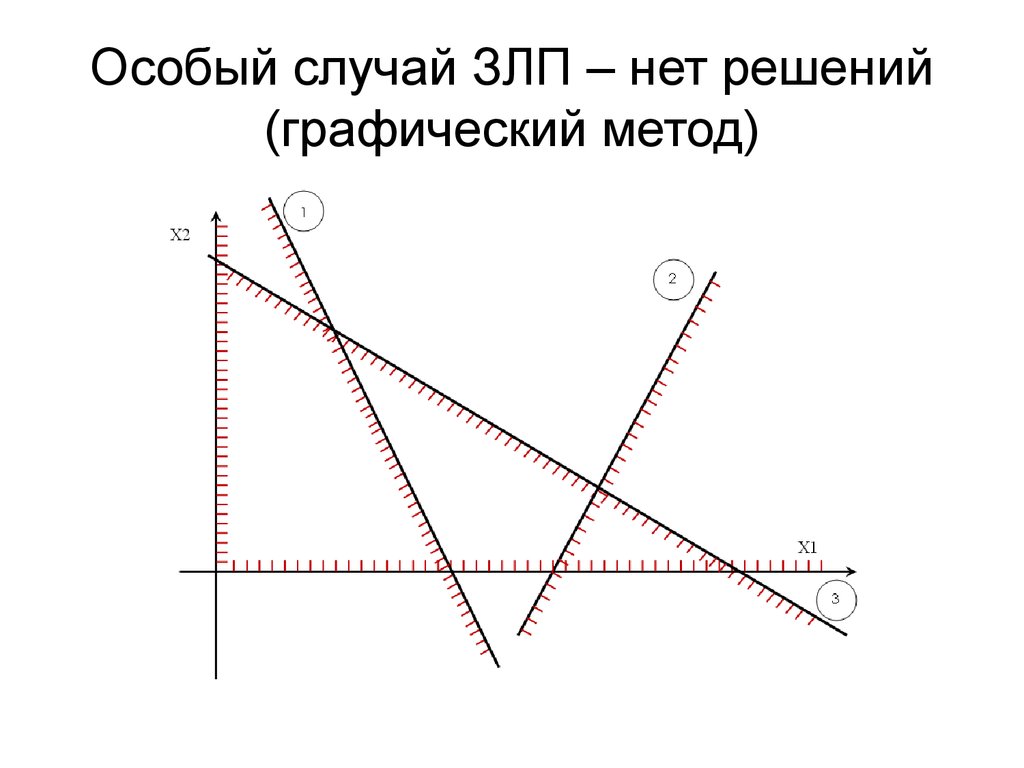
 Пусть произвольно выбранная точка М( ) принадлежит ( ), ее проекцией на прямую (L) является точка . Вектор . Координаты векторов и совпадают с координатами точек М и А, т. е. = ( ), . Вектор коллинеарен вектору , поэтому = ×l, где l некоторое число. Найдем скалярное произведение . Запишем это равенство через координаты векторов . Так как точка А принадлежит прямой (L), то , получаем .
Пусть произвольно выбранная точка М( ) принадлежит ( ), ее проекцией на прямую (L) является точка . Вектор . Координаты векторов и совпадают с координатами точек М и А, т. е. = ( ), . Вектор коллинеарен вектору , поэтому = ×l, где l некоторое число. Найдем скалярное произведение . Запишем это равенство через координаты векторов . Так как точка А принадлежит прямой (L), то , получаем .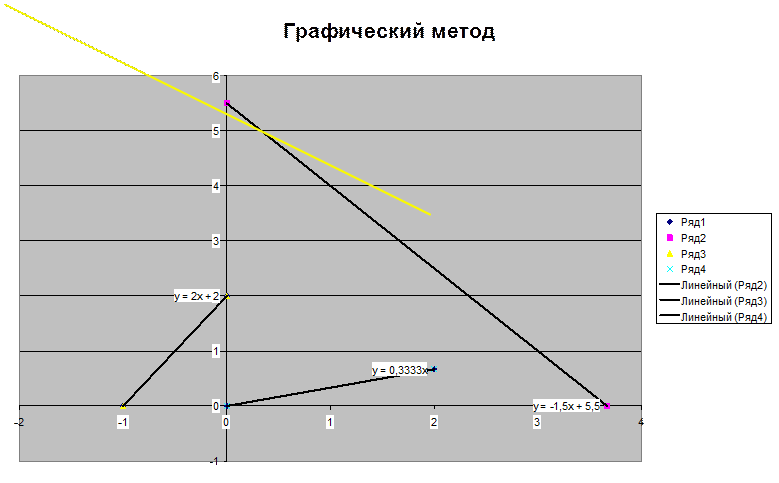

 Для нахождения оптимального решения задачи необходимо использовать опорную прямую.
Для нахождения оптимального решения задачи необходимо использовать опорную прямую.
 4
4
 Строим область допустимых решений, нормаль и одну из линий уровня (рис. 2.6). В данной задаче необходимо найти максимум целевой функции, поэтому линию уровня перемещаем в направлении нормали. Ввиду того, что в этом направлении область допустимых решений не ограничена, линия уровня уходит в бесконечность. Задача не имеет решения по причине неограниченности целевой функции.
Строим область допустимых решений, нормаль и одну из линий уровня (рис. 2.6). В данной задаче необходимо найти максимум целевой функции, поэтому линию уровня перемещаем в направлении нормали. Ввиду того, что в этом направлении область допустимых решений не ограничена, линия уровня уходит в бесконечность. Задача не имеет решения по причине неограниченности целевой функции.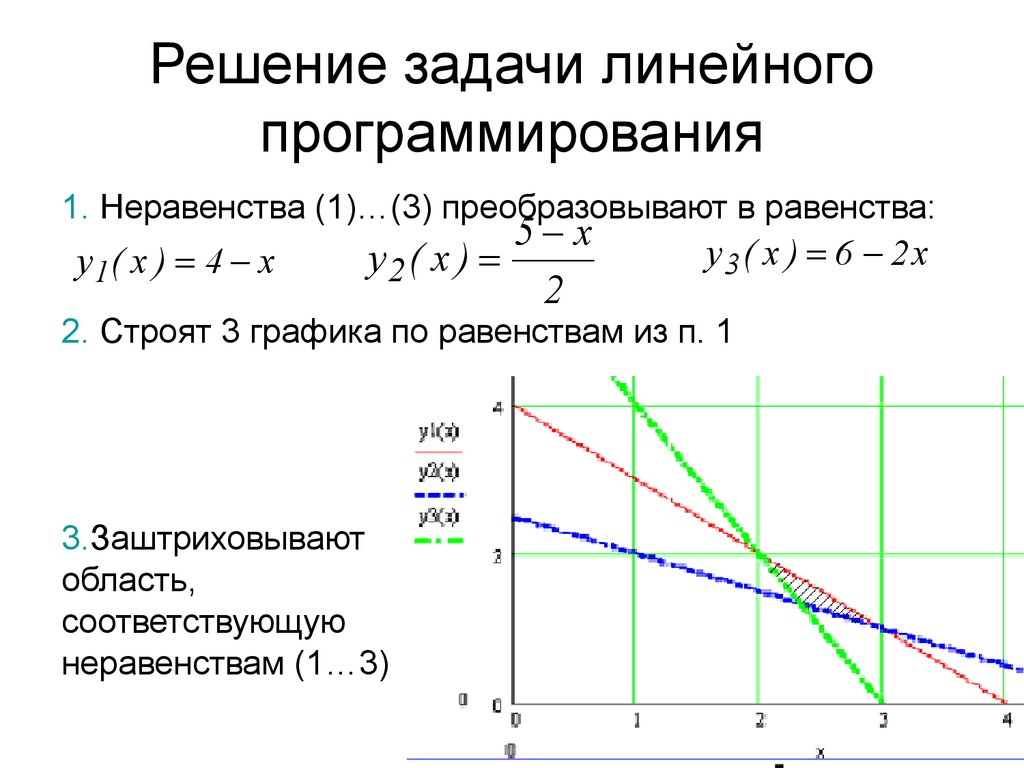 Если уравнения системы ограничений линейно независимые, то r = m.
Если уравнения системы ограничений линейно независимые, то r = m. Вычисления приведены в табл. 2.1. Задача после проведенных преобразований
Вычисления приведены в табл. 2.1. Задача после проведенных преобразований