Какими свойствами обладает произведение вектора на число: Умножение вектора на число — урок. Геометрия, 9 класс.

alexxlab / / Разное

Содержание

Произведение вектора на число / Векторы / Справочник по геометрии 7-9 класс

  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Векторы
  5. Произведение вектора на число
Определение
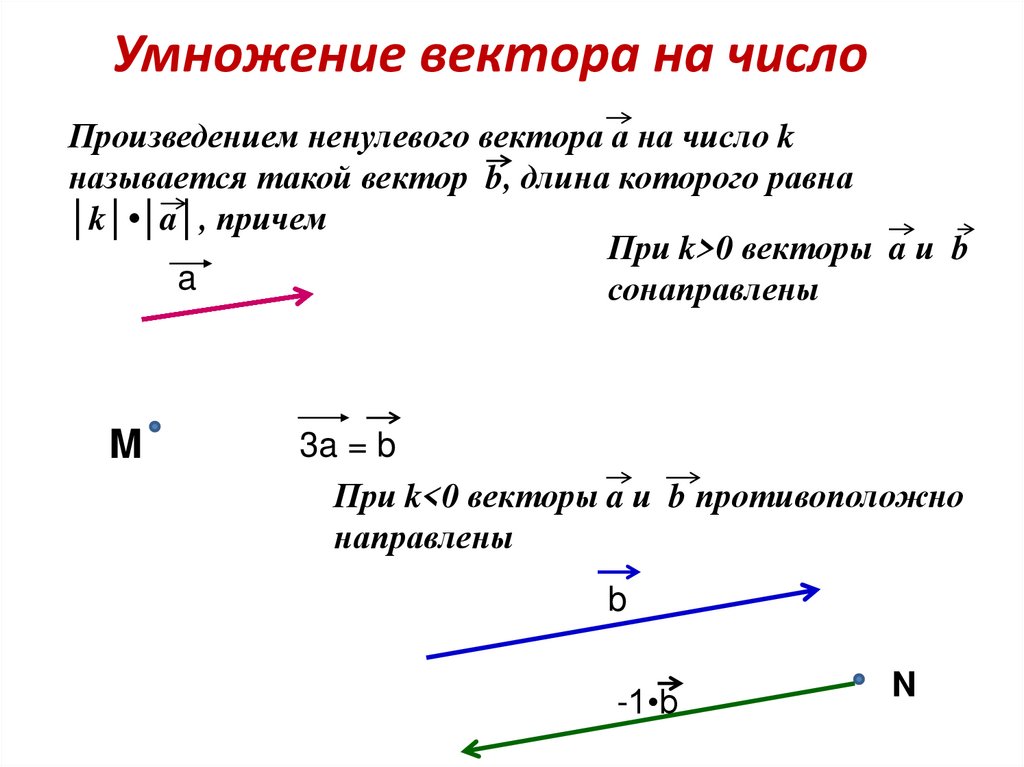
Произведением ненулевого вектора на число называется такой вектор , длина которого равна , причём векторы и сонаправлены при 0 и противоположно направлены при 0. Произведением нулевого вектора на любое число считается нулевой вектор.

Произведение вектора на число обозначается так:

Из определения следует, что:

  1. произведение любого вектора на число нуль есть нулевой вектор;
  2. для любого числа и любого вектора векторы и
    коллинеарны    .

Основные свойства умножения вектора на число:

Для любых чисел , и любых векторов , справедливы равенства:

10. () = () (сочетательный закон).

20. ( + ) = + (первый распределительный закон).

30. ( + ) = + (второй распределительный закон).

Замечание

Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, выражение = 2( — ) + ( + ) — 3( — + ) можно преобразовать так:

= 2 — 2 + + — 3 + 3 — 3= — 5 + 4.

Советуем посмотреть:

Понятие вектора

Равенство векторов

Откладывание вектора от данной точки

Сумма двух векторов

Законы сложения векторов. Правило параллелограмма

Сумма нескольких векторов

Вычитание векторов

Применение векторов к решению задач

Средняя линия трапеции

Векторы

Правило встречается в следующих упражнениях:

7 класс

Задание 775, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 781, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 804, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 805, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 806, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 903, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Свойства векторов, свойства скалярного и векторного произведения векторов.

Содержание:

  • Действия над векторами
  • Свойства операции сложения:
  • Свойства умножения вектора на число:
  • Свойства скалярного произведения:
  • Свойства векторного произведения:
  • Свойства смешанного произведения:

В данной теме мы подытожим раздел векторы, опишем все действия, которые можно совершать над векторами и какими свойствами они обладают.

Определение

Вектором называется направленный отрезок $\overline{A B}$ , где точка $A$ — начало, точка $B$ — конец вектора.

Суммой $\overline{a}+\overline{b}$ векторов $\overline{a}$ и $\overline{b}$ называют такой третий вектор $\overline{c}$, начало которого совпадает с началом $\overline{a}$, а конец — с концом $\overline{b}$ при условии, что конец вектора $\overline{a}$ и начало вектора $\overline{b}$ совпадают.

Свойства операции сложения:

1  $\overline{a}+\overline{b}=\overline{b}+\overline{a}$ — коммутативность

2  $(\overline{a}+\overline{b})+\overline{c}=\overline{a}+(\overline{b}+\overline{c})$ — ассоциативность

3  $\overline{a}+\overline{0}=\overline{a}$

4  $\overline{a}+(-\overline{a})=\overline{0}$

Определение

Разностью $\overline{a}-\overline{b}$ векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$ такой, что выполняется условие: $\overline{b}+\overline{c}=\overline{a}$.

Произведением $\alpha \overline{a}$ вектора $\overline{a}$ на число $\alpha$ называется вектор $\overline{b}$, удовлетворяющий условиям:

  1. $\overline{b} \| \overline{a}$
  2. $|\overline{b}|=|\alpha||\overline{a}|$
  3. $\overline{a} \uparrow \uparrow \overline{b}$, если $\alpha>0$, $\overline{a} \uparrow \downarrow \overline{b}$, если $\alpha \lt 0$.

Свойства умножения вектора на число:

1  $(\alpha \pm \beta) \overline{a}=\alpha \overline{a} \pm \beta \overline{a}$

2  $\alpha(\overline{a} \pm \overline{b})=\alpha \overline{a} \pm \alpha \overline{b}$

3  $\alpha(\beta \overline{a})=(\alpha \beta) \overline{a}=\beta(\alpha \overline{a})$

4  $1 \cdot \overline{a}=\overline{a}$

5  $-1 \cdot \overline{a}=-\overline{a}$

6  $0 \cdot \overline{a}=\overline{0}$

Определение

Скалярным произведением двух ненулевых векторов $\overline{a}$ и $\overline{b}$ называется число, равное произведению длин этих векторов на косинус угла между ними:

$$\bar{a} \bar{b}=\bar{a} \cdot \bar{b}=(\bar{a}, \bar{b})=|\bar{a}||\bar{b}| \cos (\bar{a}, \bar{b})$$

Свойства скалярного произведения:

1  $(\overline{a}, \overline{b})=(\overline{b}, \overline{a})$ — симметричность.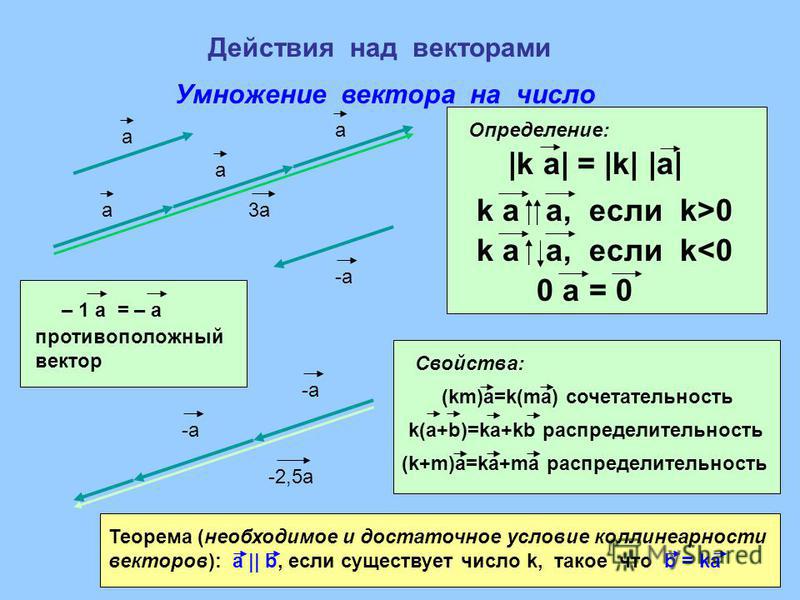 {2}$ и называется скалярный квадрат.

3  Если $\overline{a} \neq \overline{0}$, то $(\bar{a}, \bar{b})=|\bar{a}| \cdot Пр_{\bar{a}} \bar{b}$

4  Если $\overline{a} \neq \overline{0}$ и $\overline{b} \neq \overline{0}$ и $(\overline{a}, \overline{b})=0$, то $\overline{a} \perp \overline{b}$. Верно и обратное утверждение.

5  $(\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c})$

6  $(\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b})$

7  $(\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d})$

Определение

Векторным произведением ненулевых векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$, обозначаемый символом $[\overline{a}, \overline{b}]$ или $\overline{a} \times \overline{b}$, длина которого $|\bar{c}|=|\bar{a}||\bar{b}| \sin (\bar{a}, \bar{b})$.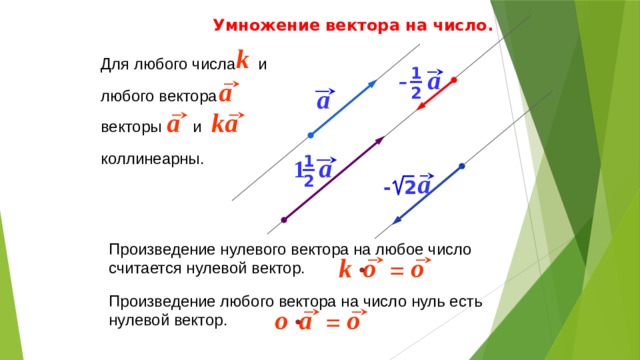

Свойства векторного произведения:

1  $[\overline{a}, \overline{b}]=\overline{0}$, тогда и только тогда, когда $\overline{a} \| \overline{b}$

2  $[\overline{a}, \overline{b}]=-[\overline{b}, \overline{a}]$

3  Модуль векторного произведения $|[\overline{a}, \overline{b}]|$ равен площади параллелограмма, построенного на заданных векторах $\overline{a}$ и $\overline{b}$ (рис. 2), т.е.

$$S=|[\bar{a}, \bar{b}]|=|\bar{a}||\bar{b}| \sin (\bar{a}, \bar{b})$$

4  $[\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}]$

5  $\left[\overline{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right]$

Определение

Смешанным произведением трех векторов $\overline{a}$, $\overline{b}$, $\overline{c}$ называется число, равное скалярному произведению вектора $\overline{a} \times \overline{b}$ на вектор $\overline{c}$: $(\overline{a}, \overline{b}, \overline{c})=([\overline{a}, \overline{b}], \overline{c})$

Свойства смешанного произведения:

1  $(\overline{a}, \overline{b}, \overline{c})=(\overline{a},[\overline{b}, \overline{c}])$

2  $(\overline{a}, \overline{b}, \overline{c})=(\overline{b}, \overline{c}, \overline{a})=(\overline{c}, \overline{a}, \overline{b})=-(\overline{b}, \overline{a}, \overline{c})=-(\overline{c}, \overline{b}, \overline{a})=-(\overline{a}, \overline{c}, \overline{b})$

3  Три вектора компланарны тогда и только тогда, когда $(\overline{a}, \overline{b}, \overline{c})=0$

4  Тройка векторов является правой тогда и только тогда, когда $(\overline{a}, \overline{b}, \overline{c})>0$. Если же $(\overline{a}, \overline{b}, \overline{c}) \lt 0$, то векторы $\overline{a}$, $\overline{b}$ и $\overline{c}$ образуют левую тройку векторов. \lt /p> \lt p>5  $(\lambda \overline{a}, \overline{b}, \overline{c})=(\overline{a}, \lambda \overline{b}, \overline{c})=(\overline{a}, \overline{b}, \lambda \overline{c})=\lambda(\overline{a}, \overline{b}, \overline{c})$

6  $\left(\overline{a}_{1}+\overline{a}_{2}, \overline{b}, \overline{c}\right)=\left(\overline{a}_{1}, \overline{b}, \overline{c}\right)+\left(\overline{a}_{2}, \overline{b}, \overline{c}\right)$

7  $\left(\overline{a}, \overline{b}_{1}+\overline{b}_{2}, \overline{c}\right)=\left(\overline{a}, \overline{b}_{1}, \overline{c}\right)+\left(\overline{a}, \overline{b}_{2}, \overline{c}\right)$

8  $\left(\overline{a}, \overline{b}, \overline{c}_{1}+\overline{c}_{2}\right)=\left(\overline{a}, \overline{b}, \overline{c}_{1}\right)+\left(\overline{a}, \overline{b}, \overline{c}_{2}\right)$

9  $([\overline{a}, \overline{b}], \overline{c})=\overline{b}(\overline{a}, \overline{c})-\overline{a}(\overline{b}, \overline{c}) ;(\overline{a},[\overline{b}, \overline{c}])=\overline{b}(\overline{a}, \overline{c})-\overline{c}(\overline{a}, \overline{b})$

10  Тождество Якоби: $(\overline{a},[\overline{b}, \overline{c}])+(\overline{b},[\overline{c}, \overline{a}])+(\overline{c},[\overline{a}, \overline{b}])=0$

Читать дальше: примеры решения задач с векторами.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Произведение векторов — определение, формула, примеры

Произведение векторов бывает двух типов. Вектор имеет как величину, так и направление, и, исходя из этого, два произведения векторов равны точечному произведению двух векторов и перекрестному произведению двух векторов. Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам.

Давайте узнаем о двух произведениях векторов, рабочих правилах, свойствах, использовании, примерах этих произведений векторов.

1. Что такое произведение векторов?
2. Рабочее правило для произведения векторов
3. Свойства произведения векторов
4. Использование произведения векторов
5. Примеры произведения векторов
6. Практические вопросы
7. Часто задаваемые вопросы о продукте Vectors

Что такое произведение векторов?

Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся больше о каждом из произведений векторов.

Скалярное произведение

Скалярное произведение векторов также называется скалярным произведением векторов. Результат скалярного произведения векторов является скалярным значением. Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.

Пусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается буквой a.b, которая определяется как:

\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ .

Здесь \(|\overrightarrow a|\) — величина \(\overrightarrow a\), \(|\overrightarrow b|\) — величина \(\overrightarrow b\), а θ — величина угол между ними.

Перекрестное произведение

Перекрестное произведение также называется векторным произведением. Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Когда два вектора перемножаются друг с другом и произведение также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.

Мы можем понять это на примере, что если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY. Символ × используется между исходными векторами. Векторное произведение или перекрестное произведение двух векторов отображается как:

\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)

Здесь \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, а \(\overrightarrow{c}\) — результирующий вектор. Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется формулой:

\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)

Рабочее правило для произведения векторов

Рабочее правило для произведения двух векторов, скалярного произведения и перекрестного произведения можно понять из приведенных ниже предложений.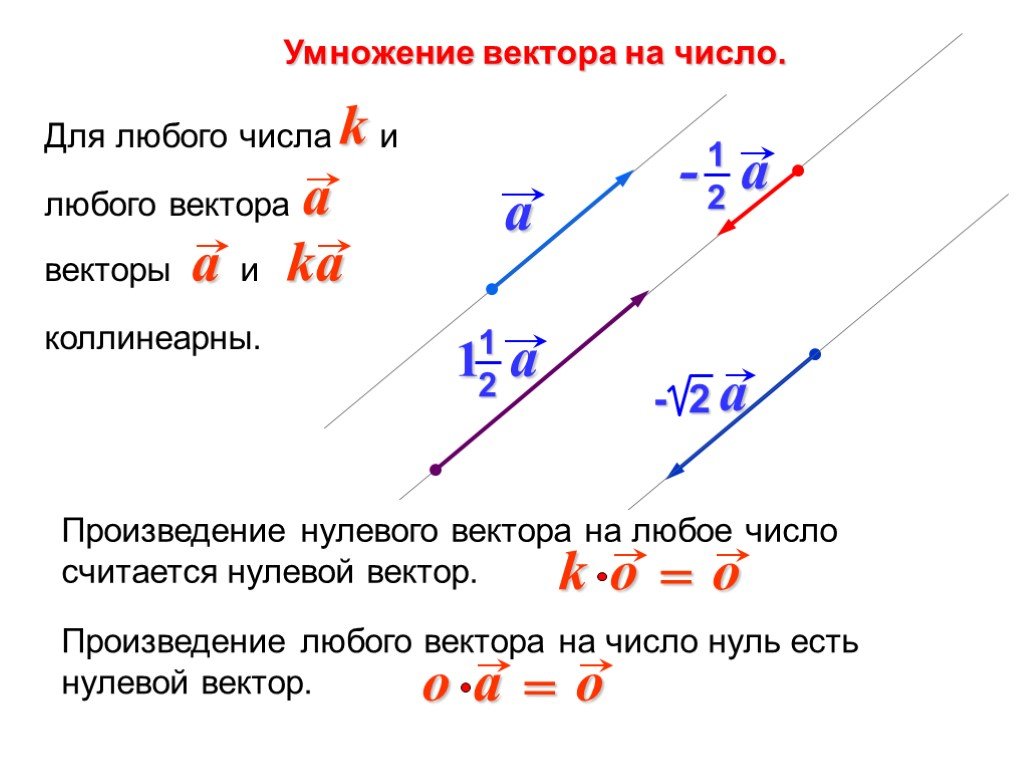

Скалярное произведение

Для скалярного произведения двух векторов два вектора выражаются через единичные векторы i, j, k вдоль осей x, y, z, затем скалярное произведение получается следующим образом:

Если \(\overrightarrow a = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow b = a_2 \hat i + b_2 \hat j + c_2\hat k\), то

\(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + b_1 \hat j + c_1 \hat k)(a_2 \hat i + b_2 \hat j + c_2 \hat k)\)

= \((a_1a_2) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)

\(\overrightarrow a. \overrightarrow b\) = \(a_1a_2 + b_1b_2+ c_1c_2\)

Перекрестное произведение

Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\ ) — два вектора, такие, что \(\overrightarrow{a}\)= \(a_1\hat i+b_1 \hat j+c_1 \hat k\) и \(\overrightarrow{b}\) = \(a_2 \ шляпа i+b_2 \ шляпа j+c_2 \ шляпа k\), то с помощью определителей мы могли бы найти перекрестное произведение и записать результат в виде формулы перекрестного произведения, используя следующую матричную запись.

Перекрестное произведение двух векторов также представляется с помощью формулы перекрестного произведения следующим образом: a_2c_1) + \hat k (a_1b_2-a_2b_1)\)

Примечание: \( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, ось и ось z соответственно.

Свойства произведения векторов

Скалярное произведение единичного вектора изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0.

  • \(\hat i.\hat i\) = \(\hat j.\hat j\) = \(\hat k.\hat k\)= 1
  • \(\шляпа i.\шляпа j\) = \(\шляпа j.\шляпа k\) = \(\шляпа k. \шляпа i\)= 0

Перекрестное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и перекрестное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их векторное произведение равно 0. А угол между двумя перпендикулярными векторами равен 90º, и их векторное произведение дает вектор, который перпендикулярен двум заданным векторам.

  • \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)

Перекрестное произведение двух векторов следует циклическому порядку, как показано на изображении ниже. Перекрестное произведение двух векторов в циклической последовательности дает третий вектор в последовательности.

  • \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}; \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}; \overrightarrow{k} \times \overrightarrow{i} = \overrightarrow{j}\)
  • \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}; \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}; \overrightarrow{i}\times \overrightarrow{k} = \overrightarrow{-j}\)

Свойства произведения векторов помогают получить подробное представление об умножении векторов, а также выполнять многочисленные вычисления с использованием векторов. Здесь перечислены несколько важных свойств произведения векторов.

  1. Перекрестное произведение двух векторов задается формулой \( \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).
  2. Скалярное произведение двух векторов определяется формулой \( \overrightarrow{a} . \overrightarrow{b} = |a| |b| \cos(\theta)\).
  3. Скалярное произведение двух векторов подчиняется свойству коммутативности. \(\vec a. \vec b = \vec b. \vec a \)
  4. Перекрестное произведение двух векторов не соответствует свойству коммутативности. \( \vec a \times \vec b\neq \vec b \times \vec a \)
  5. Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
  6. Распределительное свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
  7. Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
  8. Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
  9. Умножить на скалярную величину: \(c(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{ б}\)
  10. Скалярное произведение двух векторов является скаляром и лежит в плоскости двух векторов.
  11. Перекрестное произведение двух векторов — это вектор, который перпендикулярен плоскости, содержащей эти два вектора.

Использование произведения векторов

Ниже приведены некоторые важные области применения произведения векторов. Давайте разберемся в каждом из этих применений в следующих параграфах.

  • Проекция вектора
  • Угол между двумя векторами
  • Продукт тройного креста
  • Площадь параллелограмма
  • Объем параллелепипеда

Проекция вектора

Скалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косеканс угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.

Здесь \(\overrightarrow a\) и \(\overrightarrow b\) — два вектора, а θ — угол между двумя векторами. 2}}\)

Тройное перекрестное произведение

Перекрестное произведение вектора на произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:

\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)

Площадь параллелограмма

Две смежные стороны параллелограмма могут быть представлены векторами \(\overrightarrow a\) и \(\overrightarrow b\). Площадь параллелограмма равна произведению основания и высоты параллелограмма. Рассмотрим основание параллелограмма как \(|\overrightarrow a|\), а высоту параллелограмма как \(|\overrightarrow b|\)sin θ.

Здесь Основание = \(|\overrightarrow a|\), Высота = \(|\overrightarrow b|\)sin θ, а Площадь параллелограмма = Основание x Высота

Площадь параллелограмма = \(|\overrightarrow a|.|\overrightarrow b|\)sin θ = \(\overrightarrow a \times \overrightarrow b \)

Объем параллелепипеда

Параллелепипед равен шести двусторонняя фигура, каждая из сторон которой является параллелограммом. Здесь параллелограммы противоположных сторон одинаковы. Объем V параллелепипеда можно получить со стороны ребер a, b, c. Объем параллелепипеда можно получить из произведения площади основания на высоту параллелепипеда. Площадь основания параллелепипеда равна |b x c| а высота параллелепипеда равна |a|. Формула расчета объема параллелепипеда выглядит следующим образом.

V = a.(b x c)

Связанные темы

Следующие темы помогают лучше понять произведение векторов.

  • Коллинеарные векторы
  • Векторы
  • Типы векторов
  • Добавление векторов
  • Перекрестное произведение двух векторов

Часто задаваемые вопросы о продукте векторов

Что такое скалярное произведение векторов?

Скалярное произведение двух векторов имеет два определения. Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением.

Как рассчитать скалярное произведение векторов?

Скалярный продукт можно рассчитать в три простых шага. Сначала найдите величину двух векторов a и b, т.е. |a| и |б|. Во-вторых, найдите косеканс угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косеканса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. (a.b = |a|.|b|.Cosθ. Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.

Почему скалярное произведение называется скалярным произведением векторов?

Скалярное произведение является скалярным, поскольку все отдельные составляющие ответа являются скалярными значениями. В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные значения. Следовательно, скалярное произведение также называют скалярным произведением.

Почему мы используем косинус в скалярном произведении векторов?

Для нахождения скалярного произведения нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы находим cosθ в скалярном произведении двух векторов.

Что такое векторное произведение векторов?

В результате перекрестного произведения двух векторов при умножении третий вектор перпендикулярен двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. a × b = c, где c — векторное произведение двух векторов a и b.

Что такое скалярное произведение и векторное произведение векторов?

Векторы можно перемножать двумя разными способами: точечным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. В результате скалярное произведение дает скалярную величину, тогда как векторное произведение дает векторную величину. Скалярное произведение — это скалярное произведение двух векторов, а перекрестное произведение двух векторов — это векторное произведение двух векторов. Скалярное произведение также известно как скалярное произведение, а перекрестное произведение также известно как векторное произведение. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).

В чем разница между скалярным произведением и перекрестным произведением векторов?

При умножении векторов скалярное произведение исходных векторов дает скалярную величину, тогда как перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.

Что такое правило большого пальца правой руки для перекрестного произведения векторов?

Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора. Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.

Dot Product из двух векторов

Последняя обновленная дата: 21 апреля 2023

•

Всего просмотров: 441K

•

Просмотры сегодня: 9,28K

Векты могут быть умножены двумя различными способами, иумно, Scalar Product Product, продукт Scalar. или скалярное произведение, в котором результатом является скаляр, и векторное произведение или векторное произведение, в котором результатом является вектор. Скалярное произведение двух векторов означает скалярное произведение двух заданных векторов. Это скалярное число, которое получается путем выполнения определенной операции над различными компонентами вектора. Скалярное произведение применимо только для пар векторов с одинаковым числом измерений. Символ, используемый для скалярного произведения, — толстая точка. Это скалярное произведение широко используется в математике и физике. В этой статье мы подробно обсудим скалярное произведение векторов, определение скалярного произведения, формулу скалярного произведения и пример скалярного произведения.

Определение скалярного произведения

Скалярное произведение двух различных ненулевых векторов обозначается буквой a.b и определяется следующим образом:

0 ≤ θ ≤ π

(Изображение будет загружено в ближайшее время)

Если a = 0 или b = 0, θ не будет определено, и в этом случае

a.b= 0

Формула скалярного произведения

Вы можете определить скалярное произведение двух векторов двумя разными способами: геометрическим и алгебраическим.

Определение геометрии скалярного произведения

Геометрический смысл скалярного произведения гласит, что скалярное произведение двух заданных векторов a и b обозначается следующим образом:

a.b = |a||b| cos θ

Здесь |a| и |б| называются величинами векторов a и b, а θ — угол между векторами a и b.

Если два вектора ортогональны, то есть угол между ними равен 90, то a.b = 0, так как cos 90 = 0.

Если два вектора параллельны друг другу, то a.b =|a||b| так как cos 0 = 1,

Алгебра скалярных произведений Определение

Алгебра скалярных произведений говорит, что скалярное произведение данных двух произведений – a = (a1, a2, a3) и b= (b1, b2, b3) определяется выражением:

a.b= (a1b1 + a2b2 + a3b3)

Свойства скалярного произведения двух векторов

Ниже приведены свойства векторов:

  1. Переместительное свойство

a . b = b.a

3 ab | b|cos θ

a.b =|b||a|cos θ

  1. Распределительное свойство

a.(b + c) = a.b + a.c

  1. Билинейное свойство

a.(rb + c) = r.(a.b) + (a.c)

36 скаляр Свойство умножения

(xa) . (yb) = xy (a.b)

  1. Неассоциативное свойство

Поскольку скалярное произведение между скаляром и вектором не допускается.

  1. Ортогональное свойство

Два вектора ортогональны только тогда, когда a.b = 0

Скалярное произведение векторнозначных функций

Скалярное произведение векторнозначных функций, т. е. r(t) и u(t), каждое из которых дает вам вектор в каждой конкретной время t, и, следовательно, функция r(t)⋅u(t) называется скалярной функцией.

Решенные примеры

Пример 1:

Найдите скалярное произведение a= (1, 2, 3) и b= (4, −5, 6). Какой угол образуют векторы?

Решение:

Используя формулу скалярных произведений,

a.b = (a1b1 + a2b2 + a3b3)

Скалярное произведение можно рассчитать следующим образом: 12

Поскольку a.b — положительное число, можно сделать вывод, что векторы образуют острый угол.

Пример 2:

Два вектора A и B задаются формулой:

A = 2i − 3j + 7k и B= −4i + 2j −4k

Найдите скалярное произведение данных двух векторов.

Решение:

A.B = (2i − 3j +7k) . (−4i + 2j − 4k)

= 2 (−4) + (−3)2 + 7 (−4)

= −8 − 6 − 28

= −42

Ключевые моменты, которые следует помнить

  • продукты, выходной сигнал представляет собой вектор, ортогональный двум заданным векторам.

  • Правило большого пальца правой руки определяет направление векторного произведения двух векторов, а величина определяется площадью параллелограмма, созданного исходными двумя векторами.

  • Нулевой вектор представляет собой перекрестное произведение двух линейных векторов или параллельных векторов.

Заключение

Вектор – это величина, которая имеет как величину, так и направление. К векторам можно применить несколько математических операций, таких как сложение и умножение. Умножение векторов можно выполнить двумя способами: точечным произведением и перекрестным произведением. Скалярное произведение двух векторов представляет собой сумму произведений их соответствующих компонентов. Это произведение их величин на косинус угла между ними. Скалярное произведение вектора на самого себя равно квадрату его величины.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *