Конус. Площадь поверхности конуса. 11-й класс
Тип урока: урок изучения нового материала с применением элементов проблемно-развивающего метода обучения.
Цели урока:
- познавательные:
- ознакомление с новым математическим понятием;
- формирование новых ЗУН;
- формирование практических навыков решения задач.
- развивающие:
- развитие самостоятельного мышления учащихся;
- развитие навыков правильной речи школьников.
- воспитательные:
- воспитание навыков работы в коллективе.
Оборудование урока: магнитная доска, компьютер, экран, мультимедийный проектор, модель конуса, презентация к уроку, раздаточный материал.
Задачи урока (для учащихся):
- познакомиться с новым геометрическим понятием — конус;
- вывести формулу для вычисления площади поверхности конуса;
- научиться применять полученные знания при решении практических задач.

Ход урока
I этап. Организационный.
Сдача тетрадей с домашней проверочной работой по пройденной теме.
Учащимся предлагается узнать тему предстоящего урока, разгадав ребус (слайд 1):
Рисунок 1.
Объявление учащимся темы и задач урока (слайд 2).
II этап. Объяснение нового материала.
1) Лекция учителя.
На доске – таблица с изображением конуса. Новый материал объясняется в сопровождении программного материала «Стереометрия». На экране появляется трёхмерное изображение конуса. Учитель даёт определение конуса, рассказывает о его элементах.(слайд 3). Говорится о том, что конус – это тело, образованное при вращении прямоугольного треугольника относительно катета. (слайды 4, 5). Появляется изображение развёртки боковой поверхности конуса. (слайд 6)
2) Практическая работа.
Актуализация опорных знаний: повторить формулы для вычисления площади круга, площади сектора, длины окружности, длины дуги окружности. (слайды 7–10)
Класс делится на группы. Каждая группа получает вырезанную из бумаги развёртку боковой поверхности конуса (сектор круга с присвоенным номером). Учащиеся выполняют необходимые измерения и вычисляют площадь полученного сектора. Инструкции по выполнению работы, вопросы – постановки проблем – появляются на экране (слайды 11–14). Результаты вычислений представитель каждой группы записывает в заготовленную на доске таблицу. Участники каждой группы склеивают модель конуса из имеющейся у них развёртки.
3) Постановка и решение проблемы.
Как вычислить площадь боковой поверхности конуса, если известны только радиус основания и длина образующей конуса? (слайд 16)
Каждая группа производит необходимые измерения и пытается вывести формулу вычисления искомой площади с помощью имеющихся данных.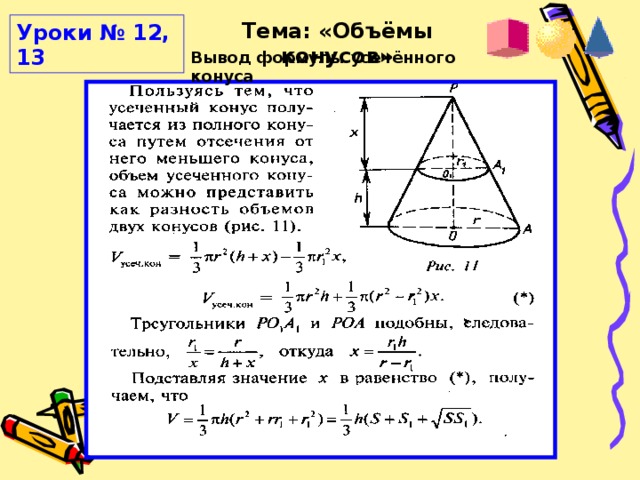 При выполнении этой работы школьники должны заметить, что длина окружности основания конуса равна длине дуги сектора – развёртки боковой поверхности этого конуса. (слайды 17–21) Используя необходимые формулы, выводится искомая формула. Рассуждения учащихся должны выглядеть примерно таким образом:
При выполнении этой работы школьники должны заметить, что длина окружности основания конуса равна длине дуги сектора – развёртки боковой поверхности этого конуса. (слайды 17–21) Используя необходимые формулы, выводится искомая формула. Рассуждения учащихся должны выглядеть примерно таким образом:
Радиус сектора – развёртки равен l, градусная мера дуги – φ. Площадь сектора вычисляется по формуле длина дуги, ограничивающей этот сектор, равна Радиус основания конуса R. Длина окружности, лежащей в основании конуса, равна С = 2πR. Заметим, что Так как площадь боковой поверхности конуса равна площади развёртки его боковой поверхности, то
Итак, площадь боковой поверхности конуса вычисляется по формуле SБПК = πRl.
После вычисления площади боковой поверхности модели конуса по выведенной самостоятельно формуле представитель каждой группы записывает результат вычислений в таблицу на доске в соответствии с номерами моделей.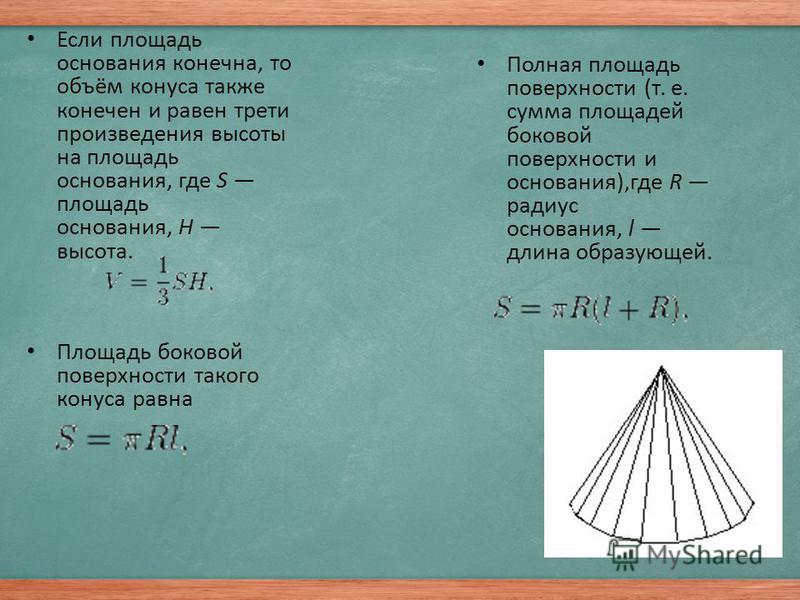 Результаты вычислений в каждой строке должны быть равны. По этому признаку учитель определяет правильность выводов каждой группы. Таблица результатов должна выглядеть таким образом:
Результаты вычислений в каждой строке должны быть равны. По этому признаку учитель определяет правильность выводов каждой группы. Таблица результатов должна выглядеть таким образом:
|
№ модели |
I задание |
II задание |
1 |
48π |
~ 48 π |
2 |
(125/3)π ~ 41,67 π |
~ 41,67 π |
3 |
75π |
~ 75 π |
4 |
(425/9)π ~ 47,22 π |
~ 47,22 π |
5 |
(539/9)π ~ 59,89 π |
~ 59,89 π |
Параметры моделей:
- l=12 см, φ =120°
- l=10 см, φ =150°
- l=15 см, φ =120°
- l=10 см, φ =170°
- l=14 см, φ =110°
Приближённость вычислений связана с погрешностями измерений.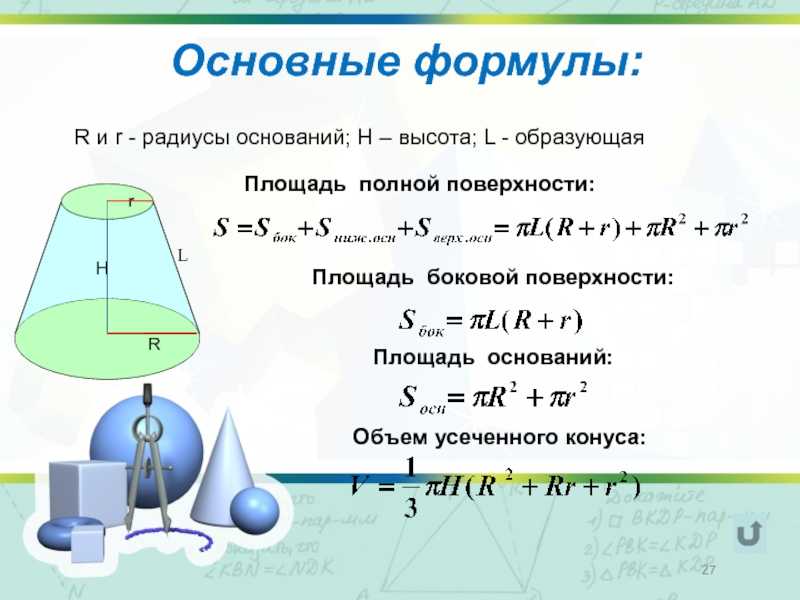
После проверки результатов вывод формул площадей боковой и полной поверхностей конуса появляется на экране (слайды 22–26), ученики ведут записи в тетрадях.
III этап. Закрепление изученного материала.
1) Учащимся предлагаются задачи для устного решения на готовых чертежах.
Найти площади полных поверхностей конусов, изображённых на рисунках (слайды 27–32).
2) Вопрос: равны ли площади поверхностей конусов, образованных вращением одного прямоугольного треугольника относительно разных катетов? Учащиеся выдвигают гипотезу и проверяют её. Проверка гипотезы осуществляется путём решения задач и записывается учеником на доске.
Дано: Δ АВС, ∠С=90°, АВ=с, АС=b, ВС=а;
ВАА’, АВВ’ – тела вращения.
Найти: SППК 1, SППК 2.
Рисунок 5. (слайд 33)
Решение:
1) R=ВС= а ; SППК 1= SБПК 1+ Sосн 1= π а с+π а2 = π а (а + с).
2) R=АС= b ; SППК 2 = SБПК 2 + Sосн 2 = π b с+π b2= π b (b + с).
Если SППК 1 = SППК 2, то а2+ас = b2 + bc, a2 — b2 + ac — bc = 0, (a-b)(a+b+c) = 0. Т.к. a, b, c – положительные числа (длины сторон треугольника), торавенство верно только в случае, если a = b.
Вывод: Площади поверхностей двух конусов равны только в случае равенства катетов треугольника.(слайд 34)
3) Решение задачи из учебника: № 565.
IV этап. Подведение итогов урока.
Домашнее задание: п.55, 56; № 548, № 561. (слайд 35)
Объявление поставленных оценок.
Выводы по ходу урока, повторение основных сведений, полученных на уроке.
Литература (слайд 36)
- Геометрия 10–11 классы – Атанасян, В.
 Ф. Бутузов, С. Б. Кадомцев и др., М., «Просвещение», 2008.
Ф. Бутузов, С. Б. Кадомцев и др., М., «Просвещение», 2008. - «Математические ребусы и шарады» – Н.В. Удальцова, библиотечка «Первого сентября», серия «МАТЕМАТИКА», выпуск 35, М., Чистые пруды, 2010.
Площадь конуса: онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Введите 1 величину
Сторона A
Диагональ фигуры (D)
Диагональ грани (d)
Введите 1 величину
Радиус (r)
Диаметр (d)
Введите 3 величины
Сторона A
Сторона B
Сторона C
Диагональ фигуры (d)
Введите 2 величины (радиус и диаметр основания приняты за одну величину)
Высота (h)
Образующая конуса (s)
Радиус (r)
Диаметр (d)
Введите H и 1 величину
Высота (h)
Радиус (r)
Диаметр (d)
Введите 3 величины
Количество сторон (n)
Высота (h)
Сторона a
Количество сторон (n)
Введите 2 величины
Сторона основания (a)
Высота (h)
Длина бокового ребра (s)
Угол (α)
Между стороной и плоскостью основания
{$ main. angles[data.angle] $}
angles[data.angle] $}
Результат расчёта
- Объём: {$ result.v|number:4 $}
- Площать: {$ result.s|number:4 $}
- Площать: {$ result.s $}
Конус представляет собой геометрическое тело вращения, которое формируется в результате вращения прямоугольного треугольника вокруг одного из его катетов. Конические фигуры не часто встречаются в реальной жизни, однако вам может понадобиться на практике узнать площадь боковой или полной поверхности конуса для решения различных бытовых или производственных вопросов.
Геометрия конуса
В переводе с греческого языка слово konos означает сосновую шишку. И действительно, форму конических фигур имеют многие природные объекты: от сосновых шишек до крон хвойных деревьев, от вулканических воронок до шляпок некоторых видов грибов. Геометрией конусов занимались древнегреческие ученые Демокрит и Архимед, которые в результате работы с цилиндрическими фигурами получили формулы для расчета объема конусов.
Геометрией конусов занимались древнегреческие ученые Демокрит и Архимед, которые в результате работы с цилиндрическими фигурами получили формулы для расчета объема конусов.
Геометрически конус образуется следующим путем. Из вершины фигуры выходит образующий луч, который движется по направляющей кривой, лежащей в основании конуса. В данном случае направляющая кривая — это окружность, вдоль которой курсирует образующий лучик, создавая при этом боковую поверхность конуса. Таким образом, конус состоит из конической поверхности и круга, лежащего в основании.
Как тело вращения коническая фигура формируется путем вращения прямоугольного треугольника около одного из катетов. При вращении гипотенуза становится образующей конуса, создающей боковую поверхность. Прилежащий катет в этой ситуации становится радиусом основания, а противолежащий — высотой конической фигуры.
Площадь поверхности конуса
Площадь поверхности конической фигуры определяется как сумма площади боковой поверхности и площади основания:
S = So + Sb
Основание конуса — это простой круг, поэтому формула для определения So предельно проста:
So = pi × R2
Площадь боковой поверхности конуса определяется как произведение длины образующей конуса l на радиус его основания r:
Sb = pi × l × r
Объединив обе формулы вместе и приведя их к удобному виду, мы получим выражение для определения площади общей поверхности конической фигуры:
S = pi × r × (r + l)
При помощи нашего онлайн-калькулятора вы можете подсчитать полную поверхность конической фигуры или только ее часть, зная всего два параметра:
- радиус и высоту конуса;
- радиус и образующую конуса.

Высота и образующая конусной фигуры связаны по формуле Пифагора, поэтому взаимозаменяемы при расчетах площади поверхности. Кроме того, вместо радиуса вы можете указать диаметр основания конуса. Выбирайте только одну пару параметров, иначе онлайн-калькулятор подгонит собственные значения других показателей для вычисления заданной площади. Рассмотрим примеры ситуаций, в которых может пригодиться использование данной формулы.
Примеры из жизни
Вигвам
Допустим, вы хотите порадовать детей и собрать им вигвам — жилище индейцев, в котором можно весело проводить время. Для этого вам понадобится пара прутьев и много ткани, но сколько? Традиционный вигвам имеет вид конуса, поэтому вам достаточно прикинуть размеры вашего домика и рассчитать площадь боковой поверхности. Это и будет площадь ткани, необходимой для выполнения «стен» индейского жилища. Вы решили сделать маленький вигвам, высота которого составит 1,5 м, а его диаметр будет равен 2 м. Введите эти параметры в форму онлайн-калькулятора и получите результат в виде:
S = 3,14 + 5,66 = 8,80
Вы получаете ответ в виде суммы площадей основания и боковой поверхности. Для построения вигвама вам не понадобится основание, так как пол в «домике» можно не строить. Таким образом, для обустройства детского места вам потребуется 5,66 квадратных метров ткани.
Для построения вигвама вам не понадобится основание, так как пол в «домике» можно не строить. Таким образом, для обустройства детского места вам потребуется 5,66 квадратных метров ткани.
Зенкеры
К примеру, вы работаете на токарном производстве и покрываете защитным составом конусы зенкеров — специальных деталей, которые используются для обработки металлических изделий. Для определения расхода защитного покрытия вам необходимо знать площадь поверхности конической детали. Пусть зенкер имеет радиус основания на уровне 5 мм, а образующая конической фигуры составляет 25 мм. В этом случае площадь обрабатываемой поверхности составляет:
S = 78,53 + 392, 69 = 471,23
Таким образом, площадь обрабатываемой поверхности равна площади боковой поверхности зенкера и составляет 392 квадратных миллиметров или 3,92 квадратных сантиметров. Зная этот параметр, вы без проблем сможете рассчитать расход защитного покрытия, которое используется для покрытия головок определенного количества зенкеров.
Заключение
Наряду с цилиндрическими телами конические фигуры широко распространены в производственной сфере. В быту конус встречается нечасто, однако вам может понадобиться рассчитать площадь поверхности фигуры для каких-либо хозяйственных задач. Кроме того, если у вас есть дети старшего школьного возраста, то определение объемов и площадей поверхностей тел вращения станет для вас практически ежедневной задачей. Пользуйтесь нашими онлайн-калькуляторами для решения любых практических и теоретических задач.
Площадь поверхности конуса — 2 формулы | Площадь изогнутой поверхности конуса
Содержание
Площадь поверхности 3D-формы (твердого объекта) — это мера общей площади поверхности объекта. Площадь поверхности конуса – это общая площадь, занимаемая его плоской и криволинейной поверхностями. Полную площадь поверхности конуса можно вычислить, если вычислить площадь его основания и площадь криволинейной грани.
Давайте узнаем, как найти площадь поверхности конуса, его методы и формулы. {2}$, и т. д.). Существует два типа площадей поверхности конуса
{2}$, и т. д.). Существует два типа площадей поверхности конуса
- Изогнутая поверхность конуса или CSA конуса
- Общая площадь поверхности конуса или TSA конуса
Изогнутая поверхность конуса или CSA конуса
Площадь криволинейной поверхности конуса относится только к изогнутой части конуса, отличной от круглого плоского основания. Чтобы найти площадь криволинейной поверхности конуса, радиус и наклонную высоту конуса умножаем на $\pi$, т. е. площадь криволинейной поверхности конуса вычисляется по формуле $\pi r l$.
Формула площади криволинейной поверхности конуса: $\pi r l$.
Общая площадь поверхности конуса или TSA конуса
Общая площадь поверхности конуса получается путем сложения площади основания и площади криволинейной поверхности. Таким образом, формула полной площади поверхности цилиндра имеет вид:
общая площадь поверхности конуса = (Площадь основания) + (Площадь криволинейной поверхности).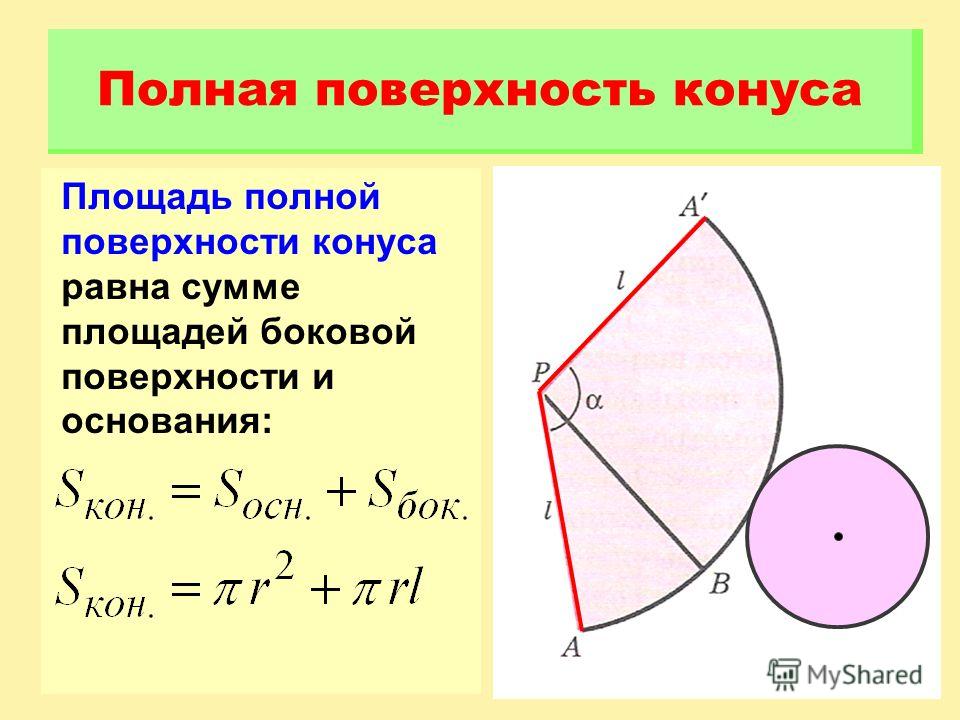 {2}$. 9{2} = \pi r \left(r + l \right)$.
{2}$. 9{2} = \pi r \left(r + l \right)$.
Формула полной площади поверхности конуса: $\pi r \left(r + l \right)$.
Типы систем координатПримеры
Пример 1: Найдите общую площадь поверхности и площадь криволинейной поверхности конуса, радиус которого составляет $3,5 см$ дюймов, а наклонная высота $3 см$.
Радиус конуса $r = 3,5 см$
Наклонная высота конуса $l = 3 см$
CSA конуса 9{2}$
Следовательно, необходимое количество валков = $\frac {150,86}{12} = 12,57$
Следовательно, количество рулонов, которые необходимо купить, = 13$.
Конус – трехмерная твердая форма
Конус представляет собой форму, образованную набором отрезков или линий, соединяющих общую точку, называемую вершиной или вершиной, со всеми точками круглого основания (которое не содержит вершины).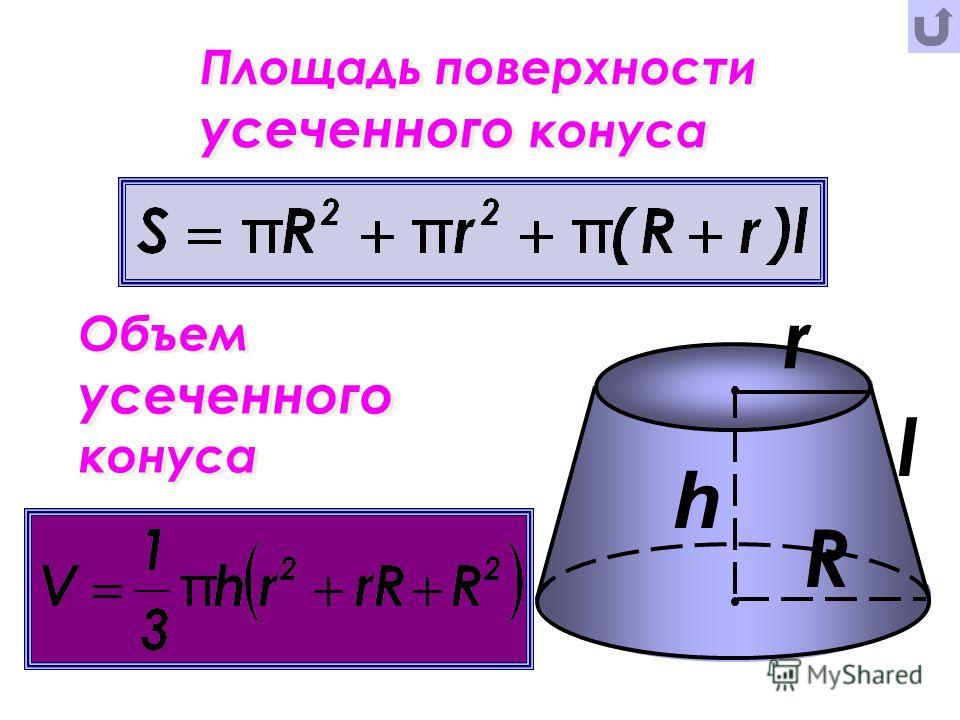 Расстояние от вершины конуса до основания и есть высота конуса. Круглое основание имеет измеренное значение радиуса. А длина конуса от вершины до любой точки на окружности основания есть высота наклона. На основе этих величин выведены формулы площади поверхности конуса.
Расстояние от вершины конуса до основания и есть высота конуса. Круглое основание имеет измеренное значение радиуса. А длина конуса от вершины до любой точки на окружности основания есть высота наклона. На основе этих величин выведены формулы площади поверхности конуса.
Типы конусов
Конусы в целом делятся на две категории.
- Прямой круговой конус: Конус с круглым основанием и осью от вершины конуса к основанию проходит через центр кругового основания. Вершина конуса лежит чуть выше центра круглого основания. Слово «право» используется здесь потому, что ось образует прямой угол с основанием конуса или перпендикулярна основанию. Это наиболее распространенные типы конусов, которые используются в геометрии. См. рисунок ниже, который является примером правильного круглого конуса.
- Наклонный конус: Конус с круглым основанием, но ось конуса не перпендикулярна основанию, называется наклонным конусом. Вершина этого конуса не расположена непосредственно над центром круглого основания.
 Поэтому этот конус выглядит как наклонный конус или наклонный конус.
Поэтому этот конус выглядит как наклонный конус или наклонный конус.
СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.
Правый круглый конус
Прямой круговой конус — это конус, ось которого перпендикулярна плоскости основания. Мы можем создать прямоугольный конус, вращая прямоугольный треугольник вокруг одного из его катетов.
На рисунке показан прямой круговой конус с круглым основанием радиуса r, ось которого перпендикулярна основанию. Линия, соединяющая вершину конуса с центром основания, является высотой конуса. Длина по внешнему краю конуса, соединяющего вершину с концом круглого основания, называется наклонной высотой. 9{2}$ и т. д.). Существует два типа площадей поверхности конуса
а) Площадь криволинейной поверхности: Формула площади криволинейной поверхности конуса: $\pi r l$.
б) Общая площадь поверхности: Формула для общей площади поверхности цилиндра: $ \pi r \left(r + l \right)$.
Что такое TSA и CSA конуса?
a) Площадь криволинейной поверхности (CSA) конуса = $\pi r l$
b) Общая площадь поверхности (TSA) конуса = $ \pi r \left(r + l \right)$
Как найти площадь поверхности?
Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей основания, верхней и боковых поверхностей (боков) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Заключение
Площадь поверхности 3D-формы (твердого объекта) — это мера общей площади поверхности объекта. Существует два типа площадей поверхности в конусе: площадь криволинейной поверхности, вычисляемая по формуле $\pi r l$, и общая площадь поверхности, вычисляемая по формуле $ \pi r \left(r + l \right)$, где $r$ и $l$ — радиус и наклонная высота конуса соответственно.
Практические задачи
- Конус имеет круглое основание с радиусом $10 см$ и наклонной высотой $30 см$.
 Вычислите площадь криволинейной поверхности и общую площадь поверхности.
Вычислите площадь криволинейной поверхности и общую площадь поверхности. - Найдите площадь криволинейной поверхности, где $r = 9см$, $h = 12см$ и $l = 15см$.
- Найдите общую площадь поверхности, где $r = 7см$, $h = 24см$.
- Конус имеет радиус $3см$ и высоту $4см$, найдите полную площадь поверхности конуса.
- Наклонная высота конуса $13см$. диаметр основания $10см$. Найдите полную площадь поверхности конуса.
- Найдите полную площадь поверхности конуса, если его наклонная высота $21м$, а диаметр основания $24м$.
Рекомендуемое чтение
- Площадь поверхности куба (определение, формула и примеры)
- Площадь поверхности прямоугольного параллелепипеда (определение, формула и примеры)
- Площадь прямоугольника – определение, формула и примеры
- Площадь квадрата – определение, формула и примеры
- Площадь треугольника – формулы, методы и примеры
- Площадь круга – формула, вывод и примеры
- Площадь ромба – формулы, методы и примеры
- Площадь воздушного змея – формулы, методы и примеры
- Периметр многоугольника (с формулой и примерами)
- Периметр трапеции – определение, формула и примеры
- Периметр воздушного змея – определение, формула и примеры
- Периметр ромба – определение, формула и примеры
- Окружность (периметр) круга – определение, формула и примеры
- Периметр квадрата – определение, формула и примеры
- Периметр прямоугольника – определение, формула и примеры
- Периметр треугольника – определение, формула и примеры
- Что такое 2D-фигуры — имена, определения и свойства
Вам также может понравиться
Как решать линейные уравнения с матрицами (с методом и примерами)
Содержание Как решать линейные уравнения с матрицамиУсловие непротиворечивости
Читать далее
Правило Крамера – определение, формулы и примеры
Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x
Читать далее
Карточки по математике для печати бесплатно – скачать PDF
Карточки по математике являются ценным пособием для учащихся всех возрастов и
Читать далее
Объем и площадь поверхности конуса формулы
Содержание
Определение конуса
Конус представляет собой трехмерную фигуру в геометрии. Объект с криволинейной (боковой) поверхностью с вершиной и круглым основанием называется круговым конусом.
Объект с криволинейной (боковой) поверхностью с вершиной и круглым основанием называется круговым конусом.
я. e Конус – это тело, имеющее круглую поверхность в основании и наклонную боковую поверхность, сходящуюся к вершине.
Его размеры определяются радиусом основания ( r), высотой ( h) и наклонной высотой ( l).
Высота конуса (h) – расстояние от вершины конуса до основания
Радиус конуса (r) – Круговое основание имеет измеренное значение радиуса
Наклонная высота конус ( l ) – Длина конуса от любой точки на окружности основания до вершины конуса
Разница между прямым круглым конусом и O наклонным конусом.
Ось конуса — это отрезок, концы которого лежат от центра основания до вершины или вершины. Если ось конуса перпендикулярна плоскости окружности, то он называется прямым круговым конусом , в противном случае это косой конус .
Формулы прямого кругового конуса
Площадь изогнутой или боковой поверхности конуса = (1/2) x высота наклона x длина всей изогнутой границы.
Здесь длина всей изогнутой границы = Окружность основания конуса = 2 π r
Площадь боковой поверхности (LSA) конуса = = π r l
LSA конуса = π r l
Примечание: Наклонная высота = l =
9002 общей площади поверхности конус = площадь боковой поверхности конуса + площадь основания конуса = π r l + π r 2
TSA конуса = π r ( l + r)
объем конуса составляет одну треть объем цилиндра с таким же радиусом основания.
Объем конуса =
Угол раскрытия = Угол сектора = ( θ) = 2 x дуга sin( r / l )
Базовый угол β = ( 180° – α ) / 2 α)
Формулы объема наклонного конуса
Для наклонного конуса высота наклона не определена, поэтому формул для площадей наклонных конусов не существует.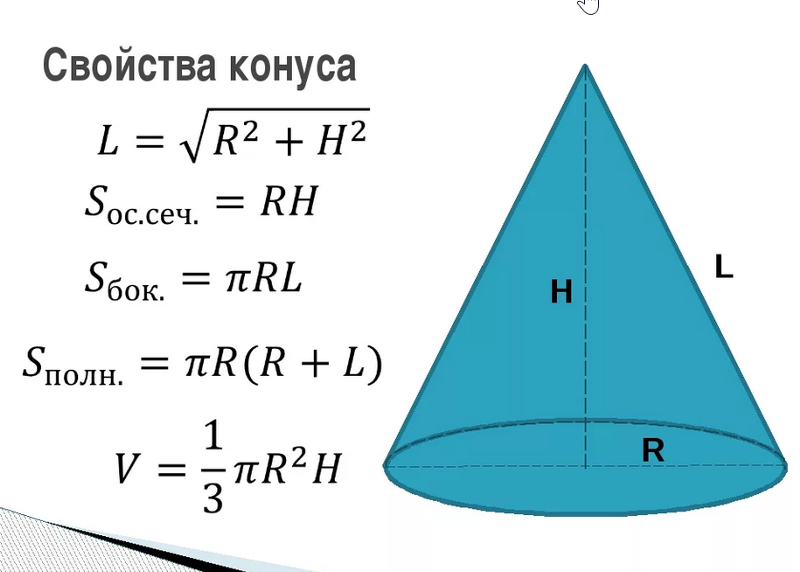
Объем косого конуса такой же, как у прямого кругового конуса.
т.е. объем косого конуса составляет одну треть произведения высоты на площадь его основания. 9Пример 1
Площадь криволинейной поверхности прямого круглого конуса = π r l = π D l /2
Наклонная высота = l = = = 17
= π x (16/2) x 17 = 136 π см 2
Пример – 2: Радиус основания прямого круглого конуса равен 7 см, а его наклонная высота равна 25 см. Найдите объем конуса.
Решение: Объем конуса =
Высота конуса = h = = = 24
Объем конуса = (1/3) x (22/7) x 7 x 7 x 24 = 1232 см 3
Пример – 3: Найдите объем наибольшего прямого круглого конуса, который можно вырезать из куба с ребром 9 см.
Решение: Объем конуса =
Здесь радиус конуса = r = 9/2 = 4,5 см
высота конуса = h = 9
Объем конуса = (1/3) x (22/ 7) х (9/2) x (9/2) x 9 = 190,93 см 3
Пример -4 : Конус вырезан параллельно его основанию таким образом, что высота двух частей одинакова.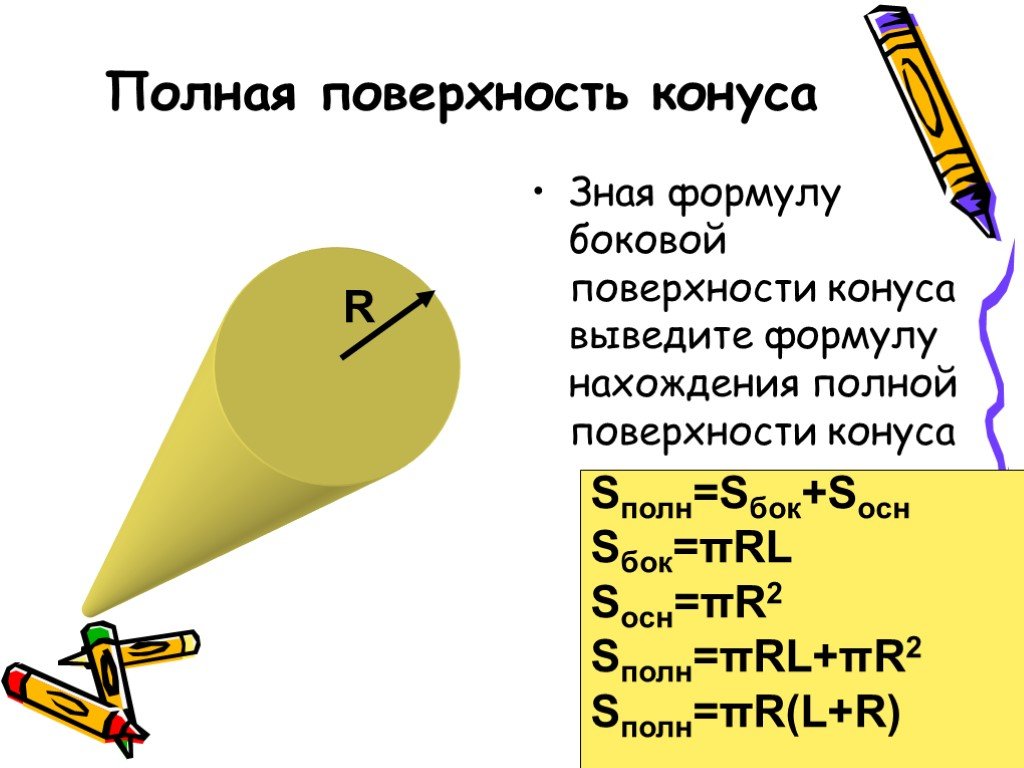 Найдите отношение объемов этих двух частей.
Найдите отношение объемов этих двух частей.
Решение: Пусть радиус малого конуса = r и высота = h
Тогда высота большого конуса = 2h и радиус = 2r
Объем конуса =
= (1/3) π r 2 h : (1/3) π (2r) 2 (2h) = 1 : 8 (Здесь всего частей 8)
Соотношение объема двух частей = 1 : 7
Пример – 5 : Конус вырезан параллельно его основанию так, что высота трех частей одинакова. Найдите отношение объемов этих трех частей.
Решение : Пусть радиус малого конуса = r и высота = h
Тогда высота среднего конуса = 2h и радиус = 2r
Тогда высота большого конуса = 3h и радиус = 3r
Объем конуса =
= (1/3) π r 2 ч : (1/3) π (2r) 2 (2h) : (1/3) π (3r) 2 (3h) = 1 : 8 : 27 (Здесь всего частей 27)
Отношение объемов трех частей конусов = 1 : 7 : 19
Пример-6 : Конус вырезан параллельно его основанию таким образом, что объем меньшего конуса в 1/729 раза больше объема большего конуса.


 Ф. Бутузов, С. Б. Кадомцев и др., М., «Просвещение», 2008.
Ф. Бутузов, С. Б. Кадомцев и др., М., «Просвещение», 2008.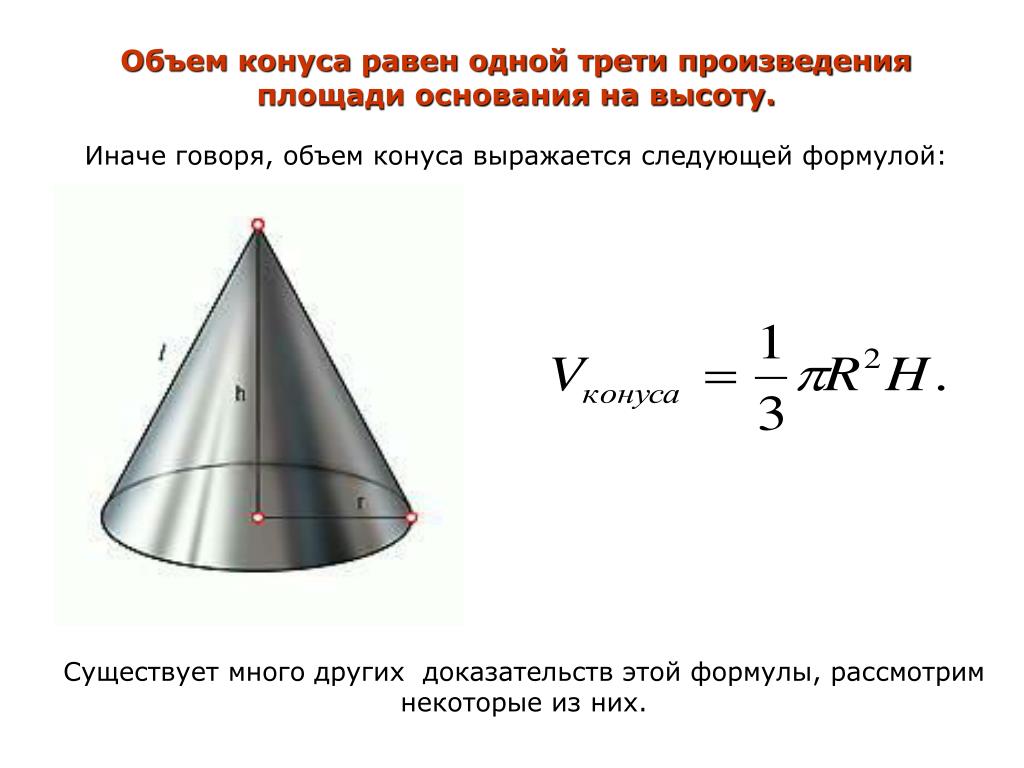
 Поэтому этот конус выглядит как наклонный конус или наклонный конус.
Поэтому этот конус выглядит как наклонный конус или наклонный конус. Вычислите площадь криволинейной поверхности и общую площадь поверхности.
Вычислите площадь криволинейной поверхности и общую площадь поверхности.