XII век | это… Что такое XII век?
Толкование
- XII век
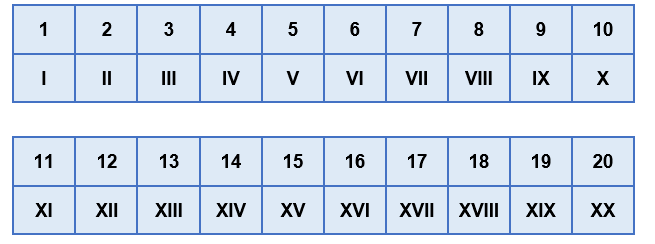
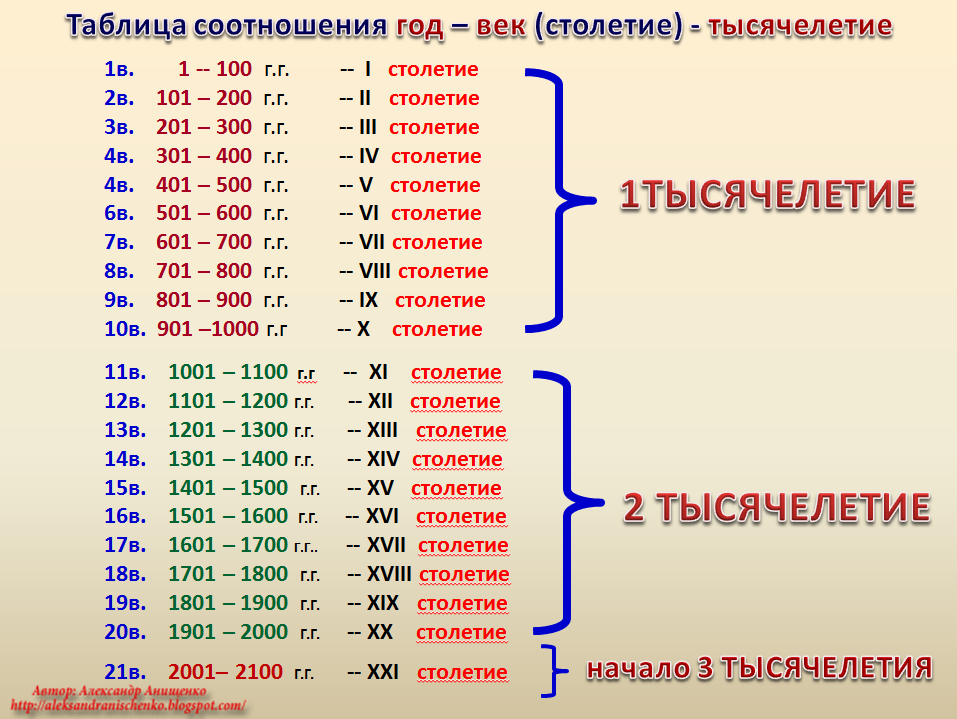
2-е тысячелетие X век — XI век — XII век — XIII век — XIV век 1090-е 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100-е 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110-е 1110 1111 1112 1113 1114 1115 1116 1117 1118 1119 1120-е 1120 1121 1122 1123 1125 1126 1127 1128 1129 1130-е 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140-е 1140 1141 1142 1143 1144 1145 1146 1147 1148 1149 1150-е 1150 1151 1152 1153 1154 1155 1156 1157 1158 1159 1160-е 1160 1161 1162 1163 1164 1165 1166 1167 1168 1169 1170-е 1170 1171 1172 1173 1174 1175 1176 1177 1178 1179 1180-е 1180 1181 1182 1183 1184 1185 1186 1187 1188 1189 1190-е 1190 1191 1192 1193 1194 1195 1196 1197 1198 1199 1200-е 1200 1201 1202 1203 1204 1205 1206 1207 1208 1209 Хронологическая таблица Двенадцатый (XII) век длился с 1101 по 1200 годы по григорианскому календарю.

Содержание
- 1 Основные события
- 1.1 Русь
- 1.2 Европа
- 2 См. также
Основные события
Русь
- 1103 — Начало целой серии походов Владимира и Святополка против половцев (1103—1120 гг).
- 1107 — Взятие Суздаля волжскими болгарами.
- 1113 — Начало княжения Владимира Мономаха (1113—1125 гг).
- 1136 — Отпадение Новгорода от Киевской Руси.
- 1139 — Волнения в Киеве и его захват Всеволодом Олеговичем.
- 1146 — Начало ожесточенной борьбы княжеских кланов за киевский престол (Мономаховичи, Ольговичи, Давидовичи) — продолжалась до 1161 г.
- 1147 — первое летописное упоминание о Москве.
- 1181 — переселенцами из Новгорода основан город Хлынов (ныне, Киров)
Европа
- 1100 — Началось правление английского короля Генриха I (1100—1135). Укрепление системы государственного управления; значительную роль стал играть постоянный королевский совет.

- 1106 — Началось правление германского короля и императора Священной Римской империи Генриха V (1106—1125). Завершил борьбу с папством за инвеституру.
- 1109 — Польско-германская война Генриха V.
- 1122 — Византийский император Иоанн II Комнин одержал победу над печенегами.
- 23 сентября 1122 — в Вормсе заключен Вормсский конкордат, завершивший борьбу за инвеституру (противоборство между папством и императорами Священной Римской империи вокруг права вводить в должность епископов).
- 1137 — Началось правление французского короля Людовика VII (1137—1180). Своим браком с Алиенорой, наследницей герцогства Аквитания, присоединил к своему домену территорию юго-западной Франции. В результате женитьбы Людовика VII на Алиеноре Аквитанской французская корона приобрела Гиень, Гасконь, Пуату, Марша, Лимузен и Перигор.
- 1146 — Поход императора Конрада III на Польшу.
- 1147 — Начался второй крестовый поход (1147—1149). Возглавляли поход французский король Людовик VII и император Священной Римской империи немецкий король Конрад III.
 Поводом послужил захват турками-сельджуками Эдессы.
Поводом послужил захват турками-сельджуками Эдессы. - 1152 — Началось правление германского короля Фридриха I Барбароссы (1152—1190), с 1155 — императора «Священной Римской империи». Пытался подчинить североитальянские города.
- 1155.02.05 — 07 — Вероятное время рождения «человека тысячелетия» Чингисхана. Или в 1167 г.
- 1159 — Начало франко-анжуйской войны (1159—1299 гг).
- 1175 — Началось правление (1175—1193) египетского султана Салах-ад-Дина (Сала-дина). Основатель династии Айюбидов. Возглавлял борьбу мусульман против крестоносцев.
- 1180 — Правление французского короля Филиппа II Августа (1180—1223). Успешно проводил политику централизации государства (увеличил королевский домен примерно в 4 раза преобразовал в нём управление; ограничил самостоятельность феодальной знати). Отвоевал у Иоанна Безземельного подвластные ему французские территории (Нормандию и др.), превратил Францию в ведущую европейскую державу.
- 1184 — Началось правление царицы Тамар (1184—1207) в Грузии.
 В её царствование Грузия добилась больших военно-политических успехов. Ей посвящена поэма Шота Руставели «Витязь в тигровой шкуре».
В её царствование Грузия добилась больших военно-политических успехов. Ей посвящена поэма Шота Руставели «Витязь в тигровой шкуре». - 1187 — Мусульмане вновь взяли Иерусалим, отобрав его у христиан: В сражении при Тивериадском озере египетский султан Салах-ад-Дин разгромил войска Иерусалимского королевства и захватил Иерусалим.
- 1189 — Началось правление английского короля Ричарда Львиное Сердце. Большую часть жизни провел вне Англии, сражаясь против французского короля и против мусульман. Возвращаясь из третьего крестового похода, попал в плен к императору Генриху VI, потребовавшему огромный выкуп, который был выплачен, в том числе благодаря повышению налогов в Англии (1194).
- 1190 — Началось правление германского короля и императора Священной Римской империи Генриха VI (1190—1197). Женитьбой на наследнице сицилийского престола присоединил к своим владениям Сицилийское королевство.
- 1198 — Папа римский Целестин III провозглашает северный крестовый поход.
 Основан Тевтонский орден (форма — белый плащ с чёрным крестом). Епископ Бертольд с войском крестоносцев приходит на Западную Двину, принудительно крестит ливов, облагает их данью.
Основан Тевтонский орден (форма — белый плащ с чёрным крестом). Епископ Бертольд с войском крестоносцев приходит на Западную Двину, принудительно крестит ливов, облагает их данью. - 1199 — Начался четвёртый крестовый поход (продолжался 1199—1204 гг).
- XII век — Победа христианства в Швеции.
- XII век — Возникновение княжества Босния.
- XII век — Перенесение столицы Волжской Болгарии в Биляр.
- XII век — Возникновение в Дагестане Аварского ханства со столицей Хунзах.
- XII век — Кильва стала центром всех арабских поселений на восточном берегу Африки. Султаны Кильвы владели Занзибаром, Мафией, Пембой, Момбасой, Аму и Пате.
- XII век — Образование движения бхакти в Индии.
- XII век — Возникновение организации «Байляньцзяо» («учение Белого лотоса») в Китае.
- XII век — Кхмеры пытаются овладеть Халипунджайей, но это им не удалось.
- XII век — От Шривиджайи отпадает княжество Малайя на Суматре, к северо-западу от Палембанга.

- XII век — Семь объединённых племен науа с севера (Нью-Мексико или Аризона) проникли в долину Мехико.
- XII век — Усиление Майяпана.
- XII век — Тои отплыл из Центральной Полинезии и оказался на Новой Зеландии.
См. также
[+] XII век
Это незавершённый список века. Вы можете помочь проекту, исправив и дополнив его. - 1 Основные события
Wikimedia Foundation. 2010.
Игры ⚽ Нужно сделать НИР?
- XIII век
- XI век
Полезное
3000 до н.э. — 12 век
3000 лет до н.э.
В древнем Вавилоне были изобретены первые счёты – абак.
1680-1620 до н.э.
Египет. Ахмес.
Ахмес был писцом, составившим так наз. «Папирус Ринда». Этот документ, найденный шотландским египтологом Генри Риндом (Henry Rhind) в 1858 г., остается основным источником информации по математике древнего Египта.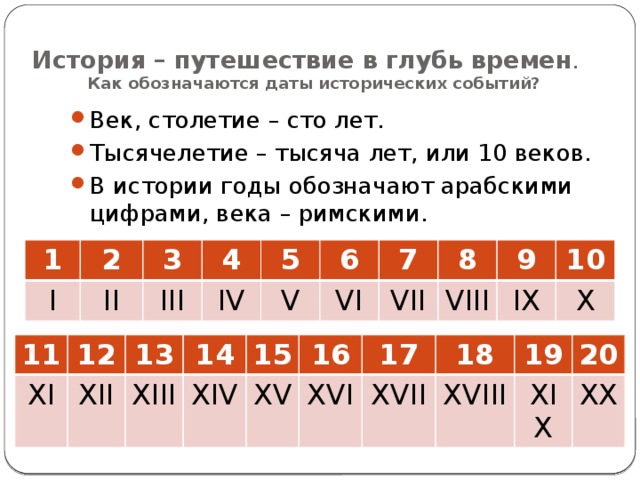 Он содержит чертежи треугольников с указаниями углов и формулами нахождения площадей, а также показывает деление числа 2 на нечётные числа от 3 до 101 в дробях и деление чисел от 1 до 9 на 10. В нём также имеется 87 задач на четыре действия арифметики, решение уравнений, прогрессии, вычисление объемов зернохранилищ, правило двух третей и т. д. В честь Ахмеса этот документ также называют « Папирус Ахмеса », однако сам он указывал, что записи составлены по более ранним материалам, относящимся примерно к 2000 до н. э.
Он содержит чертежи треугольников с указаниями углов и формулами нахождения площадей, а также показывает деление числа 2 на нечётные числа от 3 до 101 в дробях и деление чисел от 1 до 9 на 10. В нём также имеется 87 задач на четыре действия арифметики, решение уравнений, прогрессии, вычисление объемов зернохранилищ, правило двух третей и т. д. В честь Ахмеса этот документ также называют « Папирус Ахмеса », однако сам он указывал, что записи составлены по более ранним материалам, относящимся примерно к 2000 до н. э.
639-548 гг. до н.э.
Греческий философ Талий, изучив в Александрии достижения египетской науки (в основном геометрии), начал их распространение в Греции.
500 лет до н.э.
Появился абак, напоминающий современные счеты с косточками на проволоке.
409-325 гг. до н.э.
Диофант ввёл в употребление знак равенства и впервые использовал символический язык алгебры.
4 век до н.э.
Аристотель заложил основы математической логики.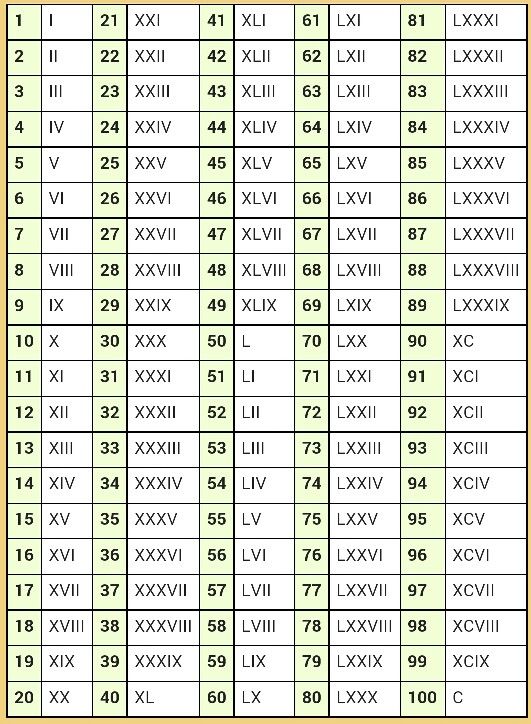 Он ввел понятие переменной в логике, применил буквы для обозначения понятий. После его работ, считавшихся верхом совершенства, в логике почти два тысячелетия наблюдался застой.
Он ввел понятие переменной в логике, применил буквы для обозначения понятий. После его работ, считавшихся верхом совершенства, в логике почти два тысячелетия наблюдался застой.
300 лет до н.э.
Евклид в одной из древнейших математических книг «Элементы» привел систематическое построение теории чисел.
276-195 гг. до н.э.
Эратосфен предложил метод нахождения простых чисел, названный впоследствии «решетом Эратосфена».
262-190 гг. до н. э.
Греция. Аполлоний из Пегры
Греческий математик, известный как «Великий геометр», оказавший большое влияние на развитие математики. В его известной книге «Конусы» введены термины парабола, гипербола и эллипс .
85 -165 н. э.
Александрия (Египет в составе Римской империи).
Клавдий Птолемей (Claudius Ptolemey)
Наиболее влиятельный греческий астроном и географ своего времени. Птолемей выдвинул геоцентрическую теорию строения вселенной, принимавшуюся в течение почти 1400 лет. В ней он приводит математическую часть, содержащую тригонометрические методы, основанные на функции, родственной синусу, и их варианты [аналоги sin(a+b), sin(a-b), sin a/2], описывает 360-угольную аппроксимацию круга, приближенное число «Pi» (3,14166), квадратный корень из числа 3 (=1,73205) и т. д. Его работы в дальнейшеи оказали огромное влияние арабских и европейских математиков.
В ней он приводит математическую часть, содержащую тригонометрические методы, основанные на функции, родственной синусу, и их варианты [аналоги sin(a+b), sin(a-b), sin a/2], описывает 360-угольную аппроксимацию круга, приближенное число «Pi» (3,14166), квадратный корень из числа 3 (=1,73205) и т. д. Его работы в дальнейшеи оказали огромное влияние арабских и европейских математиков.
500 г. н. э
Индия. Первое из известных применений десятичной системы исчисления.
Ариабата Старший (первый)
Основной письменный труд Ариабаты – «Ариабатья» – суммирует математические познания Индии вплоть до 6 в. н. э. Он указывает, что написал книгу в 499 г . в возрасте 23 лет. Книга состоит из 118 стихов на астрономические темы (индийская традиция – писать в стихотворной форме) , включая 66 математических правил, модели планет и определение времени, описание небесной сферы и затмений. Ариабата писал о вращении Земли вокруг своей оси, что создает видимость движения небесных тел.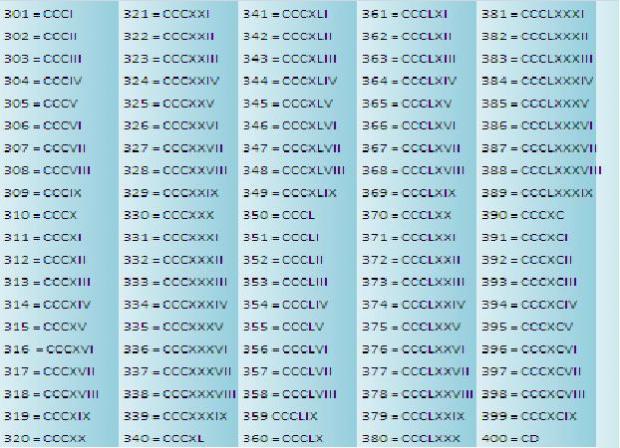 Его математическая часть включает арифметику, алгебру, геометрию, в том числе и тригонометрию. Она также содержит суммы степенных рядов, дроби, квадратные уравнения и таблицу синусов. Он писал о нахождении наименьшего общего кратного и определил число «Pi» как 3,1416 (с высокой точностью). Спецификой его трактатов было обозначение цифр (от 1 до 9 и количества десятков —20, 30 и тд.) 33 согласными индийского алфавита, а для обозначения сотен и кратных им добавлялись гласные. Такая буквенная запись позволяла представить числа до 10 в 18 степени, но была более громоздкой чем десятичная. Впрочем, Ариабата почти наверняка был знаком с понятием нуля и позиционной системой обозначения разрядов. Длину земной окружности он определил как 24 835 англ. миль (современные данные — 24 902 англ. миль) и длину года 365 дней 6 ч 12 мин и 30 с (на самом деле 365 дней и менее 6 ч).
Его математическая часть включает арифметику, алгебру, геометрию, в том числе и тригонометрию. Она также содержит суммы степенных рядов, дроби, квадратные уравнения и таблицу синусов. Он писал о нахождении наименьшего общего кратного и определил число «Pi» как 3,1416 (с высокой точностью). Спецификой его трактатов было обозначение цифр (от 1 до 9 и количества десятков —20, 30 и тд.) 33 согласными индийского алфавита, а для обозначения сотен и кратных им добавлялись гласные. Такая буквенная запись позволяла представить числа до 10 в 18 степени, но была более громоздкой чем десятичная. Впрочем, Ариабата почти наверняка был знаком с понятием нуля и позиционной системой обозначения разрядов. Длину земной окружности он определил как 24 835 англ. миль (современные данные — 24 902 англ. миль) и длину года 365 дней 6 ч 12 мин и 30 с (на самом деле 365 дней и менее 6 ч).
Ариабата трудился неподалеку от города Пталипутра – тогдашней столицы империи Гупта в северной части Индии. Это был оживленный центр международных торговых путей что облегчало общение исламского мира с индийской научной школой. Его работы тщательно изучались такими известными исламскими учеными, как Бируни и др. В ХХ веке его именем был назван первый Индийский искусственный спутник земли «Ariabhata».
Его работы тщательно изучались такими известными исламскими учеными, как Бируни и др. В ХХ веке его именем был назван первый Индийский искусственный спутник земли «Ariabhata».
598—670 гг.
Индия. Брахмагупта
Брахмагупта был самым выдающимся индийским математиком своего времени. Он сделал открытия в астрономии, но самый главный вклад он внес в систему исчисления, включая алгоритмы извлечения квадратных корней и решения квадратных уравнений
735—804 гг.
Англия – Германия – Франция. Алкуин из Йорка (Alcuin of York)
Алкуин — английский математик (один из немногих образованных людей средневековой Европы) написавший простейшие тексты по основам арифметики, геометрии и астрономии. Он происходил из знатной семьи и учился в школе архиепископа Эгберта (Ecgberht) при кафедральном соборе Йорка. По окончании остался её учителем, а с 778 г . директором, собрав там одну из лучших библиотек и сделав саму школу одним из важнейших учебных центров Европы. В 781 г. он переехал в Германию, в Аахен — столицу короля франков Карла Великого, создателя Священной Римской Империи, стремившегося возродить Европу после эпохи варварства и продолжить триумф Римской цивилизации. Карл очень заботился не только о военных успехах, но и о просвещении, сам занимался улучшением алфавита и старался привлечь в Аахен ведущие научные силы. Алкуин прибыл на организованную Карлом в Аахене встречу европейских ученых и в 782 г. был назначен там главой придворной Аахенской школы. Он развил идею Карла, составив так называемый шрифт Каролингов с ясным, удобным написанием букв, легший в основу современного европейского (латинского) алфавита.
В 781 г. он переехал в Германию, в Аахен — столицу короля франков Карла Великого, создателя Священной Римской Империи, стремившегося возродить Европу после эпохи варварства и продолжить триумф Римской цивилизации. Карл очень заботился не только о военных успехах, но и о просвещении, сам занимался улучшением алфавита и старался привлечь в Аахен ведущие научные силы. Алкуин прибыл на организованную Карлом в Аахене встречу европейских ученых и в 782 г. был назначен там главой придворной Аахенской школы. Он развил идею Карла, составив так называемый шрифт Каролингов с ясным, удобным написанием букв, легший в основу современного европейского (латинского) алфавита.
Эта работа имела почти решающее значение для сохранения уцелевших греческих трудов по математике, поскольку в IX в. их начали переписывать для удобства чтения. Большинство из дошедших до нас античных математических документов сохранилось именно в «Аахенском варианте». Алкуин стал другом Карла и учителем его детей, однако в 796 г . он уехал во Францию, в Тур, где и работал до конца жизни. Для большей доходчивости он оформлял свои научные трактаты в виде диалогов (вопросов и ответов) — классический приём, использовавшийся ещё Сократом, Платоном и др. Алкуин дал импульс к развитию математики, написав элементарные тексты по арифметике, геометрии и астрономии «…на заре Возрождения, одной из движущих сил которого стал он сам».
он уехал во Францию, в Тур, где и работал до конца жизни. Для большей доходчивости он оформлял свои научные трактаты в виде диалогов (вопросов и ответов) — классический приём, использовавшийся ещё Сократом, Платоном и др. Алкуин дал импульс к развитию математики, написав элементарные тексты по арифметике, геометрии и астрономии «…на заре Возрождения, одной из движущих сил которого стал он сам».
VIII — XII вв.
Несмотря на некоторое оживление в Европе основное развитие математики и вычислений переносится на Исламский Восток, где изучается греческое и индийское наследие и делаются новые открытия.
Около 800 г.
В Китае, вероятно под влиянием Индии, используется 0.
790—840 гг.
Персия (Иран). Абу Джафар Мухаммад ибн Муса Аль-Хорезми.
Аль-Хорезми — персидский математик, предположительно происходивший из Хорезма (сам либо родители). Автор многочисленных, весьма важных исследований по индоарабской десятичной нумерации.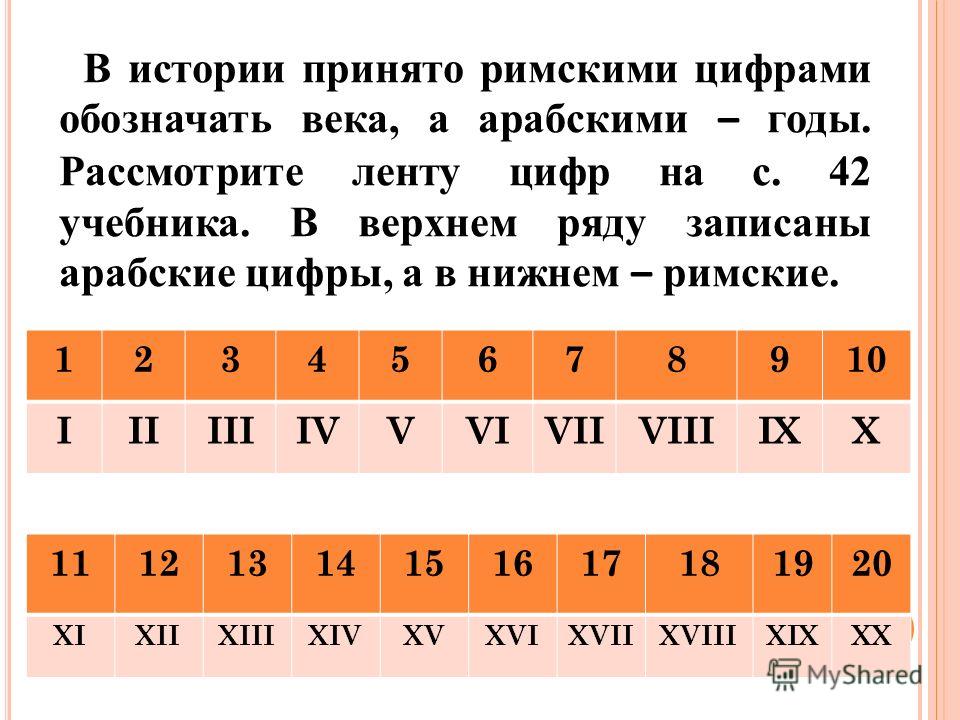 Считается что Аль-Хорезми и предложил десятичную систему счисления в арабском мире.
Он же стал одним из первых математиков, предложивших использовать знак «ноль» для обозначения десятичного разряда при записи. От имени Аль-Хорезми происходит и слово (понятие) алгоритм.
Считается что Аль-Хорезми и предложил десятичную систему счисления в арабском мире.
Он же стал одним из первых математиков, предложивших использовать знак «ноль» для обозначения десятичного разряда при записи. От имени Аль-Хорезми происходит и слово (понятие) алгоритм.
Его фундаментальное исследование «Хисаб Аль-Джебр валь-Мукабала» подарило миру слово Алгебра и может считаться первым письменным трудом по алгебре.
800—860 гг.
Ирак (Багдад). Аль-Аббас ибн Саид Аль-Джавари
Основная работа Аль-Джавари состоит в написании комментариев к «Элементам» Евклида. Имя Аль-Джавари тесно связано с Домом Мудрости в Багдаде. Знаменитый халиф Гарун Аль — Рашид (правил в 786—809)
стремился к развитию культуры и привлекал
ко двору ученых. Его сын халиф Аль-Мамун продолжил дело отца и основал академию названную Домом Мудрости . В ней изучали работы греческих философов и собирали библиотеку манускриптов (первую после Александрийской), приобретая их в Византии. Среди работавших там ученых математиков были Аль-Хорезми, Аль-Кинди, Хунаин ибн Ишаг, Тхабит ибн Кура и братья Бану. Аль-Мамун также построил ряд обсерваторий
В ней изучали работы греческих философов и собирали библиотеку манускриптов (первую после Александрийской), приобретая их в Византии. Среди работавших там ученых математиков были Аль-Хорезми, Аль-Кинди, Хунаин ибн Ишаг, Тхабит ибн Кура и братья Бану. Аль-Мамун также построил ряд обсерваторий
805—873 гг.
Ирак (Багдад). Абу Юсуф Якуб ибн Ишаг Аль-Саббах Аль-Кинди
Аль-Кинди изучал и комментировал индийскую математику и писал о её системе исчисления, геометрии и оптике.
800—870 гг.
Ирак (Багдад). Братья Бану Мусса
Три брата-математика, вместе работавшие в «Доме Мудрости» — Багдадской академии. Их труды производят впечатление частей одного целого.
— Джафар Мухаммад Бану Мусса (800 — после 873). Лучший математик из братьев. Он внес заметный вклада в геометрию и написал трактат о конусах — критический анализ работы Аполлония «Конусы» («Conics»).
— Ахмад Бану Мусса (805—873) — писал о механике.
— Аль-Хасан Бану Мусса (810 — ок. 873) — писал об эллипсах.
808—873 гг.
Ирак (Багдад). Абу Заид Хунаин ибн Ишаг аль Ибади
Его наиболее важные математические работы — переводы трудов греческих математиков, сделавшие их доступными исламским учёным
820—880 гг.
Персия — Ирак. Абу Абд-Алла Мухаммад ибн Иса Аль-Махани
Аль-Махани известен своими работами по решению задач Архимеда, связанных с сечением сфер
830—890 гг.
Индия. Пртудакасвами (Prthudakasvami)
Известен серьезными работами по решению уравнений
835—912 гг.
Ирак — Египет. Ахмед ибн Юсуф аль Мизри
Ахмед ибн Юсуф — математик, написавший комментарии к Евклидовым «Элементам». Его работа оказала значительное влияние на последующее развитие математики в Европе
836—901 гг.
Ирак. Аль-Сабри Т(х)абит ибн Кура Аль-Харрани
Математик, внёсший вклад в теорию чисел, астрономию и
статистику.
850—929 гг.
Ирак. Аль Батани ( Al-Battani, также известен как Albategnius, Albategni)
Аль Батани — исламский астроном и математик. Известен точными измерениями при изучении звезд, луны и планет. Его математические методы были использованы последующими астрономами
870—930 гг.
Индия (Бенгалия). Шридхара (Sridhara)
Шридхара много занимался практическими применениям алгебры и одним из первых вывел и доказал формулу решения квадратных уравнений
875—940 гг.
Иран — Ирак. Абуль Аббас Аль-Фадль ибн Хатим Аль-Найризи
Аль-Найризи — исламский математик, составивший объемные комментарии к работам Птолемея и Евклида
908—946 гг.
Ирак (Багдад). Ибрагим ибн Синан ибн Табит ибн Курра
Математик и астроном, изучавший геометрию, в особенности тангенсы углов в окружностях. Он внес вклад в развитие теории расчёта площадей.
920—980 гг.
Сирия (Дамаск). Абуль Хасан Ахмад ибн Ибрагим Аль-Уклидиши
Мусульманский математик, написавший две работы по арифметике. Он (предположительно) предвосхитил введение десятичных дробей.
920—1000 гг.
Индия. Ариабата (второй)
Ариабата был математиком и астрономом. Он первым составил таблицы синусов углов с точностью до пятого знака.
940—1000 гг.
Персия (Иран). Абу Саль Вайджан ибн Рустам Аль-Куи
Ведущий исламский математик, возрождавший и развивавший греческую геометрию.
9-10 век
В Европе ширится распространение арабских цифр, а также понятий нуль и позиционность. Постепенно арабские цифры вытесняют римские, но окончательно это произойдет лишь в XVII веке.
953—1029 гг.
Ирак (Багдад). Абу Бекр ибн Мухаммад ибн Аль-Хуссайн Аль-Караджи
Аль-Караджи — подробно писал о работах предшествовавших математиков. Он считается первым ученым, освободившим алгебру от геометрических операций, заменив их действиями, составляющими основу современной алгебры
973—1048 гг.
Персия (Иран). Абу Арраян Мухаммад ибн Ахмад Аль-Бируни
Бируни – одна из самых выдающихся фигур в исламской математике. Он внёс значительный вклад в астрономию, математику, физику, медицину и историю.
980—1037 гг.
Ирак. Абу Мансур ибн Тахир Аль-Багдади
Исламский математик, составивший описание различных систем арифметики в работе, имевшей принципиально важное значение в истории математики.
989—1079 гг.
Испания. Абу Абдалла Мухаммад ибн Аль-Джайани
Испанский (исламский) математик. Считается что Аль-Джайани родился в Кордове. В 1012-1017 он находился в Каире (Египет), а большую часть жизни провел в Хаене (Андалузия).
Аль-Джайани составил трактат «О соотношениях /пропорциях/» ( On ratio ) – важные комментарии к «Элементам» Евклида (к разделу называемому «книга V »). Это считается его важнейшей работой. Для определения понятия пропорция /соотношение/ он писал что основными понятиями геометрии являются число, линия, поверхность, угол и сплошная среда (твердое тело). Этот подход (число как геометрическая величина), необычный для предшествовавшей ему греческой мысли, понадобился Аль-Джайани определявшему понятие «пропорция» путем развития Арабской трактовки понятия «число». Он также написал первое исследование по сферической тригонометрии: «Книга о неизвестных дугах сферы».
Этот подход (число как геометрическая величина), необычный для предшествовавшей ему греческой мысли, понадобился Аль-Джайани определявшему понятие «пропорция» путем развития Арабской трактовки понятия «число». Он также написал первое исследование по сферической тригонометрии: «Книга о неизвестных дугах сферы».
Аль-Джайани явно испытывал большое уважение к астрономическим трудам Аль-Хорезми, свободно пользуясь данными его таблиц, но не соглашался с его астрологией, для которой он сам привлекал индийские источники.
Влияние трудов Аль-Джайани на европейских ученых весьма велико. Например многие детали его «Книги о неизвестных дугах сферы» можно найти в трудах по тригонометрии немецкого ученого Иоганна Мюллера Региомонтануса (1436-1476). С его трактовкой Евклида сходна трактовка предложенная английским математиком Исааком Барроу (1630 -1677), считавшимся первым европейским математиком правильно понявшим Евклида.
Испанское влияние также сказалось и на интересах современника Аль-Джайани, ученого монаха Герберта д’Ауриллак (Папы Сильвестра II ) как и к наукам так и к астрологии (см. ниже).
ниже).
Около 1000 г.
Зап. Европа — Ватикан
Архаичный абак модернизируется Гербертом (Gerbert d’Aurillac, 940 — 1003 г.) .
Герберт – французский монах, один из известнейших учёных средневековья, впоследствии римский Папа – Сильвестр II.
В 967 — 70 г. Герберт обучался в Барселоне под руководством местного епископа; знакомился с (индо- ) арабскими десятичными числами.
Эпоха «темного средневековья», наступившая после разорения Европы варварами, когда знание нескольких правил арифметики считалось признаком необыкновенной учёности, двигалась к своему завершению. Хозяйственная деятельность и торговля расширялись, приобретали большую организованность и выдвигали новые требования к искусству счёта.
Герберт разработал абак с 27 колонками костей (а также вспомогательными – дробными). Неизвестно, что было прототипом, египетский или римский абак (12 колонок), однако Герберт имел копию книги «Геометрия» Боэция – философа эпохи заката Рима.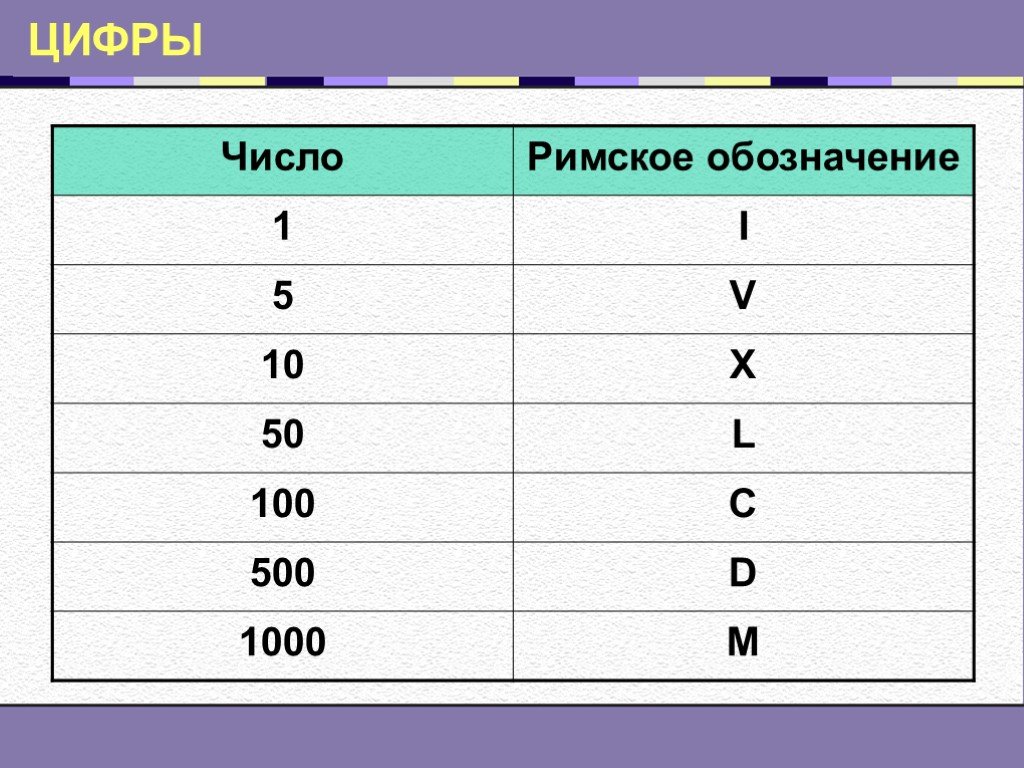 В любом случае абак Герберта был намного совершеннее: он имел «прогрессивную» конструкцию, обозначения латинскими буквами (цифрами) и позволял представлять десятичные числа до 10 в 27-й степени.
В любом случае абак Герберта был намного совершеннее: он имел «прогрессивную» конструкцию, обозначения латинскими буквами (цифрами) и позволял представлять десятичные числа до 10 в 27-й степени.
Хотя Герберт был искренним христианином, он не чуждался и астрологии. Он также писал работу в которой пытался доказать появление и деятельность Христа чисто научными методами.
Став Папой, Герберт сохранил живой интерес к науке, что принесло немало затруднений: противники обвиняли его в связях с нечистой силой, поскольку Герберт умел делить слишком большие числа.
10 век
В Китае появляются счёты «Суань-Пан». Их поле разделено на две части: одна в пять костей, другая в две.
В России. Вместе с христианством здесь вводится письменность «Кириллица», разработанная, византийскими болгарами, братьями-монахами Кириллом и Мефодием. Согласно греческой традиции цифры в ней также обозначались буквами, что создавало большие неудобства при сложных математических расчетах.
| Календарь событий | 13 век — 16 век
Порядковые числительные в английском языке Woodward English
Один, два, три… это количественных чисел.
Первый, второй, третий … это порядковых номеров.
Порядковые номера обычно показывают порядок или последовательность чего-то или кого-то.
(Подробнее об использовании порядковых числительных ниже)
Обычно порядковые числительные можно создавать, добавляя -TH в конец кардинального числительного.
- Четыре – Четыре -й
- Шестнадцать – Шестнадцать -й
Основные исключения относятся к номерам 1, 2 и 3.
- один – первый
- два – второй
- три – третьи
Также нужно быть осторожным с написанием некоторых порядковых номеров:
- пять – пятый (не « пятый »)
- девять – девятый (не « девятый »)
Порядковые номера обычно используются для:
Даты
Мы используем порядковые номера при указании даты.
- Ее день рождения 29 числа . (Двадцать девятый)
- День их независимости приходится на 4 июля года. (4 июля)
Последовательность или порядок
Мы используем порядковые номера, когда хотим показать порядок или положение кого-то или чего-то в последовательности.
- Вудворд Юнайтед финишировал второй в лиге в прошлом году.
- Я пришел третьим в гонке.
- Это первый раз, когда это произошло.
Этажи здания
- Наш офис находится на девятом этаже.
- Она живет на втором этаже .
Празднование дня рождения
- 15-летие человека является важным праздником в Мексике.
- У него была грандиозная вечеринка в честь его двадцать первое день рождения.
Столетия
- Шекспир родился в 16 веке.

- Ренессанс — период европейской истории с 14 по 17 века.
Короли и королевы
Для имени короля или королевы в письменном английском языке используются римские цифры . Однако эти римские цифры называются порядковыми номерами в разговорном английском языке.
- Генрих VIII (Генрих Восьмой)
- Людовик XVI (Людовик Шестнадцатый) был последним королем Франции перед падением монархии во время Французской революции.
Список порядковых номеров
Мы включили все порядковые номера с 1 по 31, потому что они необходимы, когда вы указываете дату на английском языке.
Порядковые номера с 1-го по 31-е на английском языке:
- 1-й – первый
- 2-й – второй
- 3-я – третья
- 4-й – четвертый
- 5-й – пятый
- 6-й – шестой
- 7-й – седьмой
- 8-8
- 9-й – 9-й
- 10-й – десятый
- 11-й – одиннадцатый
- 12-й – двенадцатый
- 13-й – тринадцатый
- 14-й – четырнадцатый
- 15-15
- 16-й – шестнадцатый
- 17 – 17
- 18-й – восемнадцатый
- 19й – девятнадцатый
- 20-й – двадцатый
- 21 – двадцать первое
- 22-й – двадцать второй
- 23 – двадцать третье
- 24 – двадцать четвертое
- 25 – двадцать пятое
- 26-26
- 27-27
- 28 – двадцать восьмое
- 29 – двадцать девятое
- 30-е – тридцатое
- 31 – тридцать первое
Сводная таблица
Теги урока: День рождения, Век, Дата, Числа, Порядковые числительные Вернуться к: Курс английского языка > Даты и время на английском языкеСильвана Патриарка.
 Числа и государственность: написание статистики в Италии девятнадцатого века. (Кембриджские исследования итальянской истории и культуры.) Нью-Йорк: Издательство Кембриджского университета. 1996. Стр. xii, 280. $49,95 | Американское историческое обозрение
Числа и государственность: написание статистики в Италии девятнадцатого века. (Кембриджские исследования итальянской истории и культуры.) Нью-Йорк: Издательство Кембриджского университета. 1996. Стр. xii, 280. $49,95 | Американское историческое обозрениеФильтр поиска панели навигации The American Historical ReviewЭтот выпускВсемирная историяКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации The American Historical ReviewЭтот выпускВсемирная историяКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Получить доступ
Патриарка
Сильвана
.
Числа и национальность: статистика письма в Италии девятнадцатого века
. (Кембриджские исследования итальянской истории и культуры.)
Нью-Йорк
:
Cambridge University Press
.
1996
. Стр. xii, 280. 49,95 долл. США.
Карл Ипсен
Карл Ипсен
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
The American Historical Review , том 103, выпуск 2, 19 апреля98, стр. 550, https://doi.org/10.1086/ahr/103.2.550
Опубликовано:
01 апреля 1998 г.
Фильтр поиска панели навигации The American Historical ReviewЭтот выпускВсемирная историяКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации The American Historical ReviewЭтот выпускВсемирная историяКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Предварительный просмотр первой страницы статьи PDF
Закрыть
Этот контент доступен только в формате PDF.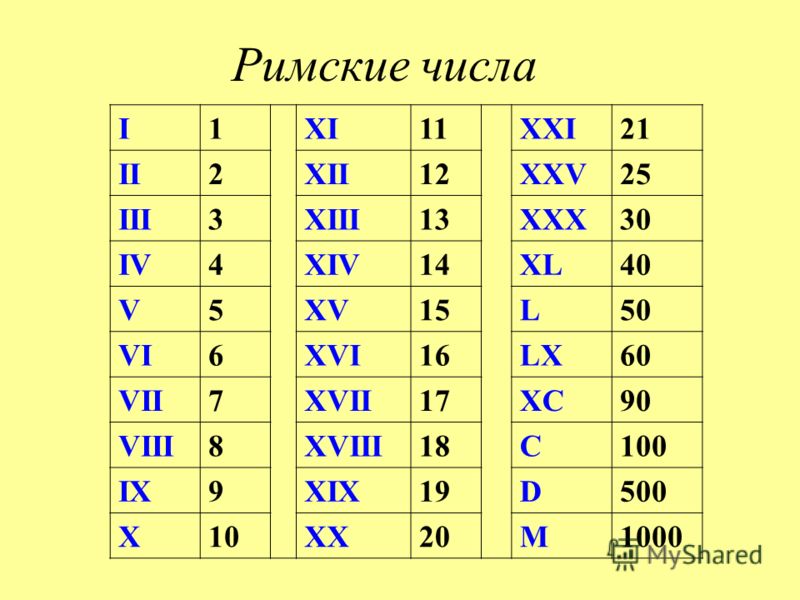
© Американская историческая ассоциация 1998
Раздел выдачи:
Современная Европа
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.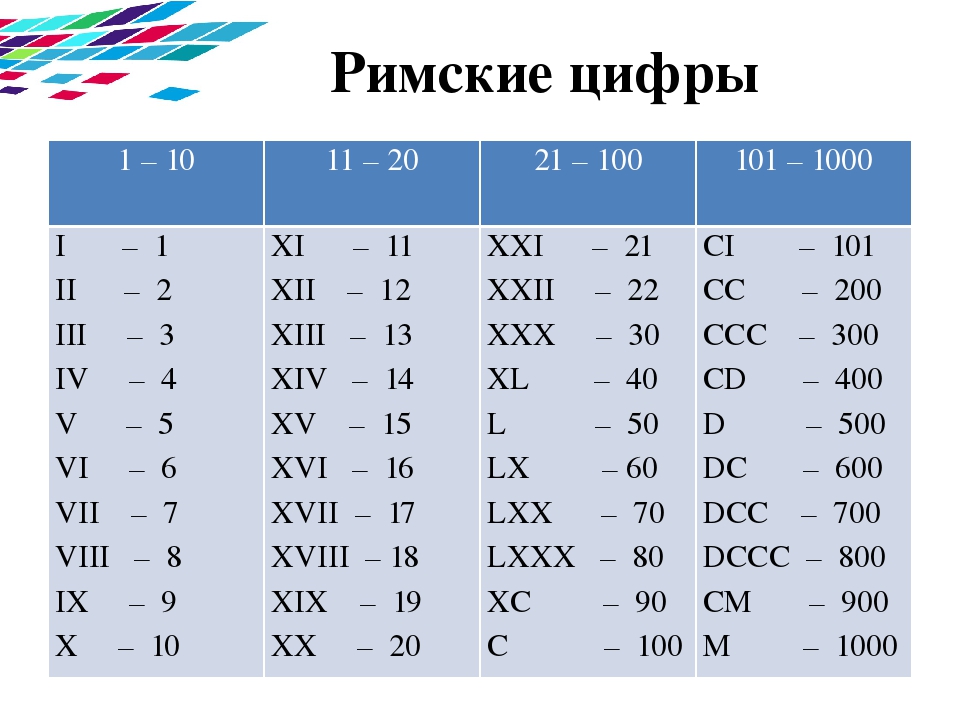
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Войти с помощью личного кабинета
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.
См. ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.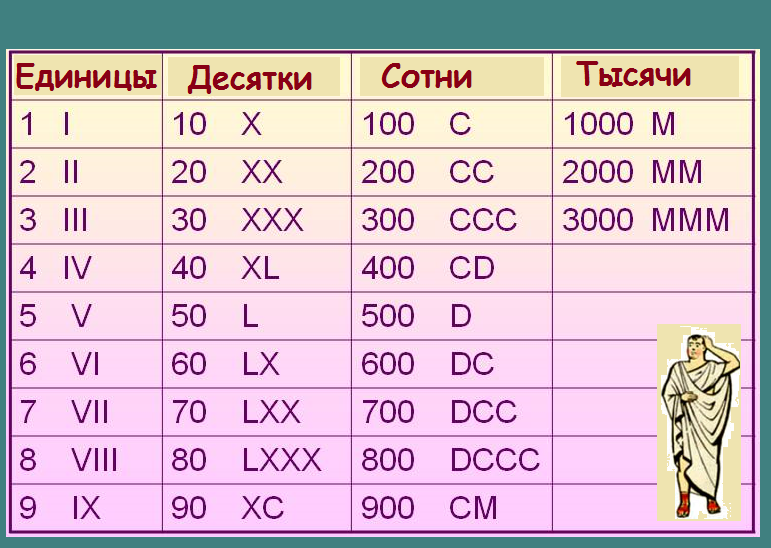
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Стоимость подписки и заказ этого журнала
Варианты покупки книг и журналов в Oxford Academic
Кратковременный доступ
Чтобы приобрести краткосрочный доступ, пожалуйста, войдите в свой личный аккаунт выше.
У вас еще нет личного кабинета? регистр
Сильвана Патриарка. Числа и национальность: статистика письма в Италии девятнадцатого века .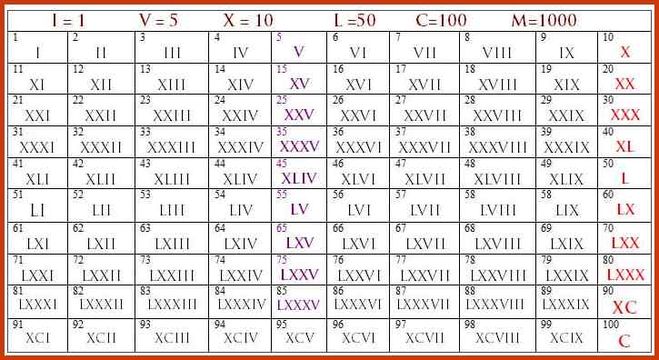 (Кембриджские исследования итальянской истории и культуры.) Нью-Йорк: Издательство Кембриджского университета. 1996. Стр. xii, 280. 49,95 долл. США — доступ в течение 24 часов
(Кембриджские исследования итальянской истории и культуры.) Нью-Йорк: Издательство Кембриджского университета. 1996. Стр. xii, 280. 49,95 долл. США — доступ в течение 24 часов
ЕВРО €36,00
32 фунта стерлингов
39 долларов США.
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Форум Проекта 1619
К.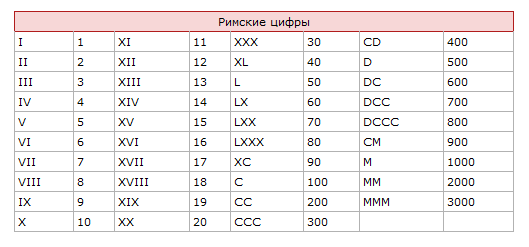



 Поводом послужил захват турками-сельджуками Эдессы.
Поводом послужил захват турками-сельджуками Эдессы. В её царствование Грузия добилась больших военно-политических успехов. Ей посвящена поэма Шота Руставели «Витязь в тигровой шкуре».
В её царствование Грузия добилась больших военно-политических успехов. Ей посвящена поэма Шота Руставели «Витязь в тигровой шкуре».
 Числа и национальность: статистика письма в Италии девятнадцатого века . (Кембриджские исследования итальянской истории и культуры.) Нью-Йорк: Издательство Кембриджского университета. 1996. Стр. xii, 280. $49,95, The American Historical Review , том 103, выпуск 2, апрель 1998 г., стр. 550, https://doi.org/10.1086/ahr/103.2.550
Числа и национальность: статистика письма в Италии девятнадцатого века . (Кембриджские исследования итальянской истории и культуры.) Нью-Йорк: Издательство Кембриджского университета. 1996. Стр. xii, 280. $49,95, The American Historical Review , том 103, выпуск 2, апрель 1998 г., стр. 550, https://doi.org/10.1086/ahr/103.2.550