Формулы в математике: Таблицы и формулы.

Основные формулы | Олимпиадный Центр МатРИЦА

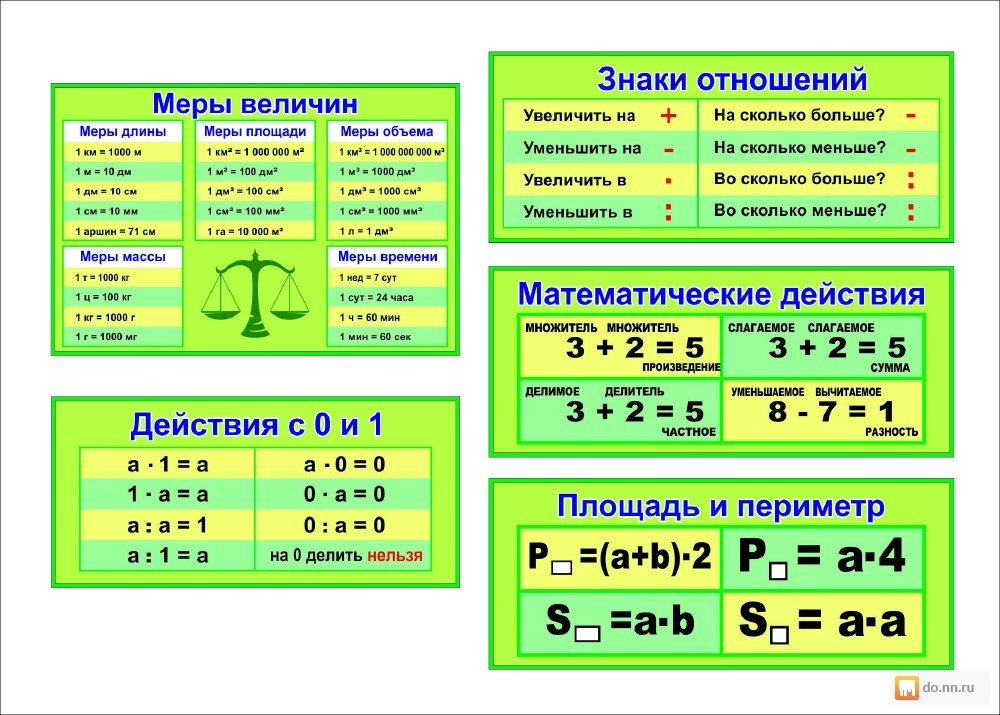
Математика: Все главные формулы

 

Оглавление:

• Таблица умножения

• Таблица квадратов двухзначных чисел

• Формулы сокращенного умножения

• Квадратное уравнение и формула разложения квадратного трехчлена на множители

• Свойства степеней и корней

• Арифметическая прогрессия

• Геометрическая прогрессия

• Геометрия на плоскости (планиметрия)

• Формулы с логарифмами

• Тригонометрия

• Тригонометрические уравнения

• Геометрия в пространстве (стереометрия)

• Координаты

• Скачать расширенную версию «Все главные формулы по школьной математике»

Весь курс алгебры для ОГЭ в схемах и таблицах >>>

Весь курс геометрии для ОГЭ в схемах и таблицах >>>

Весь курс по реальной математике для ОГЭ >>>

Все графики функций >>>

Таблица умножения

К оглавлению…

Таблица квадратов двухзначных чисел

К оглавлению…

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

#Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней.

В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

#Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

bn = b1 · q n-1

bn+1 =bn · q, где bn ≠ 0, q ≠ 0

q – знаменатель прогрессии

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника: 

Площадь треугольника через две стороны и угол между ними:  

Площадь треугольника через сторону и высоту опущенную на неё: 

Полупериметр треугольника находится по следующей формуле: 

Формула Герона для площади треугольника: 

Площадь треугольника через радиус описанной окружности: 

Формула медианы: 

Свойство биссектрисы: 

Формулы биссектрисы: 

Основное свойство высот треугольника: 

Формула высоты: 

Еще одно полезное свойство высот треугольника: 

Теорема косинусов: 

Теорема синусов: 

Радиус окружности, вписанной в правильный треугольник: 

Радиус окружности, описанной около правильного треугольника: 

Площадь правильного треугольника: 

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты): 

Радиус окружности, вписанной в прямоугольный треугольник: 

Радиус окружности, описанной вокруг прямоугольного треугольника: 

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу): 

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника: 

Длина средней линии трапеции: 

Площадь трапеции: 

Площадь параллелограмма через сторону и высоту опущенную на неё: 

Площадь параллелограмма через две стороны и угол между ними: 

Площадь квадрата через длину его стороны: 

Площадь квадрата через длину его диагонали: 

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами): 

Площадь прямоугольника через две смежные стороны: 

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними: 

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):  

Свойство касательных: 

Свойство хорды: 

Теорема о пропорциональных отрезках хорд: 

Теорема о касательной и секущей: 

Теорема о двух секущих: 

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу): 

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой): 

Свойство центральных углов и хорд: 

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

 

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом: 

Свойства логарифмов:

Логарифм произведения: 

Логарифм дроби: 

Вынесение степени за знак логарифма: 

Другие полезные свойства логарифмов:

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса: 

Определение косинуса: 

Определение тангенса: 

Определение котангенса: 

Основное тригонометрическое тождество: 

Простейшие следствия из основного тригонометрического тождества: 

Формулы двойного угла

Синус двойного угла: 

Косинус двойного угла: 

Тангенс двойного угла: 

Котангенс двойного угла: 

Тригонометрические формулы сложения

Синус суммы: 

Синус разности: 

Косинус суммы: 

Косинус разности: 

Тангенс суммы: 

Тангенс разности: 

Котангенс суммы: 

Котангенс разности: 

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов: 

Разность синусов: 

Сумма косинусов: 

Разность косинусов: 

Сумма тангенсов: 

Разность тангенсов: 

Сумма котангенсов: 

Разность котангенсов: 

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов: 

Произведение синуса и косинуса: 

Произведение косинусов: 

Формулы понижения степени

Формула понижения степени для синуса: 

Формула понижения степени для косинуса: 

Формула понижения степени для тангенса: 

Формула понижения степени для котангенса: 

Формулы половинного угла

Формула половинного угла для тангенса: 

Формула половинного угла для котангенса: 

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

К оглавлению…

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия в пространстве (стереометрия)

К оглавлению…

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (трёхмерная Теорема Пифагора):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т. е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара: 

Площадь поверхности шара (площадь сферы): 

Координаты

К оглавлению…

Длина отрезка на координатной оси: 

Длина отрезка на координатной плоскости: 

Длина отрезка в трёхмерной системе координат: 

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы): 

Как успешно подготовиться к экзамену по математике?

Для того чтобы успешно подготовиться к ОГЭ или ЕГЭ по математике,  необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к экзамену по математике, изучению теории и решению задач хотя бы по часу, но каждый день. Дело в том, что ОГЭ или ЕГЭ — это экзамены, где мало просто знать математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно, но только, решив тысячи задач.
2. Выучить все формулы и методы в математике! На самом деле, выполнить это тоже очень просто, необходимых формул по математике меньше 200. В алгебре и геометрии есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить. И, таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ОГЭ или ЕГЭ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования (РТ) по математике в нашем Центре (ЦР). Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на РТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на реальном экзамене может показаться неподготовленному человеку очень непривычным.

Успешное и ответственное выполнение этих трех пунктов позволит Вам показать на экзамене отличный результат, максимальный из того на что Вы способны!

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно через контактную форму на данном сайте. В письме укажите предмет (математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

<<< Структура сайта подготовки к ОГЭ по математике

План подготовки к ОГЭ по математике >>>

Все формулы по математике — Формулы под рукой

Не решается задачка? Наш сайт поможет тебе в учебе, подготовке к сложным экзаменам, контрольным, олимпиадам, сессиям, ЕГЭ.

ФОРМУЛЫ ПО АЛГЕБРЕ

Формулы сокращенного умноженияСвойства степени ПропорцииСвойства квадратного корня Прогрессии  Квадратное уравнение Квадратный трехчлен Неравенства Логарифмы Сравнение логарифмов Теория соединений. Бином Ньютона

ФОРМУЛЫ ПО ГЕОМЕТРИИ

 ТреугольникиЧетырехугольникиПравильные n-угольникиОкружность и кругМногогранникиПравильные многогранникиТела вращенияВекторы

ФОРМУЛЫ ПО ТРИГОНОМЕТРИИ

Градусная и радианная мера угловТригонометрические функцииТригонометрические функции
в прямоугольном треугольникеТригонометрические тождестваВыражение одних функций тригонометрии через другиеФормулы сложения тригонометрических функцийФормулы приведения тригонометрических функцийТригонометрические функции кратных угловТригонометрические функции половинного углаПонижение степени тригонометрических функцийПроизведение тригонометрических функцийФормула дополнительного углаСоотношения между обратными тригонометрическими функциями

Обладатель премии Эйнштейна, известнейший британский исследователь в области теоретический физики Стивен Хокинг однажды рассказал, что получил должность профессора математики в Оксфордском университете, не имея специального образования. На тот момент за его плечами были лишь изрядно подзабытые школьные знания по математике. Царицу наук постигал «на ходу», читая студенческий учебник с опережением программы на две недели. Впоследствии студенты Хокинга вспоминали его занятия как исключительно познавательные и захватывающие!

Такие примеры вдохновляют, вселяют уверенность, что и каждый из нас может с таким же успехом освежить «хорошо забытое». А там и новый вектор развития появится.

Чтобы вспомнить (или освоить!) школьный материал было легче, предлагаем листать не страницы учебников и справочной литературы, а воспользоваться нашим сайтом, где удобная навигация и система поиска позволят быстро отыскать нужную формулу по предметам:

• арифметика;
• алгебра;
• геометрия;
• физика;
• химия.

От теории к практике

Бывает, что и материал знаком, да и формулы, теоремы и аксиомы по нужной теме — вот они, а задачка не поддается. Педагогический «диагноз»: нет опыта. Приобретается этот опыт при помощи решения типовых уравнений и задач. Предлагаем наиболее удачные и интуитивно понятные методики, которые уже помогли не одному ученику овладеть инструментарием точных наук!

Быстрее, выше, сильнее!

Возможно, сейчас ты и считаешь, что выучить все школьные формулы невозможно. Но на самом деле формул, необходимых для решения задач школьного уровня по математике, не более двухсот, а по физике — и того меньше! А это значит, что, заглядывая в наши справочники и освоив принципы решения типовых задач, можно постепенно запомнить все базовые формулы!

Какими бы сложными ни казались тебе задания твоих преподавателей сейчас, через какое-то время школьные, да и институтские стены могут показаться тебе тесными.

На нашем сайте собраны как часто используемые, так и гораздо более сложные формулы. Если захочешь знать больше, чем написано в школьном учебнике, начни с аксиомы — слов Марка Твена, который «никогда не позволял, чтобы школьные занятия мешали образованию!».

17 важных математических формул для понимания

Автор: Вирджиния | 21 июня 2022 г.

, 8:55

Любой школьник знает, что сложные математические задачи достаточно сложны и без необходимости запоминать правильную формулу. Поэтому важно иметь все нужные инструменты в заднем кармане!

Запоминание пошаговой методологии, необходимой для решения сложных математических задач, достаточно сложно для учащихся. Последнее, что им нужно, это попытаться вспомнить хитрую формулу вдобавок ко всему!

Если вашему ребенку нужно освежиться, чтобы выполнить домашнее задание, или ему нужно вспомнить основы для большого теста или викторины, эти формулы обязательно пригодятся.

Важные математические формулы

Математика может быть забавной задачей или головной болью учащихся: эти формулы будут полезны независимо от того, к какой части спектра относится ваш ребенок. Мы обеспечим вас, несмотря ни на что.

Начальная и средняя школа

Площадь прямоугольника: площадь = длина x ширина

Детям нужно будет знать это на уроках алгебры и математики.

Периметр прямоугольника: 2(l + b)

Это рассчитает сумму внешних линий прямоугольника.

Площадь квадрата: a²

Возведите в квадрат длину обеих сторон, чтобы найти площадь квадрата.

Периметр квадрата: 4 x a

Умножьте длину стороны квадрата на 4, чтобы найти периметр.

Площадь круга: π x r²

Используйте это, чтобы найти общую площадь круга.

Длина окружности: 2π x  r

Эта формула вычисляет длину внешней стороны окружности.

Найти среднее: Сумма общих чисел, деленная на количество значений.

Полезен в статистике и многих других математических задачах.

Полезные математические формулы для старших классов и SAT®

Эти математические формулы для старших классов пригодятся в геометрии, алгебре, математических вычислениях и многом другом. Кроме того, когда наступит сезон SAT®, они помогут подросткам добиться успеха в сложной математической секции.

(Ищете дополнительную помощь по математике SAT®? Ознакомьтесь с 11 приложениями SAT® для ежедневной практики и подготовкой к тесту по математике.)

Квадратичная формула: x = −b ± √b²-4ac/2a

Это понадобится учащимся для решения квадратных уравнений по алгебре II и выше. В качестве дополнительного легочного бонуса этот легче запомнить на мелодию «Pop Goes the Weasel».

Вероятность: количество благоприятных исходов, деленное на общее количество благоприятных исходов.

Чтобы определить вероятность события, это уравнение определяет вероятность того, что что-то произойдет.

Формула расстояния: d=√(x₁ – x₂)² + (y₁ – y₂)²

Это уравнение рассчитает расстояние между двумя точками, которое понадобится в геометрии и алгебре.

Формула наклона: Наклон = y₂ – y₁ /  x₂ – x₁

Используйте это, чтобы найти угол, соединяющий две точки на графике.

Формула пересечения уклона: y=mx+b

В алгебре это находит пересечение наклона прямой линии.

Площадь треугольника: Площадь = (1/2) (основание) (высота)

Используйте это в геометрии, чтобы найти общую площадь треугольника.

Синус (SOH): Синус = противоположность / гипотенуза

Это уравнение вычисляет неизвестные углы треугольника.

Косинус (CAH): косинус = смежный / гипотенуза

Используйте это уравнение, чтобы найти неизвестные углы треугольника.

Касательная (TOA): Касательная = противоположная / смежная

Это уравнение также можно использовать для вычисления неизвестных углов треугольника.

Теорема Пифагора: a²+b²=c²

Используется для нахождения длины гипотенузы в прямоугольном треугольнике. В любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов прямоугольного треугольника.

Проблемы с математикой? У нас есть математические решения!

В дополнение к непревзойденному репетиторству по математике iD Tech предлагает множество математических ресурсов. Вот краткий обзор:

• Интересные факты о математике
• Математические соревнования 2021
• Ежедневные способы сделать математику увлекательной
• 25 занимательных математических заданий
• Лучшие образовательные каналы YouTube

Имея в руках эти полезные советы и рекомендации, вы готовы помочь своему ученику с домашними заданиями по математике, тестами, викторинами и SAT®!

Вирджиния

Вирджиния начала работать с iD Tech в Университете Денвера в 2015 году и с тех пор наслаждается каждой минутой! Бывший учитель по профессии, она имеет степень магистра в области образования и любит работать, чтобы вдохновлять следующее поколение с помощью STEM. Вне офиса вы обычно можете найти ее читающей хорошую книгу, борющейся на коврике для йоги или исследующей Скалистые горы.

Что такое формула в математике? Значение, определение, примеры, факты

Что такое формула в математике?

Формула — это факт или правило, записанное математическими символами. Обычно он связывает две или более величин со знаком равенства. Зная значение одной величины, можно найти значение другой по формуле. Помогает быстро решить вопросы. В алгебре, геометрии и других темах формулы используются для упрощения процесса получения ответа и экономии времени.

Родственные игры

Простые формулы в математике

Теорема Пифагора — один из примеров формулы в математике. Помимо этого, в математике есть много других формул. Некоторые из наиболее часто используемых формул в математике перечислены ниже:

Основные формулы геометрии

Геометрия — это раздел математики, связанный с формами, размерами, занимаемым пространством и относительным положением объектов. В геометрии мы используем формулы для нахождения размеров, периметра, площади, площади поверхности, объема и т. д. различных форм. 2D-формы плоские и имеют только два измерения: длину и ширину. Некоторые основные 2D-формулы для перечисленных ниже:

3D-объекты представляют собой твердые объекты с тремя измерениями: длиной, шириной и высотой или глубиной. Например, куб, прямоугольный параллелепипед, сфера, цилиндр и конус. Формулы для объемов основных 3D-фигур приведены ниже:

Основная алгебраическая формула

Алгебраические формулы составляют основу для различных разделов математики, таких как уравнения, многочлены, тригонометрия и т. д. Вот некоторые наиболее часто используемые алгебраические формулы.

• а ² – б ² = (а – б)(а + б)
• (а + b) ² = а ² + 2ab + b ²
• (а – б) ² = а ² – 2аб + б ²
• а ⁰ = 1
• n}$ = x ^m-n

Формула среднего арифметического

Среднее арифметическое (среднее) = $\frac{Сумма значений}{Количество значений}$

Реальные приложения математических формул

Важно понимать, что математические формулы являются частью каждой области вашей жизни. Значение формулы в математике состоит в том, чтобы выразить информацию символически и лаконично, и они получены после нескольких десятилетий исследований.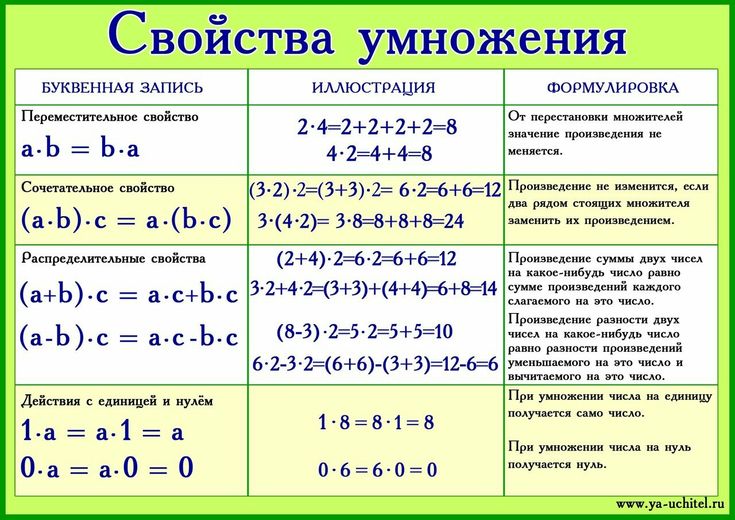 Мы широко используем их в строительстве, архитектуре, машиностроении и многом другом. Осознаете вы это или нет, но мы используем алгебраические формулы, чтобы планировать свое расписание и просто выполнять наши задачи. Формулы геометрии, такие как площадь, периметр и теорема Пифагора, обычно используются при строительстве различных типов сооружений или зданий. Мы используем алгебраические формулы в области финансового планирования и компьютерных наук. Формулы алгебры используются в медицине для измерения дозировки лекарств в зависимости от возраста и веса человека. В реальной жизни нам нужны формулы для решения большинства задач, связанных с вычислениями.

Решенные примеры

Пример 1: Найдите периметр квадрата со стороной 5 единиц.

Решение: Периметр квадрата = 4 × сторона = 4 × 5 = 20 единиц.

Пример 2: Найти значение n, когда 3 ^-7 × 3 ⁿ = 3 ^{17 18}

Решение: Используя законы экспонент , получаем

3 ^-7 × 3 ⁿ = 3 ²

3 ^-7+n = 3 ²

Так как основания одинаковы и приравнивая степени, получаем -7 + n = 2

Следовательно, должно быть 2 + 7 или 9.

No related posts.