Какой угол называется равным: Какие углы называются равными?

Углы | Математика

Две прямые линии BA и BC (черт. 13), пересекающиеся в одной и той же точке B, образуют при точке B угол.

Определение угла. Углом называется неопределенная часть плоскости, ограниченная двумя пересекающимися прямыми линиями. Угол есть величина, определяющая наклонение одной прямой линии к другой.

Стороны угла. Пересекающиеся линии называются сторонами угла.

Вершина угла. Точка пересечения двух прямых называется вершиной угла. Величина угла не зависит от длины сторон, поэтому стороны угла можно неопределенно продолжать.

Название угла. a) Углы называют буквой, стоящей при вершине; так угол на черт. 13 называют углом B. b) Если при вершине несколько углов, то углы называют тремя буквами, стоящими при вершине и двух его сторонах. При этом буква при вершине произносится и пишется в середине.

На черт. 13 угол B называют угол ABC. Линии BA и BC — две стороны, а точка B — вершина угла.

Таким образом угол ABC есть угол B или

угол ABC = углу B.

Знак угла. Слово угол заменяют иногда знаком ∠.

Таким образом предыдущее равенство изображают письменно:

∠ABC = ∠B

В том случае, когда из точки выходит несколько линий, при точке B имеется несколько углов.

На черт. 14 из точки B выходят прямые линии BA, BC, BD и при вершине B имеются углы ABC, CBD, ABD.

Прилежащие углы. Два угла называются прилежащими, когда они имеют общею вершину, по одной общей стороне, а две другие лежат по обе стороны общей стороны.

Углы ABC и CBD (черт. 14) суть прилежащие углы. Они имеют общую вершину B, общую сторону BC, а две другие стороны BA и BD лежат одна сверху, а другая снизу общей стороны BC.

Углы изменяют свою величину, если изменяется наклонение одной стороны к другой. Из двух углов, имеющих общую вершину, тот угол, внутри которого помещается другой угол, называется большим углом. На чертеже 14

уг. ABD > уг. ABC и уг. CBD < уг. ABD.

Чтобы иметь понятие о взаимной величине двух углов, имеющих разные вершины, накладывают один угол на другой. При наложении совмещают их вершины и по одной стороне, тогда направление другой стороны даст возможность сравнивать их величину. Чтобы сравнить два угла ABC и DEF (черт. 15), накладывают угол DEF на угол ABC так, чтобы сторона EF пошла по стороне BC, точка E совмещалась с точкой B; тогда сторона ED может занять три положения: она может совпасть со стороной BA, упасть внутри и вне угла ABC.

a) Если линия ED совпадет с линией BA, углы называются равными

уг. ABC = уг. DEF.

b) Если линия ED упадет внутри угла ABC и займет положение BG, угол ABC будет больше угла DEF

уг. ABC > уг. DEF.

c) Если же линия ED упадет вне угла ABC по направлению BH, угол ABC меньше угла DEF

уг. ABC < уг. DEF.

Сложение, вычитание, умножение и деление углов. Два прилежащих угла ABC и CBD (чер. 14) образуют один угол ABC. Угол ABD называется суммой углов ABC и CBD. Это выражают письменно равенством:

∠ABD = ∠ABC + ∠CBD (a)

Из равенства (а) вытекает равенство:

∠ABC = ∠ABD — ∠CBD

∠CBD = ∠ABD — ∠ABC,

т. е. угол ABC есть разность углов ABD и CBD, и угол CBD есть разность углов ABD и ABC.

Углы можно складывать и вычитать.

Если при точке O (черт. 16) находится несколько равных прилежащих углов, т. е. если

∠AOB = ∠BOC = ∠COD = ∠DOE,

то угол AOC, равный сумме углов AOB и BOC равен двум углам AOB,

∠AOC = ∠AOB + ∠BOC, след. ∠AOC = 2AOB.

Угол AOD равен трем углам AOB

AOD = 3AOB.

Обратно, угол AOB составляет половину угла AOC, треть угла AOD, четверть угла AOE.

AOB = ½ AOC = 1/3 AOD = ¼ AOE.

Отсюда выводим, что углы как величины можно не только складывать и вычитать, но также умножать и делить на отвлеченное число.

Если из двух прилежащих углов ACD и DCB (чер. 17) две стороны CA и CB лежат на одной прямой, их называют смежными.

Смежные углы. Смежными называются такие углы, у которых одна сторона общая, а две другие лежат на одной прямой.

Если линия CD, поворачиваясь около точки C, займет положение CE, то угол ACD уменьшаясь обратится в угол ACE, а угол BCD увеличиваясь обратится в угол BCE. Линия CD, продолжая поворачиваться, может принять такое положение, что два смежных угла сделаются равными. Когда два смежных угла ACD и DCB равны (чер. 18), их называют прямыми углами.

В этом случае линия CD называется перпендикулярной к линии AB или просто перпендикуляром к линии AB.

На чертеже 19 начерчен один прямой угол без другого смежного с ним.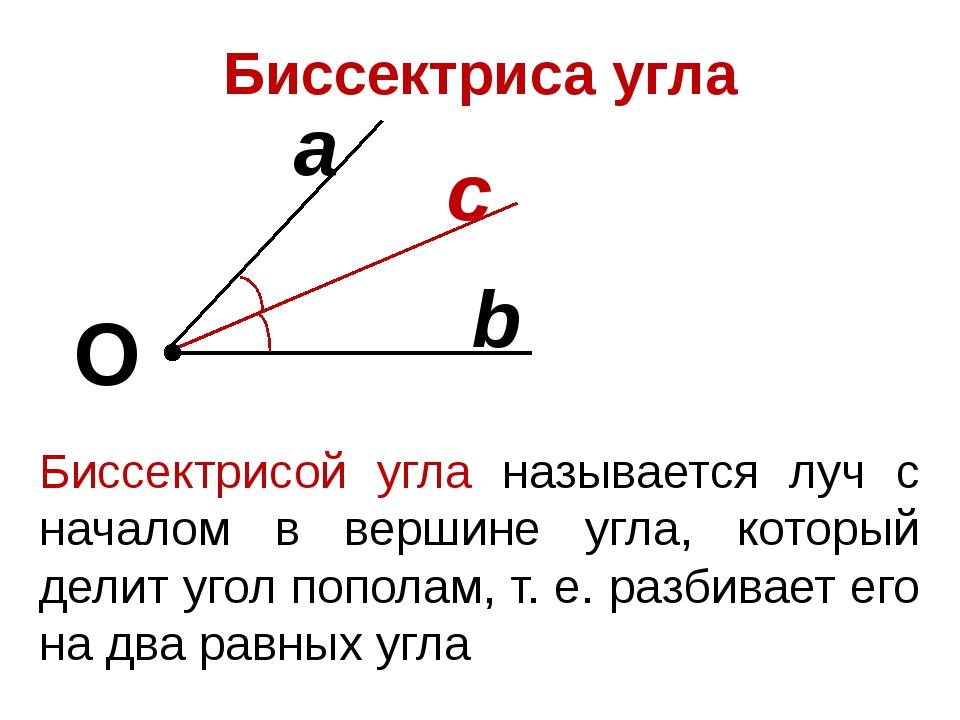

Прямой угол есть один из равных смежных углов.

Перпендикуляр есть прямая линия, образующая с другой линией прямой угол.

На чертеже 18 углы ACD и DCB, оставаясь смежными и равными, получают название прямых углов. Линия DC будет перпендикулярной к линии AB. Такое взаимное отношение двух линий выражают иногда письменно: CD ⊥ AB.

Так как линия AB будет также перпендикулярна к линии CD, то линия AB и CD будут взаимно-перпендикулярны, т. е. если CD ⊥ AB, то и AB ⊥ CD.

Подошва перпендикуляра. Точка взаимной встречи двух перпендикулярных линий называется подошвою перпендикуляра.

Точка C (чер. 18) есть подошва перпендикуляра CD.

В каждой точке линии AB можно провести перпендикуляр к линии AB.

Провести перпендикуляр к линии (AB) из точки, лежащей на линии, значит восставить перпендикуляр. Провести же перпендикуляр (DC) к линии (AB) из точки (D), лежащей вне прямой, значит опустить перпендикуляр (черт. 18).

Наклонная линия. Всякая линия неперпендикулярная к другой называется линией наклонною к ней.

На чертеже 20 линия CE будет наклона к линии AB, а линия CD перпендикулярна к линии AB.

Угол ECB меньше прямого, а угол ACE больше прямого. Угол ECB называется острым, а угол ACE тупым.

Острый угол есть всякий угол меньше прямого, а тупой угол есть угол больший прямого.

Одноименные и разноименные углы. Два острых или два тупых угла называются одноименными, а два угла, из которых один острый, а другой тупой, называются разноименными.

Наклонная линия CE образует (черт. 20) с прямою AB два смежных угла, из которых один меньше, а другой больше прямого, т. е. один острый, а другой тупой.

Теорема 3. Из точки, взятой на прямой линии, можно восставить к ней только один перпендикуляр.

Дана прямая AB и на ней точка C (черт. 20).

Требуется доказать, что можно к ней восставить только один перпендикуляр.

Доказательство. Положим, что можно из точки C к линии AB восставить два перпендикуляра (черт. 20) CD и CE. По свойству перпендикуляра

уг. DCB = уг. ACD (a)
уг. BCE = уг. ACE.

Если приложить к первой части последнего неравенства угол ECD, получим неравенство

уг. BCE + уг. ECD > уг. ACE, или уг. BCD > уг. ACE.

Заменяя в этом неравенстве уг. BCD равным ему углом ACD (a), получим

уг. DCA > уг. ACE,

неравенство очевидно нелепое, ибо часть не может быть более своего целого, следовательно предположение, что можно восставить два перпендикуляра, ведет к нелепости, поэтому оно ложно. Ложность предположения основана на том соображении, что из верного положения нельзя вывести неверного заключения, следовательно, наша теорема верна.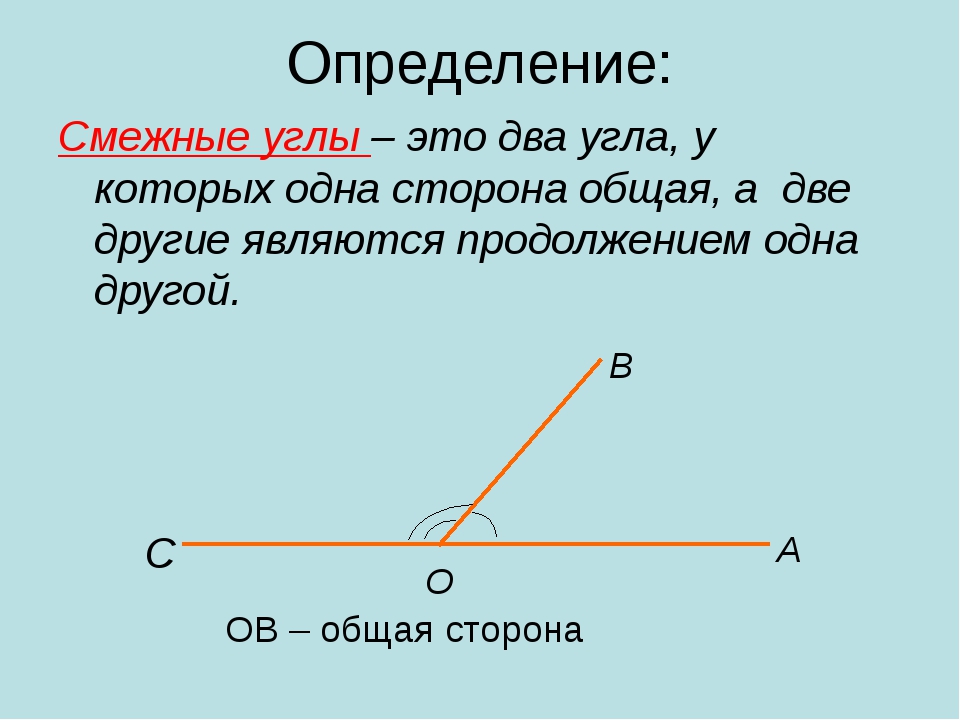

Способ доказывать справедливость данной теоремы указанием на невозможность и нелепость всякого другого предположения называется способом доказательства от противного или способом приведения к нелепости.

Теорема 4. Все прямые углы равны.

Предположим, мы имеем две пары прямых углов: одну пару составляют углы ACD и DCB, а другую углы EGH и HGF, следовательно, CD ⊥ AB и HG ⊥ EF (черт. 21).

Требуется доказать, что прямые углы равны.

Доказательство. Наложим линию EF на линию AB точкой G на точку C, тогда линия GH пойдет по линии CD, ибо из точки C можно восставить только один перпендикуляр, следовательно, прямой угол DCB = прямому углу HGF.

Заключение. Прямой угол есть величина постоянная.

Мера углов. При измерении углов прямой угол, как величину постоянную, принимают за единицу сравнения. Величину его обозначают буквою d.

В таком случае
всякий острый угол < d,
всякий тупой угол > d.

Все углы выражаются при помощи прямого. Так, например, говорят: данный угол равен ½ d, 2/3 d и т. д.

Теорема 5. Сумма двух смежных углов равна двум прямым.

Даны смежные углы ACD и DCB (черт. 22).

Требуется доказать, что ACD + DCB = 2d.

Доказательство. Из точки C восставим перпендикуляр CE, тогда

ACD = ACE + ECD = d + ECD
DCB = ECB — ECD = d — ECD

Сложив эти равенства, имеем:

ACD + DCB = ACE + ECB = 2d (что и требовалось доказать).

Два смежных угла пополняют один другой до двух прямых и потому называются углами дополнительными.

Из теоремы 5 вытекает следствие. Одна пара смежных углов равна другой паре смежных углов.

Теорема 6 (обратная теореме 5). Если сумма двух прилежащих углов равна двум прямым, то две другие стороны лежат на одной прямой.

Пусть сумма двух прилежащих углов ACD и DCB равна двум прямым (черт. 23).

ACD + DCB = 2d.

Требуется доказать, что ACB прямая линия.

Доказательство. Допустим, что ACB есть ломаная линия и что продолжение линии AC будет линия CE, тогда

ACD + DCE = 2d

Две величины равные одной и той же третьей равны (аксиома 3), следовательно

ACD + DCB = ACD + DCE

откуда выходит при сокращении

DCB = DCE

заключение нелепое (часть равна целому, см. акс. 1), следовательно линия ACB есть прямая линия (что и требовалось доказать).

Теорема 7. Сумма углов, имеющих вершину в одной точке и расположенных по одну сторону прямой линии, равна двум прямым.

Даны углы ACD, DCE, ECF, FCG, GCB, имеющие общую вершину в точке C и расположенные по одну сторону прямой AB (черт. 24).

Требуется доказать, что

ACD + DCE + ECF + FCG + GCB = 2d.

Доказательство. МЫ знаем, что сумма двух смежных углов ACF и FCB равна двум прямым (т. 5).

ACF + FCB = 2d.

Так как ACF = ACD + DCE + ECF и FCB = FCG + GCB, то заменяя углы ACF и FCB их величинами, находим:

ACD + DCE + ECF + FCG + GCB = 2d (что и требовалось доказать).

Теорема 8. Сумма всех углов, расположенных вокруг одной точки, равна четырем прямым.

Даны углы AOB, BOC, COD, DOE, EOA, имеющие общую вершину O и расположенные вокруг точки O (черт. 25).

Требуется доказать, что

AOB + BOC + COD + DOE + EOA = 4d.

Доказательство. Продолжим сторону EO по направлению OG (чер. 25), тогда

EOA + AOG = 2d.

Точно также

GOB + BOC + COD + DOE = 2d.

Сложив эти равенства, имеем:

EOA + AOG + GOB + BOC + COD + DOE = 4d.

Так как AOG + GOB = AOB, то

EOA + AOB + BOC + COD + DOE = 4d (ЧТД).

Угол ACB с углом DCE и угол BCD с углом ACE называются вертикальными (чер. 26).

Вертикальные углы. Вертикальными называются такие углы, у которых стороны одного составлены из продолжения сторон другого угла.

Теорема 9. Вертикальные углы равны между собой.

Даны вертикальные углы (чер. 26) ACB и DCE, точно также BCD и ACE.

Требуется доказать, что ACB = DCE и BCD = ACE.

Доказательство. На основании теоремы 5 имеют место равенства:

ACB + BCD = 2d (как сумма двух смежных углов)
BCD + DCE = 2d

следовательно,

ACB + BCD = BCD + DCE

откуда, отняв по равному углу BCD, находим

ACB = DCE.

Подобным же образом доказывают, что

∠BCD = ∠ACE.

Равносекущая (биссектриса) есть линия, делящая угол пополам.

На чертеже 27 BD есть биссектриса, если ∠ABD = ∠DBC.

Теорема 10. Биссектрисы двух смежных углов взаимно перпендикулярны.

Даны смежные углы ACB и BCD (чер. 28). Их биссектрисы линии CF и CE делят смежные углы BCD и BCA пополам, следовательно BCF = FCD, ACE = ECB.

Требуется доказать, что EC ⊥ CF.

Доказательство. По условию

ECB = ½ ACB, BCF = ½ BCD

Сложив эти равенства, имеем:

ECB + BCF = ½ ACB + ½ BCD = ½ (ACB + BCD).

Так как ACB + BCD = 2d, то

ECB + BCF = ½ · 2d = d.

Так как ECB + BCF = ECF, то

ECF = d

Угол ECF прямой, т. е. линии CE и CF взаимно перпендикулярны (ЧТД).

Полуплоскость и угол — презентация онлайн

1. Полуплоскость и угол

Следующее свойство является аксиомой взаимного расположения
точек на плоскости относительно данной прямой.
Каждая прямая на плоскости разбивает эту плоскость на две
части. При этом если две точки принадлежат разным частям, то
отрезок, соединяющий эти точки, пересекается с прямой. Если две
точки принадлежат одной части, то отрезок, соединяющий эти
точки, не пересекается с прямой.
Полуплоскостью называется … часть плоскости, состоящая из
точек данной прямой и точек, … лежащих по одну сторону от
этой прямой.

2. Угол

Углом называется фигура, образованная … двумя лучами с
общей вершиной и … одной из частей плоскости, ограниченной
этими лучами. Общая вершина называется… вершиной угла.
Сами лучи называются… сторонами угла.
Угол называется развернутым, если … его стороны вместе
составляют одну прямую.
Два угла называются смежными, если … одна сторона у них
общая, а две другие … вместе составляют одну прямую.
Два угла называются вертикальными, если … стороны одного
угла дополняют до прямых стороны другого угла.

3. Равенство углов

Одной из основных операций, которую можно производить с
углами, является операция откладывания данного угла в ту или
другую сторону от данного луча. Получающийся при этом угол
называется равным исходному углу.
В качестве аксиом принимаются следующие свойства.
От любого луча на плоскости в заданную сторону можно
отложить только один угол, равный данному.
Все развернутые углы равны.
Равенство углов АОВ и А1О1В1 записывается в виде АОВ =
А1О1В1. Оно означает, что если один из этих углов,
например АОВ, отложить от луча О1А1 в сторону, определяемую
лучом О1В1, то угол АОВ при этом совместится с углом А1О1В1.
Если при откладывании угла АОВ от луча О1А1 луч ОВ переходит в
луч O1B’, лежащий внутри угла А1О1В1, то говорят, что угол АОВ
меньше угла А1О1В1 и обозначают АOВ < А1O1В1.

4. Виды углов

Угол называется прямым, если …
он равен своему смежному углу.
Угол называется острым, если …
он меньше прямого угла.
Угол называется тупым, если …
он больше прямого, но меньше развернутого
угла.

5. Сложение углов

Если внутри угла АОВ провести луч ОС, то образуется два новых
угла АОС и СОВ. Угол АОВ называется суммой углов АОС и СОВ
и обозначается АОВ = АOС + СOВ. Каждый из углов АОС и СОВ
называется разностью угла АОВ и другого угла, обозначается
АOС = АOВ — СOВ, СOВ = АOВ — АOС.
Чтобы сложить два угла, например АОВ и CО1D, отложим угол
CO1D от луча ОВ так, чтобы точки A и D находились по разные
стороны от прямой ОВ. Обозначим ОЕ луч, в который перейдет луч
О1D. Тогда угол АОЕ даст сумму углов АОВ и CО1D.
Аналогичным образом поступают для вычитания из большего угла
меньшего.

6. Вопрос 1

На сколько частей прямая разбивает
плоскость?
Ответ: На две части.

7. Вопрос 2

В каком случае две точки принадлежат:
а) одной полуплоскости;
б) разным полуплоскостям относительно
данной прямой?
Ответ: а) Если отрезок, соединяющий
эти точки, пересекается с прямой.
б) если отрезок, соединяющий эти
точки, не пересекается с прямой.

8. Вопрос 3

Какая фигура называется углом? Что
называется вершиной угла? Что называется
сторонами угла?
Ответ: Фигура, образованная двумя лучами с
общей вершиной и одной из частей плоскости,
ограниченной этими лучами, называется углом.
Общая вершина называется вершиной угла, а
сами лучи — сторонами угла.

9. Вопрос 4

Какой угол называется развернутым?
Ответ: Угол называется развернутым, если его
стороны вместе составляют прямую.

10. Вопрос 5

Какие углы называются смежными?
Ответ: Два угла называются смежными, если
одна сторона у них общая, а две другие
составляют вместе прямую.

11. Вопрос 6

Какие углы называются вертикальными?
Ответ: Два угла называются вертикальными,
если стороны одного угла дополняют до
прямых стороны другого угла.

12. Вопрос 7

Как обозначаются углы?
Ответ: Угол обозначается или одной буквой,
указывающей его вершину, или тремя буквами,
средняя из которых указывает вершину угла, а
крайние – какие-нибудь точки на сторонах угла.
Например, A, AOB и т.д. Иногда углы
обозначаются цифрами, например, 1, 2 и т.д.

13. Вопрос 8

Какие два угла называются равными?
Ответ: Два угла называются равными, если один
получается из другого операцией откладывания
угла.

14. Вопрос 9

Как сложить два угла?
Ответ: Чтобы сложить два угла, например АОВ
и CО1D, отложим угол CO1D от луча ОВ так,
чтобы точки A и D находились по разные
стороны от прямой ОВ. Обозначим ОЕ луч, в
который перейдет луч О1D. Тогда угол АОЕ даст
сумму углов АОВ и CО1D.

15. Вопрос 10

Как обозначается сумма углов AOB и CQD?
Ответ: АOВ + CQD.

16. Вопрос 11

В каком случае говорят, что угол АOВ
меньше угла А1O1В1?
Ответ: Если при откладывании угла АOВ от
луча O1В1 луч OВ переходит в луч O1B’,
лежащий между лучами O1А1 и O1В1, то
говорят, что угол АOВ меньше угла А1O1В1.

17. Вопрос 12

Как обозначается то, что угол AOB меньше
угла CQD?
Ответ: АOВ < CQD.

18. Вопрос 13

Как из большего угла вычесть меньший?
Ответ: Чтобы из большего угла CQD вычесть
меньший угол AOB, от луча QC отложим угол
CQB’, равный углу AOB. Угол B’QD будет
разностью отрезков СQD и AOB.

19. Вопрос 14

Какой угол называется: а) прямым; б) острым;
в) тупым?
Ответ: а) Угол, равный своему смежному,
называется прямым.
б) угол, меньший прямого угла, называется
острым.
в) угол, больший прямого угла, но меньший
развернутого угла, называется тупым.

20. Вопрос 15

Что называется углом между пересекающимися
прямыми?
Ответ: Углом между пересекающимися
прямыми называется наименьший из углов,
образованных лучами, на которые делятся
данные прямые точкой их пересечения.

21. Вопрос 16

Какие прямые называются
перпендикулярными?
Ответ: Две прямые называются
перпендикулярными, если они образуют
прямые углы.

22. Вопрос 17

Что называется биссектрисой угла?
Ответ: Биссектрисой угла называется
внутренний луч, делящий этот угол на
два равных угла

23.

Упражнение 1На сколько частей могут разбивать
плоскость две прямые?
Ответ: На три части, если прямые параллельны и
на четыре части, если они пересекаются.

24. Упражнение 2

На сколько частей могут разбивать
плоскость три прямые?
Ответ: На четыре, шесть или семь частей

25. Упражнение 3

Назовите углы, меньшие развернутого,
изображенные на рисунке. Сколько их?
Ответ: AOB, AOC, AOD, BOC, BOD,
COD; 6 углов.

26. Упражнение 4

Назовите пары: а) вертикальных; б) смежных
углов, изображенных на рисунке.
Ответ: а) AOB и DOE, BOC и EOF, COD и
FOA, AOC и DOF, BOD и EOA;
б) AOB и BOD, BOC и COE, COD и DOF, DOE
и EOA, EOF и FOB, FOA и AOC.

27. Упражнение 5

Сколько имеется углов, смежных
данному углу?
Ответ: Два.

28. Упражнение 6

Могут ли два смежных угла быть
одновременно: а) острыми; б) прямыми; в)
тупыми?
Ответ: а) Нет. б) да. в) нет.

29. Упражнение 7

Назовите: а) острые; б) прямые; в) тупые
углы, изображенных на рисунке.
Ответ: а) AOB, AOC, BOC, BOD, COD, COE, COF,
DOE, DOF, EOF; б) AOD, BOE; в) AOE, AOF, BOF.

30. Упражнение 8

Внутри угла проведено: а) 2 луча; б) 3
луча; *в) n лучей, каждый из которых
имеет начало в вершине угла. Сколько
при этом образуется углов (вместе с
данным)?
Ответ: а) 6; б) 15; в)
(n 2)(n 1)
.
2

31. Упражнение 9

Какой угол образуют биссектрисы смежных
углов?
Ответ: Прямой.

32. Упражнение 10

Какой угол образуют биссектрисы
вертикальных углов?
Ответ: Развернутый

33. Упражнение 11

Когда часовая и минутная стрелки часов
образуют прямой угол?
Ответ: В 3 ч и 9 ч.

34. Упражнение 12*

Сколько раз за сутки часовая и минутная
стрелки образуют развернутый угол?
Ответ: 24 раза.

Конгруэнтные углы – определение, теорема, примеры, построение

Конгруэнтные углы – это углы, имеющие одинаковую меру. Таким образом, все углы, которые имеют одинаковую меру, будут называться конгруэнтными углами. Они видны повсюду, например, в равносторонних треугольниках, равнобедренных треугольниках или при пересечении секущей двух параллельных прямых. Давайте узнаем больше о равенстве углов вместе с их построением в этой статье.

1.	Что такое равные углы?
2.	Теорема о равных углах
3.	Построение равных углов
4.	Часто задаваемые вопросы о равных углах

Что такое равные углы?

В математике конгруэнтные углы определяются так: «Углы, равные по мере, называются конгруэнтными углами». Другими словами, равные углы являются конгруэнтными углами. Он обозначается символом «≅», поэтому, если мы хотим представить, что ∠A конгруэнтна ∠X, мы напишем это как ∠A ≅ ∠X. Посмотрите на пример равных углов, приведенный ниже.

На изображении выше оба угла равны по измерению (60 ^∘ каждый).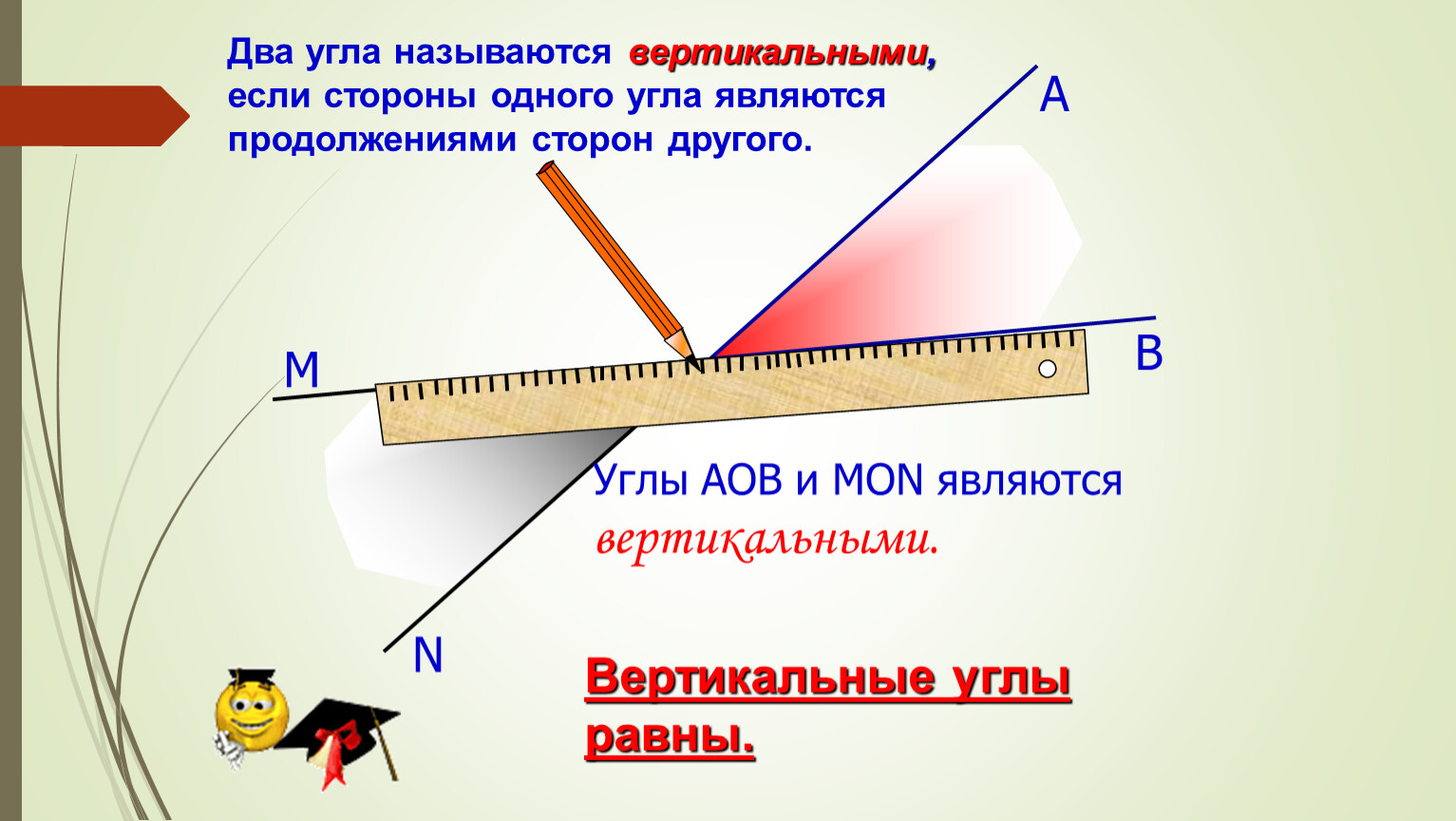 Они могут полностью перекрывать друг друга. Таким образом, согласно определению, мы можем сказать, что оба заданных угла равны.

Теорема о равных углах

Существует множество теорем, основанных на равенстве углов. Используя теорему о равных углах, мы можем легко узнать, равны ли два угла или нет. Эти теоремы перечислены ниже:

• Теорема о вертикальных углах
• Теорема о соответствующих углах
• Теорема об альтернативных углах
• Теорема о конгруэнтных дополнениях
• Теорема о конгруэнтных дополнениях

Давайте подробно разберем каждую из теорем вместе с их доказательством.

Теорема о вертикальных углах

Согласно теореме о вертикальных углах вертикальные углы всегда равны. Проверим доказательство этого.

Утверждение: Вертикальные углы равны.

Доказательство: Доказательство простое и основано на прямых углах. Мы уже знаем, что сумма углов на прямой составляет 180°.

Итак, на рисунке выше:

Заявление	Причина
∠1+∠2 = 180°	Линейная пара
∠1+∠4 = 180°	Линейная пара
∴ ∠1+∠2 = 180 ∘ = ∠1+∠4	Приравнивая два приведенных выше уравнения
∴ ∠1+∠2 =∠1+∠4	Количества, равные одному и тому же количеству, равны между собой. (Переходный: если a=b и b=c, это подразумевает a=c)
∴ ∠2 =∠4	Если из равных вычесть равные, разности равны. (путем исключения ∠1 с обеих сторон)
Кроме того, ∠1=∠3	Аналогично можно доказать для ∠1 и ∠3

Вывод: Вертикально противоположные углы всегда равны.

Соответствие углов Теорема

Определение соответствующих углов говорит нам, что когда две параллельные прямые пересекаются третьей, известно, что углы, которые занимают одно и то же относительное положение при каждом пересечении, являются соответствующими углами друг к другу.

При пересечении секущей двух параллельных прямых соответствующие углы всегда равны друг другу. На этом рисунке ∠1 = ∠2. Это постулат, поэтому нам не нужно это доказывать. Это всегда утверждается как истинное без доказательства.

Теорема о альтернативных углах

Когда секущая пересекает две параллельные прямые, каждая пара альтернативных углов конгруэнтна.

См. рисунок выше. Имеем:

∠1 = ∠5 (соответствующие углы)

∠3 = ∠5 (противоположные углы)

Таким образом, ∠1 = ∠3

Аналогичным образом мы можем доказать и другие три пары альтернативных конгруэнтных углов.

Теорема о конгруэнтных дополнениях

Дополнительными углами называются углы, сумма которых равна 180°. Эта теорема утверждает, что углы, дополняющие один и тот же угол, равны, независимо от того, являются ли они смежными углами или нет.

Мы можем доказать эту теорему, используя линейное парное свойство углов, as,

∠1+∠2 = 180° (линейная пара углов)

∠2+∠3 = 180° (линейная пара углов)

Из двух приведенных выше уравнений получаем ∠1 = ∠3.

∴ Углы, приложенные к одному углу, равны.

Теорема о конгруэнтных дополнениях

Дополнительные углы — это углы, сумма которых равна 90°. Эта теорема утверждает, что углы, дополняющие один и тот же угол, равны, независимо от того, являются ли они смежными углами или нет. Давайте поймем это с помощью изображения, приведенного ниже.

Мы можем легко доказать эту теорему, так как оба образующихся угла прямые.

∠a+∠b = 90° (∵∠a и ∠b образуют угол 90°)

∠a+∠c = 90° (∵∠a и ∠c образуют угол 90°)

Итак, из двух предыдущих уравнений, получаем ∠b ≅ ∠c.

∴ Два угла, дополняющих один и тот же угол, равны.

Построение равных углов

В этом разделе мы узнаем, как построить два равных угла в геометрии. При изучении построения конгруэнтных углов возникают два случая, а именно:

• Построение двух равных углов любой величины.
• Построение угла, равного данному углу.

Построение двух равных углов

Поэтапно изучим построение двух равных углов.

Шаг 1- Начертите две горизонтальные линии любой подходящей длины с помощью карандаша и линейки или линейки.

Шаг 2- Возьмите любую дугу компаса, меньшую, чем длина линий, нарисованных на первом шаге, и держите кончик компаса в конечной точке линии. Нарисуйте дугу, держа линии AB и PQ в качестве основания, не изменяя ширины компаса.

Шаг 3 — Держите кончик компаса в точке D и разверните ножки компаса, чтобы нарисовать дугу любой подходящей длины. Нарисуйте эту дугу и повторите тот же процесс с той же дугой, удерживая кончик компаса в точке S.

Шаг 4- Нарисуйте линии, которые соединят AC и PR.

Вот как мы получаем два равных угла в геометрии, ∠CAB и ∠RPQ.

Построение угла, равного данному углу

К настоящему моменту вы узнали, как построить два равных угла в геометрии с любым измерением. Но что, если дан какой-то один угол, и мы должны построить угол, равный ему? Давайте изучим его пошагово.

Предположим, что нам дан угол ∠ABC, и мы должны составить угол, равный ∠ABC.

Шаг 1 — Нарисуйте горизонтальную линию любого подходящего размера и назовите ее YZ.

Шаг 2 — Держите конец компаса в точке B под заданным углом и начертите дугу, взяв за основу BC, и назовите эту точку D.

Шаг 3 — Нарисуйте дугу той же ширины, удерживая кончик циркуля в точке Y, и назовите точку на линии YZ буквой O. и измерьте дугу от точки D до точки пересечения дуги на отрезке AB.

Шаг 5 — Используя ту же дугу, держите кончик циркуля в точке O и отметьте разрез на дуге, начерченной в шаге 3, и назовите эту точку X.

Шаг 6 — Проведите линию и соедините точки X и Y.

Здесь мы получаем ∠ABC ≅ ∠XYZ, что удовлетворяет определению конгруэнтного угла. Вот как мы можем построить угол, равный данному углу.

Конгруэнтные углы Советы и рекомендации:

• Конгруэнтные углы — это просто другое название равных углов.
• Все вертикально противоположные углы равны.
• Все параллельные углы и соответствующие углы, образованные пересечением двух параллельных прямых и секущей, являются конгруэнтными углами.
• Согласно определению конгруэнтных углов «Для того, чтобы любые два угла были конгруэнтными, они должны иметь одинаковую величину».

► Похожие темы

Ознакомьтесь с интересными статьями, посвященными определению конгруэнтных углов.

• Переходное свойство конгруэнтности
• Последовательные углы
• Последовательные внутренние углы
• Конгруэнтность треугольников

 

Примеры равных углов

1. Пример 1: Найдите величину угла f.

   Решение:

   Здесь ∠DOE и ∠AOC равны (вертикальные) углы. Итак, ∠DOE = ∠AOC.

   113 ^∘ = 90º+f

   f = 113°-90°

   f = 23°

   Следовательно, значение f равно 23 градусам.

2. Пример 2: У вас когда-нибудь в школе была коробка для завтрака в форме параллелограмма? Как ты закрыл эту коробку с едой? Вы пытались найти наилучшее совпадение углов на крышке, чтобы закрыть коробку. Это правильно? Можете ли вы назвать какую-либо причину, по которой вы это сделали?

   Решение:

   Причина, по которой вы это сделали, заключалась в том, что вы пытались найти наилучшее соответствие равных углов для закрытия крышки коробки. Поскольку мы знаем, что соответствующие углы конгруэнтны, вы попытались найти углы на крышке, которые лучше всего соответствуют соответствующим углам каждого угла в коробке.

   Вы наблюдали геометрию соответствующих углов, не осознавая этого.

   Ответ: Углы в коробочке для завтрака равны.

3. Пример 3: Если на данной фигуре две прямые параллельны и пересекаются секущей. Какова будет мера ∠x и ∠y?

   Решение:

   Данные прямые параллельны и, согласно теореме о конгруэнтных противоположных углах, данный угол измерения 85 ^∘ и ∠x являются альтернативно конгруэнтными углами. Итак, 85 ^∘ = ∠x.
   Точно так же 95 ^∘ и y являются конгруэнтными альтернативными углами. Итак, 95 ^∘ = ∠у.

   Следовательно, значение ∠x равно 85°, а ∠y равно 95°.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных эффектов.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по конгруэнтным углам

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о равных углах

Что означают равные углы?

Два угла называются конгруэнтными, если они имеют одинаковую величину и могут быть наложены друг на друга без каких-либо зазоров или перекрытий. Символ равных углов равен ≅.

Какие условия необходимы для равных углов?

Для равенства углов требуется только одно условие: они должны быть одинаковой величины.

У равных углов в сумме 180?

Вообще говоря, все конгруэнтные углы не являются дополнительными углами. Чтобы сумма углов составляла 180, они должны быть дополнительными углами. Таким образом, конгруэнтны только прямые углы, а также дополнительные углы, потому что они имеют одинаковую меру и в сумме дают 180.

Конгруэнтны ли прямые углы?

Прямые углы всегда равны, так как их измерение одинаково. Они всегда измеряют 90°.

Что такое конгруэнтные углы параллельных прямых?

Когда две параллельные прямые пересекаются секущей, мы получаем конгруэнтные углы, которые являются соответственными углами, вертикальными углами, альтернативными внутренними углами и альтернативными внешними углами.

Как узнать, равны ли углы?

Два угла равны, если их измерения одинаковы. Таким образом, мы можем проверить измерение заданных углов с помощью транспортира, чтобы узнать, равны ли данные углы или нет.

Равны ли конгруэнтные углы?

Да, конгруэнтные углы равны.

Как найти равные углы?

Любые два угла одной величины равны. Итак, чтобы найти конгруэнтные углы, нам просто нужно идентифицировать все равные углы. При установке друг на друга они полностью подходят друг к другу без каких-либо зазоров.

Углы какого типа всегда равны?

Вертикально противоположные углы, параллельные углы и соответствующие углы, проведенные на параллельных прямых и секущих, всегда конгруэнтны. Кроме того, углы, дополнительные к тому же углу, и углы, дополнительные к тому же углу, также являются конгруэнтными углами.

Преобразование угла | Преобразование градусов в радианы

Используйте калькулятор преобразования углов , чтобы мгновенно преобразовать радианы в градусы, градусы в градианы или многие другие угловые единицы.

Если вам интересно, как преобразовать градусы в радианы или градусы, минуты, секунды в десятичные градусы, то мы настоятельно рекомендуем прочитать текст ниже, где вы также найдете:

• Формула преобразования градусов в радианы;
• Его аналог, формула преобразования радианов в градусы;
• Почему некоторые угловые измерения выражаются в градусах, минутах, секундах; и
• Пример преобразования градусов, минут, секунд в десятичные градусы.

В физике важен правильный угол, например, в явлении дифракции. Если вам интересна эта тема, наш калькулятор дифракционных решеток — отличный инструмент для начала!

Как перевести градусы в радианы?

Радиан является наиболее часто используемой единицей измерения углов, поскольку он является предпочтительной угловой мерой в исчислении, геометрии и многих других областях математики и техники, а также является единицей измерения углов в системе СИ.

Единица измерения радиана основана на идее измерения углов по длине дуги. Величина вытянутого угла в радианах равна отношению длины дуги к радиусу окружности:

θ=s/r\маленький \theta = s/rθ=s/r

, где:

• θ — угол в радианах;
• с — длина дуги; и
• р — Радиус.

Символ радиана — это «рад» , а 1 радиан эквивалентен 57,2958 градусам или 180°/ π180°/\ \pi180°/ π. Это означает, что для преобразования угла, выраженного в градусах, в его эквивалентное значение в радианах все, что нам нужно сделать, это просто умножить на 180°/ π180°/\ \pi180°/ π.

Формула перевода градусов в радианы:

радиан=градусы ⋅180°π\маленький \text{радианы} = \text{градусы} \ \cdot \cfrac{180°}{\pi}радианы=градусы ⋅π180°​

Примером того, где мы можем найти радианы, являются единицы, используемые для выражения углового скорость.

Аналогичным образом, чтобы перейти от радианов к градусам, умножьте угол в градусах на коэффициент преобразования π/ 180°\pi/ \ 180°π/ 180°. Формула преобразования радианов в градусы выглядит следующим образом:

градуса=радианы ⋅π180°\small \text{градусы} = \text{радианы} \ \cdot \cfrac{\pi}{180°}градусы=радианы ⋅180°π​

Полярные координаты принято выражать в градусах и радианах.

Мы собрали некоторые примечательные углы в таблице ниже. Обратите внимание, что значения в радианах могут быть кратны пипипи. Это делает его практичным и простым способом их запоминания:

Градусы [°]	Радиан [рад]
0	0
30	№/6
45	№/4
60	π/3
90	π/2
180	№
270	3π/2
360	2π

Как перевести градусы минуты секунды в десятичные градусы?

Углы также используются в дисциплинах, отличных от математики и техники, таких как астрономия и навигация, в виде координат . В этих случаях удобнее выражать углы в шестидесятеричной системе счисления. Это градусов (°), минут (‘) и секунд («) (DMS).

Эквивалентность здесь аналогична той, которая используется для измерения времени. Где 1 час равен 60 минутам, а одна минута равна 60 секундам. Таким образом, если мы хотим преобразовать DMS в десятичные градусы, мы просто делим минуты на 60 и секунды на 3600, а затем прибавляем это значение к целому значению градуса.0003

Давайте рассмотрим пример преобразования DMS в десятичные градусы. Предположим, мы хотим сделать угловое преобразование координаты 33° 21′ 43″ в десятичные градусы. Мы делаем это следующим образом:

1. Вся часть угла в градусах остается неизменной. Это 33°.

2. Затем мы конвертируем секунды в градусы путем деления на 3600:
   43" = 43"/3600 = 0,012°

3. Теперь преобразуем минуты в углы, разделив на 60:
   21' = 21'/60 = 0,350°

4. Наконец, добавьте приведенное выше преобразование ко всей детали:
   33° + 0,350° + 0,012° = 33,362°

Это то, что 33° 21′ 43″ равно 33,362°.