Калькулятор арифметического квадратного корня: Калькулятор квадратных корней

Исследовательская работа по алгебре на тему «Извлечение квадратных корней из больших чисел без калькулятора».

Оглавление

 

Введение                                                                                                             3-4                                                                                                                                             Глава 1. История квадратного корня                                                                4                                          Глава 2. Способ использования таблицы квадратов двузначных чисел       5               

Глава 3.  Формула Древнего Вавилона                                                             5                                  Глава 4.  Канадский метод                                                                                 5                                   Глава 5.  Способ разложения на простые множители                                     6                           Глава 6.

Метод вычетов нечётного числа                                                         6                                   Глава 7. Метод подбора угадыванием  (метод оценки)                                 6-7                     Глава 8. Метод отбрасывания полного квадрата                                             7                                Глава 9. Извлечение квадратного корня уголком                                          7-9                                 Глава 10. Практическая часть. Диаграммы                                                     8-9

(анкетирования среди учащихся 8-11 класса).

Заключение                                                                                                         10                                 Список литературы                                                                                         11                                    

 

 

 

 

 

 

 

 

 

 

 

 

                      

 

 

Введение

Актуальность исследования. В этом году я изучал тему квадратные корни. Всё хорошо пока под рукой таблица квадратов, но однажды на уроке геометрии при решении задачи надо было извлечь квадратный корень из большого числа, а таблицы квадратов нет. Пришлось число разложить на простые множители. Корень был извлечён, но вопрос существуют ли другие способы для извлечения квадратного корня, остался.  Я решил изучить этот вопрос глубже, чем он изложен в школьной программе.

Практическая значимость: данный материал можно использовать в 8, 9, 10, 11 классах на уроках, олимпиадах, ОГЭ и ЕГЭ.

Цель работы: найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора.

   Задачи:

1.            Изучить литературу по данному вопросу.

2.            Рассмотреть особенности каждого найденного способа и его алгоритм.

3.            Показать практическое применение полученных знаний  и оценить

      степень сложности в использовании различных способов и алгоритмов.

Объект исследования: математические символы – квадратные корни.

Предмет исследования: особенности способов извлечения квадратных корней без калькулятора.

Методы исследования:

1.                  Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.

2.                  Сравнение найденных способов.

3.                  Анализ полученных способов.

Все знают, что извлечь квадратный корень из большого числа без калькулятора — это сложная задача. Когда нет под рукой калькулятора, то начинаем методом подбора стараться вспомнить данные из таблицы квадратов целых чисел, но это не всегда помогает. Также на экзаменах  ОГЭ и ЕГЭ пользование калькулятором запрещено и нет таблицы квадратов целых чисел, а надо извлечь корень из чисел больше 100 или 1000.

 Но изучая информацию по данной теме, я узнал, что извлекать корни из таких чисел возможно и без таблицы и калькулятора, люди научились делать это задолго до изобретения микрокалькулятора. Исследуя эту тему, я нашел несколько способов решения данной проблемы.

 

Глава 1. История квадратного корня

           Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически. При переводе греческое слово «сторона» превратилась в «мула» (основание, корень). Поэтому при переводе с индийского  на арабский использовался термин «джизр» (корень растения).

          Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы алгебраистов в 1525 году. Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.

          Арифметическим квадратным корнем из числа  a  называется неотрицательное число, квадрат которого равен данному числу  a.

Теорема о последней цифре квадрата числа

      Если числа оканчиваются на цифру от 1 до 9 и когда мы возводим их в квадрат, то на конце полученного числа будут стоять цифры:

…1²=…1                                    …6²=…6

…2²=…4                                   …7²=…9

…3²=…9                                   …8²=…4

…4²=…6                                   …9²=…1

…5²=…5

    Если в конце числа стоят цифры 2,3,7,8, то полный квадратный корень извлечь из него нельзя.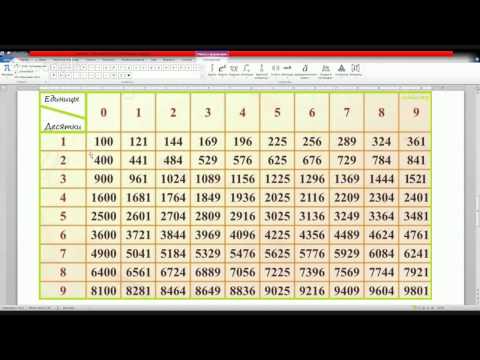

Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки умножаем на следующее, т.е. это же число плюс единица и к полученному числу справа приписываем 25. Например,

15^{2= (1∙(1+1))25 = 225}

25^{2 = (2∙(2+1))25 = 625}

85² = (8∙(8+1))25 = 7225

 

 

 

Глава 2. Способ использования таблицы квадратов двузначных чисел.

         Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 уже этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.

 

Глава 3.  Формула Древнего Вавилона.

         Число x представлено в виде суммы , где 

ближайший к числу х точный квадрат натурального числа  .

Извлечем с помощью этой формулы   квадратный корень, например из числа 40:

.

 Этот способ удобен   для нахождения приближённого значения квадратного корня.

 

Глава 4.  Канадский метод.

      Этот быстрый метод был открыт  молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух – трёх  знаков после запятой. Вот их формула: , где X — число, из которого необходимо извлечь квадратный корень, а S  — число ближайшего точного квадрата.

       Давайте попробуем извлечь  квадратный корень из 40 

             
.

 

Глава 5. Способ разложения на простые множители

          Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.

Таким способом принято пользоваться при решении заданий с корнями        

7056 3528 1764   882   441   147    49 7

2 2 2 2 3 3 7 7

 

  .  

 

            Практика показывает, что очень редко предлагаются задания с полным разложением. Чаще мы видим, что корень до конца не извлечь.

Поэтому, этот способ лишь частично решает проблему извлечения без калькулятора.

 

Глава 6. Метод вычетов нечётного числа.

        Суть метода: из подкоренного выражения нужно последовательно вычитать нечетные числа пока разность не станет равной 0 и посчитать количество вычитаний. Например, посчитаем:

256-1, 255-3, 252-5, 247-7, 240-9, 231-11, 220-13, 207-15, 192-17, 175-19, 156-21, 135-23,

112-25, 87-27, 60-29, 31-31      

Общее количество вычитаний равно 16.

       Российские ученые называют этот метод извлечения арифметического квадратного корня «методом черепахи» из-за его медлительности.
            Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее.   

 

Глава 7.   Метод  подбора  угадыванием (метод оценки).

       Данный метод эффективно применяется при вычислении квадратных корней из чисел в диапазоне от 100 до 10 000.

Алгоритм извлечения квадратного корня методом оценки.

        Рассмотрим пример извлечения квадратного корня из числа 7056.

Шаг №1 — ограничение корней.

6400 < 7056 < 8100,  80² < 7056 < 90², 80 <  < 90.

Шаг №2 – «отсев» лишних чисел. У нас есть 10 чисел — «кандидатов» на корень.

       Квадратный корень из 7056 обязательно заканчивается на 4 или на 6, получаем:

80<<90;

 =…4 или = …6

Известно, что корень лежит в пределах от 80 до 90, на котором есть только два числа, оканчивающихся на 4 и 6, это числа 84 и 86.

Шаг №3 — финальные вычисления. Итак, у нас осталось 2 числа «кандидата». Чтобы узнать, какое из них является корнем, необходимо взять «золотую середину» — число 85, и возвести его в квадрат  85² = (8∙(8+1))25 = 7225, 7225 > 7056, значит,  = 84.

 

 

Глава 8. Метод отбрасывания полного квадрата.

        Этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа. Выделяем из числа квадрат, который оканчивается той же цифрой, что и данное число.

       Извлечение корней до числа . Число 2209 представим в виде суммы, выделив из этого числа квадрат 9, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (22) прибавляем всегда 25. Получим ответ 47.

      Так можно извлекать только квадратные корни до числа.

.

       Извлечение корней после 75²= 5625, вычисляются следующим образом:

 .

 

Глава 9.  Извлечение квадратного корня уголком.

Для извлечения квадратного корня уголком   рассмотрим алгоритм:
1-й шаг. Число 7056 разбиваем на грани справа налево, каждая из которых должна содержать две цифры. Получаем две грани:  .
2-й шаг. Извлекаем квадратный корень из первой грани 70, получаем ≈ 8 с остатком. Цифра 8 –это первая цифра результата.
3-й шаг. Число 8 возводим в квадрат (8²_{= 64) и число 64 вычитаем из первой грани, получаем 70 — 64=6. Число 6 – первый остаток.
4-й шаг. К остатку 6 приписываем вторую грань 56, получаем число 656.}

5-й шаг. Удваиваем первую цифру результата 8 и, записывая слева, получаем-16

           К числу 16 нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 656, либо меньше. Это цифра 4. Она находится путем подбора: так как 164 ∙ 4 = 656, то цифра 4 – это вторая цифра результата.

 6-й шаг. Находим остаток 656 – 656 = 0. Так как остаток равен нулю, то мы получили точное значение корня – 84.

	= 8 *    64			= 8 4    64
16 *      *	6 56		16 4      4	6 56       6 56

                                                                                                                       0          

Глава 10.  Практическая часть. Диаграммы (анкетирования среди учащихся 8-11 класса).

        Получив результаты анкетирования, учащихся я свел все данные в диаграммы. В опросе участвовало 150 учащихся.

       Диаграмма № 1 — сложно ли Вам  извлекать квадратный корень из числа меньше 100, если нет таблицы квадратов?

   

 

       Диаграмма  № 2 — сложно ли Вам  извлекать квадратный корень из числа больше 100, если нет таблицы квадратов?

     

         Диаграмма  № 3 – каким образом Вы извлекаете корень их числа больше 100?

 

 

       Диаграмма  № 4 – интересно Вам было бы знать простые способы извлечение корней?

 

 

 

 

 

 

 

 

Заключение

 

        В ходе исследования было выявлено, что современной науке известно много способов извлечения квадратного корня, начиная со способа математиков Древнего Вавилона и заканчивая способом степенных рядов сложных степеней из разделов высшей математики. Были изучены и отработаны на практике все найденные способы. Предположение, что существует не менее двух способов извлечения квадратных корней без калькулятора, подтвердилось.

     Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные алгоритмы позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, их можно использовать  при проверке своего решения и не зависеть от наличия в кармане калькулятора. Тем более на экзамене в 9 и 11 классах применение калькулятора не допускается.

    Таким образом, цель работы достигнута, задачи выполнены.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Литература и сайты Интернета:

 

1.     И.Н. Сергеев, С.Н. Олехник,  С.Б. Гашков «Примени математику». – М.: Наука, 1990

2.     Керимов З., «Как найти целый корень?» Научно-популярный физико-математический журнал «Квант» №2, 1980

3.     Петраков И.С. «математические кружки в 8-10 классах»;  Книга для учителя. – М.: Просвещение,1987

4.     Тихонов А.Н., Костомаров Д.П. «Рассказы о прикладной математики». — М.: Наука. Главная редакция физико — математической литературы, 1979

5.     Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса   учебных заведений.  – Москва, Просвещение, 1994г.

6.     Жохов В.И., Погодин В.Н. Справочные таблицы по математике. — М.: ООО «Издательство «РОСМЭН-ПРЕСС», 2004.-120 с.

7.     http://translate.google.ru/translate

8.     http://www.murderousmaths.co.uk/books/sqroot.htm

9.     http://ru.wikipedia.ord /wiki /teorema/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приближенные методы извлечения квадратного корня (без использования калькулятора).

Как найти квадратный корень числа вручную

Теперь такой вопрос: как возвести число в иррациональную степень? Например, нам хочется узнать, что такое 10 √2 Ответ в принципе очень прост. Возьмем вместо √2 его приближение в виде конечной десятичной дрдби — это- рациональное число. Возводить в рациональную степень мы умеем; дело сводится к возведению в целую степень и извлечению корня. Мы получим приближенное значение числа. Можно взять десятичную дробь подлиннее (это снова рациональное число). Тогда придется извлечь корень большей степени; ведь знаменатель рациональной дроби увеличится, но зато мы получим более точное приближение. Конечно, если взять приближенное значение √2 в виде очень длинной дроби, то возведение в степень будет делом очень трудным. Как справиться с этой задачей?

Вычисление квадратных корней, кубичных корней и других корней невысокой степени — вполне доступный нам арифметический процесс; вычисляя, мы последовательно, один за другим, пишем знаки десятичной дроби. Но для того, чтобы возвести в иррациональную степень или взять логарифм (решить обратную задачу), нужен такой труд, что применить прежнюю процедуру уже не просто. На помощь приходят таблицы. Их называют таблицами логарифмов или таблицами степеней, смотря по тому, для чего, они предназначены. Они экономят время: чтобы возвести число в иррациональную степень, мы не вычисляем, а только перелистываем страницы.

Хотя вычисление собранных в таблицы значений — процедура чисто техническая, а все же дело это интересное и имеет большую историю. Поэтому посмотрим, как это делается. Мы вычислим не только х = 10 √2 , но решим и другую задачу: 10 х = 2, или x = log 10 2. При решении этих задач мы не откроем новых чисел; это просто вычислительные задачи. Решением будут иррациональные числа, бесконечные десятичные дроби, а их как-то неудобно объявлять новым видом чисел.

Подумаем, как решить наши уравнения. Общая идея очень проста. Если вычислить 10 1 и 10 1/10 , и 10 1/100 , и 10 1/1000 , и т. д., а затем перемножить результаты, то мы получим 10 1,414… или l0 √2 Поступая так, мы решим любую задачу такого рода. Однако вместо 10 1/10 и т. д. мы будем вычислять 10 1/2 , и 10 1/4 и т. д. Прежде чем начинать вычисления, объясним еще, почему мы обращаемся к числу 10 чаще, чем к другим числам. Мы знаем, что значение таблиц логарифмов выходит далеко за рамки математической задачи вычисления корней, потому что

Это хорошо известно всем, кто пользовался таблицей логарифмов, чтобы перемножить числа. По какому же основанию b брать логарифмы? Это безразлично; ведь в основу таких вычислений положен только принцип, общее свойство логарифмической функции. Вычислив логарифмы один раз по какому-нибудь произвольному основанию, можно перейти к логарифмам по другому основанию при помощи умножения. Если умножить уравнение (22.3) на 61, то оно останется верным, поэтому если перемножить все числа в таблице логарифмов по основанию b на 61, то можно будет пользоваться и такой таблицей. Предположим, что нам известны логарифмы всех чисел по основанию b. Иначе говоря, можно решить уравнение b а = с для любого с; для этого существует таблица. Задача состоит в том, как найти логарифм этого же числа с по другому основанию, например x. Нам нужно решить уравнение х а’ = с. Это легко сделать, потому что х всегда можно представить так: х = b t . Найти t, зная х и b, просто: t = log b x. Подставим теперь х = b t в уравнение х а’ = с; оно перейдет в такое уравнение: (b t) а’ = b ta’ = c. Иными словами, произведение ta’ есть логарифм с по основанию b. Значит, а’ = a/t. Таким образом, логарифмы по основанию х равны произведениям логарифмов по основа нию b на постоянное число l/t. Следовательно, все таблицы логарифмов эквивалентны с точностью до умножения на число l/log b x. Это позволяет нам выбрать для составления таблиц любое основание, но мы решили, что удобнее всего взять за основание число 10. (Может возникнуть вопрос: не существует ли все-таки какого-нибудь естественного основания, при котором все выглядит как-то проще? Мы попытаемся ответить на этот вопрос позднее. Пока все логарифмы будут вычисляться по основанию 10.)

Теперь посмотрим, как составляют таблицу логарифмов. Работа начинается с последовательных извлечений квадратного корня из 10. Результат можно увидеть в табл. 22.1. Показатели степеней записаны в ее первом столбце, а числа 10 s — в третьем. Ясно, что 10 1 = 10. Возвести 10 в половинную степень легко -это квадратный корень из 10, а как извлекать квадратный корень из любого числа, знает каждый. (Квадратный корень лучше всего извлекать не тем способом, которому обычно учат в школе, а немного иначе. Чтобы извлечь квадратный корень из числа N, выберем достаточно близкое к ответу число а, вычислим N/a и среднее а’ =1/2; это среднее будет новым числом а, новым приближением корня из N. Этот процесс очень быстро приводит к цели: число значащих цифр удваивается после каждого шага.) Итак, мы нашли первый квадратный корень; он равен 3,16228. Что это дает? Кое-что дает. Мы уже можем сказать, чему равно 10 0,5 , и знаем по крайней мере один логарифм.

Логарифм числа 3,16228 очень близок к 0,50000. Однако нужно еще приложить небольшие усилия: нам нужна более подробная таблица. Извлечем еще один квадратный корень и найдем 10 1/4 , что равно 1,77828. Теперь мы знаем еще один логарифм: 1,250 -это логарифм числа 17,78; кроме того, мы можем сказать, чему равно 10 0,75: ведь это 10 (0,5+0,25) , т. е. произведение второго и третьего чисел из третьего столбца табл. 22.1. Если сделать первый столбец таблицы достаточно длинным, то таблица будет содержать почти все числа; перемножая числа из третьего столбца, мы получаем 10 почти в любой степени. Такова основная идея таблиц. В нашей таблице содержится десять последовательных корней из 10; основной труд по составлению таблицы вложен в вычисления этих корней.

Почему же мы не продолжаем повышать точность таблиц дальше? Потому что мы кое-что уже подметили. Возведя 10 в очень малую степень, мы получаем единицу с малой добавкой. Это, конечно, происходит потому, что если возвести, например, 10 1/1000 в 1000-ю степень, то мы снова получим 10; ясно, что 10 1/1000 не может быть большим числом: оно очень близко к единице. Более того, малые добавки к единице ведут себя так, будто их каждый раз делят на 2; поглядите-ка на таблицу повнимательнее: 1815 переходит в 903, потом в 450, 225 и т. д. Таким бразом, если вычислить еще один, одиннадцатый, квадратный корень, он с большой точностью будет равен 1,00112, и этот результат мы угадали еще до вычисления. Можно ли сказать, какова будет добавка к единице, если возвести 10 в степень ∆/1024, когда ∆ стремится к нулю? Можно. Добавка будет приблизительно равна 0,0022511∆. Конечно, не в точности 0,0022511∆; чтобы вычислить эту добавку поточнее, делают такой трюк: вычитают из 10 s единицу и делят разность на показатель степени s. Отклонения полученного таким образом частного от его точного значения одинаковы для любой степени s. Видно, что эти отношения (табл. 22.1) примерно равны. Сначала они сильно различаются, но потом все ближе подходят друг к другу, явно стремясь к какому-то числу. Что это за число? Проследим, как меняются числа четвертого столбца, если опускаться вниз по столбцу. Сначала разность двух соседних чисел равна 0,0211, потом 0,0104, потом 0,0053 и, наконец, 0,0026. Разность каждый раз убывает наполовину. Сделав еще один шаг, мы доведем ее до 0,0013, потом до 0,0007, 0,0003, 0,0002 и, наконец, примерно до 0,0001; надо последовательно делить 26 на 2. Таким образом, мы спустимся еще на 26 единиц и найдем для предела 2,3025. (Позднее мы увидим, что правильнее было бы взять 2,3026, но давайте возьмем то, что у нас получилось.) Пользуясь этой таблицей, можно возвести 10 в любую степень, если ее показатель каким угодно способом выражается через I/I024.

Теперь легко составить таблицу логарифмов, потому что все необходимое для этого мы уже припасли. Процедура этого изображена в табл. 22.2, а нужные числа берутся из второго и третьего столбцов табл. 22.1.

Предположим, что мы хотим знать логарифм 2. Это значит, что мы хотим знать, в какую степень надо возвести 10, чтобы получить 2. Может быть, возвести 10 в степень 1/2? Нет, получится слишком большое число. Глядя на табл.. 22.1, можно сказать, что нужное нам число лежит между 1/4 и 1/2. Поиск его начнем с 1/4; разделим 2 на 1,778…, получится 1,124…; при делении мы отняли от логарифма двух 0,250000, и теперь нас интересует логарифм 1,124…. Отыскав его, мы прибавим к результату 1/4 = 256/1024. Найдем в табл.22.1 число, которое бы при движении по третьему столбцу сверху вниз стояло сразу за 1,124… . Это 1,074607. Отношение 1,124… к 1,074607 равно 1,046598. В конце концов мы представим 2 в виде произведения чисел из табл. 22.1:
2 = (1,77828) (1,074607) (1,036633). (1,0090350) (1,000573).
Для последнего множителя (1,000573) в нашей таблице места не нашлось; чтобы найти, его логарифм, надо представить это число в виде 10∆/1024 ≈ 1 + 2,3025∆/1024. Отсюда легко найти, что ∆ = 0,254. Таким образом, наше произведение можно представить в виде десятки, возведенной в степень 1/1024 (266 + 32+16 + 4 + 0,254). Складывая и деля, мы получаем нужный логарифм: log 10 2 = 0,30103; этот результат верен до пятого десятичного знака!

Мы вычисляли логарифмы точно так же, как это делал мистер Бриггс из Галифакса в 1620 г. Закончив работу, он сказал: «Я вычислил последовательно 54 квадратных корня из 10». На самом деле он вычислил только 27 первых корней, а потом сделал фокус с ∆. Вычислить 27 раз квадратный корень из 10, вообще-то говоря, немного сложнее, чем
10 раз, как это сделали мы. Однако мистер Бриггс сделал гораздо большее: он вычислял корни с точностью до шестнадцатого десятичного знака, а когда опубликовал свои таблицы, то оставил в них лишь 14 десятичных знаков, чтобы округлить ошибки. Составить таблицы логарифмов с точностью до четырнадцатого десятичного знака таким методом- дело очень трудное. Зато целых 300 лет спустя составители таблиц логарифмов занимались тем, что уменьшали таблицы мистера Бриггса, выкидывая из них каждый раз разное число десятичных знаков. Только в последнее время при помощи электронных вычислительных машин оказалось возможным составить таблицы логарифмов независимо от Мистера Бриггса. При этом использовался более эффективный метод вычислений, основанный на разложении логарифма в ряд.

Составляя таблицы, мы натолкнулись на интересный факт; если показатель степени ε очень мал, то очень легко вычислить 10 ε ; это просто 1+2,3025ε. Это значит, что 10 n/2,3025 = 1 + n для очень малых n. Кроме того, мы говорили с самого начала, что вычисляем логарифмы по основанию 10 только потому, что у нас на руках 10 пальцев и по десяткам нам считать удобнее. Логарифмы по любому другому основанию получаются из логарифмов по основанию 10 простым умножением. Теперь настало время выяснить, не существует ли математически выделенного основания логарифмов, выделенного по причинам, не имеющим ничего общего с числом пальцев на руке. В этой естественной шкале формулы с логарифмами должны выглядеть проще. Составим новую таблицу логарифмов, умножив все логарифмы по основанию 10 на 2,3025…. Это соответствует переходу к новому основанию — натуральному, или основанию е. Заметим, что log e (l + n) ≈ n или е n ≈ 1 + n, когда n → 0.

Легко найти само число е; оно равно 101/ 2,3025 или 10 0,4342294… Это 10 в иррациональной степени. Для вычисления е можно воспользоваться таблицей корней из 10. Представим 0,434294… сначала в виде 444,73/1024, а числитель этой дроби в виде суммы 444,73 = 256 + 128 + 32 + 16 + 8 + 4 + 0,73. Число е поэтому равно произведению чисел
(1,77828) (1,33352) (1,074607) (1,036633) (1,018152) (1,009035) (1,001643) = 2,7184.
(Числа 0,73 нет в нашей таблице, но соответствующий ему результат можно представить в виде 1 + 2,3025∆/1024 и вы—числить при ∆ = 0,73.) Перемножив все 7 сомножителей, мы получим 2,7184 (на самом деле должно быть 2,7183, но и этот результат хорош). Используя такие таблицы, можно возводить число в иррациональную степень и вычислять логарифмы иррациональных чисел. Вот как надо обращаться с иррациональностями!

ГУ « Средняя общеобразовательная школа №5 им. Бауыржана Момышулы»

отдела образования акимата г. Костаная

ПЛАН-КОСПЕКТ УРОКА

ФИО (полностью) Пластун Сергей Владимирович

Предмет алгебра

Класс 8А-8б-1

Дата 23. 09.17

Источники Алматы «Мектеп-2016»

Базовый учебник

Дополнительная литература

Нахождение приближенных значений квадратного корня.

1. Цель урока: познакомить учащихся с понятием « приближенное значение квадратного корня» и научить применять это понятие на практике.

Задачи:

Образовательные:

-научить находить приближенные значения квадратного корня;

-выработка умений рассуждать, четко формулировать правила, приводить примеры, применять свои знания и умения на практике.

корень, приводить и находить значения арифметического квадратного корня.

Развивающие:

-развивать у учащихся навык решения заданий на данную тему;

-развивать мыслительную деятельность учащихся.

Воспитательные:

— воспитывать внимательность, активность, ответственность.

2. Тип урока: комбинированный .

3. Формы работы с учащимися: фронтальная, индивидуальная.

4. Необходимое техническое оборудование.

5. Наглядные пособия, дидактические материалы, используемые на уроке.

6. Структура и ход урока.

СТРУКТУРА И ХОД УРОКА

Ход урока

1. Организационный момент .

Проверка готовности класса к уроку. Приветствие.

2. Проверка домашнего задания.

3. Повторение ранее изученного материала.

Начнем с повторения. Устная работа

Давайте вспомним, что такое квадратный корень (Квадратным корнем из неотрицательного числа а называется число, квадрат которого равен а).

(Арифметический квадратный корень) Арифметическим квадратным корнем из неотрицательного числа а называется такое неотрицательное число b , квадрат которого равен а.

Арифметический квадратный корень из числа а обозначается так:. Знак называется знаком арифметического квадратного корня, или радикалом, а –подкоренным выражением. Выражение читается так: «Арифметический квадратный корень из числа а».

По определению арифметического корня равенство
выполняется при условии, когда
.

4. Изучение нового материала.

1. Вычислите: 25 , 16, 9, 81,

Найдите значение выражения √2

— Что вам необходимо было сделать?

Что у вас получилось? (Учащиеся показывают свои варианты:)

В чём возникло затруднение?

Извлекается √2 нацело?

Как будем находить?

Какие знаем способы нахождения корней?

Ребята, видите, не всегда мы имеем дело с числами, легко представимыми в виде квадрата числа, которые извлекаются из- под корня нацело

1 МЕТОД вычислить √2 с точностью до двух знаков после запятой Будем рассуждать следующим образом.

Число √2 больше 1, так как 1 2

1

Теперь попытаемся отыскать цифру десятых.

Для этого будем дроби от единицы до двойки возводить в квадрат, пока не получим число большее двух.

Шаг деления возьмем 0,1, так как мы ищем число десятых.

Другими словами будем возводить в квадрат числа: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9

1,1 2 =1,21; 1,2 2 =1,44; 1,3 2 =1,69; 1,4 2 =1,96; 1,5 2 =2,25.

Получили число превышающее двойку, остальные числа уже не надо возводить в квадрат. Число 1,4 2 меньше 2, а 1,5 2 уже больше двух, то число √2 должно принадлежать промежутку от 1,4 до 1,5 . Следовательно, десятичная запись числа √2 в разряде десятых должна содержать 4. √2=1,4… .

1,41 2 =1,9881, 1,42 2 =2,0164.

Уже при 1.42 получаем, что его квадрат больше двух, далее возводить в квадрат числа не имеет смысла.

Из этого получаем, что число √2 будет принадлежать промежутку от 1,41 до 1,42 (1,41

Так как нам необходимо записать √2 с точностью до двух знаков после запятой, то мы уже можем остановиться и не продолжать вычисления.

√2 ≈ 1,41. Это и будет ответом. Если бы необходимо было вычислить еще более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений.

Задание

Вычислите с точностью до двух знаков после запятой

√3 = , √5 = , √6 = , √7 =, √8 =

Вывод Данный прием позволяет извлекать корень с любой заданной наперед точностью.

2 МЕТОД Чтобы узнать целую часть квадратного корня числа, можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество выполненных действий.

Например, найдем √16 так:

Выполнено 4 действия, значит, √16 = 4

Задание. Вычислите

√1 √6

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Тема приближенного вычисления корней актуальна всегда, так как задания с квадратными корнями есть в каждом курсе предметов естественнонаучного цикла. В ходе решения многих математических задач, а так же задач по геометрии, по физике, по химии и т.д. приходится сталкиваться с квадратными корнями. Для извлечения квадратного корня существуют таблицы квадратов для двухзначных чисел, но ее бывает недостаточно. Извлечение корня разложением на множители тоже непростая задача, которая не всегда приводит к желаемому результату, и я решила изучить различные способы извлечения квадратных корней с целью их практического применения.

Поэтому цель работы направлена на сопоставление различных способов приближенного извлечения квадратных корней, при этом ставятся задачи: изучение материала, выявление наиболее эффективного способа в зависимости от поставленной задачи.

Решим графически уравнение. Для этого в одной системе координат построим параболу и прямую. Абсциссы точек A и B являются корнями уравнения. Решим уравнение. Ясно, что это уравнение имеет два корня и, причем эти числа, как и в двух предыдущих случаях, равны по абсолютной величине и противоположны по знаку (). По чертежу мы не можем указать точные значения корней. Интересующее нас число x1 расположено между числами 1 и 2, но между числами 1 и 2 находится бесконечное множество рациональных чисел, например и т.д. В работе доказано, что располагая только рациональными числами, уравнение мы решить не сможем.

Математики ввели в рассмотрение новый символ, который назвали квадратным корнем, и с помощью этого символа корни уравнения записали так: и. Читается: «арифметический квадратный корень из двух». Теперь для любого уравнения вида, где, можно найти корни — ими являются числа и.

Квадратным корнем из неотрицательного числа называют такое неотрицательное число, квадрат которого равен. Это число обозначают. Если, то уравнение не имеет корней.

Операцию нахождения квадратного корня из неотрицательного числа называют извлечением квадратного корня.

В ходе исследования методов вычисления квадратного корня были найдены несколько методов, такие как: арифметический способ; метод грубой оценки; столбиком; Вавилонский способ; метод Герона и метод Ньютона; геометрический метод. В данной работе рассмотрены лишь некоторые из них.

квадратный корень извлечение приближенное

Для квадратов натуральных чисел верны следующие равенства:

То есть, чтобы узнать целую часть квадратного корня числа, можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество выполненных действий.

Например, найдем квадратный корень числа 16 так:

Выполнено 4 действия, значит, квадратный корень числа 16 равен 4. Аналогично найдем квадратный корень числа 12:

Выполнено 3 действия, квадратный корень числа 12 равен 3 целым.

Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне пригоден для грубой оценки, для учащихся, решающих простейшие математические задачи, требующие извлечения квадратного корня.

Доказательство теоремы рассмотрено в работе. Поскольку и являются приближенными значениями для по избытку и по недостатку, и является средним геометрическим чисел и, то в качестве лучшего приближения для естественно выбрать среднее арифметическое этих чисел, т.е. число. А чтобы получить ещё более точное значение для, надо взять среднее арифметическое чисел и, т.е. число. Так вычисляются одно за другим все более точные приближенные значения для. Приближения ведут до тех пор, пока два полученных значения и не совпадут в пределах заданной точности. Тогда мы имеем формулу:

Таким образом, для получилось квадратное уравнение. Если его решить, то. Мы, получается, ходим по кругу: чтобы найти, нужно сосчитать, а чтобы найти, надо вычислить. На помощь приходит следующее соображение. Погрешность приближенного значения невелика, она меньше единицы, значит число еще меньше, поэтому в равенстве (2) его можно отбросить. При этом для получается приближенное уравнение, значит. Итак, приближенное значение поправки найдено.

Работа над данным исследованием показала, что изучение квадратных корней — объективная необходимость: в реальной жизни случаются ситуации, математические модели которых содержат операцию извлечения квадратного корня. Но не всегда под рукой мы имеем калькулятор. Помимо того, бывают ситуации, когда использование калькулятора недопустимо, например, ЕГЭ.

Хотелось бы выбрать оптимально рациональный способ извлечения квадратных корней. Конечно же, арифметический способ и особенно способ грубой оценки, просты в использовании, но не точны, хотя вполне пригодны для первого приближения. К тому же при применении этих способов извлечения квадратных корней любая ошибка, допущенная в каком-то месте, полностью обесценивает дальнейшие вычисления. Иначе состоит дело при применении Вавилонского способа или способа последовательных приближений. Хоть он и трудоемкий, однако можно верно вычислить значение корня с заданной точностью.

Размещено на Allbest.ru

Подобные документы

Понятие и математическая сущность квадратного корня, его назначение и методика вычисления. Теоремы, отображающие свойства квадратного коря, их обоснование и доказательство. Применение характеристик квадратных корней в решении геометрических задач.

реферат , добавлен 05.01.2010


Выведение формулы решения квадратного уравнения в истории математики. Сравнительный анализ технологий различных способов решения уравнений второй степени, примеры их применения. Краткая теория решения квадратных уравнений, составление задачника.

реферат , добавлен 18.12.2012


Изучение способов приближенного решения уравнений с помощью графического изображения функций. Исследование метода определения действительных корней квадратного уравнения с помощью циркуля и линейки для приведенных семи уравнений, построение их графиков.

творческая работа , добавлен 04.09.2010


Метод Гаусса, LU-разложение. Прогонка для решения линейных систем с трехдиагональными матрицами коэффициентов. Метод квадратного корня для решения систем: краткая характеристика, теоретическая основа, реализация, тестирование и листинг программы.

курсовая работа , добавлен 15.01.2013


Система линейных алгебраических уравнений. Основные формулы Крамера. Точные, приближенные методы решения линейных систем. Алгоритм реализации метода квадратных корней на языке программирования в среде Matlab 6.5. Влияние мерности, обусловленности матрицы.

контрольная работа , добавлен 27.04.2011


Исследование метода квадратных корней для симметричной матрицы как одного из методов решения систем линейных алгебраических уравнений. Анализ различных параметров матрицы и их влияния на точность решения: мерность, обусловленность и разряженность.

курсовая работа , добавлен 27.03.2011


История развития формул корней квадратных уравнений. Квадратные уравнения в Древнем Вавилоне. Решение квадратных уравнений Диофантом. Квадратные уравнения в Индии, в Хорезмии и в Европе XIII — XVII вв. Теорема Виета, современная алгебраическая запись.

контрольная работа , добавлен 27.11.2010


Нахождение корней уравнений (Equation Section 1) методом: Ньютона, Риддера, Брента, Лобачевского и Лагерра. Вычисление корней многочленов по схеме Горнера. Функции произвольного вида (при использовании пакета Mathcad). Нахождение корней полиномов.

контрольная работа , добавлен 14.08.2010


Изучение истории квадратных уравнений. Анализ общего правила решения квадратных уравнений, изложенного итальянским математиком Леонардо Фибоначчи. Решение квадратных уравнений с помощью циркуля и линейки, с помощью номограммы, способом «переброски».

На практике часто приходится вычислять квадратные корни из различных чисел. Сейчас это можно сделать на калькуляторе или с помощью компьютера. Мы же рассмотрим способ, как вычислить квадратный корень из любого числа с необходимой точностью, не используя при этом компьютер, калькулятор или другие вычислительные средства.

Для примера, попробуем вычислить корень из числа 2, с точностью до 0.01, то есть до двух знаков после запятой.

Будем рассуждать следующим образом. Число √2 больше 1, так как 1 2

Теперь попытаемся отыскать цифру десятых. Для этого будем дроби от единицы до двойки возводить в квадрат, пока не получим число большее двух. Шаг деления возьмем 0,1, так как мы ищем число десятых. Другими словами будем возводить в квадрат числа: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9

• 1,1 2 =1,21; 1,2 2 =1,44; 1,3 2 =1,69; 1,4 2 =1,96; 1,5 2 =2,25.

Получи число превышающее двойку, остальные числа уже не надо возводить в квадрат. Число 1,4 2 меньше 2, а 1,5 2 уже больше двух, то число √2 должно принадлежать промежутку от 1,4 до 1,5 (1,4

• 1,41 2 =1,9881, 1,42 2 =2,0164.

Уже при 1.42 получаем, что его квадрат больше двух, далее возводить в квадрат числа не имеет смысла.

Из этого получаем, что число √2 будет принадлежать промежутку от 1,41 до 1,42 (1,41

Так как нам необходимо записать √2 с точностью до двух знаков после запятой, то мы уже можем остановиться и не продолжать вычисления. √2 ≈ 1,41. Это и будет ответом. Если бы необходимо было вычислить еще более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений.

Как уже и говорилось выше, данный прием позволяет извлекать корень с любой заданной наперед точностью.

Как вычислить квадратный корень в Python?

В этом коротком руководстве мы рассмотрим, как мы можем вычислить квадратный корень в Python. Мы рассмотрим четыре различных метода и разберем их для вас.

Содержание

• Что такое квадратный корень?
• Использование функции pow() для вычисления квадратного корня в Python
• Вычисление квадратного корня в Python с использованием оператора экспоненты
• Использование функции sqrt() для вычисления квадратного корня в Python
• Вычисление квадратного корня в Python с использованием модуля cmath
• Заключительные мысли

Что такое квадратный корень?

Квадратный корень числа — это значение, которое при умножении само на себя возвращает то же самое число.

Например, 6 x 6 = 36, поэтому квадратный корень из 36 равен 6. Однако -6 x -6 тоже равно 36, поэтому -6 также является квадратным корнем из 36.

В Python или любом другом программировании Язык у нас есть различные методы для вычисления квадратного корня числа. В этом уроке мы рассмотрим четыре различных метода вычисления квадратного корня из числа.

Использование функции pow() для вычисления квадратного корня

Функция pow() — это быстрый метод нахождения квадратного корня в Python.

Давайте сначала разберемся, как функция pow() работает в Python.

Функция pow() принимает 2 параметра, первый параметр — это числовое значение, а второй параметр — степень числового значения.

Синтаксис:

 pow(x,y) # где y - степень x 

Ввод:

 # Использование функции pow()
импортировать математику
num = float(input("Введите число:"))
sqRoot = math.pow (число, 0,5)
print("Квадратный корень из заданного числа {0} = {1}".format(num, sqRoot))
         

Вывод:

 Введите число: 25
Квадратный корень из заданного числа 25,0 = 5,0
             

Вычисление квадратного корня с использованием оператора экспоненты

Экспоненциальный оператор, обозначенный ** , выполняет операцию извлечения квадратного корня так же, как функция pow() .

Чтобы было интереснее, давайте найдем квадратный корень числа, задав собственную функцию.

Ввод:

 # Использование оператора экспоненты для вычисления квадратного корня в Python
защита sqRoot(n):
    if n 

Вывод:

 6.0 

Мы начали с определения функции с именем sqRoot(n) . Затем мы добавили уравнение n**0,5 , которое должно вычислить квадратный корень и сохранить результат в переменной 9.0034 х . Когда мы вызываем определенную нами функцию, мы вводим число, из которого хотим найти квадратный корень, вместо аргумента или параметра n . Затем вызывается функция для реализации действия и вывода результата.

Использование функции sqrt() для вычисления квадратного корня

Функция sqrt() — это предопределенный метод, используемый для нахождения квадратного корня в Python. Во-первых, мы импортируем модуль math для использования функции sqrt() .

Ввод:

 # Использование функции sqrt() для вычисления квадратного корня в Python
импортировать математику
num = int(input("Введите число:"))
sqRoot = math.sqrt(число)
print (f"Квадратный корень из {num} равен " ,sqRoot)
  

Вывод:

 Введите число:16
Квадратный корень из 16 равен 4,0 

В первой строке мы начинаем с импорта модуля math , затем в следующей строке мы принимаем ввод от пользователя. После этого находим квадратный корень числа с помощью sqrt() , и результат будет сохранен в переменной sqRoot. Последняя строка кода гарантирует, что результат будет распечатан.

Вычисление квадратного корня в Python с помощью модуля cmath

Модуль cmath используется для вычисления квадратного корня из вещественного или комплексного числа в Python. Различные методы, которые мы использовали до сих пор, будут хорошо работать для всех положительных вещественных чисел. Но для отрицательных или комплексных чисел модуль cmath оказывается полезным.

Ввод:

 # Использование модуля cmath для вычисления квадратного корня из действительных или комплексных чисел в Python
импортировать математику
num = eval(input("Введите число: ")
num_sqRoot = cmath.sqrt(число)
print("Квадратный корень из {0} равен {1:0.3f}+{2:0.3f}j".format(num, num_sqRoot.real, num_sqRoot.imag))
        

Вывод:

 Введите число: 4+4j
Квадратный корень из (4+4j) равен 2,197+0,910j 

В этой программе мы использовали функцию sqrt() в модуле cmath. Обратите внимание, что мы также использовали функцию eval() для преобразования входных данных в комплексные числа.

cmath.sqrt() также может использоваться для возврата квадратного корня из отрицательного числа. Например:

Ввод:

 импорт cmath
а = -25
печать (cmath.sqrt (а))
 

Вывод:

 5j 

Заключительные мысли

В этом уроке мы узнали, как вычислить квадратный корень числа в Python с помощью функции sqrt() , оператора экспоненты, pow() и модуль cmath.

Если вам нужно работать с целыми числами вместо чисел с плавающей запятой; math.isqrt() выводит квадрат как целое число и округляет до ближайшего целого числа. Функция sqrt() также может использоваться с библиотеками, отличными от «математической» библиотеки, такой как numPy , библиотека Python, используемая для работы с массивами.

Алгоритм вычисления квадратных корней в уме – World Mental Calculation

Существует несколько методов мысленного вычисления квадратных корней (для чисел, которые еще не являются квадратами). В этом посте объясняется один эффективный метод мысленного вычисления квадратного корня из 6-значных чисел с точностью до нескольких знаков после запятой, как в соревнованиях Кубка мира по умственным вычислениям и Мемориады. Этот метод также распространяется на квадратные корни других чисел.

Существует несвязанный, более быстрый метод извлечения квадратных корней, когда вам нужна точность всего в 3–5 цифр.

Подготовка:

Для этого метода полезно знать квадраты чисел от 31² = 961 до 99² = 9801.

Метод:

Для этого примера мы найдем квадратный корень из 6910062. Шаг 1:

Используйте свои знания квадратных чисел, чтобы найти первые две цифры ответа.

Для 661062 мы видим, что 81² = 6561 < 6610 < 82² = 6724, поэтому первые две цифры равны 81. Все деления на шаге 3 и далее будут использовать эти первые две цифры.

Step 2:

Subtract this square (810² = 656100) from the question and divide this remainder by 20.

661062 – 656100 = 4962

4962 / 20 = 248.1

Step 3:

Разделите на 81, чтобы получить следующую цифру ответа, и умножьте остаток на 10.

248,1 / 81 = 3 остатка 5,1

Ответ на данный момент равен 813, а остаток теперь равен 5,1 × 10 = 51

Шаг 4:

Удалите перекрестные произведения ответа. Перекрестные произведения проще всего объяснить на отдельном примере:

Представьте, что ответ пока равен 987,6543

Не обращайте внимания на первые две цифры (98) и умножьте первую и последнюю цифры: 7 × 3 = 21

Затем умножьте вторую и предпоследнюю цифры: 6 × 4 = 24

Продолжайте складывать эти продукты, пока не дойдете до середины. Если число цифр нечетное (например, как в этом новом примере), то, когда вы дойдете до средней цифры, возведите ее в квадрат и разделите пополам. В этом примере у нас есть нечетное количество цифр в (7, 6, 5, 4, 3), поэтому, когда мы достигнем этого среднего числа 5: 5²/2 = 12,5

Всего у нас есть 21 + 24 + 12,5 = 57,5 ​​

Итак, вернемся к нашему исходному примеру 661062 с ответом 813…

Игнорируем первые две цифры (81), и у нас осталась только одна цифра (3), поэтому из остатка (51)

51 – 4,5 = 46,5

вычитаем 3²/2 = 4,5 Примечание! Иногда остаток слишком мал, так что при вычитании перекрестных произведений получается отрицательный результат. В этом случае вернитесь к шагу 3 и уменьшите новую цифру в ответе на единицу. В этом примере у нас нет проблем (46,5 > 0), но в противном случае нам пришлось бы вернуться к шагу 3 и шагу 4 и сделать:

248,1 / 81 = 2 остатка 86,1

861 – 2²/2 = 859

Шаг 5:

Повторяйте шаги 3 и 4, пока не получите достаточную точность:

46,5 / 81 = 0 остаток 46,5 (поэтому новый ответ равен 4 600,02 903,03)

10 = 465

465 – (3 × 0) = 465

465 / 81 = 5 остаток 60 (поэтому новый ответ 813,05…)

60 × 10 = 600

600 – (3 × 5) – 0 ² / 5 2 = 585

585 / 81 = 7 остаток 18 (поэтому новый ответ 813,057…)

18 × 10 = 180

180 – (3 × 7) – (0 × 5) = 159

(и т. д.)

Шаг 6:

Для вычисления последней цифры необходимо также оцените следующую цифру, чтобы узнать, следует ли округлить вверх или вниз. В нашем примере:

159 / 81 < 5, поэтому мы округлим в меньшую сторону, и ответ (до трех знаков после запятой) будет 813,057 (не 813,058)

 

Резюме:

Этот алгоритм кажется сложным, но не слишком сложным учить.