Калькулятор дробей | Как разделить дроби?
Калькулятор дробей: Если вы хотите легко разделить 2 дроби, воспользуйтесь нашим бесплатным Калькулятором дробей. Вам просто нужно указать дроби в качестве входных данных и нажать кнопку расчета, чтобы узнать данное деление дробей с подробной работой.
Калькулятор деления дробей: Вы действительно чувствуете, что найти деление дробей сложно? Если да, то воспользуйтесь этим инструментом, чтобы легко найти ответ. На этой странице вы можете получить шаги для расчета деления дробей с решенными примерами вопросов. Кроме того, найдите шаги, чтобы использовать этот бесплатный Калькулятор деления дробей.
Получите подробное объяснение того, как решать задачи на деление дробей.
- Получите две дроби.
- Найдите обратную величину второй дроби.
- Умножьте первую дробь на обратную вторую дробь.
- Упростите дробь произведения, чтобы получить ответ.
Вопросы на деление дробей
Вопрос 1:
Разделить дроби 125/25 ÷ 780/35?
Решение:
Даны дроби 125/25 и 780/35. /35 = 125/25 x 35/780
= (125 x 35)/(25 x 780)
= 4375/19500
= 35/156
Вопрос 2: 9000 деление дробей 1208/44 и 55/164? Решение: Даны дроби 1208/44 и 55/164 Обратная величина второй дроби равна 164/55 Умножить первую дробь 1208/44 на 164/55 164 = 1208/44 x 164/55 = (1208 x 164)/(44 x 55) = 198112/2420 = 49528/605
Примеры дробления
81/66
/66FAQS на разделение FRUCTIOL FRUCTIUTUTUTUTUTURD 777 . использовать калькулятор деления дробей?
Введите дроби в соответствующие поля ввода калькулятора. Нажмите кнопку расчета после полей ввода. Тогда вы получите деление дробей на экране.
2. На какие 3 шага разделить дроби?
- Получите обратную величину второй дроби.
- Умножьте первую дробь на обратную вторую дробь.
- Упростите полученную дробь.
3. Разделить дроби 156/7÷7/218?
Даны дроби 156/7÷7/218
Чтобы разделить дроби, инвертируйте вторую дробь и умножьте ее на первую дробь.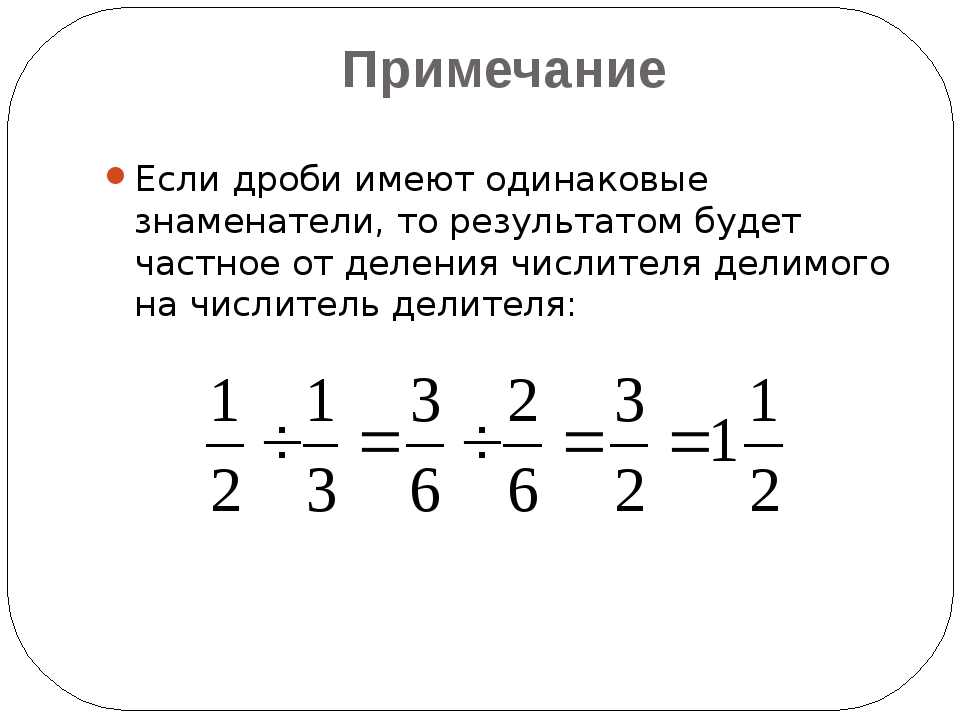
156/7÷7/218 = 156/7 х 218/7
= (156 х 218)/(7 х 7)
= 34008/49
4. Как делить дроби?
Деление дробей аналогично умножению дробей. Но нам нужно умножить первую дробь на обратную вторую дробь.
Калькулятор деления дробей
GENERATE WORK
сообщите об этом объявлении0341
использует две правильные или неправильные дроби, `a/b` и `c/d`, такие что `b,c,d\ne0`, и вычисляет частное для `a/b`, деленное на `c/d`. Это онлайн-инструмент для нахождения частного в простейшей форме двух правильных или неправильных дробей.Необходимо выполнить следующие шаги:
- Введите в поле две дроби, делимое `a/b` и делитель `c/d`. Числа `a, b, c` и `d` должны быть целыми числами, так что `b, c` и `d` должны быть ненулевыми.
- Нажмите «СОЗДАТЬ РАБОТУ» кнопка для выполнения вычислений;
- Калькулятор деления дробей вычислит частное двух чисел, представленных в виде дробей.
Ввод: Две дроби;
Вывод: Дробь в простейшей форме
Правило деления дробей: Определяется частное деления дроби `a/b` на `c/d` для `b,c,d\ne0` по следующей формуле
$$\frac{a}{b}\div\frac{c}{d}=\frac{a}{b}\times\frac{d}{c}=\frac{ a\times d}{b\times c},\quad \mbox{for}\;b,c,d\ne0$$
Как разделить дробь на дробь?
Деление дробей (или любых других чисел или переменных) может быть обозначено либо знаками деления `\div` или `:` между двумя дробями, либо записью деления в виде сложной дроби. Сложная дробь — это дробь, в которой числитель, знаменатель или оба содержат дробь. Итак, деление дробей можно представить следующим образом:
$$\frac 2 3\div \frac 5 4, \quad \frac 2 3: \frac 5 4,\quad \frac{\frac 23} {\ гидроразрыва 54} $ $
Первая дробь, в данном случае `2/3`, является делимым, вторая дробь, в данном случае `5/4`, является делителем, а результат является частным.
Одно свойство дробей, которое не действует для целых чисел и целых чисел, хорошо известно как обратное свойство дробей. Две дроби, произведение которых равно 1, называются мультипликативными обратными или обратными. Это означает, что если `\frac ab\times \frac cd=1` для `b,d\ne0`, то `\frac{a}{b} ` и `\frac{c}{d}` обратны. Произведение числа и его обратного числа равно «1». Другими словами, для каждой дроби `frac ab`, где `a, b \ne0`, существует ровно одно число `\frac b a` такое, что $$\frac ab\times \frac ba=1$$
Например, `5/7` и `7/5` обратны, потому что `\frac {5}{7}\times \frac {7}{5}=1.`
Когда мы имеем дело с делением дробей, Вот некоторые важные случаи, которые заслуживают упоминания здесь:
Деление одной дроби на другую
Деление на дробь $\frac c d$ равно умножению на дробь `\frac d c`, обратную ей. Это справедливо для любой дроби. Следовательно, чтобы разделить «a/b» на «c/d», умножьте «a/b» на «d/c», то есть умножьте их числители и умножьте их знаменатели.
$$\frac{a}{b}\div\frac{c}{d}=\frac{a}{b}\times\frac{d}{c}=\frac{a\times d} {b\times c},\quad b,c,d\ne0$$
Подводя итог, чтобы найти частное двух дробей, необходимо выполнить три шага:
- Найти обратную величину делителя
- Умножьте дивиденд на это обратное число
- При необходимости упростите произведение.
Например, разделим дроби: `8/3\разделить7/2`. Используя правило деления, описанное выше, мы получаем
$$\frac{8}{3}\div\frac{7}{2}=\frac{8}{3}\times\frac{2}{7}=\frac{8\times2}{3 \times7}=\frac{16}{21}$$
Деление дроби на целое число
Так как целое число может быть переписанный как разделенный на $1$, мы можем применить предыдущее правило деления дроби на другую дробь.
Частное дроби `\frac{a}{b},b\ne0`, деленное на целое число `c, c\ne0`, является произведением `\frac{a}{b}` и `\frac 1 c`, обратное значение `c`. Это можно записать следующим образом
$$\frac a b\div c=\frac a b\times \frac{1}{c}$$
Деление дроби на смешанные числа
Сначала нужно смешанное число преобразовать в неправильные дроби, затем разделить дроби. Например, найдите `\frac{3}{4}\div3\frac {1}{3}`. Поскольку `3\frac{1}{3}` равно `\frac{10}{3}`, частное дроби `\frac{3}{4}`, деленное на смешанное число `3\frac {1}{3}` равно частному дроби `\frac{3}{4}` на дробь `\frac {10}3`. Затем мы продолжим с правилом деления дроби на другую дробь.
Аналогичное соображение можно применить при делении алгебраических дробей.
Раздел дробей с шагами показывает полный пошаговый расчет для нахождения частного для дроби `\frac{8}{3}`, деленной на `\frac{7}{2}`, с использованием правила деления. Для любых других дробей просто введите две правильные или неправильные дроби и нажмите кнопку «СОЗДАТЬ РАБОТУ».
Учащиеся начальной школы могут использовать этот калькулятор деления на дроби для создания работы, проверки результатов деления чисел, полученных вручную, или эффективного решения домашних заданий.
Реальные задачи с использованием деления на дроби
Деление на дроби полезно при анализе размерностей. Размерный анализ — это процесс включения единиц измерения в деление. Например, сколько униформы можно изготовить, используя фабричные метры «a/b», если для каждой униформы требуется метр «c/d».
$$\mbox{метры}\div\frac{\mbox{метры}}{\mbox{uniform}}=\frac{\mbox{метры}}{1}\times\frac{\mbox{uniform }}{\mbox{meters}}=\mbox{unifrom}$$
Для дробей с маленькими числителями и знаменателями модель площади очень полезна для проверки или получения результата деления дробей. Поясним это понятие мысленным примером `1/2 \разделить 3/4`. Во-первых,
разделите два квадрата, чтобы представить каждую дробь, и заштрихуйте соответствующие их части.