Калькулятор квадратных уравнений
| Укажите коэффициенты a b и c квадратного уравнения ax2 + bx + c = 0 | |||||
|
|
|||||
| x2 + | x + | = 0 | |||
|
|
|||||
Что такое квадратное уравнение
Уравнение вида ax2 + bx + c = 0 называется квадратным.
Решить квадратное уравнение означает найти его корни, а именно x1 и x2, либо установить, что корней нет.
Числа a, b, c — называются коэфициентами квадратного уравнения, где a ≠ 0.
Каждый коэфициент квадратного уравнения имеет название:
a — старший коэфициент
b — средний коэфициент
c — свободный член
Если коэфициент b или c или оба этих коэфициента равны нулю, то такое уравнение называется неполным.
Дискриминант квадратного уравнения D выражается следующей формулой D = b2 — 4ac.
Как решить квадратное уравнение
Прежде всего при решении квадратного уравнения необходимо найти его дискрименант.
Если D > 0, то уравнение имеет два действительных корня, которые можно найти по формуле:
Приведем пример, решим уравнение 5x2 + 67x + 7 = 0
Найдем дискриминант D квадратного уравнения 5x
D = b2 — 4ac = 672 — 4 · 5 · 7 = 4349
Дискриминант уравнения больше нуля, следовательно, уравнение имеет два корня.
Подставим значения дискриминанта D, b и a в уравнения и найдем x1 и x2
| -b + D | = | |
| 2a |
| -67 + 4349 | = | |
| 2 · 5 |
-1.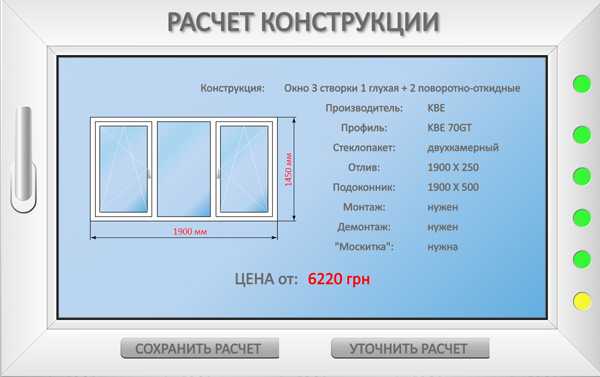 05305162480981 05305162480981 | = | |
| 10 |
| -0.105305162480981 | ||
| -b — D | = | |
| 2a |
| -67 — 4349 | = | |
| 2 · 5 |
| -132.94694837519 | = | |
| 10 |
| -13.294694837519 | ||
Если D = 0, то корни квадратного уравнения равны, по сути уравнение имеет один корень, например 9x2=0. При D = 0 необходимо воспользоваться формулой:
Приведем пример, решим уравнение x2 + 2x + 1 = 0
Найдем дискриминант D квадратного уравнения 1x2 + 2x + 1 = 0. В данном уравнении a = 1; b = 2; c = 1, тогда
В данном уравнении a = 1; b = 2; c = 1, тогда
D = b2 — 4ac = 22 — 4 · 1 · 1 = 0
Дискриминант уравнения равен нулю, следовательно, уравнение имеет один корень.
| x1,2 = | ||
| — | 2 | = |
| 2 · 1 |
| — | 2 | = |
| 2 |
Если D , например, 5x2 + 6x + 7 = 0, 20x2 + 2x + 3 = 0. При D
Приведем пример, решим уравнение 3x2 — 2x + 7 = 0
Найдем дискриминант D квадратного уравнения 3x2 — 2x + 7 = 0.
В данном уравнении a = 3; b = -2; c = 7, тогда
D = b2 — 4ac = (-2)2 — 4 · 3 · 7 = -80
Дискриминант меньше нуля, следовательно, уравнение не имеет действительных корней.
Подставим значения дискриминанта D, b и a в уравнения и найдем x1 и x2
| ( |D| )i | = | |
| 2a |
| — | -2 | + |
| 2 · 3 |
| ( 80 )i | = | |
| 2 · 3 |
| 0.333333333333333 + (1.49071198499986)i | ||
| ( |D| )i | = | |
| 2a |
| — | -2 | — |
| 2 · 3 |
| ( 80 )i | ||
| 2 · 3 |
0. 333333333333333 — (1.49071198499986)i 333333333333333 — (1.49071198499986)i | ||
Вычислить Квадратное Уравнение — Mathcracker.Com
Инструкции: Вычислите квадратное уравнение, показывая все шаги, с помощью этого калькулятора. Пожалуйста, введите квадратное уравнение, корни которого вы хотите вычислить, в поле формы ниже.
Решатель квадратных уравнений
Этот калькулятор позволит вам вычислить квадратное уравнение
который вы предоставите, показывая все шаги. Все, что вам нужно сделать, это предоставить действительное квадратное уравнение. 2 +1/3x -1, например.
2 +1/3x -1, например.
Как только вы введете правильное квадратное уравнение, все, что вам нужно сделать, это нажать кнопку «Вычислить», и вам будут представлены все шаги процесса вычисления корни квадратного уравнения который предоставляется.
Обычно для вычисления квадратных уравнений используется квадратичная формула, но это не единственный способ, как мы увидим в следующих разделах.
Как вычислить квадратное уравнение?
Существует несколько стратегий решения квадратных уравнений. Наиболее часто используемая из них — это использование метода
квадратичная формула
. Также вы можете решить
квадрат
, или вы можете решить с помощью
квадратичная факторизация
.
Наиболее часто используемая из них — это использование метода
квадратичная формула
. Также вы можете решить
квадрат
, или вы можете решить с помощью
квадратичная факторизация
.
Каковы этапы вычисления квадратных уравнений с помощью квадратичной формулы?
- Шаг 1: Определите квадратное уравнение, которое вы хотите вычислить
- Шаг 2: Убедитесь, что уравнение полностью упрощено, иначе продолжайте упрощение, пока не получите уравнение вида ax² + bx + c = 0
- Шаг 3: После приведения уравнения к упрощенной форме можно воспользоваться квадратичной формулой: \(x = \displaystyle \frac{-b \pm \sqrt{b^2 — 4ac}}{2a}\)
Возможно, использование формулы квадратного уравнения является наиболее практичным способом нахождения корней квадратного уравнения, но есть и другие причины, по которым вы можете использовать другие методы.
Как решить квадратное уравнение путем возведения в квадрат?
Вторым наиболее распространенным способом решения квадратного уравнения является использование техники квадрат . На самом деле не существует формулы для завершения квадратов (хотя технически она есть, основанная на решениях квадратного уравнения), и это скорее процесс.
Каковы шаги по заполнению квадратов
- Шаг 1: Определите квадратное уравнение, которое вы хотите решить
- Шаг 2: Вам необходимо убедиться, что уравнение полностью упрощено, и что у вас есть уравнение вида ax² + bx + c = 0
- Шаг 3: Добавьте и вычтите подходящий член (в данном случае, (b/(2a))², чтобы заставить члены квадрата бинома
Идея заставить появиться термин вида (x + «что-то)², который является конечной целью заполнения квадратов.
Почему вы используете квадратичные уравнения?
Квадратичные уравнения постоянно появляются в приложениях к алгебре в виде словесных задач. Решение квадратных уравнений — один из основных базовых навыков, которые вам необходимо приобрести.
Затем, в таких областях, как Calculus, при вычислении задач максимизации и минимизации, вам потребуется хорошее знакомство со всеми типами квадратичных уравнений.
Пример: решение квадратного уравнения
Решите следующее квадратное уравнение, используя формулу
Отвечать:
Нам необходимо решить следующее заданное квадратное уравнение \(\displaystyle 4x^2+\frac{4}{3}x+2=0\). 2+\frac{2}{3}x-\frac{4}{3}=0\) имеет два различных вещественных корня, которыми являются \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) и \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).
2+\frac{2}{3}x-\frac{4}{3}=0\) имеет два различных вещественных корня, которыми являются \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) и \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).
Графически:
Другие полезные квадратичные калькуляторы
Как мы уже видели в этом учебнике,
квадрат
играет фундаментальную роль в вычислении квадратных уравнений. Кроме того, вы можете использовать
калькулятор дискриминанта
оценить характер корней (два действительных корня, один действительный корень или два комплексных корня) без решения уравнения.
Вы также можете использовать это Вершинный калькулятор для нахождения координат вершины квадратного уравнения, и найти ось симметрии параболы . Также вы можете изучить следующее квадратичная факторизация инструмент для изучения еще одного способа вычисления квадратных уравнений.
Square Calc: find A, P, d
Создано Ханной Памула, доктором философии
Отредактировано Богной Шик и Аденой Бенн
Последнее обновление: 26 ноября 2022 г.
- Что такое квадрат?
- Расчет квадрата: найти P (периметр)
- Расчет квадрата: найти A (площадь)
- Расчет квадрата: найти d (диагональ)
- Свойства квадрата
- Как использовать калькулятор квадрата: найти пример периметра
С помощью этого простой квадратный калькулятор, вы можете найти все параметры в мгновение ока. Заполните одно поле, и калькулятор отобразит все остальные параметры: сторону, площадь, периметр и диагональ. Прокрутите вниз, если хотите напомнить себе об основных формулах вычисления квадратов.
Что такое квадрат?
Квадрат — это четырехугольник (форма, которую мы встретили в нашем калькуляторе площади четырехугольника) с четырьмя равными сторонами и четырьмя равными углами (прямые углы = 90°90\градус90°). Это одна из самых основных форм.
Это частный случай ромба, воздушного змея, трапеции, параллелограмма и прямоугольника, поэтому он обладает всеми свойствами этих фигур.
Расчет квадрата: найти P (периметр)
Периметр квадрата равен сумме всех сторон. Поскольку у квадрата все четыре стороны равны, периметр равен: 92A=a×a=a2
, где aaa — сторона квадрата
Термин в квадрате используется для описания умножения значения самого на себя, возведения его во вторую степень.
Квадраты, по большому счету, самая простая форма, когда дело доходит до вычисления площади. Для других четырехугольников формулы могут быть сложными, как вы можете видеть в нашей области калькулятора трапеций: однако, даже если есть много типов трапеций, одна формула подходит для всех. Вы также можете познакомиться с обобщением приведенных выше формул в нашем калькуляторе площади прямоугольника и узнать, что происходит, когда вы деформируете свой прямоугольник, в нашем калькуляторе площади параллелограмма.
Расчет квадрата: найти d (диагональ)
Диагонали квадрата равны по длине, они делят углы пополам и являются биссектрисами перпендикуляра друг к другу. Диагональ ddd квадрата равна длине стороны, умноженной на квадратный корень из 222:
Диагональ ddd квадрата равна длине стороны, умноженной на квадратный корень из 222:
d=a2d = a \sqrt{2}d=a2
Так, например, если сторона квадрата равна до 2 in2\ \mathrm{in}2 дюйма, тогда диагональ равна 2 in×2≈2,828 in2\ \mathrm{in}\times\sqrt 2 \приблизительно 2,828\ \mathrm{in}2 in×2≈2,828 в.
Свойства квадрата
Квадрат имеет уникальную форму. Здесь мы суммируем несколько важных признаков:
- Равенство : все четыре угла равны, все четыре стороны квадрата равны, и обе диагонали имеют одинаковую длину.
- Биссекция : диагонали делят пополам друг друга и квадратные углы.
- Перпендикулярность : все квадратные углы равны 90°90\градус90°, а диагонали пересекаются при 90°90\градус90°. 92}16 футов2.
- Чтобы определить периметр, умножьте длину стороны на 444. В нашем случае результат равен 16 ft16\ \mathrm{ft}16 ft.

- Чтобы определить диагонали, умножьте 2\sqrt{2}2 (около 1,4141,4141,414) на длину стороны. Это 5,657 футов5,657\ \mathrm{ft}5,657 футов.
- Или просто используйте наш калькулятор квадратов , чтобы найти диагонали, площадь и периметр квадрата.
- Бесконтактные платежи
- Мобильные платежи
- Платежи с чипом и PIN-кодом
- Интернет-магазин
- Онлайн-касса
- Интернет API
- Введенные транзакции
- Дистанционные карточные платежи
Ханна Памула, доктор философии
Сторона a
Диагональ
Периметр
Ознакомьтесь с 23 похожими калькуляторами 2D-геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 20
Square Payments Fee Calculator — Узнайте наши тарифы лучше
Square платежи просты и прозрачны — вы никогда не будете платить скрытые или дополнительные платежи. Кроме того, получите бесплатные услуги, такие как защита от мошенничества.
Начало работы
Сумма, которую вы сохраняете
$0.00
Начните продавать с Square
Отображаемые значения являются оценочными, основанными только на предоставленных вами данных, и не являются предложением или гарантией любого рода. Предполагаемая сумма, которую вы сохраняете, не включает налоги или другие отчисления.
Предполагаемая сумма, которую вы сохраняете, не включает налоги или другие отчисления.
Прозрачные тарифы без сюрпризов.
Лично
Скорость обработки
2,6% + 10 центов
Способ обработки
Онлайн
Скорость обработки
2,9% + 30 центов
Способ обработки
Введено вручную
Скорость обработки
3,5% + 15 центов
Метод обработки
Просмотреть все способы оплаты
Изучить варианты онлайн-оплаты
Сохраняйте больше того, что вы зарабатываете с Square.
Что вы держите
Гонорары конкурентов
Плата за квадрат
Конкуренты
Вы сохраняете 97,05%*
Квадрат
Вот разбивка того, где 2.9Комиссия 5%* взимается при продаже через Square:
63% Плата за обмен Когда Square обрабатывает транзакцию от вашего имени, Square обязан передать процент от собранных средств эмитенту карты вашего клиента. Плата за оценку Square обязана отдавать процент от суммы, полученной от вашего клиента, ассоциациям, таким как Mastercard или Visa, в качестве взносов и оценок.
3% Риск и соответствие PCI Продукты Square производятся со сквозным шифрованием и поддерживают соответствие требованиям PCI, поэтому вам не нужно доплачивать за безопасность своих данных.
34% Квадратные услуги *Эти проценты отражают сочетание наших коэффициентов наличия и отсутствия карты и предназначены для иллюстрации.

