Калькулятор онлайн дробей с иксом: Алгебраический калькулятор | Microsoft Math Solver

Калькулятор пропорций — как посчитать пропорцию

Онлайн-калькулятор пропорций, который поможет вам решить ваши проблемы с пропорциями и определить недостающее значение в пропорции. Наш решить пропорцию находит неизвестное значение двумя следующими способами:

• Крестным умножением
• По пропорции

Важно понимать основные определения, вычисления пропорций вручную и с помощью калькулятора. Что ж, мы поможем вам разобраться во всех этих терминах.

Читать дальше!

Что такое пропорция?

В математике это отношение между двумя величинами, и два утверждения должны быть равными. Результаты либо в виде дроби, либо через двоеточие (:), либо в виде десятичной дроби или процентов. Например, 3/6 = 1/2 или 3/6: 1/2. Кроме того, это можно записать как 3: 6 = 1: 2. Когда два отношения имеют равные значения, тогда значения также находятся в равной пропорции. Если вы хотите отображать результат в процентах, просто используйте наш онлайн-калькулятор процентов, который является лучшим выбором для вас, чтобы посчитать пропорцию со 100 в качестве знаменателя.

как посчитать пропорцию вручную (шаг за шагом):

Если вы хотите узнать недостающую переменную в уравнении пропорции, просто поставьте между ними знак равенства. Найдите недостающее значение путем перекрестного умножения. Наш калькулятор пропорций генерирует результат как с перекрестным умножением, так и с пропорциями. Здесь у нас есть ручной пример для пояснения.

Пример:

Уравнение имеет вид 8 / x = 6/4, найти неизвестное x?

Решение:

Крестным умножением:

Уравнение:

8 / х = 6/4

Перекрестным умножением

6х = 8 × 4

х = 8 × 4/6

х = 32/6

х = 5,33

По пропорциям:

Уравнение равно, если,

8/6 = 1,33

Итак, это правда,

х / 4 = 1,33

х = 1,33 × 4

х = 5,33

Мы настоятельно рекомендуем вам воспользоваться нашим бесплатным калькулятором пропорций, если вы собираетесь решать пропорции калькулятор для больших чисел или любых десятичных чисел.

Ценности, имеющие прямую или обратную связь:

Если термин связывает две переменные без каких-либо дополнительных уточнений, предполагается, что он напрямую связан. Например, c = y / x, где c – константа пропорциональности в уравнениях пропорциональности, x и y – переменные, напрямую связанные друг с другом.

Если произведение двух переменных равно константе k, то переменные обратно пропорциональны друг другу. Уравнение записывается как, x * y = c. После использования этого пропорционального калькулятора вы легко поймете, связаны ли два параметра обратно или напрямую.

Как использовать онлайн-калькулятор пропорций:

Этот решатель пропорций дает мгновенные и точные результаты вашей проблемы, просто следуйте данным инструкциям:

Входы:

Введите значения в поля и замените неизвестное значение любой переменной x, y или любой другой.
Затем нажмите кнопку «Рассчитать».

Выходы:

Калькулятор пропорций показывает:

• Значение отсутствующей переменной
• Пошаговое решение обоих методов (перекрестное умножение и пропорция)

Часто задаваемые вопросы (FAQ):

Каковы 3 способа решить посчитать пропорцию?

Ниже приведены три способа решить пропорцию:

• Вертикальный
• По горизонтали
• Диагональ (часто называют перекрестным произведением)

Какие бывают виды пропорций?

По сути, существует два типа пропорций:

• непосредственный
• Обратный

Заключительные слова:

В реальном мире эта пропорция используется ежедневно бизнесменами при работе с финансами. Это может помочь вам в увеличении рецепта для большого скопления людей, увеличении или уменьшении изображения для масштабирования или создании дизайна с определенными функциями и т. Д. Когда дело доходит до расчета пропорций, просто попробуйте бесплатный калькулятор пропорций, который поможет вам найти недостающие значение в уравнении.

Other Languages:Proportion Calculator, Kalkulator Proporcji, Kalkulator Proporsi, Proportions Rechner, 比例計算, Calculo De Proporção, Calculadora De Proporciones, Calcolo Proporzioni, Mittasuhteet Laskin.

Калькулятор дроби в процент — MathCracker.com

Алгебра Решатели

---

Инструкции: Используйте этот пошаговый калькулятор долей в проценты, чтобы вычислить, какой процент связан с долей \(\frac{D}{X}\).

Пожалуйста, предоставьте необходимую информацию в форме ниже:

Дробь \(D / X \) (Пример: 2/3 и т. Д.) =

You will compute the percentage associated to the given fraction \(D / X\).

---

Идея дроби и процента тесно связаны. В самом деле, процент, по его названию, показывает, сколько от общего значения будет, если бы общее значение было 100.

Это похоже на усиление членов дроби так, чтобы в знаменателе было 100. Результирующее значение в числителе — это процент. Но должен быть более простой способ увидеть это. Ну что ж, держите пари!

Как вычислить долю в процентах

Мы вычисляем требуемый процент, связанный с дробью, просто используя следующую формулу:

\[\text{Percentage} = \text{Decimal expression of } \displaystyle\frac{D}{X} \times 100\]

Это все. Вы берете десятичное выражение дроби \(\frac{D}{X}\), а затем результат этого десятичного выражения умножается на 100, и вы получаете желаемый процент.

Пример перевода дроби в процент

Пример: Какой процент 13 из 38?

Используя приведенную выше формулу, мы получаем:

\[\text{Percentage} = \displaystyle\frac{13}{38} \times 100\] \[ = 0.342105263 \times 100\] \[ = 34.21 \%\]

Связано ли это с обычным калькулятором процентов?

Да, безусловно, идея преобразования дроби в проценты тесно связана с концепцией вычисление регулярного процента .

По сути, это одно и то же. Когда вы вычисляете процент, соответствующий доле \(\frac{D}{X}\), на самом деле вы вычисляете, какой процент \(D\) составляет от \(X\).

---

Калькулятор алгебры Алгебра Решатель Базовый пакет алгебры Преобразовать дробь в процент Калькулятор дроби в процент

Fraction Calculator — Fraction Calc

Fraction Calc — это специальный калькулятор для умножения, деления, сложения и вычитания двух или более дробей и целых чисел. Он может обрабатывать несколько дробей и целых чисел одновременно. Затем он отображает пошаговые решения любой операции, которую он обработал. Иногда мало кто назовет его решателем дробей, в то время как другие могут сказать, что это калькулятор смешанных чисел или калькулятор смешанных дробей. Это онлайн-калькулятор с кнопкой дроби. На данный момент он может вычислять до десяти дробей и смешанных чисел. Это полезно для всех учащихся всех классов. Его можно использовать в качестве справочника для всех учителей математики и даже для тех специалистов, которые часто используют дроби на работе или дома.

Упростить

Backspace

Целые числа

Числители

Знаменатели

---

Как использовать?

Этот калькулятор был разработан для удобства использования.

• Сложение двух дробей

1. Нажмите любую цифру из кнопок числителя.
2. Нажмите любую цифру из кнопок знаменателя.
3. Нажмите кнопку добавления (+) .
4. Нажмите любую цифру из кнопок числителя для второй дроби.
5. Нажмите любую цифру из кнопок знаменателя для второй дроби.
6. Нажмите кнопку равно (=) , чтобы вычислить ответ. Ответ и решение будут отображаться выше.

Добавление трех или более дробей

1. Повторите шаги, описанные выше, за исключением последнего шага.
2. Нажмите кнопку добавления (+) .
3. Нажмите любую цифру из кнопок числителя для третьей дроби.
4. Нажмите любую цифру из кнопок знаменателя для третьей дроби.
5. Нажмите кнопку равно (=) , чтобы вычислить ответ, или нажмите кнопку добавления (+) , чтобы добавить другие дроби.
6. Тот же процесс будет использоваться для четвертой, пятой или любого количества фракций. Просто нажмите кнопку равно (=) для вычисления.

Вычитание двух, трех или более дробей

• Следуйте инструкциям по сложению дробей, но вместо нажатия кнопки добавления (+) нажмите кнопку вычитания (-) .

Умножение и деление двух, трех и более дробей

• Следуйте инструкциям по сложению дробей, но вместо нажатия кнопки добавления (+) нажмите кнопку умножения (x) для умножения и деления (÷) кнопку для разделение.

Сложение, вычитание, умножение и деление смешанных чисел

Важно помнить, что при работе со смешанными числами при использовании этого калькулятора никогда не забывайте вводить целые числа. Кнопки целых чисел в калькуляторе больше, чем кнопки числителя и знаменателя. Вам нужно только сначала нажать кнопку целого числа, а затем дробь, после чего вы можете перейти к любой операции, которую хотите.

Операции с дробями, целыми числами и смешанными числами

1. Нажмите кнопку целого числа, если ваша дробь состоит из целого числа, или вы можете напрямую нажать кнопку числителя, если вам не нужно целое число. Вы не можете нажать кнопку знаменателя, если вы не нажали целое число или кнопку знаменателя. Это означает, что вам нужно сначала нажать кнопку целого числа или числителя. После нажатия кнопки числителя вы больше не можете нажимать кнопку целого числа. Вы можете нажать кнопку целого числа еще раз только в том случае, если вы удалите числитель, нажав кнопку возврата. Нули не должны быть нажаты первыми. Нули будут нажаты после нажатия ненулевых чисел.
2. Нажмите кнопку знаменателя для вашего знаменателя. После нажатия вы не можете снова нажать кнопку целого числа или числителя. Вы можете нажать кнопку числителя только в том случае, если вы удалите знаменатель, нажав кнопку возврата.
3. Выберите любую операцию.
4. Нажмите кнопку Равно , если вы закончили с дробью. Решение будет отображаться выше.
5. Нажмите Backspace , если вы хотите удалить по одному номеру за раз.
6. Нажмите Кнопка AC для очистки уравнения дроби.
7. На данный момент этот калькулятор ограничен только 10 дробями.

---

Расчет дробей на мобильных телефонах Android

Выпущен наш калькулятор дробей для мобильных телефонов Android. Он может обрабатывать базовые и сложные операции с дробями и может отображать решение как методом перекрестного умножения, так и методом LCD (наименьший общий знаменатель). Вы можете получить его из магазина Google Play.

Как был выполнен расчет?

Иногда возникают сомнения в том, как выполняются вычисления при использовании нескольких операций. Используя нотацию MDAS, умножение и деление имеют такой же приоритет, но выше, чем сложение и вычитание. Сложение и вычитание имеют одинаковый приоритет. Сначала обрабатывается более высокий приоритет. Это всегда было правилом, и оно соблюдалось повсеместно. При одинаковом приоритете операция выполняется слева направо.

---

Калькулятор дроби целого числа

Fraction Calc также является калькулятором дробей целых чисел, потому что он может обрабатывать множество целых чисел. Работа с целыми числами означает, что вам придется больше учиться и делать дополнительные шаги, преобразовывая целые числа в формат, подходящий для математических операций. Выполнение математических операций с целыми числами означает, что вам нужно выполнить дополнительные действия, чтобы получить правильный ответ. Это означает дополнительную энергию и нагрузку для людей, которые оказались в ситуации, когда им нужно решать целые числа и дроби. Вот почему некоторые люди ищут калькулятор дробей и целых чисел не только с целью предоставления простых решений сложных задач, но и для экономии времени и энергии. Экономия времени и энергии на определенной задаче означает, что вы получаете дополнительные ресурсы для выполнения еще более важной задачи, которая была бы очень полезной.

---

3 Калькулятор дробей

В большинстве случаев в любой математической арифметике используются только две дроби. Очень редко в какой-либо операции участвуют 3 фракции. Но если это ваш случай, то вам очень повезло, что вы нашли этот инструмент. Вы можете легко использовать этот инструмент в качестве калькулятора 3-х дробей, потому что он может абсолютно решить эту проблему. Это основная цель этого инструмента. Некоторые люди никогда не слышали об этом инструменте, поэтому они специально искали калькулятор с тремя дробями. Но теперь, когда его инструмент создан, я думаю, у них больше нет времени беспокоиться.

---

Калькулятор кратных дробей

Большинство из созданных калькуляторов имеют ограниченные возможности до такой степени, что могут вычислять только две дроби за раз. Но Fraction Calc может даже больше. Он может решить до 10 целых чисел или дробей вместе взятых. Вот почему многие называют его калькулятором кратных дробей. Это очень специализированный калькулятор с целыми числами. С комбинацией целого числа и дроби трудно иметь дело, но с этим калькулятором кратных дробей вычисления становятся проще. Сложение смешанных чисел, преобразование дробей в целые числа, умножение дробей на целые числа, вычитание смешанных чисел и умножение смешанных дробей — вот некоторые из процессов, которые может выполнять этот калькулятор.

---

Преимущества и недостатки использования калькулятора дробей.

• Преимущества:

1. Прост в использовании.
2. Экономит больше времени и энергии.
3. Нет необходимости в ручном вычислении.
4. Вычисленный результат точен и точен.

Недостатки:

1. Это может затруднить вычисление дробей.
2. В будущем вы будете очень зависимы от него.
3. Вы можете забыть правила вычисления.

---

Правила работы с дробями

• Сложение и вычитание дробей

Сложение и вычитание дробей выполняются по одним и тем же правилам. Они должны иметь одинаковые знаменатели для выполнения выбранной операции. Вы можете сложить или вычесть две дроби, если у них один и тот же знаменатель, если нет; вы должны создать общий знаменатель, прежде чем складывать или вычитать их.

Подобные дроби — это дроби, имеющие одинаковые знаменатели. Чтобы сложить дроби с одинаковым знаменателем, добавьте его числитель. Например, 2/5 + 1/5 = 3/5.

Дроби, имеющие разные знаменатели, не похожи на дроби. Чтобы сложить разные дроби, нужно привести их к общему знаменателю. Самый простой способ сделать это — использовать метод бабочки. Чтобы выполнить метод бабочки, выполните следующие действия.

1. Умножьте числитель первой дроби на знаменатель второй дроби. Результатом будет первый числитель дроби.
2. Умножьте знаменатель первой дроби на знаменатель второй дроби. Результатом будет новый знаменатель первой дроби.
3. Умножьте числитель второй дроби на знаменатель первой дроби. Результатом будет новый числитель второй дроби.
4. Умножьте знаменатель второй дроби на знаменатель первой дроби. Результат теперь является новым знаменателем второй дроби.

Например: 2/3 + 3/5.

1. 2 х 5 = 10.
2. 3 х 5 = 15.
3. 3 х 3 = 9.
4. 5 х 3 = 15.

Новая фракция: 10/15 и 9/15.
15/10 + 15/9 = 15/19.
Новая дробь 19/15.

Чтобы вычесть дроби с одинаковым знаменателем, просто вычтите числитель второй дроби из числителя первой дроби. Пример: 4/6 – 3/6 = 1/6.

Для дробей с разными знаменателями приведите их к одному знаменателю, используя метод бабочки, а затем выполните вычитание после того, как у них будет одинаковый знаменатель.

Умножение и деление дробей

Правило умножения двух дробей простое. Умножьте числитель первой дроби на числитель второй дроби и умножьте знаменатель первой дроби на знаменатель второй дроби. Пример: 2/3 х 1/5 = 2/15.

Чтобы разделить две дроби, вы должны сначала инвертировать вторую дробь, а затем начать умножать две дроби. Пример: 2/3 разделить на 1/5 = 2/3 x 5/1 = 10/3.

Как заменить неправильную дробь смешанным числом

Когда вы сокращаете неправильную дробь до наименьшего члена, вам нужно преобразовать ее в смешанное число. Это делается делением числителя на знаменатель. Частное будет целым числом. Остаток будет новым числителем, а знаменатель останется прежним.

Как преобразовать смешанное число в неправильную дробь

При делении или умножении смешанных чисел вам нужно, чтобы оно превратилось в неправильную дробь. Это делается путем умножения целого числа на знаменатель, а затем добавления текущего числителя. Результатом будет новый числитель, а знаменатель останется прежним.

Сравнение дробей

Для дробей с одинаковыми знаменателями дробь с наибольшим числителем является большей, чем дробь с меньшим числителем.
Для дробей с одинаковыми числителями дробь с наибольшим знаменателем меньше дроби с меньшим знаменателем.

Упрощение дробей

Из темы выше мы уже знаем, что есть равнозначные дроби-дроби, одинаковые по значению, даже если у них разные числители и знаменатели. Упрощение дроби означает использование наименьшего числителя и знаменателя, но одного и того же значения. Дробь имеет простейшую форму, когда нет общего множителя для числителя и знаменателя. Например, вместо использования 7/14 мы можем использовать ½, что является самой простой формой.

Наибольший общий делитель

Наибольший общий делитель — это наибольшее число, используемое для деления числителя и знаменателя для получения простейшей формы дроби. Например, для дроби 12/30 наибольшее число, на которое можно разделить как числитель, так и знаменатель, равно 6. Разделив его на 6, вы получите его простейшую форму — 2/5.

---

Факты о дробях

Дроби являются частями целого. Например, один торт на пятерых детей. Итак, торт делится на пять частей. Каждый ребенок получит одну часть торта. Дробь будет 1/5. Каждый ребенок получит 1/5 торта.

Дробь состоит из двух частей. Верхняя половина называется числителем. Нижняя половина называется знаменателем. Числитель — это часть целого, где она используется или с которой в настоящее время имеют дело.

Существуют три типа дробей: правильная дробь, неправильная дробь и смешанные числа.

Правильная дробь — это дробь, числитель которой всегда меньше знаменателя.

Неправильная дробь – это дробь, числитель которой больше или равен знаменателю.

Смешанное число представляет собой целое число плюс дробь.

Равные дроби — это дроби, которые имеют разные числители и знаменатели, но имеют одинаковое значение, например 1/2, 2/4, 7/14, 8/16, 10/20, 20/40 и 50/100.

---

Как был создан калькулятор дробей?

Когда я был студентом, у меня был предмет по математике. Одна из тем была о дроби. Хотя эта тема сложна, меня очень удивило, почему трудно определить, правильное решение или нет. Вы должны просмотреть его несколько раз, чтобы убедиться, что ваше решение является правильным. Это произошло не только у меня. Я узнал, что большинство студентов испытывали то же самое. Так что с этого момента я мечтаю, что так или иначе буду им помогать. Я помогу им убедиться, что их решение правильное, не просматривая множество обзоров. Именно поэтому я создал этот калькулятор. Этот калькулятор был создан в качестве справочника или руководства только для того, чтобы учащийся получил правильный ответ из своих задач на дроби. От основателя FractionCalc.com

Калькулятор перекрестного умножения

Создано Maciej Kowalski, PhD

Как перекрестно умножать дроби

Пример: использование калькулятора перекрестного умножения

Часто задаваемые вопросы

Добро пожаловать в Omni’s калькулятор перекрестного умножения , где мы будем решать xxx с дробями.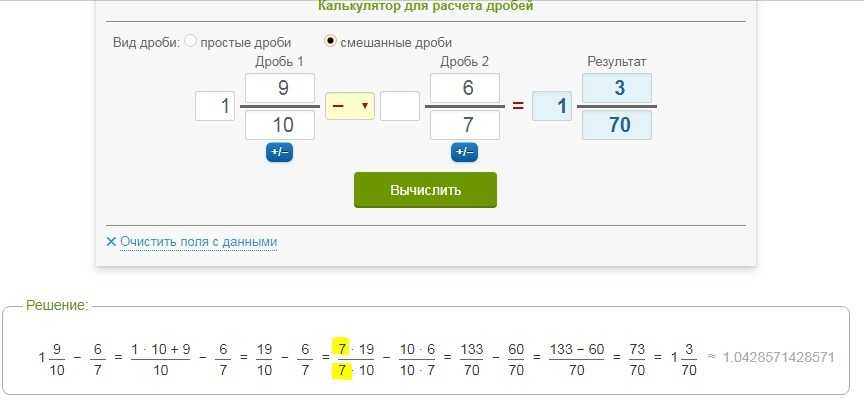 Выражения, которые мы рассматриваем здесь, часто называют пропорциями, и есть простой алгоритмический способ работы с ними: перекрестно умножить дроби . Фактически, независимо от того, какое из четырех значений неизвестно, как только мы пересечем умножение и деление, , мы обязательно получим наш результат , без каких-либо условий.

Но прежде чем забегать вперед, давайте немного замедлимся и научимся выполнять перекрестное умножение легко и просто .

Решение x с дробями

Обычно мы используем перекрестное умножение, когда имеем уравнений с одной переменной, включая дроби . Например, он включает выражения вида:

2x=57−13,4=9x1023x=218\begin{split} \frac{2}{x}& = \frac{5}{7}\\ \\[1.5em] -\frac{1}{3.4} &= \frac{9x}{10}\\ \\[1.5em] \frac{2}{3}x &= \frac{21}{8} \end{split}x2​−3.41​32​x​=75​=109x​=821​​

Обратите внимание, что мы можем иметь отрицательные числа или десятичные дроби в числителях или знаменателях. Кроме того, в последнем примере xxx находится за пределами дроби , но мы можем легко получить ее внутри, следуя основным правилам, которые говорят нам, как вычислить умножение дроби:

23x=23×x1=2×x3×1=2×3\frac{2} {3}x=\frac{2}{3}\times\frac{x}{1}=\frac{2\times x}{3\times1}=\frac{2x}{3}32​x= 32×1x=3×12×x=32x

Такие уравнения, даже если они выглядят причудливо, должны подчиняться тем же правилам, что и любые другие . В частности, мы можем прибавлять или вычитать любое число, а также умножать или делить на любое ненулевое значение, пока мы сделайте это с обеих сторон знака равенства . Для наших целей последняя пара арифметических операций оказывается решающей: мы умножим и разделим , чтобы найти значение xxx.

Как скрещивать дроби

Подсказка кроется в названии « перекрестное умножение «. Мы вычислим произведение значений в перекрестном шаблоне :

numleft×denright=numright×denleft\scriptsize \text{num}_\text{left}\times\text{den}_{\text{ right}}=\text{num}_\text{right}\times\text{den}_{\text{left}}numleft×denright​=numright×denleft​

Где num\text{num}num и den\text{den}den — соответственно числитель и знаменатель. И если бы мы использовали символы, появляющиеся в калькуляторе перекрестного умножения Omni, т. е. возьмем уравнение:

AB=CD\frac{A}{B}=\frac{C}{D}BA​=DC​

мы получим:

A×D=B×CA\times D = B\times CA×D=B×C

На самом деле, это все, что есть для решения xxx с дробями. В конце концов, когда мы перекрестим умножение, у нас больше не будет дробей, поэтому мы можем перейти к 9.0290 другие известные методы работы с уравнениями. Например, если мы хотим найти AAA из приведенной выше формулы, достаточно разделить обе части на DDD:

A×DD=B×CDA=B×CD\begin{split} \frac{A\times D}{D}&=\frac{B\times C}{D}\\ \\[1,5 см] A&=\frac{B\times C}{D} \end{split}DA×D​A​=DB×C​=DB×C​​

Обратите внимание, что какая бы буква нам ни понадобилась (т. е. какой бы ни был числитель или знаменатель), процедура останется той же: разделять. Разница лишь в том, на что мы делим на втором шаге. Чтобы быть точным, мы делим на:

• DDD при поиске AAA;
• CCC при поиске BBB;
• BBB при поиске CCC; и
• AAA при поиске DDD.

Кроме того, напомню, что мы всегда можем поменять местами стороны уравнения . Поэтому мы всегда можем изменить формулу:

numleft×denright=numright×denleft\scriptsize \text{num}_\text{left}\times\text{den}_{\text{right}}=\text{ num}_\text{right}\times\text{den}_{\text{left}}numleft​×denright​=numright​×denleft​

в:

numright×denleft=numleft×denright\scriptsize \text{num}_\text{right}\times\text{den}_{\text{left}}=\text{num}_\text {left}\times\text{den}_{\text{right}}numright​×denleft​=numleft​×denright​

Однако обратите внимание, что пары остаются теми же : нам нужно сохранить перекрестное умножение шаблон.

Хорошо, инструкции по перекрестному умножению кажутся достаточно простыми, не так ли? нам пора переходить от символов и теории к цифрам и практике . И, чтобы убить двух зайцев одним выстрелом, мы воспользуемся возможностью , чтобы наш калькулятор умножения крестов сиял .

Пример: использование калькулятора перекрестного умножения

Предположим, что вы строите модель самолета . После нескольких часов кропотливой склейки самолет готов: он будет великолепно смотреться на полке, чтобы все могли им восхищаться. Но теперь, когда часть DIY закончена, почему бы нам не узнать что-нибудь об этом? Давайте посчитаем , насколько велик реальный эквивалент 9.0291 .

На коробке написано, что модель выполнена в масштабе 1:1001:1001:100. Вы берете линейку и проверяете, что вашего творения имеет длину 3.53.53.5 дюймов . Хотите верьте, хотите нет, но это все, что нам нужно, чтобы найти ответ. Хитрость в заключается в хорошем понимании того, как работает масштабирование : единица измерения на коробке пропорциональна соотношению модельной и реальной длин. В нашем случае это означает, что 3,53,53,5 дюймов к фактической длине самолета равно 111 равно 100100100:

3. 5x=1100\frac{3.5}{x}=\frac{1}{100}x3.5​=1001​

, где xxx обозначает искомое значение. Однако, прежде чем мы бросимся решать ее самостоятельно, давайте посмотрим насколько легко решается задача, имея под рукой калькулятор перекрестного умножения Omni .

В верхней части нашего инструмента мы видим формулу:

AB=CD\frac{A}{B}=\frac{C}{D}BA​=DC​

и четыре переменных поля, соответствующие буквы. Как показывает калькулятор перекрестного умножения, достаточно ввести три значений, поэтому мы вернемся к нашей задаче и напишем:

• A=3.5A = 3.5A=3.5, C=1C = 1C=1 и D=100D = 100D=100 .

В тот момент, когда мы введем третье число, , инструмент выдаст ответ . Обратите внимание, как он также предоставляет пошаговое объяснение внизу: то же самое, что мы дадим прямо сейчас.

Начнем с того, чему научил нас предыдущий раздел: мы скрестим, умножим дроби :

3,5x=1100\frac{3,5}{x}=\frac{1}{100}x3,5​=1001​

Следовательно:

x×1=3,5×100x\times 1 = 3,5 \times 100x×1=3,5×100

Что дает:

x=350x = 350x=350

Обычно нам все равно нужно разделить результат на число, стоящее перед xxx. Однако в нашем случае это число оказалось 111, , поэтому не нужно.

Мы получили ответ! Реальный самолет имеет длину 350350350 дюймов. Что ж, нам, вероятно, следует перейти от калькулятора перекрестного умножения к преобразователю длины, чтобы получить более разумный ответ , тебе не кажется?

Модели часто строятся в разных масштабах: 1:721:721:72, 1:481:481:48 и так далее. Узнайте, как быстро перейти от одного к другому с помощью нашего масштабного калькулятора.

Часто задаваемые вопросы

Как найти x с помощью дробей?

Чтобы решить для x с дробями , вам нужно:

1. Преобразовать обе части в частные.
2. Крест умножить дроби.
3. Упростите два выражения.
4. Разделите на то, что находится перед x .
5. Наслаждайтесь , решив x с дробями.

Как скрестить дроби?

Чтобы перекрестно умножить дроби , вам необходимо:

1. Убедитесь, что у вас есть только дроби с каждой стороны.
2. Умножьте числитель первого на знаменатель второго.
3. Умножьте числитель второго на знаменатель первого.
4. Объедините шагов 2-3 в уравнение.
5. При необходимости решить полученное уравнение базовыми методами.
6. Наслаждайтесь игрой , перемножив дроби крест-накрест.

Почему работает перекрестное умножение?

Перекрестное умножение, по сути, простое умножение, выполненное дважды .

Во-первых, мы умножить обе части на знаменатель левой части , что оставляет только числитель слева (в соответствии с правилами упрощения дробей) и умножает правый числитель (в соответствии с правилами умножения дробей). Затем мы умножаем обе части на знаменатель правой части , что дает произведение слева и уничтожает знаменатель справа.

В общем, поскольку мы всегда можем умножить обе части уравнения на ненулевое число, перекрестное умножение действительно работает .

Как работает перекрестное умножение?

Чтобы использовать перекрестное умножение , вам необходимо:

1. Убедитесь, что у вас есть только дробь с каждой стороны.
2. Умножьте числитель первого на знаменатель второго.
3. Умножьте числитель второго на знаменатель первого.
4. Объедините шагов 2-3 в уравнение.
5. Если нужно, решить полученное уравнение с помощью основных методов.
6. Наслаждайтесь игрой , используя перекрестное умножение.

Как сравнивать дроби с помощью перекрестного умножения?

Чтобы сравнить дроби с помощью перекрестного умножения , вам необходимо:

1. Убедитесь, что у вас есть только дроби с каждой стороны.
2. Умножьте числитель первого на знаменатель второго.
3. Умножьте числитель второго на знаменатель первого.
4. Сравните значения из шагов 2 и 3.
5. Если на шаге 2 было:
   • Меньше , то первая дробь меньше; или
   • Больше , то первая дробь больше.
6. Если один из множителей был отрицательным, изменить отношение на противоположное.
7. Наслаждайтесь игрой , сравнив дроби с помощью перекрестного умножения.

Как решить пропорции с помощью перекрестного умножения?

Чтобы решить пропорции с помощью перекрестного умножения , вам необходимо:

1. Убедитесь, что у вас есть только дроби с каждой стороны.
2. Умножьте числитель первого на знаменатель второго.
3. Умножьте числитель второго на знаменатель первого.

   No related posts.