Среднее значение данных Калькулятор | Вычислить Среднее значение данных
✖Сумма индивидуальных значений — это общая сумма всех отдельных значений случайной величины в заданных статистических данных.ⓘ Сумма отдельных значений [Σx] | +10% -10% | ||
✖Количество отдельных значений — это общее количество отдельных значений случайной величины в заданных статистических данных, совокупности или выборке.ⓘ Количество отдельных значений [N] | +10% -10% |
|
✖Среднее значение данных — это среднее значение отдельных значений в данных статистических данных.ⓘ Среднее значение данных [μ] |
|
👎
Формула
сбросить
👍
Среднее значение данных Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Сумма отдельных значений: 160 —> Конверсия не требуется
Количество отдельных значений: 16 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
10 —> Конверсия не требуется
< 7 Иметь в виду Калькуляторы
Среднее значение данных формула
Среднее значение данных = Сумма отдельных значений/Количество отдельных значений
Что такое среднее и его значение?
В статистике наиболее часто используемым показателем центральной тенденции является среднее значение. Слово «среднее» является статистическим термином, используемым для обозначения «среднего». Среднее может использоваться для представления типичного значения и поэтому служит эталоном для всех наблюдений.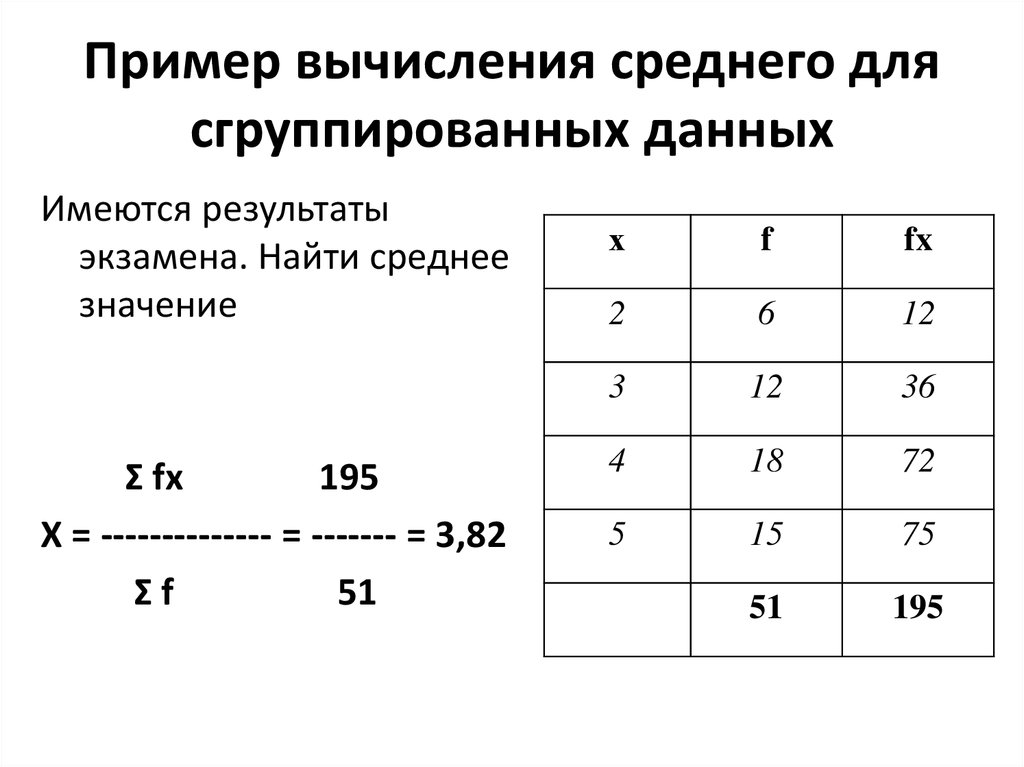
Например, если мы хотим узнать, сколько часов в среднем сотрудник тратит на обучение в год, мы можем найти среднее количество часов обучения группы сотрудников. Одним из основных преимуществ среднего значения по сравнению с другими показателями центральных тенденций является то, что среднее значение учитывает все элементы в данных данных. Он вычисляет среднее значение набора данных. Это не может быть точным измерением асимметричного распределения. Если среднее равно медиане, то распределение нормальное.
Share
Copied!
Среднее значение по способу моментов онлайн
Метод моментов приравнивает моменты теоретического распределения к моментам эмпирического распределения (распределения, построенного по наблюдениям). Из полученных уравнений находятся оценки параметров распределения. Например, для распределения с двумя параметрами первые два момента (среднее и дисперсия распределения, соответственно, m и s) будут приравнены первым двум эмпирическим (выборочным) моментам (среднему и дисперсии выборки, соответственно), и затем будет произведено оценивание.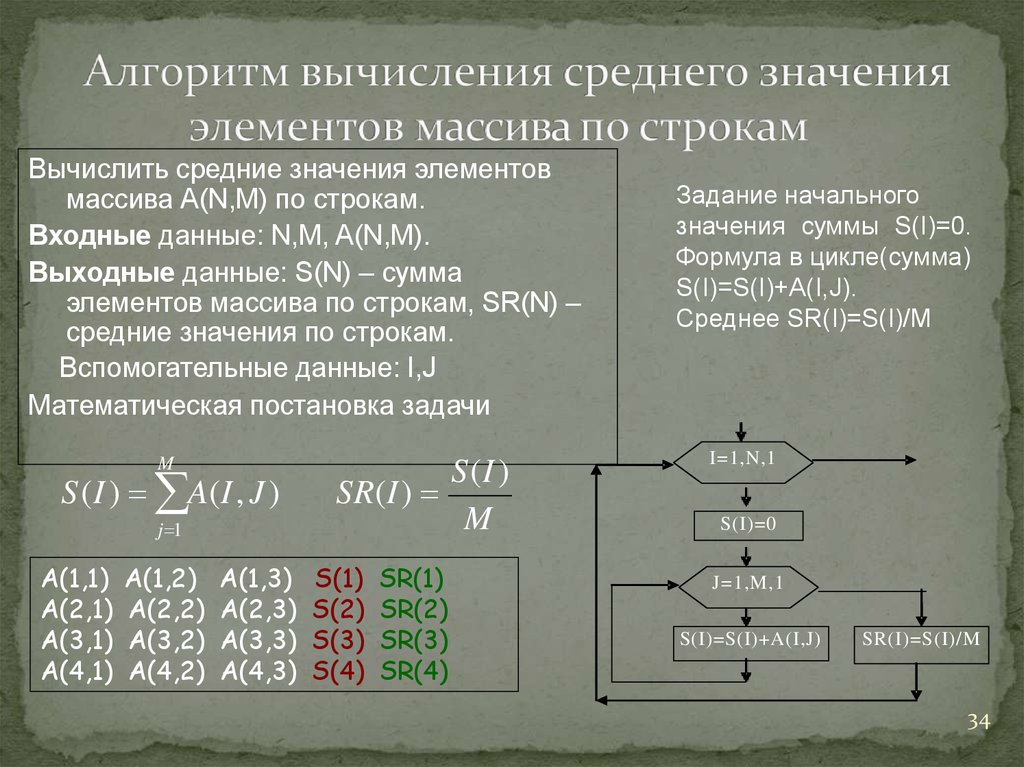
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала,Назначение сервиса. С помощью онлайн-калькулятора вычисляется среднее значение по способу моментов. Результат решения оформляется в формате Word.
- Шаг №1
- Шаг №2
- Видеоинструкция
Инструкция. Для получения решения необходимо заполнить исходные данные и выбрать параметры отчета для оформления в Word.
Количество строк
- Определяем параметр A. Вычисляем x*i
- Вычисляем x*i*fi
- Находим среднее значение по формуле
Пример. Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
Затраты времени, мин. | Число рабочих, чел. |
| до 15 | 20 |
| 15-20 | 25 |
| 20-25 | 50 |
| 25-30 | 30 |
| 30-35 | 15 |
| более 35 | 10 |
Таблица для расчета показателей.
| Группы | Середина интервала, xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)2·f |
| 5 — 10 | 7.5 | 20 | 150 | 20 | 4600.56 |
| 15 — 20 | 17.5 | 25 | 437.5 | 45 | 667.36 |
| 20 — 25 | 22.5 | 50 | 1125 | 95 | 1. 39
|
| 25 — 30 | 27.5 | 30 | 825 | 125 | 700.83 |
| 30 — 35 | 32.5 | 15 | 487.5 | 140 | 1450.42 |
| 35 — 40 | 37.5 | 10 | 375 | 150 | 2200.28 |
| 150 | 3400 | 9620.83 |
Мода
где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота.
Наиболее часто встречающееся значение ряда – 22.78 мин.
Медиана
Медианным является интервал 20 — 25, т.
к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 23 мин.
Среднее значение изучаемого признака по способу моментов.
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала.
Находим А = 22.5, шаг интервала h = 5.
Средний квадрат отклонений по способу моментов.
| xц | x*i | x*ifi | [x*i]2fi |
| 7.5 | -3 | -60 | 180 |
| 17.5 | -1 | -25 | 25 |
| 22.5 | 0 | 0 | 0 |
27. 5
| 1 | 30 | 30 |
| 32.5 | 2 | 30 | 60 |
| 37.5 | 3 | 30 | 90 |
| 5 | 385 |
мин.
Среднее квадратическое отклонение.
мин.
Коэффициент вариации — мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30% ,но v<70%, то вариация умеренная.
Пример
| Группы | x | Кол-во f | x·f | (x-x)2·f |
| 6.0 — 8.5 | 7.25 | 26 | 188.5 | 480.74 |
| 8.5 — 11.0 | 9.75 | 112 | 1092 | 362. 88
|
| 11.0 — 13.5 | 12.25 | 210 | 2572.5 | 102.9 |
| 13.5 — 16.0 | 14.75 | 52 | 767 | 532.48 |
| 400 | 4620 | 1479 |
Среднее значение изучаемого признака по способу моментов.
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала.
Находим А = 12.25.
Шаг интервала h = 2.5.
Средний квадрат отклонений по способу моментов.
| xц | x*i | x*ifi | [x*i]2fi |
7. 25
| -2 | -52 | 104 |
| 9.75 | -1 | -112 | 112 |
| 12.25 | 0 | 0 | 0 |
| 1 | 52 | 52 | |
| -112 | 268 |
Среднеквадратическое отклонение по способу моментов.
Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Формула для средневзвешенного:
Среднеквадратическое отклонение.
Каждое значение ряда отличается от среднего значения 11.55 не более, чем на 1.92.
Как видим, оценки для среднего значения m и квадрата отклонений s рассчитанные по разным формулам совпадают.
Средний Калькулятор | Калькулятор среднего
Калькулятор среднего | Калькулятор среднегоГлавная›Калькуляторы›Математические калькуляторы›Калькулятор средних значений
Калькулятор среднего Калькулятор стандартного отклонения Калькулятор дисперсии
Введите значения данных
1 2 5 2 6 6
Среднее (среднее)
Средние шаги расчета
Среднее геометрическое
Среднеквадратичное значение (RMS)
Медиана
Население SD
Образец SD:
Минимальное значение
Максимальное значение
График значений
График распределения
* SD = стандартное отклонение.
a 1 + a 2 +…+ a n n
Пример
Среднее значение 1,2,5 равно:
Среднее значение =
1+2+53
= 2,667
0 Средневзвешенное значение 3| Вес | Значение данных |
Средневзвешенное значение
Сумма весов
Расчет
Вычисление средневзвешенного значения
Средневзвешенное значение ( x ) равно сумме произведения веса (w i ), умноженного на число данных (x i ), деленного на сумму весов:
Пример
Найдите средневзвешенное значение оценок класса (с одинаковым весом) 70,70,80,80,80,90:
Поскольку веса всех оценок равны, мы можем вычислить эти оценки с помощью простого среднего или мы можем подсчитать, сколько раз встречается каждый класс, и использовать средневзвешенное значение.
2×70,3×80,1×90
x =
2×70+3×80+1×902+3+1
=
4706
= 78.33333
Калькулятор средневзвешенного значения ►
См. также
- Калькулятор стандартного отклонения
- Калькулятор дисперсии
- Калькулятор оценок
- Калькулятор среднего балла
- Математические калькуляторы
Напишите, как улучшить эту страницу
МАТЕМАТИЧЕСКИЕ КАЛЬКУЛЯТОРЫ
- Калькулятор научных данных
- Простой калькулятор
- Калькулятор средних значений
- Базовый вычислитель
- Калькулятор комплексных чисел
- Калькулятор дробей
- Калькулятор процентов
RAPID TABLES
- Рекомендовать сайт
- Отправить отзыв
- О
Калькулятор средних значений
Наш калькулятор средних значений помогает рассчитать среднее или среднее значение любого заданного набора данных.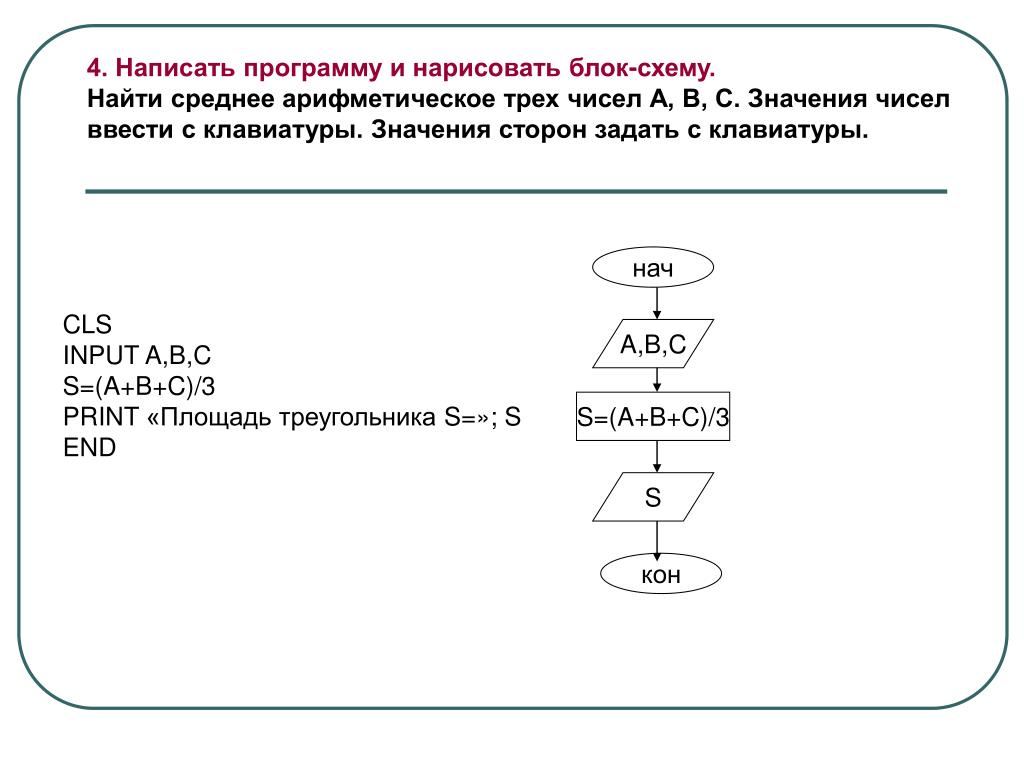
Помимо нахождения среднего или среднего числа, этот калькулятор среднего числа вычисляет и показывает график (распределение набора данных со средним), таблицу и некоторые другие параметры для данной группы чисел.
Какое среднее значение?Средний термин имеет разное количество значений. Можно сказать, что это одно число, которое используется для представления набора чисел. Когда дело доходит до математического контекста, среднее значение — это термин, который относится к среднему или среднему арифметическому.
Проще говоря, это статистическая концепция, которая широко используется в нескольких областях. Попробуйте наш калькулятор средних чисел, чтобы найти среднюю сумму онлайн.
Какие существуют типы средних значений?С точки зрения математики, мы, люди, используем три разных типа среднего: среднее, моду и медиану, каждый из которых называется отдельным «нормальным значением». что вы получите, если будете делить все поровну
Если вы хотите найти среднее значение набора чисел, просто сложив весь набор чисел и разделив их на количество чисел, которые у вас есть, для лучшего понимания, давайте взглянем на приведенная формула для среднего:
Уравнение среднего:
Среднее значение набора чисел = Сумма слагаемых / Количество слагаемых
Предположим, что имеется набор данных:
5, 6, 9, 11, 13, 12
Подставим значение в приведенную выше формулу, чтобы найти среднее значение заданных терминов:
Среднее значение набора чисел = 5 + 6 + 9 + 11 + 13 + 12 / 6
Среднее значение набора чисел = 56/6
Среднее значение набора чисел = 9,333
Таблица средних значений: Пройти по таблице ниже это специально устроено для вычисления средних значений некоторых из наиболее широко используемых пар чисел.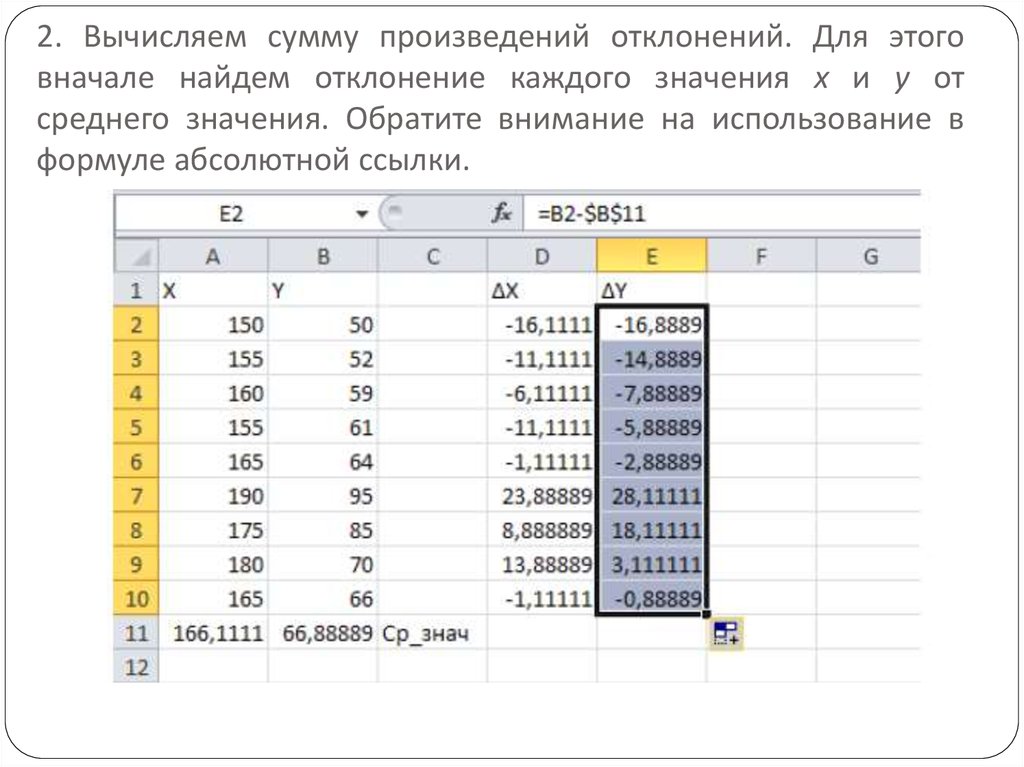
Давайте посмотрим на это:
| Старший номер | Пара номеров | Среднее 2 чисел |
| 1 | 60 и 100 | 80 |
| 2 | 90 и 100 | 95 |
| 3 | 88 и 100 | 94 |
| 4 | 95 и 100 | 97,5 |
| 5 | 92 и 100 | 96 |
| 6 | 60 и 100 | 80 |
| 7 | 86 и 100 | 93 |
| 8 | 87 и 100 | 93,5 |
| 9 | 78 и 100 | 89 |
| 10 | 70 и 100 | 85 |
| 11 | 80 и 90 | 85 |
| 12 | 84 и 100 | 92 |
| 13 | 86 и 100 | 93 |
| 14 | 93 и 100 | 96,5 |
Вы также можете проверить все эти значения, используя это лучшее среднее значение калькулятора.
Не только это, но вы также можете определить среднее значение 3 чисел с помощью этого лучшего калькулятора.
Входы:
- Прежде всего, вам просто нужно выбрать оператор, с помощью которого вы хотите разделить числа набора данных, это может быть «пробел» «запятая» или « определяется пользователем (означает определить себя)»
- После выбора все, что вам нужно, чтобы добавить набор данных или группу чисел, разделив их с помощью разделителя выбора, и нажмите кнопку расчета этого калькулятора среднего числа
Выход:
- Среднее значение
- Медиана (средний)
- Режим (наиболее распространенный)
- Диапазон (самый большой – самый маленький)
- Расчет среднего значения
- Среднее геометрическое
- Восходящий порядок
- По убыванию
- Четные числа
- Нечетные числа:
- Общая сумма
- Умножить на значения:
- Стандартное отклонение населения
- Стандартное отклонение образца
- Наибольшее значение
- Самое низкое значение
- Количество (общее количество)
- Таблица распределения по заданному набору данных
- Кроме того, этот калькулятор средних значений показывает график для «Распределения чисел со средними значениями»
Пример 1:
Есть 10 учеников, и на данный момент их суммарные оценки в процентах составляют: 78, 64, 87, 95, 88, 74, 82, 93, 79 и 82.
Итак, найдите среднюю оценку в вашем математическом классе.
Давайте начнем с суммирования всех баллов учеников:
78 + 64 + 87 + 95 + 88 + 74 + 82 + 93 + 79 + 82 = 822
Далее все, что вам нужно разделить на количество баллов, которые вы добавили. (Просто посчитайте их, или даже вы могли бы просто отметить, что поставленная задача говорит вам, что их 10)
822 ÷ 10 = 82,2
Результат равен 82,2; это средний балл в вашем классе математики.
Часто задаваемые вопросы Как найти средний процент?Для расчета среднего процента:
- Все, что вам нужно разделить общее количество предметов, представленных в процентах, на общее количество предметов. Остальную скорость также можно повысить, используя этот лучший калькулятор среднего процента.
Например:
Если из 500 карандашей было изъято 200 книг. Просто надо разделить 200 на 500, что равно 0,40.