Решение линейных неравенств: онлайн калькулятор
Выполнить {$ main.types[data.type] $}
Число A
Число B
Число C
Результаты расчёта
- {$ result[0] $}
- {$ result[1] $}
- {$ result[2] $}
Неравенство – это числовое соотношение, иллюстрирующее величину чисел относительно друг друга. Неравенства широко используются при поиске величин в прикладных науках. Наш калькулятор поможет вам разобраться с такой непростой темой, как решение линейных неравенств.
Что такое неравенство
Неравные соотношения в реальной жизни соотносятся с постоянным сравнением различных объектов: выше или ниже, дальше или ближе, тяжелее или легче. Интуитивно или зрительно мы можем понять, что один объект больше, выше или тяжелее другого, однако фактически речь всегда идет о сравнении чисел, которые характеризуют соответствующие величины.
Сравнивать объекты можно по любому признаку и в любом случае мы можем составить числовое неравенство.
Если неизвестные величины при конкретных условиях равны, то для их численного определения мы составляем уравнение. Если же нет, то вместо знака «равно» мы можем указать любое другое соотношение между этими величинами. Два числа или математических объекта могут быть больше «>», меньше «<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.
Знаки неравенств в их современном виде придумал британский математик Томас Гарриот, который в 1631 году выпустил книгу о неравных соотношениях. Знаки больше «>» и меньше «<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.
Решение неравенств
Неравенства, как и уравнения, бывают разных типов.
Линейные, квадратные, логарифмические или показательные неравные соотношения развязываются различными методами. Однако вне зависимости от метода, любое неравенство вначале требуется привести к стандартному виду. Для этого используются тождественные преобразования, идентичные видоизменениям равенств.
Тождественные преобразования неравенств
Такие трансформации выражений очень похожи на привидение уравнений, однако они имеют нюансы, которые важно учитывать при развязывании неравенств.
Первое тождественное преобразование идентично аналогичной операции с равенствами. К обеим сторонам неравного соотношения можно прибавить или отнять одно и то же число или выражение с неизвестным иксом, при этом знак неравенства останется прежним. Чаще всего этот метод применяется в упрощенной форме как перенос членов выражения через знак неравенства со сменой знака числа на противоположный. Имеется в виду смена знака самого члена, то есть +R при переносе через любой знак неравенства изменится на – R и наоборот.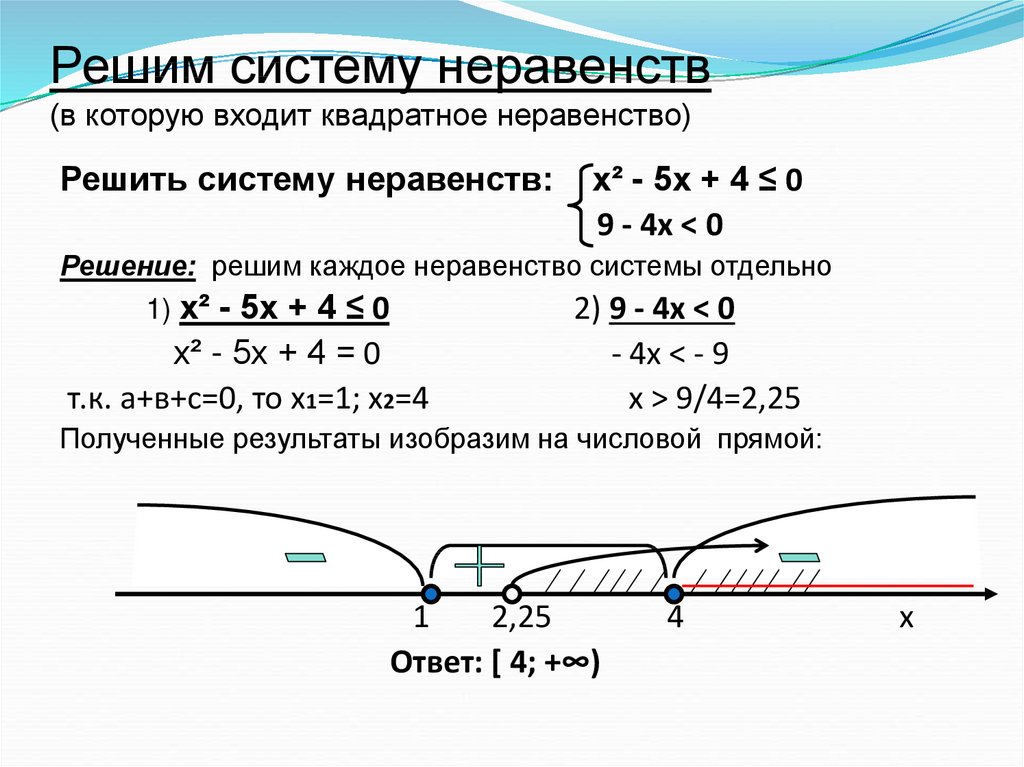
Второе преобразование имеет два пункта:
- Обе стороны неравного соотношения разрешается умножить или разделить на одно и то же положительное число. Знак самого неравенства при этом не изменится.
- Обе стороны неравенства разрешается разделить или умножить на одно и то же отрицательное число. Знак самого неравенства изменится на противоположный.
Второе тождественное преобразование неравенств имеет серьезные различия с видоизменением уравнений. Во-первых, при умножении/делении на отрицательное число знак неравного выражения всегда изменяется на обратный. Во-вторых, разделить или умножить части отношения разрешается только на число, а не на любое выражение, содержащее неизвестное. Дело в том, что мы не можем точно знать, число больше или меньше нуля скрывается за неизвестным, поэтому второе тождественное преобразование применяется к неравенствам исключительно с числами. Рассмотрим эти правила на примерах.
Примеры развязывания неравенств
В заданиях по алгебре встречаются самые разные задания на тему неравенств.
Пусть нам дано выражение:
6x − 3(4x + 1) > 6.
Для начала раскроем скобки и перенесем все неизвестные влево, а все числа – вправо.
6x − 12x > 6 + 3
−6x > 9
Нам требуется поделить обе части выражения на −6, поэтому при нахождении неизвестного икса знак неравенства изменится на противоположный.
x < −9/6
x < −1,5
При решении этого неравенства мы использовали оба тождественных преобразования: перенесли все числа справа от знака и разделили обе стороны соотношения на отрицательное число.
Наша программа представляет собой калькулятор решения числовых неравенств, которые не содержат неизвестных. В программу заложены следующие теоремы для соотношений трех чисел:
- если A < B то A–C< B–C;
- если A > B, то A–C > B–C.
Вместо вычитания членов A–C вы можете указать любое арифметическое действие: сложение, умножение или деление. Таким образом, калькулятор автоматически представит неравенства сумм, разностей, произведений или дробей.
Заключение
В реальной жизни неравенства встречаются также часто, как и уравнения. Естественно, что в быту знания о разрешении неравенств могут и не понадобиться. Однако в прикладных науках неравенства и их системы находят широкое применение. К примеру, различные исследования проблем глобальной экономики сводятся к составлению и развязыванию систем линейных или квадратных неравенств, а некоторые неравные отношения служат однозначным способом доказательства существования определенных объектов. Пользуйтесь нашими программами для решения линейных неравенств или проверки собственных выкладок.
Воспользуйтесь калькулятором неравенства Маркова — MathCracker.com
Решатели Статистика
Пожалуйста, укажите необходимые данные в форме ниже:
Среднее по совокупности (\(\mu\))
Нижняя граница события \((a)\):
Неравенство Маркова утверждает, что для значения \(a > 0\), у нас есть для любой случайной величины \(X\), которая не принимает отрицательных значений, всегда соблюдается следующая верхняя граница:
\[\Pr(X \ge a) \le \displaystyle \frac{E(X)}{a} \]
Неравенство Маркова очень важно для оценки вероятностей, учитывая его общность в том смысле, что оно применяется к любой неотрицательной случайной величине \(X\).
Действительно, неравенство Маркова имеет решающее значение для доказательства широко используемого неравенства, а именно: Неравенство Чебышева , и это основа еще более резкого неравенства — неравенства Хёффдинга.
Интуиция о неравенстве Маркова
Какая интуиция стоит за неравенством Маркова? Ну, во-первых, есть очевидный фактор: вероятность на правом хвосте имеет верхнюю границу, которая уменьшается все больше и больше по мере того, как мы получаем более дальний правый хвост, что на самом деле довольно очевидно.
Обратите внимание на характер неравенства: \(\frac{E(X)}{a}\) — это не точное значение вероятности хвоста, а только верхняя граница.
Насколько близко это ограничение? Что ж, теперь мы знаем, что это зависит от фактического распределения, но все же существуют более резкие неравенства, такие как неравенство Хёффдинга.
Но все же в математике есть очень четкое правило: чем более общие (менее конкретные) предположения, тем слабее теорема. Итак, довольно удивительно, что неравенство Маркова существует, учитывая очень общий характер его предположений.
Например, эмпирическое правило неравенство гораздо более жесткое, но оно делает гораздо более сильное предположение: лежащее в основе распределение является нормальным. Неравенство Маркова работает для любого распределения (неотрицательной переменной)
Базовый пакет статистики Калькулятор неравенства Маркова Вероятность неравенства Калькулятор статистики Статистический решатель
Калькулятор линейных уравнений и неравенств
Онлайн-калькулятор линейных уравнений и неравенств LinearEquationCalcutor помогает детям и учителям решать проблемы линейного неравенства.
Калькулятор линейных уравнений и неравенств: Знание линейных уравнений и неравенств полностью улучшит ваше понимание концепции. Что ж, предоставленное пошаговое руководство по построению графиков неравенств и линейных уравнений с одной переменной и неравенств с примерами прольет свет на ваши расчеты. Используйте наш удобный и бесплатный онлайн-калькулятор линейных уравнений и неравенств, чтобы получить и проверить свои ответы за меньшее время.
Уравнения, в которых неизвестные появляются только в первой степени, называются линейными уравнениями. Общая форма линейного уравнения с одной переменной: ax + b = 0, где x — переменная.
Линейное неравенство напоминает уравнение заменой знака равенства на символ неравенства. Как правило, диапазон значений, а не одно конкретное значение, будет решением линейного неравенства.
- х < 7
- 5 — лет ≥ 30
- х + 5 > 20
- Q ≠ 50
Этапы построения графика линейных неравенств
График линейного неравенства пересекает координатную плоскость на две части по граничной линии. Чтобы построить график неравенства, мы должны выполнить несколько основных шагов:
- Во-первых, проверить, правильно ли построено данное уравнение линейного неравенства.
- Если не переставить уравнение, где переменная будет в левой части, а остальное выражение в правой части символа неравенства
- На этом шаге подставьте значения x в уравнение и постройте график.
- Продолжайте рисовать сплошную линию для y≤ или y≥ и пунктирную линию для y< или y>.
- Наконец, заштрихуйте линию в соответствии с неравенствами, например, над линией для «больше» (y> или y≥) и под линией для «меньше» (y< или y≤).
Шаги для решения линейных уравнений и неравенств с одной переменной
Чтобы решить линейное уравнение или неравенство, имеющее только одну переменную, выполните шаги, описанные ниже, чтобы сбалансировать уравнение:
- Во-первых, добавьте или вычтите похожие термины
- Изолировать переменную
-
- Проверьте ответ.
Пример:
Найдите неравенство для 6x + 4 > 28
Решение:
Поместите переменную в левую часть и поменяйте местами все остальные члены или коэффициент при x на правую.
6x > 28 — 4
6x > 24
⇒ x > 4
Следовательно, значение x больше 4.
Просмотрите все разделы линейных уравнений на нашем надежном веб-сайте Linearequationscalculator.com и найдите бесплатные онлайн-калькуляторы, связанные с линейными уравнениями и понятия неравенства.
- Что такое неравенство в математике?
Если два математических выражения содержат такие символы, как «<» (меньше), «>» (больше), «≤» (меньше или равно) или «≥» (больше или равно), они называются неравенства.
- Какой метод лучше всего подходит для решения линейных неравенств двух переменных?
Для решения линейных неравенств двух переменных лучше всего подходит графический метод.
- Какие символы обозначают неравенства в линейных уравнениях?
В линейных неравенствах используются следующие символы:
- < (меньше)
- > (больше)
- ≤ (меньше или равно)
- ≥ (больше или равно)
- ≠ (не равно)
- Как легко решить систему линейных неравенств?
Воспользуйтесь калькулятором линейных уравнений и неравенств и легко решите вычисления линейного неравенства, просто введя уравнение в решатель неравенства.
Калькулятор неравенства
Тысячи пользователей используют наше программное обеспечение, чтобы выполнить домашнее задание по алгебре. Вот некоторые из их впечатлений:Наше вспомогательное программное обеспечение по алгебре помогает многим людям преодолеть страх перед алгеброй. Вот несколько выбранных ключевых слов, используемых сегодня для доступа к нашему сайту:
|
..