Примеры четных функций: Четные и нечетные функции

проверка функции на четность и нечетность

Что такое четность и нечетность функции

Если проанализировать графики функций, можно заметить, что некоторые из них симметричны либо относительно оси ординат, либо относительно точки начала координат.

Симметрия графика отражается в такой характеристики функции как четность или нечетность.

Исследование на четность и нечетность имеет важное значение в разделах математического анализа, описывающих разложение в числовые ряды (степенные, ряды Фурье).

Определение 1

Не все функции можно отнести к четным или нечетным. Такие функции, не являющимися четными или нечетными, принято называть функциями общего вида.

Четная функция

Дадим определение четной функции.

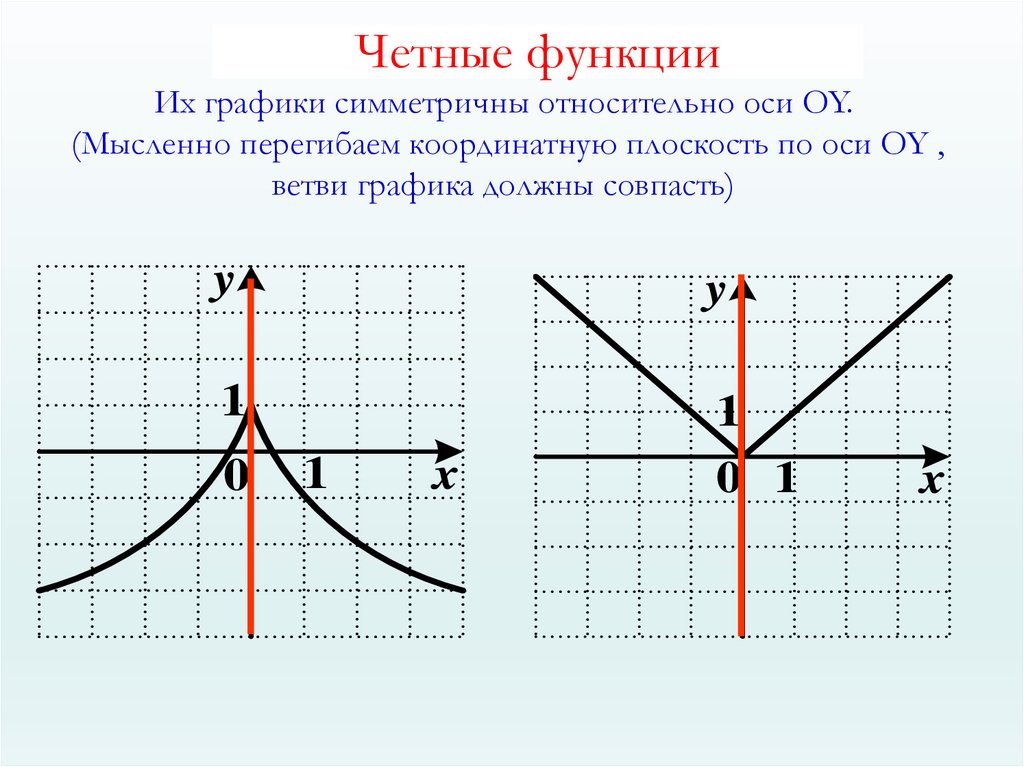
Определение 2

Функцию считают четной, если выполняется следующее условие:  для , где X — область допустимых значений.

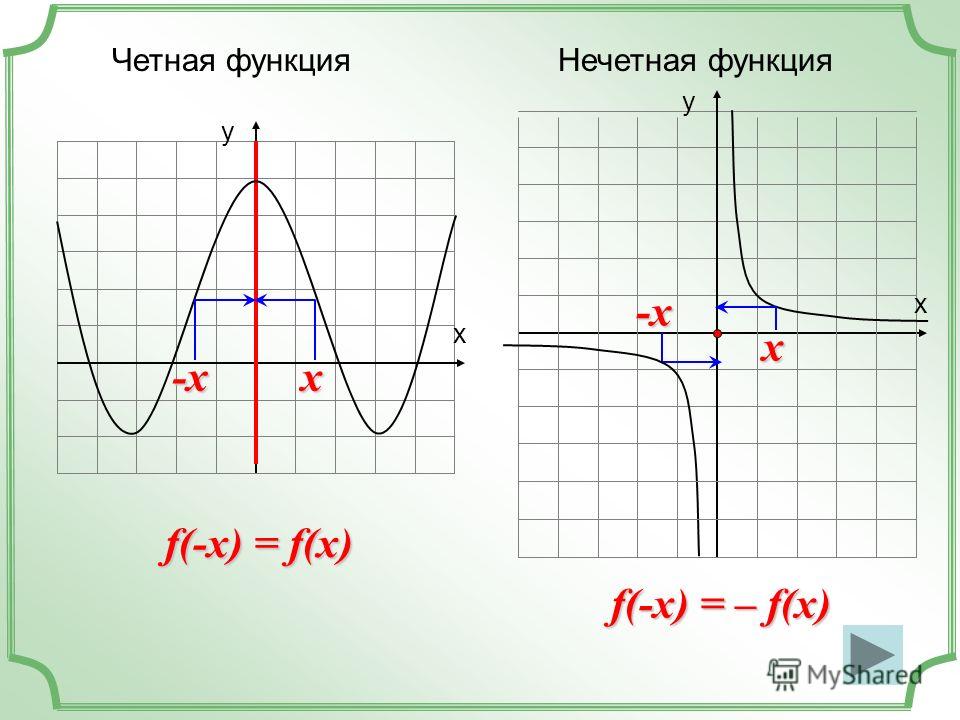
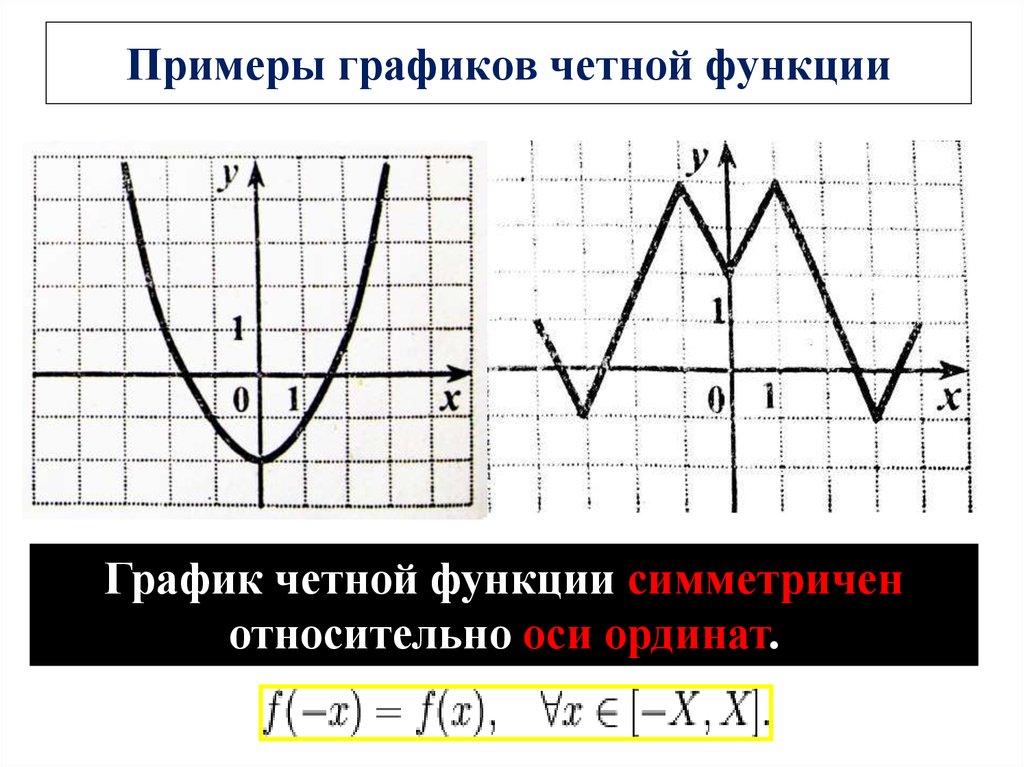
Четные функции симметричны относительно оси ординат.

Квадратичная парабола, заданная уравнением , является четной функции. В доказательство этого утверждения приведем график параболы.

Из рисунка видно, что график симметричен относительно оси Y. Проверим функцию на соответствие условию четности. В уравнении параболы  заменим x на . Получим , значит, функция четна.

К четным относится также функция модуля y=|x|.

В тригонометрии четной является функция косинуса, так как косинус обладает свойством cos(-α)=cos(α).

Сформулируем необходимые условия четности функции:

• область определения должна быть симметрична относительно оси ординат;
• должно выполняться равенство.

Условие о симметричности области определения подразумевает полную симметрию. Если на области допустимых значений имеются исключенные точки или промежутки, они также должны быть симметричны относительно оси Y.

Нечетная функция

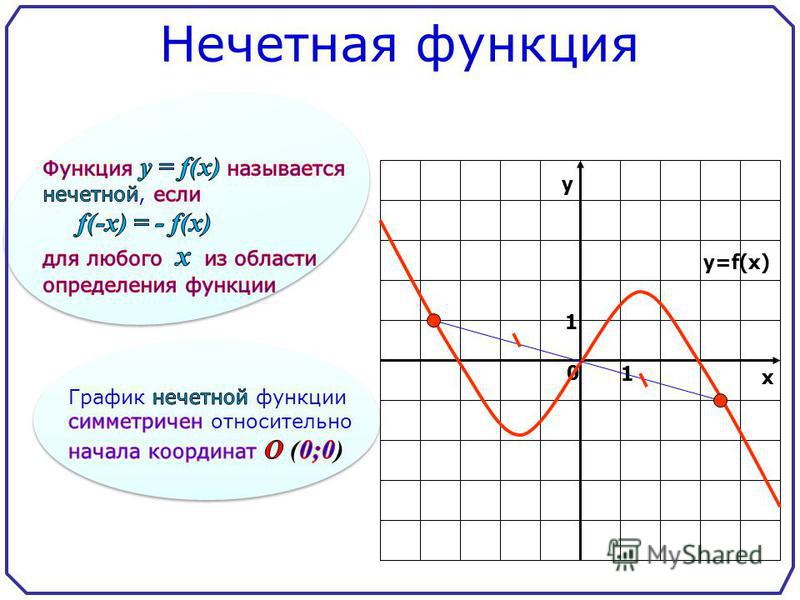
Определение 3

Функцию считают нечетной, если выполняется следующее условие:  для , где X — область допустимых значений.

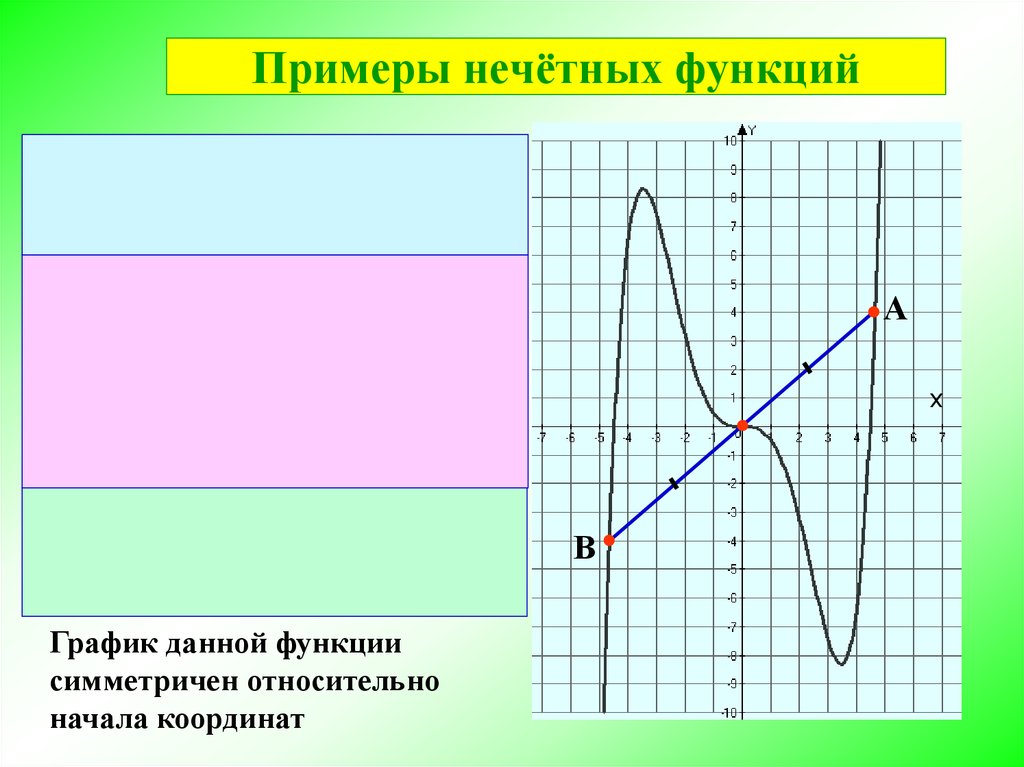
Нечетные функции симметричны относительно начала координат.

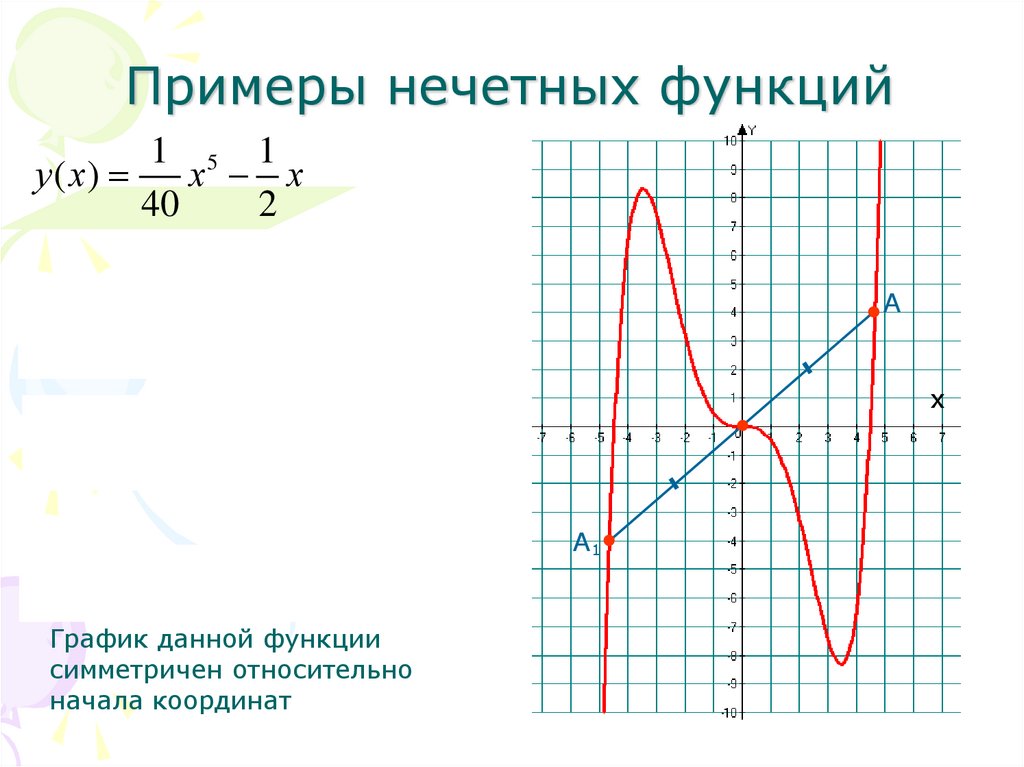
Примером нечетной функции можно назвать кубическую параболу вида .

Выясним, соблюдается ли условие нечетности, для чего подставим в формулу параболы значение . Получили, что .

Из тригонометрических функций к нечетным относится функция синуса, так как для синуса справедливо тождество 

Необходимые условия нечетности функции:

• область определения симметрична относительно начала координат;
• для всех х из области допустимых значений выполняется равенство .

Замечание относительно симметричности аналогично замечанию о четных функциях.

Свойства четных и нечетных функций

Четные и нечетные функции обладают следующими свойствами:

1. Результатом сложения или вычитания четных функций является четная функция, нечетных — нечетная функция.
2. При взятии производной результат будет противоположным. В случае четной функции производная будет нечетной, и наоборот.
3. Умножение четных функций дает четную функцию, как и умножение нечетных функций.
4. Произведение четной и нечетной функций есть нечетная функция.

Примеры на исследование функции

Прежде чем приступить к рассмотрению примеров, перечислим два способа определения четности:

• графический;
• аналитический.

При использовании графического способа строят график функции. По графику узнают о симметричности области определения, после чего делают вывод о четности функции.

В аналитическом способе в уравнении функции делают замену x на (–x). Выражение функции упрощают и проверяют соблюдения условия f(-x)=f(x) или f(-x)=-f(x).

В основном, при решении задач комбинируют два перечисленных способа.

Пример 1

Графически определить, является ли функция  четной или нечетной.

Решение

Построим график заданной функции.

Из рисунка видно, что график симметричен относительно оси ординат, значит, функция четна.

Ответ: функция четна.

Пример 2

Без построения определить, четна или нет функция .

Решение

В выражении функции имеется дробь. Нахождение точек, не входящих в область определения, сводится к решению уравнения x+4=0. Получим D(f)=(-∞; -4)∪(-4; +∞). Функция имеет одну точку разрыва, то есть область определения не симметрична относительно оси ординат. Функция не может быть четной.

Проверим четность еще раз, сделав замену x на (-x).

Получили, что y(-x)≠y(x) и y(-x)≠-y(x).

Ответ: функция общего вида.

Пример 3

Без построения графика выяснить, является функция  четной.

Решение

Область определения имеет одну точку разрыва x=0, так как в этом случае знаменатель обращается в ноль. Указанная точка совпадает с началом координат. Сделаем замену x на (-x).

Получили, что y(-x)=-y(x).

Ответ: функция нечетная.

Четные и нечетные функции | это… Что такое Четные и нечетные функции?

Толкование

Четные и нечетные функции

f(x) = x — пример нечётной функции.

f(x) = x² — пример чётной функции.

f(x) = x³, нечётная

f(x) = x³ + 1 ни чётная, ни нечётная

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Или по-другому

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Содержание 1 Определения 2 Свойства 3 Примеры 3.1 Нечётные функции 3.2 Чётные функции 4 Вариации и обобщения

Определения

• Функция называется нечётной, если справедливо равенство

• Функция f называется чётной, если справедливо равенство

• Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.

Свойства

• График нечётной функции симметричен относительно начала координат O.
• График чётной функции симметричен относительно оси ординат Oy.
• Произвольная функция может быть представлена в виде суммы нечётной и чётной функций:

f(x) = g(x) + h(x),

где

• Функция  — единственная функция, одновременно являющаяся нечётной и чётной.
• Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
• Произведение или дробь двух нечётных функций чётно.
• Произведение или дробь двух чётных функций чётно.
• Произведение или дробь нечётной и чётной функций нечётно.
• Композиция двух нечётных функция нечётна.
• Композиция двух чётных функций чётна.
• Композиция чётной функции с нечётной чётна.
• Композиция любой функции с чётной чётна (но не наоборот).
• Функция, обратная чётной, чётна, а нечётной — нечётна.
• Производная чётной функции нечётна, а нечётной — чётна.
  • То же верно про производную третьего, пятого и вообще любого нечётного порядка.
• Производная чётного порядка сохраняет чётность.

Примеры

Нечётные функции

• Нечётная степень где  — произвольное целое число.
• Синус .
• Тангенс .

Чётные функции

• Чётная степень где  — произвольное целое число.
• Косинус .

Вариации и обобщения

• Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.

Wikimedia Foundation. 2010.

Игры ⚽ Нужно сделать НИР?

• Четность функции
• Четные и нечетные числа

Полезное

Четная функция — определение, свойства, график, примеры

LearnPracticeDownload

Функция является четной, если f от x равно f от −x для всех значений x. Это означает, что функция одинакова для положительной оси x и отрицательной оси x или графически симметрична относительно оси y. Примером четной функции являются тригонометрическая четная функция, секущая функция и т. д. Давайте подробно рассмотрим четную функцию, а также ее графическое представление и свойства.

1.	Что такое четная функция?
2.	Графическое представление четной функции
3.	Свойства четной функции
4.	Часто задаваемые вопросы о функции Even

Что такое четная функция?

Давайте сначала поймем значение четных функций алгебраически. Функция четная, если f(x) = f(-x) для всех значений x. Теперь давайте посмотрим, что это значит. Для четной функции f(x), если мы подставим -x вместо x, то значение f(-x) будет равно значению f(x). Точно так же такие функции, как \(x^4, x^6, x^8, x^{10}\) и т. д., являются четными функциями.

Интересно, что указанные выше функции имеют равные силы. Обратите внимание на график ниже y = x ² , график четной функции.

Пример четной функции

Рассмотрим тригонометрическую функцию (f(x) = cos x. Определите значение f(-x) и определите, является ли она четной функцией или нет.

Решение: f(-x) = cos (-x) = cos x = f(x)

cos (-x) = cos x для всех значений x

Следовательно, f(x) = cos x равно четная функция

Графическое представление четной функции

Теперь посмотрим, как графически ведет себя четная функция. Приведенный выше график четной функции симметричен относительно оси y. Другими словами, график четной функции остается прежним после отражения относительно оси у.

Вот несколько примеров четных функций, соблюдайте симметрию относительно оси Y.

Посмотрим график для f(x) = cos x

Свойства четной функции

Поняв значение четной функции, мы собираемся исследовать ее свойства. Несколько основных свойств четной функции перечислены ниже.

• Сумма двух четных функций четна.
• Разница между двумя четными функциями четна.
• Произведение двух четных функций четно.
• Частное от деления двух четных функций четно.
• Состав двух четных функций четный.
• Композиция четной и нечетной функций четна.

☛Статьи о четной функции

Ниже приведен список тем, тесно связанных с четной функцией. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.

• Экспоненциальная функция
• Полиномиальные функции
• Квадратичные функции
• Линейные функции
• Постоянные функции

 

Примеры четных функций

1. Пример 1: Сэм хочет алгебраически определить, является ли функция f(x) = 4x ⁴ − 7x ² четной функцией или нет.

   Решение: Подставьте -x вместо x в f(x) = 4x ⁴ — 7x ² .

   f(−x) = 4(−x) ⁴ −7(−x) ²
   = 4x ​​ ⁴ − 7x ²
   = f(x)

   Поскольку f(−x) = f(x), функция f(x) является четной функцией.

2. Пример 2. Рассмотрим функцию f(x) = x ² . Определите значение f(−x). Определите, является ли это четной функцией или нет.

   Решение: f(−x) = (−x) ² = x ² = f(x)

   Следовательно, f(x) = x ² — четная функция.

   Мы можем проверить, взяв определенное значение x.

   Для x = 2 значение f(x) определяется по формуле:

   f(2) = 2 ² = 4

   Значение f(−x) определяется по формуле:

   f(− 2) = (−2) ² = 4 = f(2)

3. Пример 3: Определите, является ли функция f(x) = 6x ⁴ − x ¹² четной или нет.

   Решение: Подставьте −x вместо x в f(x) = 6x ⁴ − x ¹² .

   f(−x) = 6(−x) ⁴ − (−x) ¹²
   = 6x ⁴ − x ¹²
   = f(x)
   Поскольку f(−x) = f(x), функция f(x) является четной функцией.
   f(x) = 6x ⁴ − x ¹² — четная функция.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по четной функции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о функции Even

Что такое четные функции в исчислении?

Четные функции — это те функции в исчислении, которые одинаковы для +ve оси x и -ve оси x или графически симметричны относительно оси y. Он представлен как f (x) = f (-x) для всех x. Несколько примеров четных функций: x ⁴ , cos x, y = x ² и т. д.

Что такое уравнение четной функции?

Уравнение четной функции, математически выраженное как f(-x) = f(x) для всех x.

Как определить, является ли функция четной функцией или нет?

Если функция удовлетворяет условию f(−x) = f(x) для всех x, она называется четной функцией. Это означает, что он одинаков для +ve оси x и -ve оси x или графически симметричен относительно оси y.

• Если значение f(−x) совпадает со значением f(x) для каждого значения x, функция четная.
• Если значение f(−x) НЕ совпадает со значением f(x) для любого значения x, функция не является четной.
• Если функция имеет четную степень, функция не обязательно должна быть четной.

Является ли Cos x четной функцией?

Уравнение четной функции, математически выраженное как f(−x) = f(x) для всех x. При подстановке значения имеем cos(−x) = cosx.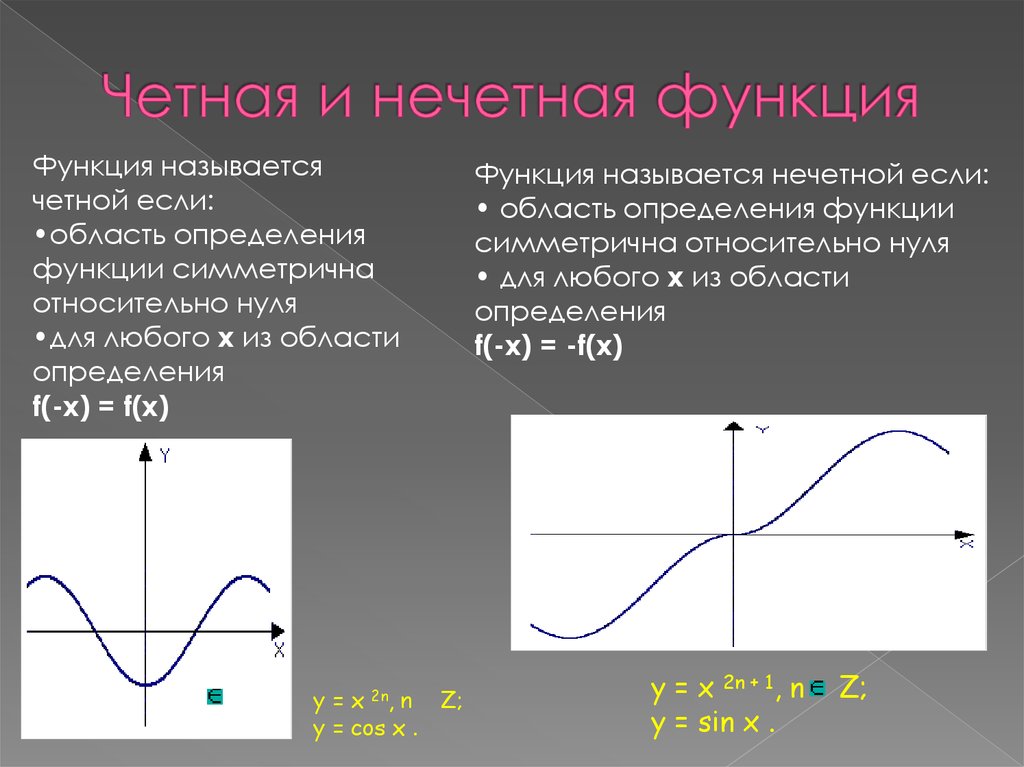 Следовательно, cos⁡ x — четная функция.

Как определить, имеет ли построенный график четную функцию?

Существуют определенные правила, позволяющие определить, является ли построенный график четной функцией или нет. Правила перечислены ниже.

• Если график симметричен относительно оси Y, функция четная.
• Если график симметричен относительно начала координат, функция нечетная.
• Если график несимметричен относительно оси Y или начала координат, функция не является ни четной, ни нечетной.

Константы даже функционируют?

Постоянная функция f(x) = k является четной функцией, поскольку f(−x) = k = f(x).

Запишите два основных свойства четной функции.

Существуют различные свойства, определяющие четную функцию. Вот два основных свойства:

• Когда мы вычитаем две четные функции, получается четная разница.
• Когда мы умножаем две четные функции, получается четное произведение.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по четным функциям

Рабочие листы по математике и
наглядный учебный план

Четный функции: определение, примеры и формула

Сидя и ожидая поезда на станции Норт-Кэмп, направляющегося в Милфорд на прогулку, я задумался над несколькими тревожными вопросами.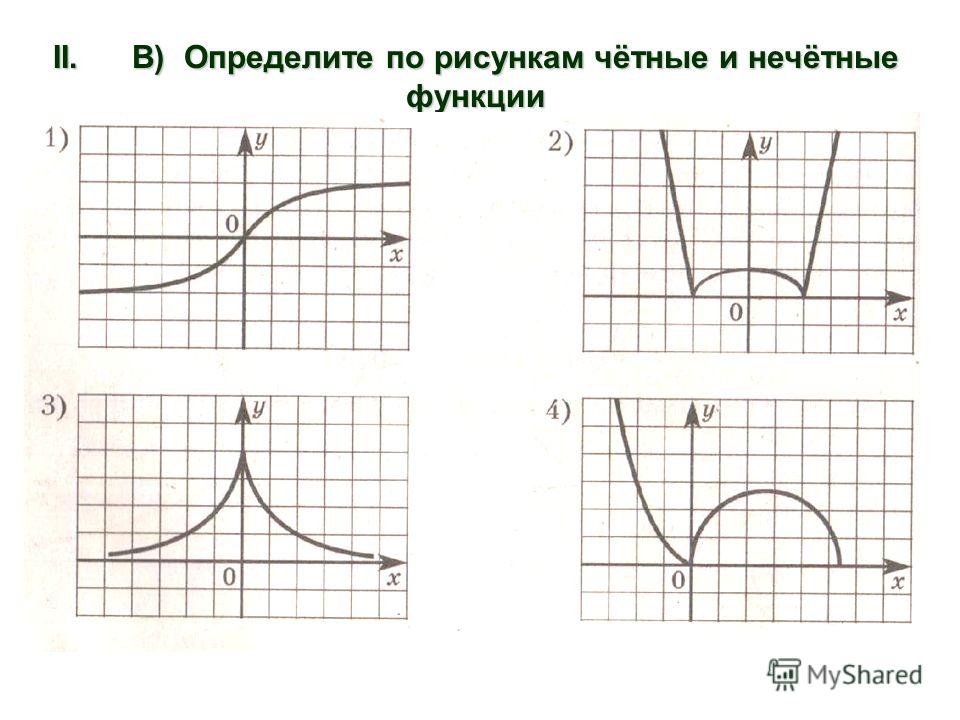

Почему произведение двух или более нечетных чисел дает нечетное число? Например, произведение 3 и 7, которые являются нечетными числами, даст 21, еще одно нечетное число. Точно так же, когда четные числа перемножаются между собой, всегда получается четное число; все еще погруженный в мысли, я опоздал на поезд. Тем не менее, мы не упустим цель этого обсуждения, далее мы узнаем о работает даже с .

Что такое четные функции?

Четные функции — это такие функции, как f(x), которые имеют те же значения при замене отрицательных независимых переменных, таких как f(-x). Следовательно, их лучше всего выражать как:

f(x)→f(-x)=f(x)

В соответствии с этой концепцией функции обычно классифицируются как четные, нечетные или никакие.

Подтвердите, что f(x) четно, когда

f(x)=x4-8

Решение:

Поскольку

f(x)=x4-8

Чтобы определить природу этой функции, мы находим f(-x), подставляя -x.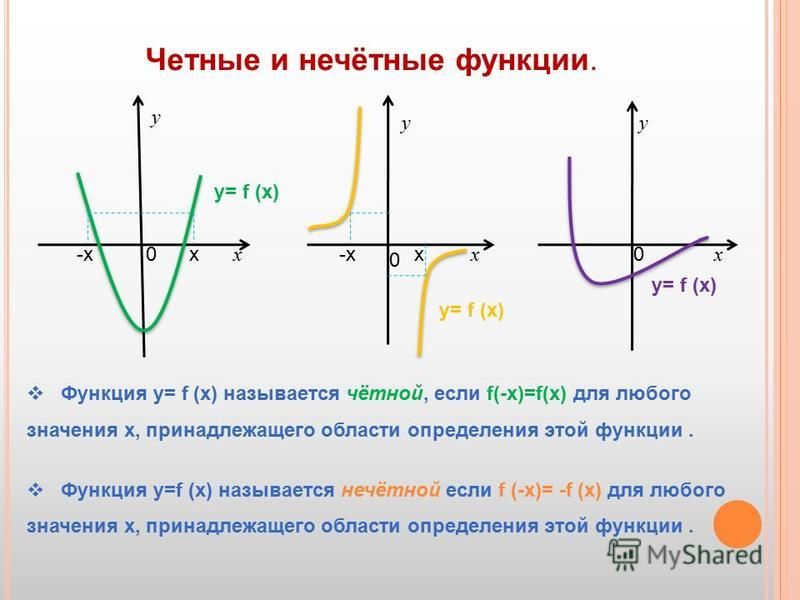

Следовательно,

f(-x)=(-x)4-8f(-x)=x4-8

Следовательно,

f(x)=f(-x)

Это доказывает, что f(x) является четной функцией для выражения x4-8.

Нечетные функции

Нечетные функции — это функции, такие как f(x), которые имеют отрицательный эквивалент при замене отрицательных независимых переменных, таких как f(-x). Следовательно, они лучше всего выражены как:

f(x)→f(-x)=-f(x)

Подтвердить, что f(x) нечетно, когда

f(x)=x3+x

Решение:

Начиная с

f(x)=x3+x

Чтобы определить природу этой функции, найдем f(-x), подставив -x. Отсюда

f(-x)=(-x)3+(-x)f(-x)=-x3-x

При факторизации по -1 получаем

f(-x)=-1(x3 +x)

Звенит ли сейчас звонок?😁

Следовательно,

f(x)→f(-x)=-f(x)

выражение х3+х.

Ни одна из функций

Ни одна из функций не является функцией, подобной f(x), которая не имеет эквивалентных значений при замене отрицательных независимых переменных, таких как f(-x). Это говорит о том, что они не являются ни четными, ни нечетными функциями. Следовательно, их лучше всего выразить как:

f(x)→f(-x)≠f(x)

и

f(x)→f(-x)≠-f(x)

Подтвердите, что f (x) четно, когда

f(x)=x4+x-1

Решение:

Так как

f(x)=x4+x-1

Чтобы определить природу этой функции, мы находим f(-x), подставляя -x. Следовательно,

f(-x)=(-x)4+(-x)-1f(-x)=x4-x-1

Выражение x4-x-1 не эквивалентно x4+x-1 , следовательно, это не четная функция. 1), следовательно, это не нечетная функция

Следовательно,

f(x)→f(-x)≠f(x)

и

f(x)→f(-x)≠-f (х)

Это доказывает, что f(x) не является функцией выражения x4+x-1.

Четные функции в тригонометрических тождествах

Можно определить характер функции (т.е. четная, нечетная или никакая) среди тригонометрических тождеств. Мы будем использовать диаграммы ниже, чтобы объяснить это.

Рисунок 1, изображение, используемое для доказательства природы функций среди тригонометрических тождеств, когда θ положительное, StudySmarter Originals

Рисунок 2, изображение, используемое для доказательства природы функций среди тригонометрических тождеств, когда θ отрицательное, StudySmarter Originals

Из первой диаграммы мы можем использовать SOHCATOA для определения cosθ.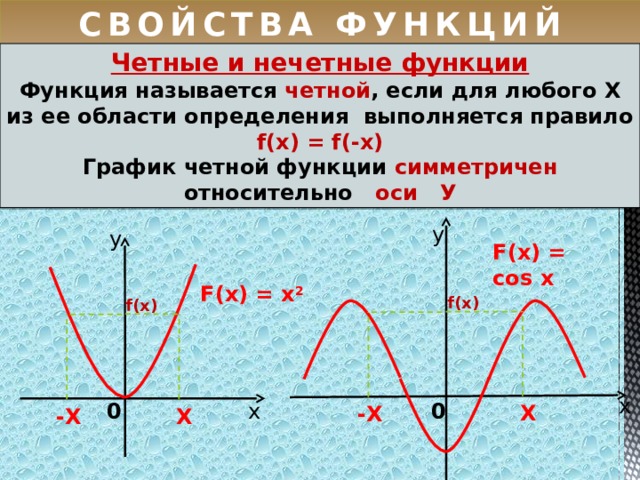 Если мы это сделаем, то обнаружим, что

cosθ=ba2+b2

Но что происходит, когда θ отрицательно? Из второй диаграммы мы замечаем, что хотя противолежащая сторона (а) изменилась (на -а) из-за поворота угла в противоположном направлении, примыкающая сторона (б) остается неизменной. В этом случае

cos(-θ)=b(-a)2+b2cos(-θ)=ba2+b2

Следовательно,

cosθ=cos(-θ)

Насколько это относится к четным функциям ? Теперь, если мы выразим косинус как функцию x, так что у нас будет cos(x) вместо cos(θ). Тогда, если

f(x)=cosx

и

f(-x)=cos-xf-x=cosx

Следовательно,

f(x)=f(-x)

В данном случае это предполагает что cos(x) — четная функция.

Функции косинуса без добавления к другим функциям равны функциям .

Как насчет функций синуса?

Если обратиться к рис. 1, то можно сделать вывод, что

sinθ=aa2+b2

Однако, когда вращение на декартовой плоскости идет в противоположном направлении на угол -θ (как показано на рис.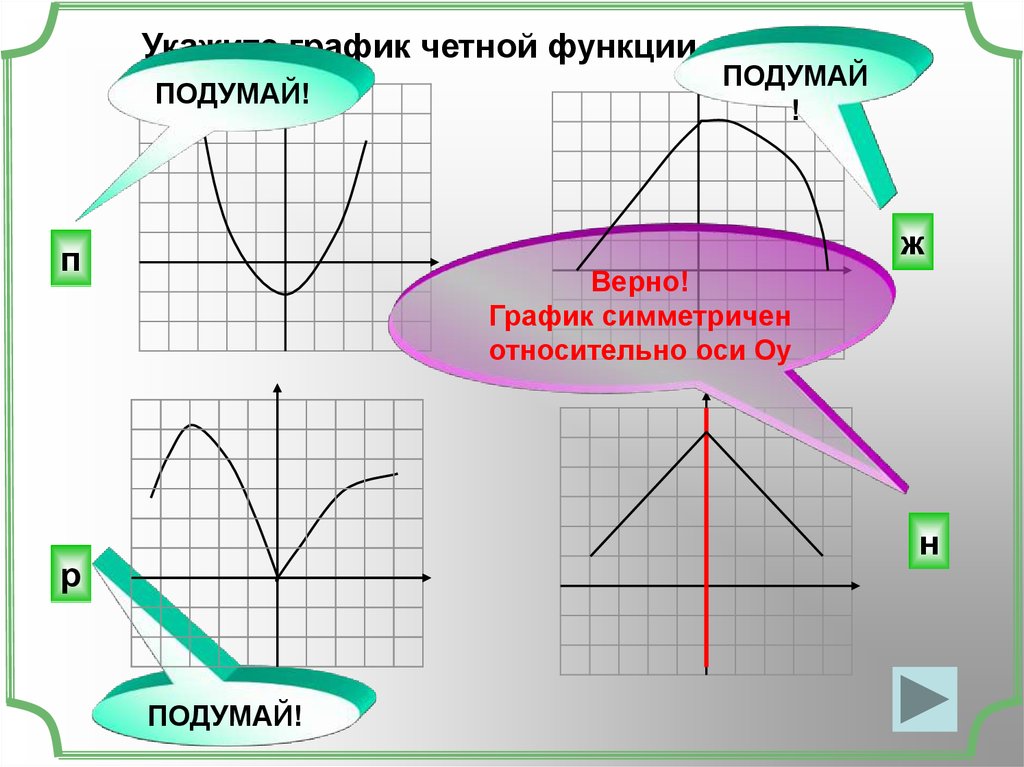

2), мы обратите внимание, что противоположная сторона «а» на рисунке 1 меняется на «-а» на рисунке 2, потому что а расположена на отрицательной оси y. Это означает, что

sin-θ=-aa2+b2

Если разложить на -1, получится

sin-θ=-1(aa2+b2)

Напомним, что

sinθ=aa2+b2

9000 2 Отсюда ,

sin-θ=-sinθ

Но насколько полезна эта деталь? Если мы выразим синус как функцию x, а не θ, чтобы мы знали, как sin(x) так же, как и sin(-x), тогда, когда

f(x)=sinx

и

f(- x)=sin(-x)f(-x)=-sin(x)

с факторизацией на -1 в правой части уравнения, мы получили бы

f(-x)=-1(sin(x))

Напомним, что

f(x)=sin(x)

Это, безусловно, означает

f(-x)=-f(x)

Это приводит к представлению, что для функции синуса

f(x)≠f(-x)

но

f(-x)=-f(x)

и, как следствие, мы можем ergo заключить, что синусоидальные функции не четные функции , а нечетные функции .

Синусоидальные функции без добавления каких-либо других функций нечетные функции .

Почему бы не поиграть с этими двумя диаграммами, чтобы определить, являются ли касательные функции четными, нечетными или ни одной из них?

Если бы вы попытались определить, какие функции являются касательными, вы бы заметили, что, поскольку

tanθ=ab

Из диаграмм мы также знаем, что

tan(-θ)=-ab

Отсюда следует, что

tan(-θ)=-tan(θ)

Следовательно, касательные функции являются нечетными функциями.

Вы были правы?

Какова формула четных функций?

Чтобы мы могли определить формулу четных функций, показатель степени независимой переменной x всегда четен с константой или без нее. Таким образом, для x ⁿ n является четным числом, таким как 2, 4, 6…n. Если a, b и c — константы, такие как 1, 2, 3… и n — четное число, то четная функция выражается как

f(x)=axn+bxn±2+c

или

f(x)=axn+bxn±2

Для нечетных функций показатель степени независимой переменной x всегда нечетен, и константа не должна присутствовать.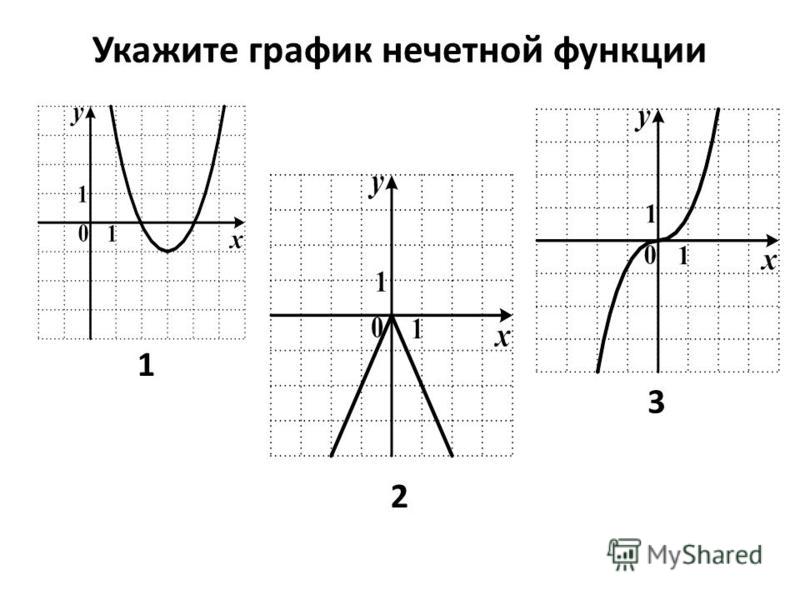 Таким образом, для x ⁿ , n — нечетное число, например 1, 3, 5…n. Если a и b — константы, такие как 1, 2, 3… и n — нечетное число, то нечетная функция выражается как

f(x)=axn+bxn±2

Ни для одной из функций показатель степени независимой переменной x может быть как четным, так и нечетным с наличием константы или без нее. Таким образом, для x ⁿ n является нечетным и/или четным числом, таким как 1, 2, 3, 4, 5…n. Если a, b и c являются константами, такими как 1, 2, 3… и n, как четными, так и нечетными числами, то ни одна из функций не выражается как

f(x)=axn+bxn±1+c

или

f(x)=axn+bxn±1

или в случае, если все показатели степени значения независимой переменной x нечетны с константой . Ни одна из функций не выражается как

f(x)=axn+bxn±2+c

, где n — нечетное число.

Графики четной функции

График четной функции симметричен относительно вертикальной оси (оси Y).

Когда график симметричен оси, при вращении вокруг точки или при отражении от линии график остается прежним, хотя точка на этой оси остается той же, а точка на другой оси будет иметь противоположный знак потому что они являются отражением, как зеркальное отражение.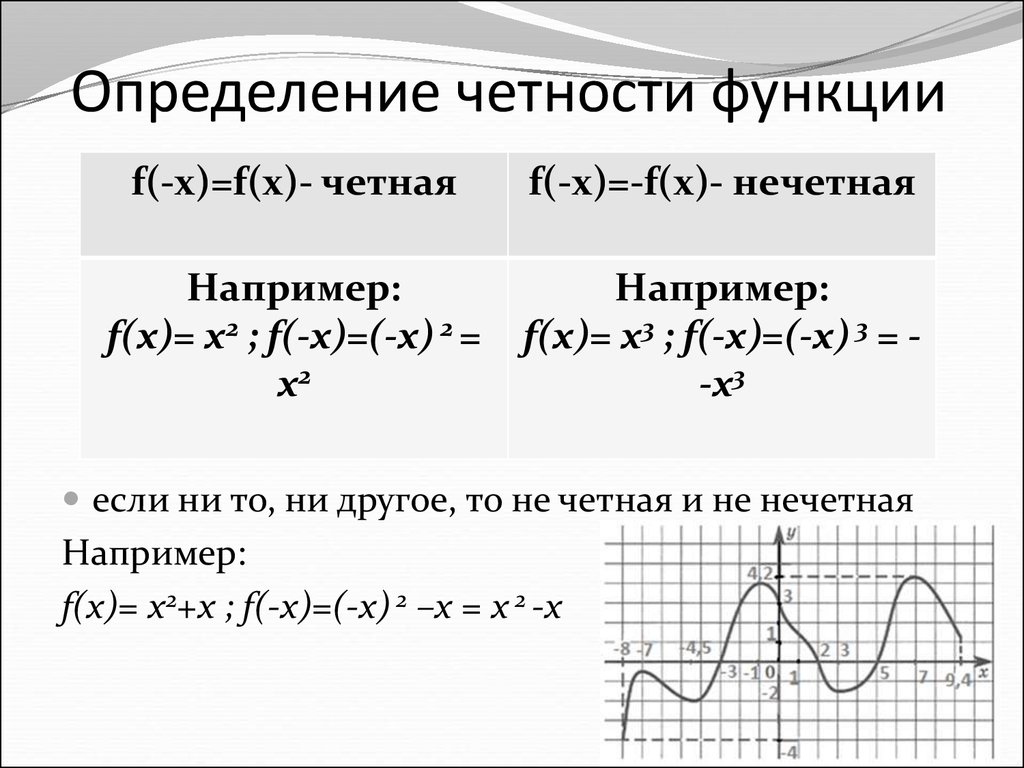

Таким образом, когда график симметричен вертикальной оси, заданные точки (p, q) на этом графике будут иметь точки (-p, q) на этом графике. Обратите внимание, что значение y (точка q на вертикальной оси) не изменилось, в то время как значение x в первой точке (p) имеет противоположное значение для второй точки (-p).

Например, четная функция

f(x)=x4-2

показана ниже

График четной функции f(x)=x ⁴ -2, StudySmarter Originals мы видим, что две точки (-1, -1) и (1, -1) графика доказывают симметрию к оси y для четной функции x4-2.

В чем разница между четными и нечетными функциями?

Четные и нечетные функции различаются двумя основными способами; в их графиках и общем выражении.

Разница в графике

Мы только что обсуждали, что график четных функций симметричен относительно вертикальной оси (оси Y).

Ты только что забыл об этом?

Но для нечетной функции ее график симметричен относительно начала координат.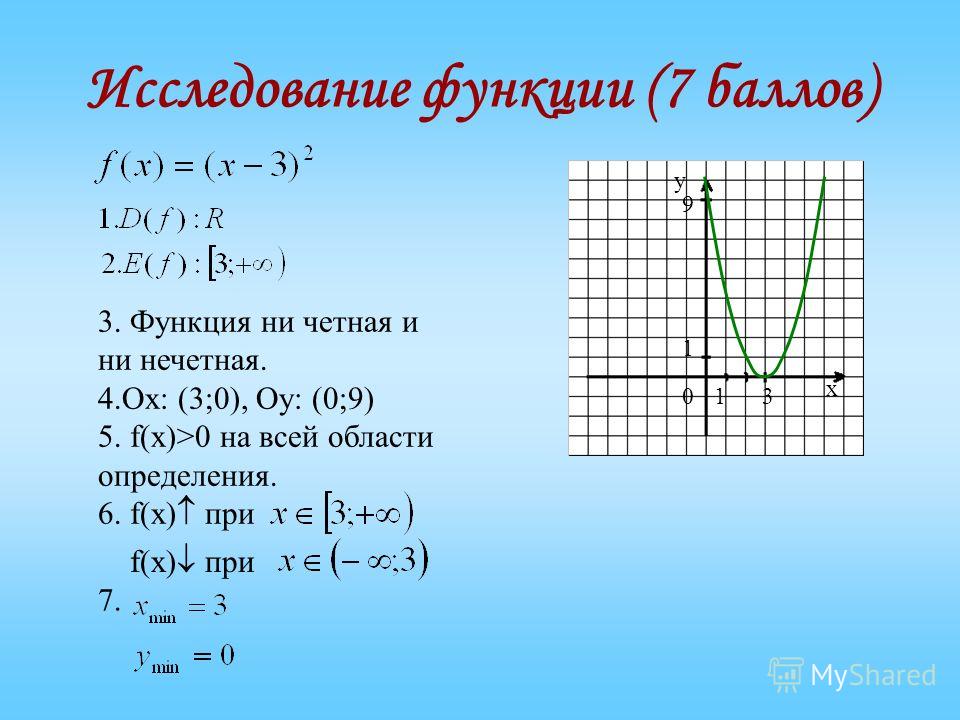 Это означает, что если кривую повернуть на 180° в начале координат (0, 0), график останется прежним.

Этого поворота можно добиться, выбрав точки (b, 0) и (0, b) на графике, если вы перетащите точку (b, 0) горизонтально в точку (-b, 0) и перетащите точку (0, b ) по вертикали до точки (0, -b) вы подтвердите, что график точно такой же. Разве это не удивительно?

Обратите внимание, как упоминалось ранее, на графиках четной функции, если вы выберете данную точку (p, q) на графике, у вас обязательно будет другая точка на противоположной горизонтальной стороне кривой, которая будет (-p, q ).

Пожалуйста, обратитесь к графику x ⁴ -2 в качестве примера.

Между тем, в нечетных функциях, если вы выберете точку (p, q), у вас будет точка (-p, -q) на противоположных вертикальной и горизонтальной осях. Например, график нечетной функции

f(x)=x3

отмечает точки (2, 8) вверх справа, а также другую точку (-2, -8), которая находится внизу слева.

График нечетной функции, f(x)=x ³ , StudySmarter Originals

Общее выражение

Четные функции также отличаются от нечетных по своему общему выражению. Даже функции выражаются в соответствии с правилом.

f(x)=f(-x)

Однако нечетные функции не подчиняются этому правилу, поскольку в их случае

f(x)≠f(-x)

к правилу

f(-x)=-f(x)

Примеры четных функций

Чтобы лучше понять четные функции, рекомендуется попрактиковаться в некоторых задачах.

Для функции

h(x)=6×6-4×4+2×2-1

Определить, является ли функция четной. Постройте график и выберите любые две точки, чтобы доказать, что это четная функция.

Решение:

Первая задача — определить, является ли функция четной. Если вы примените формулу четной функции, описанную ранее, посмотрев на выражение 6×6-4×4+2×2-1, мы можем сделать вывод, что это четная функция, поскольку все показатели степени x, т. е. 6, 4 и 2, являются четными числами. Тем не менее, для дальнейшего подтверждения мы просто применим правило:

f(x)=f(-x)

Подставляя -x в выражение, получаем

f(-x)=6(-x)6-4(-x)4+2(x2) -1f(-x)=6×6-4×4+2×2-1

Таким образом,

f(x)=f(-x)

Следовательно, мы можем сказать, что приведенное выше выражение действительно является четной функцией.

Следующая задача — построить график и, используя две точки, дополнительно доказать, что это выражение действительно является четной функцией.

Использование точек на графике для доказательства четных функций, StudySmarter Originals

Из приведенного выше графика выражения мы выбрали две точки (-1, 3) и (1, 3). Это еще раз доказывает, что выражение 6×6-4×4+2×2-1 является четной функцией, поскольку пара (-1, 3) и (1, 3) соответствует (p, q) и (-p, q).

Если

f(x)=3×2

и

g(x)=x4

Определите класс суммы обеих функций.

Решение:

f(x)+g(x)=3×2+x4

Теперь определим вид суммы.