Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х.
Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
общая сумма квадратов отклонений (TSS)
сумма квадратов отклонений, обусловленная регрессией (RSS)
остаточная сумма квадратов отклонений (ESS)
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Функция FРАСПОБР — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще.
Возвращает значение, обратное (правостороннему) F-распределению вероятностей. Если p = FРАСП(x;…), то FРАСПОБР(p;…) = x.
F-распределение может использоваться в F-тесте, который сравнивает степени разброса двух множеств данных. Например, можно проанализировать распределение доходов в США и Канаде, чтобы определить, похожи ли эти две страны по степени плотности доходов.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Чтобы узнать больше о новых функциях, см. статьи Функция F.ОБР и Функция F.ОБР.ПХ.
Синтаксис
FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)
Аргументы функции FРАСПОБР описаны ниже.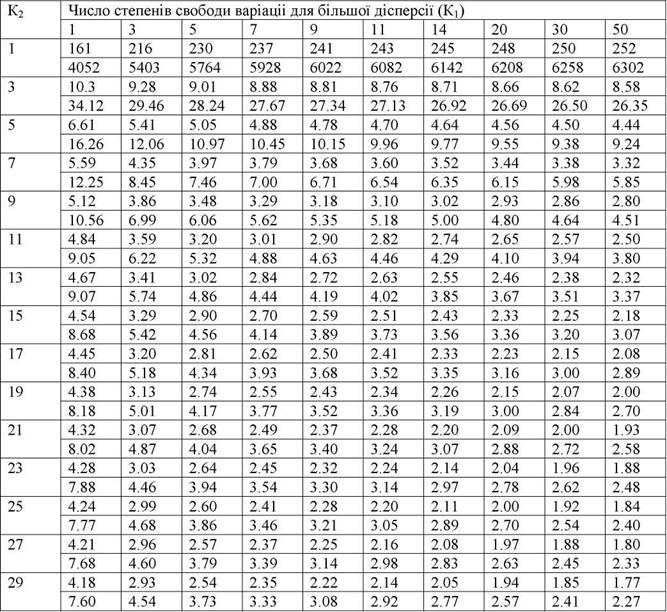
-
Вероятность — обязательный аргумент. Вероятность, связанная с интегральным F-распределением.
-
Степени_свободы1 — обязательный аргумент. Числитель степеней свободы.
Степени_свободы2 — обязательный аргумент. Знаменатель степеней свободы.
Замечания
-
Если какой-либо из аргументов не является числом, то finV возвращает #VALUE! значение ошибки #ЗНАЧ!.
10, то #NUM! значение ошибки #ЗНАЧ!.
10, то #NUM! значение ошибки #ЗНАЧ!.Функцию FРАСПОБР можно использовать для определения критических значений F-распределения. Например, результаты дисперсионного анализа обычно включают данные для F-статистики, F-вероятности и критическое значение F-распределения с уровнем значимости 0,05. Чтобы определить критическое значение F, нужно использовать уровень значимости как аргумент «вероятность» функции FРАСПОБР.
По заданному значению вероятности функция FРАСПОБР ищет значение x, для которого FРАСП(x;степени_свободы1;степени_свободы2) = вероятность. Таким образом, точность функции FРАСПОБР зависит от точности FРАСП. Для поиска функция FРАСПОБР использует метод итераций. Если поиск не закончился после 100 итераций, возвращается значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel.
Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
0,01 |
Вероятность, связанная с интегральным F-распределением |
|
|
6 |
Числитель степеней свободы |
|
|
4 |
Знаменатель степеней свободы |
|
|
Формула |
Описание |
Результат |
|
=FРАСПОБР(A2;A3;A4) |
Значение, обратное F-распределению вероятностей для приведенных выше данных |
15,206865 |
F | Вкладка ДАННЫЕ
Распределение F приходит, например.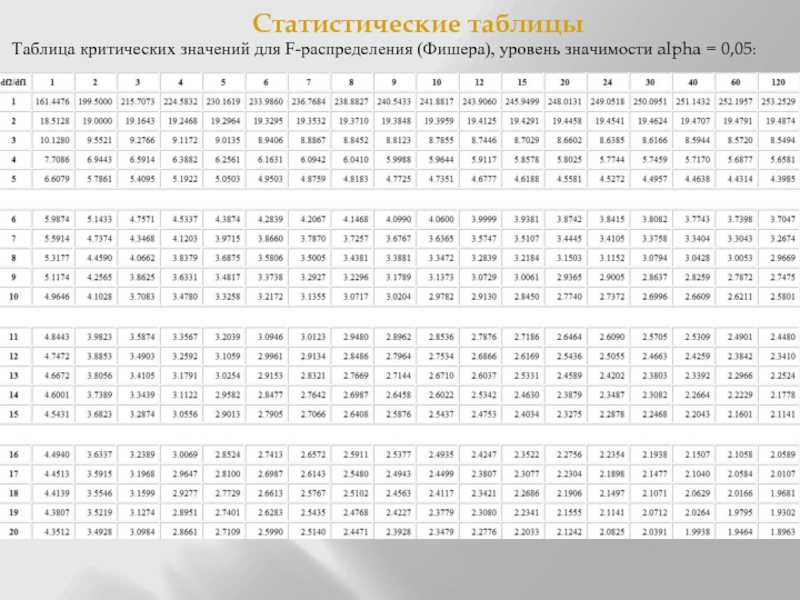
Здесь вы можете рассчитать критическое F-значение или p-значение с заданным степеней свободы, или вы можете прочитать критическое F-значение для данной альфы уровень в таблицах ниже.
F критический
альфа
д.ф. числитель
df знаменатель
p-значение
F-значение
д.ф. числитель
df знаменатель
Таблица распределения F 0,95 (a=0,05)
В следующей таблице показана обратная функция распределения
F-распределение для (1-а) = 0,95.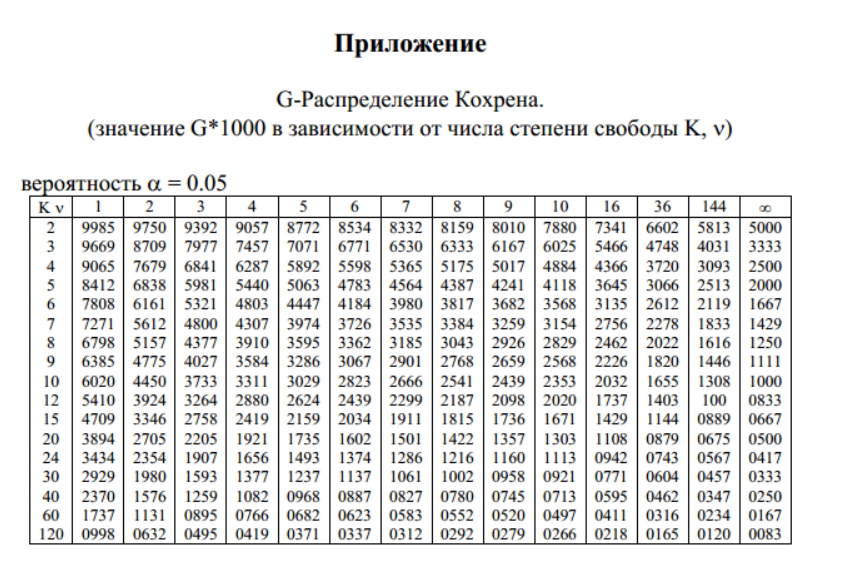
| df2\df1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 199,5 | 215,707 | 224,583 | 230,162 | 233,986 | 900 85 236,768238,883 | 240,543 | 241,882 | 242,983 | 243,906 | 244,69 900 86 | 245,364 | 245,95 | ||
| 2 | 18,513 | 19 | 19,164 | 19,247 | 19,296 | 19,33 | 19,353 | 19. 371 | 19.385 | 19.396 | 19.405 | 19.413 | 19.419 | 90 085 19.42419.429 | |
| 3 | 10,128 | 9,552 | 9,277 | 9,117 | 9,013 | 8,941 | 8,887 | 8,845 | 8,812 | 8,786 | 8,763 | 8,745 | 8,729 | 8,7 15 | 8.703 |
| 4 | 6,944 | 6,591 | 6,388 | 6,256 | 6,163 | 6,094 9 0086 | 6,041 | 5,999 | 5,964 | 5,936 | 5,912 | 5,891 | 5,873 | 5,858 | |
| 5 | 6,608 | 5,786 | 5,409 | 5,192 | 5,05 | 4,95 | 4,876 900 86 | 4,818 | 4,772 | 4,735 | 4,704 | 4,678 | 4,655 | 4,636 | 4,619 |
| 6 | 5,987 | 5,143 | 4,757 | 4,534 | 4,387 | 4,284 | 4,207 | 4,147 | 4.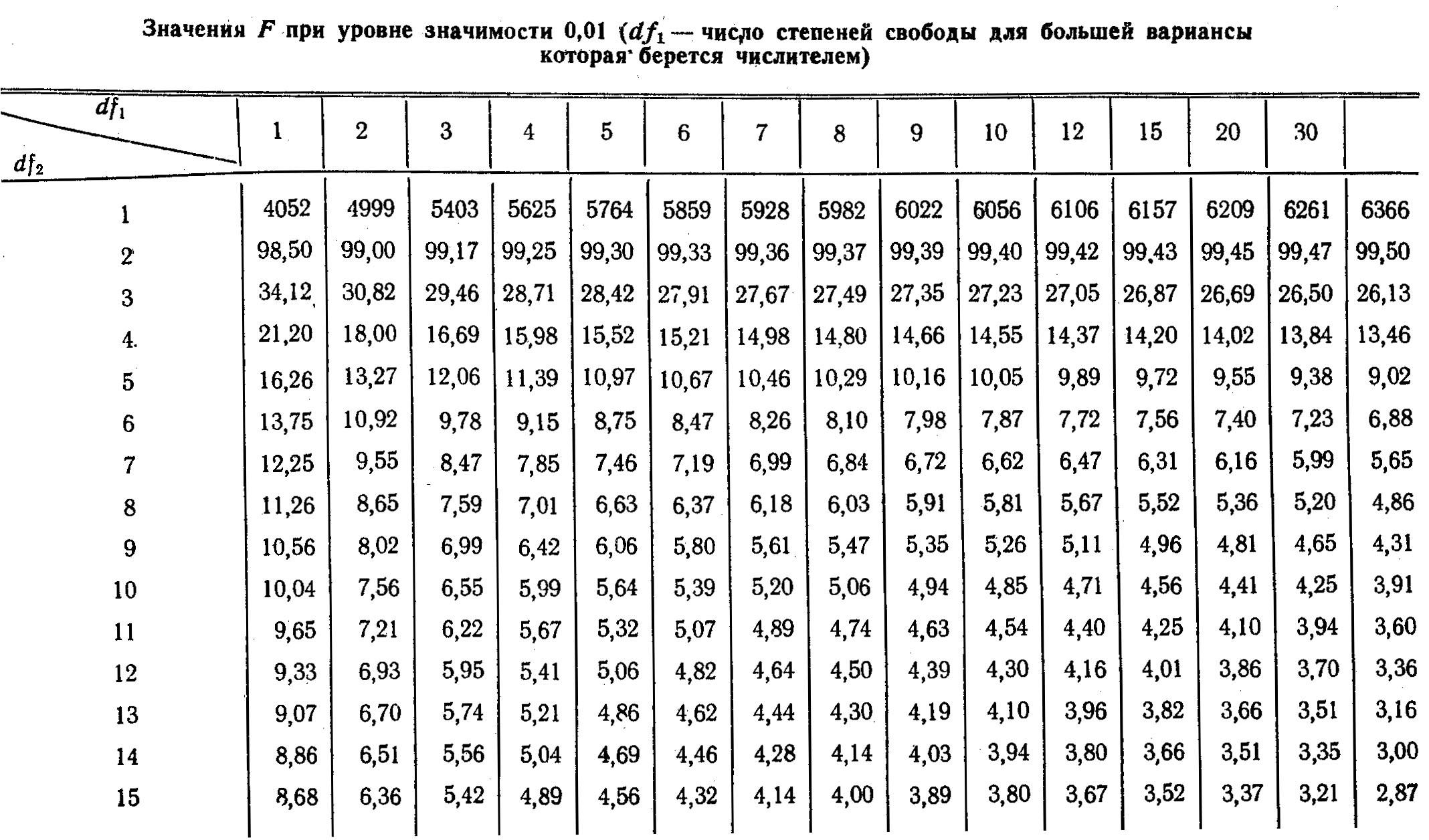 099 | 4.06 | 4.027 | 4 | 3.976 | 3.956 | 3.938 |
| 7 | 5,591 | 4,737 | 4,347 | 4,12 | 3,972 | 3,866 | 3,787 90 086 | 3,726 | 3,677 | 3,637 | 3,603 | 3,575 | 3,55 | 3,529 | 3,511 |
| 8 | 5,318 | 4,459 | 4,066 | 3,838 | 3,687 | 3,581 | 3,5 900 86 | 3,438 | 3,388 | 3,347 | 3,313 | 3,284 | 3,259 | 3,237 | 3,218 |
| 9 | 5,117 | 4,256 | 3,863 | 3,633 | 3,482 | 3,374 | 3,293 | 3,23 | 3,179 | 3,137 | 3,102 | 3,073 | 3,0 48 | 3,025 | 3,006 |
| 10 | 4,965 | 4,103 | 3,708 | 3,478 | 3,326 | 3,217 | 3,135 9 0086 | 3,072 | 3,02 | 2,978 | 2,943 | 2,913 | 2,887 | 2,865 | 2,845 |
| 11 | 4,844 | 3,982 | 3,587 | 3,357 | 3,204 | 3,095 | 3,012 9 0086 | 2,948 | 2,896 | 2,854 | 2,818 | 2,788 | 2,761 | 2,73 9 | 2,719 |
| 12 | 4,747 | 3,885 | 3,49 | 3,259 | 3,106 | 2,996 | 2,913 90 086 | 2,849 | 2,796 | 2,753 | 2,717 | 2,687 | 2,66 | 2,637 | 2,617 |
| 13 | 4,667 | 3,806 | 3,411 | 3,179 | 3,025 | 2,915 | 2,832 9 0086 | 2,767 | 2,714 | 2,671 | 2,635 | 2,604 | 2,577 | 2,55 4 | 2,533 |
| 14 | 4,6 | 3,739 | 3,344 | 3,112 | 2,958 | 2,848 | 2,764 | 2,699 | 2. 646 | 2,602 | 2,565 | 2,534 | 2,507 | 2,484 | 2,463 |
| 15 | 4,543 | 3,682 | 3,287 | 3,056 | 2,901 | 2,79 | 2,707 90 086 | 2,641 | 2,588 | 2,544 | 2,507 | 2,475 | 2,448 | 2,424 | 2,403 |
Таблица распределения F 0,99 (a=0,01)
В этой таблице F-распределения вы найдете функцию распределения
F-распределение для (1-а) = 0,99.
На осях вы найдете степени
свобода числителя и знаменателя.
| df2\df1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 052,181 | 4 999,5 | 5 403,352 | 5 624,583 | 5 763,65 | 5 858,98 6 | 5 928,356 | 5 981,07 | 6 022,473 | 6 055,847 | 6 083,317 | 6 106,321 | 6 125,865 | 6 142 674 | 6 157 285 |
| 2 | 98,503 | 99 | 99,166 | 99,249 | 99,299 | 99,333 | 99,35 6 | 99,374 | 99,388 | 99,399 | 99,408 | 99,416 | 99,422 | 9 0085 99.99.433 | |
| 3 | 34,116 | 30,817 | 29,457 | 28,71 | 28,237 | 27.911 | 27.672 | 27.489 | 27.345 | 27.229 | 27.133 | 27 0,052 | 26,983 | 26,924 | 26,872 |
| 4 | 21,198 | 18 | 16,694 | 15,977 | 15,522 | 15,207 | 14,97 6 | 14. 799 | 14.659 | 14.546 | 14.452 | 14.374 | 14.307 | 9 0085 14.24914.198 | |
| 5 | 16,258 | 13,274 | 12,06 | 11,392 | 10,967 | 10,672 | 10 .456 | 10,289 | 10,158 | 10,051 | 9,963 | 9,888 | 9,825 | 9 0085 9,779,722 | |
| 6 | 13,745 | 10,925 | 9,78 | 9. 148 | 8,746 | 8,466 | 8,26 | 8,102 | 7,976 | 7,874 | 7,79 | 7,718 | 7,657 | 7,6 05 | 7.559 |
| 7 | 12,246 | 9,547 | 8,451 | 7,847 | 7,46 | 7,191 | 6,993 9 0086 | 6,84 | 6,719 | 6,62 | 6,538 | 6,469 | 6,41 | 6,359 9 0086 | 6. 314 |
| 8 | 11,259 | 8,649 | 7,591 | 7,006 | 6,632 | 6,371 | 6,178 9 0086 | 6,029 | 5,911 | 5,814 | 5,734 | 5,667 | 5,609 | 5,55 9 | 5.515 |
| 9 | 10,561 | 8,022 | 6,992 | 6,422 | 6,057 | 5,802 | 5,613 | 5,467 | 5,351 | 5,257 | 5,178 | 5,111 | 5,055 | 5,005 | 4,962 |
| 10 | 10,044 | 7,559 | 6,552 | 5,994 | 5,636 | 5,386 | 5,2 90 086 | 5,057 | 4,942 | 4,849 | 4,772 | 4,706 | 4,65 | 4,601 | 4,558 |
| 11 | 9,646 | 7,206 | 6,217 | 5,668 | 5,316 | 5,069 | 4,886 | 4,744 | 4,632 | 4,539 90 086 | 4. 462 | 4.397 | 4.342 | 4.293 | 4.251 |
| 12 | 9,33 | 6,927 | 5,953 | 5,412 | 5,064 | 4,821 | 4,64 900 86 | 4,499 | 4,388 | 4,296 | 4,22 | 4,155 | 4,1 | 4,052 | 4,01 |
| 13 | 9,074 | 6,701 | 5,739 | 5,205 | 4,862 | 4,62 | 4,441 90 086 | 4,302 | 4,191 | 4,1 | 4,025 | 3,96 | 3,905 | 3,857 90 086 | 3. 815 |
| 14 | 8,862 | 6.515 | 5,564 | 5,035 | 4,695 | 4,456 | 4,278 | 4,14 | 4,03 | 3,939 | 3,864 | 3,8 | 3,745 | 3,698 | 3,656 |
| 15 | 8,683 | 6,359 | 5,417 | 4,893 | 4,556 | 4,318 | 4,142 9 0086 | 4,004 | 3,895 | 3,805 | 3,73 | 3,666 | 3,612 | 3,564 | 3,522 |
428Таблица дисперсионного анализа (SS, df, MS, F) в двухфакторном дисперсионном анализе – часто задаваемые вопросы 1909
Вы можете интерпретировать результаты двухфакторного дисперсионного анализа, взглянув на значения P и особенно на множественные сравнения.
Многие ученые игнорируют таблицу ANOVA. Но если вам интересны подробности, на этой странице объясняется, как рассчитывается таблица ANOVA.
Интерпретация результатов двухфакторного дисперсионного анализа
Я ввел данные с двумя строками, тремя столбцами и тремя параллельными повторениями на ячейку. Нет пропущенных значений. Итак, всего введено 18 значений. Призматический файл.
Я проанализировал данные четырьмя способами: предполагая отсутствие повторных измерений, предполагая повторные измерения с наложенными друг на друга совпавшими значениями, предполагая повторные измерения с разбросанными по строке совпавшими значениями и повторяя измерения в обоих направлениях. Таблицы ниже имеют цветовую кодировку, чтобы объяснить эти конструкции. Каждый цвет в таблице представляет один предмет. Цвета повторяются между столами, но это ничего не значит.
Файл Powerpoint
Таблица двухфакторного дисперсионного анализа
Вот таблицы дисперсионного анализа для четырех условий.
Все эти значения сообщает Prism. Я немного переставил и переименовал, чтобы все четыре можно было отобразить в одной таблице (файл Excel).
Как представить результаты двухфакторного дисперсионного анализа в виде таблицы
Сумма квадратов
Сначала сосредоточиться на столбце суммы квадратов (SS) без повторных измерений:
В первой строке показано взаимодействие строк и столбцов. Он количественно определяет, насколько вариативна из-за того, что различия между строками неодинаковы для всех столбцов. Эквивалентно, он количественно определяет степень вариации из-за того, что различия между столбцами неодинаковы для обеих строк.
- Во второй строке показана величина вариации, вызванная систематическими различиями между двумя строками.
- В третьей строке показана величина вариации из-за систематических различий между столбцами.
- В предпоследней строке показан вариант, не объясняемый ни одной из других строк. Это называется остатком или ошибкой.
- В последней строке показана общая величина вариации среди всех 18 значений.
Это называется остатком или ошибкой.Теперь посмотрите на столбцы SS для анализа тех же данных, но с различными предположениями о повторных измерениях.
- Общий SS остается прежним. Это имеет смысл. Это измеряет общую вариацию среди 18 значений.
- Значения SS для взаимодействия и систематических эффектов строк и столбцов (три верхних строки) одинаковы во всех четырех анализах.
- SS для остатка меньше, если вы предполагаете повторные измерения, так как некоторые из этих вариаций могут быть связаны с вариациями между субъектами. В последних столбцах некоторые из этих вариаций также можно отнести к взаимодействию между субъектами и строками или столбцами.
Степени свободы
Теперь посмотрим на значения DF.
Подробности о том, как вычисляются SS и DF, можно найти у Максвелла и Делани (ссылка ниже). Таблица 12.2 на стр. 576 поясняет таблицу ANOVA для повторных измерений обоих факторов.
Но обратите внимание, что они используют термин «A x B x S», где мы говорим «Остаток». Таблица 12.16 на стр. 595 поясняет таблицу ANOVA для повторных измерений одного фактора. Они говорят «B x S/A», где Prism говорит «остаток», и говорят «S/A», где Prism говорит «субъект».
Средние квадраты
Каждое среднеквадратичное значение вычисляется путем деления значения суммы квадратов на соответствующие степени свободы. Другими словами, для каждой строки в таблице ANOVA разделите значение SS на значение df, чтобы вычислить значение MS.
Коэффициент F
Каждый коэффициент F вычисляется путем деления значения MS на другое значение MS. Значение MS для знаменателя зависит от плана эксперимента.
- Для двухфакторного дисперсионного анализа без повторных измерений: Значение MS в знаменателе всегда равно MSresidual.
- Для двустороннего дисперсионного анализа с повторными измерениями в одном факторе (стр. 596 Максвелла и Делани):
- Для взаимодействия знаменатель MS равен MSresidual
- Для фактора, который не является повторным измерением, знаменатель MS равен MSsubjects
- Для коэффициента, который измеряется повторно, знаменатель MS равен MSостаток
- Для двухфакторного дисперсионного анализа с повторными измерениями обоих факторов (стр.
