Решение математических задач онлайн — Тур-инфо
Решатель математики
Решение Ваших математических задач в онлайн режиме. Бесплатная версия программы предоставляет Вам только ответы. Если вы хотите увидеть полное решение, Вы должны зарегистрироваться для полной версии.
Другие программы
Основы математики
Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.
Вы можете упростить, найти значение, объединять и умножать выражения.
Онлайн программа решения задач курса предварительной алгебры (геометрии)
Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.
Онлайн программа решения задач по алгебре
Мы рекомендуем Вам зарегистрироваться для этой онлайн программы.
Решите Ваши задачи (уравнения, неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме.
Если Ваша домашняя работа включает в себя математические уравнения, неравенства, функции, многочлены, матрицы, значит это правильный выбор.
Онлайн программа решения задач по тригонометрии
Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений, неравенств.
Строит графики тригонометрических функций.
Тригонометрия прямоугольного треугольника.
Онлайн программа решения задач курса предварительной алгебры
Включает в себя все вышеперечисленное функции плюс нахождение пределов (LIM), сумм, матриц.
Онлайн программа решения задач курса высшей математики
Решение задач c определенными, неопределенными интегралами.
Онлайн программа решения статистических задач
Решайте задач с нахождением вероятности, комбинаторные задачи.
Статистические задачи — найти среднее (арифметическое, геометрическое, квадратическое) значение, распределение, нормальное распределение, т-распределение.
Онлайн программа успешно проводит тестирование статистических гипотез
© 2005 — 2022
Копирование запрещено! В случае копирования администрация сайта обратится в компетентные органы.
Основы математики
Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.
Вы можете упростить, найти значение, объединять и умножать выражения.
Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.
Онлайн программа решения задач курса предварительной алгебры геометрии.
Www. math20.com
06.07.2018 19:52:42
2018-07-06 19:52:42
Источники:
Https://www. math20.com/ru/reshenie-zadach-onlain/
Онлайн калькуляторы для решения математических задач » /> » /> .keyword { color: red; }
Решатель математики
Онлайн калькуляторы — в этом разделе собраны написанные мною программы для решения примеров и задач по математике, алгебре, геометрии, теории вероятности, высшей математике и другим математическим дисциплинам. Для работы Вам необходимо лишь выбрать подходящий калькулятор и ввести данные, программа сама мгновенно найдет ответ и выдаст детально расписанное пошаговое решение вашей задачи. Это дает возможность не только получить результат, но и научиться решать математические задачи, найти и исправить ошибки в своем решении или проверить правильность своего решения.
Я постоянно совершенствую уже существующие калькуляторы и по мере возможностей пишу новые. Если вы не нашли необходимый вам математический калькулятор или знаете, как можно усовершенствовать уже существующие калькуляторы, пишите об этом в комментариях или отзывах.
ОНЛАЙН КАЛЬКУЛЯТОРЫ
Онлайн калькуляторы. Конвертеры величин. Конвертер единиц массы и весаКонвертер единиц расстояния и длиныКонвертер единиц площадиКонвертер единиц объемаКонвертер единиц времениКонвертер единиц скоростиКонвертер единиц температуры
Онлайн калькуляторы. Теория чиселСложение, вычитание, умножение и деление столбикомСложение и вычитание в столбикУмножение в столбикДеление в столбикДеление в столбик с остаткомОстаток при деленииНОД и НОК двух чиселРазложение числа на множителиКалькулятор квадратных корней
Онлайн калькуляторы с дробями 1 2 + 1 3 = ? Онлайн калькулятор дробей. Сложение, вычитание, умножение и деление дробей 0.1 + 1 3 = ? Вычисления с обыкновенной и десятичной дробями 0.1 = ? ? Преобразование десятичной дроби в обыкновенную дробь 3 2 → 1 1 2 Преобразование неправильных дробей в смешанные числа 1 1 2 → 3 2 Преобразование смешанных чисел в неправильные дроби 2 4 → 1 2 Сокращение дробейПриведение дробей к общему знаменателю 1 2 > 1 3 Сравнение дробей A B = C? Калькулятор пропорций 1 2 — ( 1 3 + 4 5 ) = ? Калькулятор рациональных выражений
Онлайн калькуляторы.
Калькуляторы с процентамиНайти X процентов от числа YНайти число X зная его Y процентовДобавить или вычесть X процентов от числаНайти сколько процентов составляет число X от числа YНайти на сколько процентов число X больше (меньше) числа YКалькулятор сложных процентов. Депозитный калькуляторОнлайн калькулятор скидок
Онлайн калькуляторы. Решение уравненийРешение квадратных уравненийРешение биквадратных уравненийРешение систем линейных уравненийРешение систем линейных уравнений. Метод ГауссаРешение систем линейных уравнений. Метод КрамераРешение систем линейных уравнений. Матричный метод
Онлайн калькулятор графиков
Онлайн калькуляторы. ПрогрессииЗначение n-того члена арифметической прогрессииСумма арифметической прогрессии
Онлайн калькуляторы. Пределы и производные функцийРешение пределов онлайнРешение производных онлайн
Онлайн калькуляторы. Интегралы онлайнРешение интегралов онлайнРешение определенных интегралов онлайн
Онлайн калькуляторы.
Комбинаторика. Теория вероятности. Pn Вычисление числа перестановок из n элементов An k Вычисление числа размещений из n по k Cn k Вычисление числа сочетаний из n по k M [ X ] Вычисление математического ожидания дискретного распределения D [ X ] Вычисление дисперсии дискретного распределения
Онлайн калькуляторы с комплексными числамиСложение, вычитание, умножение и деление комплексных чиселМодуль комплексного числаКонвертер алгебраической формы комплексного числа в тригонометрическую и показательную
Онлайн калькуляторы с векторамиОпределение вектора по двум точкамДлина вектора. Модуль вектораНаправляющие косинусы вектораСложение и вычитание двух векторовУмножение вектора на числоСкалярное произведение векторовУгол между векторамиПроекция вектора на векторВекторное произведение векторовСмешанное произведение векторовКоллинеарность векторовОртогональность векторовКомпланарность векторовПлощадь треугольника построенного на векторахПлощадь параллелограмма построенного на векторахОбъем пирамиды построенной на векторахПроверить являются ли вектора базисомРазложение вектора по базису
Онлайн калькуляторы с матрицами A ± B Сложение и вычитание матриц A T Транспонированная матрица 2A Умножение матрицы на число A × B Умножение матриц A 2 Возведение матрицы в степень det A Определитель матрицы.
Детерминант матрицы Rank(A) Ранг матрицы A -1 Обратная матрица A -1 Обратная матрица методом алгебраических дополнений
Онлайн калькуляторы. Аналитическая геометрия. Декартовые координатыДлина отрезка. Расстояние между точкамиСередина отрезкаУравнение прямой проходящей через две точкиТочка пересечения прямыхУгол между прямымиРасстояние от точки до прямой на плоскостиРасстояние от точки до прямой в пространствеУравнение плоскостиРасстояние от точки до плоскостиРасстояние между плоскосямиУгол между плоскостямиУгол между прямой и плоскостью
Онлайн калькуляторы. Площадь геометрических фигурПлощадь треугольника 9-ю способамиПлощадь треугольника по трем сторонам. Формула ГеронаПлощадь квадратаПлощадь прямоугольникаПлощадь параллелограммаПлощадь ромбаПлощадь трапецииПлощадь четырехугольникаПлощадь кругаПлощадь эллипса
Онлайн калькуляторы. Периметр геометрических фигурПериметр треугольникаПериметр квадратаПериметр прямоугольникаПериметр параллелограммаПериметр ромбаПериметр трапецииПериметр круга.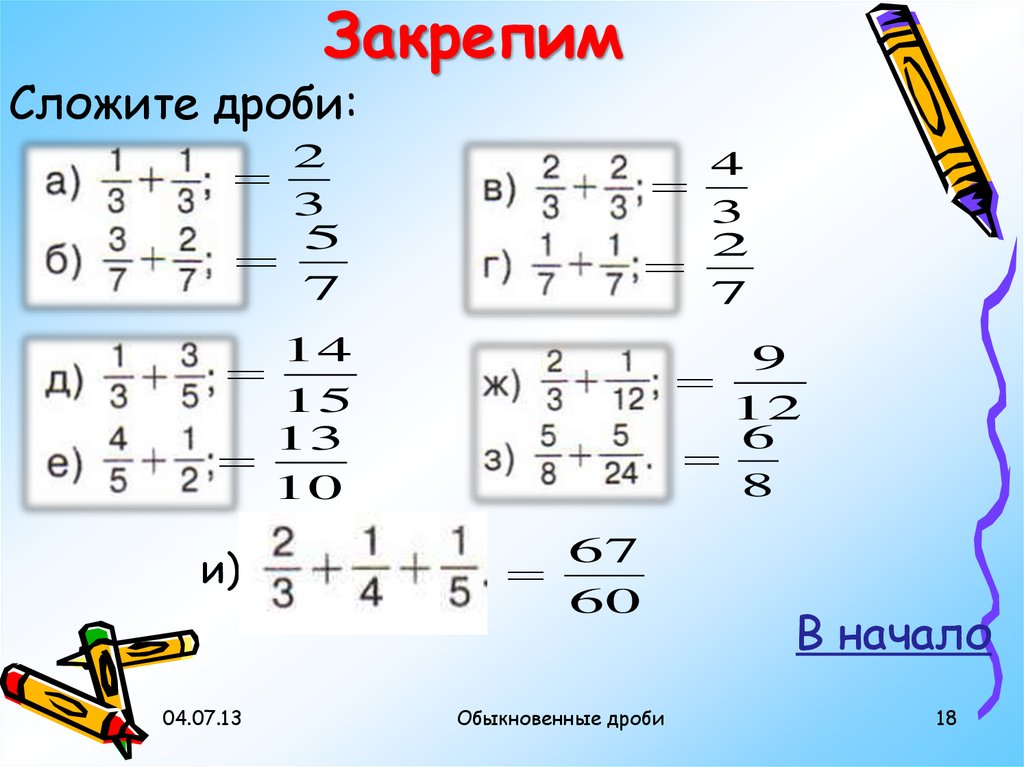
Длина окружности
Онлайн калькуляторы. Объем геометрических фигур. Объем кубаОбъем призмыОбъем прямоугольного параллелепипедаОбъем параллелепипедаОбъем пирамидыОбъем правильного тетраеэдраОбъем шараОбъем цилиндраОбъем конуса
Онлайн калькуляторы. Площадь поверхности геометрических фигурПлощадь кубаПлощадь прямоугольного параллелепипедаПлощадь цилиндраПлощадь конусаПлощадь шара
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Онлайн калькуляторы. Объем геометрических фигур. Объем кубаОбъем призмыОбъем прямоугольного параллелепипедаОбъем параллелепипедаОбъем пирамидыОбъем правильного тетраеэдраОбъем шараОбъем цилиндраОбъем конуса
Онлайн калькуляторы. Конвертеры величин. Конвертер единиц массы и весаКонвертер единиц расстояния и длиныКонвертер единиц площадиКонвертер единиц объемаКонвертер единиц времениКонвертер единиц скоростиКонвертер единиц температуры
Калькулятор пропорций 1 2 — 1 3 4 5.
Ru.
onlinemschool. com
14.04.2019 6:49:54
2020-09-12 16:21:22
Источники:
Https://ru. onlinemschool. com/math/assistance/
Mathway | Решение задач по алгебре » /> » /> .keyword { color: red; }
Решатель математики
It appears we may have a connection issue. I will end the session — please reconnect if you still need assistance.
If you click on «Tap to view steps. » you will see the steps are now numbered. Which step # do you have a question on?
Please make sure you are in the correct subject. To change subjects, please exit out of this live expert session and select the appropriate subject from the menu located in the upper left corner of the Mathway screen.
While we cover a very wide range of problems, we are currently unable to assist with this specific problem. I spoke with my team and we will make note of this for future training. Is there a different problem you would like further assistance with?
Mathway currently does not support this subject.
We are more than happy to answer any math specific question you may have about this problem.
Mathway currently does not support Ask an Expert Live in Chemistry. If this is what you were looking for, please contact support.
We are here to assist you with your math questions. You will need to get assistance from your school if you are having problems entering the answers into your online assignment.
Phone support is available Monday-Friday, 9:00AM-10:00PM ET. You may speak with a member of our customer support team by calling 1-800-876-1799.
You will need to get assistance from your school if you are having problems entering the answers into your online assignment.
Www. mathway. com
09.12.2018 12:50:02
2018-12-09 12:50:02
Источники:
Https://www. mathway. com/ru/Algebra
Научный онлайн-калькулятор с двузначной точностью для выполнения научных или академических вычислений
Помимо обычных вычислений, этот научный онлайн-калькулятор также можно использовать для выполнения научных/академических вычислений, таких как решение уравнений, выполнение вычислений с использованием комплексных чисел, тригонометрических функций и т.
д. ., решение математических и статистических задач и многое другое.
Что такое научный калькулятор?
Научные калькуляторы, широко используемые в старших классах и учащимися колледжей, используются для выполнения сложных математических и научных расчетов. Эти калькуляторы можно использовать для решения связанных с тригонометрией, алгеброй, исчислением, статистикой и т. д. задач. В них предусмотрено использование таких функций, как комплексные числа, логарифм и p, квадратный корень, экспонента, факториал и т. д. Кроме того, он также может выполнять основные арифметические вычисления, такие как сложение, вычитание, умножение и деление.
Приложения/Функции этого научного калькулятора
Это цифровой инструмент, к которому можно легко получить доступ с таких устройств, как ноутбук или мобильный телефон с работающим подключением к Интернету. Вычисления в этом научном калькуляторе можно выполнять, нажимая на соответствующие функции или просто вводя в калькулятор целое уравнение или задачу.
Ниже рассмотрены основные функции и процесс их использования.
Тригонометрические функции
Этот научный калькулятор имеет специальные кнопки для тригонометрических функций Sin, Cos и Tan, а также для обратных тригонометрических функций Sin-1, Cos-1 и Tan-1.
Например: Sin(90), Tan-1(30), Cos(5) и т.д.
Экспоненциальные функции
Этот калькулятор имеет кнопки с указанием xy, x3, x2, ex и 10x, которые можно использовать для вычислений с использованием показателей степени. Это включает в себя повышение степени числа или увеличение значения числа на определенную степень.
Например: Чтобы найти значение 63, нажмите на 6, а затем на кнопку x3; аналогично, чтобы найти значение 103, нажмите кнопку 10x, а затем 3
Радикальные функции
Эти функции помогают в вычислениях с радикалами, такими как квадратный корень или кубический корень.
Например: Чтобы найти кубический корень из 27, нажмите кнопку 3vx, а затем 27; аналогично, чтобы вычислить 10-й корень из 2563, сначала введите 2563 в калькулятор, затем нажмите кнопку yvx и затем введите 10
Функции π, e, ln и log
Здесь кнопку «p» можно использовать для ввода значения 3,1415926536 либо в уравнение, либо с другими функциями, такими как показатели степени, радикалы или основные арифметические функции. Точно так же «e» для постоянной Эйлера, а кнопки «ln» и «log» для логарифмических функций, и эти функции можно использовать в уравнениях, а также с другими функциями в калькуляторе.
Основные арифметические функции
Этот калькулятор также можно использовать для выполнения основных арифметических вычислений, включая сложение (+), вычитание (-), умножение (x) и деление (÷). Калькулятор также имеет специальные кнопки для этих математических функций, к которым можно получить доступ, просто нажав на них с помощью указателя мыши.
Например: 1256 + 489, 96 x 58, 56784936 ÷ 67484 и т. д.
Калькулятор кратности
Онлайн-калькулятор кратности позволяет найти нулей уравнения.
Онлайн-калькулятор кратности — это мощный инструмент, используемый математиками и физиками для нахождения нулей или корней уравнения. Калькулятор кратности играет жизненно важную роль в решении сложных математических задач.
Что такое калькулятор кратности?
Калькулятор кратности — это онлайн-калькулятор, который позволяет находить нули или корни полиномиального уравнения, которое вы вводите.
Калькулятор кратности требует единственного ввода, уравнения, которое вы вводите в Калькулятор кратности . Для работы калькулятора кратности уравнение должно быть полиномиальной функцией.
Калькулятор кратности мгновенно вычисляет результаты и отображает их в новом окне.
Калькулятор кратности отображает несколько результатов, таких как корни уравнения, график корней уравнения, числовая линия уравнения, сумма корней и произведение корней.
Как пользоваться калькулятором кратности?
Вы можете использовать Калькулятор кратности , введя уравнение полинома и нажав кнопку «Отправить». Результаты будут мгновенно отображаться на вашем экране.
Пошаговые инструкции по использованию Калькулятора кратности приведены ниже:
Шаг 1
На первом этапе вы вставляете уравнение полинома в поле ввода , предусмотренное в калькуляторе кратности . .
Шаг 2
После ввода уравнения полинома в Калькулятор кратности нажмите кнопку «Отправить». Калькулятор отобразит результаты в отдельном окне. 9{2} + bx + c $ обычно пересекает или касается оси x графика; уравнения решаются и приравниваются к нулю для вычисления корней уравнения.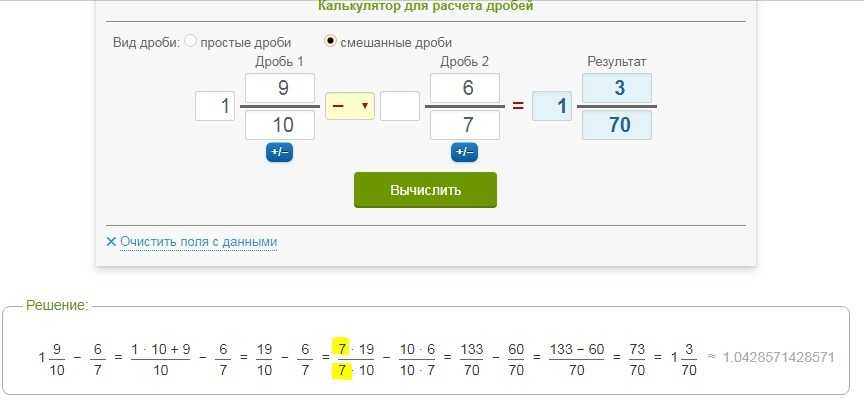
Давайте обсудим некоторые важные понятия, связанные с работой этого калькулятора.
Что такое нули многочленов?
Нули полиномов — это точки, в которых уравнения полиномов становятся равными нулю. Проще говоря, можно сказать, что нули многочлена — это переменные значения, при которых многочлен равен 0,9.0003
Нули полинома часто называют корнями уравнения и часто записывают как $\alpha$,$\beta$ и $\gamma$.
В математической терминологии значения x, удовлетворяющие уравнению полинома f(x) = 0, представляют собой нулей полинома . В этом случае нули полинома являются значениями x, для которых значение функции f(x) равно нулю. Степень уравнения f(x) = 0 определяет, сколько нулей имеет многочлен.
Как найти нули многочленов?
Вы можете найти нулей полинома, подставив их равными 0 и найдя значения задействованной переменной, которые являются нулями полинома.
Нахождение нулей многочлена можно выполнить разными способами. Степень уравнения полинома определяет, сколько нулей имеет полином.
Чтобы определить нули многочлена, каждое из многочисленных уравнений, которые были классифицированы как линейный, квадратичный, кубический и полиномы высших степеней — рассматриваются отдельно.
Различные полиномиальные уравнения с методами их решения приведены ниже:
Нахождение нулей для линейных уравнений
Линейные уравнения обычно записываются как y = ax + b. Вы можете найти решение этого уравнения, подставив y = 0, и при упрощении мы получим ax + b = 0, или $x = \frac{-b}{a} $.
Нахождение нулей в квадратных уравнениях 9{2} + cx + d$ можно разложить на множители. Переменная x = $\alpha$ может быть заменена любым меньшим значением в соответствии с теоремой об остатках, и если значение y дает
ноль , y = 0, то (x – $\alpha$ ) является одним корнем уравнения.
Мы можем разделить кубическое уравнение на $(x – \alpha )$, используя длинное деление , чтобы получить квадратное уравнение .
Квадратное уравнение может быть окончательно решено либо с помощью формулы, либо с помощью факторизации 9{n-2} + ….. px + q$.
После вычисления квадратной формулы из этих многочленов высшей степени их можно разложить на множители для получения корней уравнения.
Что такое кратность многочлена?
Кратность полинома означает, сколько раз корень значений появляется в полиномиальном уравнении. Если у нас есть факторизованная версия многочлена, вычислить количество корней несложно. С другой стороны, также возможно определить количество корней, изучив полиномиальный график.
$x$-пересечения графика многочлена являются действительными корнями многочлена. В результате мы можем узнать, сколько у него действительных корней, изучив полиномиальный граф.
Аналогичным образом, исследуя нулей многочлена или его факторизованную форму, мы можем предсказать, как часто график будет касаться или пересекать ось x.
Кратность нуля или корня — это количество раз, когда связанный с ним множитель появляется в многочлене.
Например, квадратное уравнение (x+5)(x-3) имеет корень x= -5 и x = 3. Это объясняет, что линия уравнения проходит через точки x= -5 и x = 3 один раз.
Если полином не учитывается, мы должны факторизовать его или получить график полинома, чтобы исследовать, как он ведет себя при пересечении или контакте с осью x.
Примеры решения
Калькулятор кратности — это эффективный способ вычисления нулей или корней полиномиального уравнения.
Вот несколько решенных примеров, которые решены с помощью Калькулятора множественности .
Решенный пример 1
Учащемуся старшей школы дано следующее полиномиальное уравнение: 9{2} – 6x \]
Учащийся должен вычислить нулей и построить график, используя это полиномиальное уравнение. Найдите нулей и постройте график, используя полиномиальное уравнение.
Решение
Используя калькулятор кратности , мы можем вычислить нулей полиномиального уравнения и построить график. Сначала вводим уравнение полинома в Калькулятор кратности .
После ввода уравнения полинома мы нажимаем кнопку «Отправить» на 9{3}$. Чтобы завершить свое исследование, математику необходимо найти корней полиномиального уравнения.
Найдите корней многочлена высшей степени.
Решение
Чтобы решить уравнение и найти корни с помощью Калькулятора кратности, сначала мы вставляем полученное полиномиальное уравнение в соответствующее поле ввода.
После подстановки полиномиального уравнения все, что нам нужно сделать, это нажать кнопку «Отправить» на 9{3} = 0 \]
Результаты:
x = -2 (кратность 3)
x = -1 (кратность 2)
x = 0 (кратность x = 0 (кратность 9000 0 1) :
Рисунок 3
Численная линия:
Рисунок 4
Сумма корней:
-8
Продукт корней:
0
Решенный пример 3
.
студент колледжа наткнулся на следующее уравнение: 9{3}(x+3)(x+2) \]
Учащийся должен найти кратность нулей в полиномиальном уравнении. Найдите кратность нулей данного полиномиального уравнения.
Решение
Мы можем использовать Калькулятор кратности , чтобы найти кратность нулей полиномиального уравнения . Чтобы использовать калькулятор, мы сначала добавляем уравнение полинома в поле ввода.
После добавления уравнения полинома в 9{3}(x+3)(x+2) = 0 \]
Результаты:
x = -3 (кратность 3)
x = -2 (кратность 2)
x = 1 (множественность 1)
Корневой график:
Рисунок 5
Линия номеров:
Рисунок 6
Сумма корней:
-2
Продукт корней:
6
. Пример 4
Рассмотрим следующее полиномиальное уравнение:
9{3} \] Используя приведенное выше уравнение, вычислите кратность нулей .