Калькулятор скалярного произведения
Калькулятор скалярного произведения является бесплатным инструментом для нахождения равнодействующей двух векторов путем умножения друг на друга. Этот калькулятор для скалярного произведения двух векторов помогает выполнять вычисления с:
- Компоненты вектора, это может быть либо 2D, либо 3D вектор.
- Величина и угол.
Когда дело доходит до компонентов, вы можете выполнять расчеты по:
- Координатам.
- баллов.
Он также известен как скалярное произведение и может быть определен как «сумма покомпонентных произведений». Скалярное произведение двух векторов равно произведению их величин. Значит, он равен нулю для двух взаимно перпендикулярных векторов. И это обозначается символом «.» между двумя векторами. Основное различие между точечным и перекрестным произведением заключается в том, что произведение точечной операции представляет собой одно число, а результатом перекрестной операции является вектор.
Формула скалярного умножения двух векторов выглядит следующим образом:
a.b = |a| |б| cosΘ
Где
a и b — два вектора, а |a| & |б| являются модулями вектора a и b соответственно.
Θ — угол между двумя векторами.
Наш онлайн-калькулятор скалярного произведения также позволяет найти угол Θ между векторами, используя следующее уравнение:
Θ = Cos-1 a.b / |a| |б|
Как сделать скалярное произведение вручную:Формула для вычислений обсуждалась выше, теперь у нас есть ручные примеры для обоих методов.
Расчет с компонентой вектора:Из этих входных параметров мы должны знать две координаты, для которых мы собираемся выполнять вычисления. Здесь у нас есть пример:
Пример:
Если вектор a = [2,-4,3] и второй вектор b = [-4,3,5]. Что такое скалярное произведение двух векторов?
Решение:
Шаг 1:
Найдите произведение первой компоненты каждого вектора.
Итак, (2)*(-4) = -8
Шаг 2:
Найдите произведение второго компонента каждого вектора.
Итак, (-4)*(3) = -12
Шаг 3:
Найдите произведение третьего компонента каждого вектора.
Итак, (3)*(5) = 15
Шаг 4:
Сложите все эти значения, чтобы найти скалярное произведение (точечный продукт). Итак, (2)*(-4) = -8
(-8)+(-12)+15
-8 – 12 + 15
a.b = -5
Если нам нужно найти угол между двумя векторами, то используйте формулу как:
Θ = Cos-1 а.б / |а| |б|
Шаг 1:
Величина вектора a.
|а| = √ (2)2 + (-4)2 + (3)2
|а| = √ 4+ 16 + 9
|а| = √ 29
|а| = 5,38
Шаг 2:
Величина вектора b.
|б| = √ (-4)2 + (3)2 + (5)2
|б| = √ 16+ 9 + 25
|b| = √ 50
|б| = 7,07
Шаг 3:
Θ = Cos-1 a.
b / |a| |б|
Θ = Cos-1 -5 / 5,38* 7,07
Θ = Cos-1 -5 / 38,03
Θ = Cos-1 -0,1314
Θ = 97,53 град.
Расчеты становятся очень простыми с помощью этого бесплатного онлайн-калькулятора. Этот инструмент определяет скалярное произведение векторов двумя разными методами, которые мы собираемся обсудить:
Читайте дальше!
Компоненты вектора:Для расчетов по этому методу просто придерживайтесь следующих точек:
Входные данные:
- Прежде всего, выберите измерение на вкладке. Это либо 2D, либо 3D.
- Далее выберите векторное представление для первого вектора из раскрывающегося списка калькулятора.
- Затем выберите векторное представление для второго вектора из раскрывающегося списка этого инструмента.
- Введите во все поля в соответствии с выбранной опцией.
- Наконец, нажмите кнопку расчета.
Для расчетов по этому методу просто следуйте следующим пунктам:
Входные данные:
- Прежде всего, введите величину первого вектора.
- Далее введите величину второго вектора в указанное поле.
- После этого подставьте угол между векторами.
- Наконец, нажмите кнопку расчета.
Выходы:
После ввода во все поля калькулятор показывает:
- Скалярное произведение между векторами.
- Величина вектора A.
- Величина вектора B.
- Угол между векторами.
- Пошаговые расчеты.
Взято из официального источника Википедии: Определение и свойства скалярного произведения.
Калькулятор скалярного произведения — Примеры, Онлайн-калькулятор скалярного произведения
Калькулятор скалярного произведения вычисляет скалярное произведение двух заданных векторов. Когда два вектора умножаются с помощью скалярного произведения, полученная таким образом величина будет скаляром. Скалярный продукт может быть положительным или отрицательным действительным числом.
Что такое калькулятор скалярного произведения?
Калькулятор скалярного произведения – это онлайн-инструмент, который помогает определить скалярную величину, являющуюся результатом скалярного произведения заданных двух векторов. Величина, полученная после скалярного произведения, будет находиться в той же плоскости, что и два заданных вектора. Чтобы использовать калькулятор скалярного произведения, введите значения в соответствующие поля ввода.
Калькулятор скалярного произведения
Как пользоваться калькулятором скалярного произведения?
Выполните следующие шаги, чтобы вычислить скалярное произведение двух заданных векторов с помощью калькулятора скалярного произведения.
Как найти калькулятор скалярного произведения?
Скалярное произведение определяется как произведение величины двух векторов и косинуса угла между двумя заданными векторами. Если \(\overrightarrow{a}\) и \(\overrightarrow{b}\) являются двумя векторами, то скалярное произведение дается следующим образом:
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = |\(\overrightarrow{a}\)|.|\(\overrightarrow{b}\)|cosθ.
Предположим, что нам даны два вектора, которые выражены в виде их единичных векторов i, j, k вдоль осей x, y и z. Затем шаги, необходимые для нахождения скалярного произведения между двумя векторами, приведены ниже:
\(\overrightarrow{a}\) = \(a_{1}\hat{i} + a_{2}\hat{ j} + a_{3}\шляпа{k}\)
\(\overrightarrow{b}\) = \(b_{1}\шляпа{i} + b_{2}\шляпа{j} + b_{ 3}\hat{k}\)
Чтобы найти скалярное произведение
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\))
= \((a_{1}b_{1})(\hat{i}.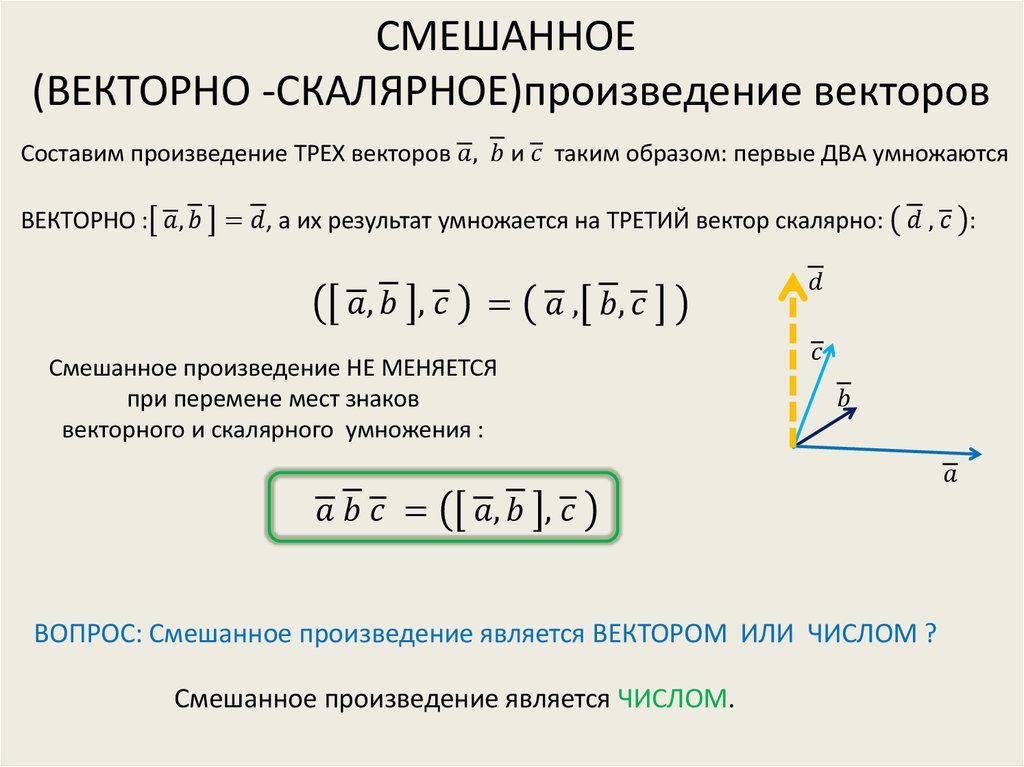
\hat{i}) + (a_{1}b_{2})(\hat{i}.\hat{j }) + (a_{1}b_{3})(\шляпа{i}.\шляпа{k})\) + \((a_{2}b_{1})(\шляпа{j}.\шляпа {i}) + (a_{2}b_{2})(\hat{j}.\hat{j}) + (a_{2}b_{3})(\hat{j}.\hat{k })\) + \((a_{3}b_{1})(\шляпа{k}.\шляпа{i}) + (a_{3}b_{2})(\шляпа{k}.\шляпа {j}) + (a_{3}b_{3})(\шляпа{k}.\шляпа{k})\)
\(\шляпа{i}.\шляпа{j}\) = \( \hat{i}.\hat{k}\) = \(\hat{k}.\hat{j}\) = cos 90 = 0. Это потому, что эти векторы ортогональны.
\(\шляпа{i}.\шляпа{i}\) = \(\шляпа{k}.\шляпа{k}\) = \(\шляпа{j}.\шляпа{j}\) = cos 0 = 1. Потому что эти векторы сонаправлены.
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = \(a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\)
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры на калькуляторе скалярного произведения
Пример 1:
Найти скалярное произведение двух векторов \(\overrightarrow{a}\) = \(4\hat{i} + 2\шляпа{j} — 5\шляпа{k}\) и \(\overrightarrow{b}\) = \(3\шляпа{i} — 2\шляпа{j} — \шляпа{k}\).
Проверьте результат с помощью калькулятора скалярного произведения.
Решение:
Учитывая \(\overrightarrow{a}\) = \(4\hat{i} + 2\hat{j} — 5\hat{k}\) и \(\overrightarrow{b }\) = \(3\шляпа{i} — 2\шляпа{j} — \шляпа{k}\)
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = \(a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\)
\(\overrightarrow{a}\ ). \(\overrightarrow{b}\) = (4 . 3) + (2 . (-2)) + ((-5) . 1)
= 12 — 4 — 5
= 3
Следовательно, скалярное произведение двух векторов равно 3.
Пример 2:
Найдите скалярное произведение двух векторов \(\overrightarrow{a}\) = \(2,3\hat{i} — 1,2\hat{j} + 8,9\hat{k}\) и \(\overrightarrow{ b}\) = \(-4,6\шляпа{i} + 2,8\шляпа{j} + 5,5\шляпа{k}\). Проверьте результат с помощью калькулятора скалярного произведения.
Решение. }\) = (-4,6\шляпа{i} + 2,8\шляпа{j} + 5,5\шляпа{k}\)
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = \(a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\)
\(\overrightarrow{a}\).