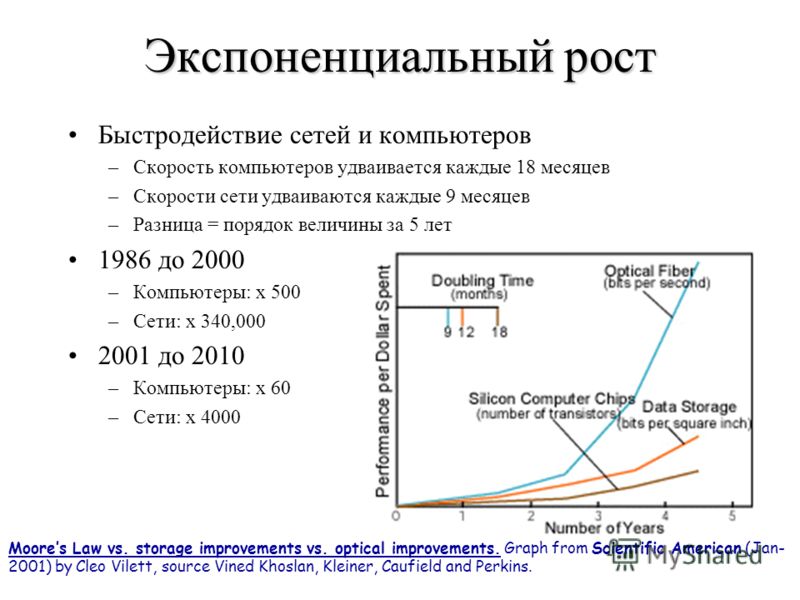
График экспоненциальный: Экспоненциальный рост • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Содержание

Экспоненциальный рост • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Если прирост численности популяции пропорционален количеству особей, численность популяции будет расти экспоненциально.

Выражение «экспоненциальный рост» вошло в наш лексикон для обозначения быстрого, как правило безудержного увеличения. Оно часто используется, например, при описании стремительного роста числа городов или увеличения численности населения. Однако в математике этот термин имеет точный смысл и обозначает определенный вид роста.

Экспоненциальный рост имеет место в тех популяциях, в которых прирост численности (число рождений минус число смертей) пропорционален числу особей популяции. Для популяции человека, например, коэффициент рождаемости примерно пропорционален количеству репродуктивных пар, а коэффициент смертности примерно пропорционален количеству людей в популяции (обозначим его N). Тогда, в разумном приближении,

\[ \begin{array}{lcl} \text{прирост населения}&=&{\text{число рождений}}-\text{число смертей}\\ &\propto& N\\ &=&rN \end{array}\]

(Здесь r — так называемый коэффициент пропорциональности, который позволяет нам записать выражение пропорциональности в виде уравнения. )

Пусть dN — число особей, добавившихся к популяции за время dt, тогда если в популяции в общей сложности N особей, то условия для экспоненциального роста будут удовлетворены, если

dN = rN dt

После того как в XVII веке Исаак Ньютон изобрел дифференциальное исчисление, мы знаем, как решать это уравнение для N — численности популяции в любое заданное время. (Для справки: такое уравнение называется дифференциальным.) Вот его решение:

N = N₀ e^rt

где N₀ — число особей в популяции на начало отсчета, а t — время, прошедшее с этого момента. Символ е обозначает такое специальное число, оно называется

основание натурального логарифма (и приблизительно равно 2,7), и вся правая часть уравнения называется экспоненциальная функция.

Чтобы лучше понять, что такое экспоненциальный рост, представьте себе популяцию, состоящую изначально из одной бактерии. Через определенное время (через несколько часов или минут) бактерия делится надвое, тем самым удваивая размер популяции. Через следующий промежуток времени каждая из этих двух бактерий снова разделится надвое, и размер популяции вновь удвоится — теперь будет уже четыре бактерии. После десяти таких удвоений будет уже более тысячи бактерий, после двадцати — более миллиона, и так далее. Если с каждым делением популяция будет удваиваться, ее рост будет продолжаться до бесконечности.

Существует легенда (скорее всего, не соответствующая действительности), будто бы человек, который изобрел шахматы, доставил этим такое удовольствие своему султану, что тот пообещал исполнить любую его просьбу. Человек попросил, чтобы султан положил на первую клетку шахматной доски одно зерно пшеницы, на вторую — два, на третью — четыре и так далее. Султан, посчитав это требование ничтожным по сравнению с оказанной им услугой, попросил своего поданного придумать другую просьбу, но тот отказался. Естественно, к 64-му удвоению число зерен стало таким, что во всем мире не нашлось бы нужного количества пшеницы, чтобы удовлетворить эту просьбу.

В той версии легенды, которая известна мне, султан в этот момент приказал отрубить голову изобретателю. Мораль, как я говорю моим студентам, такова: иногда не следует быть чересчур умным!

Пример с шахматной доской (как и с воображаемыми бактериями) показывает нам, что никакая популяция не может расти вечно. Рано или поздно она попросту исчерпает ресурсы — пространство, энергию, воду, что угодно. Поэтому популяции могут расти по экспоненциальному закону лишь некоторое время, и рано или поздно их рост должен замедлиться. Для этого нужно изменить уравнение так, чтобы при приближении численности популяции к максимально возможной (которая может поддерживаться внешней средой) скорость роста замедлялась. Назовем эту максимальную численность популяции

K. Тогда видоизмененное уравнение будет выглядеть так:

dN = rN(1 — (N/K)) dt

Когда N намного меньше K, членом N/K можно пренебречь, и мы возвращаемся к первоначальному уравнению обычного экспоненциального роста. Однако когда N приближается к своему максимальному значению K, значение 1 — (N/K) стремится к нулю, соответственно стремится к нулю и прирост численности популяции. Общая численность популяции в этом случае стабилизируется и остается на уровне

K. Кривая, описываемая этим уравнением, а также само уравнение, имеют несколько названий — S-кривая, логистическое уравнение, уравнение Вольтерры, уравнение Лотки—Вольтерры. (Вито Вольтерра, 1860–1940 — выдающийся итальянский математик и преподаватель; Альфред Лотка, 1880–1949 — американский математик и страховой аналитик.) Как бы она ни называлась, это — достаточно простое выражение численности популяции, резко возрастающей экспоненциально, а затем замедляющейся при приближении к некоему пределу. И она гораздо лучше отражает рост численности реальных популяций, чем обычная экспоненциальная функция.

Моделирование экспоненциального роста

Чтобы лучше усвоить материал, рекомендуем вам использовать данные для примера и Python Notebook.

Почему именно экспоненциальный рост?

Экспоненциальный рост — это математическая функция, которая может использоваться в нескольких ситуациях. С ее формулой можно вычислить количество случаев в определенный момент времени. В случае с коронавирусом — число зараженных людей.

Причиной использования экспоненциального роста для моделирования вспышки коронавируса является то, что, согласно исследованиям специалистов, первая вспышка эпидемии следует принципу экспоненциального роста.

Формула экспоненциального роста

Экспоненциальный рост выражается следующей формулой:

Функция экспоненциального роста

Где:

x (t) — количество случаев в момент времени t;
x0 — количество случаев в начале эпидемии, также называемое начальным значением;
b — количество людей, зараженных каждым больным человеком, скорость роста (фактор роста).

Рассмотрим гипотетический случай, в котором:

начальное значение = 1 ( первый зараженный человек), поэтому x0 = 1;
каждый больной заражает 2 других людей, поэтому скорость роста будет b = 2;
мы проанализируем развитие эпидемии начиная с периода 0 и заканчивая периодом 14.

Сначала подставляем значения a и b, чтобы получить формулу для нашей эпидемии:

Далее мы используем эту формулу, чтобы вычислить значение y для каждого значения t от 0 до 14. Таким образом, мы получим число зараженных людей в каждый промежуток времени, как видно из таблицы ниже. При 1 зараженном в период 0 и факторе роста 2, получаем более 16000 случаев в период 14.

В графическом представлении мы получаем кривую, очень напоминающую те, которые видим в ситуации с коронавирусом:

График экспоненциального роста с фактором роста 2

Нахождение точной формулы для эпидемии коронавируса

Чтобы найти реальный фактор роста эпидемии коронавируса, рассмотрим данные о ее распространении:

Данные о коронавирусе. Источник: https://covid.ourworldindata.org/data/full_data.csv

Находим фактор роста с помощью линейной регрессии

На первый взгляд эти данные говорят только о количестве случаев в день, а не о факторе роста заражений. Лучший способ найти фактор роста, основываясь на эмпирических ежедневных наблюдениях, — это использовать статистическую модель, называемую линейной регрессией.

Линейная регрессия позволяет определить наилучшие значения для a и b в указанной ниже формуле, учитывая эмпирические наблюдения для y и x. В этой формуле у — количество случаев, а х — время. Однако необходимо слегка переписать функцию экспоненциального роста, так как линейная регрессия может работать только с формулами следующего вида:

Тип формулы, который нужен для линейной регрессии

Переписываем экспоненциальную формулу для линейной регрессии

Для начала необходимо переписать формулу в виде линейной регрессии. Для этого воспользуемся логарифмами:

мы используем логарифм количества инфекций вместо количества инфекций;
мы используем логарифм фактора роста вместо фактора роста.

Применяем модель линейной регрессии к нашим данным

Шаг 1. Первым делом импортируем данные в Python Notebook и применяем преобразование логарифма:

Шаг 2. Далее используем библиотеку Statsmodels для определения функции линейной регрессии:

Шаг 3. Составляем функцию прогнозирования на основе таблицы.

Вернемся к нашей формуле линейной регрессии:

Тип формулы, который нужен для линейной регрессии

Таблица statsmodels дает значения для a и b под coef (в середине):

Коэффициент const — это значение для a в нашей модели линейной регрессии: 0.4480.
Коэффициент Time — это значение для b: 0.1128.

Теперь мы можем заполнить функцию линейной регрессии:

Обратите внимание, что:

a в линейной регрессии является логарифмом начального значения;
b в линейной регрессии является логарифмом фактора роста.

Следовательно:

логарифм начального значения равен 0. 4480;
логарифм фактора роста 0.1128.

Чтобы найти действительные значения, нам нужно вычислить их с помощью экспоненты:

Теперь можно вернуться к исходной формуле экспоненциального роста и вставить эти значения, чтобы узнать фактическое значение в случае коронавируса:

Фактическая формула для эпидемии коронавируса

Прогнозируем ситуацию на две недели вперёд

Полученную выше формулу можно использовать для прогнозирования ситуации на любую дату. Стоит отметить, что данные прогнозы являются лишь примером, показывающим, как математика и статистика могут использоваться в эпидемиологии. Эпидемиологи из реальной жизни, помимо экспоненциального роста, тестируют разные типы моделей, а также проделывают большую работу по валидации моделей, что было пропущено в данном примере.

Как только лучшая модель будет найдена, ее можно использовать для прогнозирования. Используя функцию, которую мы нашли с помощью кривой экспоненциального роста, можно сделать прогноз на 2 недели после последнего 68-го дня в нашем наборе данных. Для этого просто помещаем t = 68 в формулу, и модель предсказывает количество заражений на этот день: 3355.

Возможности для дальнейшего анализа:

Мы рассмотрели применение модели линейной регрессии для прогнозирования процесса экспоненциального роста. Обратите внимание на следующие меры предосторожности:

Линейная модель — это только приблизительная функция экспоненциального роста и она имеет определенный предел погрешности.
Функция экспоненциального роста не является идеальным представлением эпидемии. Мы определили наиболее подходящую функцию экспоненциального роста, но в дальнейшем возможно изучение, например, логистического роста.
Экспоненциальный рост соответствует эпидемии только на ее начальных этапах. В какой-то момент вылечившиеся люди больше не будут распространять инфекцию. Когда (почти) все окажутся зараженными или вылечившимися, рост прекратится.

Как построить график экспоненциальной функции — Объяснение!

Пошаговые примерыБольше примеров

Purplemath

Графики экспоненциальных функций аналогичны графикам, которые вы делали ранее. Однако по природе экспоненциальных функций их точки, как правило, либо очень близки к одному фиксированному значению, либо слишком велики, чтобы их можно было удобно изобразить на графике.

На самом деле будет всего несколько точек, которые «разумно» использовать для рисования вашего изображения.

Содержание продолжается ниже

MathHelp.com

Чтобы выбрать разумные точки, вам потребуется хорошее понимание общего поведения экспоненты, чтобы вы могли заполнить пробелы.

Какое основное свойство экспонент?

Помните, что основное свойство экспонент состоит в том, что они изменяются в заданной пропорции в течение заданного интервала. Например, медицинский изотоп, который распадается наполовину по сравнению с предыдущим количеством каждые двадцать минут, и бактериальная культура, которая удваивается каждый день, демонстрируют экспоненциальное поведение, потому что за заданный промежуток времени (двадцать минут и один день соответственно) количество изменилась в постоянной пропорции (в полтора и два раза соответственно).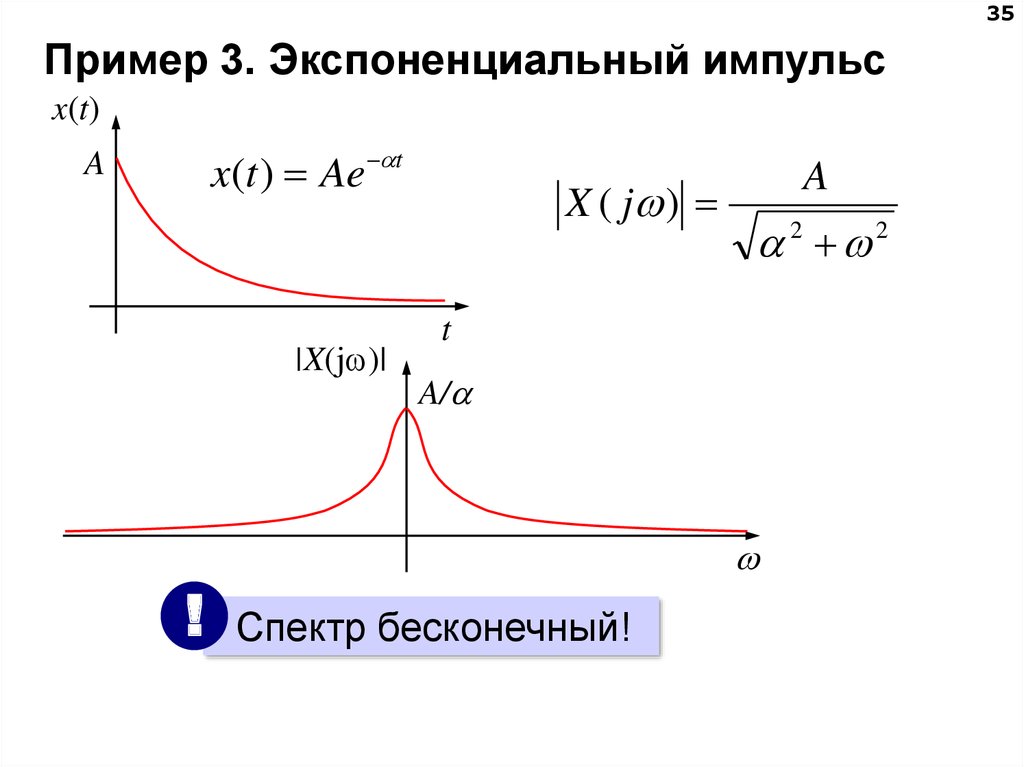

(Примечание: многие [«самые»?] экспоненты будут иметь беспорядочное время удвоения/уменьшения пополам, поэтому часто полезнее работать с точки зрения утроения, учетверения и т. д. времени, или данное упражнение может полностью игнорировать проблему , Если основание экспоненты не равно 2 [или ½], то не ожидайте, что время удвоения/уменьшения пополам будет подчеркнуто — или же не ожидайте, что время удвоения/уменьшения пополам будет красивым целым числом.)

Эта черта — наличие фиксированного времени деления пополам или удвоения — является основной для экспоненциальных функций. Но это может сделать график немного рискованным.

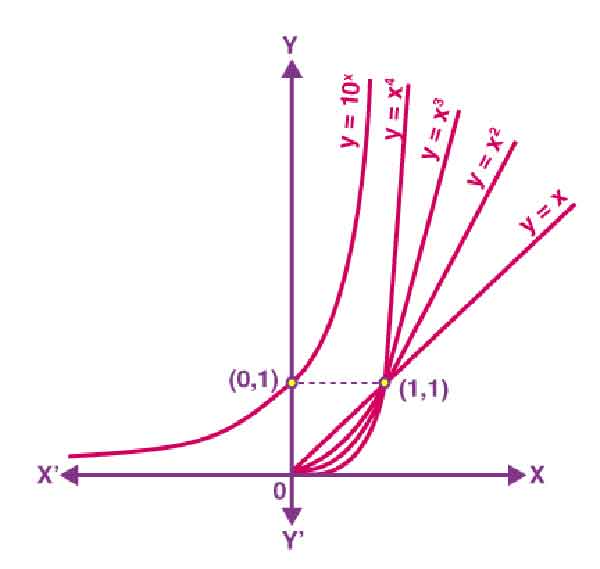
Такое поведение можно увидеть в любой базовой экспоненциальной функции, поэтому мы будем использовать y = 2 ^x как представление всего класса функций:

В левой части x -ось, график отображается на оси x . Но ось x представляет y = 0. Сможете ли вы когда-нибудь превратить 2 в 0, возведя его в степень? Конечно, нет.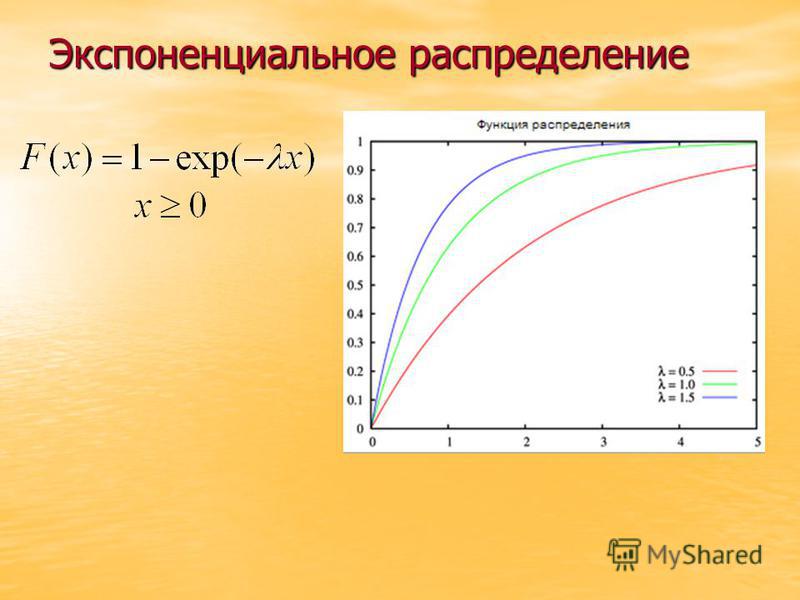 И положительная 2 не может превратиться в отрицательное число, если возвести его в степень.

Итак, линия, несмотря на свой внешний вид, никогда не опускается ниже оси x в отрицательные значения

y ; график y = 2 ^x всегда фактически выше оси x , даже если только на исчезающе малую величину.

Так почему он выглядит так, как будто он прямо на оси? Помните, что делают отрицательные экспоненты: они говорят вам перевернуть основание на другую сторону дробной черты. Итак, если, скажем, x = -4, приведенная выше экспоненциальная функция даст нам 2 ⁻⁴ , что составляет 2 ⁴ = 16, а затем переворачивается снизу, чтобы получить

1/16, что довольно мало.

По характеру экспонент каждый раз, когда мы возвращаемся назад (то есть всякий раз, когда мы двигаемся дальше влево) на 1 по оси x , линия только наполовину меньше высоты над осью x , чем она. было для предыдущего значения x

. То есть, в то время как

y = 1/16 для x = -4, линия будет вдвое короче, на y = 1/32, для x = -5.

Итак, хотя линия на самом деле никогда не касается и не пересекает ось x , она чертовски близка! Вот почему, говоря практически, левая часть основной экспоненты имеет тенденцию быть направленной вдоль оси. Если вы увеличите график достаточно близко, вы в конечном итоге сможете увидеть, что график действительно выше оси x , но достаточно близко, чтобы не иметь никакого значения, по крайней мере, в том, что касается графика.

Если вы используете TABLE или другую подобную функцию вашего графического калькулятора для поиска точек графика для вашего графика, вы должны знать, что ваш калькулятор будет возвращать y -значение 0 для сильно отрицательных x -значений. Ваш калькулятор может содержать только определенное количество знаков после запятой, и в конце концов он просто сдается и говорит: «Эй, ноль уже достаточно близко»:

Но вы не должны забывать, что это всего лишь признак ограничений технологии.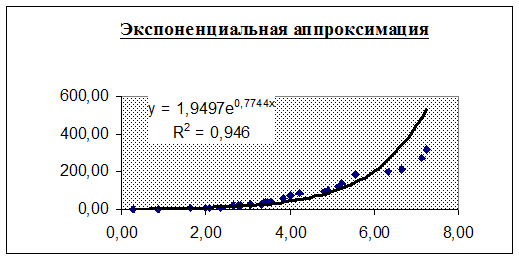 Как я часто говорю своим ученикам: «Ученик умный, калькулятор глупый». Нужно помнить, что что бы ни говорил калькулятор, график все равно выше х — ось; значения и по-прежнему положительны, хотя и очень, очень, очень малы.

Давайте снова посмотрим на график y = 2 ^x :

Вы можете видеть, что в правой части оси x график взлетает до небес. Это опять-таки из-за удвоения экспоненты. Как только функции начинают заметно расти, они продолжают удваиваться, поэтому очень быстро становятся очень большими.

Обычно вы не будете наносить много точек в левой части графика, потому что y -значения становятся настолько близкими к нулю, что делают точки графика неотличимыми от оси

x . Вы будете рисовать ту сторону графика, которая движется поверх оси.

И, как правило, вы не будете строить много точек в правой части графика, потому что значения и становятся слишком большими. Вот почему я подробно рассказал об общей форме и поведении экспоненты: вам понадобятся эти знания, чтобы помочь вам в построении графика, поэтому убедитесь, что вы достаточно хорошо его понимаете.

Что нужно знать при построении графика экспоненты:

Переменная функции будет в степени.
Число, на котором стоит сила, называется базовым.
Экспоненциальные функции имеют время удвоения (или деления пополам).
Графики обычно выглядят довольно горизонтально для одной половины.
Для второй половины графики обычно растут безумно быстро.
С недоверием относитесь к тому, что говорит вам ваш калькулятор.
Тщательно и аккуратно делайте графики.

URL: https://www.purplemath.com/modules/graphexp.htm

Страница 2Страница 3Страница 4

Графики и конечное поведение экспоненциальных функций

Теперь, когда мы рассмотрели формулу экспоненциальной функции, мы посвятим этот раздел изучению графиков, включая конечное поведение 9x\text{,}\) возможны две формы графика:

(a) Экспоненциальный рост: \(b\gt1\)(b) Экспоненциальный спад: \(b\lt1\) Рисунок 14.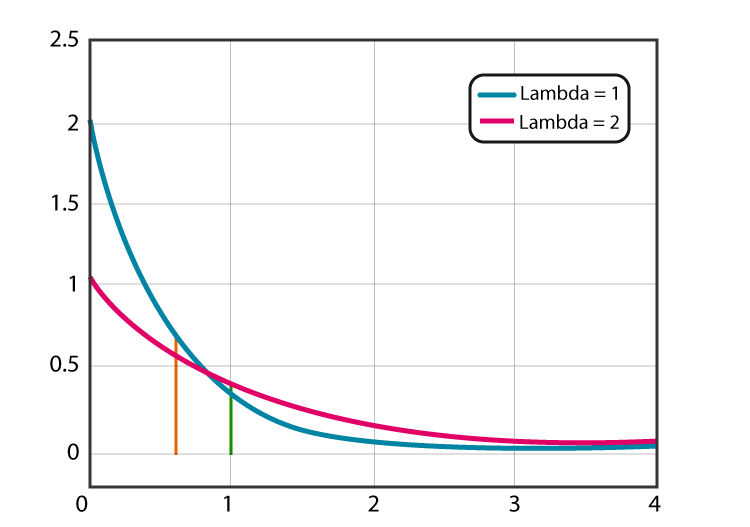

13. Две возможные формы графика экспоненциальной функции.

Глядя на два графика, мы видим, что конечное поведение отличается от того, что мы видели раньше: у него есть горизонтальная асимптота на одной стороне, а другая увеличивается до \(\infty\text{.}\)

Факт 14.14. Нахождение конечного поведения экспоненциальной функции.

Чтобы найти конечное поведение экспоненциальной функции, нам сначала нужно выяснить, представляет ли она рост или убывание. После этого мы можем использовать форму графика для определения конечного поведения.

Для функций с экспоненциальным ростом мы имеем следующее конечное поведение.

Конечное поведение слева (как \(x\стрелка вправо -\infty\)), оно имеет горизонтальную асимптоту в точке \(y=0\)*
Конечное поведение справа (как \(x\стрелка вправо \infty\)), \(y\стрелка вправо \infty\text{.}\)

Для функций с экспоненциальным убыванием мы имеем следующее конечное поведение.

Конечное поведение слева (как \(x\стрелка вправо -\infty\)), \(y\стрелка вправо \infty\) 9х\текст{. }\)
Ответ.
- Как \(x\стрелка вправо -\infty\текст{,}\) \(y\стрелка вправо \infty\текст{.}\)
- Как \(x\стрелка вправо \infty\текст{,}\) \(y\стрелка вправо 0\текст{.}\)
Раствор.
Так как \(b=0.01\lt 1\text{,}\) мы можем видеть, что это экспоненциальное затухание. Основываясь на форме графика экспоненциального затухания, мы имеем следующее конечное поведение: ) 9{x+3}-2\text{.}\) Поскольку \(b=1,56\gt 1\text{,}\) мы видим, что это экспоненциальный рост. Итак, мы знаем, как выглядит форма графика, но обратите внимание, что здесь есть некоторые преобразования. \(+3\) — это сдвиг по горизонтали, который не повлияет на наше конечное поведение, поэтому мы можем его игнорировать. Однако \(-2\) сдвигает весь граф вниз. Это не повлияет на сторону, ведущую к \(\infty\) (поскольку \(\infty-2\) по-прежнему \(\infty\)), но сдвинет нашу горизонтальную асимпоту вниз на 2.
No related posts.