Решение четырехэтажных дробей. Дроби. Умножение и деление дробей
Инструкция
Принято разделять обыкновенные и десятичные дроби , знакомство с которыми начинается еще в средней школе. В настоящее нет такой области знаний, где не применялось бы это . Даже в мы говорим первая 17 века, и все сразу , что имеются ввиду 1600-1625 года. Также часто приходится сталкиваться с элементарными действиями над , а также их преобразованием из одного вида в другой.
Приведение дробей к общему знаменателю является, пожалуй, наиболее важным действием над . Это основа проведения абсолютно всех вычислений. Итак, допустим есть две дроби a/b и c/d. Тогда, для того чтобы привести их к общему знаменателю, нужно найти наименьшее общее кратное (М) чисел b и d, и далее умножить числитель первой дроби на (М/b), а числитель второй на (M/d).
Сравнение дробей, еще одна немаловажная задача. Для того чтобы это сделать, приведите заданные простые дроби к общему знаменателю и потом сравните числители, чей числитель окажется больше, та дробь и больше.
Для того чтобы выполнить сложение или вычитание обыкновенных дробей, нужно привести их к общему знаменателю, а после произвести нужное математическое с этих дробей. Знаменатель же остается без изменения. Допустим нужно из a/b вычесть c/d. Для этого требуется найти наименьшее общее кратное M чисел b и d, и после вычесть из одного числителя другой, не меняя при этом знаменатель: (a*(M/b)-(c*(M/d))/M
Достаточно просто умножить одну дробь на другую, для этого следует просто перемножить их числители и знаменатели:
(a/b)*(c/d)=(a*c)/(b*d)Чтобы разделить одну дробь на другую, нужно дробь делимого умножить на дробь обратную делителю. (a/b)/(c/d)=(a*d)/(b*c)
Стоить напомнить, что для того чтобы получить обратную дробь, нужно числитель и знаменатель поменять местами.
Дробные выражения сложны для понимания ребёнком. У большинства возникают сложности, связанные с . При изучении темы «сложение дробей с целыми числами», ребёнок впадает в ступор, затрудняясь решить задание.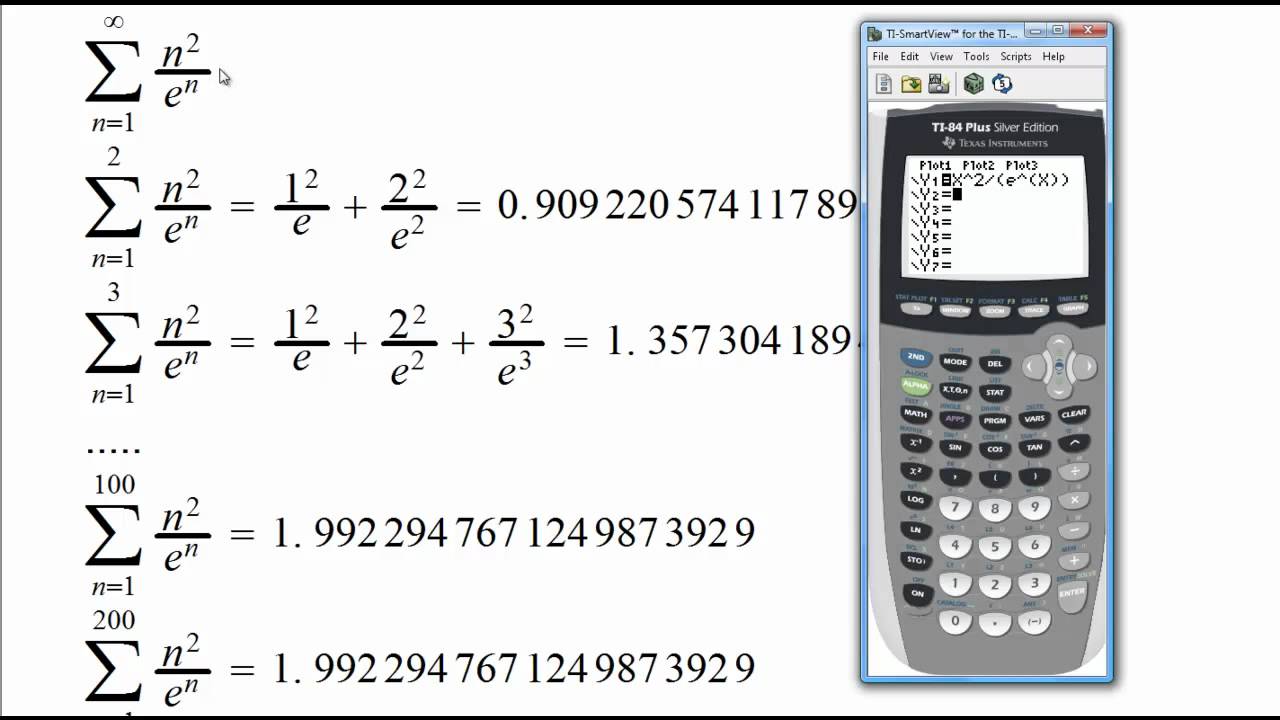
Объясним ребёнку наглядно. Возьмём три яблока, два из которых будут целыми, а третье разрежем на 4 части. От разрезанного яблока отделим одну дольку, а остальные три положим рядом с двумя целыми фруктами. Получим ¼ яблока в одной стороне и 2 ¾ — в другой. Если мы их соединим, то получим целых три яблока. Попробуем уменьшить 2 ¾ яблока на ¼, то есть уберём ещё одну дольку, получим 2 2/4 яблока.
Рассмотрим подробнее действия с дробями, в составе которых присутствуют целые числа:
Для начала вспомним правило вычисления для дробных выражений с общим знаменателем:
На первый взгляд всё легко и просто. Но это касается только выражений, не требующих преобразования.
Как найти значение выражения где знаменатели разные
В некоторых заданиях необходимо найти значение выражения, где знаменатели разные.
3 2/7+6 1/3
Найдём значение данного выражения, для этого найдём для двух дробей общий знаменатель.
Для чисел 7 и 3 – это 21. Целые части оставляем прежними, а дробные – приводим к 21, для этого первую дробь умножаем на 3, вторую – на 7, получаем:
6/21+7/21, не забываем, что целые части не подлежат преобразованию. В итоге получаем две дроби с одним знаменателям и вычисляем их сумму:
3 6/21+6 7/21=9 15/21
Что если в результате сложения получается неправильная дробь, которая уже имеет целую часть:
2 1/3+3 2/3
В данном случае складываем целые части и дробные, получаем:
5 3/3, как известно, 3/3 – это единица, значит 2 1/3+3 2/3=5 3/3=5+1=6
С нахождением суммы всё понятно, разберём вычитание:
Из всего сказанного вытекает правило действий над смешанными числами, которое звучит так:
- Если же от дробного выражения необходимо вычесть целое число, не нужно представлять второе число в виде дроби, достаточно произвести действие только над целыми частями.
Попробуем самостоятельно вычислить значение выражений:
Разберём подробнее пример под буквой «м»:
4 5/11-2 8/11, числитель первой дроби меньше, чем второй. Для этого занимаем одно целое число у первой дроби, получаем,
3 5/11+11/11=3 целых 16/11, отнимаем от первой дроби вторую:
3 16/11-2 8/11=1 целая 8/11
- Будьте внимательны при выполнении задания, не забывайте преобразовывать неправильные дроби в смешанные, выделяя целую часть. Для этого необходимо значение числителя разделить на значение знаменателя, то что получилось, встаёт на место целой части, остаток – будет числителем, например:
19/4=4 ¾, проверим: 4*4+3=19, в знаменателе 4 остаётся без изменений.
Подведём итог:
Перед тем как приступить к выполнению задания, связанного с дробями, необходимо проанализировать, что это за выражение, какие преобразования нужно совершить над дробью, чтобы решение было правильным. Ищите более рациональные способ решения.
Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Чтобы не произошло путаницы при решении дробных выражений, необходимо руководствоваться правилом последовательности. Решайте всё внимательно, не торопясь.
Практически каждый пятиклассник после первого знакомства с обыкновенными дробями находится в небольшом шоке. Мало того, что нужно еще понять суть дроби, так с ними еще придется выполнять арифметические действия. После этого маленькие ученики будут систематически допрашивать своего учителя, разузнавать когда же эти дроби кончатся.
Чтобы избежать подобных ситуаций, достаточно всего лишь как можно проще объяснить детям эту нелегкую тему, а лучше в игровой форме.
Суть дроби
Перед тем, как узнать что такое дробь, ребенок должен познакомиться с понятием доля . Здесь лучше всего подойдет ассоциативный метод.
Представьте целый торт, который поделили на несколько равных частей, допустим на четыре.
Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.
Доли бывают разные, потому что, целое можно поделить на совершенно разное количество частей. Чем больше долей в целом, тем они меньше, и наоборот.
Чтобы доли можно было обозначить, придумали такое математическое понятие, как обыкновенная дробь . Дробь позволит нам записать столько долей, сколько потребуется.
Составными частями дроби являются числитель и знаменатель, которые разделены дробной чертой либо наклонной чертой. Многие дети не понимают их смысла, поэтому и суть дроби им не понятна. Дробная черта обозначает деление, здесь нет ничего сложного.
Знаменатель принято записывать снизу, под дробной чертой или справа от накл.черты. Он показывает количество долей целого. Числитель, он записывается сверху над дробной чертой или слева от накл.черты, определяет сколько долей взяли.К примеру дробь 4/7. В данном случае 7-это знаменатель, показывает, что есть всего 7 долей, а числитель 4 указывает на то, что из семи долей взяли четыре.
Основные доли и их запись в дробях:
Помимо обыкновеной, существует еще и десятичная дробь.
Действия с дробями 5 класс
В пятом классе учатся выполнять все арифметические действия с дробями.
Все действия с дробями выполняются по правилам, и надеяться на то, что не выучив правило все получится само сабой не стоит. Поэтому не стоит пренебрегать устной частью домашнего задания по математике.
Мы уже поняли, что запись десятичной и обыкновенной дроби различны, следовательно и арифметические действия будут выполняться по-разному. Действия с обыкновенными дробями зависят от тех чисел, которые стоят в знаменателе, а в десятичной-после запятой справа.
Для дробей, у которых знаменатели одинаковые, алгоритм сложения и вычитания очень прост. Действия выполняем только с числителями.
Для дробей с разными знаменателями нужно найти Наименьший Общий Знаменатель (НОЗ). Это то число, которое будет делиться без остатка на все знаменатели, и будет наименьшим из таких чисел, если их несколько.
Для сложения либо вычитания десятичных дробей, нужно записать их в столбик, запятая под запятой, и уравнить количество десятичных знаков если это требуется.
Чтобы перемножить обыкновенные дроби просто найди произведение числителей и знаменателей. Очень простое правило.
Деление выполняется по следующему алгоритму:
- Делимое записать без изменения
- Деление превратить в умножение
- Делитель перевернуть (записать обратную дробь делителю)
- Выполнить умножение
Сложение дробей, объяснение
Давайте более подробно разберем, как складывать обыкновенные и десятичные дроби.
Как видно на изображении выше, у дроби одна третья и две третьих общий знаменатель три. Значит требуется сложить только числители единицу и два, а знаменатель оставить без изменения. В итоге получается сумма три третьих. Такой ответ, когда числитель и знаменатель дроби равны, можно записать как 1, так как 3:3 = 1.
Требуется найти сумму дробей две третьих и две девятых. В этом случае знаменатели различны, 3 и 9. Чтобы выполнить сложение, нужно подобрать общий. Есть очень простой способ. Выбираем наибольший знаменатель, это 9. Проверяем делится ли он на 3. Так как 9:3 = 3 без остатка, следовательно 9 подходит как общий знаменатель.
Следующим шагом находим дополнительные множители для каждого числителя. Для этого общий знаменатель 9 делим поочередно на знаменатель каждой дроби, полученные числа и будут допол. множ. Для первой дроби: 9:3 = 3, дописываем к числителю первой дроби 3. Для второй дроби: 9:9 = 1, единицу можно не дописывать, так как при умножении на нее получится то же самое число.
Теперь умножаем числители на их дополнительные множители и складываем результаты. Полученная сумма дробь восемь девятых.
Сложение десятичных дробей выполняется по тому же правилу, что и сложение натуральных чисел. В столбик, разряд записывается под разрядом. Единственное отличие в том, что в десятичных дробях нужно правильно поставить запятую в результате.
Для этого дроби записываются запятая под запятой, и в сумме требуется лишь снести запятую вниз.
Найдем сумму дробей 38, 251 и 1, 56. Чтобы было удобнее выполнять действия, мы уровняли количество десятичных знаков справа, добавив 0.
Складываем дроби не обращая внимания на запятую. А в полученной сумме просто опускаем запятую вниз. Ответ: 39, 811.
Вычитание дробей, объяснение
Чтобы найти разность дробей две третьих и одна третья, нужно вычислить разность числителей 2-1 = 1, а знаменатель оставить без изменения. В ответе получаем разность одну третью.
Найдем разность дробей пять шестых и семь десятых. Находим общий знаменатель. Используем способ подбора, из 6 и 10 наибольший 10. Проверяем: 10: 6 без остатка не делится. Добавляем еще 10, получается 20:6, тоже без остатка не делится. Снова увеличиваем на 10, получили 30:6 = 5. Общий знаменатель 30. Так же НОЗ можно найти по таблице умножения.
Находим дополнительные множители. 30:6 = 5 — для первой дроби.
30:10 = 3 — для второй. Перемножаем числители и их доп.множ. Получаем уменьшаемое 25/30 и вычитаемое 21/30. Далее выполняем вычитание числителей, а знаменатель оставляем без изменения.
В результате получилась разность 4/30. Дробь сократимая. Разделим ее на 2. В ответе 2/15.
Деление десятичных дробей 5 класс
В этой теме рассматривается два варианта действий:
Умножение десятичных дробей 5 класс
Вспомните, как вы умножаете натуральные числа, точно таким же способом и находят произведение десятичных дробей. Сначала разберемся, как умножить десятичную дробь на натуральное число. Для этого:
При умножении десятичной дроби на десятичную, действуем точно также.
Смешанные дроби 5 класс
Пятиклашки любят называть такие дроби не смешанные, а >, наверное так легче запомнить. Смешанные дроби называются так от того, что они получились путем соединения целого натурального числа и обыкновенной дроби.
Смешанная дробь состоит из целой и дробной части.
При чтении таких дробей сначала называют целую часть, затем дробную: одна целая две третьих, две целых одна пятая, три целых две пятых, четыре целых три четвертых.
Как же они получаются, эти смешанные дроби? Все довольно просто. Когда мы получаем в ответе неправильную дробь (дробь у которой числитель больше знаменателя), мы ее должны всегда переводить в смешанную. Достаточно разделить числитель на знаменатель. Это действие называется выделением целой части:
Перевести смешанную дробь обратно в неправильную тоже несложно:
Примеры с десятичными дробями 5 класс с объяснением
Много вопросов у детей вызывают примеры на несколько действий. Разберем пару таких примеров.
(0,4 · 8,25 — 2,025) : 0,5 =
Первым действием находим произведение чисел 8,25 и 0,4. Выполняем умножение по правилу. В ответе отсчитываем справа налево три знака и ставим запятую.
Второе действие находится там же в скобках, это разность.
От 3,300 вычитаем 2,025. Записываем действие в столбик, запятая под запятой.
Третье действие-деление. Полученную разность во втором действии делим на 0,5. Запятая переносится на один знак. Результат 2,55.
Ответ: 2,55.
(0, 93 + 0, 07) : (0, 93 — 0, 805) =
Первое действие сумма в скобках.Складываем в столбик, помним, что запятая под запятой. Получаем ответ 1,00.
Второе действие разность из второй скобки. Так как у уменьшаемого меньше знаков после запятой, чем у вычитаемого, добавляем недостающий. Результат вычитания 0 ,125.
Третьим действие делим сумму на разность. Запятая переносится на три знака. Получилось деление 1000 на 125.
Ответ: 8 .
Примеры с обыкновенными дробями с разными знаменателями 5 класс с объяснением
В первом примере находим сумму дробей 5/8 и 3/7. Общим знаменателем будет число 56. Находим дополнительные множ., разделим 56:8 = 7 и 56:7 = 8. Дописываем их к первой и второй дроби соответственно.
Перемножаем числители и их множители, получаем сумму дробей 35/56 и 24/56. Получили сумму 59/56. Дробь неправильная, переводим ее в смешанное число.Остальные примеры решаются аналогично.
Примеры с дробями 5 класс для тренировки
Для удобства переведите смешанные дроби в неправильные и выполняйте действия.
Как научить ребенка легко решать дроби с помощью лего
С помощью такого конструктора можно не только хорошо развивать воображение ребенка, но и объяснить наглядно в игровой форме, что такое доля и дробь.
На картинке ниже показано, что одна часть с восемью кружками это целое. Значит, взяв пазл с четырьмя кружками, получается половина, или 1/2. На картинке наглядно показано, как решать примеры с лего, если считать кружки на деталях.
Вы можете построить башенки из определенного количества частей и подписать каждую из них, как на картинке ниже. Например возьмем башенку из семи частей. Каждая часть зеленого конструктора будет 1/7.
Если вы к одной такой части добавите еще две, то получится 3/7. Наглядное объяснение примера 1/7+2/7 = 3/7.
Чтобы получать пятерки по математике не забывайте учить правила и отрабатывать их на практике.
Удобный и простой онлайн калькулятор дробей с подробным решением может:
- Складывать, вычитать, умножать и делить дроби онлайн,
- Получать готовое решение дробей картинкой и удобно его переносить.
Результат решения дробей будет тут…
0
1
2
3
4
5
6
7
8
9
Знак дроби «/»
+
—
*
:
_cтереть
Очистить
У нашего онлайн калькулятора дробей быстрый ввод . Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7 в калькулятор и нажмите кнопку «Решать дроби «.
Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку .
Знаки используемые для записи в калькуляторе
Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.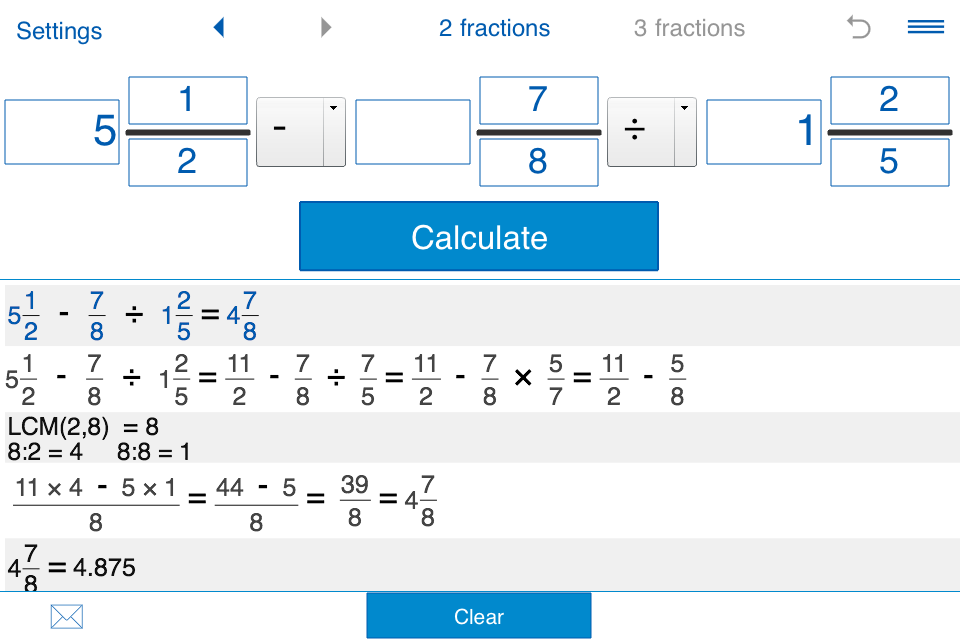
Возможности онлайн калькулятора дробей
Калькулятор дробей может выполнить операции только с 2-мя простыми дробями. Они могут быть как правильными(числитель меньше знаменателя), так и неправильными(числитель больше знаменателя). Числа в числителе и знаменатели не могут быть отрицательными и больше 999.Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду — сокращает дробь и выделяет целую часть, если потребуется.
Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса.
При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными. То есть минус на минус в данном случае дает плюс, а от перестановки слагаемых сумма не меняется. Этими же правилами мы пользуемся при вычитании дробей одна из которых отрицательная.
Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю.
Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.
В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей !
Понятие дроби вводится в курс математики начиная с 6 класса средней школы.
Дроби имеют вид: ±X/Y, где Y — знаменатель, он сообщает на сколько частей разделили целое, а X — числитель, он сообщает, сколько таких частей взяли.
Для наглядности возьмем пример с тортом:
В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.
Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.
Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.
Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.
Если числитель меньше знаменателя — дробь является правильной, если наоборот — неправильной. В состав дроби может входить целое число.
Например, 5 целых 3/4.
Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.
Если вы хотите запомнить, как решать дроби за 6 класс , вам надо понять, что решение дробей , в основном, сводится к понимаю нескольких простых вещей.
- Дробь по сути это выражение доли. То есть числовое выражение того, какую часть составляет данное значение от одного целого. К примеру дробь 3/5 выражает, что, если мы поделили что то целое на 5 частей и количество долей или частей это этого целого — три.
- Дробь может быть меньше 1, например 1/2(или по сути половина), тогда она правильная. Если дробь больше 1, к примеру 3/2(три половины или один с половиной), то она неправильная и для упрощения решения, нам лучше выделить целую часть 3/2= 1 целая 1/2.
- Дроби это такие же числа, как 1, 3, 10, и даже 100, только числа это не целые а дробные. С ними можно выполнять все те же операции, что с числами. Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.
Как решать дроби. Примеры.
К дробям применимы самые разные арифметические операции.
Приведение дроби к общему знаменателю
Например, необходимо сравнить дроби 3/4 и 4/5.
Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.
е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
Наименьший общий знаменатель(4,5) = 20
Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю
Ответ: 15/20
Сложение и вычитание дробей
Если необходимо посчитать сумму двух дробей, их сначала приводят к общему знаменателю, затем складывают числители, при этом знаменатель останется без изменений. Разность дробей считается аналогичным образом, различие лишь в том, что числители вычитаются.
Например, необходимо найти сумму дробей 1/2 и 1/3
Теперь найдем разность дробей 1/2 и 1/4
Умножение и деление дробей
Тут решение дробей несложное, здесь все достаточно просто:
- Умножение — числители и знаменатели дробей перемножаются между собой;
- Деление — сперва получаем дробь, обратную второй дроби, т.е. меняем местами ее числитель и знаменатель, после чего полученные дроби перемножаем.
Например:
На этом о том, как решать дроби , всё.
Если у вас остались какие то вопросы по решению дробей , что то непонятно, то пишите в комментарии и мы обязательно вам ответим.
Если вы учитель, то возможно скачать презентацию для начальной школы (http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) будет вам кстати.
Калькулятор алгебры без дробей
Рабочий пример, иллюстрирующий работу калькулятора решения:
Калькулятор алгебры без дробей
В природе в большинстве случаев используются дроби. В результате большинство математических задач состоит из дробей или десятичных знаков. В отличие от натуральных чисел или целых чисел, вы не можете напрямую складывать или вычитать дроби. Тем не менее, вы можете решить любую задачу с дробями, используя правильный метод. Калькулятор алгебры с дробями помогает эффективно и точно решать такие задачи.
Первым шагом в решении или сложении дробей является определение знаменателей. Если знаменатели совпадают, то вам повезло.
Знаменатели похожи, что означает, что вы можете складывать или вычитать дроби напрямую.
Алгебраический калькулятор с дробями пригодится, когда вы пытаетесь решить алгебраические задачи, содержащие дроби.
Например, \frac{2}{5}+\frac{1}{5}можно вычислить напрямую, так как знаменатели являются общими.
Другие примеры без подобных знаменателей:
\frac{1}{2}+\frac{3}{5}
\frac{2}{5}-\frac{4}{6}
В последних примерах необходимо иметь выражения под общим знаменателем, прежде чем пытаться их решить. Это похоже на нахождение эквивалентных дробей с общим знаменателем. Для этого вы просто находите НОК знаменателей, а затем выражаете каждую дробь по новому найденному знаменателю. Вот как представить дроби под общим знаменателем:
- Найдите НОК (наименьшее общее кратное знаменателей)
- Выразите или перепишите дроби под новым найденным знаменателем. Это будет включать в себя деление НОК на знаменатель, умножение результата на числитель и выражение результатов в виде новой дроби под общим знаменателем.
LCM или наименьший общий знаменатель — это общий термин, используемый для LCM знаменателей дробей.
Примеры:
\frac{1}{3}+\frac{2}{5}=\frac{5+6}{15}=\frac{11}{12}
\frac{7} {14}+\frac{1}{7}+\frac{7+2}{14}
Как складывать дроби с одинаковым знаменателем с помощью калькулятора алгебры
Складывать дроби с общим знаменателем легко и просто. Обычно вы просто добавляете числители и записываете результаты над исходным знаменателем. Независимо от того, сколько членов у вас есть в выражении, просто добавьте все числители, а затем запишите результаты над исходным знаменателем.
Однако вам может понадобиться сократить ответ на более простые дроби. Это называется упрощением дробей. Алгебраический калькулятор для дробей распечатает ваши ответы в упрощенной дробной форме. Если вы не используете калькулятор, вам просто нужно разделить числитель и знаменатель на общий множитель, чтобы упростить его.
Пример
\frac{36}{48}=\frac{12}{12}*\frac{3}{4}
Таким образом, дробь \frac{36}{48}можно записать как \frac {3}{4}
Из приведенного выше примера легко и возможно записать данную дробь по-разному, просто умножив ее на множитель или разделив на общий множитель.
Как найти общий множитель или НОК без калькулятора алгебры
Поиск МОК может оказаться сложной задачей, особенно если числа маловероятны. Однако есть верный способ найти LCM. Использование нашего калькулятора LCM гарантирует, что вы получите точный LCM.
Основной или наиболее фундаментальный метод состоит в том, чтобы разложить заданные числа на простые множители. Простой множитель — это число или множитель, который является простым. Это означает, что у него нет других делителей, кроме одного и самого себя.
Например, давайте найдем НОК 36 и 24
24 = 2*2*2*3
36 = 2*2*3*3
После того, как вы разложили два числа на соответствующие простые множители как показано, вы продолжаете и выбираете общие факторы. Легко видеть, что 2,2,3 являются общими в обоих выражениях. Таким образом, LCM сводится к нахождению произведения этих факторов.
Помогает ли ваш алгебраический калькулятор найти НОК дробей?
Да, действительно, калькулятор решает дроби, а также помогает найти НОК.
У нас есть отдельные калькуляторы как для LCM, так и для расчета дробей.
Чтобы складывать или вычитать дроби с помощью калькулятора, просто поместите математическое выражение в текстовую область. Выберите Решать дроби в качестве метода. Затем нажмите кнопку расчета, чтобы получить результаты.
Допустимые математические символы и их использование 9Используется для экспоненты или для возведения в степень
Перейти к решаемым примерам алгебры с шагами
Подробнее о решении
Калькулятор абсолютного значения — MathCracker.com
Алгебра Решатели
Инструкции: Введите любое число или числовое выражение, и решатель вычислит его абсолютное значение.
Например, для дробей введите «-2/3».
Введите число, чтобы вычислить его абсолютное значение =
Абсолютное значение — это математическая операция, применяемая к действительным числам, которая определяется следующим образом:
- Для действительного числа \(x\), если \(x\) положительно (или равно нулю), абсолютное значение \(x\) равно \(x\)
- С другой стороны, если \(x\) отрицательно, абсолютное значение \(x\) равно \(-x\)
Что такое символ абсолютного значения?
С математической точки зрения наиболее распространенным символом, используемым для абсолютного значения, является \(| x |\), который представляет абсолютное значение заданного числа \(x\).
Но это не всегда так, поскольку некоторые калькуляторы могут использовать свои собственные специальные обозначения, такие как \(abs(x)\), которые также широко используются.
Уравнения с абсолютными значениями
Одним из наиболее распространенных применений абсолютных значений, помимо простого вычисления абсолютных значений чисел, является их использование в уравнениях. Например
\( |х — 1 | = 3\)соответствует уравнению с абсолютным значением, потому что есть уравнение, которое необходимо решить относительно \(x\), и в нем участвует абсолютное значение. Этот с таким уравнением может быть сложнее иметь дело из-за необходимости правильно обращаться с абсолютным значением.
Примеры расчета абсолютных значений
Например:
\[ |3| = 3\] потому что 3 положительный.