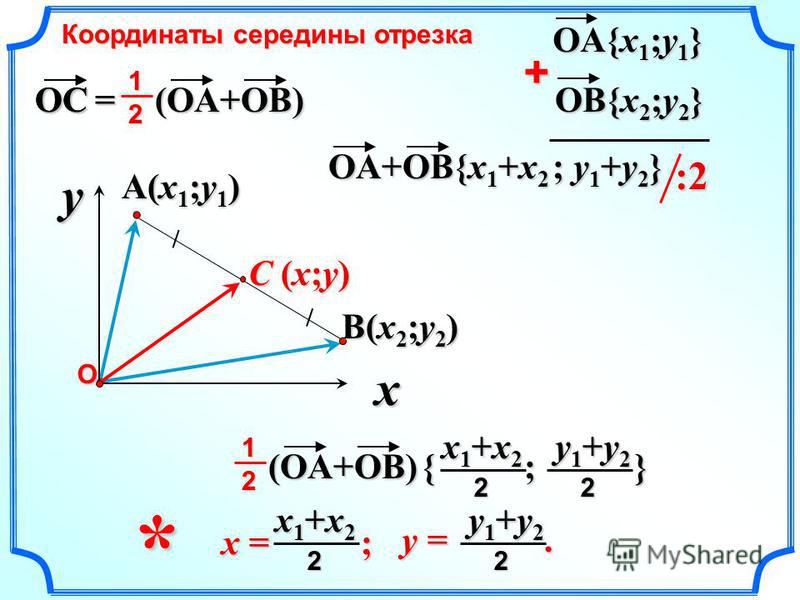
Координаты точки на плоскости, координаты середины отрезка, расстояние между двумя точками
Запомнить
Восстановить пароль
Регистрация
Конспект
Каждой точке координатной плоскости соответствуют две координаты. Координаты точки на плоскости – это пара чисел, в которой на первом месте стоит абсцисса, а на втором – ордината точки.
Например, точка \(A\) с координатами \((x; y)\) обозначается как \(A(x; y)\).
У точки, лежащей на оси абсцисс, ордината равна нулю; у точки, лежащей на оси ординат, абсцисса равна нулю. Обе координаты начала координат равны нулю.
Середина отрезка – это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек. Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка. 2}\).
2}\).
Порядок точек не играет роли.
Даны точки \(M(-4; 1), N(2; -2), P(1; 3)\). Определите координаты точки О, если\(\ \vec{MN} = \vec{OP}\).
Точка М – середина отрезка АВ. Найдите координаты точки А, если В(–8; –3), М(–12; 4).
Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Связь между координатами вектора и координатами его начала и конца 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 27.
Связь между координатами вектора и координатами его начала и конца.
Ты уже знаком с понятием координат вектора. Ими называют коэффициенты разложения данного вектора по единичным координатным векторам i⃗ и j⃗.
Сегодня мы ответим на вопрос «Как связаны координаты вектора с координатами его начала и конца?».
Но для начала вернёмся к координатам точки в прямоугольной системе координат.
Напомним, что для их определения нужно опустить перпендикуляры из данной точки к осям.
Точки пересечения данных прямых с осями обозначим как M1 и M2.
Абсциссой точки М является число x, которое является длиной отрезка OM1. А ординатой — число y, которое является длиной отрезка OM2.
M(x; y) x = OM1, y = OM2
Мы вспомнили, как определять координаты точек, а теперь вернёмся к общему случаю и, уже рассмотренной, точке M.
Проведём вектор из точки O к точке M. Запомни, вектор OM⃗ называют радиус-вектором точки M.
Сейчас докажем следующее утверждение: координаты точки M равны соответствующим координатам её радиус-вектора.
Доказать: M(x;y)=OM⃗x;y
Понятно, что вектор OM⃗=ОM1⃗+ОM2⃗ по правилу параллелограмма.
Теперь необходимо доказать, что вектор
OM1⃗=xi⃗, а вектор OM2⃗=yj⃗
Тем самым мы докажем, что вектор OM⃗x;y.
Если x > 0, то x = OM1, а векторы OM1⃗ и i⃗ сонаправлены, поэтому
OM1⃗=OM1∙i⃗=xi⃗
Если x x = OM1, а векторы OM1⃗ и i⃗ противоположно направлены. Поэтому OM1⃗=-OM1∙i⃗=xi⃗.
Наконец, если x = 0
OM1⃗=0⃗ и равенство OM1=xi⃗ в этом случае так же справедливо. Таким образом, в любом случае ОM1⃗=xi⃗. Аналогично доказывается, что ОM2⃗=yj⃗.
Следовательно,OM⃗=ОM1⃗+ОM2⃗=xi⃗+yj⃗
Отсюда следует, что координаты радиус-вектора OM равны (x
; y), то есть равны соответствующим координатам точки M.
Пользуясь доказанным утверждением, выразим координаты вектора AB⃗ через координаты его начала A и конца B. Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
Вектор AB⃗ равен разности векторов OB⃗ и OA⃗, поэтому его координаты равны разностям соответствующих координат векторов OB⃗ и OA⃗. Но OB⃗ и OA⃗ – радиус-векторы точек B и A, и, значит, OB⃗ имеет координаты x2;y2, а OA⃗ имеет координаты x1;y1. Следовательно, вектор AB⃗ имеет координаты x2-x1;y2-y1.
Таким образом, каждая координата вектора равна разности соответствующих координат его конца и начала.
Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.
Рассмотрим три вспомогательные задачи:
-
Как найти координаты середины отрезка.
Пусть в системе координат Oxy точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
 Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
OC⃗=12OA⃗+OB⃗.
x=x1+x22; y=y1+y22
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
-
Вычисление длины вектора по его координатам.
Пусть вектор a⃗x;y, тогда длина вектора вычисляется по формуле:
a⃗=x2+y2
-
Вычисление расстояния между двумя точками. Пусть точка M1 имеет координаты (x1; y1), точка M2 – координаты (x2; y2). Выразим расстояние d между точками M1 и M2 через их координаты.
Рассмотрим вектор M1M2⃗. Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:
Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:
M1M2⃗=x2-x12+y2-y12
Пример:
-
Найти длину вектора a⃗-3;4
a⃗=x2+y2=-32+42=25=5
Ответ: 5
-
Найти расстояние между точкой A(2; 7) и точкой B(-2; 7)
d=-2-22+7-72=16=4
Ответ: 4
Midpoint Calculator
Использование калькулятора
Середина отрезка — это точка, которая находится посередине между двумя точками. Средняя точка находится на одинаковом расстоянии от каждой конечной точки.
Используйте этот калькулятор, чтобы вычислить среднюю точку, расстояние между двумя точками или найти конечную точку, зная среднюю и другую конечные точки.
Решения для расчета средней и конечной точек
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор средней точки показывает работу, которую нужно найти:
Калькулятор средней точки показывает работу, которую нужно найти:
- Средняя точка между двумя заданными точками
- Конечная точка задана одной конечной точкой и средней точкой
- Расстояние между двумя конечными точками
Калькулятор также предоставляет ссылку на Калькулятор уклона, который решит и продемонстрирует работу по нахождению уклона, уравнениям линии и точкам пересечения x и y для заданных двух точек.
Как вычислить середину
Вы можете найти середину отрезка по двум конечным точкам (x 1 , у 1 ) и (х 2 , у 2 ). Добавьте каждую координату x и разделите на 2, чтобы найти x средней точки. Добавьте каждую координату y и разделите на 2, чтобы найти y средней точки.
Вычислите среднюю точку (x M , y M ), используя формулу средней точки:
\( (x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_ {2}} {2} , \dfrac {y_{1} + y_{2}} {2}\right) \)
Важно отметить, что середина — это средняя точка на линии сегмент . Истинная линия в геометрии бесконечно длинна в обоих направлениях. Но отрезок прямой имеет 2 конечные точки, поэтому можно вычислить среднюю точку. Луч имеет один конец и бесконечно длинный в другом направлении.
Истинная линия в геометрии бесконечно длинна в обоих направлениях. Но отрезок прямой имеет 2 конечные точки, поэтому можно вычислить среднюю точку. Луч имеет один конец и бесконечно длинный в другом направлении.
Пример: найти середину
Допустим, вы знаете две точки на отрезке, и их координаты (6, 3) и (12, 7). Найдите середину по формуле средней точки.
\( (x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2} , \dfrac {y_{1} + y_{2}} { 2}\справа) \)
- Сначала добавьте координаты x и разделите на 2. Это даст вам координату x средней точки, x M
- Во-вторых, добавьте координаты y и разделите на 2. Это даст вам координату y средней точки, y М
- Возьмите каждый результат, чтобы получить среднюю точку.
 В этом примере средняя точка (9, 5).
В этом примере средняя точка (9, 5).
\(x_{M} = \dfrac {x_{1} + x_{2}} {2} \)
\(x_{M} = \dfrac {6 + 12} {2} \)
\(x_{M} = \dfrac {18} {2} \)
\( х_{М} = {9} \)
\(y_{M} = \dfrac {y_{1} + y_{2}} {2} \)
\(y_{M} = \dfrac {3 + 7} {2} \)
\(y_{M} = \dfrac {10} {2} \)
\(у_{М} = {5} \)
Как рассчитать расстояние между двумя точками
Если вы знаете конечные точки отрезка, вы можете использовать их для расчета расстояния между двумя точками. Здесь вы на самом деле находите длину отрезка. Используйте формулу для расстояния между 2 точками: 92} \)
\(d = \sqrt {36 + 64} \)
\(d = \sqrt {100} \)
\(d = 10\)
Подобно этому калькулятору средней точки, наш Калькулятор двухмерного расстояния. Расстояние между 2 точками в 3 измерениях с координатами (x, y, z) см. 3-х мерный калькулятор расстояний.
Как вычислить конечную точку
Если вы знаете конечную точку и середину отрезка, вы можете вычислить отсутствующую конечную точку.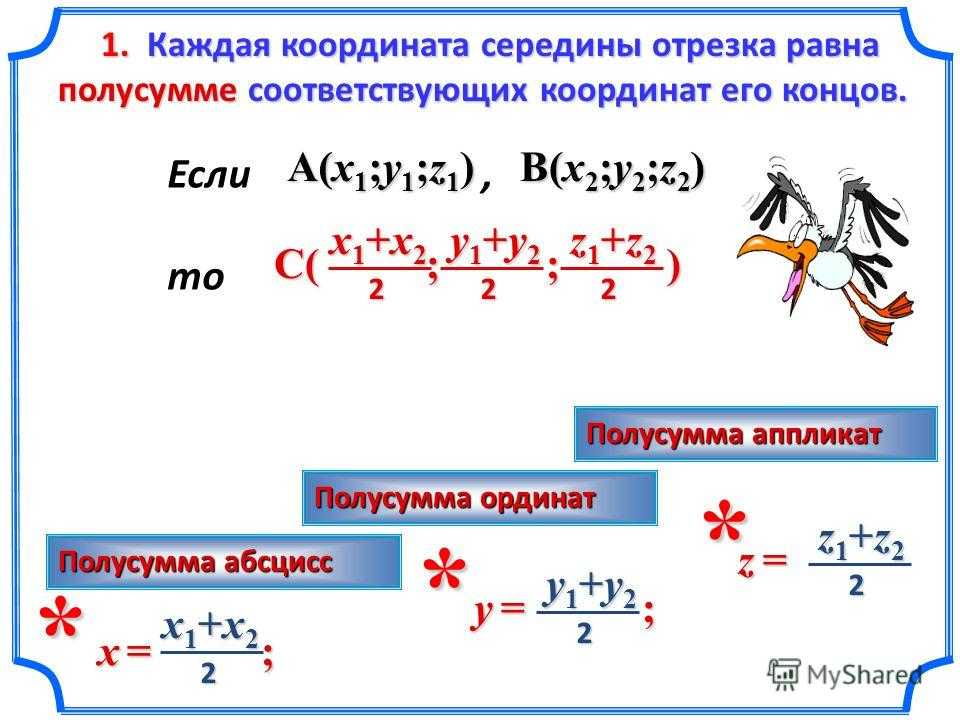 Начните с формулы средней точки сверху и определите координаты неизвестной конечной точки.
Начните с формулы средней точки сверху и определите координаты неизвестной конечной точки.
- Сначала возьмем формулу средней точки:
- И разбить его, чтобы у вас были отдельные уравнения для координат x и y средней точки
- Переставьте каждое уравнение так, чтобы вы решали x 2 и y 2
\( x_{2} = 2x_{M} — x_{1} \)
\(у_{2} = 2у_{М} — у_{1} \)
- Поскольку вы знаете середину, вставьте ее координаты вместо x M и y M в каждом уравнении
- Вставьте координаты вашей известной конечной точки в значения для x 1 и г 1
- Наконец, решите каждое уравнение, чтобы найти x 2 и y 2 , которые будут координатами вашей отсутствующей конечной точки
\((x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2}, \dfrac {y_{1} + y_{2}} {2 }\справа) \)
\(x_{M} = \dfrac {x_{1} + x_{2}} {2} \)
\(y_{M} = \dfrac {y_{1} + y_{2}} {2} \)
Пример: найти конечную точку
Используя приведенные выше шаги, давайте найдем конечную точку отрезка, где мы знаем, что одна конечная точка (6, -4), а средняя точка (1, 7). Конечная точка – это (x 1 , y 1 ) координата. Середина – это (x M , y M ) координата.
Конечная точка – это (x 1 , y 1 ) координата. Середина – это (x M , y M ) координата.
- Сначала возьмем формулу средней точки:
- И переставьте уравнения так, чтобы вы решали x2 и y2
- Вставьте координаты вашей средней точки (1, 7) вместо x M и y M в каждом уравнении
- Вставьте координаты вашей известной конечной точки (6, -4) в значения для x 1 и у 1
- Решите каждое уравнение, чтобы найти x 2 и y 2 .

- Ваша отсутствующая конечная точка (x 2 , y 2 ) равно (-4, 18)
\((x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2}, \dfrac {y_{1} + y_{2}} {2 }\справа) \)
\( х_{2} = 2х_{М} — х_{1} \)
\(у_{2} = 2у_{М} — у_{1} \)
\( х_{2} = 2(1) — х_{1} \)
\(у_{2} = 2(7) — у_{1} \)
\( х_{2} = 2(1) — 6 \)
\(у_{2} = 2(7) — (-4) \)
\( х_{2} = 2 — 6 \)
\(х_{2} = -4 \)
\( у_{2} = 14 + 4 \)
\( у_{2} = 18 \)
Калькулятор средней точки
Создано Матеушем Мухой и Петром Малеком
Отзыв от Jack Bowater
Последнее обновление: 10 февраля 2023 г.
Содержание:- Как найти среднюю точку
- Формула средней точки
- Другие связанные темы
- Часто задаваемые вопросы их . Эта точка часто используется в геометрии. В качестве дополнения к этому калькулятору мы написали статью ниже, в которой обсуждается, как найти среднюю точку и что такое формула средней точки.
Если вы хотите понять, как меняется одна координата относительно другой, рекомендуем проверить калькулятор средней скорости изменения.

Как найти середину
- Обозначьте координаты (x₁,y₁) и (x₂,y₂) .
- Введите значения в формулу.
- Сложите значения в скобках и разделите каждый результат на 2.
- Новые значения формируют новые координаты средней точки.
- Проверьте свои результаты с помощью калькулятора средней точки.
Предположим, у нас есть отрезок, и мы хотим разрезать его на две равные части. Для этого нам нужно знать центр. Мы можем добиться этого, найдя среднюю точку. Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.
Формула средней точки
Если у нас есть координаты (x₁,y₁) и (x₂,y₂) , то середина этих координат определяется как (x₁ + x₂)/2, (y₁ + y₂)/2 . Это формирует новую координату, которую вы можете назвать (x₃,y₃) .
 Калькулятор средней точки решит это мгновенно, если вы введете координаты. Выполните шаги, описанные выше, если рассчитываете вручную.
Калькулятор средней точки решит это мгновенно, если вы введете координаты. Выполните шаги, описанные выше, если рассчитываете вручную.Для небольших чисел легко вычислить среднюю точку вручную, но для больших и десятичных значений калькулятор является самым простым и удобным способом вычисления средней точки.
Отрезок можно разделить в любом соотношении, а не только 1:1. Используйте наш калькулятор соотношений направленных отрезков, чтобы узнать, как это сделать.
Как в геометрии часто требуется найти среднюю точку, так и найти расстояние между двумя точками. Расстояние между двумя точками на горизонтальной или вертикальной линии легко вычислить, но процесс усложняется, если точки не выровнены как таковые. Это часто имеет место при работе со сторонами треугольника. Поэтому калькулятор расстояний является удобным инструментом для выполнения этой задачи.
В некоторых геометрических случаях мы хотим вписать треугольник внутрь другого треугольника, где вершины вписанного треугольника лежат в середине исходного треугольника.
 Калькулятор средней точки чрезвычайно полезен в таких случаях.
Калькулятор средней точки чрезвычайно полезен в таких случаях.Часто задаваемые вопросы
Как найти середину класса?
- Найти нижний предел класса . Для диапазона 2-5 это 2.
- Найти верхний предел класса . Для того же диапазона это 5, .
- Сложите два числа вместе. Для нас это дает 7,
- Разделите результат на 2. Среднее значение класса 2-5 равно 3,5.
Как найти конечную точку со средней и другой конечной точкой?
- Удвойте среднюю точку.
- Вычтите известную конечную точку, чтобы получить другую. Это , не имеет значения, верхняя это или нижняя граница .
- Поразитесь своим математическим способностям!
Как найти середину треугольника?
Чтобы найти середину треугольника, технически известного как его центроид , выполните следующие действия:
Найдите середины сторон треугольника.
 Если вы знаете, как это сделать, перейдите к шагу 5 .
Если вы знаете, как это сделать, перейдите к шагу 5 .Измерьте расстояние между двумя конечными точками и разделите результат на 2. Это расстояние от любого конца является серединой этой линии.
Можно также добавить две координаты x конечных точек и разделить на 2. Сделайте то же самое для координат y. Результаты дают вам координаты средней точки.
Проведите линию между средней точкой и ее противоположным углом.
Повторить как минимум для одной пары средней и угловой точек или для обеих наивысшей степени точности .
Место пересечения всех линий находится в центре треугольника.
Что такое середина окружности?
Чтобы найти середину или центр окружности, следуйте этим инструкциям:
Найдите на окружности две точки, полностью противоположные друг другу , т.
 е. разделенные диаметром окружности.
е. разделенные диаметром окружности.Если вы знаете их координаты, сложите две координаты x вместе и разделите результат на 2. Это координата x центра.
Сделайте то же самое для 2-х координат y, что даст вам координату y.
Объедините два, чтобы получить координаты центроида .
Если вы не знаете координат, измерьте расстояние между двумя точками и половину его.
Эта половина расстояния между одной конечной точкой и другой является средней точкой.
Как найти середину квадрата?
Чтобы найти середину или центр тяжести квадрата, следуйте этому простому руководству:
Если у вас есть координаты двух противоположных углов квадрата, сложите 2 x координаты вместе и разделите результат на 2.
Сделайте то же самое для координаты y.
Используйте эти два рассчитанных числа, чтобы найти центр квадрата, поскольку они являются его координатами x и y соответственно.

В качестве альтернативы проведите линию от одного угла к противоположному углу и еще одну для оставшейся пары.
Место пересечения этих двух точек является центром тяжести квадрата.
Вы округляете середину?
В общем, вы не округляете средние точки . Вы определенно не используете непрерывные данные , так как эта точка является реальной точкой в наборе данных. Для дискретных данных вы обычно не делаете , вместо этого отмечая, что средняя точка является значением обоих значений по обе стороны от вычисления средней точки.
Что такое середина 0 и 5?
2,5 . Чтобы найти середину любого диапазона, сложите два числа вместе и разделите на 2. В этом случае 0 + 5 = 5, 5 / 2 = 2,5.
Как найти середину трапеции?
Вы можете найти середину или центр тяжести трапеции одним из двух способов:
- Проведите линию от одного угла трапеции к ее противоположному углу.

- Проделайте то же самое с оставшейся парой углов.
- Там, где эти две линии пересекаются, находится центр тяжести .
- Идеально сбалансируйте трапецию на ее центроиде!
Альтернативно:
- Возьмите координаты двух противоположных сторон.
- Сложите координаты x этих точек вместе и разделите на 2. Это координата x средней точки .
- Повторите для 2-х координат y, получив координату y средней точки .
Какая средняя точка между 0,2 и 2,8?
- Сложите 0 и 2, чтобы получить 2.
- Разделите результат на 2, чтобы получить 1. Это координата x средней точки.
- Сложите 2 и 8, получится 10.
- Разделить 10 на 2, получится 5; это координата y средней точки.
- Соедините две координаты вместе; середина (0,2) и (2,8) равна (1,5) .
Что такое среднее между 30 и 60?
45 .


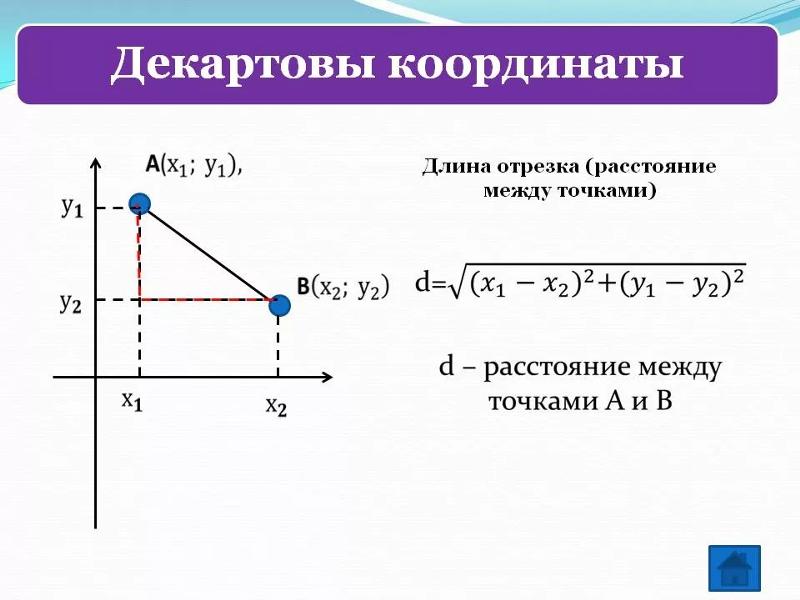 Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
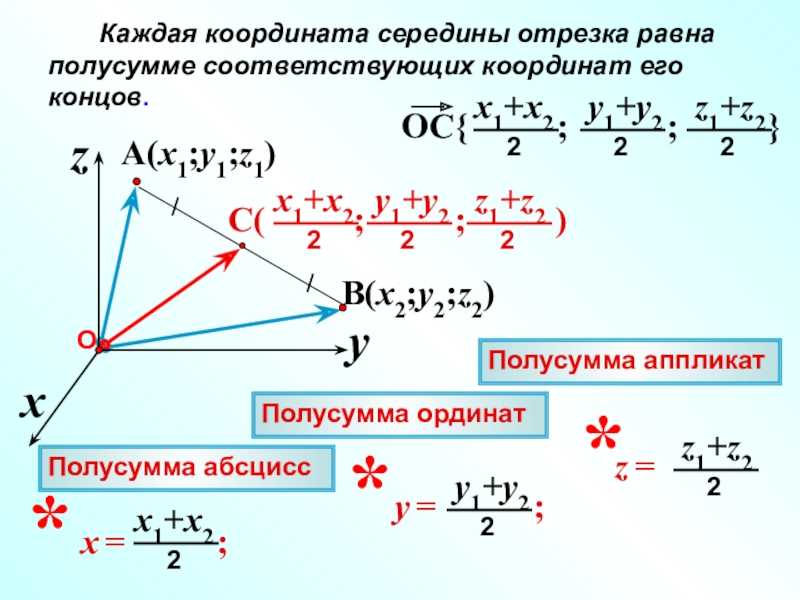 В этом примере средняя точка (9, 5).
В этом примере средняя точка (9, 5).

 Калькулятор средней точки решит это мгновенно, если вы введете координаты. Выполните шаги, описанные выше, если рассчитываете вручную.
Калькулятор средней точки решит это мгновенно, если вы введете координаты. Выполните шаги, описанные выше, если рассчитываете вручную.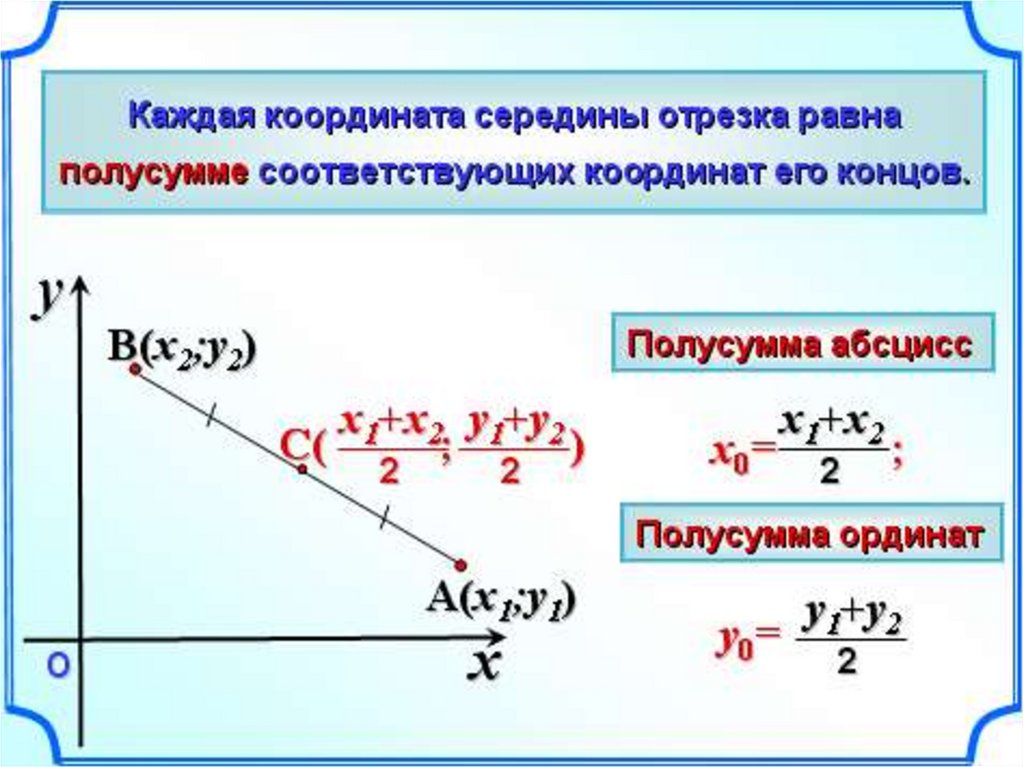 Калькулятор средней точки чрезвычайно полезен в таких случаях.
Калькулятор средней точки чрезвычайно полезен в таких случаях. Если вы знаете, как это сделать, перейдите к шагу 5 .
Если вы знаете, как это сделать, перейдите к шагу 5 . е. разделенные диаметром окружности.
е. разделенные диаметром окружности.