Калькулятор котангенса | Calculators.vip
Котангенс это отношение косинуса к синусу.
.
Поделиться расчетом:
Найти величину
X=SIN(A)X=COS(A)X=TAN(A)X=CTN(A)
A=ARC SIN(X)A=ARC COS(A)A=ARC TAN(X)A=ARC CTN(X)
Первоначальные данные
Градус
Радиан
Вычислить
| Угол в градусах | Ctg (Котангенс) |
|---|---|
| 0° | ∞ |
| 1° | 57.29 |
| 2° | 28.6363 |
| 3° | 19.0811 |
| 4° | 14.3007 |
| 5° | 11.4301 |
| 6° | 9.5144 |
| 7° | 8.1443 |
| 8° | 7.1154 |
| 9° | 6.3138 |
| 10° | 5.6713 |
| 11° | 5.1446 |
| 12° | 4.7046 |
| 13° | 4.3315 |
| 14° | 4. 0108 0108 |
| 15° | 3.7321 |
| 16° | 3.4874 |
| 17° | 3.2709 |
| 18° | 3.0777 |
| 19° | 2.9042 |
| 20° | 2.7475 |
| 21° | 2.6051 |
| 22° | 2.4751 |
| 23° | 2.3559 |
| 24° | 2.246 |
| 25° | 2.1445 |
| 26° | 2.0503 |
| 27° | 1.9626 |
| 28° | 1.8807 |
| 29° | 1.804 |
| 30° | 1.7321 |
| 31° | 1.6643 |
| 32° | 1.6003 |
| 33° | 1.5399 |
| 34° | 1.4826 |
| 35° | 1.4281 |
| 36° | 1.3764 |
| 37° | 1.327 |
| 38° | 1.2799 |
| 39° | 1.2349 |
| 40° | 1.1918 |
| 41° | 1.1504 |
| 42° | 1. 1106 1106 |
| 43° | 1.0724 |
| 44° | 1.0355 |
| 45° | 1 |
| 46° | 0.9657 |
| 47° | 0.9325 |
| 48° | 0.9004 |
| 49° | 0.8693 |
| 50° | 0.8391 |
| 51° | 0.8098 |
| 52° | 0.7813 |
| 53° | 0.7536 |
| 54° | 0.7265 |
| 55° | 0.7002 |
| 56° | 0.6745 |
| 57° | 0.6494 |
| 58° | 0.6249 |
| 59° | 0.6009 |
| 60° | 0.5774 |
| 61° | 0.5543 |
| 62° | 0.5317 |
| 63° | 0.5095 |
| 64° | 0.4877 |
| 65° | 0.4663 |
| 66° | 0.4452 |
| 67° | 0.4245 |
| 68° | 0.404 |
| 69° | 0.3839 |
| 70° | 0. 364 364 |
| 71° | 0.3443 |
| 72° | 0.3249 |
| 73° | 0.3057 |
| 74° | 0.2867 |
| 75° | 0.2679 |
| 76° | 0.2493 |
| 77° | 0.2309 |
| 78° | 0.2126 |
| 79° | 0.1944 |
| 80° | 0.1763 |
| 81° | 0.1584 |
| 82° | 0.1405 |
| 83° | 0.1228 |
| 84° | 0.1051 |
| 85° | 0.0875 |
| 86° | 0.0699 |
| 87° | 0.0524 |
| 88° | 0.0349 |
| 89° | 0.0175 |
| 90° | 0 |
Калькулятор тригонометрических функций
SmartCalculator.online
Калькулятор тригонометрических функций вычислит: синус, косинус, тангенс, котангенс, секанс, косеканс, гиперболический синус, гиперболический косинус, гиперболический тангенс, гиперболический котангенс, гиперболический секанс, гиперболический косеканс. Значением угла могут быть любые числа и выражения. Угловая мера может быть выражена в градусах, минутах и секундах, а также в радианах.
Значением угла могут быть любые числа и выражения. Угловая мера может быть выражена в градусах, минутах и секундах, а также в радианах.
Введите значение угла
Угловая мера
в градусах, минутах, секундахв радианах
*Чтобы найти значение арксинуса, арккосинуса, арктангенса, арккотангенса, арксеканса, арккосеканса, а также обратных гиперболических функций воспользуйтесь калькулятором обратных тригонометрических функций.
| Угол | ||
|---|---|---|
| Градусы, минуты, секунды | Градусы | Радианы |
| Тригонометрическая функция |
Обозначение | Десятичное представление |
Значение |
|---|---|---|---|
| Синус | sin | ||
| Косинус | cos | ||
| Тангенс | tg, tan | ||
| Котангенс | ctg, cot | ||
| Секанс | sec | ||
| Косеканс | csc, cosec | ||
| Гиперболический синус | sh, sinh | ||
| Гиперболический косинус | ch, cosh | ||
| Гиперболический тангенс | th, tanh | ||
| Гиперболический котангенс | cth, coth | ||
| Гиперболический секанс | sch, sech | ||
| Гиперболический косеканс | csch, csch |
Самыми распространенными системами измерения углов являются: градусная и радианная.
В градусной системе измерения углов:
1° (1 градус) равен 1/180 части развернутого угла, либо 1/360 часть окружности.
1′ (1 минута) равна 1/60 части градуса.
1» (1 секунда) равна 1/60 части минуты.
1° (1 градус)
1′ (1 минута) = 60 секунд.
1 радиан – угол длина дуги которого равна радиусу окружности.
1° = π/180 радиан ≈ 0.0174 рад
1 рад = 180/π градусов ≈ 57.2958°
Как перевести градусы, минуты и секунды в градусы
Чтобы перевести градусы, минуты и секунды в градусы необходимо минуты разделить на 60 и прибавить к градусам, затем секунды разделить на 3600 и прибавить к градусам.
Градусы = градусы + (минуты / 60) + (секунды / 3600)
Например, переведем 2 градуса 12 минут 34 секунды в градусы:
2° 12′ 34» = 2 + (12/60) + (34/3600) ≈ 2. 21°
21°
Переведем 27 минут 44 секунды в градусы:
27′ 44» = (27/60) + (44/3600) ≈ 0.462°
Переведем 7 секунд в градусы
7» = 7/3600 ≈ 0.00194°
Как перевести градусы в радианы
Чтобы перевести градусы в радианы нужно значение угла в градусах умножить на π и разделить на 180°.
x° = πx°/180° рад
Например, переведем 45 градусов в радианы:
45° = 3.14*45°/180° рад ≈ 0.785 рад
Как перевести радианы в градусы
Чтобы перевести радианы в градусы необходимо значение угла в радианах умножить на 180 и разделить на π.
x рад = (180x/π)°
Например, переведем 2 радиана в градусы:
2 рад = (180*2/π)° ≈ 114.592°
Тригонометрические функции
Дать определение тригонометрическим функциям можно построив в декартовой системе координат окружность единичного радиуса с центром в точки O. Угол определим, как поворот против часовой стрелки от положительного направления оси x до некоторой точки B на окружности. Если значение точки B по оси x обозначить как Bx, а по оси y как By, то тригонометрические функции можно определить, как:
Если значение точки B по оси x обозначить как Bx, а по оси y как By, то тригонометрические функции можно определить, как:
Синус α
Косинус α = Bx
Тангенс α = By/Bx
Котангенс α = Bx/By
Секанс α = 1/Bx
Косеканс α = 1/By
Гиперболические функции
sh = 12(eπ4-e-(π4))
ch = 12(eπ4+e-(π4))
th = e2(π4)-1e2(π4)+1
cth = e2(π4)+1e2(π4)-1
sch = 2eπ4+e-(π4)
csch = 2eπ4-e-(π4)
Другие калькуляторы
Калькулятор функции котангенса
Предположим, что после краткого знакомства с увлекательным миром тригонометрии ваш учитель решил, что пора проверить, сколько из сказанного им осталось в ваших мозгах . Они объявили о тестировании определений и формул функций, которые появятся позже на этой неделе.
Количество материала для изучения не так уж велико, и осталось еще немало дней, но будучи хорошим учеником, которым вы , вы решили начать подготовку сегодня. Вы убираете свой стол и для практики решаете вычислить значения всех тригонометрических функций для следующих углов:
Вы убираете свой стол и для практики решаете вычислить значения всех тригонометрических функций для следующих углов: 30° , 45° , 60° и 75° . В этой статье нас больше всего интересует как найти котангенс этих углов .
Прежде всего, давайте посмотрим, насколько легко решается задача с калькулятором кроватки Omni . Там нам нужно заполнить только одно переменное поле: угол . Мы вводим вышеуказанные числа одно за другим, и калькулятор котангенса выдает ответ под цифрой 9.0004 . Обратите внимание, что, хотя калькулятор котангенса стремится к точности, вы можете уменьшить количество значащих цифр, если собираетесь использовать значения в некоторых дальнейших вычислениях.
Также обратите внимание, как для 30° и 60° , он дает точные значения до их округления в большую сторону, то есть в виде дроби с квадратными корнями. Мы поговорим подробнее о том, почему это так, через секунду.
Мы поговорим подробнее о том, почему это так, через секунду.
Теперь пришло время оставить калькулятор котангенса на некоторое время и использовать то, что мы узнали из этой статьи. Другими словами, мы вычислим значения сами используя определение котангенса из первого раздела. (Конечно, если вы предпочитаете, вы можете использовать любую из трех других формул раскладушки.)
Для каждого угла мы начнем с рисунка прямоугольного треугольника с соответствующим углом. Начнем с первого: 30° .
Заметим, что это совершенно особый треугольник, в котором мы знаем отношения между сторонами , т. е. мы можем быть уверены, что если более короткая сторона имеет длину x , тогда гипотенуза будет 2x . Это потому, что наша фигура на самом деле является половиной равностороннего треугольника. Таким образом, у нас есть другой острый угол, равный 60° , поэтому мы можем использовать ту же картинку для этого случая .
Напомним, что кроватка в математике равна отношению катета, следующего за углом, к другому . Что такое котангенс в этом случае? Имеем:
раскладушка(30°) = x√3 / x = √3 ,и:
раскладушка(60°) = х / х√3 = 1 / √3 = √3 / 3 . Далее переходим к углу 45° .
Опять же, нам посчастливилось знать отношения между сторонами треугольника . На этот раз это потому, что форма на самом деле представляет собой половину квадрата.
Используя определение котангенса, получаем:
cot(45°) = x / x = 1 . Остался последний ракурс. Чему равен котангенс числа 75° ?
Ну, как оказалось, ответ не так прост . У нас нет специального треугольника для использования здесь. Мы могли бы, например, вспомнить предыдущий раздел и найти ответ, вычислив сначала tan(75°) . Однако для этого нам пришлось бы использовать, например, формулы половинного угла, что, в свою очередь, потребовало бы от нас найти
Однако для этого нам пришлось бы использовать, например, формулы половинного угла, что, в свою очередь, потребовало бы от нас найти cos(150°) . Эта задача, в конце концов, не так уж сложна, поскольку 150° = 180° - 30° , а оба 30° и 180° являются довольно простыми углами .
Урок здесь состоит в том, что в целом вычисление тригонометрических функций — это не прогулка в парке. На самом деле, мы обычно используем внешние инструменты для этого , такие как калькулятор котангенса Omni.
Тем не менее, эти несколько простых вычислений, несомненно, были хорошей подготовкой к предстоящему испытанию . Получив итоговую оценку по математике, вспомните все воспоминания, которыми вы поделились с помощью Omni Calculator, которые помогли вам на этом пути, и довольный кивок головы . Бедные разработчики контента жаждут этого. 😀
Калькулятор — cotan(pi/6) — Solumaths
Котан, расчет онлайн
Резюме:
Тригонометрическая функция котана для вычисления котана угла в радианах,
градусов или градианов.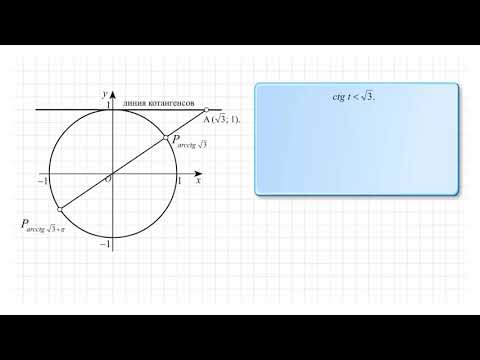
котанг онлайн
Описание:
Тригонометрическая функция котангенс отметил котан ,
это калькулятор котангенса , он позволяет онлайн расчет
котангенс угла, можно использовать разные угловые единицы: градусы, грады
или радианы, которые являются угловыми единицами по умолчанию.
Котангенс является обратным тангенсу: `cotan(x)=1/tan(x)` .
- Расчет котангенса
- Первообразная котангенса
Вычисление котангенса угла в радианах
Для расчета котангенса котангенса угла в радианах необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого действия вы можете начать свои расчеты.
Итак, чтобы вычислить котангенс `pi/6`, введите
cotan(`pi/6`), после вычисления,
результат возвращается.
Вычисление котангенса угла в градусах
Чтобы рассчитать онлайн котангенс
Чтобы вычислить котангенс котангенс числа 60, введите cotan(60), после вычисления, результат возвращается.
Вычисление котангенса угла в градусах
Чтобы вычислить котангенс угла в градусах, вы должны сначала выбрать нужную единицу, нажав на кнопку параметров расчетного модуля. После этого действия вы можете начать свои расчеты.
Чтобы вычислить котангенс числа 50, введите cotan(50), после вычисления
результат возвращается. 92`.
92`.
Первообразная котангенса равна `ln(sin(x))`.
Синтаксис:
cotan(x), где x — число.
Примеры:
cotan(`1/2`), возвращает 1.83048772171
Производный котангенс :
Чтобы дифференцировать котангенс функции онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции котангенса 92`
Первообразная котангенса :
Калькулятор первообразной позволяет вычислить первообразную функции котангенса.
Первопроизводная от cotan(x) является первообразной(`»»cotan»»(x)`)=`ln(sin(x))`
Предельный котангенс :
пределы функции котангенса.предел cotan(x) is limit(`»»cotan»»(x)`)
Графический котангенс:
Графический калькулятор может отображать функцию котангенса в заданном интервале.
Свойство котангенса функции:
Функция котангенса является нечетной функцией.
Расчет онлайн с котангенсом
См. также
Список связанных калькуляторов:
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.- Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.


 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.