Свойства функции y 3 в степени x. Степенная функция, ее свойства и графики
На данном уроке мы продолжим изучение степенных функций с рациональным показателем, рассмотрим функции с отрицательным рациональным показателем.
1. Основные понятия и определенияНапомним свойства и графики степенных функций с целым отрицательным показателем.
При четных n, :
Пример функции:
Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;1). Особенность функций данного вида — их четность, графики симметричны относительно оси ОУ.
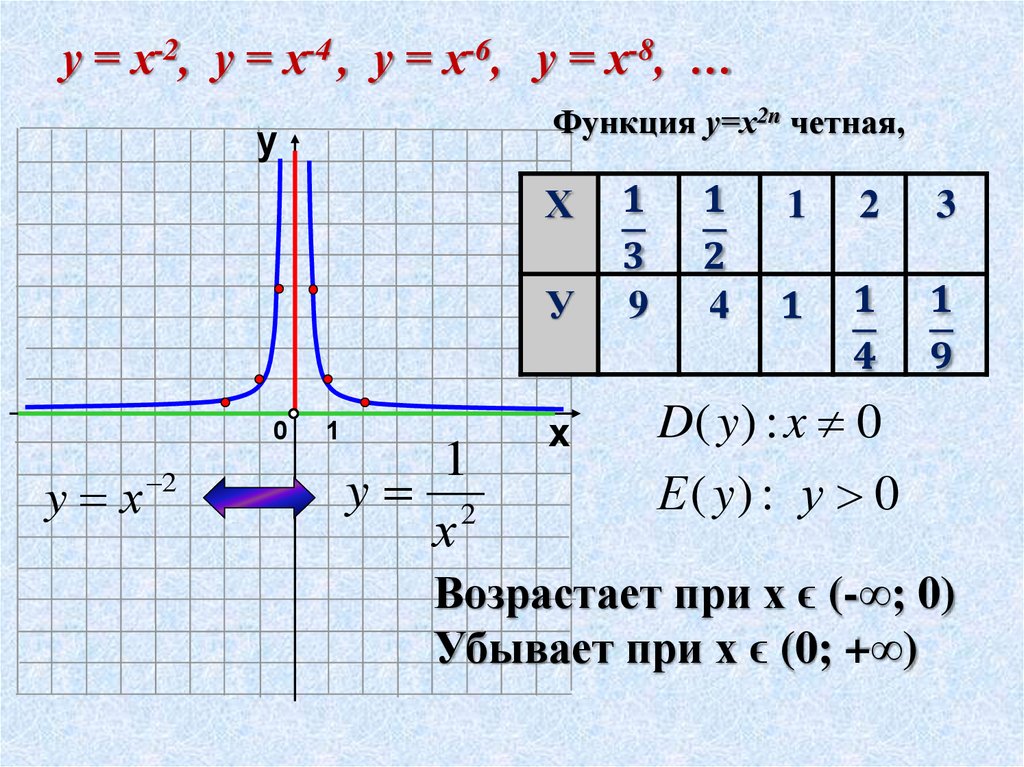
Рис. 1. График функции
При нечетных n, :
Пример функции:
Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;-1). Особенность функций данного вида — их нечетность, графики симметричны относительно начала координат.
Рис. 2. График функции
2. Функция с отрицательным рациональным показателем степени, графики, свойстваНапомним основное определение.
Степенью неотрицательного числа а с рациональным положительным показателем называется число .
Для выполняется равенство:
Например: ; — выражение не существует по определению степени с отрицательным рациональным показателем; существует, т. к. показатель степени целый,
Перейдем к рассмотрению степенных функций с рациональным отрицательным показателем.
Например:
Для построения графика данной функции можно составить таблицу. Мы поступим иначе: сначала построим и изучим график знаменателя — он нам известен (рисунок 3).
Рис. 3. График функции
График функции знаменателя проходит через фиксированную точку (1;1). При построении графика исходной функции данная точка остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 4).
Рис. 4. График функции
Рассмотрим еще одну функцию из семейства изучаемых функций.
Важно, что по определению
Рассмотрим график функции, стоящей в знаменателе: , график данной функции нам известен, она возрастает на своей области определения и проходит через точку (1;1) (рисунок 5).
Рис. 5. График функции
При построении графика исходной функции точка (1;1) остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).
Рис. 6. График функции
Рассмотренные примеры помогают понять, каким образом проходит график и каковы свойства изучаемой функции — функции с отрицательным рациональным показателем.
Графики функций данного семейства проходят через точку (1;1), функция убывает на всей области определения.
Область определения функции:
Функция не ограничена сверху, но ограничена снизу. Функция не имеет ни наибольшего, ни наименьшего значения.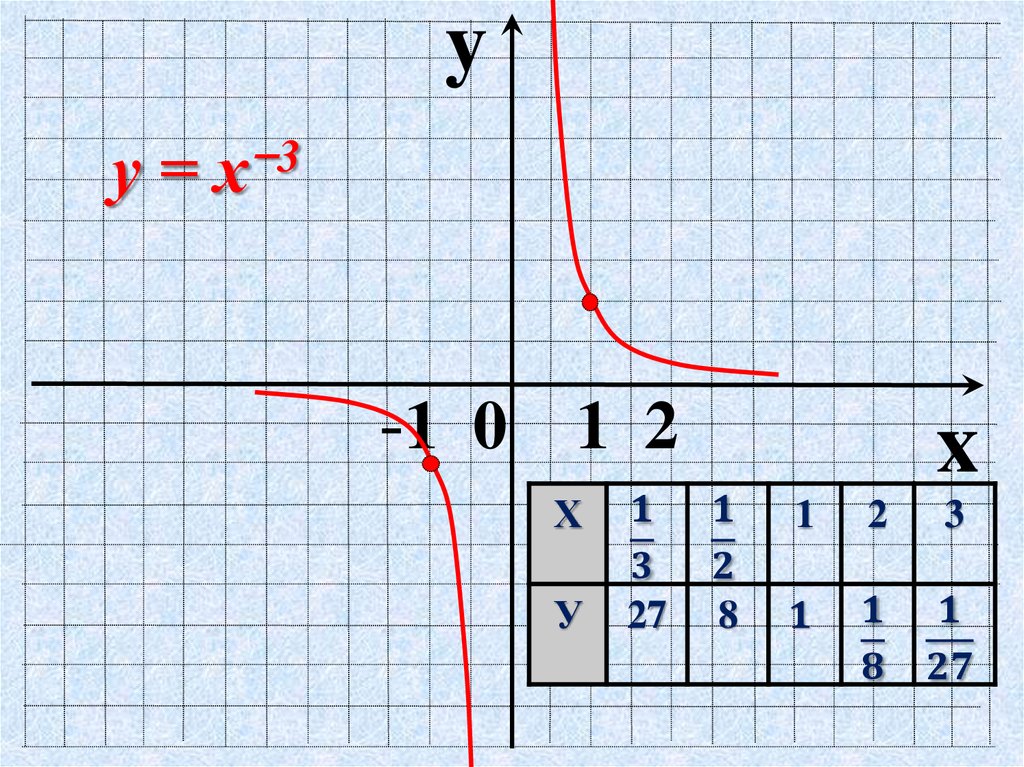
Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем
Свойства степенной функции с отрицательным целым показателем
Область определения — $\left(-\infty ,0\right)(0,+\infty)$.
Если показатель четный, то функция четна, если нечетный, то функция нечетна.
$f(x)$ — непрерывна на всей области определения.
Область значения:
Если показатель четный, то $(0,+\infty)$, если нечетный, то $\left(-\infty ,0\right)(0,+\infty)$.
При нечетном показателе функция убывает, при $x\in \left(-\infty ,0\right)(0,+\infty)$. При четном показателе функция убывает при $x\in (0,+\infty)$. и возрастает, при $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ на всей области определения
Для удобства рассмотрения степенной функции будем рассматривать 4 отдельных случая: степенная функция с натуральным показателем, степенная функция с целым показателем, степенная функция с рациональным показателем и степенная функция с иррациональным показателем.
n$ ($n\in Z)$ называется степенной функцией с целым показателем.
Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем
Свойства степенной функции с отрицательным целым показателем
Область определения — $\left(-\infty ,0\right)(0,+\infty)$.
Если показатель четный, то функция четна, если нечетный, то функция нечетна.
$f(x)$ — непрерывна на всей области определения.
Область значения:
Если показатель четный, то $(0,+\infty)$, если нечетный, то $\left(-\infty ,0\right)(0,+\infty)$.
При нечетном показателе функция убывает, при $x\in \left(-\infty ,0\right)(0,+\infty)$. При четном показателе функция убывает при $x\in (0,+\infty)$. и возрастает, при $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ на всей области определения
Степенной называется функция вида y=x n (читается как y равно х в степени n), где n – некоторое заданное число.
Частными случаями степенных функций является функции вида y=x, y=x 2 , y=x 3 , y=1/x и многие другие. Расскажем подробнее о каждой из них.
Линейная функция y=x 1 (y=x)
График прямая линия, проходящая через точку (0;0) под углом 45 градусов к положительному направлению оси Ох.
График представлен ниже.
Основные свойства линейной функции:
- Функция возрастающая и определена на всей числовой оси.
- Не имеет максимального и минимального значений.
Квадратичная функция y=x 2
Графиком квадратичной функции является парабола.
Основные свойства квадратичной функции:
- 1. При х =0, у=0, и у>0 при х0
- 2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
- 3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
Предыдущая статья: Создание landing page на WordPress Следующая статья: Стул мелена – опасный симптом, требующий срочной медицинской помощи Мелена бывает
Как найти экспоненциальную функцию с учетом двух точек калькулятора
AllebildervideosbüchermapsNewshopping
Sucoptionen
Калькулятор экспоненциальной функции-MathCracker.
com
MathCracker.com ›Функциональный функционирующий функция
. Калькулятор, чтобы найти функцию, описывающую экспоненциальную функцию, проходящую через две заданные точки.
экспоненциальная функция из заданных двух точек — YouTube 9x через два …
Dauer: 5:55
Прислан: 28.10.2019
Найти экспоненциальную функцию (2,25) — Mathway
www.mathway.com найти экспоненциальную функцию, f(x)=ax f ( x ) = a x , содержащую точку, установить f(x) f ( x ) в функции на значение y y 25 25 точки, …
Ähnliche Fragen
Как найти показательную функцию с двумя точками?
Как найти показательную функцию на калькуляторе?
Как найти экспоненциальную функцию из таблицы значений?
Экспоненциальная функция, проходящая через две заданные точки — GeoGebra
www.geogebra.org › eBHzJyKt
Визуализируйте экспоненциальную функцию, проходящую через две точки, которые можно перетаскивать в плоскости x-y.
Точки будут привязаны к точкам сетки (с помощью …
Как найти экспоненциальную функцию, учитывая, что точки — Socratic
socratic.org › вопросы › как-вы-находите-выставку. ..
Объяснение: ; Умножьте обе части первого уравнения на ·, чтобы найти ; Подставьте это во второе уравнение и найдите · : ; Два уравнения …
Калькулятор экспоненциальной регрессии
www.omnicalculator.com › статистика › экспоненциально-р… набор точек данных. Это очень похоже на другие …
Функция поиска уравнений из таблицы баллов — онлайн-калькулятор
www.dcode.fr › function-equation-finder
Инструмент для поиска уравнения функции по ее точкам, ее координатам x, y=f(x) в соответствии с некоторыми методами интерполяции и алгоритмами поиска уравнений.
Калькулятор экспоненциальных уравнений — Symbolab
www.symbolab.com › … › Алгебра › Уравнения
Бесплатный калькулятор экспоненциальных уравнений — шаг за шагом решайте экспоненциальные уравнения.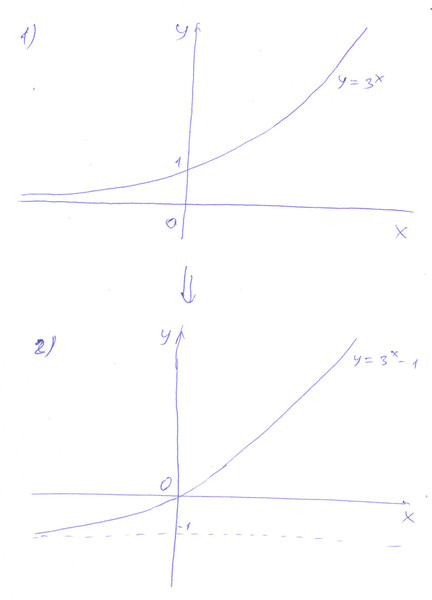
Как найти экспоненциальное уравнение с двумя точками — Наука
sciencing.com › … › Экспоненты и логарифмы
13.03.2018 · Если у вас есть две точки (x1, y1) и (x2, y2), вы можете определить экспоненциальную функцию, которая проходит через эти точки, с помощью подставив их в …
Ähnlichesuchanfragen
Найти экспоненциальную функцию из двух точек
Найти логарифмическое уравнение из калькулятора точек
Экспоненциальная функция, которая проходит через две точки
Калькулятор экспоненциального уравнения с шагами
Exponential growth equation
Get function from points
Linear function calculator
Exponential regression
exponential and logarithmic functions test pdf
AlleBilderVideosBücherMapsNewsShopping
Suchoptionen
[PDF] Math 30-1: Logarithms Practice Exam
lzinnick.weebly.com › загрузки › exponents_and_logs
1.
Математика 30-1: экспоненциальные и логарифмические функции. ПРАКТИЧЕСКИЙ ЭКЗАМЕН. Все нижеперечисленные функции являются экспоненциальными, кроме:
[PDF] Экспоненциальные и логарифмические функции Урок №9: Практический тест
jennanolan.weebly.com › загрузки › explogspracticetestkey
Экспоненциальные и логарифмические функции Урок №9: Практический тест … Графический калькулятор можно использовать для остаток теста.
[PDF] Test 5 Exponents and Logarithms REVIEW.tst — WordPress.com
утверждение или ответ на вопрос. … Эта таблица значений представляет собой экспоненциальную функцию.
[PDF] ExamView — Logariths Practice Test.tst
www.misternolfi.com › Курсы › Logariths Practice Test
Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. … График экспоненциальной или логарифмической функции можно использовать для …
[PDF] Экспоненциальные и логарифмические функции Test Review Key.
pdf
www.ddtwo.org › site › handlers › filedownload › FileName= Expose…
Определите, является ли каждая функция примером экспоненциального роста или затухания. Затем найдите y-перехват. 12. у = 3(0,55)*. 13. у = 123(1,98)-2х.
[PDF] Honors Math 3 Unit 2 TEST, экспоненциальные и логарифмические функции
www.cabarrus.k12.nc.us › cms › lib › Centricity › Domain
. Большой выбор. Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на …[PDF] Math 120 — Обзорный лист Экспоненциальные и логарифмические функции
www.unm.edu › ~efryer › Рабочие листы › Экспоненциальные и логарифмические…
Период____. Датировать________________. Обзорный лист: экспоненциальные и логарифмические функции. Разверните каждый логарифм. 1) лог (щ. 2 в). 3. 2) лог. 6.
[PDF] ПРЕДВЫЧИСЛЕНИЕ: ЧАСТЬ 5 ПРАКТИКА
www.scasd.org › cms › lib › Centricity › Domain
= 4[ln + ln( + 5)] − 2ln( − 5).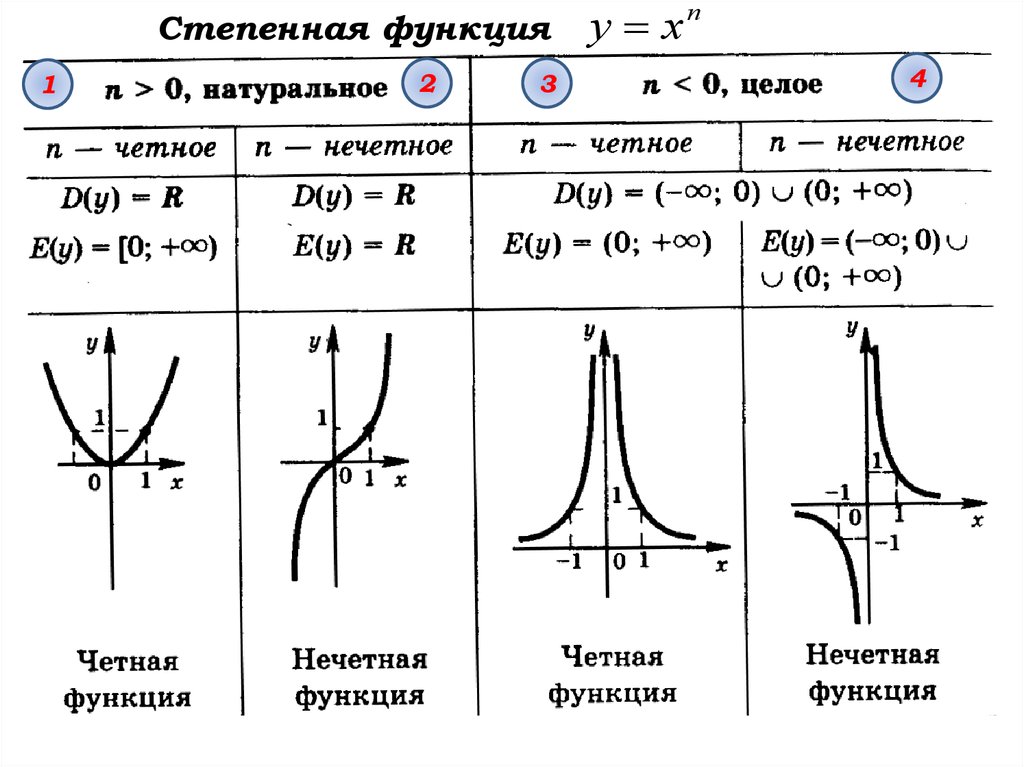
Стр. 26. ЛТ 1-8. Экспоненциальные и логарифмические функции. Практика викторины. Графики и свойства логарифмов. Глава 3.1 – …
[PDF] Блок № 6 – Экспоненциальные и логарифмические функции – mrsk.ca
mrsk.ca › TABexpLogReview
Целью проверки прогресса является диагностика областей, в которых вам нужно больше практики перед тестом. 1. Просмотрите свои записи, прежде чем пытаться ответить на вопросы в …
[PDF] Экспоненциальные и логарифмические функции MHF4U 1) Нарисуйте график …
static1.squarespace.com › static › Unit+3+Review+ +Logarithms
Раздел 3 Предтестовый обзор – экспоненциальные и логарифмические функции … Затем нарисуйте график обратной функции для каждой функции. Подпишите каждый график его уравнением.
Ähnliche Fragen
Как узнать, является ли функция экспоненциальной или логарифмической?
Каковы 7 правил логарифмирования?
Что такое экспоненциальные и логарифмические примеры функций?
Какие бывают 3 типа логарифмов?
Anzeige·www.