Калькулятор sin cos tg: Инженерный калькулятор онлайн, Научный калькулятор

Отредактировано Barni090 (26.01.2012 11:22:22, 10 лет 9 месяцев назад)

Тема закрыта и находится в архиве, не беспокойте автора без особой необходимости!

СайтBarni090

2 Ответ от Sin 15.12.2011 20:03:55 (10 лет 11 месяцев назад)

• Sin
• Участник
• Неактивен

Re: Калькулятор с Sin. Cos. Tg и др.функциями

так то лютый калькуль!)

3 Ответ от Athlon82 15.12.2011 21:25:09 (10 лет 11 месяцев назад)

• Athlon82
• МАСТЕРю
• Неактивен

Re: Калькулятор с Sin. Cos. Tg и др.функциями

у меня такой был лет 12-13 назад

сели батарейки.щас им доча играет

Отредактировано (15.12.2011 21:25:45, 10 лет 11 месяцев назад)

4 Ответ от Barni090 16.12.2011 09:19:20 (10 лет 11 месяцев назад)

• Barni090
• Участник
• Автор темы
• Неактивен

Re: Калькулятор с Sin.

Cos. Tg и др.функциями

Все новое, хорошо забытое старое 

Покупаем, есть в наличии!

Отредактировано (19.12.2011 16:44:35, 10 лет 11 месяцев назад)

Тема закрыта и находится в архиве, не беспокойте автора без особой необходимости!

СайтBarni090

Сообщений [ 4 ] Просмотров: 1 374

[Закрыто]

Просматривают тему:

1 гость, 0 пользователей

Страницы 1

Чтобы отправить ответ, вы должны войти или зарегистрироваться

Перейти в раздел:
КомпьютерыНоутбукиПланшетыКомплектующие для стационарных ПККомплектующие для мобильных ПКМониторыСетевое оборудованиеПериферияИгровые приставки, консолиКуплюМеняюТелефоны, смартфоныАксессуары для мобильных устройствКуплюМеняюТелевизоры, ВидеоАудиоФото и видеокамерыКуплюМеняюАвтомузыка, автоэлектроникаАвтошины, дискиАвтомобилиМотоциклы, мопеды, велосипедыАвтозапчастиКуплюИщу работуВакансииПродаюКуплюМебель, интерьерОдежда, обувьУкрашения, ювелирные изделия, аксессуарыКоллекционированиеТехническая продукция и строительствоСпортивный и туристический инвентарьЖивотные, растения и сопутствующие товарыПродаюКуплюМеняюУслугиНедвижимостьОтдам даром, приму в дарГде??Выбор и оценкаАукционыБеседкаТехническая поддержкаВопросы по форуму

16. 11.2022 11:09:03 | © Price-Altai.ru

Чем пользоваться на ЕГЭ | ШКОЛА № 35 Василеостровского района

Перечень дополнительных устройств, которыми разрешается пользоваться во время экзаменов по каждому предмету ЕГЭ, ежегодно утверждается  приказом Минобрнауки России.

Кроме того, в комплекты КИМ по некоторым предметам включены справочные материалы.

Ниже дан полный перечень разрешенных дополнительных устройств и материалов, составленный на основе спецификаций по предметам.

ЕГЭ по математике

Разрешается пользоваться линейкой.

Справочные материалы, которые можно использовать во время экзамена, выдаются каждому участнику ЕГЭ вместе с текстом его экзаменационной работы.

ЕГЭ по географии

Разрешено использование непрограммируемого калькулятора (на каждого ученика), линейки и транспортира.

Непрограммируемый калькулятор должен обеспечивать арифметические вычисления (сложение, вычитание, умножение, деление, извлечение корня) и вычисление тригонометрических функций (sin, cos, tg, ctg, arcsin, arcos, arctg).  

Калькулятор не должен предоставлять возможность сохранения в своей памяти баз данных экзаменационных заданий и их решений, а также любой другой информации, знание которой прямо или косвенно проверяется на экзамене.

Калькулятор не должен предоставлять экзаменующемуся возможности получения извне информации во время сдачи экзамена. Коммуникационные возможности калькулятора не должны допускать беспроводного обмена информацией с любыми внешними источниками.

ЕГЭ по химии

 Разрешено использование непрограммируемого калькулятора с возможностью вычисления тригонометрических функций (cos, sin, tg) и линейки.

Также к каждому варианту экзаменационной работы прилагаются следующие материалы:

• периодическая система химических элементов Д.И. Менделеева;
• таблица растворимости солей, кислот и оснований в воде;
• электрохимический ряд напряжений металлов.

ЕГЭ по физике

Разрешено использование непрограммируемого калькулятора (на каждого ученика) с возможностью вычисления тригонометрических функций (cos, sin, tg) и линейки.

Кроме того, каждый КИМ содержит справочные данные, которые могут понадобиться при выполнении работы.

ЕГЭ по иностранным языкам

Дополнительные материалы и оборудование на экзамене по иностранному языку включают звуковоспроизводящую аппаратуру, аудиокассеты или компакт-диски (CD) с материалами для выполнения заданий раздела 1 «Аудирование».

По остальным предметам использование дополнительного оборудования и материалов на экзамене не предусмотрено.

Всё, что не входит в спецификацию КИМ ЕГЭ по предмету, иметь и использовать на экзамене запрещено, в том числе:

• мобильные телефоны или иные средства связи;
• любые электронно-вычислительные устройства и справочные материалы и устройства.

При нарушении этих правил и отказе в их соблюдении  организаторы совместно с уполномоченным представителем ГЭК вправе удалить участника ЕГЭ с экзамена с внесением записи в протокол проведения экзамена в аудитории с указанием причины удаления.

На бланках и в пропуске проставляется метка о факте удаления с экзамена.

Калькулятор касательной tan(x) | Определение

Создано Ханной Памула, кандидатом наук

Отзыв от Bogna Szyk

Последнее обновление: 02 ноября 2022 г.

Содержание:

• Что такое тангенс? Определение тангенса, формула тангенса
• Тангенс — sin over cos
• Закон тангенса
• Калькулятор тангенса — пример использования

Этот калькулятор тангенса поможет вам найти тангенс любого угла, который вы хотите. Просто введите угол в градусах или радианах, и тангенс появится мгновенно. Если вы хотите понять, что такое тангенс, вас интересует определение тангенса или вывод формулы тангенса, продолжайте читать! Также 9Мем 0019 sin over cos ждет тебя там внизу.

Что такое тангенс? Определение тангенса, формула тангенса

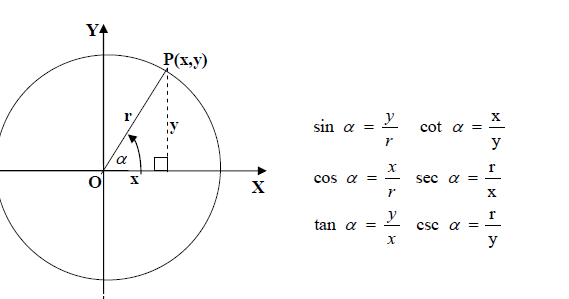
Тангенс — одна из трех наиболее распространенных тригонометрических функций (наряду с синусом и косинусом). Его можно определить как

отношение сторон: противолежащих и прилежащих к углу, в прямоугольном треугольнике.

Чтобы узнать больше о коэффициентах, воспользуйтесь нашим калькулятором коэффициентов!

НО! Есть еще одна геометрическая концепция, называемая 9.0019 тангенс . Это линия или плоскость, которая касается кривой или криволинейной поверхности в точке, но если ее продолжить, она не пересекает ее в этой точке.

Слово тангенс происходит от латинского tangere , что означает «касаться». И название нашей тригонометрической функции также происходит от этого значения! Взгляните на рисунок ниже:

Нарисуйте единичный круг. Точка C является пересечением линии, содержащей радиус, и линии x=1. Тогда tan(α) — это просто координата y точки C.

Тангенс — sin over cos

Тангенс угла может быть также определен как его синус, деленный на его косинус. Но почему это так? Взгляните на изображение единичного круга, и все должно быть ясно:

Зная определение синуса — напротив гипотенузы — мы можем узнать, что для прямоугольного треугольника из изображения sin(α) = у . Аналогично, косинус можно определить как , примыкающий к гипотенузе , поэтому в нашем случае он равен x. Затем в предыдущем абзаце вы узнали, что тангенс равен напротив соседней стороны . Итак, для нашего примера tan(α) = y/x, и его можно заменить синусом и косинусом интересующего нас угла, чтобы получить окончательную формулу:

tan(α) = sin(α) / cos(α)

Не так давно в интернете можно было найти математические анекдоты — sin over cos мемы . Мы почти уверены, что после прочтения этого абзаца вы получите этот!

А как насчет загара герина 🍊? Загар идти 🎶? Ти загар ic 🚢? Или даже sa tan ism? Подумайте, какие еще слова могли бы составить такой ребус!

Закон тангенсов

Закон тангенсов описывает отношение между тангенсами двух углов треугольника и длинами противоположных сторон. В частности, в нем говорится, что:

(a - b) / (a ​​+ b) = тангенс (0,5 (α - β)) / тангенс (0,5 (α + β))

Хотя закон тангенсов не столь популярными, как закон синусов или закон косинусов, может оказаться полезным, если мы дали:

• две стороны и угол между ними;
• два угла и сторона.

🙋 Посетите наш калькулятор закона косинусов и калькулятор закона синусов, если вы не совсем помните, о чем эти теоремы!

Калькулятор тангенса — пример использования

Все, что вам нужно сделать, это ввести в калькулятор одно значение — угол , в радианах или градусах. Чтобы переключиться между единицами измерения, нажмите на название единицы и выберите из раскрывающегося списка. Тогда вы сразу увидите результат — значение тангенса интересующего вас угла. Помните, что загар может быть неопределенным . Эта ситуация возникает, когда cos(α) равен 0, потому что мы никогда не можем делить на ноль (другое объяснение: прямые будут параллельны, поэтому они никогда не пересекутся и не образуют точку C).

Ханна Памула, кандидат наук

Посмотреть 19 похожих тригонометрических калькуляторов 📐

ArccosArcsinArctan… еще 16

Косинус. Калькулятор | Определение | График

Автор: Ханна Памула, кандидат наук

Рецензент: Богна Шик

Последнее обновление: 20 октября 2022 г.

Содержание:

• Что такое косинус? Определение косинуса
• График и таблица косинуса (cos 0, cos 30 градусов, cos 45 градусов…)
• Пример: как использовать калькулятор косинуса

Калькулятор косинуса является двойным инструментом нашего калькулятора синуса — добавьте в калькулятор тангенсов, и у вас будет пакет самых популярных тригонометрических функций. Просто введите угол — в градусах или радианах — и вы сразу найдете значение косинуса. Читайте дальше, чтобы понять что такое косинус и найти определение косинуса , а также аккуратную таблицу со значениями косинуса для основных углов, таких как cos 0°, cos 30° или cos 45°.

Что такое косинус? Определение косинуса

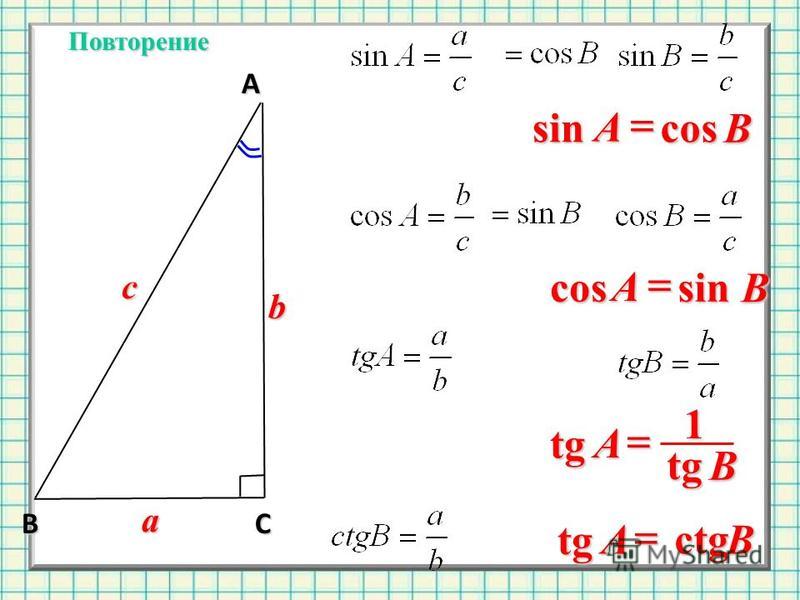
Косинус — одна из самых основных тригонометрических функций. Его можно определить на основе прямоугольного треугольника или единичного круга, аналогично тому, как определяется синус:

Косинус угла равен длине прилежащей стороны, деленной на длину гипотенузы .

cos(α) = смежная / гипотенуза = b / c

Если вы не уверены, что такое , смежная с и гипотенуза (а также напротив ), ознакомьтесь с объяснением в калькулятор синусов.

Название косинуса происходит от латинского префикса co- и функции синуса, поэтому оно буквально означает дополнение синуса . И действительно, функцию косинуса можно определить так: как синус дополнительного угла — другого непрямого угла. Аббревиатура косинуса

cos , например. cos(30°) .

Важные свойства функции косинуса:

• Диапазон значений косинуса: -1 ≤ cos(α) ≤ 1
• Косинус Период равен 2π
• Это четная функция (в то время как синус нечетный!), что означает, что cos(-α) = cos(α)
• Определение косинуса необходимо для понимания закона косинусов — очень полезного закона для решения любого треугольника. Откройте для себя это с помощью нашего калькулятора закона косинусов!

Lucas Vieira / Public domain

График и таблица косинуса (cos 0, cos 30 градусов, cos 45 градусов.

..)

На изображении ниже показана функция косинуса в диапазоне <-2π, 2π>. Кроме того, если вы хотите научиться играть с ним, обязательно проверьте калькулятор фазового сдвига.

диапазон»>

Точное значение косинуса особенно легко запомнить и определить для определенных углов — возможно, вы узнали, что cos 0° = 1, cos 30° = √3/2 или cos 45° = √2/2. Остальные основные углы указаны в таблице:

α (угол)	sin(α)
Градусы	Радиан	Точный	Десятичный
0°	0	1	1
15°	№/12	(√6 + √2) / 4	0,9659258263
30°	№/6	√3/2	0,8660254038
45°	№/4	√2/2	0,7071067812
60°	№/3	0,5	0,5
75°	5π/12	(√6 — √2) / 4	0,25881
90°	№/2	0	0
105°	7π/12	-(√6 — √2) / 4	-0,25881
120°	2π/3	-0,5	-0,5
135°	3π/4	-√2/2	-0,7071067812
150°	5π/6	-√3/2	-0,8660254038
165°	11π/12	-(√6 + √2) / 4	-0,9659258263
180°	№	-1	-1

Кроме того, вы можете наблюдать, как функция косинуса ведет себя в зависимости от квадранта, в котором она находится.

Помните о периодичности функции косинуса cos(α + 360°) = cos(α) , если ваш угол выходит за пределы таблицы ниже.

Квадрант/граница	Градусы	Радиан	Значение	Знак	Монотонность	Выпуклость
	0°	0	1		максимум
1-й квадрант	0° < α < 90°	0 < α < π/2	0 < cos(α) < 1	+	по убыванию	вогнутый
	90°	№/2	0		корень, перегиб
Второй квадрант	90° < α < 180°	π/2 < α < π	-1 < cos(α) < 0	—	по убыванию	выпуклый
	180°	№	-1		минимум
3-й квадрант	180° < α < 270°	π < α < 3π/2	-1 < sin(α) < 0	—	увеличение	выпуклый
	270°	3π/2	0		корень, перегиб
4-й квадрант	270° < α < 360°	3π/2 < α < 2π	0 < sin(α) < 1	+	увеличение	вогнутый

Пример: как пользоваться калькулятором косинуса

Теперь вы разобрались, что такое косинус, пользоваться этим калькулятором косинуса проще простого!

1. Введите угол .

   No related posts.