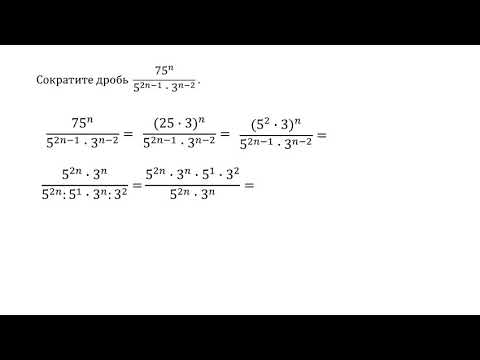Уменьшение дроби до наименьших значений
Алгебра Решатели
Инструкции: Сократите дробь до наименьшего (простейшего) члена с помощью этого калькулятора. Введите числитель и знаменатель (используйте неотрицательные целые числа), и решатель покажет шаг за шагом, как уменьшить дробь до ее простейшего выражения.
Сократите дробь до наименьшего (простейшего) значения.
Введите дробь, которую вы хотите уменьшить =
Идея сокращения дроби до наименьшего числа означает взять дробь и выразить ее в ее простейшей возможной форме, имея дробь, имеющую то же значение, что и исходная дробь, но все возможные общие множители между числителем и знаменатель были упрощены. Это достигается путем вычисления наибольшего общего делителя (НОД) между двумя числителем и знаменателем, а затем упрощения дроби с его помощью.
● Давайте посмотрим на следующий пример: Сократите эту дробь до наименьшего числа.
\[\frac{165}{1575}\]
Сначала мы вычисляем GCD для \(n_1 = 165\) и \(n_2 = 1575\).
1 = 3 \cdot 5 = 15 \]
Теперь все, что нам нужно сделать, это упростить исходную дробь на 15: \[\frac{165}{1575} = \frac{165/15}{1575/15} = \frac{11}{105} \]
что соответствует дроби в ее наименьшем значении, поскольку ее нельзя упростить.
Возникает вопрос: почему мы сокращаем дроби до наименьших значений? Что ж, ответ прост. Как и во всем в математике, простота — самое желанное условие. Зачем работать с громоздкой дробью, если мы можем сократить ее до более простой эквивалентной дроби?
Для других калькуляторов алгебры вы можете попробовать наш раздел
алгебраические решатели и калькуляторы
, где вы найдете множество других калькуляторов.
Алгебра Решатель Базовый пакет алгебры Уменьшение фракции Уменьшение дроби до наименьших членов Фракции Упрощение калькулятора дробей
App Store: Фракция Калькулятор + Десятич
Описание
Представляем первый в мире калькулятор дробей с дополнительными функциями, такими как сокращение или упрощение дробей, возможность перевода обыкновенных дробей в десятичные и обратно.
ФУНКЦИИ:
— БЕСПЛАТНЫЙ калькулятор дробей и конвертер десятичных дробей в обыкновенные.
— Автоматическое преобразование обыкновенных дробей в десятичные.
— Поддержка неправильных и правильных дробей, смешанных и целых чисел.
— Теперь вы можете также считать и в обратном порядке: превращайте десятичные дроби в обыкновенные
— Большая и четкая клавиатура для быстрого и легкого расчета.
— Помощь в домашних делах: нужна дополнительная помощь для понимания дробей? Вы можете БЕСПЛАТНО проигрывать интерактивные видео и постичь основные знания о дробях.
000Z» aria-label=»23 ноября 2020 г.»>23 нояб. 2020 г.
Версия 2.1.4
— Исправлены некоторые ошибки
Оценки и отзывы
Оценок: 17
Супер пупер
Клевое приложение помогало на контрольных всем рекомендую
Потрясающе!
Отличное приложение, занимает мало места и экономит время. Спасибо разработчикам! 💝
Отзыв
Все платное не качайте
Разработчик Visual Math Interactive Sdn. Bhd. не сообщил Apple о своей политике конфиденциальности и используемых им способах обработки данных.
Подробные сведения доступны в политике конфиденциальности разработчика.
Нет сведений
Разработчик будет обязан предоставить сведения о конфиденциальности при отправке следующего обновления приложения.
Информация
- Провайдер
- Visual Math Interactive Sdn Bhd
- Размер
- 151,2 МБ
- Категория
- Производительность
- Возраст
- 4+
- Copyright
- © Visual Math Interactive
- Цена
- Бесплатно
- Сайт разработчика
- Поддержка приложения
- Политика конфиденциальности
Другие приложения этого разработчика
Вам может понравиться
Упроститель дробей — MathCracker.
comРешатели Алгебра
Дробь, которую вы хотите упростить (пример: 9/6 и т. д.)
Об этом упростителе для калькулятора дробей
Этот калькулятор позволяет упростить дробь, полученную путем приведения дроби к наименьшим возможным выражениям.
Вам нужно дать калькулятор
дробь, просто набрав ее.
Например, вы можете написать что-то простое, например «3/9», или что-то вроде «(1+3)/(6+8)». Затем, когда вы написали допустимое выражение дроби, вам просто нужно нажмите на кнопку с надписью «Рассчитать». Затем вам будет представлен пошаговый расчет упрощения дроби.
Если вы вводите дробь с операциями в числителе и/или знаменателе, этот калькулятор сначала выполнит эти вычисления.
Как упростить дробь
Приведение дроби к минимуму довольно просто, и оно включает в себя упрощение любого общего множителя, который может иметь числитель и знаменатель.
Каковы шаги для упрощения дробей?
- Шаг 1: Четко определите числитель и знаменатель дроби
- Шаг 2: Найдите множители для каждого числителя и знаменателя
- Шаг 3. Отмените эти общие факторы
Зачем сокращать дроби?
Существует множество причин для уменьшения дроби.
Во-первых, уменьшенная дробь имеет то же значение, что и исходная, но проще, имеет смысл сохранить
упрощенная версия исходной дроби.
Очевидно, это зависит от случая. Возможно, исходная дробь имеет конкретное значение, и сокращать ее бесполезно. Таким образом, вам необходимо оценить, в зависимости от обстоятельств, независимо от того, уместно ли упрощение или нет.
Пример: расчет упрощения дроби
Упростите следующую дробь \(\displaystyle \frac{32}{48}\).
Решение:
Нам нужно упростить следующую заданную дробь: \(\displaystyle \frac{32}{48}\).
Получается следующий расчет:
\( \displaystyle \frac{32}{48}\)
Мы можем вынести 16 как в числителе, так и в знаменателе.
знак равно
\(\displaystyle \frac{ 16 \times 2}{ 16 \times 3}\)
Теперь сокращаем 16 из числителя и знаменателя.
знак равно
\(\displaystyle \frac{ \cancel{ 16} \times 2}{ \cancel{ 16} \times 3}\)
Отменив 16, мы получим эту упрощенную дробь.
знак равно
\(\displaystyle \frac{2}{3}\)
, что завершает расчет.
Пример: еще одно сокращение дроби
Упростите теперь следующую дробь \(\displaystyle \frac{3+9}{6\times 3}.
Решение:
Нам нужно упростить следующую заданную дробь: \(\ displaystyle \frac{3+9}{6\cdot 3}\).
Получается следующее вычисление:
\( \displaystyle \frac{3+9}{6\cdot 3}\)
Упрощение целых чисел, которые можно умножать: \(\displaystyle 6\times3 = 18\)
знак равно
\(\displaystyle \frac{3+9}{18}\)
Сокращение целых чисел, которые можно сложить вместе: \(\displaystyle 3+9= 12\)
знак равно
\(\displaystyle \frac{12}{18}\)
Мы можем вынести 6 как в числителе, так и в знаменателе.
знак равно
\(\displaystyle \frac{ 6 \times 2}{ 6 \times 3}\)
Теперь мы сокращаем 6 из числителя и знаменателя.
знак равно
\(\displaystyle \frac{ \cancel{ 6} \times 2}{ \cancel{ 6} \times 3}\)
После сокращения 6 out мы получаем эту упрощенную дробь.
знак равно
\(\displaystyle \frac{2}{3}\)
, что завершает расчет.
Другие калькуляторы дробей
Дроби — это вездесущие объекты в алгебре, и они используются во многих контекстах. Калькуляторы дробей играют важную роль в помощи вы видите, как завершается процесс и как выполняется алгебра.
Ключевым процессом сокращения дроби является вычисление наибольшего общего делителя, который является наибольшим значением
с помощью которого мы можем упростить как числитель, так и знаменатель.
Кроме того, в другом аспекте дробей, особенно на более элементарных уровнях, вас может заинтересовать работа со смешанными дробями и их преобразование в правильные дроби.
Дроби будут появляться везде, как часть общего алгебраического выражения и в контексте полиномиальные вычисления и функции в целом.
Дробные операции Граф тригонометрических функций Калькулятор дробей Числовые выражения
Калькулятор упрощения дробей — ezcalc.me
Этот онлайн-калькулятор упрощения дробей представляет собой бесплатный онлайн-инструмент, который предлагает возможность упростить дробь. Позволяет упростить правильные и неправильные дроби, а также смешанные числа (смешанные дроби), как положительные, так и отрицательные.
В дроби числитель и знаменатель разделяются косой чертой (/). Важно оставлять пробел между целым числом и дробной частью смешанного числа. В случае отрицательного числа знак минус (-) предшествует дроби или целому числу в смешанной дроби без пробела между ними.
Дробь:
Результат:
Упрощение дробей
Упрощение дробей (или сокращение дробей) представляет собой процесс представления дроби в виде несократимой правильной дроби. Дробь неприводима, если наибольший общий делитель их числителя и знаменателя равен 1 . Наш калькулятор уменьшенной дроби также преобразует неправильную дробь в смешанное число (смешанную дробь).
Как упростить дроби
При работе с дробями всегда удобнее иметь дело с дробями, приведенными к простейшему виду. Например, гораздо проще производить вычисления с дробью 3/7 , чем с дробью 39/91 , хотя обе дроби эквивалентны в том смысле, что они выражают одну и ту же часть целого.
Чтобы убедиться, что обе эти дроби эквивалентны, просто обратите внимание, что числитель и знаменатель дроби 39/91 одновременно делятся на 13 : 39/13 = 3 и 91/13 = 7 . В результате этого деления получаем упрощенную дробь 3/7 .
Важно отметить, что дробь 3/7 не может быть упрощена дальше, потому что числитель и знаменатель этой дроби не имеют общего делителя, кроме 1 . Итак, 3/7 называется несократимой дробью. В этом примере 13 был наибольшим общим множителем числителя и знаменателя числа 39/91 .
В итоге приходим к следующему простому алгоритму упрощения дробей.
Шаг 1 . Найдите наибольший общий делитель числителя и знаменателя данной дроби.
Шаг 2 . Разделите числитель и знаменатель на этот наибольший общий делитель.
Если найденный наибольший общий делитель не равен 1 то после деления получится упрощенная форма исходной дроби.
В качестве другого примера рассмотрим дробь 42/231 .
1. Наибольшим общим делителем чисел 42 и 231 является число 21 .
2. Итак, эту дробь можно сократить до меньших членов, разделив числитель и знаменатель на 21 , получив в результате дробь 2/11 .
Приведенный выше алгоритм можно переформулировать следующим образом:
Шаг 1 . Найдите все делители числителя и знаменателя данной дроби.
Шаг 2 . Определите общие делители числителя и знаменателя.
Шаг 3 . Последовательно разделите числитель и знаменатель на общие делители, пока у них не будет общего делителя, отличного от 1.
В приведенном выше примере дроби 42/231 вы можете действовать следующим образом.
1. Делители числителя 42 равны 1, 2, 3, 6, 7, 14, 21, 42 , а множители знаменателя 231 это 1, 3, 7, 11, 21, 33, 77, 231 .