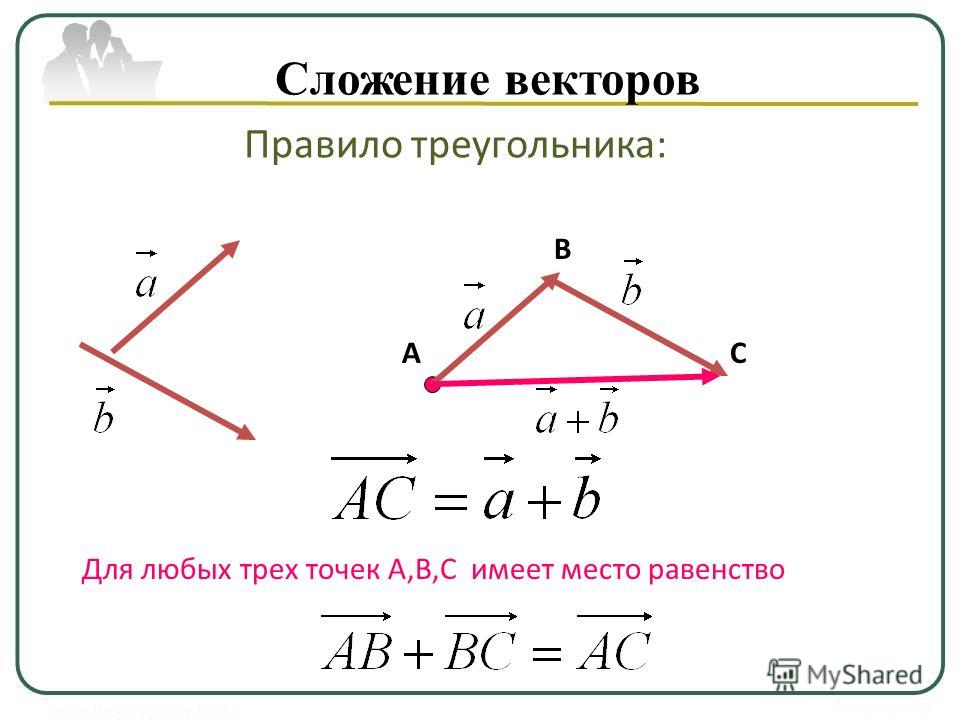
Сложение комплексных чисел
|
|
|
|||||||||||||||||||||||||||||||
Вышла новая версия семантического калькулятора RusVectōrēs
В канун праздников Школа лингвистики НИУ ВШЭ решила сделать подарок всем, кто занимается дистрибутивной семантикой, и выпустила новую версию сервиса RusVectōrēs 2. 0.
0.
RusVectōrēs вычисляет семантические отношения между словами русского языка c помощью векторных семантических моделей, обученных на больших текстовых корпусах. Что это такое? В дистрибутивной семантике слова обычно представляются в виде векторов в многомерном пространстве их контекстов. Семантическое сходство вычисляется как косинусная близость между векторами двух слов и может принимать значения в промежутке от 0 до 1. Значение 0 означает, что у этих слов нет похожих контекстов и их значения не связаны друг с другом. Значение 1, напротив, свидетельствует о полной идентичности их контекстов и, следовательно, о близком значении. RusVectōrēs позволяет на основе нейронных моделей, обученных на НКРЯ, новостном и веб корпусах, работать с векторами слов: вычислять ближайших семантических соседей слова, находить коэффициент сходства между парами слов, складывать и вычитать лексические вектора. Модели обучаются при помощи алгоритмов Skip-Gram и CBOW, реализованных в широко известной утилите word2vec.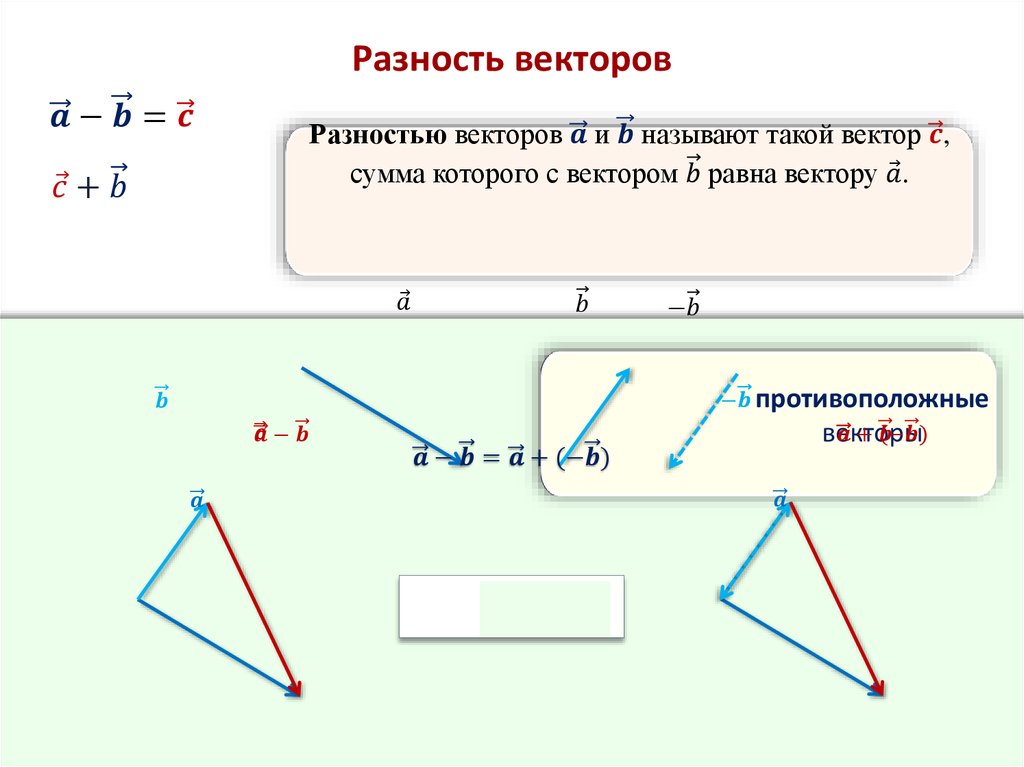
О сервисе было рассказано на семинаре «Quantitative Approaches to the Russian Language» в Хельсинки в августе и на тьюториале по дистрибутивной семантике на конференции AINL-FRUCT в Санкт-Петербурге в ноябре. С тех пор функционал RusVectōrēs существенно расширился, и теперь у пользователей есть ещё больше возможностей для исследований. Основные изменения в новой версии таковы:
1) Появился API, так что теперь к сервису можно обращаться автоматически. С помощью API можно для любого слова получить список слов, семантически близких к данному в выбранной модели. Для этого необходимо выполнить GET-запрос по адресу следующего вида: http://ling.go.mail.ru/dsm/MODEL/WORD/api, где MODEL — идентификатор для выбранной модели, а WORD — слово запроса. По запросу отдаётся текстовый файл в формате tab-separated values, в котором перечислены ближайшие десять соседей слова.
2) Создан инструментарий для визуализации данных. Сервис строит карту взаимного расположения слов, которые ввёл пользователь, в выбранной модели, а затем отображает двумерную проекцию этой карты (поскольку изначально мы имеем дело с векторным пространством высокой размерности).
3) Доступна также визуализация вектора для каждого слова в выбранной модели, которая находится по уникальной для этого слова ссылке.
4) Семантический калькулятор теперь может выполнять операции двух видов: решение пропорции вида «найти слово D, связанное со словом C таким же образом, как слово A связано со словом B» (analogical inference) и алгебраические операции над векторами(сложение, вычитание, нахождение центра лексического кластера)
5) Как и раньше, пользователи могут обучать нейронные модели с заданными параметрами на собственных корпусах, чтобы затем использовать их в работе.
6) Вы всегда можете быть в курсе текущих изменений в работе сервиса, подписавшись на новостную ленту.
Калькулятор добавления векторов
Онлайн-калькулятор для сложения двух векторов, дающих компоненты равнодействующей, ее величину и направление. Пусть u и v — два вектора, заданные в компонентной форме формулой Использование калькулятора сложения векторовЕсть два калькулятора, которые можно использовать для сложения двух векторов в зависимости от того, знаете ли вы компоненты или величину и направление складываемых векторов.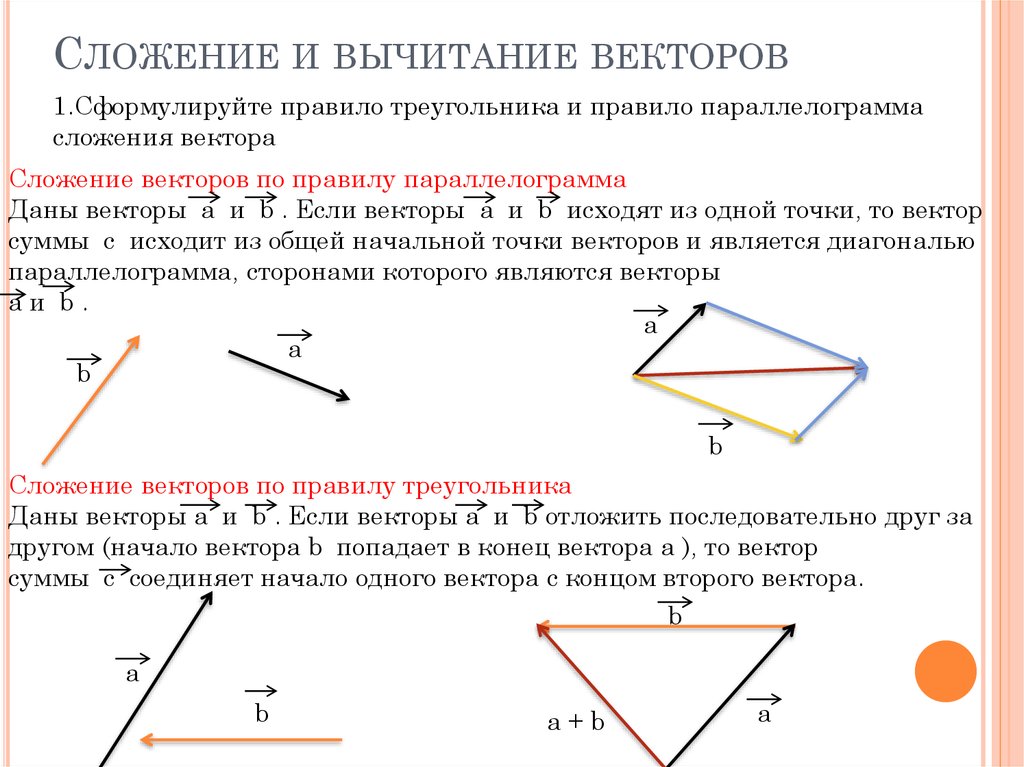 1 — Введите компоненты u 1 , u 2 и v 1 , v 2 двух векторов u и v соответственно как действительные числа и нажмите «Добавить два вектора». Выходами являются компоненты вектора u + v, его величина и направление в градусах. 2 — Введите величины (неотрицательные действительные числа) и направления в градусах двух векторов u и v соответственно как действительные числа и нажмите «Добавить два вектора». Выходами являются компоненты вектора u + v, его величина и направление в градусах. Дополнительные ссылкиНайти величину и направление векторов.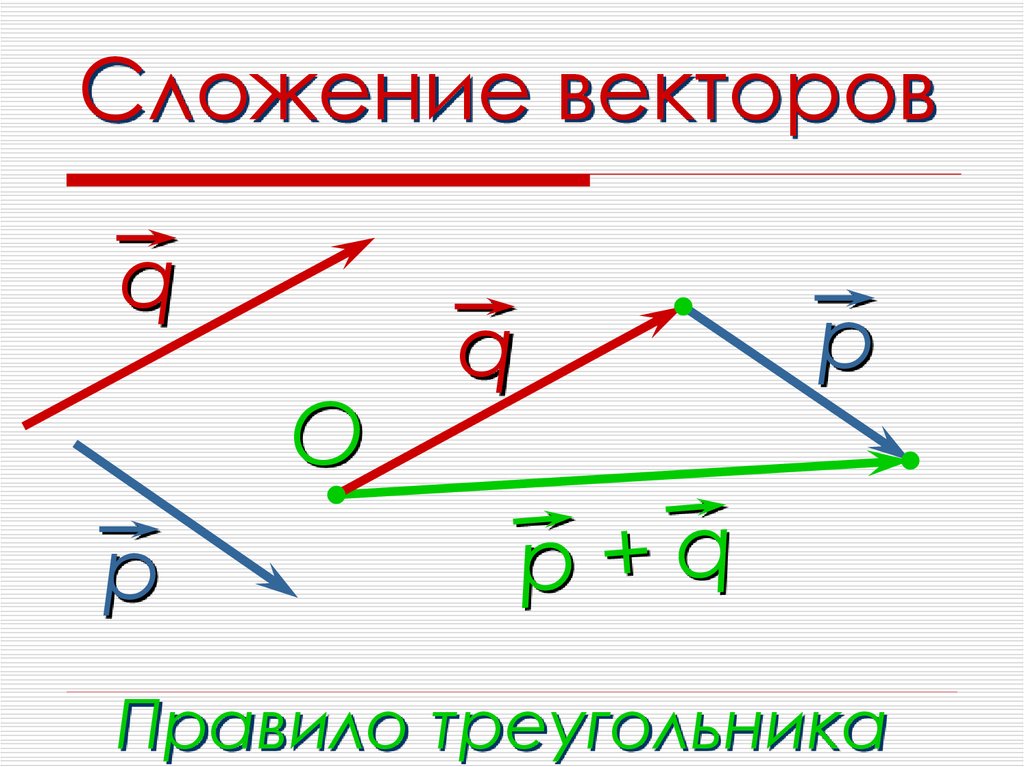 векторные калькуляторы векторные калькуляторы Сложение векторов и скалярное умножение. |
{ezoic-объявление-1}
Калькулятор сложения векторов
Калькулятор сложения и вычитания векторов для сложения и вычитания двух векторов. Калькулятор можно использовать для сложения и вычитания 2D или 3D векторов.
Калькулятор сложения векторов:
| ВХОДНЫЕ ПАРАМЕТРЫ | |||
| ДВА ВЕКТОРА | |||
| Вектор | |||
Примечание.


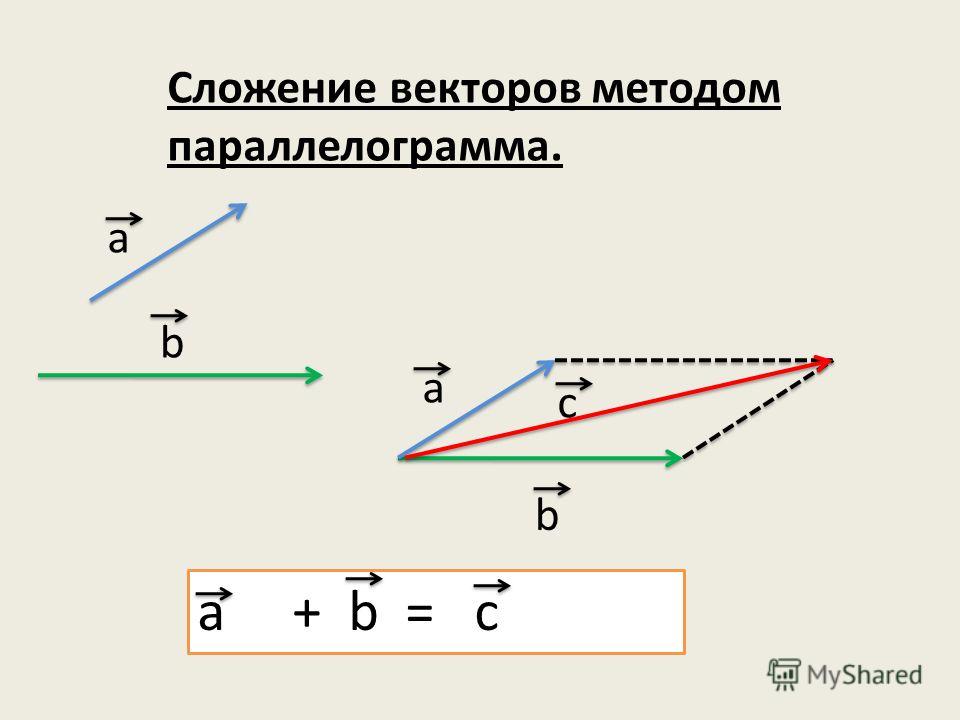

 Но, это только для вычислений, а так я верю в величие церкви и что все планеты вращаются вокруг Земли.
Но, это только для вычислений, а так я верю в величие церкви и что все планеты вращаются вокруг Земли.
 Настройка.
Настройка. .
.