Калькулятор степеней
Онлайн калькулятор помогает возвести число в любую степень и найти корень любой степени из числа (квадратные, кубические корни, а также корни других степеней). Основанием степени могут быть любые числа, показателем степени также может быть любые числа, в том числе и отрицательные.
Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Как возвести число в степень?
Чтобы возвести число X в степень n, достаточно всего лишь умножить число X его само на себя n раз.
Что такое отрицательная степень числа?
Отрицательная степень числа — это единица, поделённая на число в степени n, то есть a-n = 1/ an.
Основные действия со степенями
- Число 34— это 3×3×3×3, где перемножаются четыре одинаковых множителя. Если умножить 34 на 32, то мы получим (3×3×3×3)×(3×3), то есть 36. Отсюда первое правило возведения в степень: при умножении чисел, возведенных в степень, их показатели суммируются. Математически: xm * xn = x(m+n).
- Число 35разделить на 32, это означает следующее: (3×3×3×3×3)/(3×3), то есть останется (3×3×3) или 33.Отсюда второе правило действий со степенями: при делении чисел, возведенных в степень, их показатели вычитаются. Математически: xm / xn = x(m-n).
- Число 54возвести в куб, то есть в третью степень. Для этого нужно вычислить выражение (5×5×5×5)×(5×5×5×5)×(5×5×5×5). Получилось 12 сомножителей. Отсюда третье правило: при возведении в n-ную степень числа в степени m, показатели перемножаются. Математически: (xm)n = x(m×n).
- Любое положительное число в степени 0 всегда равно единице. Математически: x0= 1. Например можно представить 70 как 74 разделить на 74 или 74/74=1.
- При возведении числа в отрицательную степень необходимо единицу разделить на число в положительной степени. Например, если разделить 82на 84, то получим 8-2 или (8×8)/(8×8×8×8). Если сократить восьмерки в числителе и знаменателе, то получим 1/(8×8). Математически: x-m = 1 / xm.
- Если в качестве степени выступает дробное число, то знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически: x(m/n)есть корень n-ной степени из xm. Например, 4(2/3) означает, что нужно найти корень третьей степени от числа 42.
Навигация по записям
Возведение дроби в степень. Онлайн калькулятор
Данный калькулятор может возвести любую дробь в положительную, отрицательную и дробную степень и дать подробное решение. Если у дроби нет целой части оставьте это поле пустым, если дробь отрицательна, задайте ее знак при помощи кнопки (+/-). Чтобы записать дробную степень, воспользуйтесь знаком “/”, например, 3/5 или -3/5
Правила возведения дроби в степень
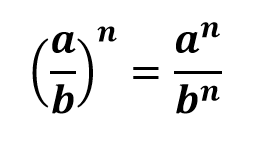
Чтобы возвести дробь в степень n, необходимо числитель и знаменатель дроби возвести в степень n. Например,
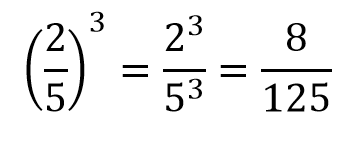
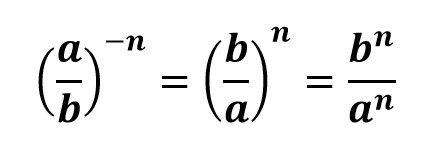
Чтобы возвести дробь в степень -n с отрицательным показателем, необходимо числитель и знаменатель дроби поменять местами, при этом знак степени заменить на противоположенный. Затем необходимо возвести в степень числитель и знаменатель дроби. Например,
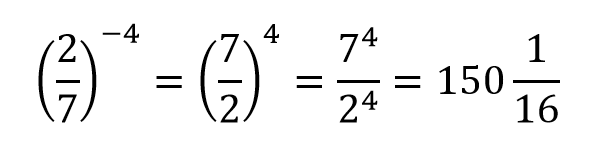
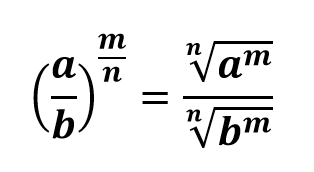
Для того чтобы возвести дробь в степень с дробным показателем необходимо числитель и знаменатель дроби представить в виде подкоренного числа, возведенного в степень равную числителю степени и в качестве показателя корня записать знаменатель степени. Например,
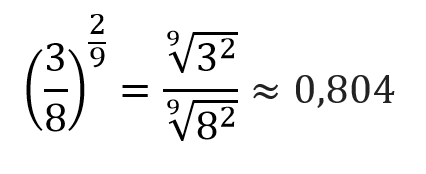
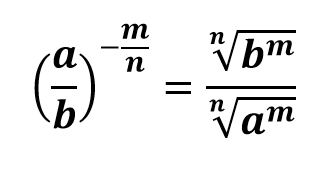
Для того чтобы возвести дробь в степень с отрицательным дробным показателем необходимо числитель и знаменатель дроби поменять местами, при этом знак степени измениться на противоположенный. Затем числитель и знаменатель дроби представить в виде подкоренного числа, возведенного в степень равную числителю степени и в качестве показателя корня записать знаменатель степени. Например,
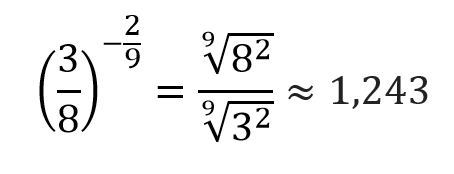
| Вам могут также быть полезны следующие сервисы |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер сложения |
| Тренажёр вычитания |
| Тренажёр умножения |
| Тренажёр деления |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Данный калькулятор возводит полином в степень. Для этого калькулятор производит несколько умножений используя Умножение многочленов. Полином можно задать последовательностью вещественных, рациоанльных или комплексных коэффициентов. Алгоритм описан сразу за калькулятором.
Возведение полинома в степень
Точность вычисленияЗнаков после запятой: 2
Дерево степеней
save Сохранить extension Виджет
Алгоритм возведения в степень
Известно несколько алгоритмов, позволяющих оптимально возвести число в целую степень. Один из самых оптимальных: дерево степеней. Он описан в Искусстве программирования Дональда Кнута том 2 . Алгоритм умножает результирующую величину на значения, полученные на предыдущих шагах, согласно заранее построенному дереву степеней (см. граф Дерево степеней).
К примеру, для того чтобы получить x23 нужно только 6 умножений:
| Номер | Операция | Результат |
|---|---|---|
| 1 | x*x | x2 |
| 2 | x2 * x | x3 |
| 3 | x3 * x2 | x5 |
| 4 | x5 * x5 | x10 |
| 5 | x10 * x3 | x13 |
| 6 | x13 * x10 | x23 |
Реализация алгоритма может использовать заранее просчитанное до какого-нибудь разумного значения дерево степеней.
Само дерево строится следующим алгоритмом:
- для каждого значения степени на последнем уровне дерева:
- сохранить показатель степени в переменную e
- для каждого значения в цепочке степеней pi, (включая e и всех его родителей вплоть до 1) выполняем следующее:
- к текущему узлу дерева добавим дочерний элемент со степенью pi + e , но только если он до сих пор еще не добавлен в другие узлы дерева
Двоичный алгоритм возведения в степень
Примечателен также двоичный алгоритм. Его производительность не уступает алгоритму дерева степеней до 22 степени включительно, далее он начинает несущественно проигрывать (количество умножений становится больше).
- представим показатель степени в двоичной форме
- создадим строку операций путем замены 1 на SX
- заменим все двоичные нули на X
- удалим первый SX
- начиная слева направо выполняем для каждого символа строки операций:
- умножаем на x если символ = ‘X’
- умножаем само на себя если символ = ‘S’
Например, алгоритм требует 7 операций умножения для получения x23. Так как число 23 в двоичной форме это 10111 , то наша строка операций будет выглядеть так: SXXSXSXSX. Шаги умножения представлены далее:
| Код | Операция | Результат |
|---|---|---|
| X | x * x | x2 |
| S | (x2 )2 | x4 |
| X | x4 * x | x5 |
| S | (x5 )2 | x10 |
| X | x10 * x | x11 |
| S | (x11 )2 | x22 |
| X | x22 * x | x23 |
Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: .
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
Корни 3 степени также называют кубическими корнями.
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .
Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень четной степени из отрицательного числа не существует для вещественных чисел.
Корень любой степени из нуля
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби .Обратная операция также верна , любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Число является обратным числом 5, т.е. их произведение равно единице , такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1
Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Основные действия со степенями
В первую очередь степень — это повторяющееся умножение. Число 134 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 134 на 132, то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 136. Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:
am × an = a(m+n).
Если разделить 134 на 132, то нам потребуется вычислить дробь вида:
(13 × 13 × 13 × 13) / (13 × 13).
Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 132. Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так:
am / an = a(m – n).
Теперь давайте возведем 114 в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так:
(am)n = a(m × n).
Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 150? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 154 на 154, что запишется как дробь:
154 / 154.
Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 150. Следовательно:
154 / 154 = 150 = 1.
Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так:
a0 = 1.
При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 82 на 84 и запишем выражение в виде дроби.
(8 × 8) / (8 × 8 × 8 × 8).
Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:
a-m = 1 / am
При этом для значения -1 правило трансформируется в элегантную формулу:
a-1 = 1 / a.
И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка. Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат. Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как:
a(m/n) есть корень n-ной степени из am.
Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.
Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.
Примеры из реальной жизни
Депозит в банке
Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:
Рост = a × e(kt),
где a – начальное значение, e – константа, равная 2,718; k – коэффициент роста; t – время.
Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.
Школьная задача
Пусть в школьной задаче требуется построить график функции y = x2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции. Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.
Заключение
Возведение в степень — арифметическая операция последовательного умножения. Степени имеют больше значение в прикладных науках, так как большинство реальных процессов описываются при помощи степенных функций. Используйте наш калькулятор для расчетов любых практических или школьных задач.
Пример 1. Возведем число 250 без модуля.
10010 = 1100102 , считаем длину в двоичной записи n = 6. Следовательно, нам надо посчитать a1 … a6 по формулам 2 из теории.
a1 = 2; a2 = 22 = 4, a3 = 42 = 16, a4 = 162 = 256, a5 = 2562 = 65536, a6 = 655362 = 4294967296
x1 = 0, x2 = 1, x3 = 0, x4 = 0, x5 = 1, x6 = 1 — двоичная запись в обратном порядке (от младших разрядов к старшим).
Перемножаем ai-ые по второй формуле пункта 2. Другими словами, перемножаем между собой те ai-ые, у которых на соответствующей позиции в двоичной записи степени стоят единицы — это a2, a5 и a6;
250 = 4 * 65536 * 4294967296 = 1125899906842624
Пример 2. Возведем число 250 по модулю 100. Все аналогично, только считаем ai-ые и произведения ai-ых по модулю 100.
10010 = 1100102 , считаем длину в двоичной записи n = 6. Следовательно, нам надо посчитать a1 … a6 по формулам 2 из теории.
a1 = 2; a2 = 22 = 4, a3 = 42 = 16, a4 = 162 = 56, a5 = 562 = 36, a6 = 362 = 96 по модулю 100
x1 = 0, x2 = 1, x3 = 0, x4 = 0, x5 = 1, x6 = 1 — двоичная запись в обратном порядке (от младших разрядов к старшим).
Перемножаем ai-ые по второй формуле пункта 2. Другими словами, перемножаем между собой те ai-ые, у которых на соответствующей позиции в двоичной записи степени стоят единицы — это a2, a5 и a6;
250 = 4 * 36 * 96 = 24 по модулю 100.
Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an = an.
Например, а=2, n=3: 2 * 2 * 2=2^3 = 8.
Вообще возведение в степень часто используется в различных формулах по математике и физике. Эта функция имеет более научное предназначение, чем четыре основные: Сложение, Вычитание, Умножение, Деление.
Возведение числа в степень
Возведение числа в степень – операция не сложная. Оно связано с умножением подобно связи умножения и сложения. Запись an – краткая запись n-ого количество чисел «а» умноженных друг на друга.
Рассмотри возведение в степень на самых простых примерах, переходя к сложным.
Например, 42. 42 = 4 * 4 = 16. Четыре в квадрате (во второй степени) равно шестнадцати. Если вам не понятно умножение 4 * 4, то читайте нашу стать об умножении.
Рассмотрим еще одни пример: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125. Пять в кубе (в третьей степени) равно ста двадцати пяти.
Еще один пример: 9^3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729. Девять в кубе равняется семи сотням двадцати девяти.
Формулы возведения в степень
Чтобы грамотно возводить в степень нужно помнить и знать формулы, указанные ниже. В этом нет ничего сверх естественного, главное понять суть и тогда они не только запомнятся, но и покажутся легкими.
Возведение одночлена в степень
Что из себя представляет одночлен? Это произведение чисел и переменных в любом количестве. Например, двух – одночлен. И вот именно о возведении в степень таких одночленов данная статья.
Пользуясь формулами возведения в степень вычислить возведение одночлена в степень будет не трудно.
Например, (3x^2y^3)^2= 3^2 * x^2 * 2 * y^(3 * 2) = 9x^4y^6; Если возводить одночлен в степень, то в степень возводится каждая составная одночлена.
Возводя в степень переменную уже имеющую степень, то степени перемножаются. Например, (x^2)^3 = x^(2 * 3) = x^6;
Возведение в отрицательную степень
Отрицательная степень – обратное число. Что такое обратное число? Любому числу Х обратным будет 1/X. То есть Х-1=1/X. Это и есть суть отрицательной степени.
Рассмотрим пример (3Y)^-3:
(3Y)^-3 = 1/(27Y^3).
Почему так? Так как в степени имеется минус, то просто переносим в знаменатель данное выражение, а затем возводим в его в третью степень. Просто не так ли?
Возведение в дробную степень
Начнем рассмотрение вопрос на конкретном примере. 43/2. Что означает степень 3/2? 3 – числитель, означает возведение числа (в данном случае 4) в куб. Число 2 – знаменатель, это извлечение корня второй степени из числа (в данном случае 4).
Тогда получаем квадратный корень из 43 = 2^3 = 8. Ответ: 8.
Итак, знаменатель дробной степени может быть, как 3, так и 4 и до бесконечности любым числом и это число определяет степень квадратного корня, извлекаемого из заданного числа. Конечно же, знаменатель не может быть равным нулю.
Возведение корня в степень
Если корень возводится в степень, равной степени самого корня, то ответом будет подкоренное выражение. Например, (√х)2 = х. И так в любом случае равенства степени корня и степени возведения корня.
Если (√x)^4. То (√x)^4=x^2. Чтобы проверить решение переведем выражение в выражение с дробной степенью. Так как корень квадратный, то знаменатель равен 2. А если корень возводится в четвертую степень, то числитель 4. Получаем 4/2=2. Ответ: x = 2.
В любом случае лучший вариант просто перевести выражение в выражение с дробной степенью. Если не будет сокращаться дробь, значит такой ответ и будет, при условии, что корень из заданного числа не выделяется.
Возведение в степень комплексного числа
Что такое комплексное число? Комплексное число – выражение, имеющее формулу a + b * i; a, b – действительные числа. i – число, которое при возведение в квадрат дает число -1.
i^2=-1.
Рассмотрим пример. (2 + 3i)^2.
(2 + 3i)^2 = 22 +2 * 2 * 3i +(3i)^2 = 4+12i^-9=-5+12i.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Возведение в степень онлайн
С помощью нашего калькулятора, Вы сможете посчитать возведение числа в степень:
Загрузка калькулятора…
Возведение в степень 7 класс
Возведение в степень начинают проходить школьники только в седьмом классе.
Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an=an.
Например, а=2, n=3: 2 * 2 * 2 = 2^3 = 8.
Примеры для решения:
Возведение в степень презентация
Презентация по возведению в степень, рассчитанную на семиклассников. Презентация может разъяснить некоторые непонятные моменты, но, вероятно, таких моментов не будет благодаря нашей статье.
Скачать презентацию
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
90000 Exponent Calculator 90001 90002 Enter values into any two of the input fields to solve for the third. 90003 90004 RelatedScientific Calculator | Log Calculator | Root Calculator 90005 90006 What is an exponent? 90007 90002 Exponentiation is a mathematical operation, written as 90009 a 90010 n 90011 90012, involving the base 90009 a 90012 and an exponent 90009 n 90012. In the case where 90009 n 90012 is a positive integer, exponentiation corresponds to repeated multiplication of the base, 90009 n 90012 times.90003 90022 a 90010 n 90011 = a × a × … × a 90005 n times 90003 90002 The calculator above accepts negative bases, but does not compute imaginary numbers. It also does not accept fractions, but can be used to compute fractional exponents, as long as the exponents are input in their decimal form. 90003 90006 Basic exponent laws and rules 90007 90002 When exponents that share the same base are multiplied, the exponents are added. 90003 90022 a 90010 n 90011 × a 90010 m 90011 = a 90010 (n + m) 90011 90005 EX: 2 90010 2 90011 × 2 90010 4 90011 = 4 × 16 = 64 90005 2 90010 2 90011 × 2 90010 4 90011 = 2 90010 (2 + 4) 90011 = 2 90010 6 90011 = 64 90003 90002 When an exponent is negative, the negative sign is removed by reciprocating the base and raising it to the positive exponent.90003 90057 90058 90059 EX: 2 90010 (-3) 90011 = 1 ÷ 2 ÷ 2 ÷ 2 90062 90059 = 90062 90065 90066 90067 90002 When exponents that share the same base are divided, the exponents are subtracted. 90003 90057 90058 90059 EX: 90062 90065 90059 = 90062 90065 90059 = 90062 90065 90059 90062 90066 90067 90057 90058 90065 90059 = 2 90010 (2-4) 90011 = 2 90010 -2 90011 = 90062 90065 90059 = 90062 90065 90066 90067 90002 When exponents are raised to another exponent, the exponents are multiplied.90003 90022 (A 90010 m 90011) 90010 n 90011 = a 90010 (m × n) 90011 90005 EX: (2 90010 2 90011) 90010 4 90011 = 4 90010 4 90011 = 256 90005 (2 90010 2 90011) 90010 4 90011 = 2 90010 (2 × 4) 90011 = 2 90010 8 90011 = 256 90003 90002 When multiplied bases are raised to an exponent, the exponent is distributed to both bases. 90003 90022 (A × b) 90010 n 90011 = a 90010 n 90011 × b 90010 n 90011 90005 EX: (2 × 4) 90010 2 90011 = 8 90010 2 90011 = 64 90005 (2 × 4) 90010 2 90011 = 2 90010 2 90011 × 4 90010 2 90011 = 4 × 16 = 64 90003 90002 Similarly, when divided bases are raised to an exponent, the exponent is distributed to both bases.90003 90057 90058 90059 EX: (90062 90065 90059) 90010 2 90011 90062 90059 = 90062 90065 90059 × 90062 90065 90059 = 90062 90065 90066 90067 90002 When an exponent is 1, the base remains the same. 90003 90022 a 90010 1 90011 = a 90003 90002 When an exponent is 0, the result of the exponentiation of any base will always be 1, although some debate surrounds 0 90010 0 90011 being 1 or undefined.For many applications, defining 0 90010 0 90011 as 1 is convenient. 90003 90022 a 90010 0 90011 = 1 90003 90002 Shown below is an example of an argument for a 90010 0 90011 = 1 using one of the previously mentioned exponent laws. 90003 90022 If a 90010 n 90011 × a 90010 m 90011 = a 90010 (n + m) 90011 90005 Then a 90010 n 90011 × a 90010 0 90011 = a 90010 (n + 0) 90011 = a 90010 n 90011 90003 90002 Thus, the only way for 90009 a 90010 n 90011 90012 to remain unchanged by multiplication, and this exponent law to remain true, is for a 90010 0 90011 to be 1.90003 90002 When an exponent is a fraction where the numerator is 1, the n 90010 th 90011 root of the base is taken. Shown below is an example with a fractional exponent where the numerator is not 1. It uses both the rule displayed, as well as the rule for multiplying exponents with like bases discussed above. Note that the calculator can calculate fractional exponents, but they must be entered into the calculator in decimal form. 90003 90022 90220 90003 90002 It is also possible to compute exponents with negative bases.They follow much the same rules as exponents with positive bases. Exponents with negative bases raised to positive integers are equal to their positive counterparts in magnitude, but vary based on sign. If the exponent is an even, positive integer, the values will be equal regardless of a positive or negative base. If the exponent is an odd, positive integer, the result will again have the same magnitude, but will be negative. While the rules for fractional exponents with negative bases are the same, they involve the use of imaginary numbers since it is not possible to take any root of a negative number.An example is provided below for reference, but please note that the calculator provided can not compute imaginary numbers, and any inputs that result in an imaginary number will return the result «NAN,» signifying «not a number.» The numerical solution is essentially the same as the case with a positive base, except that the number must be denoted as imaginary. 90003 90022 90225 90003 .90000 Exponents Calculator 90001 90002 Calculator Use 90003 90004 This is an online calculator for exponents. Calculate the power of large base integers and real numbers. You can also calculate numbers to the power of large exponents less than 1000, negative exponents, and real numbers or decimals for exponents. 90005 90004 For larger exponents try the Large Exponents Calculator 90005 90004 90009 For instructional purposes 90010 the solution is expanded when the base x and exponent n are small enough to fit on the screen.{4}} \) 90005 90004 \ (= \; \ dfrac {1} {3 \ cdot 3 \ cdot 3 \ cdot 3} \) 90005 90004 \ (= \; \ dfrac {1} {81} \) 90005 90004 \ (= 0.012346 \) 90005 90036 Exponent Notation: 90003 90004 90009 Note that -4 90040 2 90041 and (-4) 90040 2 90041 result in different answers: -4 90040 2 90041 = -1 * 4 * 4 = -16, while (-4) 90040 2 90041 = (-4) * (-4) = 16. If you enter a negative value for x, such as -4, this calculator assumes (-4) 90040 n 90041 90010.90005 90004 «When a minus sign occurs with exponential notation, a certain caution is in order. For example, (-4) 90040 2 90041 means that -4 is to be raised to the second power. Hence (-4) 90040 2 90041 = (-4) * (-4) = 16. On the other hand, -4 90040 2 90041 represents the additive inverse of 4 90040 2 90041. Thus -4 90040 2 90041 = -16. It may help to think of -x 90040 2 90041 as -1 * x 90040 2 90041 … «[1] 90005 90068 Examples: 90069 90070 90071 3 raised to the power of 4 is written 3 90040 4 90041 = 81.90074 90071 -4 raised to the power of 2 is written (-4) 90040 2 90041 = 16. 90074 90071 -3 raised to the power of 3 is written (-3) 90040 3 90041 = -27. Note that in this case the answer is the same for both -3 90040 3 90041 and (-3) 90040 3 90041 however they are still calculated differently. -3 90040 3 90041 = -1 * 3 * 3 * 3 = (-3) 90040 3 90041 = -3 * -3 * -3 = -27. 90074 90071 For 0 raised to the 0 power the answer is 1 however this is considered a definition and not an actual calculation.m} \) 90005 90068 References 90069 90004 [1] Algebra and Trigonometry: A Functions Approach; M. L. Keedy and Marvin L. Bittinger; Addison Wesley Publishing Company; 1982, page 11. 90005 90004 The Math Forum: Exponents and Negative Numbers. 90005 90004 For more detail on Exponent Theory see Exponent Laws. 90005 90004 To calculate fractional exponents use our Fractional Exponents Calculator.90005 90004 To calculate root or radicals use our Roots Calculator. 90005 .90000 Expontent Calculator 90001 90002 Use this exponentiation calculator to easily calculate the power of a given base, raised by a given exponent. 90003 90004 Exponentiation. How to calculate exponents? 90005 90002 Exponentiation is a mathematical operation in which a number called the base is raised to a power, which is given by the exponent. The exponent is usually written as a superscript, for example if the base is 90007 b 90008 and the exponent 90007 e 90008 the exponentiation of b by e will be 90007 b 90012 e 90013 90008.This is the operation this online exponent calculator performs for you. 90003 90002 When the exponent is a positive integer the operation is equal to multiplying the base by itself 90007 e times 90008. If the exponent is a negative, for example -5, the operation is 1 divided by the base raised to the absolute value of the exponent: 90007 b 90012 -5 90013 = 1 / b 90012 5 90013 90008. The formula below expresses this. The most commonly computed exponents are the square of a number (b 90012 2 90013, b raised to the second power / b to the power of two) and the cube of a number (b 90012 3 90013, b raised to the 3-rd power / b to the power of 3), and their reverse functions: square root and cube root.90003 90002 Exponents are related to 90007 logarithms 90008 so that the natural logarithm ln (e) is the inverse of the exponential function b 90012 e 90013, however defining exponentiation using logarithms is more common when dealing with complex numbers. 90003 90002 In 90007 combinatorics 90008 exponents express the number of possible 90007 permutations 90008, that is — how many unique ways there are to select a part of a collection, or a set of things in which 90007 the order matters 90008.You can use our permutation calculator for these calculations as well. 90003 90004 Exponent formula 90005 90002 The formula for exponentiation is: 90047 where 90007 n 90008 is the exponent and 90007 b 90008 is the base. An exponent with base 0 does not technically exist, so it is not supported by our exponent calculator. 90003 90004 Practical application of exponents 90005 90002 Exponentiation has uses in economics (eg compound interest), biology (population growth), chemistry, physics, and, of course — computer science where storage capacity units are traditionally based off the powers of two, while public-key cryptographic functions rely on the hard reversibility of exponentiation.Practitioners of these disciplines often end up using an exponent calculator. 90003 90002 In physics we have exponential decay related to light, sound, gravity, dangerous chemicals, and radiation (see radioactive decay & half-life). In marketing and the spreading of ideas, memes, viral videos, etc. we talk about exponentially increasing reach. Moore’s law about the increase of computing power is in essence an exponential law. The scale for measuring Earthquakes is also exponential, so a magnitude 5 earthquake is 32 times stronger than a magnitude 4 earthquake (10 90012 1.5 90013), while a magnitude 6 earthquake releases 1,000 times more energy (10 90012 3 90013) than a 4. The decibel scale used to measure volume is also exponential: 20 dB = 10 90012 2 90013 dB = 100 power ratio, 30 dB = 10 90012 3 90013 = 1,000 power ratio, so a 30 dB sound level is 10 times louder than a 20 dB sound level. 90003 90002 90068 90003 90002 In the graph above, you can think of each exponent as a generation (in biology), or as a tier of people who have seen a viral video or read a viral article (in marketing), or the power released from an earthquake of a magnitude equal to the exponent.As you can see by step 10 an exponential process that started with a base of 2 is completely dwarfed by one started with a base of 3 to such an extent that the base 2 line looks almost like a flat line next to the base 3 exponential curve , which is why we had to provide a zoom-in. The graph was compiled using our calculator. 90003 90002 In complex systems exponential processes often precede cataclysmic events, such as ruptures and explosions. The distribution of work contribution, ability / talent, and wealth in humans and other species is exponential according to work 90012 [1] [2] 90013 often cited by the famous psychometrician Jordan B.Peterson. In the human studies circles it is known as Paretian distribution (Pareto distribution). 90003 90002 Financial crisis, economic crisis and bubbles have exponential nature before they pop according to Didier Sornette & colleagues 90012 [3] 90013. The size of cities is well predicted using power law (Zipf’s Law) 90012 [4] 90013 which follows an exponential function and can thus be computed using an exponent calculator. 90003 90082 References 90083 90002 [1] O’Boyle E.Jr., Aguinis H. (2012) «The Best and the Rest: Revisiting the Norm of Normality of Individual Performance» 90085 Personnel Psychology 90086 65 (1): 79-119 90003 90002 [2] Yu S., Liang J., Liu H. (2016) «Existence of Hierarchies and Human’s Pursuit of Top Hierarchy Lead to Power Law» 90085 arXiv: 1609.07680 90086 90003 90002 [3] D.Sornette (2009) «Dragon-Kings, Black Swans and the Prediction of Crises» 90085 International Journal of Terraspace Science and Engineering 90086 2 (1): 1-18 90003 90002 [4] Gabaix X.(1999) «Zipf’s Law for Cities: An Explanation» 90085 The Quarterly Journal of Economics 90086 114 (3): 739-767 90003 .90000 Exponential function Calculator — High accuracy calculation 90001 90002 90003 [1] 2020/01/17 3:54 Male / Under 20 years old / High-school / University / Grad student / Not at All / 90004 90005 Purpose of use 90006 90007 homework beacause my jerk teacher makes me eo 6 20 question assignments every day 90008 90005 Comment / Request 90006 90007 its all good 90008 90013 90002 90003 [2] 2020/01/07 19:49 Male / 40 years old level / High-school / University / Grad student / Very / 90004 90005 Purpose of use 90006 90007 Getting familiar with functions on new scientific calculator.90008 90013 90002 90003 [3] 2019/11/20 10:42 Female / Under 20 years old / High-school / University / Grad student / A little / 90004 90005 Purpose of use 90006 90007 homework 90008 90013 90002 90003 [4] 2019 / 11/16 15:34 Male / Under 20 years old / Elementary school / Junior high-school student / Not at All / 90004 90005 Purpose of use 90006 90007 calculate the time it takes for a blackhole to die 90008 90013 90002 90003 [5 ] 2019/05/28 4:19 Female / Under 20 years old / High-school / University / Grad student / A little / 90004 90005 Purpose of use 90006 90007 homework 90008 90013 90002 90003 [6] 2018/09/03 21: 22 Male / Under 20 years old / High-school / University / Grad student / Useful / 90004 90005 Purpose of use 90006 90007 To easily understand the complex problems with regards on Exponential fuction.90008 90005 Comment / Request 90006 90007 I guess, it shoul have a tutorial or steps how to use it because some people don»t know how to use it yet 90008 90013 90002 90003 [7] 2018/01/31 5:31 Male / 60 years old level or over / A teacher / A researcher / Very / 90004 90005 Purpose of use 90006 90007 Computing odds ratios 90008 90013 90002 90003 [8] 2017/12/06 14:39 Male / 30 years old level / High- school / University / Grad student / Useful / 90004 90005 Purpose of use 90006 90007 Calculation 90008 90013 90002 90003 [9] 2017/10/20 2:00 Female / Under 20 years old / High-school / University / Grad student / A little / 90004 90005 Purpose of use 90006 90007 Project Euler 90008 90005 Comment / Request 90006 90007 I would like for it to show more digits 90008 90013 90002 90003 [10] 2017/03/11 7:15 Female / Under 20 years old / Elementary school / Junior high-school student / Not at All / 90004 90005 Comment / Request 90006 90007 What is 1/3814697265625 i n exponential form ?! 90008 90013.